Астрономический журнал, 2022, T. 99, № 1, стр. 3-14
Неравновесная нейтронизация и крупномасштабная конвекция при гравитационном коллапсе
А. Г. Аксенов 1, *, В. М. Чечеткин 1, 2
1 Институт автоматизации проектирования РАН
Москва, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: aksenov@icad.org.ru
Поступила в редакцию 27.08.2021
После доработки 30.09.2021
Принята к публикации 30.09.2021
- EDN: ZTTKAA
- DOI: 10.31857/S0004629922010029
Аннотация
Большая часть энергии, высвобождаемой при гравитационном коллапсе ядер массивных звезд, уносится нейтрино. С помощью 2D газовой динамики с учетом спектрального переноса нейтрино в рамках диффузии с ограничением потоков решается самосогласованная задача о гравитационном коллапсе. Показано, что крупномасштабная конвекция развивается в области вблизи нейтриносферы и приводит к увеличению средней энергии нейтрино до 15–18 МэВ, что в 1.5 раза выше результатов 1D расчетов. В данной работе уточнена простая модель нейтронизации в центральной непрозрачной области, строго говоря, применимая только в прозрачной области. Используемая 2D модель правильно воспроизводит высокий химический потенциал вырожденных электронов $ \sim {\kern 1pt} 60$ MэВ в центре с высокой плотностью вещества, как в сферически симметричных расчетах с точным учетом слабого взаимодействия. Поскольку из-за запертых нейтрино нейтронизация в центре обратима, процесс развития неустойчивости в центре подавлен, высокий химический потенциал электронов в центре в уточненной модели нейтронизации не сказывается на энергии уходящих нейтрино. Полученные энергии нейтрино важны как для объяснения явления сверхновой, так и для постановки эксперимента по регистрации нейтрино от сверхновой.
1. ВВЕДЕНИЕ
Сверхновые типа II (СН II), так называемые коллапсирующие, связаны с эволюцией массивных звезд с массой $ \gtrsim {\kern 1pt} 10{{M}_{ \odot }}$. В центре массивной звезды образуется железное ядро с массой $(1.2{\kern 1pt} - {\kern 1pt} 1.6)\,{{M}_{ \odot }}$ в результате термоядерного горения [1]. Этот результат близок к Чандрасекаровскому пределу массы белых карликов (политропа $n = 3$ для вырожденных релятивистских электронов) ${{M}_{{{\text{Ch}}}}} = 5.83Y_{e}^{2}\,{{M}_{ \odot }}$, где ${{Y}_{e}}$ – число электронов на нуклон [2]. Полная энергия, высвобождаемая при коллапсе, достигает значения ${{10}^{{54}}}$ эрг и уносится, в основном, нейтрино. Малая доля этой энергии ($ \sim {\kern 1pt} {{10}^{{51}}}$ эрг) поглощается веществом звезды. При коллапсе массы $1.4\,{{M}_{ \odot }}$ в нейтронную звезду с радиусом $ \sim {\kern 1pt} 10$ км выделяется $ \sim 100$ МэВ на нуклон в виде нейтрино, в то время как термоядерная энергия может обеспечить только 8 МэВ на нуклон. Соответственно нейтринный механизм взрыва, связанный с поглощением энергии от нейтрино, является наиболее перспективным [3].
Нейтринные процессы в ядрах звезд впервые рассмотрены в работе [3]. Вопрос доли поглощения энергии нейтрино (1%) в предсверхновой остается до конца нерешенной задачей [4–6] из‑за необходимости кинетического описания переноса нейтрино, наличия разных масштабов времени для слабого взаимодействия и газодинамического времени, многомерности задачи на фоне разных пространственных масштабов предсверхновой, нейтронной звезды и области развития неустойчивости. От указанных процессов зависят количество поглощенной энергии нейтрино и сброс оболочки, наблюдаемый как СН II.
Впервые физика процесса гравитационного коллапса, пригодная для расчетов на доступных вычислительных мощностях, была сформулирована в работах [7, 8] путем введения нейтринной теплопроводности и введением в расчеты двух областей, прозрачной и непрозрачной для нейтрино, разделенных нейтриносферой. Принципиальное ограничение подхода состоит в зависимости нейтриносферы от энергий нейтрино и их типа. Вообще говоря, нейтриносфер надо вводить несколько. А в случае конвекции в многомерном случае прозрачная и непрозрачная области, разделенные нейтриносферой, могут становиться не односвязными.
Следующий шаг состоял в рассмотрении спектрального переноса нейтрино в рамках диффузии с ограничением потоков [9]. Этот подход точный в двух случаях: в оптически плотном веществе – обычная диффузия, а в прозрачной области – свободное распространение нейтрино. Ограничение потока осуществляется путем введения нелинейной теплопроводности, т.е. произвольной сшивки потоков в промежуточном случае [10–12]. Сферически симметричные расчеты в рамках диффузии с ограничением потоков [13–17] дали большее значение средней энергии нейтрино в сравнении с нейтринной теплопроводностью.
Вероятная причина неопределенности в построении модели взрыва коллапсирующей СН состоит в определяющей роли 3D неустойчивостей при коллапсе и учете конвекции. Одна область конвективной неустойчивости формируется в центре коллапсирующего ядра звезды, является протяженной и существует в течение $ \gtrsim {\kern 1pt} 10$ мс, в то время как другая неустойчивая область в области аккреции тонкая, но существует все время коллапса. Конвекция в центре может иметь два важных эффекта: помимо увеличения потока энергии нейтрино центр содержит много высокоэнергичных нейтрино в сравнении с нейтрино вблизи нейтриносферы в 1D модели [18, 19]. Модели 2D [20, 21] и 3D [22, 23] демонстрируют крупномасштабный характер конвекции и приводят к взрыву СН. В то же время уточненные расчеты 3D ставят под сомнение крупномасштабную конвекцию и взрыв [24–26].
Крупномасштабная конвекция в центре звезды впервые предложена для СН в работе [27]. Начальное условие выбрано стационарным с плотностью в центре $2 \times $ 1013 г · см–3 и постоянной энтропией, за исключением центральной области с избытком энтропии. 3D расчеты газовой динамики показывают развитие крупномасштабной конвекции в неустойчивой области ${\mathbf{g}}\nabla s > 0$. Конвекция в центральной области протонейтронной звезды в 3D идеальной газовой динамике с начальным реалистичным профилем удельной энтропии, соответствующей решению 1D с кинетическим переносом нейтрино, рассмотрена в работах [28, 29] без учета переноса нейтрино в 3D газовой динамике. Предположение о применимости критерия конвективной неустойчивости Шварцшильда для газовой динамики было спорным. Оказалось, помимо нейтронизации, есть потери нейтрино, и имеет место сильное вырождение [30, 31]. Тем не менее упрощенная газодинамическая модель с уравнением состояния идеального газа (идеальный газ с показателем адиабаты 4/3 точно описывает вырожденные релятивистские электроны, если использовать удельную внутреннюю энергию вместо температуры) позволила получить количественно правильные результаты. Конвекция развилась за газодинамическое время ~10 мс в центральной области с плотностью ${{\rho }_{c}} \sim $ 1012 г · см–3, ее масштаб крупный из-за протяженной неустойчивой центральной области, а также наличия небольшого вращения звезды. Был сделан вывод о необходимости учитывать конвекцию в расчетах коллапса, а вращение способствовало выделению длинноволновых возмущений и приближает 3D расчеты к 2D случаю. Это было проверено как для газодинамической модели развития неустойчивости [29], так и в 3D самосогласованном расчете коллапса с учетом переноса нейтрино без учета их спектра [32].
Неравновесная нейтронизация вследствие учета процессов слабого взаимодействия при начальной высокой плотности энергии исследована в работе [33] в рамках однородной изотропной модели для функций распределения нейтрино при расширении однородного пузыря. Сделан вывод о предположительно высокой энергии ($ \gtrsim {\kern 1pt} 40$ МэВ) при наступлении непрозрачности. Это много больше нейтрино с энергиями 10 МэВ в 1D сферически симметричной модели с излучением вблизи нейтриносферы. Задание средней энергии нейтрино в интервале 30–60 МэВ даже при неизменной светимости нейтрино обеспечивает кинетическую энергию оболочки в интервале $(1.5{\kern 1pt} - {\kern 1pt} 50) \times {{10}^{{51}}}$ эрг [28]. Это следствие пропорциональности сечения рассеяния и доли передаваемой энергии веществу средней энергии нейтрино [34–36].
Самосогласованная 2D задача о коллапсе с переносом нейтрино рассмотрена в работах [30, 31, 37] с упрощенной моделью взаимодействия нейтрино с веществом. Газодинамический код для описания переноса использует явную схему и оригинальный решатель задачи Римана для многокомпонентной смеси газов с табличным уравнением состояния, включая нейтрино [38–40]. Процессы обмена энергиями между компонентами (вещество и нейтрино разных энергий) рассматриваются на отдельном шаге с применением неявного метода Гира. В литературе присутствует единственная альтернатива – код Castro [21], отличающийся приближенным “решателем” задачи Римана. Другие модели газовой динамики для расчета коллапса используют раздельное описание газовой динамики для вещества, перенос нейтрино, например, код Fornax [41].
С точки зрения математики отличие от совместного описания нейтрино с веществом в газовой динамике не принципиально, поскольку учет реакций взаимодействия вещества и нейтрино уравнивают оба подхода. Но для расчетов реальной задачи раздельное описание упирается в доступные ограничения вычислительных мощностей. В методе разделения задачи по физическим процессам газовая динамика используется явная. В оптически плотной области число временных шагов для расчета обмена энергиями между нейтрино разных энергий будет определять толща для наиболее быстрой реакции, поскольку независимый перенос вещества и нейтрино – это большое возмущение для последующего шага расчета кинетики реакций. Поэтому авторам кода Fornax [41] приходится искусственно подавлять неустойчивости, корректируя потоки для нейтрино при расчетах для непрозрачных областей с временным шагом, определяемым скоростью звука вещества. При совместном рассмотрении вещества и нейтрино перенос слабо меняет тепловое равновесие, а реакции слабого взаимодействия, вычисляемые по неявной схеме на отдельном шаге, не влияют на количество временных шагов газодинамического переноса. Естественно, в расчетах для непрозрачных областей с временными шагами, определяемыми газовой динамикой, разностная схема должна быть консервативной. Единственное существенное ограничение на временной шаг в сравнении с газовой динамикой получается из-за прозрачной области, где скорость переноса нейтрино $c$ по крайней мере на порядок больше скорости звука и газодинамической скорости вещества с запертым излучением.
Моделирование коллапса с переносом нейтрино подтвердило развитие крупномасштабной конвекции в центре за время $ \sim {\kern 1pt} 10$ мс благодаря неравновесной нейтронизации из-за потерь части нейтрино. А учет небольшого вращения ядра привел к выделению крупномасштабных мод [32, 42]. Как показано в наших прошлых расчетах коллапса, с переносом нейтрино конвекция в центре успевает развиться за время существования неустойчивого профиля энтропии [31, 30, 35 ]. Благодаря потере части нейтрино нейтронизация оказывается необратимой, реализуется сценарий неустойчивости, близкий к Шварцшильду [30, 31].
Нас в первую очередь интересует влияние конвекции на спектр исходящих нейтрино. Если интересоваться только спектром нейтрино, но не интересоваться взаимодействием выходящих нейтрино с оболочкой, можно использовать разработанную простую модель взаимодействия нейтрино с веществом [37]: спектральная плотность энергии нейтрино релаксирует к равновесному значению с температурой и химическим потенциалом, определяемыми температурой вещества и химическим потенциалом электронов, с характерным постоянным сечением слабого взаимодействия ${{\sigma }_{0}} = 1.7 \times {{10}^{{ - 40}}}$ см2. А количество электронов на нуклон (точнее разница чисел электронов и позитронов на нуклон) релаксирует к приближенному аналитическому табличному значению из работы [43], где исследовалось $\beta $ равновесие для реакций слабого взаимодействия электронов и позитронов со свободными нуклонами при условии свободного выхода нейтрино. Такое же приближение свободного выхода нейтрино было использовано в более ранней работе [44] при изучении термодинамических свойств вещества при высокой плотности из-за нейтронизации для выводов об устойчивости относительно коллапса звезды. Строго говоря, упрощенная модель $\beta $ равновесия реализуется вблизи нейтриносферы, там где важно учесть потоки энергии нейтрино. В глубоко непрозрачной области нейтрино никуда не уходят, простая модель $\beta $ равновесия количественно неправильная, но и потоки энергии нейтрино в непрозрачной области пренебрежимо малы.
В работе [37] мы произвели самосогласованный аксиально симметричный 2D расчет газодинамического коллапса со спектральным переносом энергии нейтрино с целью выяснения влияния конвекции на спектр уходящих нейтрино и получили энергию уходящих нейтрино на уровне 15 МэВ в соответствии с энергией Ферми вырожденных электронов в зоне развития конвекции. При упрощенном описании процессов слабого взаимодействия мы переоценили скорость нейтронизации вещества при большой плотности, и химический потенциал электронов в центре при повышении плотности от начального значения 2 × 1012 до 4 × 1012 г см–3 даже снизился с 20 до 13 МэВ. Такое несоответствие приближенной кинетики нейтронизации строгому учету всех реакций слабого взаимодействия в сферически симметричном расчете [34] с энергиями Ферми десятки МэВ следует исправить, ожидая при больших допустимых энергиях вырожденных электронов в ходе конвекции больших энергий уходящих нейтрино. Целью данной работы является уточнение спектра нейтрино в более правильной математической модели.
Несомненно, для подтверждения модели коллапса и взрыва важно наблюдение нейтрино от СН. От СН1987А зарегистрировано только 20 нейтринных событий, первые публикации указывают на высокие энергии: 20–40 МэВ IMB [45], 9–35 МэВ Kamiokande-II [46], 20 МэВ Ba-ksan-LSD [47, 48], что ближе к модели крупномасштабной конвекции, чем к сферически симметричному коллапсу.
2. КОНВЕКЦИЯ ПРИ КОЛЛАПСЕ ВРАЩАЮЩЕГОСЯ ЯДРА ЗВЕЗДЫ С УЧЕТОМ СПЕКТРАЛЬНОГО ПЕРЕНОСА НЕЙТРИНО
Физическая задача о гравитационном коллапсе включает плотность нуклонов, разницу чисел электронов и позитронов, уравнение для плотности энергии вещества, определение гравитационного поля, кинетические уравнения для нейтрино разных сортов. Помимо зависимости от пространственных переменных и времени функции распределения нейтрино зависят от импульса (двух углов и энергии частицы). Решение усложняет наличие прозрачных и непрозрачных областей для нейтрино. Из-за различных характерных времен процессов полная физическая задача может быть численно рассмотрена только в сферически симметричном случае в рамках неявного кинетического кода. В многомерном случае привлекательна модель диффузии с ограничением потоков, впервые предложенная в работе [9] для сферически симметричного коллапса. В этой модели нет зависимости функций распределений от углов, содержится неопределенный на границе прозрачной и непрозрачной областей параметр сшивки потоков в прозрачной и непрозрачной областях. Сами потоки пропорциональны градиентам спектральных плотностей энергий нейтрино. Модель легко расширяется на многомерный случай, как только решена проблема разрешения численного решения многокомпонентной газовой динамики на неподвижной эйлеровой сетке.
Наш многокомпонентный гидродинамический код [38, 39, 49] содержит независимые переменные: плотности компонентов ${{\rho }_{i}}$ (или плотности концентраций ${{n}_{i}} = \rho {\text{/}}{{m}_{p}}$), внутренние энергии ${{\epsilon }_{i}}$ компонентов $i$, плотность импульса $\rho {\mathbf{v}}$ (скорости всех компонентов предполагаются одинаковыми, но безмассовые частицы могут переносить энергию относительно вещества). Имеем систему уравнений Эйлера для описания гравитационного коллапса. Уравнение для плотности числа барионов
(1)
$\frac{{\partial \rho {\text{/}}{{m}_{p}}}}{{\partial t}} + \operatorname{div} (\rho {\text{/}}{{m}_{p}}{\mathbf{v}}) = 0,$(2)
$\frac{{\partial \Delta {{n}_{e}}}}{{\partial t}} + \operatorname{div} (\Delta {{n}_{e}}{\mathbf{v}}) = {{\dot {Y}}_{e}}\rho {\text{/}}{{m}_{p}},$(3)
$\frac{{\partial \rho {{v}_{j}}}}{{\partial t}} + {{\nabla }_{i}}\Pi _{{ij}}^{{\text{m}}} = \rho {{g}_{j}} + \rho {{f}_{\nu }},$(4)
$\frac{{\partial \rho {{E}_{{\text{m}}}}}}{{\partial t}} + \operatorname{div} ({{E}_{{\text{m}}}}\rho + {{P}_{{\text{m}}}}){\mathbf{v}} = \rho {\mathbf{vg}} + \rho {{q}_{{\text{m}}}},$(6)
$\frac{1}{c}\frac{{\partial {{f}_{\nu }}({\mathbf{r}},{\mathbf{p}},t)}}{{\partial t}} + \frac{{\mathbf{p}}}{p}\nabla {{f}_{\nu }} = \sum\limits_q \,(\eta _{\nu }^{q} - \chi _{\nu }^{q}{{f}_{\nu }})$(7)
$f_{\nu }^{{{\text{eq}}}} = \frac{2}{{\mathop {(2\pi \hbar c)}\nolimits^3 }}\frac{1}{{1 + exp\left( {\tfrac{{\varepsilon - {{\mu }_{\nu }}}}{{k{{T}_{\nu }}}}} \right)}},\quad {{\mu }_{\nu }} \approx {{\mu }_{e}}.$Для получения спектра уходящих нейтрино требуется ввести сетку для энергий нейтрино и использовать спектральные плотности энергии нейтрино и антинейтрино,
(8)
$\Delta \rho {{\varepsilon }_{{\nu ,\omega }}} \equiv \int\limits_{{{\varepsilon }_{{\omega - 1/2}}}}^{{{\varepsilon }_{{\omega + 1/2}}}} \,d\varepsilon {{\varepsilon }_{\nu }}{{f}_{\nu }}$(9)
$\frac{{\partial \rho \Delta {{\varepsilon }_{{\nu ,\omega }}}}}{{\partial t}} + {\mathbf{v}}\nabla (\rho \Delta {{\varepsilon }_{{\nu ,\omega }}}) = \operatorname{div} \Delta {{{\mathbf{F}}}_{{\nu ,\omega }}} - \rho \Delta {{q}_{{{\text{m}},\omega }}},$(10)
$\mathop {\Delta {\mathbf{F}}}\nolimits_{\nu ,\omega } = \frac{{\mathop {\Delta {\mathbf{F}}}\nolimits_{\nu ,\omega }^{{\text{thick}}} }}{{\left| {\mathop {\Delta {\mathbf{F}}}\nolimits_{\nu ,\omega }^{{\text{thick}}} } \right|{\text{/}}\Delta F_{{\nu ,\omega }}^{{max}} + 1}}.$Обмен энергиями между нейтрино и веществом описывается релаксацией к тепловому равновесию $\rho \Delta {{q}_{{\text{m}}}} = c\chi (\Delta {{U}_{{\nu ,\omega }}} - \Delta U_{{\nu ,\omega }}^{{{\text{th}}}})$, где $\sum\nolimits_\omega \,\Delta U_{{\nu ,\omega }}^{{{\text{th}}}}({{T}_{{{\text{eq}}}}}) + $ $ + \;\rho \epsilon (\rho ,{{T}_{{{\text{eq}}}}},{{Y}_{e}})$ = $\sum\nolimits_\omega \,\Delta {{U}_{{\nu ,\omega }}} + \rho \epsilon $, скорость релаксации выбрана пропорциональной концентрации свободных нуклонов ($c\chi \approx c{{\sigma }_{0}}\rho {\text{/}}{{m}_{n}}$) с постоянным сечением ${{\sigma }_{0}} = 1.7 \times {{10}^{{ - 40}}}$ см2. Данная модель позволит определить спектр испускаемых нейтрино, а для точного учета их поглощения в оболочке постоянного сечения недостаточно. Сечение рассеяния с веществом оболочки для энергий выходящих нейтрино от 10 МэВ (много больше энергии Ферми электронов оболочки) оказывается пропорциональным энергии нейтрино [34].
Уравнение состояния ${{P}_{{\text{m}}}} = {{P}_{{\text{m}}}}(\rho ,{{\varepsilon }_{{\text{m}}}},{{Y}_{e}})$ ядра в статистическом равновесии со свободными нуклонами: $({{A}_{i}},{{Z}_{i}}) \rightleftarrows ({{A}_{i}} - {{Z}_{i}})n + {{Z}_{i}}p$, дает связь химических потенциалов ${{\mu }_{i}} = ({{A}_{i}} - {{Z}_{i}}){{\mu }_{n}} + {{Z}_{i}}{{\mu }_{p}}$); “число электронов” ${{Y}_{e}}$ определяется из кинетики нейтронизации $\tfrac{{\partial {{Y}_{e}}}}{{\partial t}} + {\mathbf{v}}\nabla {{Y}_{e}} = {{\dot {Y}}_{e}}(\rho ,{{T}_{{\text{m}}}},{{\varepsilon }_{\nu }})$. Ограничиваясь упрощенным описанием кинетики вместо всех реакций слабого взаимодействия, принимаем время релаксации ${{Y}_{e}}$: ${{\dot {Y}}_{e}} = - (c{{\sigma }_{0}}({{n}_{n}} + {{n}_{p}}))({{Y}_{e}} - $ $ - \;Y_{e}^{{{\text{eq}}}}(\rho ,T(\rho ,\varepsilon )))$ к $\beta $ равновесию $Y_{e}^{{{\text{eq}}}}(\rho ,T)$ из работы [43], где рассмотрены только две реакции, ${{e}^{ - }} + p \to n + \nu $ и ${{e}^{ + }} + n \to p + \tilde {\nu }$, со свободным выходом нейтрино. Расширение этой модели, количественно применимой только в прозрачной области около нейтриносферы, на непрозрачную область оправдывает малость диффузии нейтрино в непрозрачной области. Для $ln{{(Y_{e}^{{{\text{eq}}}})}^{{ - 1}}}$ приближенно применима линейная интерполяция по переменной $Z = \ln \rho {\text{/}}{{T}^{3}}$ в интервале $({{Y}_{{e,{\text{min}}}}},{{Y}_{{e,0}}})$. В работе [37] с малым допустимым значением ${{Y}_{{e,min}}} = 0.001$ получалась переоцененная нейтронизация в непрозрачной области, сопровождаемая уменьшением химического потенциала электронов при росте плотности в центре. В данных расчетах минимальное значение числа электронов на нуклон $Y_{e}^{{{\text{eq}}}}$ ограничено снизу величиной 0.05, что воспроизводит химический потенциал электронов в 2D задаче на рис. 1 как в сферически симметричном расчете коллапса с точным расчетом реакций слабого взаимодействия [34].
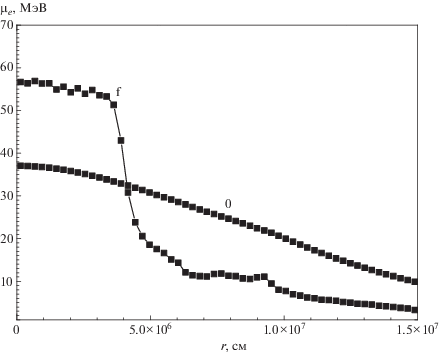
Рис. 1.
Химический потенциал электронов в начале расчетов ($t \approx 0$) и в конце (${{t}_{f}} = 11.72$ мс) 2D расчетов в экваториальной плоскости.
Для электронов используется уравнение состояния ультрарелятивистских пар ${{k}_{{\text{B}}}}T \ll \rho \epsilon {\text{/}}{{m}_{p}}$, ${{\mu }_{e}}\, \gg \,{{m}_{e}}{{c}^{2}}$: $\tfrac{{{{Y}_{e}}\rho }}{{{{m}_{p}}}}\, = \,\tfrac{1}{{2{{\pi }^{2}}}}\mathop {\left( {\tfrac{{kT}}{{\hbar c}}} \right)}\nolimits^3 (\mu _{e}^{3}\, + \,{{\pi }^{2}}{{\mu }_{e}})$, ${{P}_{e}}\, = \,\left( {\tfrac{4}{3} - 1} \right)\rho {{\epsilon }_{e}}$ = = $\tfrac{1}{{12{{\pi }^{2}}{{{(\hbar c)}}^{3}}}}\left( {\mu _{e}^{4} + 2{{\pi }^{2}}\mu _{e}^{2}{{{({{k}_{{\text{B}}}}T)}}^{2}} + \tfrac{7}{{15}}{{\pi }^{4}}{{{({{k}_{{\text{B}}}}T)}}^{4}}} \right)$.
В качестве начальных данных принята связь давления и плотности как в политропе $P \propto {{\rho }^{{1 + 1/n}}}$ с индексом $n = 3$, соответствующему ультрарелятивистским электронам с небольшим начальным вращением. Закон вращения выбран в виде постоянного отношения центробежной силы к силе тяжести ($\alpha = {\text{const}}$ – обобщение твердотельного вращения для несжимаемой жидкости) из [51]. Отношение полярного радиуса ${{r}_{p}}$ к экваториальному ${{r}_{{{\text{eq}}}}}$ выбрано 0.9, энергия вращения получилась 1.25% от гравитационной. Небольшое вращение обеспечивает аксиальную симметрию и способствует выделению крупномасштабной конвекции, как было показано в 3D расчетах с учетом переноса нейтрино без учета их спектра [32].
Политропная начальная модель содержит три независимых физических параметра, например гравитационная постоянная $G$, центральная плотность ${{\rho }_{0}}$ и экваториальный радиус ${{r}_{{{\text{eq}}}}}$. Для выбранной центральной плотности ${{\rho }_{c}} = 2 \times {{10}^{{12}}}$ г · см–3 для заданной типичной массы коллапсирующего ядра $1.4\,{{M}_{ \odot }}$ политропа дает экваториальный радиус ${{r}_{{{\text{eq}}}}} = 2.68 \times {{10}^{7}}$ см, гравитационную энергию Egr = –2.93 × 1052 эрг, энергию вращения ${{E}_{{\text{k}}}}{\text{/}}( - {{E}_{{{\text{gr}}}}})\, = $ $ = 0.0125$, момент импульса ${{J}_{z}} = 9.87 \times {{10}^{{48}}}$ эрг · с.
Выбранный закон дифференциального вращения (угловая скорость зависит от цилиндрического радиуса) позволяет рассматривать сколь угодно большие энергии вращения, вплоть до тонкого диска, достижимые только в конце сжатия, когда, после потерь энергии на нейтринное излучение, гравитационная сила в основном удерживается центробежной силой. С другой стороны, в начале гравитационного коллапса для ядра звезды с радиусом ~109 см следовало выбрать твердотельное вращение политропы $n = 3$, поскольку процессы горения в массивной звезде сопровождаются конвекцией, и происходит выравнивание угловой скорости. Пространственное распределение плотности в политропе $n = 3$ получается достаточно рыхлым, и максимально сильное твердотельное вращение для неe возможно при достижении на экваторе первой космической скорости с энергией вращения ${{E}_{{\text{k}}}}{\text{/}}( - {{E}_{{{\text{gr}}}}}) = 0.009$ и моментом импульса $6.4 \times {{10}^{{49}}}$ эрг с [52]. Поэтому выбранное дифференциальное вращение в постановке задачи уже на стадии коллапса импульса можно считать слабым относительно максимально возможного. Для рыхлой конфигурации политропы $n = 3$ при твердотельном вращении роль центробежной силы велика к краю звезды, в случае принятого в начале расчетов дифференциального закона вращения отношение центробежной силы к силе тяжести во всей экваториальной плоскости постоянно в точности, как для жесткого уравнения состояния несжимаемой жидкости. Эффекты вращения затрагивают центральную область, конвекция в которой нас интересует.
Для заданных профилей плотности и давления надо пересчитать параметры $T$, ${{Y}_{e}} = Y_{e}^{{{\text{eq}}}}(\rho ,T)$ с температурой $T = T(\rho ,\epsilon = 3P{\text{/}}\rho )$, обеспечивающие начальное равновесие (без учета потерь энергии нейтрино) в момент времени $t = 0$ (см. рис. 2). Выбранная центральная плотность в начальном равновесии соответствует уже продолжающемуся коллапсу реального ядра звезды. Малый начальный радиус позволяет обойтись меньшей неподвижной эйлеровой расчетной сеткой. Требуется разрешить формирование нейтронной звезды с радиусом ~10 км. В реальности коллапс начинается при радиусе звезды ~108 см, однако начальная стадия потерь энергии нейтрино продолжается несколько секунд и значительно превышает газодинамическое время ${{(G\rho )}^{{ - 1/2}}}$ даже для малой начальной центральной плотности ~109 г см–3 [34].
Рис. 2.
Вверху – начальная модель ($t \approx 0$) и окончание расчетов (${{t}_{f}} = 11.72$ мс) в экваториальной плоскости в 2D расчетах. Зависимости плотности $\rho $ (сплошные линии) и температуры $T$ (штриховые линии) от радиуса. Внизу – зависимости энтропии на нуклон $s{\text{/}}{{k}_{{\text{B}}}}$ (сплошные линии), числа электронов ${{Y}_{e}}$ (штриховые линии) и показателя адиабаты $\Gamma $ (пунктирные линии) от радиуса.
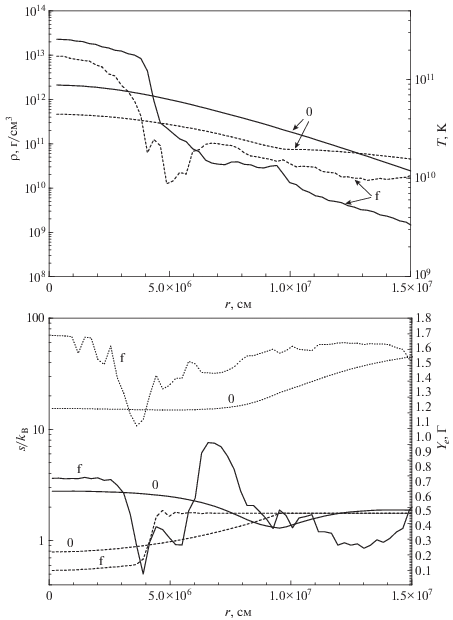
В результате реконструкции решения в 2D задаче мы получаем тот же снижающийся в центре профиль энтропии $ds{\text{/}}dr < 0$ (см. рис. 2), как в сферически симметричном расчете коллапса с большим реалистичным начальным радиусом [34]. Спадающий профиль возникает из-за нейтронизации. Нейтронизация уменьшает число электронов ${{Y}_{e}}$, и удельная энергия из электронного компонента переходит к нуклонам. Дополнительно рис. 2 показывает переход показателя адиабаты $\Gamma \equiv (\rho c_{s}^{2}{\text{/}}P)$ от релятивистских электронов, 4/3, к нуклонам, 5/3 при высокой плотности ~1013 г · см–3. В задаче о коллапсе [34] мы получали две предположительно неустойчивые области для конвекции (если использовать критерий устойчивости Шварцшильда $\tfrac{{ds}}{{dr}} < 0$ без учета нейтрино). Первая область вблизи центра звезды существует в течение $ \gtrsim {\kern 1pt} 10$ мс. Области соответствует спадающей профиль энтропии на рис. 2. Вторая узкая область формируется вблизи аккрецирующей ударной волны и существует длительное время. Другой критерий возникновения конвекции для газовой динамики с химическим превращением (нейтронизация вещества происходит за газодинамическое время) есть критерий устойчивости Леду [53, 54]. Критерий Леду не учитывает перенос нейтрино, который оказывается важным.
Для расчетов 2D задачи в сферических координатах $(r,0 < \theta < \pi {\text{/}}2)$ использовалась сетка $60 \times 30$ для большой части политропы (расчетная область ограничена $r \leqslant 0.6{{r}_{{{\text{eq}}}}}$) в предположении аксиальной симметрии $\partial {\text{/}}\partial \phi = 0$, и плоскости симметрии $\theta = \pi {\text{/}}2$. Для учета спектра нейтрино используется логарифмическая сетка из 15 интервалов до 40 МэВ. Пространственная сетка при приближении к началу координат сгущается по угловой переменной, а при расчете по явной схеме действует ограничение Куранта на временнóй шаг $\Delta t \lesssim \Delta r\Delta \theta {\text{/}}({{c}_{s}} + \left| v \right|)$. Скиннер и др. [41] использовали менее подробную сетку по углам при приближении к началу координат, объединяли интервалы по углам. Мы же в своих расчетах сетку не меняли, а дробили временные шаги интегрирования по углам на несколько при приближении к началу координат, т.е. огрубляли описание в угловом направлении вблизи начала координат.
Граничные условия задачи. На внешней границе заданы непротекание вещества и гладкая стенка, нейтрино свободно покидают расчетную область. В данном расчете мы не претендуем на описание сброса оболочки, а если бы ставили такую цель, то выбрали достаточно большую расчетную область, ограниченную гладкой стенкой для вещества, чтобы контролировать результаты счета. Масса сохраняется с машинной точностью, потери полной энергии, связанные с неточностью гидродинамического описания в условиях гравитации на конечной сетке, много меньше потерь энергии нейтрино, несохранение $z$-компонента момента импульса также связано с ошибками аппроксимации (присутствуют “схемная” вязкость и трение слоев вещества) и не превышает долей процента в методе даже для нескольких оборотов вещества в случае сильного вращения [29]. В данном расчете вращение слабое, в формирующейся нейтронной звезде из-за потерь энергии нейтрино угловая скорость выходит на значение 0.4 мс, получается менее одного оборота в центральной части за все время расчетов.
Вычислительная сложность задачи заключается в малых газодинамических скоростях вещества и звука в сравнении со световой скоростью переноса нейтрино только в прозрачной области, $\Delta t \lesssim \Delta r{\text{/}}({{c}_{s}} + \left| v \right|)$. Хотя диффузия и обмен энергиями с нейтрино считаются по неявной схеме, нет возможности за один временной шаг просчитать перенос нейтрино через несколько пространственных интервалов расчетной сетки без потери точности. Непрозрачная область не ограничивает временны́е шаги явной газодинамической схемы. На практике временнóй шаг газовой динамики выбирается из требования ограниченного числа временны́х шагов неявной схемы, описывающей перенос энергии нейтрино на один газодинамический шаг. Это требование автоматически приводит к условию временнóго шага $\Delta t \lesssim \Delta r{\text{/}}c$ в прозрачной области, в которой энергию переносят нейтрино со световой скоростью, а не все вещество (его газодинамическая скорость и скорость звука много меньше скорости света). Другая особенность задачи – использование консервативной схемы при наличии большого вырождения электронов. В каждом объеме пространственной сетки для построения консервативной схемы мы используем объемные плотности энергии вещества и спектральной плотности энергии нейтрино. Это решает проблему непрозрачной области, в которой временны́е шаги определяют газодинамический перенос и скорость звука, и нет нужды рассчитывать многократное испускание и поглощение нейтрино. Однако при небольшой ошибке в определении энергии вещества получается большая погрешность в определении температуры, так что можно попасть в физически недопустимую область параметров ядерного статистического равновесия $(\rho ,\rho \epsilon ,{{Y}_{e}})$. На практике на использованной расчетной сетке удается просчитать развитие неустойчивости для сильного вырождения ${{\mu }_{e}} \sim 60$ МэВ при температуре $kT \lesssim 10$ МэВ. Наконец, газовая динамика включает перенос числа электронов на нуклон ${{Y}_{e}}$ вместе с веществом – это естественная независимая переменная для лагранжева описания задачи на сетке, движущейся с веществом [34]. Оказалось, высокое разрешение эйлеровой схемы на неподвижной сетке не всегда обеспечивает получение физически допустимых параметров $(\rho ,\rho \epsilon ,{{Y}_{e}})$ в переходной области нейтронизации между железом и свободными нуклонами для уравнения состояния ядерного статистического равновесия, если в качестве независимой переменной использовать число электронов на нуклон ${{Y}_{e}}$. А использование для независимой переменной разницы концентраций электронов и позитронов $\Delta {{n}_{e}}$ в уравнении (2) эту проблему снимает.
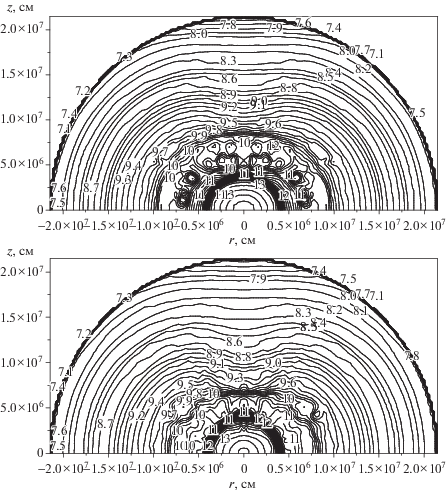
Линии уровня плотности на рис. 3 в момент времени $t = 11.72$ мс показывают развитие крупномасштабной конвекции за газодинамическое время ${{(G\bar {\rho })}^{{ - 1/2}}} = 4$ мс для средней плотности $\bar {\rho } \approx {{10}^{{11}}}$ г · см–3. При этом происходит перестройка спадающего наружу неустойчивого профиля энтропии (рис. 2). В этой части нейтрино теряются, благодаря необратимой нейтронизации реализуются условия конвекции, близкие к условию Шварцшильда. Расчеты с учетом вращения демонстрируют выделение более длинноволновых возмущений, чем в случае без вращения [30, 31]. В более реалистичном 3D случае вращение способствует выделению тех же самых длинноволновых возмущений [32, 55].
Рис. 3.
Линии уровня плотности в плоскости $y = 0$ ($\phi = 0$) в задаче о коллапсе массы $1.4\,{{M}_{ \odot }}$ с учетом переноса нейтрино и их спектра в моменты $t = 11.72$ мc (вверху) и $t = 12.59$ мc (внизу) для параметров $lg{{\rho }_{{{\text{min}}}}} = 7$, $lg{{\rho }_{{{\text{max}}}}} = 13$, $\Delta \lg \rho = 0.1$, единица плотности г ⋅ см–3 демонстрируют развитие крупномасштабной конвекции.
В центральной части с высокой плотностью нейтрино захвачены веществом, нейтронизация обратима, конвекция развивается хуже. С выключенным переносом нейтрино задача является математически строгой задачей об устойчивости. И конвекция во всей расчетной области развивалась за длительное время (100 мс), начинаясь с периферийной разреженной области. Пересчет удельной энтропии в предположении быстрой релаксации числа электронов ${{Y}_{e}}$ к равновесному значению $Y_{e}^{{{\text{eq}}}}$ убирает неустойчивый профиль энтропии.
Важный результат расчетов – это спектральный поток нейтрино $dL{\text{/}}d\epsilon $ вблизи нейтриносферы $r = 5.5 \times {{10}^{6}}$ см (см. рис. 4). 2D расчет демонстрирует повышение средней энергии нейтрино в сравнении с 1D [34] в 1.5 раза. Спектр уходящих нейтрино становится жестче в сравнении со сферически симметричным расчетом из-за конвекции в центральной области с высокоэнергичными нейтрино, запертыми оптически плотным веществом в 1D. Максимум спектральной светимости достигается при 18 МэВ. Как показывает приведенный на рис. 1 профиль химического потенциала электронов (и близкого к нему химического потенциала нейтрино в непрозрачной области), энергия выходящих частиц примерно соответствует максимальным значениям химического потенциала в конвективной области, не затрагивающей центр с высоким химическим потенциалом $ \approx {\kern 1pt} 60$ МэВ.
Рис. 4.
Спектральная нейтринная светимость при коллапсе, $dL{\text{/}}d\epsilon $ в момент $t = 11.72$ мc вблизи нейтриносферы $r = 5.5 \times {{10}^{6}}$ см.

Сравнивая результаты данной работы с современными газодинамическими моделями (без учета магнитного поля) зарубежных авторов, следует отметить использование в 3D моделях упрощенного переноса нейтрино вместо решения уравнений Больцмана. Авторы Мирфи, Микин, Барроуз, Жанг, Котч, Отт, Радис используют более точное уравнение состояния при ядерных плотностях, полный набор реакций взаимодействия нейтрино с веществом, иногда включают эффекты ОТО, которые не важны при размерах формирующейся прото-нейтронной звезды десятки километров. Основной упор этих моделей делается на объяснение сброса оболочки без детального объяснения физики процессов. В частности, ключевой вопрос о масштабе конвекции в области аккреции и выводах о сбросе оболочки СН оказывается зависящим от принятой размерности математической задачи. В 2D моделях [20, 21] взрыв СН получается одновременно с крупномасштабной конвекцией. В более реалистичной 3D постановке [24, 25] конвекция в области аккреции остается мелкомасштабной, а необходимого энерговложения в оболочку предсверхновой часто не происходит [26]. В нашем анализе это означает недостаточное влияние мелкомасштабной конвекции в 3D постановке прежде всего на энергию выходящих нейтрино. И наши расчеты коллапса в 3D с учетом переноса нейтрино наглядно показывают, что небольшое начальное вращение превращает 3D задачу в 2D постановку и снимает проблему развития крупномасштабных возмущений [32].
Аксиально симметричные расчеты Доленс, Барроуз, Жанг, Накамура, Вартанян [21, 56] демонстрируют средние энергии нейтрино 12–20 МэВ и светимость нейтрино на десятки процентов выше, чем в сферически симметричной модели. Напомним, что в сферически симметричной модели искусственного повышения средней энергией нейтрино до величины 30 МэВ было бы достаточно для объяснения СН даже при неизменной светимости нейтрино [35, 36]. Большинство 3D моделей [24, 25] сосредоточены на анализе развития неустойчивости, а спектров нейтринного излучения не дают. Однако в последнее время появились работы о возможности регистрации нейтрино от коллапсирующих сверхновых, для чего расчет спектра нейтрино обязателен. Если при взрыве последней близкой СН1987А в соседней галактике в 1987 г. было зарегистрировано несколько нейтринных событий, связанных с последующей вспышкой света от взрыва сверхновой (фотоны возникают из расходящейся по веществу протяженной предсверхновой звезды ударной волны, и наблюдаются позже нейтрино из гравитационном коллапса компактной центральной массы $1.4\,{{M}_{ \odot }}$), то современные установки с большим количеством рабочего вещества обещают в тысячу раз большее количество регистраций нейтринных событий от близкой сверхновой и даже возможность регистрации нейтрино от далеких коллапсирующих сверхновых на расстоянии 100 кпк, например Супер-Камиоканда [57]. Рассчитанная нейтринная светимость (полная энергия сравнима с гравитационной энергией нейтронной звезды, испускается несколько секунд) вместе со спектром нейтрино (типичные средние энергии от 10 до 20 МэВ), дает отклик детектора в зависимости от расстояния до Земли. Темп регистрации нейтринных событий оказывается различим для рассчитанных моделей коллапса с разными спектрами нейтрино. Но неопределенность в расчете нейтринных осцилляций вносит неопределенность в предсказание темпа нейтринных событий. Так, средние энергии нейтрино на уровне 5–10 МэВ дают существенно меньший темп регистрируемых событий и всегда оказываются отличимы от нейтрино 15 МэВ (мало энергичные нейтрино тяжелее регистрировать), а средние энергии нейтрино 30 МэВ могут оказаться неотличимы от нейтрино 15 МэВ [57]. Мы же утверждаем, что ключом проверки модели крупномасштабной конвекции является возможность отличить в эксперименте средние энергии нейтрино 15 МэВ от 30 МэВ. Просто регистрации нейтринных событий для проверки теории взрыва недостаточно, нужен спектр нейтрино. Оказывается спектр нейтрино, проинтегрированный по времени, даже при допустимости нейтринных осцилляций можно воспроизвести с помощью регистрации нейтрино на нескольких типах детекторов [58].
3. ЗАКЛЮЧЕНИЕ
Рассмотрена крупномасштабная конвекция в задаче о коллапсе ядра звезды со слабым вращением с учетом переноса нейтрино и их спектра. Конвекция возникает в центральной части за газодинамическое время $ \sim {\kern 1pt} 10$ мс благодаря неравновесной нейтронизации при выходе нейтрино из этой области. Выделению длинноволновой моды способствует небольшое начальное вращение, поскольку начальная конфигурация отличается от сферической. Полученное значение средней энергии нейтрино 15 МэВ в 1.5 раза превышает значение сферически симметричных расчетов и в соответствующее число раз увеличит энергию, передаваемую от нейтрино расширяющейся оболочке. Этот эффект существенный для объяснения взрыва СН.
Уточнение модели относилось к расчету нейтронизации при высокой плотности. В расчетах удалось воспроизвести правильное увеличение химического потенциала электронов при росте центральной плотности, как при полном учете кинетики слабых взаимодействий в сферически симметричном расчете [34], за счет коррекции минимального значения равновесного числа электронов на нуклон. Имеют место два эффекта при высокой плотности вещества – смещение в сторону обратимой нейтронизации и рост химического потенциала электронов. Первый эффект подавляет развитие крупномасштабной конвекции, а второй эффект должен увеличивать средние энергии уходящих нейтрино. В итоге решения задачи с существенным отличием от публикации [37] получились прежние энергии уходящих нейтрино: средняя энергия $ \sim {\kern 1pt} 15$ МэВ с максимумом нейтринной светимости при $ \sim {\kern 1pt} 18$ МэВ. Таким образом, вблизи формирующейся нейтриносферы в области неравновесной нейтронизации реализуются условия устойчивости газовой динамики Шварцшильда. А в самом центре с запертыми нейтрино с высоким химическим потенциалом $ \gtrsim {\kern 1pt} 60$ МэВ нейтронизация обратима, конвекция подавлена в соответствии с критерием Леду.
Учет процессов взаимодействия нейтрино с оболочкой в нашей модели осложнен значительным увеличением времени счета пропорционально кубу числа энергетических интервалов в неявной схеме, описывающей реакции слабого взаимодействия. Вероятно, для объяснения сброса оболочки сверхновой с вложением необходимой энергии 1051 эрг важно как увеличение средней энергии, так и рост светимости из-за крупномасштабной конвекции.
Список литературы
K. Nomoto and M. aki Hashimoto, Phys. Rep. 163, 13 (1988).
S. Chandrasekhar and E. A. Milne, Monthly Not. Roy. Astron. Soc. 91, 456 (1931).
W. A. Fowler and F. Hoyle, Astrophys. J. Suppl. 9, 201 (1964).
V. S. Imshennik and D. K. Nadezhin, Astrophys. Space Sci. Rev. 8, 1 (1989).
H. A. Bethe, Rev. Modern Physics 62, 801 (1990).
H.-T. Janka, K. Langanke, A. Marek, G. Martínez-Pinedo, and B. Müller, Phys. Rep. 442, 38 (2007), arXiv:astro-ph/0612072.
V. S. Imshennik and D. K. Nadezhin, Sov. J. Experim. Theoret. Phys. 36, 821 (1973).
D. K. Nadezhin, Astrophys. Space Sci. 49, 399 (1977).
S. W. Bruenn, Astrophys. J. Suppl. 58, 771 (1985).
L. Dessart, A. Burrows, E. Livne, and C. D. Ott, Astrophys. J. 673, L43 (2008), arXiv:0710.5789 [astro-ph].
F. D. Swesty and E. S. Myra, Astrophys. J. Suppl. 181, 1 (2009).
B. Müller, H.-T. Janka, and H. Dimmelmeier, Astrophys. J. Suppl. 189, 104 (2010), arXiv:1001.4841 [astro-ph.SR].
A. Mezzacappa and S. W. Bruenn, Astrophys. J. 405, 637 (1993).
A. Mezzacappa and S. W. Bruenn, Astrophys. J. 405, 669 (1993).
A. Mezzacappa and S. W. Bruenn, Astrophys. J. 410, 740 (1993).
A. Mezzacappa, M. Liebendörfer, O. E. Messer, W. R. Hix, F.-K. Thielemann, and S. W. Bruenn, Phys. Rev. Lett. 86, 1935 (2001), arXiv:astro-ph/0005366.
E. J. Lentz, A. Mezzacappa, O. E. B. Messer, M. Liebendörfer, W. R. Hix, and S. W. Bruenn, Astrophys. J. 747, id. 73 (2012), arXiv:1112.3595 [astro-ph.SR].
M. Herant, W. Benz, W. R. Hix, C. L. Fryer, and S. A. Col-gate, Astrophys. J. 435, 339 (1994), arXiv:astro-ph/9404024.
A. Burrows, J. Hayes, and B. A. Fryxell, Astrophys. J. 450, 830 (1995), arXiv:astro-ph/9506061.
J. W. Murphy and C. Meakin, Astrophys. J. 742, id. 74 (2011), arXiv:1106.5496 [astro-ph.SR].
J. C. Dolence, A. Burrows, and W. Zhang, Astrophys. J. 800, id. 10 (2015), arXiv:1403.6115 [astro-ph.SR].
S. M. Couch and C. D. Ott, Astrophys. J. 778, id. L7 (2013), arXiv:1309.2632 [astro-ph.HE].
A. Wongwathanarat, E. Müller, and H.-T. Janka, Astron. and Astrophys. 577, id. A48 (2015), arXiv:1409.5431 [astro-ph.HE].
S. M. Couch and C. D. Ott, Astrophys. J. 799, id. 5 (2015), arXiv:1408.1399 [astro-ph.HE].
D. Radice, C. D. Ott, E. Abdikamalov, S. M. Couch, R. Haas, and E. Schnetter, Astrophys. J. 820, id. 76 (2016), arXiv:1510.05022 [astro-ph.HE].
A. Burrows and D. Vartanyan, Nature 589, 29 (2021), arXiv:2009.14157 [astro-ph.SR].
V. M. Chechetkin, S. D. Ustyugov, A. A. Gorbunov, and V. I. Polezhaev, Astron. Letters 23, 30 (1997).
I. V. Baikov, V. M. Suslin, V. M. Chechetkin, V. Bychkov, and L. Stenflo, Astron. Rep. 51, 274 (2007).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 60, 655 (2016).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 62, 251 (2018).
V. M. Chechetkin and A. G. Aksenov, Phys. Atomic Nuclei 81, 128 (2018).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 65, 916 (2021).
V. M. Suslin, S. D. Ustyugov, V. M. Chechetkin, and G. P. Churkina, Astron. Rep. 45, 241 (2001).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 56, 193 (2012).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 58, 442 (2014).
I. V. Baikov and V. M. Chechetkin, Astron. Rep. 48, 229 (2004).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 63, 900 (2019).
A. G. Aksenov, Comp. Math. and Math. Physics 55, 1752 (2015).
G. Vereshchagin and A. Aksenov, Relativistic Kinetic Theory With Applications in Astrophysics and Cosmology (Cambridge University Press, 2017).
A. G. Aksenov, Astron. Letters 24, 482 (1998).
M. A. Skinner, J. C. Dolence, A. Burrows, D. Radice, and D. Vartanyan, Astrophys. J. Suppl. 241, id. 7 (2019).
A. G. Aksenov and V. M. Chechetkin, Astron. Rep. 62, 834 (2018).
G. S. Bisnovatyi-Kogan, Astrophysics 55, 387 (2012), arXiv:1203.0997 [astro-ph.HE].
V. S. Imshennik and V. M. Chechetkin, Soviet Astron. 14, 747 (1971).
R. M. Bionta, G. Blewitt, C. B. Bratton, D. Casper, and A. Ciocio, Phys. Rev. Lett. 58, 1494 (1987).
K. Hirata, T. Kajita, M. Koshiba, M. Nakahata, and Y. Oyama, Phys. Rev. Lett. 58, 1490 (1987).
E. N. Alekseev, L. N. Alekseeva, V. I. Volchenko, and I. V. Krivosheina, Sov. J. Experim. Theoret. Phys. Lett. 45, 589 (1987).
R. Schaeffer, Y. Declais, and S. Jullian, Nature 330, 142 (1987).
A. G. Aksenov, V. F. Tishkin, and V. M. Chechetkin, Math. Models Computer Simulations 11, 360 (2019).
A. G. Aksenov, Astron. Lettets 25, 185 (1999).
A. G. Aksenov and S. I. Blinnikov, Astron. and Astrophys. 290, 674 (1994).
A. G. Aksenov, S. I. Blinnikov, and V. S. Imshennik, A-stronomicheskii Zhurnal 72, 717 (1995).
P. Ledoux, Astrophys. J. 105, 305 (1947).
G. S. Bisnovatyj-Kogan, Physical problems of the theory of stellar evolution (Moscow: Nauka, 1989).
S. Chandrasekhar and N. R. Lebovitz, Astrophys. J. 138, 185 (1963).
H. Nagakura, A. Burrows, and D. Vartanyan, Monthly Not. Roy. Astron. Soc. 506, 1462 (2021).
K. Abe, P. Adrich, H. Aihara, R. Akutsu, et al., Astrophys. J. 916, 15 (2021).
H. Nagakura, Monthly Not. Roy. Astron. Soc. 500, 319 (2021), arXiv:2008.10082 [astro-ph.HE].
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


