Астрономический журнал, 2022, T. 99, № 1, стр. 75-87

1. ВВЕДЕНИЕ

В движении земного полюса, как известно [1–3], выделяются основные составляющие – чандлеровское и годичное колебания, долгопериодический тренд, а также нерегулярные колебания, в том числе стохастического характера [4]. Проблема построения модели и прогноза движения земного полюса связана в первую очередь с нерегулярным поведением его основных компонентов [2, 5].

Факторы, влияющие на движение Земли относительно центра масс, можно условно разделить на астрономические и геофизические. Движение Земли в космическом пространстве, а также перемещение ее подвижных сред происходит под влиянием тел Солнечной системы и в первую очередь Солнца и Луны. Поэтому в вопросах исследования движения Земли естественным является совместный учет геофизических и астрономических факторов в совокупности. Лунно-солнечные гравитационные возмущающие силы приводят к прецессии и нутации Земли [6]. В отличие от прецессии и нутации свойство деформируемости Земли и подвижность ее различных сред являются уже определяющими для движения мгновенной оси вращения в теле Земли. И в этом случае важным может являться не только учет подвижности сред, но и влияющих на них астрономических факторов, поскольку за время эволюции Солнечной системы многие процессы надо полагать синхронизированными [7–9].

Этой теме посвящено немало научных работ. Например, в исследовании [9] рассмотрена идеализированная модель влияния Луны на изменения параметров чандлеровского колебания, основанная на дифференциальных уравнениях связанных осцилляторов. В работе [10] изучено влияние параметрического резонанса в системе Земля–Луна на чандлеровское колебание и приведено качественное сравнение с “эмпирическими законами Мельхиора” [3]. В работах [11, 12] установлена взаимосвязь вариаций амплитуды и фазы чандлеровского компонента с геофизическими процессами в атмосфере и океанах. В ряде работ [13–15] рассмотрены вопросы о связи пространственного движения лунной орбиты с чандлеровским колебанием, обсуждена синхронизация чандлеровского колебания с 18-летним приливным циклом. В частности, в [13] установлено наличие 18-летнего цикла функции возбуждения чандлеровского колебания, приводящего к удвоенному периоду в амплитудной модуляции чандлеровского компонента. В работе [15] с помощью обработки и анализа данных наблюдений и измерений ряда C04 о движении земного полюса Международной службы вращения Земли (МСВЗ) [1] показано наличие колебательного процесса, синфазного с прецессионным движением орбиты Луны. Однако вопросы о синхронизации колебаний полюса с прецессией лунной орбиты и о влиянии Луны на его колебательный процесс еще мало изучены и требуют более детального рассмотрения.

Цель данной работы состоит в развитии работы [15], т.е. в дальнейшем исследовании свойств колебательного процесса земного полюса с периодом прецессии орбиты Луны и особенностей их синхронизации на более длительном интервале времени. Для этого использовался ряд C01 данных МСВЗ [1] о движении земного полюса, начиная с 1900 г. Численная обработка и анализ длительного ряда C01 проводились во многих исследованиях, например, в [16, 17]. Однако проблемы колебаний параметров движения земного полюса (параметров чандлеровских и годичных компонентов), происходящих с частотой, близкой к частоте прецессии лунной орбиты, обсуждаются достаточно редко.

В первой части данной статьи с помощью обработки длительного ряда наблюдений C01 МСВЗ рассматривается преобразование координат земного полюса, позволяющее определить 18‑летнюю цикличность и исследовать ее средние параметры на 120-летнем временнóм интервале наблюдений. Во второй ее части обсуждается кинематика движения земного полюса в полярных координатах. Основные кинематические свойства движения полюса используются для модификации преобразования, когда на интервале обработки данных происходит смена доминирующей гармоники (гармоники с большей амплитудой). В третьей части устанавливается синфазность 18-летних колебаний полюса после выполненного преобразования и колебаний параметров ориентации плоскости лунной орбиты.

2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЗЕМНОГО ПОЛЮСА НА ДЛИТЕЛЬНОМ ИНТЕРВАЛЕ ВРЕМЕНИ

В работе [15] с помощью анализа и численной обработки астрометрических данных измерений положения земного полюса на временнóм интервале 1945–2016 гг. показана зависимость вариаций параметров его компонентов от прецессионного движения орбиты Луны. А именно, в рамках совместного рассмотрения чандлеровского и годичного компонентов (без разложения основного движения полюса на составляющие) найдено преобразование от исходной к новой системе координат, в которой движение полюса оказывается синхронизированным с прецессионным движением орбиты Луны. Это преобразование состоит из двух этапов.

На первом этапе необходимо центрировать квазипериодическую траекторию полюса вычетом трендовой составляющей и исключить его среднее движение вокруг центральной точки. В результате полюс будет совершать циклическое квазипериодическое движение с шестилетним периодом, равным периоду амплитудной модуляции чандлеровского и годичного компонентов.

На втором этапе исключается полученная после первого преобразования шестилетняя цикличность аналогично первому этапу преобразования. В окончательной системе координаты земного полюса представлены как совокупность некомпенсированных после преобразования основных слагаемых (остаток от регулярных составляющих чандлеровского и годичного компонентов с постоянными амплитудами и фазами) и колебательного процесса, в котором выделяется колебание с частотой, близкой к частоте прецессии лунной орбиты. При этом наблюдается совпадение фаз найденного колебания и колебания параметров ориентации плоскости лунной орбиты к экватору Земли. Если применить обратное преобразование за вычетом некомпенсированной части, то получим гармоники в дополнение к регулярным составляющим колебаний полюса с чандлеровской и годичной частотами. Эти дополнительные слагаемые будут модулированы гармоникой с частотой, близкой к частоте прецессии орбиты Луны. Однако основная частота полученных слагаемых может принимать значения частоты либо чандлеровского, либо годичного компонента и зависит от преобразования (точнее от того, амплитуда какого компонента оказывается наибольшей).

Действительно, на временнóм интервале 1945–2006 гг. чандлеровский компонент был доминирующим по амплитуде (рис. 1) и, значит, средняя частота обращения полюса вокруг центральной точки была близка к чандлеровской частоте [18]. В течение последующих шести лет (2006–2012 гг.) амплитуды чандлеровского и годичного компонентов были близки, а после их равенства в окрестности 2011 г. произошла смена доминирующей гармоники. Это в свою очередь повлияло на рассмотренное преобразование, так как при изменении амплитудного соотношения изменится и средняя частота обращения полюса вокруг центральной точки. Как отмечалось в работе [15], на временнóм интервале с 2011 г. (в окрестности которого произошло изменение колебательного режима полюса) до 2016 г. выделить гармоники обработкой данных наблюдений было проблематичным ввиду слишком короткого для разделения гармоник с близкими частотами временнóго интервала.

Рассмотрим теперь этот вопрос более полно, воспользовавшись данными ряда C01, предоставляемого Международной службой вращения Земли [1]. Предложенное ранее преобразование исходной системы координат ($x$, $y$) можно представить в матричном виде [15]:

Здесь ${{a}_{h}}$ и ${{a}_{{ch}}}$ – амплитуды годичного и чандлеровского колебания полюса, а ${{w}_{h}}$ и ${{w}_{{ch}}}$ – их фазы; ${{\omega }_{*}}$ – среднее движение Земли по орбите вокруг Солнца; $N \cong 0.843$, $\nu = 1$ – чандлеровская и годичная частоты, измеряемые в циклах/год; $\Pi $ – матрица плоского поворота; ${{a}_{0}}$ – среднее значение амплитуды колебаний полюса при его движении вокруг “средней точки” (т.е. без трендовой составляющей); ${{c}_{x}}$, ${{c}_{y}}$ задают положение “средней точки” полюса и содержат константы, вековые слагаемые и вариации с периодами более шести лет; ${{\dot {w}}_{2}} - {{\dot {w}}_{1}} = \pm {{\nu }_{T}}{{\omega }_{*}}$ – частота шестилетней цикличности движения полюса.

Из выражения (1) видно, что смена доминирующей гармоники отразится как на первом этапе преобразования, так и на втором. На первом этапе поворот исходной системы координат выполняется в сторону движения полюса на угол ${{w}_{1}}$, соответствующий либо фазе чандлеровского колебания, либо фазе годичного колебания. На втором этапе направление поворота может быть как прямым, так и обратным, и зависит от доминирующей гармоники, а абсолютная величина угла $\left| {{{w}_{2}} - {{w}_{1}}} \right|$, на который выполняется поворот, оказывается инвариантной к выбору доминирующей гармоники.

Необходимые повороты удобно выполнить в полярных координатах. Например, для первого поворота перейдем от декартовых координат $x$, $y$ к полярным – амплитуде ${{a}_{p}}$ и фазе (полярному углу) ${{\psi }_{p}}$ с помощью выражений $x = {{c}_{x}} + {{a}_{p}}\cos {{\psi }_{p}}$, $y = {{c}_{y}} + {{a}_{p}}\sin {{\psi }_{p}}$. Тогда первому повороту будет соответствовать преобразование полярных координат, при котором амплитуда ${{a}_{p}}$ не меняется, а из полярного угла ${{\psi }_{p}}$ вычитается линейная часть. Вариацию полярного угла после первого поворота обозначим через $\delta {{\psi }_{p}}$. Величины ${{a}_{p}}$ и $\delta {{\psi }_{p}}$ являются полярными координатами полюса после первого этапа преобразования. На рис. 2 приведены декартовы координаты полюса ${{x}_{p}} = x - {{c}_{x}}$, ${{y}_{p}} = y - {{c}_{y}}$, построенные согласно данным ряда C01 МСВЗ за вычетом трендовой составляющей, а также вычисленные амплитуда ${{a}_{p}}$ и вариация полярного угла $\delta {{\hat {\psi }}_{p}}$.

График $\delta {{\hat {\psi }}_{p}}$ получен вычетом линейной части из вычисленного ряда ${{\psi }_{p}}$ на временнóм интервале 1900–2020 гг. На этот интервал приходится несколько эпизодов смены доминирующей гармоники. Поэтому средняя частота за весь рассматриваемый интервал не совпадает ни с чандлеровской частотой, ни с годичной, а имеет значение между 0.843 и 1 циклов в год. На графике $\delta {{\hat {\psi }}_{p}}$ визуально хорошо выделяются интервалы с доминирующим чандлеровским (с возрастающей линейной частью) и годичным (с убывающей линейной частью) компонентами. Этим интервалам соответствуют разные значения средней частоты ${{\langle {{\dot {\psi }}_{p}}\rangle }_{T}}$ (средней за шестилетний период модуляции), которая равна либо 0.843 циклов в год, либо 1 цикл в год.

Следует отметить, что наибольшие скачки в фазе чандлеровского колебания [19] происходили на интервалах с доминирующим годичным компонентом. Такое соответствие обусловлено, вероятно, взаимосвязью амплитуды и фазы чандлеровского колебания, так как изменения фазы наблюдались в окрестностях минимумов амплитуды.

3. ИСПОЛЬЗОВАНИЕ КИНЕМАТИЧЕСКИХ СВОЙСТВ ДВИЖЕНИЯ ЗЕМНОГО ПОЛЮСА В ПРЕОБРАЗОВАНИИ ЕГО КООРДИНАТ

Согласно выражению (1) в момент изменения средней частоты ${{\dot {\psi }}_{p}}$ рассмотренное преобразование может иметь особенность, так как на первом этапе значение ${{w}_{1}}$ скачкообразно меняется (значения ${{w}_{{ch}}}$ и ${{w}_{h}}$ в произвольный момент времени не равны), а на втором этапе меняется направление поворота. Это создает определенные неудобства, однако их нетрудно устранить.

Для этого рассмотрим сумму чандлеровской и годичной составляющих колебаний полюса. Его координаты (${{x}_{p}}$, ${{y}_{p}}$) приближенно можно записать в виде:

Примем во внимание, что амплитуды ${{a}_{{ch}}}$, ${{a}_{h}}$ подвержены медленным изменениям и содержат долгопериодические вариации с периодами более шести лет, а также, что на более коротких интервалах времени их можно считать квазипостоянными величинами. Тем самым в дальнейшем будем пренебрегать скоростью их изменения. Тогда при этих предположениях получим выражения для частоты ${{\dot {\psi }}_{p}}$:

Как показано в [18], средняя частота ${{\langle {{\dot {\psi }}_{p}}\rangle }_{T}}$ за период $T$ модуляции чандлеровской и годичной гармоник при постоянстве их частот $N = {\text{const}}$, $\nu = {\text{const}}$ и неравенстве амплитуд (${{a}_{{ch}}} \ne {{a}_{h}}$) принимает одно из значений $N{{\omega }_{*}}$ или $\nu {{\omega }_{*}}$.

Отсюда следует, что вариацию частоты $\delta {{\dot {\psi }}_{p}}$ можно ввести различными способами в зависимости от колебательного режима (от того, какая гармоника является доминирующей). Так, если доминирующим является чандлеровский компонент, то вариация частоты (в рамках принятых упрощений) определяется выражением:

которое получается вычетом из ${{\dot {\psi }}_{p}}$ частоты $N{{\omega }_{*}}$. Оно достаточно точно описывает наблюдаемые вариации. На рис. 3 для интервала с доминирующей чандлеровским компонентом (без изменения колебательного режима) приведено сравнение вариации $\delta {{\psi }_{p}}$, вычисленной двумя способами. Первым способом вариация $\delta {{\hat {\psi }}_{p}}$ вычислена вычетом непосредственно из функции полярного угла его линейной части. Второй способ заключается в вычислении $\delta \dot {\psi }_{p}^{N}$ по формуле (4) с последующим ее интегрированием. Для применения (4) предварительно были найдены зависимости ${{a}_{{ch}}}(t)$, ${{a}_{h}}(t)$ с помощью фильтрации на основе Фурье-преобразования (рис. 1) и зависимость ${{a}_{p}}(t)$ (рис. 2в). Также на графике даны невязки двух графиков $\Delta {{\psi }_{p}} = \delta {{\hat {\psi }}_{p}} - \delta \psi _{p}^{N}$. Так как вариация $\delta {{\psi }_{p}}$ не является гармонической, то аккуратно сгладить и отфильтровать высокочастотные колебания из $\delta {{\psi }_{p}}$ с помощью амплитудно-частотного анализа оказывается проблематичным. И если требуется получить сглаженную функцию $\delta {{\psi }_{p}}$, то применение (4) оказывается предпочтительным. Из сравнения графиков видно, что интеграл от выражения (4) адекватно описывает сглаженные колебания $\delta {{\psi }_{p}}$. Это в свою очередь показывает, что скорости изменения амплитуд основных гармоник колебаний полюса достаточно малы и для вычисления вариации полярного угла $\delta {{\psi }_{p}}$ ими можно пренебречь.

Теперь, если амплитуда годичного компонента окажется больше амплитуды чандлеровского компонента, то вариация частоты примет вид

и получается из (3) вычетом частоты $\nu {{\omega }_{*}}$.

Однако, если на рассматриваемый интервал приходится смена доминирующей гармоники, то вариация, определяемая выражениями (4), (5), будет содержать разрыв. Из (4) и (5) видно, что значения вариаций частоты $\delta \dot {\psi }_{p}^{\nu }$ и $\delta \dot {\psi }_{p}^{N}$ не равны при равенстве амплитуд ${{a}_{{ch}}} = {{a}_{h}}$ (в том числе и при ${{a}_{p}} = 0$, так как их пределы при ${{a}_{p}} \to 0$ не равны). Значит, при ${{a}_{{ch}}} = {{a}_{h}}$ будет разрывной и вариация полярного угла $\delta {{\psi }_{p}}$, если только при интегрировании уравнений (4) и (5) не добавить фазу, устраняющую разрыв. Чтобы избежать особенности в точке перехода, вариацию $\delta {{\dot {\psi }}_{p}}$ можно определить более удобным образом:

Действительно, вычитая из (4) или прибавляя к (5) полуразности частот чандлеровской и годичной гармоник, получим одно и то же выражение, записанное в (6). Оно получается сразу и из (3) вычетом полусуммы чандлеровской и годичной частот. Вариации $\delta {{\dot {\psi }}_{p}}$ и $\delta {{\psi }_{p}}$, определенные таким образом, не будут содержать разрывов при равенстве амплитуд ${{a}_{{ch}}} = {{a}_{h}}$.

Заметим, что среднее значение вариации частоты (6) (за время, в которое укладывается целое число периодов модуляции) может быть равно нулю, только если время наблюдения обоих колебательных режимов (когда ${{a}_{{ch}}} > {{a}_{h}}$ и ${{a}_{h}} > {{a}_{{ch}}}$) одинаковое. При произвольном выборе интервала среднее значение окажется ненулевым, что качественно никак не повлияет на дальнейшее преобразование. Однако вариация частоты, определенная выражением (6), будет уже непрерывной и, следовательно, будет непрерывной вариация полярного угла $\delta {{\psi }_{p}}$.

Из выражения (6) для $\delta {{\dot {\psi }}_{p}}$ найдем функцию полярного угла ${{\psi }_{p}}$:

где скобки $[...]$ обозначают целую часть соответствующего выражения. Первые два слагаемых в выражении (7) представляют собой вариацию полярного угла $\delta {{\psi }_{p}}$. Она содержит помимо периодической части и линейную часть, равную либо $ - (\nu - N)t{\text{/}}2$ при ${{a}_{{ch}}} > {{a}_{h}}$, либо $(\nu - N)t{\text{/}}2$ при ${{a}_{h}} > {{a}_{{ch}}}$. При равенстве амплитуд ${{a}_{{ch}}} = {{a}_{h}}$ вариация $\delta {{\psi }_{p}}$ отсутствует.

Как показано в [18], экстремумы мгновенной частоты ${{\dot {\psi }}_{p}}$, которые достигаются при минимумах амплитуды ${{a}_{p}}$, изменят знак после смены доминирующей гармоники, а вариации полярного угла $\delta {{\psi }_{p}}$ изменят фазу на противоположную (т.е. произойдет зеркальное отражение графика вариации полярного угла $\delta {{\psi }_{p}}$ относительно оси абсцисс при условии одинаковых постоянных соотношений ${{a}_{{ch}}}{\text{/}}{{a}_{h}}$, ${{a}_{h}}{\text{/}}{{a}_{{ch}}}$ до и после изменения колебательного режима). Тогда для устранения особенности преобразования при изменении средней частоты можно изменить знак вариации $\delta {{\psi }_{p}}$ (отразив тем самым ее график относительно оси абсцисс), величина которой и является полярным углом после первого этапа преобразования. Это следует непосредственно из того, что

где $T = 2\pi {\text{/}}(\nu - N)$, и из выражений (6) и (7) для $\delta {{\dot {\psi }}_{p}}$, $\delta {{\psi }_{p}}$.

Действительно, из (8) следует, что средняя частота ${{\langle {{\dot {\psi }}_{p}}\rangle }_{T}}$ равна либо $N{{\omega }_{*}}$, либо $\nu {{\omega }_{*}}$, средняя частота ${{\langle \delta {{\dot {\psi }}_{p}}\rangle }_{T}}$ в пределах каждого из колебательных режимов равна $ \pm (\nu - N){{\omega }_{*}}{\text{/}}2$ и меняет знак при смене доминирующей гармоники, а из (6) и (7) следует, что при смене доминирующей гармоники изменят знаки функция $\delta {{\dot {\psi }}_{p}}$ и с точностью до постоянной фазы функция $\delta {{\psi }_{p}}$ (в пределах одного колебательного режима $\delta {{\dot {\psi }}_{p}}$ и $\delta {{\psi }_{p}}$ знак не меняют). При этом $\delta {{\dot {\psi }}_{p}}$ пройдет через ноль при ${{a}_{{ch}}} = {{a}_{h}}$. В частности, при одинаковых соотношениях амплитуд ${{a}_{{ch}}}{\text{/}}{{a}_{h}}$ и ${{a}_{h}}{\text{/}}{{a}_{{ch}}}$ до и после изменения средней частоты выполняются равенства:

Теперь, если при смене доминирующей гармоники для $\delta {{\psi }_{p}}$ выполнить инверсию (под которой здесь и далее будем понимать зеркальное отражение относительно оси абсцисс), то полученная в результате вариация $\delta \psi _{p}^{{inv}}$ фазу менять не будет. Значит и полюс не будет менять направление своего движения после первого этапа преобразования с учетом выполненной инверсии.

Пусть известен момент смены доминирующей гармоники, когда ${{a}_{{ch}}} \approx {{a}_{h}}$ и требуется выполнить инверсию вариации полярного угла. К вариации полярного угла $\delta {{\psi }_{p}}$ инверсию допустимо применить и не точно в момент равенства амплитуд ${{a}_{{ch}}}$ и ${{a}_{h}}$, а позднее – до момента прохождения локального экстремума (включительно) функции $\delta {{\psi }_{p}}$. Сдвиг начала инверсии при таком подходе имеет смысл, так как ее выполнение в произвольный момент времени (когда окажется, что ${{a}_{{ch}}} = {{a}_{h}}$) технически менее удобно, чем в момент прохождения локального экстремума функцией $\delta {{\psi }_{p}}$, а искажение результата будет мало. Это связано с тем, что в любой момент времени, когда ${{a}_{p}} \ne 0$ при ${{a}_{{ch}}} \to {{a}_{h}}$ выполняется равенство:

Следовательно, при ${{a}_{{ch}}} = {{a}_{h}}$ функция ${{\dot {\psi }}_{p}}$ будет постоянной всюду за исключением точек, когда ${{a}_{p}} = 0$. При ${{a}_{p}} = 0$ полярный угол ${{\psi }_{p}}$ оказывается неопределен (при прохождении ${{a}_{p}}$ через ноль его фаза скачкообразно изменится на $\pi $), а вариация частоты $\delta {{\dot {\psi }}_{p}}$ обращается в $ \pm \infty $. То есть предела у $\delta {{\dot {\psi }}_{p}}$ при ${{a}_{p}} \to 0$ и ${{a}_{{ch}}} \to {{a}_{h}}$ не существует. Но в этот момент (когда ${{a}_{p}} \to 0$ и ${{a}_{{ch}}} \to {{a}_{h}} \pm 0$) изменение фазы полярного угла можно учесть в знаке амплитуды ${{a}_{p}}$. Тогда, приняв ${{a}_{p}} \in ( - \infty ,\infty )$, пределы справа и слева окажутся равны и равенство (10) будет выполнено всюду (т.е. предельный случай совпадет с простейшим, когда ${{a}_{{ch}}} = {{a}_{h}} = {\text{const}}$).

Таким образом, при близких значениях амплитуд ${{a}_{{ch}}}$ и ${{a}_{h}}$ графики функции ${{\dot {\psi }}_{p}}$ для случаев с ${{a}_{{ch}}} > {{a}_{h}}$, $k = {{a}_{{ch}}}{\text{/}}{{a}_{h}}$ и ${{a}_{h}} > {{a}_{{ch}}}$, $k = {{a}_{h}}{\text{/}}{{a}_{{ch}}}$ будут близки друг к другу всюду за исключением окрестностей минимумов амплитуды ${{a}_{p}}$. И чем больше будут различаться значения амплитуд ${{a}_{{ch}}}$ и ${{a}_{h}}$, тем большим будет значение минимума амплитуды ${{a}_{p}}$ и шире окажутся эти окрестности. Границы этих окрестностей определяются соседними локальными экстремумами вариации $\delta {{\psi }_{p}}$ с наименьшим расстоянием между локальными минимумом и максимумом при ${{a}_{{ch}}} > {{a}_{h}}$ (или, наоборот, при ${{a}_{h}} > {{a}_{{ch}}}$), в середине которого положительная амплитуда ${{a}_{p}}$ достигает минимума (а при ${{a}_{h}} = {{a}_{{ch}}}$ амплитуда ${{a}_{p}}$ обращается в ноль). В момент прохождения локального экстремума функцией $\delta \psi _{p}^{N}$ (или $\delta \psi _{p}^{\nu }$) выполняется условие $\delta \dot {\psi }_{p}^{N} = 0$ (или $\delta \dot {\psi }_{p}^{\nu } = 0$), а момент смены доминирующей гармоники определяется условием $\delta {{\dot {\psi }}_{p}} = 0$.

Остается заметить, что идентификация рассматриваемого 18-летнего колебательного процесса слабо чувствительна к ошибке определения момента смены доминирующей гармоники (хотя на временнóй шкале она может достигать и нескольких лет). Это связано с тем, что на периоде 18 лет такие ошибки качественно не отличимы от квазидвухлетних флуктуаций. Таким образом, малой оказывается ошибка и от указанного сдвига начала инверсии для вариации $\delta \varphi $ и от погрешности определения момента равенства амплитуд чандлеровской и годичной гармоник.

Нужно заметить, что в отличие от вариации полярного угла $\delta {{\psi }_{p}}$ амплитуда ${{a}_{p}}$ не требует каких-либо особенных преобразований, а ее сглаженный график легко получить с помощью Фурье-преобразования. Так, на рис. 4а приведены исходная и сглаженная амплитуды.

Рассмотренный способ выполнения инверсии $\delta \varphi $ достаточно наглядный, но не является самым простым в реализации и может приводить к некоторым погрешностям вблизи момента смены доминирующей гармоники (хотя и к несущественным для качественного анализа). Можно предложить и более простой способ построения инверсии сглаженной вариации $\delta {{\psi }_{p}}$, который показывает корректность выполненной инверсии первым способом.

Второй способ основан на приближенной зависимости (6) вариации частоты от амплитуд чандлеровской и годичной гармоник. Как легко видеть, инверсия вариации частоты $\delta {{\dot {\psi }}_{p}}$ получается естественным образом из (6):

Тогда, после интегрирования выражения (11) получим вариацию полярного угла с учетом инверсии, выполненной столько раз, сколько было переходов от одной доминирующей гармоники к другой:

На рис. 4б приведено сравнение величины $\delta \psi _{p}^{{inv}}$, найденной двумя способами: негладкая кривая получена первым способом, а гладкая кривая – вторым способом. Недостатком второго способа является необходимость определения зависимостей амплитуд ${{a}_{{ch}}}(t)$ и ${{a}_{h}}(t)$ от времени, что требует предварительного разделения колебания земного полюса на компоненты. Последнее не может быть выполнено абсолютно точно, поэтому результат будет зависеть от определения чандлеровской и годичной гармоник (от того, какие вариации отнесены к той или иной гармонике). Этот фактор вносит больше неопределенности, чем ошибка от неучета производных амплитуд в формуле (12). Однако второй способ получения инвертированной величины $\delta \psi _{p}^{{inv}}$ более естественный и простой в описании.

4. ВАРИАЦИИ ПАРАМЕТРОВ ДВИЖЕНИЯ ЗЕМНОГО ПОЛЮСА В ПЕРИОД С 1900 г.

Вносимые ошибки в результате выполняемой инверсии согласно двум рассмотренным выше способам кардинально различны по сути. Поэтому качественное и хорошее количественное совпадения результатов получения $\delta \psi _{p}^{{inv}}$ позволяют заключить о корректности проведенных преобразований. Особенно важно совпадение результатов в окрестностях изменения доминирующей гармоники. Но поскольку неопределенность в амплитудах ${{a}_{{ch}}}(t)$ и ${{a}_{h}}(t)$ носит более глобальный характер и может влиять на результат преобразования на всем рассматриваемом интервале, то далее предпочтительнее использовать $\delta \psi _{p}^{{inv}}$, полученную первым способом.

На рис. 5 приведена траектория движения полюса после первого этапа преобразования с учетом выполненной инверсии и после вычета трендовой составляющей ($c_{x}^{1}$, $c_{y}^{1}$). Положение полюса в полученной системе задается координатами: ${{x}_{1}} = {{a}_{p}}\cos \delta \psi _{p}^{{inv}} - c_{x}^{1}$, ${{y}_{1}} = {{a}_{p}}\sin \delta \psi _{p}^{{inv}} - c_{y}^{1}$. Из рисунка видно, что полюс направления своего движения в системе (${{x}_{1}},{{y}_{1}}$) не меняет. Период обращения полюса в этой системе равен 6-летнему периоду модуляции чандлеровской и годичной гармоник, который подвержен небольшим изменениям. Полученное колебание содержит одну основную частоту, поэтому на втором этапе преобразование осуществляется простейшим образом в полярной системе, аналогично первому этапу. Для этого координаты полюса представим в виде ${{x}_{1}} = b\cos {{\varphi }^{{inv}}}$, ${{y}_{1}} = b\sin {{\varphi }^{{inv}}}$. Тогда для центрированной 6-летней периодической траектории определим величину $b$ и вариацию полярного угла $\delta {{\varphi }^{{inv}}}$. В отличие от первого этапа вариацию $\delta {{\varphi }^{{inv}}}$ определить легко, так как после первого этапа с учетом выполненной инверсии не происходят ни смена доминирующей гармоники, ни направления движения полюса.

Далее, на интервалах инверсий первого этапа преобразования следует выполнить обратную инверсию вариации полярного угла $\delta {{\varphi }^{{inv}}}$, так как направление движения полюса было изменено. В результате получим вариацию $\delta \varphi $, состоящую из вариаций полярных углов на участках с различными доминирующими гармониками. Обратная инверсия выполняется так, чтобы график был непрерывным и не содержал скачков. Такая процедура носит отчасти формальный характер, так как может изменить тренд составной вариации $\delta \varphi $, но позволяет построить непрерывный график функции $\delta \varphi $ для нескольких колебательных режимов. Тренд долгопериодического (с периодами вдвое большими 18-летнего периода) и векового характера в данном случае на результат не оказывает влияния, так как подлежит удалению.

Составную вариацию $\delta \varphi $ можно получить и, непосредственно рассматривая колебательные режимы по отдельности, если их длительности для этого достаточны. Но короткие интервалы с доминирующей годичной гармоникой уверенно (без дополнительных пояснений) этого сделать не позволяют. Поэтому в данной работе была выбрана стратегия преобразования не частей ряда с различными режимами колебаний, а целого ряда. Хотя рассмотренный способ инверсии, основанный на выражении (12), позволяет заключить, что преобразование ряда можно выполнить частями, так как это будет эквивалентно первому способу инверсии.

На рис. 6 даны амплитудные спектры построенных рядов $b$, $\delta \varphi $. На их основании можно заключить о наличии колебаний с частотой, близкой к частоте прецессии орбиты Луны в исследуемых параметрах. Изменение границ интервала данных приводит к небольшой вариации этой частоты (около 0.053–0.055 циклов в год) в амплитудном спектре. Однако, если временнóй интервал данных выбрать кратным периоду 18.6 лет (например, сдвинув конец интервала на 5 лет), то, как показано на рис. 6, частота этого пика в амплитудном спектре совпадет с частотой прецессии лунной орбиты, равной 0.05373 цикла в год [20]. Как показано далее, фаза колебаний в параметре $b$ отличается на $\pi {\text{/}}2$ от фазы соответствующих колебаний в полярном угле $\delta \varphi $. Можно заметить, что аналогично и фаза колебаний угла I наклона лунной орбиты к экватору Земли отличается на $\pi {\text{/}}2$ от фазы угла $\theta $ отклонения вдоль экватора точки пересечения лунной орбиты с экватором.

Для сравнения полученных величин $b$, $\delta \varphi $ с параметрами I, $\theta $ ориентации орбиты Луны по отношению к экватору Земли в них были отфильтрованы колебания из низкочастотных спектральных областей (расположенных левее вертикальных сплошных линий, отмеченных на рис. 6).

Сравнение колебаний амплитуды $b$ после фильтрации и сглаживания с колебаниями угла наклона I плоскости лунной орбиты к экватору показано на рис. 7. Одновременно с амплитудой $b$ на графике приведено ее сглаженное значение, а также построена стационарная гармоника с частотой 0.05371 циклов в год, выделенная из амплитудного спектра построенного ряда $b$. Колебание угла I было вычислено, используя лунные эфемериды [21]. Штриховые вертикальные линии, проведенные между двумя графиками, показывают совпадение экстремумов колебаний $b$ и I, в особенности хорошее совпадение фаз стационарной гармоники, выделенной из спектра $b$ и колебаний угла I.

Вариации угла $\delta \varphi $ также содержат значимые вариации с частотой, близкой к частоте прецессии орбиты Луны. На рис. 8 приведено сравнение вариаций $\delta \varphi $ и колебаний угла $\theta $ вдоль земного экватора точки пересечения экватора с лунной орбитой, вычисленного с использованием лунных эфемерид [21]. Также на графике приведено сглаженное значение $\delta \varphi $. Для наглядной иллюстрации применимости рассмотренного преобразования к различным доступным рядам координат полюса ряд $\delta \varphi $ построен с использованием составного ряда координат полюса. Он состоит из трех интервалов с данными измерений различной точности (1890–1945; 1945–1962; 1962–2016). Сглаживание применялось только к первому интервалу, т.е. для ряда C01 до 1945 г. Границы интервалов, соответствующих разным рядам, хорошо различимы на графике. В частности, сильные флуктуации, присутствующие в средней части графика $\delta \varphi $, обусловлены низкой точностью измерений положения земного полюса. Однако это не является препятствием ни выполнению преобразования, ни выделению рассматриваемого колебания. В первой половине графика $\delta \varphi $ (левее зашумленной его части) ряд строился, используя сглаженные данные C01 координат полюса, аналогично построению ряда амплитуды $b$. На втором и третьем временн${\text{ы}}\prime $х интервалах использовались несглаженные данные рядов C01 и C04 соответственно.

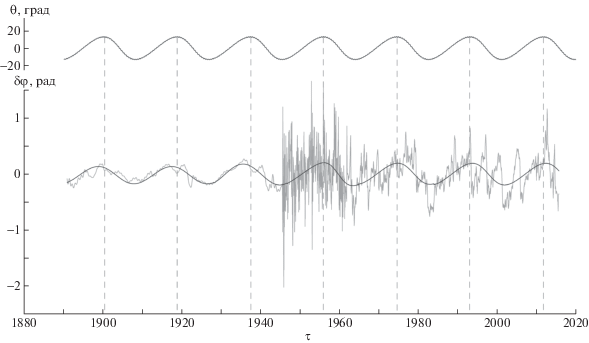
Рисунок 8 показывает, что найденное колебание удается выделить из различных рядов данных о движении полюса, как сглаженных, так и несглаженных. Это позволяет уверенно говорить о наличии колебательного процесса земного полюса, синхронизированного с прецессионным движением орбиты Луны, иными словами – о наличии долгопериодического лунного возмущения, влияющего на колебания земного полюса.

5. ЗАКЛЮЧЕНИЕ

В результате обработки данных наблюдений и измерений рядов C01 и C04 МСВЗ с помощью предложенного в работе [16] подхода установлено наличие 18-летней цикличности в движении земного полюса на 120-летнем интервале времени. Используя основные кинематические свойства движения полюса, рассмотрена модификация преобразования, которая может применяться на длительном интервале времени с учетом смены доминирующей гармоники. Выполненное преобразование зависит только от средних параметров движения земного полюса и не зависит явно от времени.

Показана синфазность 18-летних колебаний координат полюса и колебаний параметров ориентации плоскости лунной орбиты. Найденный квазистационарный колебательный процесс обладает стабильными частотой и фазой, которые совпадают с частотой и фазой колебаний угла наклона плоскости лунной орбиты к экватору Земли. Точнее говоря, в результате преобразования полярный радиус полюса совершает колебания, синфазные с колебаниями угла наклона плоскости лунной орбиты к земному экватору, а колебания его полярного угла происходят синфазно с отклонением вдоль экватора точки пересечения лунной орбиты с экватором.

Расширенность пиков, соответствующих найденной 18-летней цикличности в амплитудном спектре исследуемых параметров, указывает на вовлеченность в механизм возбуждения этих колебаний геофизических сред. Таким образом, можно предположить, что найденный колебательный процесс обусловлен астрономическими и геофизическими факторами в совокупности.