Астрономический журнал, 2022, T. 99, № 11, стр. 979-990

1. ВВЕДЕНИЕ

В последние десятилетия было открыто множество экзопланет, относящихся к классу горячих юпитеров – планет с массой порядка массы Юпитера и имеющих большую полуось орбиты менее 0.1 а.е. Примерно половина из тех горячих юпитеров, для которых определена величина эксцентриситета орбиты, имеют эллиптичные орбиты, при этом величина эксцентриситета может, в некоторых случаях, превышать 0.5 (по данным сайта http://exoplanet.eu). Столь явное разделение горячих юпитеров на две группы (с нулевым и ненулевым эксцентриситетом) ставит множество вопросов как о механизмах их образования, так и о физических различиях между двумя этими группами. Для получения ответов на эти вопросы необходимо детальное исследование горячих юпитеров, имеющих как нулевой, так и отличный от нуля эксцентриситет. В частности, важным является вопрос о влиянии эксцентриситета орбиты на структуру и параметры атмосфер и протяженных оболочек горячих юпитеров, так как внешние части атмосфер и вещество оболочек в значительной мере определяют наблюдательные проявления этих планет.

Газовые оболочки горячих юпитеров могут достигать больших размеров и простираться далеко за пределы полостей Роша планет [1–6]. В работах [7, 8] было показано, что (в отсутствие магнитного поля) оболочка горячего юпитера может относиться к одному из трех типов: быть замкнутой, квазизамкнутой и открытой, в зависимости от положения точки лобового столкновения, в которой динамическое давление звездного ветра уравновешивает давление атмосферы планеты. Если эта точка находится внутри полости Роша планеты, оболочка является замкнутой и лишь небольшое количество массы теряется атмосферой, образуя шлейф за планетой. В случае, когда на границе полости Роша планеты давление атмосферы превышает динамическое давление ветра, образуются истечения из окрестностей точек L₁ и L₂. Далее, в зависимости от параметров системы, может реализовываться либо случай квазизамкнутой оболочки, когда поток из L₁ может быть остановлен динамическим давлением звездного ветра за пределами полости Роша, либо, в случае открытой оболочки, вещество атмосферы не может быть остановлено и формирует аккреционный диск вокруг звезды [9]. Как было показано в работе [10], общий темп потери массы в случае квазизамкнутой оболочки сравнительно невелик, так как существенная часть массы, покинувшей планету через окрестность точки L₁, возвращается обратно в атмосферу, в то время, как интенсивной потере массы через окрестность точки L₂ мешает вихревое течение, устанавливающееся за планетой. Позднее, в работах [11–13] было показано, что наличие магнитного поля существенно не меняет картины течения, приводя, в основном, к сдвигу диапазона параметров, при котором оболочка может быть квазизамкнутой.

Результаты, полученные в работах [7–13], относятся к горячим юпитерам с круговыми орбитами. В рамках данной работы представлена газодинамическая численная модель, адаптированная для моделирования течения в оболочках горячих юпитеров, движущихся по эллиптическим орбитам. Можно предположить, что при движении по эллиптической орбите темп потери массы атмосферой горячего юпитера будет переменным, достигая максимума вблизи точки периастра и минимума в апоастре. На рис. 1 показана зависимость расстояния от центра масс планеты до ${\text{L}}_{1}^{*}$ – аналога точки L₁ в модели с эллиптической орбитой для планеты с параметрами HD 209458b, аналогичными тем, что использовались в работе [8] (см. также описание модели в разде-ле 2), при эксцентриситете $e = 0.2$. Положение ${\text{L}}_{1}^{*}$ может быть определено как точка, лежащая между центрами масс звезды и планеты, где в данный момент уравновешиваются силы, связанные с гравитацией и (радиальными) центробежными силами в системе координат, связанной с планетой. В отличие от классической внутренней точки Лагранжа L₁, в ${\text{L}}_{1}^{*}$ уравновешены не все потенциальные силы – сила инерции, связанная с угловым ускорением системы, остается не скомпенсированной. Как видно из рис. 1, ${\text{L}}_{1}^{*}$ перемещается в пределах $ \sim {\kern 1pt} 1{{R}_{{{\text{pl}}}}}$, расстояние до нее от центра масс планеты достигает минимума в $ \sim {\kern 1pt} 1.3{{R}_{{{\text{pl}}}}}$ на фазе 0.5 и максимума $ \sim {\kern 1pt} 2.3{{R}_{{{\text{pl}}}}}$ на фазе 0. В модели с круговой орбитой при том же размере большой полуоси точка L₁ находилась на расстоянии $ \sim {\kern 1pt} 1.75{{R}_{{{\text{pl}}}}}$ (показана штриховой линией на рис. 1). Точка ${\text{L}}_{1}^{*}$ находится ближе, чем $1.75{{R}_{{{\text{pl}}}}}$ на фазах 0.3–0.7, т.е. на протяжении половины орбитального периода. Однако на темп потери массы атмосферой, кроме приливных сил, влияет множество параметров, связанных как с динамическим давлением звездного ветра, так и с нестационарными процессами в самой атмосфере. Для получения оценки темпа потери массы и возможных наблюдательных проявлений горячего юпитера с эксцентричной орбитой необходимо проведение трехмерного численного моделирования.

В разделе 2 статьи приведено описание модели горячего юпитера с эллиптической орбитой, в разделе 3 приведены результаты расчета для планеты с параметрами HD 209458b и эксцентриситетом орбиты 0.2, проведенного в рамках данной модели, а раздел 4 содержит основные выводы статьи.

2. ЧИСЛЕННАЯ МОДЕЛЬ

Движение планеты по эллиптической орбите описывается, в идеальном случае, уравнениями Кеплера. В рамках нашей модели мы будем считать, что вся масса планеты сосредоточена в одной точке и что ее масса пренебрежимо мала по сравнению с массой родительской звезды. К сожалению, уравнения, определяющие положение, скорость и ускорение планеты, не могут быть записаны явным образом как функции от времени. Чтобы получить нужные нам параметры в каждый момент времени, мы итерационным методом решаем уравнение Кеплера:

где $E$ – эксцентрическая аномалия, параметр, значение которого мы ищем, $e$ – эксцентриситет орбиты, а $M = t{\text{/}}{{P}_{{{\text{orb}}}}} + 0.5$ – средняя аномалия, равная времени $t$, выраженном в орбитальных периодах системы ${{P}_{{{\text{orb}}}}} = 2\pi {\text{/}}\sqrt {G{{M}_{*}}{\text{/}}{{A}^{3}}} $, $G$ – гравитационная постоянная, ${{M}_{*}}$ – масса звезды, $A$ – большая полуось орбиты системы. Смещение 0.5 добавляется к средней аномалии, чтобы момент времени $t = 0$ соответствовал прохождению планетой точки апоастра. После того, как вычислена величина $E$, остальные параметры могут быть найдены аналитически. Расстояние между центрами масс звезды и планеты $r$: угол (равный 0 при $t = 0$) между большой полуосью и линией, соединяющей центры масс звезды и планеты: мгновенная угловая скорость планеты: где мгновенная радиальная скорость планеты: мгновенное радиальное ускорение планеты: и мгновенное угловое ускорение планеты:

Зная эти параметры, мы можем перейти в систему координат, в центре которой будет находиться планета, а сама система координат будет поворачиваться таким образом, чтобы звезда всегда находилась слева от планеты, имея декартовы координаты $( - r,0,0)$. Такая система координат будет неинерциальной, так как сама планета движется с ускорением, более того, система координат будет вращаться с переменной угловой скоростью, чтобы поддерживать постоянным направление на звезду. В предельном случае, когда $e = 0$, эта система координат переходит в классическую, где определяется потенциал Роша.

В выбранной нами системе координат возникают дополнительные ускорения, связанные с силами инерции (см. Приложение):

где первый член отвечает за центробежное ускорение, аналогично случаю кругового движения с мгновенной угловой скоростью $\Omega $, второй член соответствует радиальному ускорению системы отсчета, третий член связан с угловым ускорением системы отсчета, а четвертый является аналогом силы Кориолиса, связанной с радиальным ускорением системы отсчета. В приводимых в этой статье расчетах четвертый член не учитывался, однако, это не повлияло существенно на результат, так как его вклад в общую сумму сил составляет менее процента. Также в системе присутствует ускорение, связанное с классической силой Кориолиса: где ${\mathbf{v}}$ – скорость частицы.

Используемый в данной работе численный код является модификацией трехмерного кода, описанного в работе [8]. В коде решается стандартная система уравнений идеальной газовой динамики:

Здесь $\rho $ – плотность, ${\mathbf{v}}$ – скорость, ${\mathbf{f}}$ – удельная внешняя сила, являющаяся суммой ${{{\mathbf{a}}}_{i}}$, ${{{\mathbf{a}}}_{c}}$ а также силы гравитационного притяжения звезды и планеты, $\varepsilon $ – удельная внутренняя энергия. Вещество может рассматриваться как идеальный газ, поэтому систему уравнений можно замкнуть с помощью уравнения состояния:

где $\gamma = 5{\text{/}}3$ – показатель адиабаты.

Вычисления проводятся на декартовой сетке с разрешением $472 \times 472 \times 250$ ячеек, сгущающейся к центру планеты. Общий размер сетки составлял $(42 \times 42 \times 10){\kern 1pt} {{R}_{{{\text{pl}}}}}$ по осям ${\mathbf{x}}$, ${\mathbf{y}}$ и ${\mathbf{z}}$ соответственно. В процессе расчета ось ${\mathbf{x}}$ всегда соединяет центры масс планеты и звезды, ось ${\mathbf{z}}$ направлена перпендикулярно экваториальной плоскости системы и коллинеарна вектору угловой скорости системы $\Omega $, а ось ${\mathbf{y}}$ дополняет тройку векторов $({\mathbf{x}},{\mathbf{y}},{\mathbf{z}})$ до правой.

В ячейках, находящихся на границах сетки, искусственно поддерживаются условия, соответствующие параметрам звездного ветра в этих точках. Так как сетка в процессе расчета меняет свое положение относительно звезды, значения в граничных ячейках также меняются на каждом шаге вычислений. Плотность ветра зависит от расстояния как $1{\text{/}}{{r}^{2}}$, его радиальная скорость остается постоянной, а тангенциальная скорость в выбранной системе отсчета равна $\Omega \cdot r$, где $r$ – расстояние от центра масс звезды до центра ячейки. Такой подход оправдан, так как для типичных горячих юпитеров скорость набегающего потока всегда будет сверхзвуковой (см., напр., [14]). В центре счетной области, в точке с координатами $(0,0,0)$, находится центр масс планеты. В сферическом слое, на расстояниях $(0.56{\kern 1pt} - {\kern 1pt} 1.0){{R}_{{{\text{pl}}}}}$, где ${{R}_{{{\text{pl}}}}}$ – фотометрический радиус моделируемой планеты, искусственно поддерживается распределение, соответствующее равновесной экспоненциальной атмосфере:

где $\rho $ – плотность атмосферы на радиусе $r$, ${{\rho }_{{{\text{atm}}}}}$ – плотность атмосферы на фотометрическом радиусе ${{R}_{{{\text{pl}}}}}$, ${{R}_{{{\text{gas}}}}}$ и ${{T}_{{{\text{atm}}}}}$ – газовая постоянная и температура атмосферы соответственно. В момент начала счета экспоненциальное распределение, соответствующее равновесной изотермической атмосфере, задавалось до радиуса $3{\kern 1pt} {{R}_{{{\text{pl}}}}}$, вся остальная счетная область была заполнена параметрами, соответствующими звездному ветру.

Ранее, в работе [8], нами было проведено численное моделирование газодинамики оболочки горячего юпитера с параметрами HD 209458b. Чтобы провести сравнение с ранее полученными результатами, в данной работе параметры планеты были взяты аналогичными HD 209458b, однако с эксцентриситетом орбиты $e = 0.2$. Массы планеты и звезды полагались равными M_pl = = $0.69{{M}_{{{\text{jup}}}}}$ и ${{M}_{*}} = 1.1\;{{M}_{ \odot }}$. Большая полуось была задана равной $A = 10.2\;{{R}_{ \odot }}$. Фотометрический радиус планеты ${{R}_{{{\text{pl}}}}}$ был задан равным $1.38{{R}_{{{\text{jup}}}}}$. Концентрация и температура газа на фотометрическом радиусе взяты равными $n = {{10}^{{11}}}$ и $T = 7500$ K, аналогично модели 3 из работы [8]. Радиальная скорость, температура и концентрация вещества ветра также были взяты аналогично использованным в работе [8]: ${{{v}}_{w}} = 100$ км/с, $T = 7.3 \times {{10}^{5}}$ K, $n = 1.4 \times {{10}^{4}}$.

Вычисления проводились с использованием 324 процессорных ядер, между которыми была распределена вычислительная сетка. Счет проводился до достижения 4.0 орбитальных периодов.

3. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

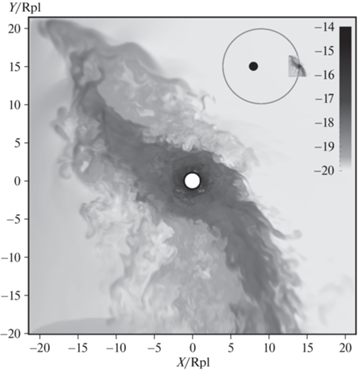
Квазистационарное течение установилось начиная, приблизительно, с $t = 2.5{{P}_{{{\text{orb}}}}}$, так что рассмотрим динамику течения на протяжении одного орбитального периода $t = (3.0{\kern 1pt} - {\kern 1pt} 4.0){{P}_{{{\text{orb}}}}}$. На рис. 2 показано распределение плотности в логарифмическом масштабе и вектора скорости в экваториальной плоскости системы в момент прохождения планетой апоастра при $t = 3.0{{P}_{{{\text{orb}}}}}$. На рисунке видна оболочка неправильной формы вокруг планеты, имеющая выступ в направлении звезды (звезда находится слева от планеты, за пределами показанной области). Этот выступ, имеющий протяженность примерно $10{{R}_{{{\text{pl}}}}}$, является остатком выброса, произошедшего на предыдущем орбитальном периоде. Перед ним виды остатки выброса, разрушенного в результате взаимодействия со звездным ветром, сносимые ветром в сторону планеты. В направлении, противоположном направлению на звезду, видно истечение, аналогичное истечению из окрестности точки L₂, получаемому в решениях с круговой орбитой. Вокруг планеты видна область с радиусом порядка $5{{R}_{{{\text{pl}}}}}$, заполненная сравнительно плотным веществом, где течение сильно турбулизовано.

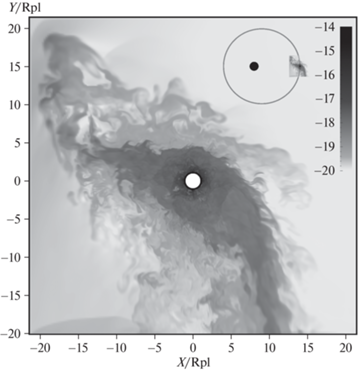
Для сравнения, на рис. 3 показано решение для аналогичного момента времени ($t = 3.0{{P}_{{{\text{orb}}}}}$), полученное в модели с такими же параметрами, но при нулевом эксцентриситете орбиты планеты. Здесь также имеется область вокруг планеты, заполненная турбулизованным веществом, но несколько меньшего размера, с радиусом $ \sim {\kern 1pt} 3{{R}_{{{\text{pl}}}}}$, а также существенно более выраженное истечение вещества через окрестность точки L₁.

На рис. 4 показано решение для момента времени $t = 3.25{{P}_{{{\text{orb}}}}}$. Планета находится на половине пути к периастру, и в окрестности точки L₁ начинается новое истечение, длина которого уже достигает $ \sim {\kern 1pt} 25{{R}_{{{\text{pl}}}}}$. Перед истечением видна отошедшая ударная волна. Само истечение существенно шире и плотнее, чем в случае круговой орбиты (см. рис. 3), оно также является неоднородным, в нем видны сгустки более плотного вещества. Истечение из окрестности точки L₂ также существенно более интенсивное, чем в апоастре, и более интенсивное, чем в случае круговой орбиты.

На рис. 5 показано решение для момента времени $t = 3.5{{P}_{{{\text{orb}}}}}$. Истечение из окрестности L₁ уже достигло края счетной области, вытеснив отошедшую ударную волну. Как видим, в этом решении вещество не может быть остановлено динамическим давлением звездного ветра, как это происходило в случае круговой орбиты, и вещество атмосферы покидает планету, формируя тороидальную оболочку вокруг звезды. Истечения из окрестностей точек L₁ и L₂ более плотные и узкие, чем в момент времени $t = 3.25{{P}_{{{\text{orb}}}}}$. Также уменьшилась область вокруг планеты, заполненная плотным веществом. Перед планетой отчетливо видна отошедшая ударная волна, которая до этого была менее выражена, так как планета находилась за отошедшей ударной волной от струи, а также плотность звездного ветра в окрестности планеты была меньше.

На рис. 6 показано решение для момента времени $t = 3.75{{P}_{{{\text{orb}}}}}$. Планета находится на пути к апоастру, и истечение из точки L₁ начинает разрушаться. При этом в окрестности L₁ остается выступ, который имеет примерно такую же протяженность, как в момент времени $t = 3.0{{P}_{{{\text{orb}}}}}$ – порядка $10{{R}_{{{\text{pl}}}}}$. Истечение из окрестности L₂ в этот момент как бы “отстает” от планеты, в выбранной системе координат его положение меняется, в нем появляются разрывы. Перед планетой еще видна отошедшая ударная волна.

На рис. 7 показано решение для момента времени $t = 4.0{{P}_{{{\text{orb}}}}}$. В целом течение в этот момент аналогично тому, что было показано на рис. 2, что говорит о том, что решение близко к квазистационарному. Анимация для данного решения доступна по ссылке: https://bit.ly/3PRmIIq.

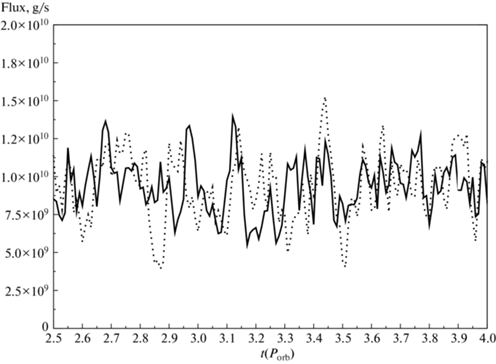
На рис. 8 показана зависимость темпа потери массы планетой (поток через сферу с радиусом $3{\kern 1pt} {{R}_{{{\text{pl}}}}}$ вокруг центра планеты) от времени для периода $(2.5{\kern 1pt} - {\kern 1pt} 3){\kern 1pt} {{P}_{{{\text{orb}}}}}$ от начала счета для решений с эллиптической и круговой орбитами. Как видно из рисунка, в целом поток практически не отличается для этих двух решений. Выбранный радиус находится за пределами полости Роша планеты, а также его эквивалента для эллиптической орбиты. Тем не менее, как показывают результаты расчета, в этой области в обоих случаях наблюдается более-менее стационарное облако газа, течение в котором в большей степени определяется газодинамическими процессами, а не гравитацией. Средний темп потери массы в обоих случаях составляет ~10¹⁰ г/с.

На рис. 9 показан аналогичный поток массы через сферу с радиусом $7{\kern 1pt} {{R}_{{{\text{pl}}}}}$. К сожалению, счетная область ограничена $ \pm 5{\kern 1pt} {{R}_{{{\text{pl}}}}}$ по оси ${\mathbf{z}}$, что не позволяет определить поток точно, однако, показанная величина дает хорошее представление о влиянии эксцентриситета орбиты на интенсивность выбросов вещества. Как и предполагалось, наибольшая потеря массы ($ \sim {\kern 1pt} 1.2 \times {{10}^{{10}}}$ г/с) наблюдается вблизи периастра, а наименьший ($\sim {\kern 1pt} 7.5 \times {{10}^{9}}$ г/с – в апоастре, т.е. меняется приблизительно в 1.5 раза в течение орбитального периода. При этом, как показывает анализ решения, темп потери массы через окрестности L₁ и L₂ примерно одинаков.

4. ВЫВОДЫ

Нами была разработана трехмерная численная модель, позволяющая проводить газодинамическое моделирование течения в окрестности горячих юпитеров с эллиптическими орбитами. Как правило, подобное моделирование проводится в лабораторной системе координат, где компоненты двойной системы движутся по сетке (см., напр., работы [15–17]). Однако при моделировании оболочек горячих юпитеров такой подход не позволяет добиться нужной точности при разумных вычислительных затратах, так как счетная область должна включать в себя, как минимум, всю орбиту планеты; кроме того, при этом невозможно обеспечить сгущение сетки вблизи планеты, так как планета движется. Нами был выбран более сложный подход – численное моделирование в неинерциальной системе координат, в которой планета является неподвижной, а ось ${\mathbf{x}}$ всегда совпадает с линией, соединяющей центры масс звезды и планеты. Это потребовало учета дополнительных сил, связанных с неинерциальностью системы координат – сил инерции и силы Кориолиса, переменных во времени. Плюсами такого подхода являются более высокая точность задания граничных условий для атмосферы планеты, так как ее центр не перемещается по сетке, возможность использования неоднородных сеток, сгущающихся к центру планеты, а также возможность использования сравнительно небольшой сетки, охватывающей только интересующую нас область вблизи горячего юпитера.

При помощи разработанной модели был проведен расчет, для которого были взяты параметры, ранее использовавшиеся нами для моделирования оболочки планеты HD 209458b в работе [8], модель с температурой атмосферы 7500 K. Для тестового расчета был задан эксцентриситет орбиты $e = 0.2$. Полученная картина течения существенно отличается от результатов моделирования с нулевым эксцентриситетом орбиты. Прежде всего, что ожидаемо, течение становится нестационарным, демонстрируя выбросы вещества при прохождении точки периастра. В модели с круговой орбитой атмосфера являлась квазизамкнутой, истечение из окрестности точки L₁ останавливалось за пределами полости Роша планеты за счет динамического давления звездного ветра, в то время как в случае эллиптической орбиты истечения периодически преодолевали давление ветра и оболочка становилась открытой.

Интересным результатом численного моделирования оказалось то, что темп потери массы планетой в случае эллиптической орбиты оказался приблизительно равным темпу потери массы для круговой орбиты. Это можно объяснить тем, что планета, находясь достаточно глубоко внутри полости Роша (или ее аналога в случае эллиптической орбиты), подвержена приливному воздействию в меньшей степени, чем газодинамическим эффектам, и темп потери массы атмосферой определяется турбулентной вязкостью. При этом, как показали расчеты, вокруг планеты образуется облако газа существенно большего размера, чем ее полость Роша, оно имеет радиус $ \sim {\kern 1pt} (3{\kern 1pt} - {\kern 1pt} 4){\kern 1pt} {{R}_{{{\text{pl}}}}}$. Это облако не является полностью стационарным, но сохраняется на протяжении всего орбитального периода. При движении к апоастру вещество накапливается в этом облаке, а при движении к периастру оно теряет вещество. На рис. 10 показано изменение массы газа в сферическом слое между $1{\kern 1pt} {{R}_{{{\text{pl}}}}}$ и $4{\kern 1pt} {{R}_{{{\text{pl}}}}}$ на протяжении одного орбитального периода. Как видно из графика, вещество накапливается в этой области на протяжении большей части орбитального периода (с фазы ~0.7 до фазы ~0.5 следующего орбитального периода), после чего, довольно быстро (на фазах ~0.5–0.7) все накопленное вещество сбрасывается. Сбрасывается сравнительно небольшая доля массы (менее одного процента от всей массы слоя), однако при этом поток в выбросах через окрестности точек L₁ и L₂ меняется приблизительно в 1.5 раза между максимумом в периастре и минимумом в апоастре. Такой резкий сброс связан, вероятно, с нарушением равновесия в оболочке при прохождении периастра.

В целом, по результатам моделирования, следует отметить, что эллиптичность орбиты существенным образом влияет на картину течения в оболочке горячего юпитера. При заданных в работе параметрах наблюдается периодическое переключение режима течения между открытой и квазизамкнутой типами оболочки. Это влечет существенное изменение формы и размера оболочки в разных фазах, что может повлиять на наблюдательные проявления планеты.