1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 99, № 5, 2022

Астрономический журнал, 2022, T. 99, № 5, стр. 417-427

Изменения орбитального периода затменно-двойной системы W Del

А. И. Халиуллина *

Московский государственный университет им. М.В. Ломоносова, Государственный Астрономический институт им. П.К. Штернберга
Москва, Россия

* E-mail: hfh@sai.msu.ru

Поступила в редакцию 12.12.2021
После доработки 07.01.2022
Принята к публикации 24.01.2022

Полный текст (PDF)

Аннотация

Проведен анализ изменений орбитального периода затменно-двойной системы W Del. Показано, что изменения периода с почти одинаковой точностью можно представить либо суперпозицией двух циклических изменений, либо суперпозицией векового увеличения периода и двух циклических изменений. Вероятнее всего, циклические изменения орбитального периода W Del как в случае представления моментов минимумов в виде суммы линейных элементов и двух периодических колебаний, так и в случае их представления в виде суммы квадратичных элементов и двух периодических колебаний являются следствием магнитной активности вторичного компонента. Вековое увеличение периода, которое получается в случае квадратичного представления, можно объяснить обменом веществом между компонентами.

Ключевые слова: двойные звезды, затменные звезды, отдельные – W Del

1. ВВЕДЕНИЕ

Переменноcть звезды W Del (BD +17 4367, V = = 9.69m, P = 4.806d) открыла мисс Уэллс из фотографических наблюдений [1]. Пикеринг [2] построил первую (визуальную) кривую блеска и определил фотометрические элементы орбиты. В работах [3, 4] были построены кривые блеска в главном минимуме, как по визуальным, так и по фотографическим наблюдениям. Главный минимум оказался очень глубоким и показывал полное затмение. Вторичный минимум в этих наблюдениях не был зафиксирован. Полные фотоэлектрические кривые блеска W Del в фотометрических системах B и V были получены в работе [5]. На этих кривых блеска уже виден вторичный минимум на фазе 0.5. Фотометрические элементы орбиты W Del определялись в работах [5–10]. Кривая лучевых скоростей для главного компонента была получена в работе [11], из нее получалось, что орбита системы эллиптическая с эксцентриситетом е = 0.20. Спектр главного компонента был определен как B9 или А0. Позднее в работе [12] для него было получено значение В9.5V. Cпектр вторичного компонента в работе [11] оценен как G5, что согласуется и с фотометрическими наблюдениями. Эксцентриситет, полученный из кривой лучевых скоростей, противоречит фотометрическим данным. Однако в работе [13], этот эксцентриситет был подтвержден. Все дело в асимметричности кривой лучевых скоростей, которая может быть вызвана газовыми потоками. По этой причине эксцентриситеты, полученные из кривых лучевых скоростей, часто оказываются ложными. В этом вопросе лучше полагаться на фотометрические наблюдения.

Еще в работе [2] при построении кривой блеска W Del было отмечено, что наблюдения указывают на небольшое изменение периода. Расселл и др. [4], сравнивая фотографические и визуальные наблюдения W Del, полученные в разные годы, также заметили, что период меняется. Цесевич [14] отметил, что диаграмма О – С имеет, по-видимому, циклический характер. Плавец [15] провел подробное исследование изменений периода W Del с использованием имевшихся к тому времени данных. Он представил эти изменения суммой линейных элементов и периодического члена с периодом 50.9 года и пришел к выводу, что для объяснения циклических изменений периода не подходят ни апсидальное движение, ни третье тело. Позже он вернулся к этому вопросу и предположил, что апсидальное движение все-таки может иметь место, однако для этого он постулировал существование небольшого эксцентриситета [16]. Крайнер [17] представил изменения периода W Del суммой квадратичных элементов и синусоидального члена с периодом ∼50 лет. В работе [18] было показано, что кривую О – С после исключения квадратичного члена можно описать двумя периодическими кривыми. Представленный в этой работе график показывает хорошее совпадение теоретической кривой с наблюдениями. Авторы усомнились в реальности существования двух дополнительных тел в системе на основании слишком больших значений их масс. Однако бо́льшие сомнения вызывают близкие значения их периодов. Альтернативные причины таких изменений периода в этой работе не рассматривались. В работе [19] изменения периода W Del были представлены суммой квадратичных элементов и одного синусоидального члена с периодом 53.4 года. Из рисунка, приведенного в этой статье, видно, что данное представление плохо удовлетворяет наблюдениям. Рассмотрев разные возможные причины циклических изменений периода, автор пришел к выводу, что они могут быть следствием магнитной активности вторичного компонента (G5).

В настоящей работе были использованы наблюдения от JD = 2412002 до JD = 2458664, т.е. в интервале 46 662 сут или 127.8 года. Этот диапазон намного шире, чем в работах [14–17], ненамного шире, чем в работе [18] и мало отличается от диапазона наблюдений, использованных в работе [19]. В работах [15, 17, 19] авторы представляли изменения орбитального периода суммой векового увеличения и только одного циклического члена, для которого в этих работах получены близкие по величине периоды. В работе [18] остатки после исключения параболы были представлены суммой двух световых уравнений с периодами 58.7 и 36.8 года. Возможность представления моментов минимумов W Del в виде суммы линейных элементов и двух периодических колебаний никем не рассматривалась.

2. ИЗМЕНЕНИЯ СО ВРЕМЕНЕМ ОРБИТАЛЬНОГО ПЕРИОДА W DEL

Для исследования изменений периода затменно-двойной системы W Del были использованы моменты минимумов из базы данных B.R.N.O. [20]. Всего имеется 234 момента главного минимума: 179 визуальных, 34 фотографических и 21 из фотоэлектрических и ПЗС-наблюдений. На рис. 1 приведены отклонения (O – C)1 наблюдаемых (О) моментов минимумов W Del от вычисленных (C) с линейными элементами, полученными методом наименьших квадратов с использованием всех имеющихся моментов главного минимума:

(1)
$\begin{gathered} C \equiv {\text{HJD}}({\text{Min}}\,{\text{I}}) = 2\,443\,328.557(4) + \\ + \;4.8060693{{(12)}^{{\text{d}}}}T, \\ \end{gathered} $
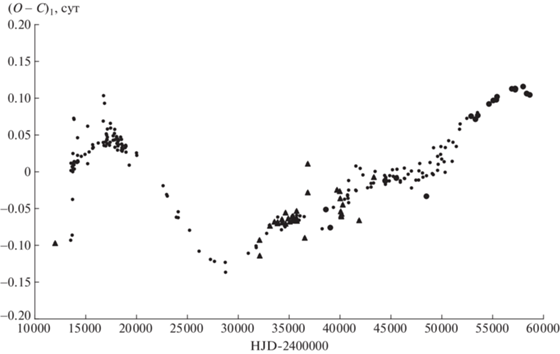
где T – эпоха наблюдения. На этом рисунке фотоэлектрические наблюдения представлены большими точками, визуальные – маленькими точками и фотографические – треугольниками. Из рисунка видно, что существуют некие долговременные изменения периода, на которые накладываются периодические или квазипериодические колебания. Похожая диаграмма О – С была получена для RT Per, и было показано, что изменения периода этой системы с почти одинаковой точностью можно представить либо суперпозицией двух циклических изменений, либо суперпозицией векового увеличения периода и двух циклических изменений [21]. Для W Del также были рассмотрены два возможных представления моментов минимумов.

Рис. 1.

Отклонения (O – C)1 наблюдаемых моментов минимумов W Del от вычисленных с линейными элементами (1). Фотографические наблюдения представлены в виде треугольников, визуальные – маленькими точками, фотоэлектрические и ПЗС – большими точками.

2.1. Линейные элементы

Отклонения наблюдаемых моментов минимумов от теоретических, вычисленных с линейными элементами, были представлены суперпозицией двух световых уравнений. Параметры световых уравнений определялись методом перебора в области их возможных значений. Одновременно (тоже перебором) уточнялись линейные элементы. Поиск подходящих световых уравнений осуществлялся методом последовательных приближений, подробно описанным в работе [21]. В результате изменения орбитального периода W Del были представлены в виде:

(2)
$\begin{gathered} {\text{HJD}}({\text{Min}}\,{\text{I}}) = 2\,443\,328.575(1) + \\ + \;4.8060840{{(1)}^{{\text{d}}}}T + LTE1 + LTE2, \\ \end{gathered} $
где выражения для световых уравнений LTE1 и LTE2 имеют вид [22]:
(3)
$LTE = ({{a}_{{\text{i}}}}\sin {{i}_{{\text{i}}}}{\text{/}}c)(1--{{e}_{{\text{i}}}}\cos E)\sin ({v} + {{\omega }_{{\text{i}}}}).$
В выражении для светового уравнения использованы следующие обозначения для элементов орбиты затменно-двойной системы относительно центра тяжести i-кратной системы: аi – большая полуось, ii – наклонение, еi – эксцентриситет и ωi – долгота периастра; ${v}$ и Е – истинная и эксцентрическая аномалии, соответственно, которые отсчитываются в той же орбите; c – скорость света. Окончательно параметры каждого светового уравнения уточнялись методом дифференциальных поправок [23] при фиксированных линейных элементах (2). Одновременно вычислялись ошибки определения параметров. Отклонение наблюдаемых точек от теоретической кривой, вычисленной согласно соответствующему представлению, характеризовалось величиной стандартного отклонения: $\sigma = $$\sqrt {\frac{{\sum\nolimits_{k = 1}^N {(O - C)_{k}^{2}} }}{{N - 1}}} $, где N – число наблюдений. Поскольку линейные элементы определялись только методом перебора, для них в скобках указана величина шага перебора.

В табл. 1 приведены параметры световых уравнений для случая линейного представления моментов минимумов. Параметры с индексом G относятся к орбите с бо́льшим периодом, а с индексом L – к орбите с меньшим периодом. Здесь PG – период обращения в долгопериодической орбите с бо́льшим периодом, PL – период обращения в долгопериодической орбите с меньшим периодом, JDG, L – момент прохождения через периастр соответствующей орбиты, АG,L = (${{a}_{{G,L}}}\sin {{i}_{{G,L}}}$)/c. На рис. 2 приведены отклонения (O – C)11 наблюдаемых моментов минимумов W Del от вычисленных с линейными элементами (2). Сплошная кривая – сумма теоретических кривых для световых уравнений с параметрами из табл. 1. В нижней части рис. 2 приведены значения (О – С)10, полученные вычитанием из (О – С)11 обоих световых уравнений. Из этого рисунка видно, что полученное представление хорошо удовлетворяет наблюдениям. На рис. 3 приведены разности (О – С)12, полученные вычитанием из отклонений наблюдаемых моментов минимумов от вычисленных с линейными элементами (2), (О – С)11, теоретической кривой для светового уравнения с параметрами из табл. 1 с индексом L, и на рис. 4 – разности (О – С)13, полученные вычитанием из тех же значений (О – С)11 теоретической кривой для светового уравнения с параметрами из табл. 1 с индексом G. Сплошной линией на рис. 3 показана теоретическая кривая для светового уравнения с параметрами из табл. 1 с индексом G. Сплошная линия на рис. 4 – теоретическая кривая для светового уравнения с параметрами из табл. 1 с индексом L.

Таблица 1.  

Параметры гипотетических долгопериодических орбит в W Del для представления с линейными элементами

Параметр Значение Параметр Значение
PG (36 600 ± 200) сут = (100.2 ± 0.5) лет PL (23 300 ± 300) сут = (63.8 ± 0.8) лет
AG (0.085 ± 0.002) сут AL (0.051 ± 0.001) сут
${{e}_{G}}$ 0.60 ± 0.02 ${{e}_{L}}$ 0.49 ± 0.03
${{\omega }_{G}}$ 51° ± 4° ${{\omega }_{L}}$ 257° ± 10°
JDG 2 451 300 ± 300 JDL 2 427 400 ± 660
${{a}_{G}}\sin {{i}_{G}}$ (2.20 ± 0.05 ) × 109 км = (14.7 ± 0.3 ) а.е. ${{a}_{L}}\sin {{i}_{L}}$ (1.32 ± 0.03 ) × 109 км = (8.8 ± 0.2) а.е.
f(M3) 0.318 ${{M}_{ \odot }}$ f(M3) 0.170 ${{M}_{ \odot }}$
Рис. 2.

Отклонения (O – C)11 наблюдаемых моментов минимумов W Del от вычисленных с линейными элементами (2). Обозначения на этом рисунке те же, что на рис. 1. Сплошная кривая – сумма теоретических кривых для световых уравнений с параметрами из табл. 1. В нижней части рисунка приведены значения (О – С)10, полученные вычитанием из (О – С)11 обоих световых уравнений.

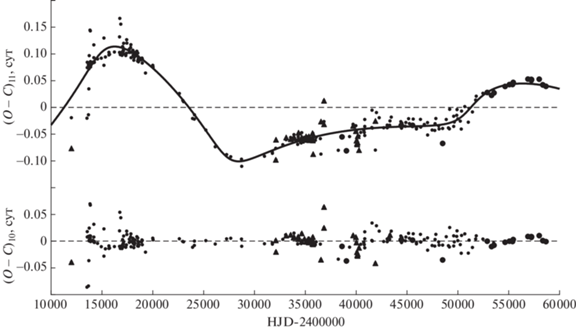
Рис. 3.

Разности (О – С)12, полученные вычитанием из отклонений (О – С)11 наблюдаемых моментов минимумов W Del от вычисленных с линейными элементами (2) теоретической кривой для светового уравнения с параметрами из табл. 1 с индексом L. Сплошной линией показана теоретическая кривая для светового уравнения с параметрами из табл. 1 с индексом G. Обозначения те же, что на рис. 1.

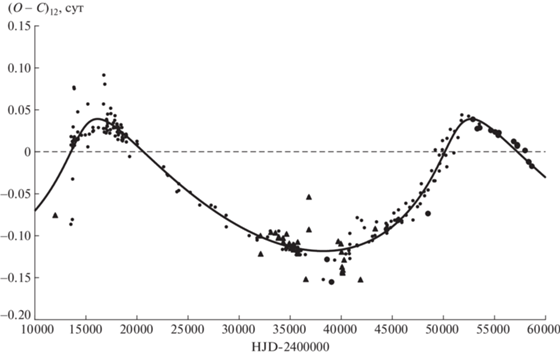
Рис. 4.

Разности (О – С)13, полученные вычитанием из отклонений (О – С)11 наблюдаемых моментов минимумов W Del от вычисленных с линейными элементами (2) теоретической кривой для светового уравнения с параметрами из табл. 1 с индексом G. Сплошной линией показана теоретическая кривая для светового уравнения с параметрами из табл. 1 с индексом L. Обозначения такие же, как на рис. 1.

2.2. Квадратичные элементы

Изменения периода W Del можно представить и квадратичной зависимостью, параметры которой также определялись методом наименьших квадратов:

(4)
$\begin{gathered} {\text{HJD}}({\text{Min}}\,{\text{I}}) = 2\,443\,328.530(3) + \\ + \;4.8060975{{(16)}^{{\text{d}}}}T + 6.5{{(3)}^{{\text{d}}}} \times {{10}^{{--9}}}{{T}^{2}}. \\ \end{gathered} $

На рис. 5 показаны остатки (O – C)2, полученные вычитанием из отклонений наблюдаемых моментов минимумов от теоретических, вычисленных по формуле (4), теоретической параболы с параметрами из представления (4). Эти остатки оказалось невозможным представить одной синусоидальной кривой, поэтому они были представлены суммой двух световых уравнений. Параметры этих световых уравнений искались тем же способом, что и для линейного представления. В процессе подбора суперпозиции двух световых уравнений уточнялись и квадратичные элементы. В результате было получено следующее представление для моментов минимумов:

(5)
$\begin{gathered} {\text{HJD}}({\text{Min}}\,{\text{I}}) = 2\,443\,328.5494(1) + \\ + \;4.8061054{{(1)}^{{\text{d}}}}T + 7.2{{(1)}^{{\text{d}}}} \times {{10}^{{--9}}}{{T}^{2}} + \\ + \;LTE1 + LTE2. \\ \end{gathered} $
Как и в предыдущем случае, параметры каждого светового уравнения уточнялись методом дифференциальных поправок [23] при фиксированных квадратичных элементах (5). Одновременно вычислялись ошибки определения параметров. В выражении (5) для квадратичных элементов в скобках приводится шаг перебора. Параметры световых уравнений для этого случая приведены в табл. 2, в которой использованы те же обозначения, что в табл. 1. Период и амплитуда светового уравнения с бо́льшим периодом близки к значениям этих параметров в работе [18], остальные параметры этого колебания и параметры светового уравнения с меньшим периодом заметно отличаются.

Рис. 5.

Остатки (O – C)2, полученные вычитанием из отклонений наблюдаемых моментов минимумов W Del от теоретических, вычисленных по формуле (4), теоретической параболы с параметрами из представления (4). Обозначения те же, что на рис. 1.

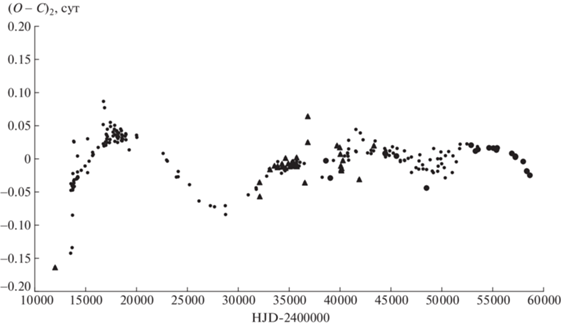
Таблица 2.  

Параметры гипотетических долгопериодических орбит в W Del для представления с квадратичными элементами

Параметр Значение Параметр Значение
PG (21 800 ± 150) сут = (59.7 ± 0.4) лет PL (18 400 ± 110) сут = (50.4 ± 0.3) лет
AG (0.053 ± 0.002) сут AL (0.049 ± 0.002) сут
${{e}_{G}}$ 0.0 ${{e}_{L}}$ 0.43 ± 0.04
${{\omega }_{G}}$ 0.0 ${{\omega }_{L}}$ 60° ± 10°
JDG 2 433 600 ± 100 JDL 2 433 700 ± 420
${{a}_{G}}\sin {{i}_{G}}$ (1.37 ± 0.05 ) × 109 км = (9.2 ± 0.3 ) а.е. ${{a}_{L}}\sin {{i}_{L}}$ (1.27 ± 0.05) × 109 км = (8.5 ± 0.3) а.е.
f(M3) 0.217 ${{M}_{ \odot }}$ f(M3) 0.241 ${{M}_{ \odot }}$

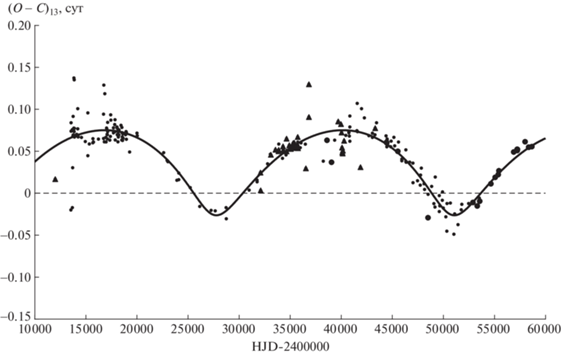
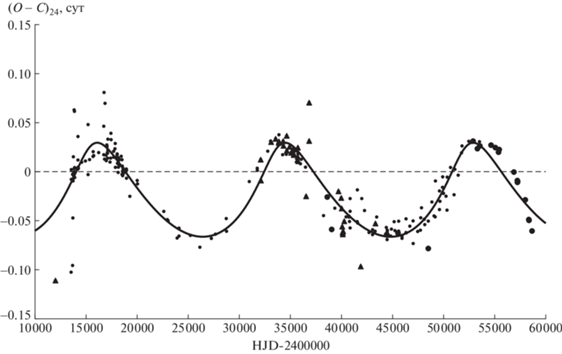
На рис. 6 приведены остатки (О – С)22, полученные вычитанием теоретической параболы из отклонений наблюдаемых моментов минимумов W Del от теоретических, вычисленных с квадратичными элементами (5). Сплошная кривая на этом рисунке – сумма теоретических кривых для световых уравнений с параметрами из табл. 2. В нижней части рис. 6 приведены значения (О – ‒ С)20, полученные вычитанием из (О – С)22 обоих световых уравнений. Отметим, что эта кривая несколько хуже представляет наблюдения, особенно самые последние, чем кривая для линейного представления. На рис. 7 приведены разности (О – С)23, полученные вычитанием из отклонений (О – С)22 наблюдаемых моментов от вычисленных с квадратичными элементами (5) теоретической кривой для светового уравнения с параметрами из табл. 2 с индексом L, и на рис. 8 – разности (О – С)24, полученные вычитанием из тех же значений (О – С)22 теоретической кривой для светового уравнения с параметрами из табл. 2 с индексом G. Сплошной линией на рис. 7 показана теоретическая кривая для светового уравнения с параметрами из табл. 2 с индексом G. Сплошной линией на рис. 8 показана теоретическая кривая для светового уравнения с параметрами из табл. 2 с индексом L.

Рис. 6.

Остатки (О – С)22 , полученные вычитанием из отклонений наблюдаемых моментов минимумов W Del от теоретических, вычисленных с квадратичными элементами (5), теоретической параболы (5). Сплошная кривая – сумма теоретических кривых для световых уравнений с параметрами из табл. 2. В нижней части рисунка приведены значения (О – С)20, полученные вычитанием из (О – С)22 обоих световых уравнений. Обозначения те же, что на рис. 1.

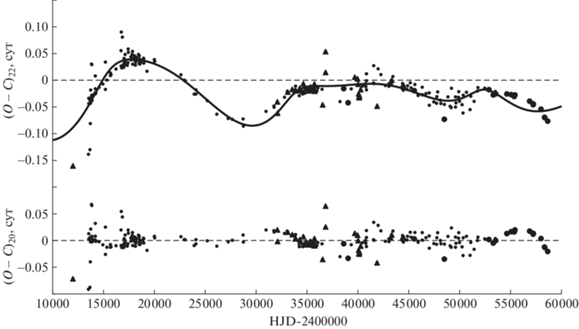
Рис. 7.

Разности (О – С)23, полученные вычитанием из отклонений (О – С)22 наблюдаемых моментов минимумов W Del от вычисленных с квадратичными элементами (5) теоретической кривой для светового уравнения с параметрами из табл. 2 с индексом L. Сплошной линией показана теоретическая кривая для светового уравнения с параметрами из табл. 2 с индексом G. Обозначения такие же, как на рис. 1.

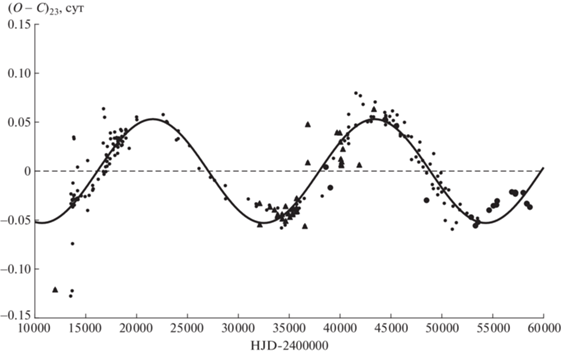
Рис. 8.

Разности (О – С)24, полученные вычитанием из отклонений (О – С)22 наблюдаемых моментов минимумов W Del от вычисленных с квадратичными элементами (5) теоретической кривой для светового уравнения с параметрами из табл. 2 с индексом G. Сплошной линией показана теоретическая кривая для светового уравнения с параметрами из табл. 2 с индексом L. Обозначения такие же, как на рис. 1.

3. ВОЗМОЖНЫЕ ПРИЧИНЫ ИЗМЕНЕНИЙ ОРБИТАЛЬНОГО ПЕРИОДА W DEL

Вековое увеличение периода, которое получается в случае квадратичного представления, можно объяснить обменом веществом между компонентами. В случае равномерного перетекания вещества от менее массивного к более массивному компоненту без изменения общего углового момента [24]:

(6)
${{\dot {M}}_{2}} = - {{M}_{2}}\dot {P}{{P}^{{ - 1}}}\frac{1}{{3(1 - q)}},$
где q = M2/M1. При квадратичной зависимости моментов минимумов
(7)
${\text{JD}}({\text{Min}}\,{\text{I}}) = {\text{J}}{{{\text{D}}}_{0}} + {{P}_{0}}T + Q{{T}^{2}},$
где P0 – орбитальный период в момент времени JD0. Производная от JD по T дает нам значение периода в любой момент времени
(8)
$P = {\text{dJD/d}}T = {{P}_{0}} + 2QT.$
Дифференцируя это выражение по времени, получаем
(9)
$\dot {P} = \frac{{dP}}{{dt}} = \frac{{dP}}{{dT}}\frac{{dT}}{{dt}} = \frac{{2Q}}{{{{P}_{0}}}},$
поскольку $T = \frac{{t - {{t}_{0}}}}{{{{P}_{0}}}}$, $\frac{{dT}}{{dt}} = \frac{1}{{{{P}_{0}}}}$. Подставляя найденное выражение (9) для $\dot {P}$ в уравнение (6), получим (в приближении P ≈ P0)
(10)
${{\dot {M}}_{2}} = - {{M}_{2}}\frac{{2Q}}{{{{P}^{2}}}}\frac{1}{{3(1 - q)}}.$
Для W Del: M1 = 2.01 ${{M}_{ \odot }}$, M2 = 0.42 ${{M}_{ \odot }}$ [25], q = = 0.21, Q = 7.2 × 10–9, P = 4.8061054d. Подставляя эти значения в выражения (9) и (10), получаем dP/dt = = 1.09 × 10–6 сут/год, ${{\dot {M}}_{2}}$= – 4.04 × 10–8${{M}_{ \odot }}$/год.

Хотя мы представили циклические колебания орбитального периода затменно-двойной системы W Del, как в случае линейных элементов, так и в случае квадратичного представления суперпозицией двух световых уравнений, на самом деле, эти циклические изменения орбитального периода могут быть следствием нескольких причин. Кроме светового уравнения, они могут вызываться вращением линии апсид орбиты двойной системы или влиянием магнитных циклов одного из компонентов.

3.1. Вращение линии апсид

Вращение линии апсид наблюдается в двойных системах с эксцентричной орбитой. Из кривой лучевых скоростей W Del для главного компонента был получен эксцентриситет орбиты е = = 0.20 [11]. Фотометрические наблюдения, сначала визуальные и фотографические, не подтверждали это значение. Наконец, была получена фотоэлектрическая кривая блеска, в которой уже виден вторичный минимум на фазе 0.5. Следует отметить, что эксцентриситеты, полученные из кривых лучевых скоростей, часто оказываются ложными и не подтверждаются фотоэлектрическими наблюдениями. На форму кривой лучевых скоростей могут влиять, во-первых, осевое вращение компонентов, а во-вторых, деформация кривой лучевых скоростей, главным образом, около фазы главного затмения, из-за газовых потоков. Поэтому в вопросе об эксцентриситете следует полагаться на результаты фотометрии. Отметим, что фотометрические наблюдения W Del показывают асимметрию главного минимума [5], которая может быть следствием наличия газовых потоков. На основании вышесказанного для W Del принимается круговая орбита, и вращение линии апсид как причина изменений периода не рассматривается.

3.2. Световое уравнение

Полученные параметры долгопериодических орбит позволяют вычислить функции масс для каждого светового уравнения:

(11)
$f({{M}_{3}}) = \frac{{4{{\pi }^{2}}}}{G}\frac{{a_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{P_{3}^{2}}},$
где G – гравитационная постоянная.

Для иерархических тройной и четырехкратной систем функция масс связана с массами компонентов следующими соотношениями:

(12)
$f({{M}_{3}}) = \frac{{M_{3}^{3}{{{\sin }}^{3}}{{i}_{3}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}})}}^{2}}}},$
(13)
$f({{M}_{4}}) = \frac{{M_{4}^{3}{{{\sin }}^{3}}{{i}_{4}}}}{{{{{({{M}_{1}} + {{M}_{2}} + {{M}_{3}} + {{M}_{4}})}}^{2}}}}.$
Здесь М1 и М2 – массы компонентов затменно-двойной системы, М3 и М4 – массы дополнительных тел.

3.2.1. Линейные элементы. На рис. 3 и 4 видно, что каждое из синусоидальных представлений хорошо описывает наблюдения, причем наблюдения охватывают по два периода для каждого из циклических изменений. Используя приведенные выше значения масс компонентов и предполагая, что только одно циклическое изменение периода вызвано световым уравнением, получаем для третьего тела с меньшим периодом f(M3) = = 0.170 ${{M}_{ \odot }}$, соответствующая минимальная масса третьего тела равна 1.34 ${{M}_{ \odot }}$. Для предполагаемого третьего тела с бо́льшим периодом f(M3) = 0.318 ${{M}_{ \odot }}$, а минимальная масса 1.78 ${{M}_{ \odot }}$. Если же предположить четырехкратную систему, минимальная масса более удаленного тела получается равной 2.26 ${{M}_{ \odot }}$. Фотометрические наблюдения не обнаруживают третий свет в системе. Так что дополнительное тело должно быть либо звездой пониженной светимости, либо, в свою очередь, двойной (или кратной) системой. При этом присутствие сразу двух дополнительных тел маловероятно.

3.2.2. Квадратичные элементы. В этом случае получаются два циклических изменения периода с близкими периодами, такая четырехкратная система вряд ли может существовать. Для меньшего периода функция масс равна 0.241 ${{M}_{ \odot }}$ и минимальная масса третьего тела 1.57 ${{M}_{ \odot }}$. Для бо́льшего периода имеем соответственно 0.217 ${{M}_{ \odot }}$ и 1.50 ${{M}_{ \odot }}$. Присутствовать в системе может только одно из этих дополнительных тел, и это может быть либо звезда пониженной светимости, либо, в свою очередь, двойная (или кратная) система.

3.3. Магнитные колебания

В качестве альтернативы гипотезе о третьем теле может служить предположение, что наблюдаемые модуляции периода являются проявлением магнитной активности. Вторичный компонент в затменно-двойной системе W Del имеет спектральный класс G5, и должен иметь конвективную оболочку и, следовательно, магнитное поле. В работе [26] была предложена модель, в которой гравитационное квадрупольное взаимодействие обеспечивает механизм, посредством которого орбита реагирует на изменения внутренней структуры активной звезды. В этой модели амплитуда модуляций орбитального периода ΔP и амплитуда осцилляций Δ(О – С) на диаграмме О – С связаны соотношением: ΔP/P0 = 2π Δ(О – ‒ С)/Pmod. Используя соответствующее значение периода двойной системы, находим ΔP для всех значений Δ(О – С) и Pmod. Принимая оценки масс компонентов и абсолютного радиуса вторичного компонента R2 = 3.88 ${{R}_{ \odot }}$ из [25] и используя последовательность формул, приведенную в [26], для каждого значения модулирующего периода находим оценки величины переносимого (от ядра звезды к ее оболочке и обратно) углового момента ΔJ, количества энергии, необходимого для переноса углового момента во внешнюю часть звезды, ΔE, напряженности магнитного поля B активного компонента и изменений его светимости ΔL. Эти величины приведены в табл. 3 для представления с линейными элементами и в табл. 4 для квадратичного представления изменений периода. Светимости компонентов затменно-двойной системы определим, исходя из оценок массы и относительной светимости главного компонента, приведенных в [25]. Главный компонент затменно-двойной системы является звездой Главной последовательности, и его светимость можно найти из соотношения масса–светимость в соответствующем диапазоне масс [27]: L1 = 20.43 ${{L}_{ \odot }}$. Согласно [25], его относительная светимость равна 0.857, тогда абсолютная светимость вторичного компонента получается равной L2 = 3.41 ${{L}_{ \odot }}$.

Таблица 3.  

Величины, характеризующие циклы магнитной активности вторичного компонента W Del для разных значений модулирующего периода для представления с линейными элементами

Величина Значение
Рmod 36 600 сут 23 300 сут
Δ(О – С) 0.085 сут 0.051 сут
ΔP 6.06 с 5.71 с
ΔJ 9.54 × 1047 г см2/с 9.00 × 1047 г см2/с
ΔE 4.49 × 1041 эрг 3.98 × 1041 эрг
B 1.70 × 103 Гаусс 2.07 × 103 Гаусс
ΔL 4.46 × 1032 эрг/с = 0.116 ${{L}_{ \odot }}$ = 0.034L2 6.22 × 1032 эрг/с = 0.162 ${{L}_{ \odot }}$ = 0.048L2
Таблица 4.  

Величины, характеризующие циклы магнитной активности вторичного компонента W Del для разных значений модулирующего периода для представления с квадратичными элементами

Величина Значение
Рmod 21 800 сут 18 400 сут
Δ(О – С) 0.053 сут 0.049 сут
ΔP 6.34 с 6.95 с
ΔJ 9.99 × 1047 г см2/с 1.09 × 1048 г см2/с
ΔE 4.62 × 1041 эрг 5.90 × 1041 эрг
B 2.25 × 103 Гаусс 2.57 × 103 Гаусс
ΔL 8.20 × 1032 эрг/с = 0.21 ${{L}_{ \odot }}$ = 0.062 L2 1.16 × 1033 эрг/с = 0.30 ${{L}_{ \odot }}$ = 0.088 L2

Из табл. 3 и 4 видно, что для всех модулирующих периодов полученные оценки магнитных и энергетических величин вполне укладываются в допустимые рамки. Возможные колебания светимости невелики. Кроме того, оценки требуемой энергии, основанные на формулах из [26], следует рассматривать как верхние пределы. В работах [28, 29] было показано, что за счет использования большей скорости вращения звезды или более эффективного механизма превращения вращательной кинетической энергии в магнитную и обратно, затраты энергии и соответствующие изменения светимости могут быть заметно меньше. Таким образом, магнитные колебания можно использовать для объяснения циклических изменений орбитального периода затменно-двойной системы W Del.

Циклические колебания орбитального периода вследствие магнитных циклов могут иметь не строго периодический характер, а также непостоянную амплитуду, причем могут существовать несколько циклов различной продолжительности [26]. При линейном представлении моментов минимумов получаем сочетание двух циклических изменений, подобных наблюдаемым у Алголя [30]. В случае Алголя два цикла приписываются магнитной активности вторичного компонента. То же самое можно предположить и для W Del. В случае квадратичного представления моментов минимумов оба циклических изменения орбитального периода имеют близкие периоды, и теоретические кривые для световых уравнений не очень хорошо представляют наблюдения (рис. 6, 7). Для их объяснения лучше подходят магнитные циклы вследствие магнитной активности вторичного компонента. Кроме того, изменения периода, показанные на рис. 5, можно рассматривать как квазициклические колебания с непостоянными периодом и амплитудой, не разделяя их на составляющие.

4. ЗАКЛЮЧЕНИЕ

Исследование изменений орбитального периода затменно-двойной системы W Del, имеющих довольно сложный характер, показало, что их можно представить суперпозицией двух циклических изменений либо суперпозицией векового увеличения периода и двух циклических изменений с мало различающейся точностью (σ = = 0.0167d в первом случае и σ = 0.0176d во втором случае). При использовании линейных элементов остаточные изменения периода очень хорошо представляются суммой двух синусоидальных кривых. Если предположить четырехкратную систему, то масса более удаленного тела получается слишком большой. Поэтому можно допустить существование только одного дополнительного тела, вероятнее всего, с меньшим периодом, и оно должно быть звездой пониженной светимости или двойной (или кратной) системой. Тогда второе колебание, по-видимому, является следствием магнитной активности вторичного компонента. Следствием магнитной активности вторичного компонента могут быть также оба вида колебаний. Формально представление моментов минимумов W Del с использованием линейных элементов лучше описывает наблюдения. Однако существование газовых потоков, на которое указывают как спектральные, так и фотометрические наблюдения, предполагает обмен веществом между компонентами, которое должно приводить к вековому изменению периода. В случае квадратичного представления моментов минимумов остаточные изменения периода после исключения параболы не очень хорошо представляются строгими синусоидами. Для их объяснения лучше подходят магнитные колебания. Можно также предположить, что изменения периода в этом случае носят квазициклический характер с непостоянными амплитудой и периодом. Кроме того, свой вклад в нерегулярность изменений периода может вносить нестационарность потока вещества между компонентами.

Для уточнения характера изменений орбитального периода в затменно-двойной системе W Del нужны дальнейшие наблюдения моментов минимумов, а также высокоточные кривые блеска для уточнения орбитальных параметров и прояснения вопроса о третьем свете в блеске системы. Желательно также получение более современной кривой лучевых скоростей для надежного определения масс компонентов.

Список литературы

  1. E. C. Pickering and L. D. Wells, Astrophys. J. 3, 77 (1896).

  2. E. C. Pickering, Astrophys. J. 4, 320 (1896).

  3. H. N. Russel, Astrophys. J. 36, 133 (1912).

  4. H. N. Russel, M. Fowler, and M. C. Borton, Astrophys. J. 45, 306 (1917).

  5. K. Walter, Astron. Nachr. 292, 145 (1970).

  6. H. Shapley, Astrophys. J. 38, 158 (1913).

  7. В. П. Цесевич, Переменные звезды 11, 403 (1957).

  8. В. М. Табачник, А. М. Шульберг, Астрон. журн. 42, 590 (1965).

  9. М. И. Лавров, Астрон. журн. 48, 951 (1971).

  10. K. Mezzetti, Astrophys. and Space Sci. 39, 273 (1980).

  11. O. Struve, Astrophys. J. 104, 253 (1946).

  12. G. Hill, R.W. Hilditch, F. Younger, and W. A. Fisher, Mem. Roy. Astron. Soc. 79, 131 (1975).

  13. L. B. Lucy and M. A. Sweeney, Astron. J. 76, 544 (1971).

  14. В. П. Цесевич, Астрон. цирк. № 174, 17 (1956).

  15. M. Plavec, Bull. of the Astron. Inst. of Czechoslovakia 10, 185 (1959).

  16. M. Plavec, Bull. of the Astron. Inst. of Czechoslovakia 11, 148 (1960).

  17. J. M. Kreiner, Acta Astron. 21, 365 (1971).

  18. T. Borkovits, and T. Hegedues, Astron. and Astrophys. Suppl. Ser. 120, 63 (1996).

  19. M. A. Hanna, J. Korean Astron. Soc. 39, 129 (2006).

  20. B. R. N. O. Project – Eclipsing Binaries database, http://var2.astro.cz/EN/brno/index.php

  21. А. И. Халиуллина, Астрон. журн. 96, 196 (2019).

  22. Д. Я. Мартынов, в кн. М. С. Зверев, Б. В. Кукаркин, Д. Я. Мартынов, П. П. Паренаго, Н. Ф. Флоря, В. П. Цесевич, Переменные звезды, т. 3, Гостехиздат (1947), стр. 464–490.

  23. А. И. Халиуллина, Х. Ф. Халиуллин, Астрон. журн. 61, 393 (1984).

  24. Х. Ф. Халиуллин, Астрон. журн. 51, 395 (1974).

  25. L. P. Surkova and M. A. Svechnikov, Vizier On-line Data Catalog: Semi-detached eclipsing binaries (2004).

  26. J. H. Applegate, Astrophys. J. 385, 621 (1992).

  27. Z. Eker, F. Soudugan, E. Soydugan, S. Bilir, E. Yaz Gökçe, I. Steer, M. Tüysüz, T. Şenyüz, and O. Demircan, Astron. J. 149, 131 (2015).

  28. A. F. Lanza, M. Rodono, and R. Rosner, Monthly Not. Roy. Astron. Soc. 296, 893 (1998).

  29. A. F. Lanza and M. Rodono, Astron. and Astrophys. 349, 887 (1999).

  30. S. O. Selam and O. Demircan, Turk. J. Phys. 23, 301 (1999).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал