Астрономический журнал, 2022, T. 99, № 7, стр. 576-594
Сверхскоростные свободные планеты как продукт столкновения их родительских систем со сверхмассивными черными дырами
Г. Н. Дремова 1, *, В. В. Дремов 1, **, А. В. Тутуков 2, ***
1 Российский федеральный ядерный центр
Снежинск, Челябинская область, Россия
2 Институт астрономии Российской академии наук
Москва, Россия
* E-mail: G.N.Dryomova@mail.ru
** E-mail: V.V.Dryomov@vniitf.ru
*** E-mail: atutukov@inasan.ru
Поступила в редакцию 20.03.2022
После доработки 30.04.2022
Принята к публикации 16.05.2022
- EDN: OWZZYP
- DOI: 10.31857/S0004629922080047
Аннотация
Данная статья продолжает поиск механизмов образования свободных планет и рассматривает проблему динамического захвата планетной системы окрестностью сверхмассивной черной дыры (СМЧД) с массой в миллион солнечных масс. Используется упрощенная модель планетной системы, включающей родительскую звезду солнечной массы, планету-гигант с массой Юпитера и $N$ малых тел типа астероидов, комет и карликовых планет (АКП объекты), коорбитальных с планетой-гигантом. Постановка численного моделирования сводится к задаче четырех тел, дублированной $N$ раз. Изучены спектры скоростей рассеяния АКП объектов в зависимости от параметров столкновения: перицентрического сближения и угла подлета планетной системы к СМЧД. Отмечается эффективность гравитационного рассеяния планетной системы на СМЧД: до 50% всех малых планетных тел получают статус свободных объектов, включая ~1% сверхскоростных АКП со скоростями до тысячи и больше километров в секунду. Анализируется доля АКП объектов, разрушенных или поглощенных СМЧД. В работе приведена оценка частоты столкновений планетных систем с СМЧД, исходя из которой допускается существование хорошо населенного компонента свободных планет, астероидов и комет в плотных ядрах галактик.
1. ВВЕДЕНИЕ
Сегодня хорошо установлено, что в ядрах массивных галактик находятся сверхмассивные черные дыры (СМЧД). И хотя условия их возникновения в ранней Вселенной остаются предметом оживленной дискуссии (космология, сверхэддингтоновская аккреция, сверхмассивные звезды), сам факт присутствия СМЧД в ядрах галактик не вызывает сомнений [1–3]. Главная проблема связана с условиями появления СМЧД во Вселенной с возрастом менее одного миллиарда лет при ограничении скорости аккреции эддингтоновским пределом. Один из возможных путей ее решения – допущение больших масс (порядка миллиона солнечных) первых звезд – предшественниц СМЧД, которые, будем надеяться, откроет космический телескоп “Джеймс Уэбб”. Такие массы могут быть достигнуты в ядрах галактик за счет высоких температур газа и очень малой, исходной космологической его металличности [4]. Высокая температура газа повышает величину предела Джинса на массу коллапсирующих газовых облаков, а низкая металличность уменьшает интенсивность звездного ветра молодой звезды, препятствующего росту массы массивных звезд. Масса наблюдаемых СМЧД (${{M}_{{{\text{SMBH}}}}}$) коррелирует с массой (${{M}_{g}}$) родительских галактик: ${{M}_{{{\text{SMBH}}}}}\sim 0.001{\kern 1pt} {{M}_{g}}$, хотя дисперсия этого соотношения остается довольно большой [5].
Ядра галактик являются очень плотными скоплениями старых звезд, в основном, солнечной и меньшей массы. Большая пространственная плотность звезд и присутствие СМЧД предопределяют активную эволюцию звездного и газового состава галактических ядер. Главными наблюдаемыми проявлениями этой активности являются мощные вспышки звездообразования и аккреция газа в ядре. И то и другое носит подчеркнуто рекуррентный характер, задавая хорошо наблюдаемые проявления – мощные инфракрасные источники излучения ядер галактик и квазары [6–8], вспышки излучения квазаров продолжительностью в несколько десятков дней в ультрафиолете [9–11] и рентгене [12].
С момента осознания природы квазаров как аккрецирующих СМЧД взаимодействие звезд ядра галактики с этими объектами стало одной из популярных задач современной астрофизики. Большая переменность светимости и, следовательно, скорости аккреции является результатом неоднородности аккреционного диска. Изучение временнóго поведения яркости квазаров позволило выделить сравнительно однородную группу вспышек излучения продолжительностью 10–100 дней, отмечающую периоды усиления аккреционной активности СМЧД с массами (105–108) ${{M}_{ \odot }}$. Эти вспышки были приписаны приливному разрушению звезд, оказавшихся вблизи СМЧД. Явления такого рода были впервые независимо рассмотрены Хиллзом [13, 14], Франком [15] и Докучаевым и Озерным [16].
Хорошо известно, что пространственная плотность звездного компонента растет с приближением к ядру галактик. Массы СМЧД коррелируют с массами балджей (${{M}_{b}}$) с большой дисперсией корреляции: ${{M}_{{{\text{SMBH}}}}} \approx 0.001{\kern 1pt} {{M}_{b}}$ [17]. Скорости звездообразования в ядрах ($d{{M}_{g}}{\text{/}}dt$) и темпы аккреции газа СМЧД ($d{{M}_{{{\text{SMBH}}}}}{\text{/}}dt$) снова при достаточно большой дисперсии обнаруживают признаки скоррелированности: $d{{M}_{g}}{\text{/}}dt \approx 30{\kern 1pt} d{{M}_{{{\text{SMBH}}}}}{\text{/}}dt$ при наблюдаемых скоростях звездообразования ${{(10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}})\,{{M}_{ \odot }}$/год [18], что, вероятно, свидетельствует об общих причинах их активизации. Одной из них может быть накопительная неустойчивость газового компонента в ядре галактики или столкновения галактик. В пользу последнего говорит то, что наблюдения демонстрируют: доля галактик с активными ядрами заметно растет при увеличении плотности их окружения [19, 20]. В то же время обнаружение двойных СМЧД в ядрах некоторых галактик и СМЧД, расположенных вне ядер своих галактик, является наглядной демонстрацией роли столкновений и слияния галактик во всесторонней активизации их ядер [21], включая приливные разрывы звезд с аккрецией вещества на СМЧД [14, 22, 23].
Оценка частоты приливных разрушений звезд Главной последовательности солнечной массы СМЧД в ядрах галактик остается пока довольно неопределенной. Наблюдательная оценка осложнена, как обычно, эффектами наблюдательной селекции и, весьма вероятно, значительной дисперсией энергетики этих событий. Рассмотрим варианты теоретических оценок частоты столкновений звезд с СМЧД.
2. ОЦЕНКИ ЧАСТОТЫ ПРИЛИВНЫХ РАЗРУШЕНИЙ ЗВЕЗД
Теоретические оценки частоты приливных разрушений звезд и их планетных систем в поле СМЧД осложнены рядом важных неопределенностей, а также остаются целиком зависящими от предположений о плотности звездного окружения СМЧД и распределения орбит звезд ядра галактики по угловым моментам, ибо только звезды с предельно малыми угловыми моментами разрушаются СМЧД. Верхний предел этой частоты может быть найден в предположении, что вся масса СМЧД является результатом аккреции вещества разрушенных приливами звезд. Поскольку характерное отношение массы балджа галактики (${{M}_{b}}$) к массе СМЧД (${{M}_{{{\text{SMBH}}}}}$) около тысячи [17, 24], верхняя оценка частоты будет ${{10}^{{ - 13}}}\,{{M}_{b}}{\text{/}}{{M}_{ \odot }}$/год, что для нашей Галактики составляет ${{10}^{{ - 3}}}$ в год. Однако ясно, что основную часть своей массы СМЧД получает в результате аккреции стационарного газового вещества окружающего ее диска. И первые модельные оценки частоты приливных разрушений звезд существенно понизили ее до ${{10}^{3}}\,{{M}_{ \odot }}{\text{/}}{{M}_{{{\text{SMBH}}}}}$ [25].
Сложность эмпирического подхода к оценке частоты приливных разрушений звезд в ядрах галактик отражается в большом разбросе величины этих оценок, относимых обычно к некой условной галактике: ${{10}^{{ - 6}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 3}}}$ в год [26] при массах разрушаемых звезд порядка солнечной массы [27, 28]. Верхняя оценка ${{10}^{{ - 3}}}$ в год [29] приводится для самых плотных звездных ядер галактик, населенных самыми массивными СМЧД. Согласно результатам моделирования событий приливного разрушения звезд в ОТО [30] частота приливных разрушений составляет $ \sim {\kern 1pt} {{10}^{{ - 6}}}$/год/Мпк3 или около ${{10}^{{ - 6}}}$ в год в расчете на галактику с массой, равной массе нашей Галактики, при плотности, равной космологической. Эта частота почти на три порядка ниже частоты SNe Ia [31]. За хаббловское время рост массы СМЧД за счет приливных распадов звезд с массой порядка солнечной не превысит несколько тысяч солнечных масс. Этот рост много меньше ожидаемой массы СМЧД у галактики с массой порядка массы нашей Галактики $ \sim {\kern 1pt} {{10}^{6}}\,{{M}_{ \odot }}$ [5]. Поэтому следует признать, что приливный распад звезд в ядрах галактик не увеличивает существенно массы их СМЧД. Возникновение и рост масс СМЧД остаются в тени предельно ранних стадий эволюции Вселенной и галактик, а также наблюдаемой аккреции окружающего их газа.
Теоретическая оценка нижнего предела частоты приливного разрушения звезд СМЧД может быть найдена в рамках однородной модели балджа, состоящего из звезд одинаковой массы ($m$) и одного радиуса ($r$), исходя из времени полного перераспределения между всеми звездами балджа их скоростей, или времени релаксации, ${{t}_{{{\text{rlx}}}}}$ [32–35]. И хотя ясно, что приливному разрушению подвергаются только звезды с предельно малыми угловыми моментами, заполняющие в перицентрах своих орбит свои полости Роша, это время может быть записано согласно [36] через кулоновский логарифм ${{t}_{{{\text{rlx}}}}} = N{\kern 1pt} {{T}_{K}}{\text{/}}\ln N$, тогда оценка частоты разрушений как $N{\text{/}}{{t}_{{{\text{rlx}}}}}$, где $N$ – число звезд в сферической системе, ${{T}_{K}}$ – ее кеплеровское время. При $N{{ = 10}^{{11}}}$ оценка искомой частоты равна ${{10}^{{ - 6}}}\,{{M}_{ \odot }}$/год.
Рассмотрим сферически симметричное скопление звезд с массой ${{M}_{{{\text{cl}}}}}$ и радиусом $R$ вокруг СМЧД с массой ${{M}_{{{\text{SMBH}}}}}$ в центре этого скопления. Связь массы и радиуса скопления для численных оценок может быть представлена соотношением: ${{M}_{{{\text{cl}}}}}{\text{/}}{{M}_{ \odot }} \approx {{10}^{3}}{{(R{\text{/пк}})}^{2}}$ [37]. Плоский характер кривой вращения и его постоянство для массивных галактик [38]: ${{V}_{{{\text{rot}}}}} = 250({{M}_{{{\text{cl}}}}}{\text{/}}{{10}^{{11}}}\,{{M}_{ \odot }}{{)}^{{1/4}}}$ км/с [39] вплоть до ядра галактики с радиусом 0.01 $R$ [40] или 0.1 $R$ [41] позволяют ввести параметр $q = {{R}_{N}}{\text{/}}R$, учитывающий увеличение плотности галактики с приближением к ядру, где ${{R}_{N}}$ – радиус центральной околоядерной (nuclear) области галактики, за пределами которой сохраняется плоский характер кривой вращения галактики. Для оценки прицельного параметра $b$ орбит звезд, заполняющих в перицентрах их орбит свои полости Роша, используем условие сохранения их орбитального момента относительно СМЧД: $bv = (Gm{{r}_{t}}{{)}^{{1/2}}}$. Здесь $G$ – постоянная гравитации, $v$ – кеплеровская скорость звезды в скоплении, ${{r}_{t}} = 2.5({{M}_{{{\text{SMBH}}}}}{\text{/}}m{{)}^{{1/3}}}r$ – приливный радиус СМЧД для звезды с массой $m$ и радиусом $r$. Итоговая оценка $b$:
(1)
$b = ({{M}_{{{\text{SMBH}}}}}{\text{/}}{{M}_{{{\text{cl}}}}}{{)}^{{1/2}}}{{({{M}_{{{\text{SMBH}}}}}{\text{/}}m)}^{{1/6}}}{{(r{{R}_{N}})}^{{1/2}}}.$Частота приливных разрушений звезд может быть оценена из выражения $f = \pi {\kern 1pt} {{b}^{2}}v{{M}_{{{\text{cl}}}}}{\kern 1pt} /{\kern 1pt} R_{N}^{3}{\text{/}}m$ или, подставляя выражение для $b$ и ${{R}_{N}}$:
где ${{T}_{k}} = R{\text{/}}v$ – кеплеровское время для звезд балджа. Принимая радиусы и массы звезд равными солнечным, найдем оценку частоты приливных разрушений звезд:(3)
$\begin{gathered} f{{ = 10}^{{ - 7}}}{\text{/}}{{q}^{2}}{{({{M}_{{{\text{SMBH}}}}}{\text{/}}{{10}^{9}}\,{{M}_{ \odot }})}^{{4/3}}} \times \\ \, \times {{{{(10}^{{11}}}\,{{M}_{ \odot }}{\text{/}}{{M}_{{{\text{cl}}}}})}^{{1/2}}}{{(10}^{7}}{\text{/}}{{T}_{k}}){\text{/год}}{\text{.}} \\ \end{gathered} $Приведенная оценка включает все определяющие ее параметры в рамках этой простой модели. Частота разрушений звезд Главной последовательности растет с массой СМЧД вследствие увеличения радиуса захвата и падает с массой скопления из-за увеличения скорости движения звезд. Эта оценка сопоставима c эмпирическими оценками частоты приливного разрушения звезд. Стоит отметить, что частота приливных разрушений мала, и роль приливного разрушения звезд в росте массы СМЧД за хаббловское время несущественна.
Для нас сейчас особенно важна зависимость частоты столкновений (см. (2)) от радиуса звезды и ее планетной системы. Это ведет к нескольким важным следствиям. Во-первых, звезды на стадии гигантов увеличивают свои размеры в сотни раз, уменьшая одновременно время жизни на этой фазе в сто раз [41]. В результате согласно (2) частота приливного разрушения сверхгигантов может оказаться сопоставимой с частотой наблюдаемых разрушений звезд Главной последовательности. Однако эти события могут оставаться пока незамеченными наблюдателями, поскольку при разрушении оболочки гиганта образуется протяженный аккреционный диск со слишком большим для его регистрации временем аккреции СМЧД. Во-вторых, ясно, что число вырожденных карликов в ядре галактики сопоставимо с числом звезд Главной последовательности. При заполнении этими карликами своих полостей Роша в парах с плотными СМЧД с массами последних менее примерно миллиона солнечных масс они разрушаются, порождая короткие рентгеновские вспышки излучения. Однако частота таких вспышек согласно (2) должна быть почти в сто раз меньше частоты разрушения звезд Главной последовательности, поэтому такие события пока не зарегистрированы. Интересно, что СМЧД с массами, большими порядка миллиона солнечных, поглощают вырожденные карлики, не разрушая их. Такие события отмечены только короткими вспышками излучения гравитационных волн. В-третьих, размеры планетной части планетных систем на примере Солнечной системы почти в десять тысяч раз превышают размеры их центральных звезд, что, соответственно, повышает частоту взаимодействия планетных систем с СМЧД в ядрах галактик. В результате разрушения СМЧД многих планетных систем в плотных ядрах галактик появляется обильный твердотельный компонент, состоящий из астероидов, ядер комет и планет. Последние теряются планетными системами в результате гравитационного взаимодействия планетных систем ядра с СМЧД и звездами поля.
Очевидно, что звезды сфероидального ядра галактики с угловым моментом, меньшим $vb$, будут разрушены СМЧД за кеплеровское время ядра. Дальнейшая эволюция системы зависит от скорости заполнения интервала малых угловых моментов, “конуса потерь”, за счет парных столкновений звезд балджа галактики. Для заполнения “конуса потерь” скорость звезды балджа должна измениться на малую величину порядка $\Delta v = vb{\text{/}}R$. Величина изменения скорости звезды при близком, на расстоянии ${{R}_{c}}$, прохождении соседней звезды составляет $\Delta v = Gm{\text{/}}(v{{R}_{c}})$. Из двух последних условий найдем ${{R}_{c}} = Gm{\text{/}}{{v}^{2}} \times $ $ \times \;{{({{M}_{{{\text{cl}}}}}{\text{/}}{{M}_{{{\text{SMBH}}}}})}^{{1/2}}}{{(m{\text{/}}{{M}_{{{\text{SMBH}}}}})}^{{1/6}}}{{(R{\text{/}}r)}^{{1/2}}}$, а характерное время для изменения скорости звезд скопления на указанную величину есть
Для поддержания стационарности процесса заполнения “конуса потерь” звездами последнее время должно быть короче времени истощения этого конуса ${{T}_{K}}$, или при ${{M}_{{{\text{cl}}}}}{\text{/}}{{M}_{ \odot }} = {{10}^{3}}{{(R{\text{/пк}})}^{2}}$ [37]:
(5)
${{M}_{{{\text{SMBH}}}}}{\text{/}}{{M}_{ \odot }} < 4 \times {{10}^{8}}{{({{M}_{{{\text{cl}}}}}{\text{/}}{{10}^{{11}}}\,{{M}_{ \odot }})}^{{3/8}}}.$Последнее условие эквивалентно при ${{M}_{{{\text{SMBH}}}}} \approx $ $ \approx 0.001{{M}_{{{\text{cl}}}}}$ [17] для ${{M}_{{{\text{SMBH}}}}}{{ < 10}^{9}}\,{{M}_{ \odot }}$. Оно выполняется практически для всех галактик, поэтому предположение о стационарности процесса питания СМЧД звездами балджа, использованное при оценке скорости приливных распадов (см. (3)), можно считать выполненным. При этом важно отметить, что согласно (4) скорость заполнения “конуса потерь” увеличивается с уменьшением массы СМЧД, что, вероятно, исключает наиболее массивные СМЧД из наблюдаемых активных разрушителей звезд. Хотя наблюдаемый эффект концентрации наблюдаемых актов приливного разрушения звезд к СМЧД умеренных масс ${{(10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{8}})\,{{M}_{ \odot }}$ [42, 43]) может быть следствием эффектов наблюдательной селекции.
Вполне вероятно, что высокая частота взаимодействия звезд с СМЧД может определяться не только большими массами СМЧД и их галактик, но и эффективно поддерживаться в их скоплениях столкновениями и слияниями галактик между собой, приводящими к быстрому перераспределению звезд по угловым моментам [44–46]. Радиус ${{r}_{{{\text{capture}}}}}$ зоны гравитационного влияния СМЧД с массой ${{M}_{{{\text{SMBH}}}}}$ на движение звезд, предположим, сферического балджа с массой ${{M}_{b}}$ и радиусом ${{R}_{b}}$: ${{r}_{{{\text{capture}}}}} = G{\kern 1pt} {{M}_{{{\text{SMBH}}}}}{\text{/}}{{v}^{2}}$. Скорость движения звезд балджа $v = (G{{M}_{b}}{\text{/}}{{R}_{b}}{{)}^{{1/2}}}$. Звезды, попавшие в ходе своего движения в сферу с радиусом ${{r}_{{{\text{capture}}}}}$, изменят свою пространственную скорость на величину, превосходящую $v$, т.е. эффективно провзаимодействуют с СМЧД.
За динамическое время ~108 лет некоторая часть звезд, около ${{({{M}_{{{\text{SMBH}}}}}{\text{/}}{{M}_{b}})}^{2}}$, пройдет через сферу гравитационного влияния СМЧД. При ${{M}_{{{\text{SMBH}}}}}{\text{/}}{{M}_{b}} = {{10}^{{ - 3}}}$ [17] это составит $ \sim {\kern 1pt} {{10}^{{ - 6}}}{{M}_{b}}$ или $ \sim {\kern 1pt} {{10}^{5}}$ звезд солнечной массы для балджа с массой, равной массе нашей Галактики. Дальнейшее заполнение “конуса потерь” в пространстве скоростей звезд балджа будет осуществляться, как показывают простые оценки, за счет парных столкновений звезд балджа рассматриваемой галактики и столкновения этой галактики с ее близкими массивными спутниками. В результате стационарный процесс взаимодействия СМЧД со звездами и их планетными системами будет, вероятно, время от времени прерываться сравнительно короткими периодами усиленной активности этого процесса, вызванными уже столкновениями галактик. Количественная оценка скорости этого процесса обременена целым рядом параметров и остается поэтому довольно неопределенной.
Из приведенных выше полуэмпирических оценок частоты приливных разрушений звезд в ядрах галактик [11, 25, 28–30] следуют два вывода. Первый: рост массы СМЧД за счет аккреции вещества разрушенных звезд по сравнению с наблюдаемой их массой [17] невелик, если учесть, что на каждый грамм аккрецированного газа аккреционный диск теряет в форме его индуцированного облучением ветра десятки грамм газа [47]. Основной путь пополнения массы СМЧД квазара – аккреция газа аккреционного диска, пополняемого старыми звездами балджа галактики. Второй вывод из приведенного выше анализа: потенциальная важность и большая частота гравитационного взаимодействия планетных систем с СМЧД в ядрах галактик. Последнее следует из того, что при “наблюдаемой” частоте разрушения компактных звезд ${{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 6}}}$ в год [11, 25, 28], взаимодействия СМЧД с планетными системами, размеры которых превосходят размеры звезд в тысячи раз, должны быть обыденными явлениями в ядрах всех галактик. Частота образования планетных систем высока, около трети звезд обладают ими [48–51]. Но численная оценка частоты взаимодействия планетных систем с СМЧД осложнена проблемами количественной оценки сохранности далеких членов планетных систем, слабо связанных с родительскими звездами, в ходе диффузии звезд в пространстве угловых моментов под действием близких прохождений звезд балджа.
Итогом распада неустойчивых планетных систем звезд плотного ядра и взаимодействие СМЧД с планетными системами в ядре галактики является обильный компонент свободных АКП объектов. Их число в ядре галактики может оказаться сопоставимым с числом звезд ядра. Важно, что члены этого АКП компонента непрерывно взаимодействуют со звездами ядра, получая при парном взаимодействии приращения пространственной скорости. И при $m{\text{/}}{{r}_{d}} > {{M}_{b}}{\text{/}}{{R}_{b}}$ или ${{V}_{d}} > {{V}_{b}}$ АКП объекты могут быть потеряны ядром галактики. Здесь $m$ и ${{M}_{b}}$ – массы звезды и ядра галактики, а ${{r}_{d}}$ и ${{R}_{b}}$ – расстояние АКП от звезды балджа и радиус балджа, тогда как ${{V}_{d}}$ и ${{V}_{b}}$ – параболические скорости АКП на расстоянии ${{r}_{d}}$ от звезды и на границе ядра галактики ${{R}_{b}}$ соответственно [52]. Следует подчеркнуть, что АКП объекты с размерами менее 100 км могут сближаться со звездами Главной последовательности гораздо теснее, вплоть до их радиусов, ускоряясь до соответствующих скоростей, что связано с электростатической природой связи тела АКП, превалирующей над самогравитацией (подробнее см. в Разделе 3). Если при близких прохождениях окажется, что ${{V}_{d}} > {{V}_{b}}$, члены АКП компонента ядра могут быть выброшены как из ядра галактики, так и из самой галактики. Вырожденные одиночные и тесные двойные вырожденные карлики ядра являются еще более эффективными “ускорителями” из-за более высоких параболических скоростей для них. То есть, наряду с рассмотренным в этой статье ускоряющим действием СМЧД на члены околозвездных планетных систем ядер, звезды ядра также могут поддерживать АКП “ветер” ядра галактики.
Интенсивность этого ветра задается в конечном итоге массой и плотностью звездного ядра галактики. Для оценки интенсивности примем, что для ускорения АКП объектов ядра до параболической скорости прицельное расстояние пролета АКП объекта около звезды ядра ${{r}_{d}}$ должно быть меньше ${{R}_{b}}{\kern 1pt} m{\text{/}}{{M}_{b}}$. Тогда доля пространства, заметаемого звездами однородного ядра галактики за хаббловское время ${{T}_{H}}$, будет ${{(m{\text{/}}{{M}_{b}})}^{2}}{{T}_{H}}{\text{/}}{{T}_{k}}N$, где $N$ – число звезд в балдже, ${{T}_{k}}$ – кеплеровское время ядра, определяемое его средней плотностью. NGC 3593 с массой ${{M}_{b}}\;\, = \;\,2\;\, \times \;\,{{10}^{7}}\,{{M}_{ \odot }}$, $N \sim {{10}^{7}}$ и ${{T}_{k}} = 3 \times {{10}^{4}}$ лет показывает, что около 10% АКП ядра могут быть ускорены до сверхпараболических скоростей [38].
Процесс взаимодействия планетных систем с СМЧД в плотных ядрах галактик остается пока слабо изученным, но его возможные продукты – члены планетных систем, выброшенные из ядер, привлекают внимание. К их довольно очевидному числу можно отнести АКП, теряемые планетными системами в процессе гравитационного рассеяния [52]. Естественно, планеты и кометы в силу функции масс редки, но поиски внесолнечных метеоров в последние годы после обнаружения межзвездных объектов Oumuamua и Borisov становятся популярными [53–56]. Среди межзвездных объектов и, даже, межгалактических объектов могут быть астероиды и метеоры, выброшенные из ядер галактик. Пока среди 160 000 метеоров, зарегистрированных радарным методом [54], было найдено только пять с потенциально гиперболическими орбитами относительно Солнца. Редкость межзвездных объектов по сравнению с солнечными очевидна. Интересно, что сейчас предпринимаются первые попытки выяснения условий для поиска пылинок с субрелятивистскими скоростями [52]. Среди них могут быть пылинки, ускоренные до больших скоростей вблизи СМЧД в ядрах галактик. Но пока оценки скоростей рассеяния АКП объектов, выброшенных из ядра галактики, можно получить с помощью численного моделирования.
3. ПОСТАНОВКА ЗАДАЧИ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Методом прямого численного моделирования рассчитывается прохождение планетной системы вблизи СМЧД с массой ${{M}_{{{\text{SMBH}}}}} = {{10}^{6}}\,{{M}_{ \odot }}$. Перицентрическое сближение родительской звезды с СМЧД моделировалось в трех вариантах: 100 ${{R}_{ \odot }}$, 50 ${{R}_{ \odot }}$ и 25 ${{R}_{ \odot }}$. Планетная система включает одиночную родительскую звезду (Солнце), планету-гигант (Юпитер) и центрированный по его орбите тор, заполненный случайным образом невзаимодействующими друг с другом малыми космическими телами ($N = {{10}^{4}}$), такими как астероиды, кометы и карликовые планеты (АКП). Такая модель планетной системы исследовалась нами ранее в [52] для моделирования начальной стадии формирования облака Оорта, сопровождающейся образованием свободных планет путем гравитационного рассеяния АКП объектов планетами-гигантами. Анализ распределений АКП объектов по их полной энергии (кинетическая энергия движения и энергия гравитационного взаимодействия с планетой-гигантом и родительской звездой), полученных на разные моменты времени, показал процесс “разогрева” начального тора под действием планеты-гиганта, постепенно “забрасывающей” АКП объекты все дальше от начального положения тора. Как показали расчеты [52], за время 105 лет механизм гравитационного рассеяния успевает произвести АКП с положительной полной энергией, эквивалентной остаточной скорости 1–2 км/с.
В настоящей постановке мы также пренебрегаем гравитационным взаимодействием АКП объектов друг с другом и решаем задачу четырех тел (СМЧД, родительская звезда, планета-гигант и АКП объект) $N$ раз. Орбитальное движение АКП-тора и планеты-гиганта задаются с сохранением основных параметров Солнечной системы: масса (${{M}_{S}}$) и размер (${{R}_{S}}$) родительской звезды как у Солнца, большая полуось орбиты планеты-гиганта 5.2 a.e., ее размер (${{R}_{J}}$) и масса (${{M}_{J}}$) как у Юпитера. Начальные положения АКП распределены случайным образом равномерно вдоль орбиты Юпитера в слое толщиной $h = 0.01$ a.e. Такой характер распределения является следствием разыгрывания отклонений начальных скоростей от кеплеровской орбитальной скорости, не превышающих 10%, чтобы “распушить” тор до состояния, когда его толщина в перпендикулярном плоскости орбиты направлении была бы сравнима с его толщиной в плоскости орбиты. Обозначим начальную конфигурацию такой планетной системы – модель $A$.
В противоположность организованной структуре, какой можно назвать АКП-тор в модели $A$, интересно рассмотреть возмущенную конфигурацию планетной системы в качестве начальной. В результате механизма гравитационного рассеяния АКП объектов на гиганте-Юпитере и Солнце часть АКП объектов сходит со своих первоначальных орбит, “упакованных” в торе, и образует пространственно неоднородную конфигурацию. Мы рассмотрели два варианта такой конфигурации, соответствующих проэволюционировавшим пространственным распределениям АКП объектов к моментам времени $ \sim {\kern 1pt} {\kern 1pt} 2400$ лет и ~16 900 лет согласно расчетам [52]. Условно обозначим эти конфигурации модель $B$ и модель $C$ соответственно. В этих конфигурациях начальная численность АКП (${{N}_{0}}$) – 8140 и 5966 соответственно.
В расчетах мы имитируем приход планетной системы из бесконечности, задавая ее орбиту в форме эллипса с большим эксцентриситетом. Основные параметры орбиты приведены в табл. 1: расстояние в апоцентре ${{r}_{a}}$, расстояние в перицентре ${{r}_{p}}$, начальная скорость орбитального движения планетной системы ${{V}_{{{\text{orb}}}}}$ и ее орбитальный период ${{P}_{{{\text{orb}}}}}$, рассчитанный по обобщенному третьему закону Кеплера. Движение планетной системы в поле СМЧД интегрируется с использованием численной схемы скоростной формулировки Верлета и Вейса [57], обеспечивающей сохранение всех интегралов движения с учетом адаптивного шага по времени.
Таблица 1.
Начальные параметры орбиты планетной системы относительно СМЧД с массой ${{10}^{6}}\,{{M}_{ \odot }}$ в моделях $A$, $B$ и $C$
| Модель $A$ $h$ = 0.01 a.e. |
|||
|---|---|---|---|
| ${{r}_{a}} = {{10}^{4}}\,{{R}_{ \odot }}$ ${{P}_{{{\text{orb}}}}} \approx 39$ дней | |||
| ${{r}_{p}}$, ${{R}_{ \odot }}$ | 100 | 50 | 25 |
| ${{V}_{{{\text{orb}}}}}$, км/с | 615 | 435 | 308 |
| Модель $B$ Модель $C$ $h$ = 0.27 a.e. $h$ = 0.59 a.e. |
|||
| ${{r}_{a}} = {{10}^{5}}\,{{R}_{ \odot }}$ ${{P}_{{{\text{orb}}}}} \approx $ 44.3 года | |||
| ${{r}_{p}}$, ${{R}_{ \odot }}$ | 100 | 50 | 25 |
| ${{V}_{{{\text{orb}}}}}$, км/с | 61.7 | 43.6 | 30.8 |
Примечание. $h$ – диаметр сечения тора; ${{r}_{a}}$ – расстояние в апоцентре, ${{r}_{p}}$ – расстояние в перицентре, ${{V}_{{{\text{orb}}}}}$ – начальная скорость орбитального движения планетной системы с орбитальным периодом ${{P}_{{{\text{orb}}}}}$, рассчитанным по обобщенному третьему закону Кеплера.
Так как движение АКП объекта рассматривается в мультицентровом поле, создаваемом СМЧД, звездой и планетой-гигантом, шаг интегрирования ${{h}_{t}}$ выбирается из условия минимума отношения расстояния ${{d}_{i}}$ в шести парах (1: АКП и СМЧД; 2: АКП и звезда; 3: АКП и планета-гигант; 4: СМЧД и звезда; 5: СМЧД и планета-гигант; 6: звезда и планета-гигант) ко второй космической скорости для менее массивного объекта из пары:
(6)
${{h}_{t}} = 1{\text{/}}2000 \times \mathop {\min }\limits_{i = 1...6} \left\{ {2\pi {{d}_{i}}{\text{/}}\sqrt {2G{{M}_{i}}{\text{/}}{{d}_{i}}} } \right\}.$Величина дробления характерного времени ($1{\text{/}}2000$) оказывается достаточной для обеспечения сохранения всех интегралов движения. Интегрирование проводилось до времени 2/3 ${{P}_{{{\text{orb}}}}}$. Критерием окончания счета послужило резкое замедление после прохождения перицентра процесса обмена импульсами между объектами планетной системы, которым можно пренебречь на оставшемся (1/3 ${{P}_{{{\text{orb}}}}}$) сегменте орбиты.
При расчете прохождения планетной системы вблизи СМЧД учитывались ограничения на приливные разрушения звезды, планеты-гиганта и АКП объектов под действием СМЧД. Из равенства ускорения свободного падения на Солнце (${{g}_{ \odot }} \sim 274$ м/c2) и приливного ускорения со стороны СМЧД, $\Delta a = - G{{M}_{{{\text{SMBH}}}}}(1{\text{/}}d_{4}^{2} - 1{\text{/}}{{({{d}_{4}} - {{R}_{ \odot }})}^{2}})$ можно получить оценку приливного радиуса ${{r}_{{{\text{tidal}}}}} \sim 125\,{{R}_{ \odot }}$, на котором звезда будет разорвана приливными силами СМЧД с массой ${{10}^{6}}\,{{M}_{ \odot }}$. Аналогичную оценку критического радиуса можно получить для планеты-гиганта, учитывая ускорение свободного падения на Юпитере (${{g}_{J}} \sim 25$ м/c2) и приливное ускорение со стороны СМЧД, $\Delta a = - G{{M}_{{{\text{SMBH}}}}}(1{\text{/}}d_{5}^{2} - 1{\text{/}}{{({{d}_{5}} - {{R}_{J}})}^{2}})$, которая составила $ \sim {\kern 1pt} 130\,{{R}_{ \odot }}$. Учитывая эффект приливного туннелирования, т.е. способности звезды на короткое время проникать “под барьер” приливного радиуса без последствий разрушения согласно результатам, полученным в [58, 59], мы использовали ограничение в виде $3{\text{/}}4{\kern 1pt} {{r}_{{{\text{tidal}}}}} \sim 85\,{{R}_{ \odot }}$. Если планета-гигант или родительская звезда подходит к СМЧД ближе этого расстояния, она будет разорвана приливными силами. Для АКП объектов с радиусом больше ${{R}_{{{\text{lim}}}}} \sim 100$ км требуется проверка границ полости Роша, внутри которой АКП объект в безопасности от приливных эффектов СМЧД. Значение ${{R}_{{{\text{lim}}}}}$ находится из баланса самогравитации и напряжения на разрыв (${{P}_{{{\text{cri}}}}}$), определяемого электростатической природой АКП объекта. Эти величины сравнимы при ${{R}_{{{\text{lim}}}}}\sim {{({{P}_{{{\text{cri}}}}}{\text{/}}G)}^{{1/2}}}{\text{/}}{{\rho }_{{{\text{AKP}}}}} \approx 100$ км, что является критерием разделения планет от астероидов.
Для АКП объектов с размерами менее 100 км оценка разрушения выполняется из анализа механической прочности вещества астероида, уравновешенной действием приливных сил. Согласно [60] предельное напряжение разрыва для метеоритного вещества варьирует в диапазоне ${{P}_{{{\text{cri}}}}} \sim 50{\kern 1pt} - {\kern 1pt} 100$ МПа. Это напряжение следует сравнить с напряжением ${{P}_{{{\text{tidal}}}}}$, создаваемым приливными силами. Cо стороны СМЧД ${{P}_{{{\text{tidal}}}}} = {{F}_{{{\text{tidal}}}}}{\text{/}}\pi R_{{{\text{AKP}}}}^{2}$, где ${{R}_{{{\text{AKP}}}}}$ – радиус астероида и ${{F}_{{{\text{tidal}}}}} = - G{{M}_{{{\text{SMBH}}}}}{\kern 1pt} {{m}_{{{\text{AKP}}}}}(1{\text{/}}d_{1}^{2} - 1{\text{/}}{{({{d}_{1}} - {{R}_{{{\text{AKP}}}}})}^{2}})$. Исходя из средней плотности астероида $ \sim {\kern 1pt} 3$ г/см3 и его массы $ \sim {\kern 1pt} {{10}^{{15}}}$ кг можно оценить ${{R}_{{{\text{AKP}}}}} \sim 5.3$ км. Давление приливных сил ${{P}_{{{\text{tidal}}}}}$ оказывается сравнимым по величине с прочностью астероида на разрыв ${{P}_{{{\text{cri}}}}} \sim 75$ МПа при ${{d}_{1}} \sim 10.6\,{{R}_{ \odot }}$. На этом расстоянии, которое вдвое превосходит собственный радиус СМЧД с массой ${{10}^{6}}\,{{M}_{ \odot }}$, АКП объект будет разорван приливными силами СМЧД. Аналогичные оценки прочности АКП объекта в гравитационном поле Солнца и Юпитера дают ограничение на предельное сближение $0.106\,{{R}_{ \odot }}$ и $0.0106\,{{R}_{ \odot }}$ соответственно, что означает, что АКП объект будет скорее “проглочен”, чем разрушен.
Программа расчетов организована следующим образом: три пространственные конфигурации планетной системы (модели $A$, $B$, $C$), заданные в плоскости $xy$, используются в качестве начальных данных и тестируются в двух взаимоположениях – сизигийном и квадратурном. В первом случае начальные положения СМЧД, звезды и планеты-гиганта заданы вдоль оси $y$, во втором – изменяется положение СМЧД, которое задается вдоль оси $z$ перпендикулярно линии соединения звезды и планеты. Каждая из этих конфигураций рассчитывается в шести вариантах с учетом направления вектора начальной скорости орбитального движения (вдоль осей $x$ или $z$ для сизигийного положения и вдоль осей $x$ или $y$ для квадратурного) и перицентрического сближения: $100\,{{R}_{ \odot }}$, $50\,{{R}_{ \odot }}$, $25\,{{R}_{ \odot }}$. Результаты 36 вариантов моделирования обсуждаются в следующем разделе.
4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
4.1. Модель $A$
Рассмотрим конфигурацию планетной системы из [52], соответствующую моменту времени ${{t}_{0}} = 0$, заданную в плоскости $xy$ в сизигийном положении по отношению к СЧМД с массой ${{10}^{6}}\,{{M}_{ \odot }}$, вокруг которой совершается орбитальное движение. Направление орбитального движения в начальный момент выбрано вдоль оси z. На рис. 1 в качестве иллюстрации представлена последовательность пространственных конфигураций планетной системы при перицентрическом сближении ее родительской звезды с СМЧД на $100\;{{R}_{ \odot }}$. Действие приливных сил хорошо видно по деформации АКП-тора по мере его приближения к перицентру СМЧД.
Рис. 1.
Последовательность пространственных конфигураций планетной системы в модели $A$, рассчитанной в варианте с сизигийной начальной конфигурацией для перицентрического сближения родительской звезды с СМЧД (${{10}^{6}}\,{{M}_{ \odot }}$) на ${{r}_{p}} = 100\,{{R}_{ \odot }}$. Кружками желтого, оранжевого и фиолетового цветов обозначены звезда, планета-гигант и СМЧД соответственно. АКП объекты показаны зелеными точками.

Следующий расчет в модели $A$ был проведен для варианта с квадратурной начальной конфигурацией. СМЧД задана на оси $z$, перпендикулярно линии, соединяющей положения звезды и планеты, расположенных вдоль оси $y$. После прохождения перицентра часть АКП объектов получает ускорение, позволяющее им освободиться от гравитационного влияния звезды и планеты-гиганта. Это хорошо иллюстрирует рис. 2, приведенный на финальный момент расчета, на котором видно два симметричных “АКП-фонтана”, бьющих из околозвездного тора. Их происхождение связано с выбросами АКП объектов из тех участков тора, которые при прохождении перицентра СМЧД оказываются из-за приливной деформации ближе всего к Солнцу. Также на этом графике (впереди) виден разрыв тора вокруг “Юпитера”, расчищающего себе орбитальную трассу, группируя АКП в облако спутников радиусом $ \sim {\kern 1pt} 0.112$ a.e. ($ \sim {\kern 1pt} 230{\kern 1pt} {{R}_{J}}$). Отметим, что в варианте с сизигийной начальной конфигурацией подобные разрывы вокруг “Юпитера” и “АКП-фонтаны” также образовались после прохождения перицентра, но в менее выраженной форме.
Рис. 2.
Финальный вид АКП-тора в модели $A$, рассчитанной для варианта с квадратурной начальной конфигурацией для перицентрического сближения родительской звезды с СМЧД (${{10}^{6}}\,{{M}_{ \odot }}$) на ${{r}_{p}} = 100\,{{R}_{ \odot }}$.

Для выяснения статуса АКП объекта после прохождения им перицентра рассчитывалось изменение его полной энергии (сумма кинетической и гравитационной энергий взаимодействия с СМЧД, звездой и планетой-гигантом) по сравнению с ее величиной в апоцентре, $\Delta E = ({{E}_{{{{r}_{p}}}}} - {{E}_{{{{r}_{a}}}}})$, который условно заменяет уход на бесконечность. Если $\Delta E$ превышает начальную энергию связи с родительской звездой и планетой-гигантом, $U_{b}^{0} = - G{{m}_{{{\text{AKP}}}}}({{M}_{ \odot }}{\text{/}}{{d}_{{2,0}}} + {{M}_{J}}{\text{/}}{{d}_{{3,0}}})$, то АКП объект будет свободным, унеся весь прирост энергии на бесконечность. Таким образом, из условия прироста полной энергии после прохождения перицентра, $\Delta E + U_{b}^{0} > 0$, выделяется статистика свободных АКП объектов (${{N}^{{ub}}}$), и, соответственно, согласно условию убыли полной энергии после прохождения перицентра, ΔE + $ + \;U_{b}^{0} < 0$, отбираются связанные c планетной системой АКП объекты (${{N}^{b}}$). Также были оценены статистики АКП, упавших на планету-гигант, звезду или разрушенных приливной гравитацией СМЧД: $N_{{{\text{fall}}}}^{J}$, $N_{{{\text{fall}}}}^{ \odot }$, $N_{{{\text{fall}}}}^{{{\text{SMBH}}}}$ соответственно (см. табл. 2).
Таблица 2.
АКП-статистики в модели $A$. ${{N}_{0}} = {{10}^{4}}$
| ${{\vec {V}}_{{{\text{orb}}}}}$ | АКП-статистики | ||||||
|---|---|---|---|---|---|---|---|
| ось | ${{N}_{{{{r}_{p}}}}}$ | $N_{{{\text{fall}}}}^{J}$ | $N_{{{\text{fall}}}}^{ \odot }$ | $N_{{{\text{fall}}}}^{{{\text{SMBH}}}}$ | ${{N}^{{ub}}}$ | ${{N}^{b}}$ | $N_{{{\text{HVA}}}}^{{}}$ |
| ${{r}_{p}} = 100\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 9980 | 20 | 0 | 0 | 5257 | 4723 | 3 |
| $z$ | 9979 | 21 | 0 | 0 | 4836 | 5143 | 9 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 9975 | 25 | 0 | 0 | 7284 | 2691 | 37 |
| $y$ | 9972 | 28 | 0 | 0 | 6035 | 3937 | 46 |
| ${{r}_{p}} = 50\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 9979 | 21 | 0 | 0 | 5260 | 4719 | 1 |
| $z$ | 9979 | 21 | 0 | 0 | 4654 | 5325 | 6 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 9972 | 27 | 1 | 0 | 8583 | 1389 | 49 |
| $y$ | 9970 | 28 | 2 | 0 | 8171 | 1799 | 78 |
| ${{r}_{p}} = 25\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 9978 | 22 | 0 | 0 | 5217 | 4761 | 1 |
| $z$ | 9979 | 21 | 0 | 0 | 4277 | 5702 | 5 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 9973 | 27 | 0 | 0 | 9010 | 963 | 2 |
| $y$ | 9972 | 28 | 0 | 0 | 9868 | 104 | 2 |
Примечание. ${{N}_{0}}$ – начальная численность АКП; $N_{{{\text{fall}}}}^{J}$, $N_{{{\text{fall}}}}^{ \odot }$, $N_{{{\text{fall}}}}^{{{\text{SMBH}}}}$ – число АКП, упавших на планету-гигант, звезду и СМЧД соответственно. ${{N}_{{{{r}_{p}}}}}$ – число АКП, сохранившихся после прохождения перицентра, из них выделены статистики свободных, ${{N}^{{ub}}}$ ($\Delta E + U_{b}^{0} > 0$), и связанных ${{N}^{b}}$ ($\Delta E + U_{b}^{0} < 0$) с родительской системой. Приведена статистика сверхскоростных АКП, ${{N}_{{{\text{HVA}}}}}$. Расчеты проведены для начальных состояний планетной системы в сизигийной и квадратурной конфигурациях для двух вариантов направления начальной скорости орбитального движения планетной системы (указана ось, вдоль которой задана ${{V}_{{{\text{orb}}}}}$ в начальный момент) и вариантов сближений ${{r}_{p}} = 100\,{{R}_{ \odot }}$; $50\,{{R}_{ \odot }}$; $25\,{{R}_{ \odot }}$.
На рис. 3 приведены спектры скоростей АКП объектов с приростом полной энергии, значение которого позволило вычислить скорость выброса АКП объекта из окрестности СМЧД:
(7)
${{v}_{{{\text{eject}}}}} = \sqrt {2{\kern 1pt} (\Delta E + U_{b}^{0}){\text{/}}{{m}_{{{\text{AKP}}}}}} .$Рис. 3.
Рассчитанные в модели $A$ спектры скоростей АКП объектов, гравитационно рассеянных СМЧД с массой ${{10}^{6}}\,{{M}_{ \odot }}$, для вариантов перицентрического сближения на $100\,{{R}_{ \odot }}$ (слева), $50\,{{R}_{ \odot }}$ (центр) и $25\,{{R}_{ \odot }}$ (справа) в ряду соответственно. Графики верхнего ряда соответствуют варианту с начальной сизигийной конфигурацией, нижнего – для квадратурной. Правее штриховой линии расположена область сверхскоростных АКП (${{V}_{{{\text{eject}}}}} > 750$ км/с).
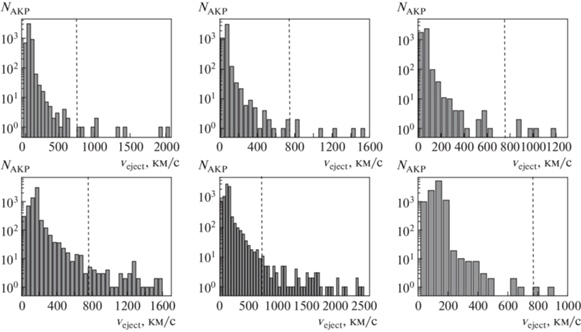
Из анализа спектра скоростей производится отбор кандидатов в сверхскоростные АКП объекты (статистика ${{N}_{{{\text{HVA}}}}}$ в табл. 2) согласно критерию преодоления гравитационного поля центральной области галактики ${{v}_{{{\text{eject}}}}} > 750$ км/с, найденному Ву и др. [61]. Как видно из табличных данных, число сверхскоростных выбросов АКП объектов возрастает в варианте с квадратурной начальной конфигурацией планетной системы. Это справедливо для расчетов с ${{r}_{p}} = 100\,{{R}_{ \odot }}$ и ${{r}_{p}} = 50\,{{R}_{ \odot }}$. Объяснение этой корреляции, возможно, связано с переходом в перицентре орбиты первоначально квадратурной конфигурации трех тел (СМЧД, звезды и планеты-гиганта) в сизигийную, при котором приливный эффект трех тел усиливается, создавая благоприятные для выброса условия.
Подчеркнем, что планетная система “забывает” о начальных условиях – важен тип конфигурации не в начальный момент времени, а в момент перицентрического сближения. Сизигийные начальные конфигурации в перицентре оказались квадратурными и независимо от перицентрического сближения ($100\,{{R}_{ \odot }}$, $50\,{{R}_{ \odot }}$, $25\,{{R}_{ \odot }}$) показали стабильную статистку АКП объектов с приростом полной энергии после прохождения перицентра ($ \sim {\kern 1pt} 53\% $). В то же время начальные квадратурные конфигурации в перицентре трансформировались в сизигийные, суммарный приливный эффект в которых способствовал эффективному рассеянию АКП объектов с приростом энергии после прохождения перицентра. Хорошо просматривается корреляция роста численности АКП объектов с приростом энергии 70, 86 и 98% при уменьшении ${{r}_{p}}$ на $100\,{{R}_{ \odot }}$, $50\,{{R}_{ \odot }}$ и $25\,{{R}_{ \odot }}$ соответственно.
Интересно сравнить моменты прохождения перицентра и финальный вид АКП-тора, рассчитанные в модели $A$ для варианта с начальной квадратурной конфигурацией при ${{r}_{p}} = 50\,{{R}_{ \odot }}$ (верхний ряд графиков рис. 4) и ${{r}_{p}} = 25\,{{R}_{ \odot }}$ (нижний ряд графиков рис. 4). Хорошо видно, что при подлете к перицентру при ${{r}_{p}} = 50\,{{R}_{ \odot }}$ (левый график верхнего ряда рис. 4) звезда заметно сместилась со своего первоначального центрального положения внутри АКП-тора к его образующей (сместилась на 5.2 a.e.) и оказалась приподнята приливной гравитацией СМЧД на $ \sim {\kern 1pt} 0.25$ a.e. над плоскостью АКП-тора. При сближении на ${{r}_{p}} = 25\,{{R}_{ \odot }}$ (левый график нижнего ряда рис. 4) звезда в момент прохождения перицентра вообще вылетела из тора, удалившись от положения центра АКП-тора на 6.2 a.e. Возможно, это объясняет резкое снижение статистики сверхскоростных АКП и отсутствие “АКП-фонтанов” (правый график нижнего ряда рис. 4), поскольку оставшись без “АКП-свиты”, звезда уединенно проходит область перицентра. На правом верхнем графике рис. 4 показан АКП-тор после прохождения перицентра ${{r}_{p}} = 50\,{{R}_{ \odot }}$ с тремя разрывами: на заднем плане графика разрыв соответствует месту нахождения Юпитера, который расчистил вокруг себя пространство от АКП, а на переднем плане графика два приливных “АКП-фонтана” – места эффективного выброса АКП объектов, оказавшихся рядом со звездой при ее прохождении перицентра. На финальных графиках отсутствуют обозначения планеты-гиганта и звезды, как разрушенные под действием приливных сил при перицентрических сближениях, меньших $85\,{{R}_{ \odot }}$.
Рис. 4.
Пространственные конфигурации планетной системы в модели $A$, рассчитанные для варианта с начальной квадратурной конфигурацией для ${{r}_{p}} = 50\,{{R}_{ \odot }}$ (верхний ряд графиков) и ${{r}_{p}} = 25\,{{R}_{ \odot }}$ (нижний ряд графиков). Графики слева соответствуют моменту прохождения звездой перицентра СМЧД, справа – финальный вид АКП-тора. Описание графиков в тексте.

В расчетах, проведенных для ${{r}_{p}} = 100\,{{R}_{ \odot }}$ и $50\,{{R}_{ \odot }}$, “АКП-фонтаны” образуются в обоих конфигурациях, но в расчетах с начальной квадратурной конфигурацией они заметнее выражены. Также следует отметить, что расстояние между “АКП-фонтанами”, полученными в квадратурных расчетах для ${{r}_{p}} = 50\,{{R}_{ \odot }}$, сокращается, поскольку звезда при прохождении перицентра сместилась на край АКП-тора и ее сопровождает лишь небольшая доля АКП объектов, тогда как при ${{r}_{p}} = 100\,{{R}_{ \odot }}$ звезда оставалась внутри тора. В расчетах с ${{r}_{p}} = 25\,{{R}_{ \odot }}$ звезда вылетела из тора, в результате чего вообще не сложились условия для обмена импульсом в классической задаче трех тел.
Основные выводы из проведенных расчетов в пределах изученного диапазона ${{r}_{p}}$:
• в расчетах для варианта с начальной сизигийной конфигурацией, которая в перицентре трансформируется в квадратурную, генерация свободных АКП объектов (${{N}^{{ub}}}$) оказывается стабильной ($ \sim {\kern 1pt} 50\% $) и не зависит от перицентрического сближения;
• в расчетах с квадратурной начальной конфигурацией генерация свободных АКП эффективнее ($ \sim {\kern 1pt} 70\% $) и возрастает (до $ \sim {\kern 1pt} 98\% $) с уменьшением ${{r}_{p}}$;
• генерация сверхскоростных АКП (${{N}_{{{\text{HVA}}}}}$) эффективнее в вариантах с начальной квадратурной конфигурацией, которая в перицентре переходит в сизигийную с максимальным приливным эффектом; однозначной корреляции с ${{r}_{p}}$ нет, поскольку с уменьшением перицентрического расстояния звезда постепенно выталкивается из АКП-тора, проходя перицентр СМЧД уединенно.
• независимо от типа начальной конфигурации примерно одинаковое число АКП падает на Юпитер при прохождении перицентра ($ \sim {\kern 1pt} 0.2\% $).
4.2. Модели $B$ и $C$
Рассмотрим в качестве начальной конфигурации возмущенное состояние планетной системы, приобретенное в результате гравитационного рассеяния АКП объектов на гиганте-Юпитере и Солнце. Для этого были использованы записи динамической эволюции планетной системы на моменты времени 2400 лет (модель $B$) и 16 800 лет (модель $C$) [52]. Начальные параметры орбиты приведены в табл. 1.
Численное моделирование проводилось аналогично так же, как для модели $A$: 12 расчетов, описывающих варианты для сизигийной и квадратурной начальной конфигураций, с учетом вариации перицентрического сближения родительской звезды с СМЧД на $100\,{{R}_{ \odot }}$, $50\,{{R}_{ \odot }}$ и $25\,{{R}_{ \odot }}$, а также вариации направления вектора скорости орбитального движения ${{V}_{{{\text{orb}}}}}$ в начальный момент времени (табл. 3 и 4).
Таблица 3.
АКП-статистики, полученные в расчетах для модели $B$. ${{N}_{0}} = 8{\kern 1pt} 140$
| ${{\vec {V}}_{{{\text{orb}}}}}$ | АКП-статистики | ||||||
|---|---|---|---|---|---|---|---|
| ось | ${{N}_{{{{r}_{p}}}}}$ | $N_{{{\text{fall}}}}^{J}$ | $N_{{{\text{fall}}}}^{ \odot }$ | $N_{{{\text{fall}}}}^{{{\text{SMBH}}}}$ | ${{N}^{{ub}}}$ | ${{N}^{b}}$ | $N_{{{\text{HVA}}}}^{{}}$ |
| ${{r}_{p}} = 100\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 8120 | 8 | 12 | 0 | 3937 | 4183 | 8 |
| $z$ | 8116 | 10 | 14 | 0 | 3928 | 4188 | 10 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 8137 | 3 | 0 | 0 | 4499 | 3638 | 2 |
| $y$ | 8135 | 5 | 0 | 0 | 4672 | 3463 | 0 |
| ${{r}_{p}} = 50\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 8117 | 9 | 14 | 0 | 3939 | 4178 | 9 |
| $z$ | 8115 | 10 | 15 | 0 | 3918 | 4197 | 9 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 8135 | 5 | 0 | 0 | 4597 | 3538 | 1 |
| $y$ | 8135 | 5 | 0 | 0 | 4781 | 3354 | 0 |
| ${{r}_{p}} = 25\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 6629 | 7 | 19 | 1485 | 3902 | 2727 | 7 |
| $z$ | 8117 | 9 | 14 | 0 | 3934 | 4183 | 10 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 7845 | 3 | 0 | 292 | 4604 | 3241 | 0 |
| $y$ | 7892 | 4 | 0 | 244 | 4747 | 3145 | 0 |
Примечание. Структура и описание данных аналогичны табл. 2.
Таблица 4.
АКП-статистики, полученные в расчетах для модели $C$. ${{N}_{0}} = 5{\kern 1pt} 966$
| ${{\vec {V}}_{{{\text{orb}}}}}$ | АКП-статистики | ||||||
|---|---|---|---|---|---|---|---|
| ось | ${{N}_{{{{r}_{p}}}}}$ | $N_{{{\text{fall}}}}^{J}$ | $N_{{{\text{fall}}}}^{ \odot }$ | $N_{{{\text{fall}}}}^{{{\text{SMBH}}}}$ | ${{N}^{{ub}}}$ | ${{N}^{b}}$ | $N_{{{\text{HVA}}}}^{{}}$ |
| ${{r}_{p}} = 100\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 5940 | 14 | 12 | 0 | 2710 | 3230 | 6 |
| $z$ | 5946 | 10 | 10 | 0 | 2704 | 3242 | 6 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 5964 | 2 | 0 | 0 | 3200 | 2764 | 0 |
| $y$ | 5965 | 1 | 0 | 0 | 3488 | 2477 | 0 |
| ${{r}_{p}} = 50\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 5946 | 14 | 6 | 0 | 2722 | 3224 | 5 |
| $z$ | 5943 | 11 | 12 | 0 | 2705 | 3238 | 5 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 5965 | 1 | 0 | 0 | 3259 | 2706 | 0 |
| $y$ | 5964 | 2 | 0 | 0 | 3533 | 2431 | 1 |
| ${{r}_{p}} = 25\,{{R}_{ \odot }}$ $y$-сизигийная начальная конфигурация |
|||||||
| $x$ | 5014 | 10 | 7 | 935 | 2681 | 2333 | 3 |
| $z$ | 5941 | 10 | 15 | 0 | 2708 | 3233 | 7 |
| $z$-квадратурная начальная конфигурация | |||||||
| $x$ | 5699 | 3 | 0 | 264 | 3180 | 2519 | 0 |
| $y$ | 5680 | 3 | 0 | 283 | 3395 | 2285 | 0 |
Примечание. Структура и описание данных аналогичны табл. 2.
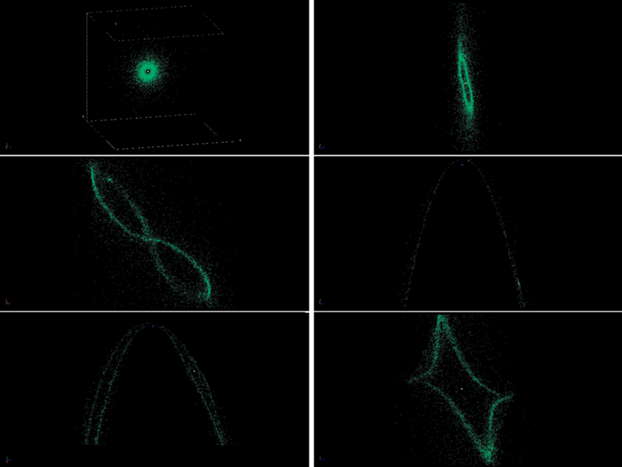
Рассмотрим особенности динамической эволюции планетной конфигурации в модели $B$ при сближении родительской звезды с СМЧД на расстояние ${{r}_{p}} = 100\,{{R}_{ \odot }}$. На рис. 5 (вверху, слева) показана начальная сизигийная конфигурация планетной системы, заданная в плоскости $xy$, в апоцентре. Направление ее орбитального движения в начальный момент времени ориентировано вдоль оси $x$. На правом графике верхнего ряда показана деформация АКП-тора, вытянутого приливными силами по направлению к СМЧД с заметным сужением к центральной звезде ($t \sim 12$ лет). Это сужение (стягивание тора) становится более выраженным к моменту $ \sim {\kern 1pt} 26$ лет (все еще до прохождения перицентра), когда родительская звезда своей гравитацией стягивает к себе орбиты близких АКП, собирая их в центральное облако, что придает тору форму восьмерки, в верхней части которой заметно еще одно облако (радиуса $4.4 \times $ × 10–3 a.e.) АКП объектов, захваченных Юпитером. Следующие два графика (правый график центрального ряда и левый график нижнего ряда) отражают процесс “спагеттизации” АКП-тора в перицентре СМЧД, соответствующий моментам прохождения перицентра Юпитером ($ \sim {\kern 1pt} 30.5$ лет) и Солнцем ($ \sim {\kern 1pt} 33$ лет). На правом графике нижнего ряда представлена финальная конфигурация планетной системы после сближения с СМЧД ($t \sim $ ~ 44 лет) с остаточной приливной деформацией в форме суперэллипса (3D-аналог кривой Ламе с $n = 1{\text{/}}2$).
Рис. 5.
Пространственные конфигурации планетной системы в модели $B$ для варианта с начальной сизигийной конфигурацией с ${{r}_{p}} = 100\,{{R}_{ \odot }}$. Описание графиков в тексте.
На рис. 6 показана расчетная орбита (против часовой стрелки), составленная из конфигураций планетной системы в модели $B$ для варианта c начальной квадратурной конфигурацией. В этих расчетах получается заметно меньше выбросов АКП с высокими скоростями (${{N}_{{{\text{HVA}}}}}$) по сравнению с расчетами для модели $A$, что объясняется, вероятно, относительно меньшей плотностью АКП объектов в окрестности Солнца при прохождении им перицентра.
Рис. 6.
Пространственные конфигурации планетной системы, рассчитанные в модели $B$ для варианта с начальной квадратурной конфигурацией при ${{r}_{p}} = 100\,{{R}_{ \odot }}$. Описание графика в тексте.

Расчеты, проведенные для модели $B$ в сизигийной начальной конфигурации c перицентрическим сближением звезды с СМЧД на расстояниях ${{r}_{p}} = 50\,{{R}_{ \odot }}$ и ${{r}_{p}} = 25\,{{R}_{ \odot }}$, позволили выделить более сложные по форме деформации планетной системы: перекрученный планетный тор с центральным суперэллипсом, как, например, показано на графиках рис. 7.
Рис. 7.
Слева – финальная конфигурация планетной системы в модели $B$ с ${{r}_{p}} = 50\,{{R}_{ \odot }}$. Справа – момент прохождения перицентра Юпитером в модели $B$ с ${{r}_{p}} = 25\,{{R}_{ \odot }}$. Графики демонстрируют расчеты для варианта с сизигийной начальной конфигурацией.

Анализ статистик свободных и связанных АКП после прохождения перицентра ${{r}_{p}} = 100\,{{R}_{ \odot }}$ показывает, что в расчетах с квадратурной начальной конфигурацией генерация свободных АКП немного эффективнее ($ \sim {\kern 1pt} 55\% $) по сравнению с сизигийной ($ \sim {\kern 1pt} 50\% $). С уменьшением перицентрического расстояния процент освободившихся АКП в расчетах с начальной сизигийной конфигурацией почти не меняется, тогда как в расчетах с начальной квадратурной конфигурацией проявляется слабая тенденция увеличения статистики свободных АКП (с $ \sim {\kern 1pt} 55$ до $ \sim {\kern 1pt} 60\% $).
Спектры скоростей, полученные в расчетах для модели $B$, представлены на рис. 8. Интересно, что генерация сверхскоростных объектов из “распушенной” планетной системы в модели $B$ не столь эффективна, как в случае с упорядоченной структурой в Модели $A$. В “распушенной” системе АКП рассеяны по большему объему и в момент прохождения перицентра их оказывается не так много вблизи звезды. С другой стороны, в модели $B$ появилась статистика АКП, упавших на Солнце, Юпитер и СМЧД, причем при ${{r}_{p}} = 25\,{{R}_{ \odot }}$ число АКП, упавших на СМЧД, резко возрастает, особенно в варианте с начальной сизигийной конфигурацией и начальным направлением орбитальной скорости вдоль оси $x$.
Основные выводы, которые можно сделать из проведенных расчетов для модели $B$:
• в вариантах с начальной сизигийной конфигурацией генерация свободных АКП объектов (${{N}^{{ub}}}$) стабильна ($ \sim {\kern 1pt} 50\% $) и не зависит от перицентрического сближения;
• в квадратурных начальных конфигурациях генерация свободных АКП также близка к стабильной ($ \sim {\kern 1pt} 55\% $) и слабо возрастает ($ \sim {\kern 1pt} 55{\kern 1pt} - {\kern 1pt} 60\% $) с уменьшением ${{r}_{p}}$;
• результаты генерации сверхскоростных АКП объектов (${{N}_{{{\text{HVA}}}}}$) в вариантах с начальной сизигийной конфигурацией такие же, как в модели $A$;
• в вариантах с квадратурной начальной конфигурацией сверхскоростные АКП почти не образуются в отличие от модели $A$. Это связано с изначально высокой рассеянностью АКП объектов в модели $B$, в которой оказывается лишь малая их концентрация вблизи звезды или планеты-гиганта при прохождении перицентра СМЧД;
• статистика АКП, выпавших на Юпитер, несколько меньше по сравнению с результатами расчетов, полученных в модели $A$;
• в расчетах с сизигийной начальной конфигурацией появилась статистика АКП, выпавших на Солнце, в то время как в расчетах с квадратурной начальной конфигурацией их статистика отсутствует из-за того, вероятно, что Солнце, изначально находясь ближе всех к СМЧД, выталкивается ее гравитацией из тора и проходит область перицентра уединенно;
• обращает внимание статистика АКП, поглощенных СМЧД, которая проявилась в расчетах с ${{r}_{p}} = 25\,{{R}_{ \odot }}$: $ \sim {\kern 1pt} 20\% $ в расчетах с сизигийной начальной конфигурации, $ \sim {\kern 1pt} 4\% $ – с квадратурной. Возможно, в этом причина снижения статистики сверхскоростных АКП – их кандидаты оказались проглоченными СМЧД.
Интерпретация результатов расчетов, полученных в Модели $C$, остается такой же, как в модели $B$. По этой же причине для модели $C$ не приведены графики приливной деформации планетной системы. На рис. 9 приведены спектры скоростей АКП объектов в модели $C$, полученные в ходе гравитационного рассеяния на СМЧД с массой ${{10}^{6}}\,{{M}_{ \odot }}$ с вариацией перицентрического расстояния ($100\,{{R}_{ \odot }}$, $50\,{{R}_{ \odot }}$, $25\,{{R}_{ \odot }}$) и вариантом конфигурации: сизигийная (верхний ряд графиков) или квадратурная (нижний ряд графиков).
Основные выводы, которые можно сделать из проведенных расчетов для модели $C$:
• в вариантах с начальной сизигийной конфигурацией генерация свободных АКП объектов (${{N}^{{ub}}}$) стабильна ($ \sim {\kern 1pt} 45\% $) и не зависит от ${{r}_{p}}$;
• в квадратурных начальных конфигурациях генерация свободных АКП слабо возрастает от ~53 до 60% с уменьшением перицентрического расстояния;
• результаты генерации сверхскоростных АКП объектов (${{N}_{{{\text{HVA}}}}}$) в вариантах с начальной сизигийной конфигурацией на уровне статистик в моделях $A$ и $B$;
• в вариантах с квадратурной начальной конфигурацией сверхскоростные АКП не образуются. Причина такая же, как для модели $B$: низкая концентрация АКП объектов (ввиду их разбросанности по планетному диску) вблизи звезды или планеты-гиганта во время прохождения ими перицентра СМЧД и высокая статистика АКП объектов как возможных кандидатов в HVA, поглощенных СМЧД;
• статистики АКП, выпавших на Юпитер и Солнце, как в расчетах для модели $B$;
• в расчетах с ${{r}_{p}} = 25\,{{R}_{ \odot }}$ отмечается высокий процент АКП объектов, поглощенных СМЧД: $ \sim {\kern 1pt} 16\% $ в сизигийной начальной конфигурации, $ \sim {\kern 1pt} 5\% $ – для квадратурной.
Главный вывод расчетов, проведенных в моделях $A$, $B$ и $C$ – демонстрация механизма образования свободных планет и астероидов в результате прохождения их родительской звезды вблизи СМЧД и возможность генерации сверхскоростных АКП объектов со скоростями ${{v}_{{{\text{eject}}}}} \geqslant 750$ км/c.
5. ЗАКЛЮЧЕНИЕ
Рассмотренный в статье сценарий динамического захвата родительской звезды с планетной системой в окрестность СМЧД продемонстрировал одну из возможностей образования свободных планет в галактиках с СМЧД в ядрах. Изученные в статье модели были нацелены на поиск сверхскоростных АКП, а потому рассматривались близкие перицентрические расстояния ($ < {\kern 1pt} 0.5$ a.e.), тогда как реальный интервал допустимых прицельных расстояний $ \sim {\kern 1pt} 100$ a.e. Взаимодействие АКП объектов планетных систем звезд ядер галактик с массивными планетами этих систем и с СМЧД создает в итоге хорошо населенный компонент свободных АКП объектов ядер и гало галактик. При этом часть АКП объектов получают скорости, достаточные для их освобождения не только из ядер своих галактик, но и покидания самих галактик. Так рождается АКП компонент скоплений галактик.
Звездный высокоскоростной компонент с относительной населенностью ~10–5 сегодня хорошо известен [62]. Межзвездные галактические астероиды (например, Borisov) уже найдены, очередь за межгалактическими астероидами. Отличительная особенность, которая указывает на сценарий образования межгалактической АКП при участии СМЧД, это ее высокая пространственная скорость ($ \geqslant {\kern 1pt} 1000$ км/с), которая на несколько порядков превосходит диапазон скоростей, достижимых в других механизмах освобождения планет.
К числу других механизмов можно отнести возмущающие прохождения звезд поля вблизи внешних слоев облака Оорта родительской звезды. Во-вторых, это может быть связано с влиянием Галактического прилива. Детальное изучение этих сценариев [63] показало, что за 5 млрд. лет облако Оорта может испытать $ \sim {\kern 1pt} 40{\kern 1pt} {\kern 1pt} 000$ звездных прохождений, вследствие которых лишиться до 30% малых планетных тел. Альтернативным вариантом является стадия планетарной туманности: в результате сброса своей оболочки “похудевшая” звезда не в состоянии контролировать пространство на рубеже внешних планет. Рожденные в таких сценариях свободные планеты приобретают пространственные скорости порядка нескольких км/с, что позволяет отнести их к классу “дрейфующих”.
Теоретические оценки и “наблюдаемая” частота приливного разрушения звезд ${{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 6}}}$ в год [11, 25, 28] в результате их взаимодействия с СМЧД, а также высокая распространенность звезд с планетными системами, позволяют говорить об астероидно-кометно-планетном компоненте как полноправном наряду со звездным и газовым в строении галактик. Быстрые астероиды – главный многочисленный продукт этой работы. Кроме того, планеты обрели статус инструмента, позволяющего открывать себе подобные далеко за пределами нашей Галактики.
Гравитационное нанолинзирование открыло новую страницу в обнаружении внегалактических свободных планет. Современная оценка числа свободных планет, вытекающая из наблюдений [64], допускает, что их число в Галактике может в десятки раз превышать число звезд в ней. По данным Subaru в технике пиксельного линзирования Ниикура и др. [65] детектировали пока одну свободную планету в туманности Андромеды. Из анализа сигнатур и каустик искаженного гравитационным линзированием квазарного света по данным наблюдений с обсерватории Bhatiani и др. [66] получили ограничения на распределение объектов планетных масс в диапазоне от массы Луны до массы Юпитера, находящихся внутри галактик или их скоплений, составляющих массовую долю от массы их гало 3 × 10–4 и 10–4 для галактики QJ0158–4325 на $z = 0.317$ и скопления галактик SDSS J1004+4112 на $z = 0.68$ соответственно. Важно, что эти объекты планетных масс не имеют родительской звезды, иначе ее радиус кольца Эйнштейна “поглотил” бы все производимые планетами искажения.
Таким образом, свободные планеты весьма распространены в галактиках, а фактор СМЧД позволяет им легко преодолевать межгалактические масштабы, чтобы однажды оказаться в Солнечной системе.
Список литературы
E. Opik, Astron. J. 10, 153 (1971).
I. Feain, P. Papapoulos, P. Ekers, and E. Middelberg, A-strophys. J. 662, 872 (2007).
J. Shangguan, L. C. Ho, F. E. Bauer, R. Wang, and E. Treister, Astrophys. J. 899, id. 112 (2020).
A. Tutukov and A. Fedorova, Astron. Rep. 52, 985 (2008).
A. DeGraf, D. Sijacki, T. Di Matteo, K. Holley-Bockelmann, G. Snyder, and V. Springel, Monthly Not. Roy. Astron. Soc. 503, 3629 (2021).
E. Kruegel, A. Tutukov, and H. Loose, Astron. and A-strophys. 124, 89 (1983).
A. C. Robleto-Orús, J. P. Torres-Papaqui, A. L. Longinotti, R. A. Ortega-Minakata, et al., Astrophys. J. Letters 906(2), id. 6 (2021).
J. S. Clark, L. R. Patrick, F. Najarro, C. J. Evans, and M. Lohr, Astron. and Astrophys. 649, id. A43 (2021).
S. Gezari, D. C. Martin, B. Milliard, S. Basa, et al., A-strophys. J. Letters 653, L25 (2006).
S. Gezari, T. Heckman, C. B. Cenko, M. Eracleous, et al., Astrophys. J. 698, 1367 (2009).
T. W.-S. Holoien, C. S. Kochanek, J. L. Prieto, K. Z. Sta-nek, et al., Monthly Not. Roy. Astron. Soc. 455, 2918 (2016).
S. Komossa, J. High Energy Astrophys. 7, 148 (2015).
J. Hills, Astrophys. J. Letters 17, 96 (1975).
J. Hills, Nature 254, 295 (1976).
J. Frank and M. Rees, Monthly Not. Roy. Astron. Soc. 176, 633 (1976).
V. I. Dokuchaev and L. M. Ozernoi, Soviet Astron. Letters 3, 209 (1977).
H. Zhang, P. Behroozi, M. Volonteri, J. Silk, X. Fan, P. F. Hopkins, J. Yang, J. Aird, arXiv:2105.10474 [astro-ph.GA] (2021).
M. McDonald, B. R. McNamara, M. S. Calzadilla, C.‑T. Chen, M. Gaspari, R. C. Hickox, E. Kara, and I. Korchagin, Astron. and Astrophys. 908, id. 85 (2021).
E. A. Shah, J. S. Kartaltepe, C. T. Magagnoli, I. G. Cox, et al., Astrophys. J. 904, id. 107 (2020).
J. Aird and A. Coil, Monthly Not. Roy. Astron. Soc. 502, 5962 (2021).
C. Ward, S. Gezari, S. Frederick, E. Hammerstein, et al., Astrophys. J. 913, id. 102 (2021).
M. Rees, Nature 333, 523 (1988).
V. Stoeger, A. Pacholczyk, and T. Stepinski, Astrophys. J. 391, 550 (1992).
S. Kisaka and Ya. Kojima, Monthly Not. Roy. Astron. Soc. 405, 1285 (2010).
D. Syer and A. Ulmer, Monthly Not. Roy. Astron. Soc. 306, 35 (1999).
N. Stone and B. Metzger, Monthly Not. Roy. Astron. Soc. 455, 859 (2016).
T. Ryu, J. Krolik, and T. Piran, Astrophys. J. 904, id. 73 (2020).
H. Pfister, M. Volonteri, and J. Dai, Monthly Not. Roy. Astron. Soc. 497, 2276 (2020).
N. Stone and S. van Velzen, Astrophys. J. Letters 825, id. 14 (2016).
N. Stone, M. Kesden, R. Cheng, and S. van Velsen, General Relativ. and Gravit. 51, 30 (2019).
I. Iben and A. Tutukov, Astrophys. J. Suppl. 54, 335 (1984).
S. Chandrasekhar, Astrophys. J. 93, 285 (1941).
S. Tremaine, Astrophys. J. 625, 143 (2005).
E. V. Polyachenko, P. Berczik, A. Just, I. G. Shukhman, Monthly Not. Roy. Astron. Soc. 492, 645 (2020).
E. V. Polyachenko, P. Berczik, A. Just, and I. G. Shukh-man, Monthly Not. Roy. Astron. Soc. 492, 4819 (2020).
S. Chandrasekhar, Rev. Modern Physics 15, 1 (1943).
A. Tutukov, Astron. Rep. 63, 79 (2019).
J. Ostriker and P. Peebles, Astrophys. J. 186, 467 (1973).
E. M. Di Teodoro, L. Posti, P. M. Ogle, S. M. Fall, and T. Jarrett, Monthly Not. Roy. Astron. Soc. 507, 5820 (2021).
D. D. Nguyen, M. Bureau, S. Thater, K. Nyland, et al., arXiv:2110.08476 [astro-ph.GA] (2021).
А. Масевич, А. Тутуков, Эволюция звезд: теория и наблюдения (М.: Наука, 1988).
T. Wevers, S. van Velzen, P. G. Jonker, N. C. Stone, T. Hung, F. Onori, S. Gezari, and N. Blagorodnova, Monthly Not. Roy. Astron. Soc. 471, 1694 (2017).
T. Wevers, N. Stone, S. van Velzen, P. G. Jonker, et al., Monthly Not. Roy. Astron. Soc. 487, 4136 (2019).
E. Athanassoula, J. Makino, and A. Bosma, Monthly Not. Roy. Astron. Soc. 286, 825 (1997).
R. J. McLure, H. J. Pearce, J. S. Dunlop, M. Cirasuolo, et al., Monthly Not. Roy. Astron. Soc. 428, 1088 (2013).
J. A. O’Leary, B. P. Moster, T. Naab, and R. S. Somerville, Monthly Not. Roy. Astron. Soc. 501, 3215 (2021).
A. Vayner, N. L. Zakamska, R. A. Riffel, R. Alexandroff, et al., Monthly Not. Roy. Astron. Soc. 504, 4445 (2021).
A. Tutukov, Soviet Astron. 31, 663 (1987).
D. Barbato, A. Bonomo, A. Sozzetti, and R. Morbidelli, Proc. IAU Symp. 348 21st Century Astrometry: crossing the Dark and Habitable frontiers, (2018), arXiv:1811.08249 [astro-ph.EP].
M. Tuomi, H. R. A. Jones, R. P. Butler, P. Arriagada, et al., arXiv:1906.04644 [astro-ph.EP] (2019).
J. H. Checlair, G. L. Villanueva, B. P. C. Hayworth, S. L. Olson, et al., Astron. J. 161, 150 (2021).
A. Tutukov, G. Dryomova, and V. Dryomov, Astron. Rep. 64, 946 (2020).
A. Do, M. Tucker, and J. Tonry, Astrophys. J. Letters 855, id. 10 (2018).
A. Siraj and A. Loeb, arXiv:2002.01476 [astro-ph.EP] (2020).
M. Froncisz, P. Brown, and R. Weryk, arXiv:2005.10896 [astro-ph.EP] (2020).
G. V. Borisov and B. M. Shustov, Solar System Res. 55, 124 (2021).
L. Verlet and J. J. Weis, Phys. Rev. A 5, 939 (1972).
G. Dremova, V. Dremov, and A. Tutukov, Astron. Rep. 58, 291 (2014).
G. Dryomova, V. Dryomov, and A. Tutukov, Baltic Astronomy 24, 1 (2015).
G. Flynn, G. Consolmagno, P. Brown, and R. Macke, Chemie der Erde 78, 269 (2018).
X. Wu, B. Famaey, G. Gentile, H. Perets, and H. Zhao, Monthly Not. Roy. Astron. Soc. 386, 2199 (2008).
T. Marchetti, Monthly Not. Roy. Astron. Soc. 503, 1374 (2021).
J. A. Correa-Otto and M. F. Callandra, Monthly Not. Roy. Astron. Soc. 490 2495 (2019).
E. Bachelet, D. Specht, M. Penny, M. Hundertmark, et al., arXiv:2202.09475 [astro-ph.EP] (2022).
H. Niikura, M. Takada, N. Yasuda, R. H. Lupton, et al., Nature Astron. 3, 524 (2019).
S. Bhatiani, X. Dai, and E. Guerras, Astrophys. J. 885 id. 77 (2019).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал




