1. На главную
  2. Электронные версии
  3. Астрономический журнал
  4. T. 99, № 8, 2022

Астрономический журнал, 2022, T. 99, № 8, стр. 650-674

Сравнение углов между магнитным моментом и осью вращения для двух групп радиопульсаров

З. В. Кенько 1, Ф. Малов 2, *

1 Пущинский государственный естественно-научный институт
Пущино, Россия

2 Физический институт им. П.Н. Лебедева РАН, Пущинская радиоастрономическая обсерватория им. В.В. Виткевича, Астрокосмический центр
Пущино, Россия

* E-mail: malov@prao.ru

Поступила в редакцию 11.04.2022
После доработки 28.05.2022
Принята к публикации 21.06.2022

Полный текст (PDF)

Аннотация

Проведены вычисления углов $\beta $ между осью вращения и магнитным моментом в двух группах радиопульсаров, отличающихся периодами ($P > 2$ с и $0.1{\text{ с}} < P < 2$ с). Использованы два метода. Первый основан на наблюдаемых ширинах импульса и дает минимальные значения угла ${{\beta }_{1}}$. Распределения этих углов значимо отличаются для указанных групп объектов. Во втором методе используются поляризационные данные, позволяющие вычислить более точные величины ${{\beta }_{2}}$. Намечается бимодальность в распределении значений ${{\beta }_{2}}$ для пульсаров с $P > 2$ с. Близость средних величин ${{\beta }_{2}}$ ($47.6^\circ $ для долгопериодических пульсаров и 35.6° для источников с более короткими периодами) не позволяет объяснить обнаруженное ранее различие поведения этих двух групп на диаграмме $(dP{\text{/}}dt) - (P)$ уменьшением роли магнитодипольного излучения из-за уменьшения $\beta $. Проведенные нами оценки показали, что наблюдаемое различие может быть объяснено разной зависимостью мощностей пульсарного ветра и магнитодипольного торможения от периода пульсара. Торможение пульсаров с $P > 2$ с вызвано в основном пульсарным ветром.

Ключевые слова: нейтронные звезды, радиопульсары, структура магнитосферы, механизмы торможения

1. ВВЕДЕНИЕ

Одним из инструментов, используемых для анализа путей эволюции радиопульсаров, остается исследование положения этих объектов на диаграмме $(dP{\text{/}}dt) - (P)$, которая описывает зависимость производной периода между последовательными импульсами от самого периода. Это связано с тем обстоятельством, что указанные величины измеряются непосредственно в процессе достаточно длительных наблюдений и не связаны с различными предположениями о природе пульсаров и их моделях. В работе [1] были исследованы соответствующие диаграммы для трех групп пульсаров, отличающихся величиной периода: $P > 2$ с, $0.1{\text{ с}} < P < 2$ с и $P < 0.1$ с. Было показано, что вращение пульсаров первой группы замедляется выносом углового момента релятивистскими частицами (пульсарным ветром). В этом случае потеря энергии вращения описывается следующим выражением [2]:

(1)
$I\Omega \frac{{d\Omega }}{{dt}} = - \frac{{L_{p}^{{1/2}}BR_{*}^{3}{{\Omega }^{2}}}}{{{{{(6{{c}^{3}})}}^{{1/2}}}}}.$
Здесь $I$ – момент инерции нейтронной звезды, ${{R}_{*}}$ – ее радиус, $\Omega = 2\pi {\text{/}}P$ – угловая скорость вращения, $B$ – магнитное поле на поверхности, ${{L}_{p}}$ – мощность ветра, $c$ – скорость света.

Во второй группе к пульсарному ветру подключается магнитодипольное излучение нейтронной звезды [3]:

(2)
$I\Omega \frac{{d\Omega }}{{dt}} = - \frac{{{{B}^{2}}R_{*}^{6}{{\Omega }^{4}}{{{\sin }}^{2}}\beta }}{{6{{c}^{3}}}}.$

Источники третьей группы тормозятся обоими механизмами. В [1] было высказано предположение о том, что малый вклад магнитодипольного излучения в первой популяции определяется значением угла $\beta $ между магнитным моментом нейтронной звезды и осью ее вращения. Действительно, из выражения (2) следует, что чем меньше этот угол при прочих равных параметрах, тем меньше вклад магнитодипольного механизма. Для проверки такого предположения необходимо провести вычисления угла $\beta $ для пульсаров с разными периодами и проанализировать отличие этого угла в различных популяциях.

В течение всех лет исследования пульсаров предпринимались многочисленные попытки вычисления углов $\beta $ с использованием различных методов [4–8]. Важно было также понять, как эволюционирует этот угол с возрастом пульсара. В работе [9] построена модель магнитосферы, в которой угол $\beta $ должен увеличиваться со временем, т.е. пульсары стремятся стать ортогональными ротаторами. Однако дальнейшие магнитогидродинамические расчеты [10] показали, что наклон магнитного момента к оси вращения с возрастом уменьшается по степеннóму закону.

Мы здесь анализируем отличие угла $\beta $ для двух групп пульсаров с $P > 2$ с и $0.1{\text{ с}} < P < 2$ с. Что касается объектов с $P < 0.1$ с, то в них начинают играть роль релятивистские эффекты [11] и для вычисления $\beta $ могут потребоваться другие методы, отличающиеся от описываемых в следующем разделе.

2. ИСПОЛЬЗУЕМЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ УГЛА $\beta $

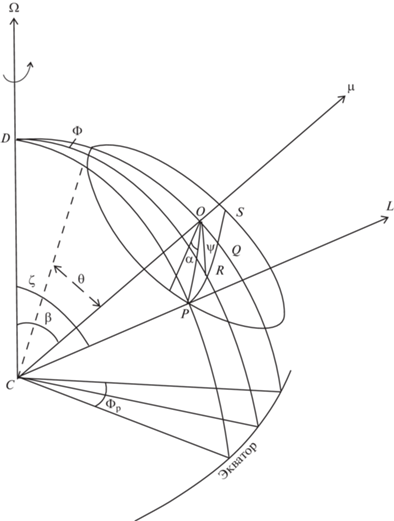
В дальнейшем используется модель полярной шапки, представленная на рис. 1. Сферическая тригонометрия позволяет записать уравнение, связывающее углы $\beta ,\zeta $ и $\theta $,

(3)
$\cos \theta = \cos \beta \cos \zeta + \sin \beta \sin \zeta \cos \Phi .$
Рис. 1.

Геометрия конуса излучения пульсара в модели полярной шапки: ${{\Phi }_{р}}$ – половина наблюдаемой ширины импульса, $\vec {\Omega }$ – ось вращения пульсара, $\mu $ – вектор дипольного магнитного момента, $L$ – луч зрения наблюдателя, $\theta $ – угловой радиус конуса излучения, $\zeta $ – угол между лучом зрения и осью вращения, $\beta $ – угол между осью вращения и вектором магнитного момента, $\psi $ – позиционный угол плоскости поляризации излучения, $\Phi $ – долгота.

Для определения всех трех углов необходимы еще два уравнения.

Самый простой метод оценки связан с предположением о прохождении луча зрения через центр конуса излучения. В этом случае

(4)
$\beta = \zeta ,$
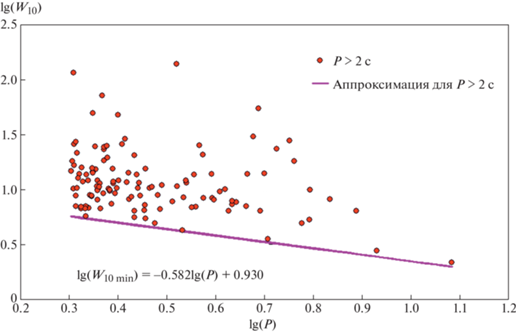
а в качестве третьего уравнения можно использовать статистическую зависимость ширины импульса по уровню 10% от периода ${{W}_{{10}}}(P)$, полагая, что наблюдаемая ширина профиля связана с положением конуса излучения относительно оси вращения. Реальному радиусу конуса будет соответствовать $\beta = 90^\circ $, что на диаграмме (${{W}_{{10}}}){\kern 1pt} - {\kern 1pt} (P)$ определяется нижней границей массива наблюдаемых значений:
(5)
$\theta = {{W}_{{10\min }}}(P){\text{/}}2,$
что на основе уравнения (3) дает возможность оценки угла $\beta $, используя следующее выражение:

(6)
$\beta = \arcsin \left( {\frac{{\sin \frac{{{{W}_{{10\min }}}}}{4}}}{{\sin \frac{{{{W}_{{10}}}}}{4}}}} \right).$

Поскольку мы считали, что наблюдаемое уширение импульса связано исключительно с приближением конуса излучения к оси вращения пульсара, вычисленные по формуле (6) значения угла $\beta $ представляют собой нижние пределы этого угла.

В дальнейшем мы будем использовать параметры пульсаров, приведенные в каталоге ATNF (последняя версия 1.67) [12].

Считается общепризнанным, что наблюдаемое радиоизлучение пульсаров генерируется механизмом излучения кривизны (curvature radiation). В этом случае позиционный угол $\psi $ линейной поляризации определяется проекцией магнитного поля, и его зависимость от других углов может быть представлена в виде [13]:

(7)
${\text{tg}}\psi = \frac{{\sin \beta \sin \Phi }}{{\sin \zeta \cos \beta - \cos \zeta \sin \beta \cos \Phi }}.$

Наблюдательные данные показывают, что для многих пульсаров ход позиционного угла измеряется только в пределах главного импульса на небольшом участке долгот $\Phi $. Скорость изменения позиционного угла достигает максимальной величины ${{(d\psi {\text{/}}d\Phi )}_{{\max }}}$, когда луч зрения пересекает меридиан, где находится магнитная ось ($\Phi = 0$).

(8)
${{\left| {\frac{{d\psi }}{{d\Phi }}} \right|}_{{\max }}} = \frac{{\sin \beta }}{{\sin (\zeta - \beta )}}.$

Величина ${{\Phi }_{p}}$ для наблюдаемого профиля, определяемая уравнением (3), задается углом $\beta $ (видимым уширением импульса при приближении к оси вращения) и угловым расстоянием ($\zeta - \beta $), на котором луч зрения пересекает конус излучения. Последний эффект уменьшает наблюдаемую ширину ${{\Phi }_{p}}$. Вклад каждого из этих эффектов заранее не известен, поэтому в среднем их можно считать равными, т.е. компенсирующими друг друга. Тогда зависимость $\theta (P)$ можно определить прямой, вписанной в массив ${{W}_{{10}}}(P)$ по методу наименьших квадратов, и положить

(9)
$\theta = \frac{{\langle {{W}_{{10}}}\rangle }}{2}.$

Выражения (3), (8) и (9) образуют систему трех уравнений, которая путем преобразований сводится к алгебраическому уравнению 4-й степени:

(10)
$\begin{gathered} C{{(1 - D)}^{2}}{{y}^{4}} + 2C(1 - D){{y}^{3}} + \\ + \;[1 + 2{{C}^{2}}D(1 - D)]{{y}^{2}} + 2C(D - {{B}^{2}})y + \\ \, + {{C}^{2}}{{D}^{2}} - {{B}^{2}}(1 + C2) = 0, \\ \end{gathered} $
где введены обозначения:
(11)
$\begin{gathered} B = \cos \theta ,\quad C = {\text{|}}d\psi {\text{/}}d\Phi {\kern 1pt} {{{\text{|}}}_{{\max }}}, \\ D = \cos \langle {{W}_{{10}}}\rangle {\text{/}}2,\quad y = \cos \zeta . \\ \end{gathered} $
Используя выражения (11), соотношение (8) можно переписать в виде:
(12)
${\text{tg}}{\kern 1pt} {\kern 1pt} \beta = \frac{{C{{{(1 - {{y}^{2}})}}^{{1/2}}}}}{{1 + Cy}}.$
Решив уравнение (10) относительно $y$, из (12) находим искомый угол $\beta $.

Уравнение (10) имеет 4 решения, из которых находятся 4 значения $\beta $. Некоторые решения могут оказаться комплексными и должны быть отброшены. Знак производной $C = (d\psi {\text{/}}d\Phi {{)}_{{\max }}}$ по наблюдениям только в пределах главного импульса определить нельзя, поскольку не известен знак $d\Phi $, пульсар может вращаться как по часовой стрелке, так и против нее, в связи с чем решать систему уравнений (10) и (12) необходимо при $C > 0$ и $C < 0$. Уравнение (10) может дать отрицательное значение $y = \cos \zeta $. Это соответствует $\zeta > 90^\circ $, что вполне возможно в реальных пульсарах.

При расчете углов $\beta $ этим методом использовался каталог поляриметрических данных для 600 пульсаров [14]. Исключались объекты в шаровых скоплениях и в двойных системах, где на их параметры влияют компаньоны. Учитывались также следующие факторы.

1) Скачок позиционного угла на $180^\circ $ соответствует простому его продолжению, т.е. поляриметрические кривые необходимо “сшить” в точке разрыва. Пример такого случая представлен на рис. 2.

Рис. 2.

Вверху: оцифрованный профиль хода позиционного угла $\psi (\Phi )$ в пределах импульса пульсара J2346$ - $0609 по данным каталога [14]; внизу – “сшитые” ветки $\psi (\Phi )$ и аппроксимация их полиномиальной функцией: $\psi (\Phi )$ = = $0.1014{{\Phi }^{3}}$ – $2.1966{{\Phi }^{2}}$ + $2.0967\Phi $ – $45.318$.

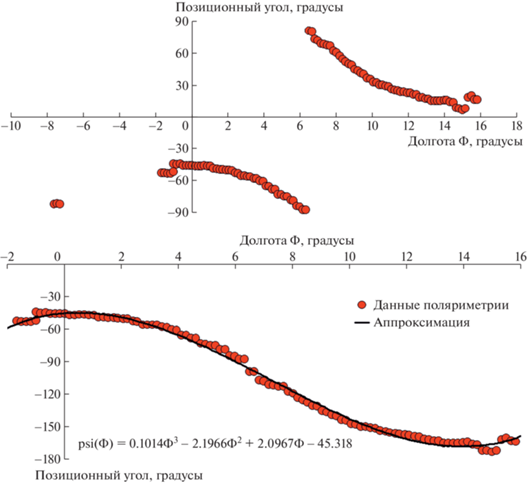
2) Скачк${\text{и}}\prime $ на $90^\circ $ или на меньшие значения свидетельствуют о наличии другой моды (или других поляризационных мод), и такие пульсары исключались из дальнейшего рассмотрения.

3) Также были исключены источники с затянутым правым “хвостом” в их импульсах. Эти “хвосты” вызваны рассеянием в среде между пульсаром и наблюдателем, которое может существенно исказить поляризационные свойства.

4) На S-образных зависимостях $\psi (\Phi )$ максимальная производная соответствует прямолинейной части кривой.

Следует отметить, что решение системы уравнений (10) и (12) существует не при любых значениях $B$, $C$ и $D$, полученных из наблюдений. Это может означать, что в ряде пульсаров рассмотренная модель, описывающая поведение позиционного угла, не работает.

Можно использовать и другие методы определения угла $\beta $ [11], но мы ограничимся здесь рассмотренными в данном разделе.

3. РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ УГЛА $\beta $

Как уже упоминалось, мы используем для анализа данные, приведенные в каталогах [12, 14].

Для дальнейших вычислений нужно выразить ширину $W$ импульса в градусах:

(13)
${{W}_{{10}}}\;[^\circ ] = 360^\circ \frac{{{{W}_{{10}}}\;{\text{[мс]}}}}{{P\;{\text{[мс]}}}}.$
На рис. 3 приведена диаграмма $({{W}_{{10}}}){\kern 1pt} - {\kern 1pt} (P)$ для пульсаров с $P > 2$ с.

Рис. 3.

Зависимость ширины импульса от периода для радиопульсаров с $P > 2$ с.

Для диапазона $0.1{\text{ с}} < P < 2$ с полученная выборка содержала 1381 пульсар с известными значениями ${{W}_{{10}}}$, в диапазоне $P > 2$ с выборка включала 119 пульсаров (см. табл. 1–2).

Таблица 1.  

Значения углов β для выборки пульсаров с периодами в интервале $0.1\;{\text{c}} < P < 2$ c

№ Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, ° № Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, ° № Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, °
1 J0006+1834 2.1 – 46 J0242+62 9 – 91 J0533+0402 23.6 –
2 J0014+4746 4.9 – 47 J0243+6027 10.1 – 92 J0536–7543 7.4 39.9
3 J0025–19 7.8 – 48 J0255–5304 28 – 93 J0540+3207 18.7 –
4 J0026+6320 4.1 – 49 J0301+35 7.9 – 94 J0540–7125 10.4 61.2
5 J0033+57 10.2 – 50 J0302+2252 11.6 – 95 J0555+3948 12.4 –
6 J0033+61 20.6 – 51 J0304+1932 12.8 77.5 96 J0601–0527 10 –
7 J0034–0721 4.5 – 52 J0324+5239 2.6 – 97 J0608+00 20.2 –
8 J0038–2501 10.7 – 53 J0325+6744 29.6 – 98 J0611+1436 5.1 –
9 J0040+5716 27 – 54 J0329+1654 14 – 99 J0612+3721 10.4 –
10 J0048+3412 22.4 – 55 J0332+5434 13.4 – 100 J0612+37216 10.3 –
11 J0051+0423 6.4 – 56 J0335+4555 16.6 – 101 J0613+3731 13.1 –
12 J0054+6946 15.7 – 57 J0335+6623 19 – 102 J0614+2229 16 67.6
13 J0056+4756 9.1 – 58 J0341+5711 14 – 103 J0614+83 7.3 –
14 J0058+4950 11.5 – 59 J0343+06 8.9 – 104 J0621+0336 32.1 –
15 J0058+6125 22.6 – 60 J0343+5312 13.9 – 105 J0624–0424 9.5 33.3
16 J0059+69 10.9 – 61 J0344–0901 29.5 – 106 J0627+0649 12.5 –
17 J0100+8023 12.5 – 62 J0357+5236 4.8 – 107 J0627+0706 32.3 –
18 J0102+6537 8.5 – 63 J0358+4155 8.9 – 108 J0629+2415 12.5 –
19 J0103+54 16.9 – 64 J0401–7608 12.1 – 109 J0630–0046 13.9 –
20 J0104+64 9.5 – 65 J0402+4825 3.5 – 110 J0636–23 10.6 –
21 J0107+1322 19.3 – 66 J0406+6138 10.9 – 111 J0636–4549 30.8 –
22 J0108+6608 13.3 – 67 J0408+552 5 – 112 J0645+80 7.3 –
23 J0108+6905 9.4 – 68 J0410–31 21.6 – 113 J0646+0905 12.5 –
24 J0108–1431 7.7 9.2 69 J0413+58 7.3 – 114 J0647+0913 23.1 –
25 J0110–22 11.2 – 70 J0414+31 12.7 – 115 J0652–0142 22.7 –
26 J0122+1416 18 – 71 J0415+6954 20 – 116 J0653+8051 16.6 –
27 J0125+62 15.7 – 72 J0417+35 21.9 – 117 J0656–2228 24.6 –
28 J0133–6957 15.6 – 73 J0417+61 7 – 118 J0656–5449 11.5 –
29 J0134–2937 12.6 – 74 J0418–4154 16.5 – 119 J0659–36 10.8 –
30 J0137+1654 4.1 – 75 J0421+3255 1 – 120 J0700+6418 12.5 –
31 J0137+6349 7.3 – 76 J0426+4933 19.3 – 121 J0709–5923 32.2 –
32 J0139+5621 15.7 – 77 J0448–2749 13 58.2 122 J0711+0931 16.6 –
33 J0139+5814 17.9 – 78 J0450–1248 7.4 – 123 J0719–2545 20.3 –
34 J0141+6009 6.7 – 79 J0452–1759 8.8 – 124 J0725–1635 26.5 –
35 J0147+5922 12.4 – 80 J0454+4529 16.3 – 125 J0733–2345 17.3 –
36 J0151–0635 5.5 – 81 J0454+5543 7.2 – 126 J0737–2202 7.1 –
37 J0152–1637 20.5 – 82 J0458–0505 26.8 – 127 J0738–4042 5.9 –
38 J0156+3949 6.3 – 83 J0459–0210 15.1 – 128 J0745–5353 4.5 25.5
39 J0201+7005 15.6 – 84 J0502+4654 10.3 – 129 J0747+6646 11.8 –
40 J0206–4028 19.9 – 85 J0517+2212 3.7 – 130 J0749–4247 23.7 –
41 J0210+5845 12.9 – 86 J0518+5416 10.5 – 131 J0750+57 6.4 –
42 J0211–8159 4.8 – 87 J0520–2553 11.7 – 132 J0754+3231 8.1 –
43 J0212+5222 11.5 – 88 J0525+1115 12.8 – 133 J0758–1528 39.3 80.2
44 J0215+6218 3.1 – 89 J0529–0715 15.5 – 134 J0758–30 12.5 –
45 J0231+7026 18.1 – 90 J0530–39 12.5 – 135 J0803–0942 21.9 –
136 J0807–5421 18.8 – 181 J0922–4949 21.4 – 226 J1046+0304 14.4 –
137 J0808–3937 16.9 – 182 J0924–5302 19.2 – 227 J1046–5813 16.3 –
138 J0809–4753 13.1 – 183 J0924–5814 5.3 17.7 228 J1047–3032 4.7 –
139 J0812–3905 6.2 – 184 J0930–2301 16.8 – 229 J1047–6709 11.5 –
140 J0814+7429 8.2 – 185 J0932–3217 26.8 – 230 J1048–5838 1.8 –
141 J0815+0939 2.1 – 186 J0934–4154 12.6 – 231 J1054–5943 37.3 –
142 J0815+4611 12.6 – 187 J0934–5249 19.6 – 232 J1054–5946 5 –
143 J0818–3049 5.3 – 188 J0941–5244 16.3 – 233 J1054–6452 31.3 –
144 J0820–1350 21 – 189 J0942–5552 8.5 – 234 J1055–6236 19.6 –
145 J0820–3826 6.3 – 190 J0942–5657 38.9 – 235 J1056–6258 7.1 –
146 J0820–3921 5.8 – 191 J0943+1631 4.3 – 236 J1057–7914 18.3 21.9
147 J0820–4114 1.9 – 192 J0944–1354 32.4 – 237 J1058–5957 17.6 –
148 J0821–4221 10.5 – 193 J0945–4833 18.8 – 238 J1059–5742 22.2 –
149 J0823+0159 15.3 – 194 J0947+2740 10.1 – 239 J1103–6025 28.1 –
150 J0826+2637 26.4 – 195 J0949–6902 25.9 – 240 J1104–6103 12.5 –
151 J0828–3417 1.2 – 196 J0952–3839 11.1 – 241 J1105–4353 9 –
152 J0831–4406 12.1 – 197 J0953+0755 7.5 – 242 J1107–5907 1.1 –
153 J0835–3707 30.7 – 198 J0954–5430 15.9 47.8 243 J1107–5947 10.6 –
154 J0836–4233 16.8 – 199 J0955–5304 16.8 – 244 J1107–6143 20.2 –
155 J0837+0610 21.6 – 200 J0957–5432 20.5 – 245 J1110+58 11.6 –
156 J0837–4135 25.1 – 201 J0959–4809 3.3 14.9 246 J1110–5637 11.9 –
157 J0838–2621 5.3 – 202 J1000–5149 18.6 – 247 J1112–6613 9.8 –
158 J0840–5332 13.3 – 203 J1001–5507 31.2 – 248 J1112–6926 13.7 –
159 J0842–4851 30.5 – 204 J1001–5559 17 – 249 J1114–6100 7.6 –
160 J0843–5022 12.1 10.6 205 J1002–5919 6.1 – 250 J1115+5030 27.2 –
161 J0846–3533 8.5 – 206 J1003–4747 11.2 – 251 J1115–6052 16.4 44.6
162 J0849+8028 9.6 – 207 J1006–6311 18.9 – 252 J1116–2444 14.9 –
163 J0849–6322 9.4 – 208 J1012–5857 22.1 – 253 J1116–4122 28.2 –
164 J0855–3331 25.4 – 209 J1013–5934 7.4 – 254 J1117–6154 11.7 –
165 J0855–4658 14.3 – 210 J1015–5719 1.6 – 255 J1120–24 23.5 –
166 J0856–6137 14.7 – 211 J1016–5345 29.2 – 256 J1121–5444 12.3 –
167 J0857–4424 11.2 – 212 J1017+3011 7 – 257 J1123–4844 11.8 40.6
168 J0901–4624 7.6 24.1 213 J1017–5621 23.8 38.1 258 J1123–6102 15.9 –
169 J0902–6325 14 – 214 J1018–1642 20.7 – 259 J1123–6259 12.1 60.4
170 J0904–4246 18.1 – 215 J1020–5921 21 – 260 J1123–6651 6.4 –
171 J0904–7459 10.9 33 216 J1020–6026 3.5 – 261 J1126–2737 11 –
172 J0905–4536 3 – 217 J1032–5911 16.6 – 262 J1126–38 8.9 –
173 J0905–5127 19.6 – 218 J1034–3224 2.2 – 263 J1126–6054 13.9 –
174 J0905–6019 16.2 – 219 J1035–6345 27.4 – 264 J1126–6942 13.8 –
175 J0907–5157 6.9 26.1 220 J1036–4926 18.2 – 265 J1130–5826 14.6 –
176 J0908–1739 11.1 – 221 J1036–6559 20.2 – 266 J1130–6807 2.6 –
177 J0909–7212 9.1 – 222 J1038–5831 18.8 – 267 J1132+25 23.6 –
178 J0912–3851 19.2 – 223 J1041–1942 12.6 55.6 268 J1132–4700 7.2 –
179 J0919–6040 15.8 – 224 J1042–5521 17.7 – 269 J1132–5627 18 –
180 J0921+6254 17.9 – 225 J1043–6116 15 – 270 J1133–6250 1.8 –
271 J1136–5525 8.6 – 316 J1252–6314 12 – 361 J1346–4918 10.3 –
272 J1136–6527 19.1 – 317 J1255–6131 20.8 – 362 J1347–5947 18.3 –
273 J1137–6700 2.8 – 318 J1255–62 1.9 – 363 J1349–6130 10.8 19.6
274 J1141–3107 12.4 – 319 J1257–1027 11.4 – 364 J1349–63 4.6 –
275 J1141–3322 8.2 – 320 J1259–6741 15.1 – 365 J1350–5115 25.1 –
276 J1142–6230 9 – 321 J1300–6602 6.8 – 366 J1352–6803 9.1 8.2
277 J1143–5158 22.6 – 322 J1305–6203 8.4 – 367 J1355–5153 30.5 –
278 J1143–5536 19.5 – 323 J1305–6455 6.9 – 368 J1355–5925 15.4 –
279 J1144–6217 16.1 – 324 J1306–6617 4.9 – 369 J1356–5521 9.8 –
280 J1146–6030 12.2 – 325 J1308–4650 9.8 – 370 J1357–62 6.5 –
281 J1152–6012 12.1 – 326 J1308–5844 22 – 371 J1358–2533 10.4 –
282 J1156–5707 10.5 14.7 327 J1311–1228 25.2 – 372 J1359–6038 15.5 –
283 J1156–5909 31.1 – 328 J1312–5402 10.7 – 373 J1401–6357 30 –
284 J1157–6224 6.4 – 329 J1312–5516 14.2 – 374 J1402–5021 12.6 –
285 J1159–6409 1.7 – 330 J1316–6232 1.3 – 375 J1403–6310 7.1 –
286 J1159–7910 15.8 – 331 J1317–6302 6.5 – 376 J1403–7646 10.7 –
287 J1202–5820 18.4 – 332 J1319–6056 14.8 – 377 J1405–5641 16.8 –
288 J1204–6843 16 – 333 J1319–6105 9.5 – 378 J1409–6953 10.2 –
289 J1210–5559 26.4 – 334 J1320+67 10.2 – 379 J1410–7404 65.7 –
290 J1210–6322 5.7 – 335 J1320–3512 9.2 – 380 J1412–6111 15.2 –
291 J1211–6324 11.9 – 336 J1320–5359 11.6 55.3 381 J1412–6145 6.1 –
292 J1214–5830 32.5 – 337 J1321+8323 10.4 – 382 J1413–6141 3.1 –
293 J1215–5328 7.2 – 338 J1321–5922 36.7 – 383 J1413–6222 3.3 –
294 J1220–6318 6 – 339 J1322–6241 23.9 – 384 J1413–6307 29.4 –
295 J1222–5738 39.1 – 340 J1326–5859 12.5 – 385 J1415–6621 17.2 –
296 J1223–5856 2.2 – 341 J1326–6408 10.8 – 386 J1416–5033 18.8 –
297 J1224–6208 16.7 – 342 J1326–6700 5.9 – 387 J1416–6037 9.6 –
298 J1225–5556 19.1 – 343 J1327–6222 17.8 – 388 J1418–3921 11.8 –
299 J1225–6035 53.5 – 344 J1327–6301 6.6 – 389 J1420–5416 18.2 –
300 J1225–6408 12.2 – 345 J1327–6400 1.6 – 390 J1423–6953 8.9 –
301 J1227–63 7.8 – 346 J1328–4357 17.9 – 391 J1424–5556 13.3 –
302 J1231–4609 9.6 – 347 J1328–4921 12.6 – 392 J1424–5822 10.7 44
303 J1232–4742 3 – 348 J1331–5245 8.9 – 393 J1424–6438 6.6 –
304 J1234–3630 16.3 – 349 J1332–3032 3.5 – 394 J1425–5723 18.3 –
305 J1235–54 5.4 – 350 J1333–4449 24.7 – 395 J1425–6210 19.1 –
306 J1236–5033 11.4 – 351 J1334–5839 11 – 396 J1427–4158 15.2 –
307 J1239+2453 14.8 – 352 J1335–3642 6.4 – 397 J1428–5530 15.5 –
308 J1239–6832 19.6 – 353 J1336–2522 12 – 398 J1430–5712 7.4 –
309 J1240–4124 34.1 – 354 J1338–6204 3.6 – 399 J1430–6623 19.4 –
310 J1243–5735 3.9 – 355 J1339–4712 19.2 – 400 J1434–5943 11 –
311 J1243–6423 30.9 – 356 J1339–6618 9.5 – 401 J1435–5954 8.4 43.9
312 J1244–6359 4.2 – 357 J1340–6456 11.6 – 402 J1439+7655 17.8 –
313 J1246+2253 18 – 358 J1341–6023 21 – 403 J1440–6344 13.3 –
314 J1248–6444 11.3 – 359 J1344–5855 6.6 – 404 J1443–5122 5.1 19.4
315 J1251–7407 20.7 – 360 J1345–6115 21.9 – 405 J1449–5846 10.4 –
406 J1452–6036 6.3 – 451 J1532–56 5.8 – 496 J1559–5545 23.5 –
407 J1453–6413 14.6 – 452 J1534–4428 3.9 – 497 J1600–5044 9.4 –
408 J1456–6843 6.3 – 453 J1534–5334 16.2 – 498 J1600–5751 5.4 –
409 J1457–5122 11.4 – 454 J1534–5405 9 – 499 J1600–5916 4.8 –
410 J1457–5902 17.2 – 455 J1535–4114 11.9 58.6 500 J1602–5100 19.5 –
411 J1501–0046 17.7 – 456 J1535–4415 2.2 – 501 J1603–2531 16.1 –
412 J1502+4653 24.3 – 457 J1535–5848 19.3 – 502 J1603–2712 14.3 –
413 J1502–5653 23.4 – 458 J1536–30 15.8 – 503 J1603–3539 6.1 –
414 J1502–6128 8.4 – 459 J1536–3602 7.7 – 504 J1603–5312 10.6 –
415 J1504–5621 12 – 460 J1536–5433 7.7 47.1 505 J1603–5657 45.1 –
416 J1504–5659 15.5 – 461 J1537–4912 5.8 – 506 J1604–4718 15.1 –
417 J1505–25 21.7 – 462 J1537–5153 19.3 – 507 J1604–4909 17 –
418 J1506–5158 14 – 463 J1538–5621 17.6 – 508 J1604–7203 6.4 –
419 J1507–4352 21.6 19.2 464 J1538–5732 17.7 – 509 J1605–5257 5 –
420 J1507–5800 8 – 465 J1538–5750 2.2 – 510 J1607–0032 15.1 –
421 J1507–6640 46.7 – 466 J1539–4828 16.5 – 511 J1607–6449 11.6 –
422 J1509+5531 16.6 – 467 J1539–5626 8 – 512 J1609–1930 34.3 –
423 J1510–4422 5.4 – 468 J1539–6322 11 – 513 J1609–4616 22.5 –
424 J1511–5414 18.4 – 469 J1540–5736 13.5 – 514 J1610–1322 6.5 –
425 J1511–5835 4.1 – 470 J1542–5034 34.1 – 515 J1610–5006 1.9 –
426 J1512–5759 5.6 – 471 J1542–5133 16.9 – 516 J1611–4949 6.9 –
427 J1513–5739 18.9 – 472 J1542–5303 9.7 – 517 J1611–5209 46.3 –
428 J1513–6013 17 – 473 J1543+0929 1.7 – 518 J1611–5847 39.7 –
429 J1514–4834 23.4 – 474 J1543–0620 25.1 – 519 J1612–2408 16.9 –
430 J1514–5316 11.4 – 475 J1543–5459 4.4 – 520 J1612–49 1.8 –
431 J1517–4356 17.6 – 476 J1544–5308 10.4 – 521 J1612–5022 15.4 –
432 J1517–4636 20 – 477 J1546–5302 19.4 – 522 J1612–55 8.7 –
433 J1518–0627 10.1 – 478 J1547–0944 20.8 – 523 J1612–5805 21.8 –
434 J1518–3952 5.4 – 479 J1547–5750 6.3 – 524 J1613–4714 16.8 16.1
435 J1519–5734 3.8 – 480 J1547–5839 3.6 – 525 J1614+0737 28.4 –
436 J1519–6308 18.4 – 481 J1548–4927 20.2 – 526 J1614–3846 6.3 –
437 J1522–5525 26.9 – 482 J1548–5607 5 – 527 J1614–3937 9.2 –
438 J1522–5829 8.9 – 483 J1549+2113 32.6 – 528 J1615–4958 5.4 –
439 J1523–3235 8.7 – 484 J1549–4848 15 55.3 529 J1615–5444 14.8 –
440 J1524–5706 16 – 485 J1550–5242 19.3 – 530 J1615–5537 21.3 –
441 J1525–5417 66.4 – 486 J1551–4424 5.2 – 531 J1616–5017 14.5 –
442 J1525–5523 5.3 $ - $ 487 J1551–6214 19.4 – 532 J1617–4608 20.2 –
443 J1527–5552 15.5 – 488 J1553–5456 4.8 – 533 J1618–4723 8.6 –
444 J1528–4109 23 41.7 489 J1555–0515 30.8 – 534 J1621–5039 14.8 –
445 J1529–26 15.1 – 490 J1555–2341 11.8 – 535 J1621–5243 6.5 –
446 J1530–21 10.5 – 491 J1555–3134 9.4 – 536 J1622–3751 8.9 –
447 J1530–5327 10.9 – 492 J1557–4258 12 – 537 J1622–4332 13 –
448 J1530–6343 17.7 – 493 J1557–5151 3.9 – 538 J1622–4347 18.6 –
449 J1531–4012 18.4 – 494 J1558–5756 30.3 – 539 J1622–4802 3.9 –
450 J1532+2745 18.2 – 495 J1559–4438 9.5 – 540 J1622–4845 10.2 –
541 J1623–0908 41.3 – 586 J1639–4604 9.7 – 631 J1658–4958 9.4 –
542 J1623–4256 7.7 – 587 J1640–4715 3.8 – 632 J1659–1305 5.6 –
543 J1623–4949 13.8 – 588 J1641–2347 6.9 16.8 633 J1700–3312 15.7 –
544 J1624+5850 14.3 – 589 J1643+1338 20.6 – 634 J1700–3611 14 29.8
545 J1624+8643 20.4 – 590 J1643–4505 7.8 – 635 J1700–4012 6.5 –
546 J1624–4411 2.9 – 591 J1643–4550 15.1 – 636 J1700–4422 6.1 –
547 J1624–4613 2.6 – 592 J1644–33 4.3 – 637 J1700–4939 4.4 –
548 J1625–4913 9.5 – 593 J1644–4559 21 – 638 J1701–3130 10.6 –
549 J1626–4537 9.4 – 594 J1645+1012 12.5 – 639 J1701–4533 4.7 –
550 J1626–6621 12.4 – 595 J1645–0317 31.3 – 640 J1702–4310 6.6 16.3
551 J1627+1419 7.4 – 596 J1646–5123 13.3 – 641 J1703–1846 20.7 –
552 J1627–4706 4 – 597 J1646–6831 10.1 – 642 J1703–3241 14.1 –
553 J1627–4845 2.2 – 598 J1647+6608 16.4 – 643 J1703–4442 17.5 –
554 J1627–49 3.8 – 599 J1647–3607 9 – 644 J1703–4851 14.4 –
555 J1627–51 16.5 – 600 J1648–3256 25.5 – 645 J1704–3756 8.9 –
556 J1627–5547 9 – 601 J1648–6044 12.9 – 646 J1704–5236 6 –
557 J1627–5936 1.9 – 602 J1649+2533 15.4 – 647 J1704–6016 1.6 –
558 J1628–4804 2 – 603 J1649–3805 5.1 – 648 J1705–3423 7.6 –
559 J1629+33 14.3 – 604 J1649–3935 9.9 – 649 J1705–3950 5.8 –
560 J1629+43 7.7 – 605 J1649–4349 2.7 – 650 J1705–4331 9.4 –
561 J1629–3825 23 – 606 J1650–1654 15.8 – 651 J1705–6135 5.5 –
562 J1630–4719 17.7 – 607 J1650–4126 14.8 – 652 J1706+59 14.9 –
563 J1631–4155 11.8 – 608 J1650–4502 12.3 32.8 653 J1706–4434 12.1 –
564 J1632–1013 12.4 – 609 J1651–1709 16.6 – 654 J1706–6118 46.5 –
565 J1632–4621 23.1 – 610 J1651–4246 3.3 12.6 655 J1707–4053 4.4 –
566 J1633–4453 8.8 – 611 J1651–5222 17.2 – 656 J1707–4341 18.6 –
567 J1633–5015 10.3 – 612 J1651–5255 7.9 – 657 J1707–4729 4 –
568 J1634–49 6.4 – 613 J1651–7642 9.3 45.4 658 J1708–3426 11.6 –
569 J1634–5107 7.8 – 614 J1652+2651 11 – 659 J1708–3641 4.5 –
570 J1634–5640 8.8 – 615 J1652–1400 8.2 36.7 660 J1708–4522 20.1 –
571 J1635+2418 16.2 – 616 J1652–2404 18.4 – 661 J1708–7539 15.1 –
572 J1635–1511 2.6 – 617 J1653–3838 13.5 – 662 J1709–1640 20.6 –
573 J1635–4944 4.2 – 618 J1653–4030 3.7 – 663 J1709–3626 8.2 –
574 J1635–5954 9.6 – 619 J1653–4105 6.7 – 664 J1709–4401 25.8 –
575 J1636–2614 24.1 – 620 J1653–4249 10.4 – 665 J1710–2616 5.7 9.2
576 J1637–4450 1.6 – 621 J1653–45 19.1 – 666 J1710–37 4.4 –
577 J1637–4553 13.3 – 622 J1654–2636 6 – 667 J1711–1509 25.9 –
578 J1638+4005 15.2 – 623 J1654–2713 14.5 – 668 J1711–4322 4.3 –
579 J1638–35 13 – 624 J1654–3710 17.1 – 669 J1711–5350 23.1 –
580 J1638–3815 5.9 – 625 J1655–3048 3 – 670 J1712–2715 2.5 –
581 J1638–4233 7 – 626 J1656+6203 15 – 671 J1713+7810 10.9 –
582 J1638–44 6.7 – 627 J1656–3621 11.9 – 672 J1714–1054 5 –
583 J1638–4725 3.4 – 628 J1657+3304 17.8 – 673 J1715–3859 4.2 –
584 J1638–5226 7.2 – 629 J1657–4432 11.7 – 674 J1716–3720 3.6 –
585 J1639–4359 10 – 630 J1658–47 5.2 – 675 J1716–4111 18.2 –
676 J1716–4711 21.1 – 721 J1733–2533 6.8 – 766 J1745+1252 5.8 –
677 J1717–3425 9.7 – 722 J1733–2837 22.9 – 767 J1745–0129 33.2 –
678 J1717–3737 5.9 – 723 J1733–3716 3.7 – 768 J1745–2758 6.9 –
679 J1717–3953 1.8 – 724 J1733–4005 20 – 769 J1745–3040 10.7 –
680 J1717–4054 39.6 – 725 J1733–5515 8.4 51 770 J1745–3812 17.3 –
681 J1717–5800 6.6 – 726 J1734–0212 11.7 – 771 J1746+2540 18.6 –
682 J1718–41 4.7 – 727 J1734–2415 7.4 – 772 J1748–1300 12 –
683 J1718–4539 9.7 – 728 J1734–2859 7 – 773 J1748–30 3 –
684 J1719–2330 15.3 – 729 J1734–3058 14.4 – 774 J1749+5952 10.1 –
685 J1719–3458 11.5 – 730 J1735–0243 4.3 – 775 J1749–3002 4.1 –
686 J1719–4006 8.6 36.2 731 J1735–0724 11.6 – 776 J1749–4931 35.8 –
687 J1719–4302 18 – 732 J1737–3102 14.6 – 777 J1749–5417 8.6 –
688 J1720+2150 12.9 – 733 J1737–3555 15.2 – 778 J1749–5605 11.6 –
689 J1720–0212 3.5 – 734 J1738–2330 15.9 – 779 J1750–2438 22.5 –
690 J1720–1633 19.3 – 735 J1738–2736 15.8 – 780 J1750–28 21.3 –
691 J1720–2446 9 – 736 J1738–2955 4.3 – 781 J1750–3157 6.2 –
692 J1720–2933 10.8 79.9 737 J1738–3211 18.2 – 782 J1750–3503 3.6 –
693 J1720–3659 10.3 – 738 J1739+0612 9.8 – 783 J1751–3323 9.6 –
694 J1721–3532 2.6 – 739 J1739–1313 86.2 – 784 J1751–4657 22.2 –
695 J1722+35 9.4 – 740 J1739–2903 20.2 – 785 J1752+2359 23.1 –
696 J1722–3207 14.4 – 741 J1739–3131 3.3 – 786 J1752–2806 29 –
697 J1722–3632 6.2 – 742 J1739–3951 11.1 – 787 J1752–2821 19.2 –
698 J1722–3712 15.4 – 743 J1740+1311 9.7 – 788 J1753–2501 3.4 –
699 J1722–4400 20 – 744 J1740+27 16.5 – 789 J1753–38 18.1 –
700 J1723–3659 7.6 16.9 745 J1740–3015 38.6 – 790 J1754–3443 11.7 –
701 J1723–38 12.8 – 746 J1740–3327 13.5 – 791 J1754–3510 20.2 –
702 J1724–4500 19.7 – 747 J1741+2758 19.4 – 792 J1755–0903 12.6 –
703 J1725–0732 7.5 – 748 J1741+3855 12.5 – 793 J1755–1650 16.7 –
704 J1725–2852 9 – 749 J1741–2719 7.1 – 794 J1755–2521 20.6 –
705 J1725–3546 6.1 – 750 J1741–2733 9.4 – 795 J1755–2550 7.6 –
706 J1725–4043 8.3 – 751 J1741–3016 9.4 – 796 J1755–26 10.2 –
707 J1726–3635 2.7 – 752 J1741–34 11.7 – 797 J1755–2725 5.8 –
708 J1727–2739 6.5 – 753 J1741–3927 12.3 – 798 J1756–2435 10.1 –
709 J1728–0007 7.6 – 754 J1742–0203 8.6 – 799 J1756–25 13.1 –
710 J1728–3733 20.6 – 755 J1742–3957 4.9 – 800 J1757–1500 24.6 –
711 J1728–4028 4.2 – 756 J1742–4616 6.8 29.2 801 J1757–2223 24.2 –
712 J1730–2900 19.8 – 757 J1743–0339 15 – 802 J1758+3030 13 –
713 J1731–33 4.1 – 758 J1743–1351 9.9 – 803 J1758–2846 15 –
714 J1731–3322 4.6 – 759 J1743–35 10 – 804 J1759–1736 10.6 –
715 J1732–1930 12.7 – 760 J1743–4212 12.7 – 805 J1759–2205 26 –
716 J1732–3426 6.2 – 761 J1744–1610 24.4 – 806 J1759–2307 6.4 –
717 J1732–35 5.9 – 762 J1744–2335 16 – 807 J1759–24 5.1 –
718 J1732–4128 15.6 – 763 J1744–3130 22.2 – 808 J1759–2922 17.2 –
719 J1733–01 11.7 – 764 J1744–3922 18 – 809 J1759–3107 26.5 –
720 J1733–2228 6 – 765 J1744–5337 5.2 – 810 J1800+5034 17.4 –
811 J1800–0125 9 – 856 J1812–2526 10.3 – 901 J1824–0132 6.3 –
812 J1801–0357 16.3 – 857 J1812–3039 14.6 – 902 J1824–1118 5.2 –
813 J1801–2920 10.1 – 858 J1813+1822 10.4 – 903 J1824–1350 13.6 –
814 J1801–3458 7.1 – 859 J1813+4013 19.5 – 904 J1824–1423 7.9 –
815 J1802+0128 15.1 – 860 J1813–2113 11.3 – 905 J1824–1945 39.4 –
816 J1802–0523 6.4 – 861 J1814–0521 13.6 – 906 J1824–2233 21 –
817 J1803–2712 6.4 32.6 862 J1814–0618 4 – 907 J1824–2328 16.7 –
818 J1803–3329 18 – 863 J1814–1649 9.5 – 908 J1825+0004 13.8 –
819 J1804–28 10.8 – 864 J1815+5546 14.4 – 909 J1825–1108 15.5 –
820 J1805+0306 11.5 – 865 J1815–1910 13.7 – 910 J1825–1446 6.2 –
821 J1805–0619 10.2 – 866 J1816–1729 12.4 73.5 911 J1827–0750 4.5 –
822 J1805–1504 2 11.1 867 J1816–2650 5.4 – 912 J1827–0958 2.7 –
823 J1805–2447 17.9 – 868 J1816–5643 6.1 – 913 J1828–0611 9.9 –
824 J1805–2948 11.8 – 869 J1817–0743 7.8 – 914 J1828–2119 9.1 –
825 J1806–1154 8 – 870 J1817–3618 13.9 – 915 J1829+0000 6 –
826 J1806–2125 5.3 – 871 J1817–3837 24 – 916 J1829–0734 10.3 –
827 J1807+0756 10.4 – 872 J1818–0151 13.9 – 917 J1829–1011 3.9 –
828 J1807–0847 8.8 – 873 J1818–1422 3.4 – 918 J1829–1751 10.6 –
829 J1807–2715 19.5 – 874 J1819+1305 7.4 – 919 J1830–0052 13.3 –
830 J1808+00 7.6 – 875 J1819–0925 15.1 – 920 J1830–0131 5.5 –
831 J1808–0813 13.4 – 876 J1819–1114 2.5 – 921 J1830–10 12.1 –
832 J1808–1020 13.7 – 877 J1819–1318 21.1 – 922 J1830–1059 26.7 41.5
833 J1808–1517 18.3 – 878 J1819–1510 4.8 – 923 J1830–1414 20.8 –
834 J1808–2057 6.3 – 879 J1819–37 9.6 – 924 J1831–04 22.1 –
835 J1808–3249 12.4 – 880 J1820–0427 18.9 – 925 J1831–0823 18.3 –
836 J1809–0119 19.2 – 881 J1820–0509 9.9 – 926 J1832+0029 21.7 –
837 J1809–0743 10.8 – 882 J1820–1346 3.5 – 927 J1832–0644 7.3 –
838 J1809–1429 21.1 – 883 J1820–1818 6.8 – 928 J1832–0827 16.8 –
839 J1809–2109 28.5 – 884 J1821+1715 12.1 – 929 J1832–1021 8.5 38.7
840 J1809–3547 2.7 – 885 J1821+4147 16.4 – 930 J1833–0209 5.9 –
841 J1810+0705 1.6 – 886 J1821–0256 10.1 – 931 J1833–0338 21.7 –
842 J1810–1709 2.2 – 887 J1821–1432 10.9 – 932 J1833–6023 13.1 –
843 J1810–1820 3.2 – 888 J1822+02 9.1 – 933 J1834–0010 9 –
844 J1810–5338 7.4 – 889 J1822+1120 16.9 – 934 J1834–0031 15.7 –
845 J1811–0154 15.4 – 890 J1822+2617 27.3 – 935 J1834–0426 1.8 –
846 J1811–1717 4.1 – 891 J1822–0719 16.3 – 936 J1834–0602 8.4 –
847 J1811–1736 1.3 – 892 J1822–0848 8.8 – 937 J1834–0731 2.3 –
848 J1811–2439 10.5 – 893 J1822–0902 13.6 – 938 J1834–09 2.1 –
849 J1811–4930 21 – 894 J1822–1400 8 – 939 J1834–1202 4.8 –
850 J1812+0226 23.7 – 895 J1822–2256 12.8 34.3 940 J1834–1710 10.5 –
851 J1812–15 17.2 – 896 J1822–4209 9.8 – 941 J1834–1855 11.6 –
852 J1812–1718 11.4 – 897 J1823+0550 7.3 – 942 J1835–0349 17.6 –
853 J1812–1733 1.8 – 898 J1823–0154 30.9 – 943 J1835–0643 3.2 –
854 J1812–20 2.7 – 899 J1823–1126 23.8 – 944 J1835–0847 4.6 –
855 J1812–2102 10.5 74.4 900 J1823–3106 20.1 44.6 945 J1835–09242 3.3 –
946 J1835–0928 5.7 – 991 J1842–0415 11.7 – 1036 J1851+1259 36.4 –
947 J1835–0944 5 – 992 J1842–0800 13.7 – 1037 J1851–0029 9.7 –
948 J1835–0946 33.9 – 993 J1842–0905 10.6 – 1038 J1851–0053 24.6 –
949 J1835–1020 17.2 – 994 J1842–39 4 – 1039 J1851–0114 12.5 –
950 J1835–1106 12.7 44.3 995 J1843–0000 13.5 69.8 1040 J1851–0633 19.5 –
951 J1835–1548 9.4 – 996 J1843–0459 4.9 – 1041 J1852–0118 5.7 –
952 J1836+51 11.6 – 997 J1843–0510 11 – 1042 J1852–0127 3.2 –
953 J1836–0436 12.1 – 998 J1843–0702 17.4 – 1043 J1852–0635 2.8 –
954 J1836–1008 20 – 999 J1843–1507 18.5 – 1044 J1852–2610 7.4 –
955 J1836–11 5.4 – 1000 J1844+00 6.5 – 1045 J1853+0011 11.7 25.1
956 J1836–1324 7.1 – 1001 J1844+1454 14.4 – 1046 J1853+0505 2.7 –
957 J1837+0053 2.7 – 1002 J1844–0030 12.2 – 1047 J1853+0545 3.2 –
958 J1837+1221 24.1 – 1003 J1844–0244 6.6 – 1048 J1854+36 5.2 –
959 J1837–0045 11.8 – 1004 J1844–0302 20.8 – 1049 J1854–0524 14 –
960 J1837–0653 5.8 – 1005 J1844–0433 21.5 – 1050 J1854–1421 14 –
961 J1837–0822 11.7 – 1006 J1844–0538 7 – 1051 J1855+0307 19.1 –
962 J1837–1837 19.5 – 1007 J1845+0623 32.2 – 1052 J1855–0941 4.7 –
963 J1838+1523 4.9 – 1008 J1845–0434 11.7 – 1053 J1856+0102 13.4 –
964 J1838+1650 11.4 – 1009 J1845–0545 19.2 – 1054 J1856–0526 5.7 –
965 J1838–0107 6 – 1010 J1845–0635 8.4 – 1055 J1857+0057 6.1 –
966 J1838–1046 20.7 – 1011 J1845–0743 7.4 – 1056 J1857+0143 2.2 –
967 J1839–0223 10.6 – 1012 J1845–0826 12.1 – 1057 J1857+0212 10.5 –
968 J1839–0402 19.8 – 1013 J1845–1114 23.9 – 1058 J1857+0526 7.2 –
969 J1839–0436 8.1 – 1014 J1846+0051 11 – 1059 J1859+00 3.5 –
970 J1839–0627 10.1 – 1015 J1846–0749 12.7 – 1060 J1859+1526 17 –
971 J1839–0643 3.7 – 1016 J1846–07492 13.9 – 1061 J1859+7654 15.5 –
972 J1839–1238 21.9 – 1017 J1847–0402 12.3 – 1062 J1900+0634 11.7 –
973 J1840+0214 21.5 – 1018 J1847–0427 3.4 – 1063 J1900+30 18.1 –
974 J1840+5640 16.1 – 1019 J1847–0438 27.1 – 1064 J1900–0051 16.9 –
975 J1840–0445 4.8 – 1020 J1847–0605 12.3 – 1065 J1900–0134 17.8 –
976 J1840–0559 11.1 – 1021 J1848+0647 11.3 – 1066 J1900–0933 3.2 –
977 J1840–0809 15.9 – 1022 J1848+0826 5.5 – 1067 J1900–2600 5.6 –
978 J1840–0815 18.7 – 1023 J1848–0023 13.4 – 1068 J1900–7951 8.5 –
979 J1840–1207 21.4 – 1024 J1848–0123 10.5 – 1069 J1901+0156 12.8 –
980 J1841+0912 16.8 – 1025 J1848–0601 6.4 – 1070 J1901+0331 11.1 –
981 J1841–0157 9.8 – 1026 J1848–1150 17.8 – 1071 J1901+0716 9.5 –
982 J1841–0345 6.5 26.9 1027 J1848–1414 6.2 – 1072 J1901+1306 15.5 –
983 J1841–0425 12.2 31.6 1028 J1849+0409 28.8 – 1073 J1901–0312 4.6 –
984 J1841–1404 6.2 – 1029 J1849+2423 6.4 – 1074 J1901–0315 23.9 –
985 J1841–7845 5.2 – 1030 J1849–0317 11.3 – 1075 J1901–0906 17.8 –
986 J1842+0358 18.6 – 1031 J1849–0614 18.5 – 1076 J1901–1740 9 –
987 J1842+0638 9.7 – 1032 J1849–0636 32.9 – 1077 J1902+0556 15.7 –
988 J1842+1332 2 – 1033 J1850+0026 6.3 – 1078 J1902+0615 32 –
989 J1842–0153 9.1 – 1034 J1850+1335 17.9 64.3 1079 J1902+0723 5.2 –
990 J1842–0359 3 15.6 1035 J1850–0026 2 – 1080 J1902–1036 24.8 –
1081 J1903+0135 23 – 1126 J1912+1036 8.3 – 1171 J1923+4243 13.1 –
1082 J1903+2225 14.9 – 1127 J1912+2525 23.5 – 1172 J1924+2040 5.3 –
1083 J1903–0258 5.5 – 1128 J1913+0446 15.1 – 1173 J1925+19 8.1 –
1084 J1903–0632 16.5 – 1129 J1913+0936 13.9 – 1174 J1926+0431 23.3 –
1085 J1903–0848 14.3 – 1130 J1913+1000 7.8 – 1175 J1926+1434 5 –
1086 J1904+0004 6 12.5 1131 J1913+1145 6.8 – 1176 J1926+1648 18.4 –
1087 J1904+1011 6 – 1132 J1913+1400 15.7 – 1177 J1926+1928 8.6 –
1088 J1904+33 7.7 – 1133 J1913+3732 16.6 – 1178 J1926–0652 3.6 –
1089 J1904–0150 18 – 1134 J1913–0440 27.6 – 1179 J1927+0911 25 –
1090 J1904–1224 17.8 – 1135 J1914+0219 12.6 68.4 1180 J1927+1852 10.4 –
1091 J1904–1629 29.1 – 1136 J1914+0631 15.4 – 1181 J1927+1856 4.3 –
1092 J1905+0600 7.6 – 1137 J1914+1122 15.6 – 1182 J1927+2234 9.6 –
1093 J1905+0616 28.1 – 1138 J1915+0227 7 – 1183 J1928+1923 5 –
1094 J1905+0709 6.1 – 1139 J1915+0738 48.5 – 1184 J1928+28 10.9 –
1095 J1905–0056 48.5 – 1140 J1915+0838 8.4 – 1185 J1929+00 12.3 –
1096 J1906+0641 6.2 – 1141 J1915+1009 26.7 – 1186 J1929+1844 14.2 –
1097 J1906+0649 12.2 – 1142 J1915+1410 7.7 – 1187 J1929+1955 10.1 –
1098 J1906+0746 72.4 – 1143 J1915+1647 19.4 – 1188 J1929+2121 27.4 –
1099 J1906+1854 6.3 – 1144 J1916+0748 1.5 – 1189 J1929+3817 5.6 –
1100 J1907+0249 6.7 – 1145 J1916+0844 9.2 – 1190 J1929+62 17.2 –
1101 J1907+0731 13.1 – 1146 J1916+0951 14.1 – 1191 J1929+66 12.4 –
1102 J1907+0740 16.4 – 1147 J1916+1030 9.5 – 1192 J1930+1316 21.5 –
1103 J1907+0918 36.1 – 1148 J1916+1312 18.5 – 1193 J1930–1852 13.1 –
1104 J1907+1149 29.7 – 1149 J1916+3224 14 – 1194 J1931+1536 7.2 –
1105 J1907+1247 14.7 – 1150 J1916–2939 11.6 – 1195 J1931+1952 21.9 –
1106 J1907+4002 9.7 – 1151 J1917+1353 14.8 58.7 1196 J1931+30 15.8 –
1107 J1907+57 10.3 – 1152 J1917+2224 6.8 – 1197 J1931–0144 8.7 –
1108 J1908+0457 8.3 – 1153 J1918+1444 25.6 – 1198 J1932+1059 11.9 21.3
1109 J1908+0500 35.5 – 1154 J1918+1541 8.9 – 1199 J1932+2020 4.2 –
1110 J1908+0734 7.5 – 1155 J1918–1052 23.8 – 1200 J1932–3655 16.3 –
1111 J1908+0909 11.5 – 1156 J1919+0021 20.3 – 1201 J1933+0758 18.3 –
1112 J1908+0916 5.1 – 1157 J1919+0134 11.2 – 1202 J1933+1304 17.5 –
1113 J1908+2351 16.6 – 1158 J1919+2621 21 – 1203 J1933+2421 11.6 –
1114 J1909+0007 28.8 – 1159 J1920+2650 16.4 – 1204 J1934+2352 10.1 –
1115 J1909+0254 17.4 – 1160 J1920–0950 9.9 – 1205 J1934+5219 7.5 –
1116 J1909+0749 14 – 1161 J1921+0812 41.4 – 1206 J1935+1159 3.8 –
1117 J1909+1102 16.2 – 1162 J1921+1419 9.2 – 1207 J1935+1616 24.8 –
1118 J1909+1450 6.7 – 1163 J1921+1948 3.6 – 1208 J1935+1745 26.5 –
1119 J1909+1859 11.6 – 1164 J1921+2003 9.5 – 1209 J1937+2544 6.4 –
1120 J1910+0225 6.9 – 1165 J1921+2153 17.7 – 1210 J1937+2950 7.7 –
1121 J1910+0728 10 – 1166 J1922+1733 12.4 – 1211 J1938+0650 31.9 –
1122 J1910+1231 19.6 – 1167 J1922+2018 8.3 – 1212 J1938+2213 8.9 –
1123 J1910–0112 8.6 – 1168 J1922+2110 19.1 – 1213 J1939+2449 11.2 –
1124 J1910–0309 12.1 – 1169 J1922+58 16 – 1214 J1940+0239 11.7 –
1125 J1911+1758 13.9 – 1170 J1923+1706 11.7 – 1215 J1940–2403 14.7 –
1216 J1941+0121 4.1 – 1261 J2013+3845 3.6 – 1306 J2116+1414 12.1 –
1217 J1941+1026 17 – 1262 J2013–0649 14.4 – 1307 J2122+2426 7.9 –
1218 J1941+1341 10.1 – 1263 J2017+2043 15.4 – 1308 J2123+36 18.5 –
1219 J1941+4320 16.4 – 1264 J2017+5906 3.6 – 1309 J2123+5434 12.9 –
1220 J1941–2602 22.7 – 1265 J2017–2737 2.3 – 1310 J2124+1407 14.1 –
1221 J1942+1743 4.5 – 1266 J2018+2839 15.1 – 1311 J2127–6648 5.9 –
1222 J1942+3941 6.7 – 1267 J2019+72 2.5 – 1312 J2129+4119 15.1 –
1223 J1942+8106 21.9 – 1268 J2022+2854 13.4 – 1313 J2136–1606 11.2 –
1224 J1943+0609 12.9 – 1269 J2022+5154 10.8 – 1314 J2137+6428 18.2 –
1225 J1943–1237 26.2 – 1270 J2023+5037 15.4 – 1315 J2138+4911 6.9 –
1226 J1944+1755 5.8 – 1271 J2027+2146 11.6 – 1316 J2139+00 6 –
1227 J1944–1750 16.1 – 1272 J2027+4557 5.2 – 1317 J2139+2242 13 –
1228 J1945+1834 12.5 – 1273 J2027+7502 3.5 – 1318 J2145+21 17.9 –
1229 J1945–0040 8.1 – 1274 J2029+3744 15.9 – 1319 J2148–34 15 –
1230 J1946+1805 5.2 – 1275 J2030+2228 12.5 – 1320 J2149+6329 6.6 –
1231 J1946+2244 20.7 – 1276 J2030+55 9.8 – 1321 J2150+5247 8.2 –
1232 J1946–1312 15.7 – 1277 J2033–1938 15.2 – 1322 J2151+2315 5.2 –
1233 J1946–2913 24.6 – 1278 J2036+2835 21.7 – 1323 J2154–2812 38.8 –
1234 J1947+0915 14.1 – 1279 J2036+6646 9.5 – 1324 J2155+2813 21.8 –
1235 J1947–4215 11.1 – 1280 J2037+3621 7.5 – 1325 J2155–3118 19.3 –
1236 J1948+3540 8.4 – 1281 J2038+35 8.6 – 1326 J2155–5641 8.6 –
1237 J1948–27 18.8 – 1282 J2038+5319 14.9 – 1327 J2156+2618 17.8 –
1238 J1949+3426 4.5 – 1283 J2038–3816 21.3 – 1328 J2157+4017 7.5 –
1239 J1949–2524 27.1 – 1284 J2040+1657 6.3 – 1329 J2158–27 11.1 –
1240 J1951+4724 1.7 – 1285 J2040–21 11.2 – 1330 J2203+50 6 –
1241 J1953+1149 21.9 – 1286 J2043+7045 14.6 – 1331 J2205+1444 9.3 –
1242 J1953+2732 17.3 – 1287 J2044+28 15.4 – 1332 J2206+6151 4.1 –
1243 J1954+2923 14.7 – 1288 J2044+4614 3.7 – 1333 J2207–15 11.2 –
1244 J1954+3852 22.1 – 1289 J2045+0912 8.9 – 1334 J2208+5500 18.2 –
1245 J1954+4357 5.7 – 1290 J2046+1540 13 – 1335 J2209+22 24.6 –
1246 J1955+5059 24.1 – 1291 J2046+5708 11.6 – 1336 J2212+2933 9.8 –
1247 J1956+0838 7 – 1292 J2046–0421 25.9 – 1337 J2215+1538 29.7 –
1248 J1957–0002 19.9 – 1293 J2048+2255 9.8 – 1338 J2217+5733 6 –
1249 J2001+4258 21.5 – 1294 J2048–1616 12.9 – 1339 J2219+4754 25.2 –
1250 J2002+1637 10.8 – 1295 J2053–7200 5.8 26.9 1340 J2222+2923 8 –
1251 J2002+30 3.3 – 1296 J2054–39 15.3 – 1341 J2222+5602 6.2 –
1252 J2002+3217 10.1 – 1297 J2055+2209 21.1 – 1342 J2227+30 15.4 –
1253 J2002+4050 11.2 – 1298 J2055+3630 8.3 – 1343 J2228+6447 14 –
1254 J2006+4058 15.9 – 1299 J2102+38 10.3 – 1344 J2229+6205 7.6 –
1255 J2006–0807 3.6 – 1300 J2105+28 20.9 – 1345 J2234+2114 2.8 –
1256 J2007+0910 21.7 – 1301 J2108+4441 2.5 – 1346 J2241+6941 45.9 –
1257 J2008+2513 10.9 – 1302 J2108–3429 33.7 – 1347 J2242+6950 16.7 –
1258 J2010+2845 14.7 – 1303 J2113+2754 30.2 – 1348 J2243+1518 12.2 –
1259 J2012–2029 9.8 – 1304 J2113+4644 3.8 – 1349 J2244+63 12.1 –
1260 J2013+3058 25.2 – 1305 J2113+67 11.8 – 1350 J2248–0101 17 –
1351 J2251+24 11.7 – 1362 J2315+58 11.3 – 1372 J2333+6145 4.6 –
1352 J2253+1516 10 – 1363 J2317+2149 24.5 – 1373 J2338+4818 9.3 –
1353 J2257+5909 7 – 1364 J2319+6411 1.8 – 1374 J2343+6221 10.2 –
1354 J2257–16 26.5 – 1365 J2325+6316 5.4 – 1375 J2346–0609 11 59.7
1355 J2302+6028 19.3 – 1366 J2325–0530 19.6 – 1376 J2347+02 19.8 –
1356 J2305+3100 26.6 – 1367 J2326+6113 6.4 – 1377 J2351+8533 17.8 –
1357 J2305+4707 10.2 – 1368 J2326+6141 10 – 1378 J2352+65 5.6 –
1358 J2307+2225 15.3 – 1369 J2327+62 6.4 – 1379 J2354+6155 14.8 –
1359 J2308+5547 8.3 – 1370 J2329+4743 25.8 – 1380 J2354–22 16 –
1360 J2312+6931 14.9 – 1371 J2330–2005 29.8 – 1381 J2355+2246 8.9 –
1361 J2313+4253 14.8 –
Таблица 2.  

Значения углов β для выборки пульсаров с периодами $P > 2$ с

№ Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, ° № Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, ° № Name ${{\beta }_{1}}$, ° ${{\beta }_{2}}$, °
1 J0021–0909 51.8 – 41 J1404+1159 36.3 – 81 J1839–0332 34.1 –
2 J0055+5117 20.6 – 42 J1414–6802 14.8 – 82 J1840–0840 8 –
3 J0111+6624 30 – 43 J1432–5032 2.9 – 83 J1842+0257 23.8 –
4 J0152+0948 20.5 – 44 J1444–5941 27.2 – 84 J1843–0211 18.3 –
5 J0157+6212 16.5 – 45 J1503+2111 1.9 – 85 J1843+2024 80.5 –
6 J0323+3944 30.2 – 46 J1512–5431 12.7 – 86 J1845–1351 24.9 –
7 J0343–3000 9.8 19.9 47 J1519–6106 54.5 – 87 J1846–4249 29.8 –
8 J0421–0345 73.6 – 48 J1527–3931 31.7 – 88 J1846–7403 3.6 –
9 J0528+2200 11.1 38.7 49 J1528–5547 21.2 – 89 J1848+0604 37.7 –
10 J0546+2441 45.8 – 50 J1615–2940 33 – 90 J1848+1516 6.3 –
11 J0600–5756 20.5 – 51 J1617–4216 29.6 – 91 J1848–1952 27.8 –
12 J0633–2015 33.6 – 52 J1625–4048 13.1 – 92 J1853+0853 27.7 –
13 J0648–27 21.7 – 53 J1629–3636 65.7 – 93 J1857–1027 9.1 –
14 J0737–3039B 24.3 – 54 J1634–4229 22.7 – 94 J1901+0511 29.8 –
15 J0738+6904 20 – 55 J1701–3726 19.1 – 95 J1910+0358 4.3 –
16 J0746–4529 32.3 – 56 J1707–4417 9.9 – 96 J1910+0714 48.4 –
17 J0804–3647 53.2 – 57 J1715–4034 15.1 – 97 J1912+2104 22.4 –
18 J0818–3232 51 – 58 J1732–3729 26.7 – 98 J1915+0752 53.1 –
19 J0847–4316 37.5 – 59 J1736–2457 20.2 – 99 J1917+0834 28 –
20 J0928+06 39.8 – 60 J1741–0840 19.8 58.9 100 J1919+1745 26.1 –
21 J0932–5327 28.2 – 61 J1741–2019 16.2 – 101 J1921–05 20.1 –
22 J0944+4106 21.8 – 62 J1741–21 11.1 – 102 J1945+1211 6.6 –
23 J1001–5939 24.1 – 63 J1743–3150 31.2 – 103 J1951+1123 69 –
24 J1012–2337 24.5 – 64 J1746+2245 20.2 – 104 J2004+3137 53.1 –
25 J1032–5206 30.1 – 65 J1749–2146 13.6 – 105 J2005–0020 32.6 40.8
26 J1049–5833 37.5 – 66 J1750–2043 6.5 – 106 J2015+2524 30 –
27 J1055–6905 26.5 – 67 J1754+5201 15.3 – 107 J2033+0042 13.9 –
28 J1059+6459 35.4 – 68 J1759–1029 6.1 – 108 J2037+1942 32.9 –
29 J1106–6438 58.7 – 69 J1802–3346 26.6 – 109 J2053+4718 32.2 –
30 J1119–7936 40.9 – 70 J1803–1857 58.6 – 110 J2111+2106 28.5 –
31 J1148–5725 36.2 – 71 J1808–2701 25.5 – 111 J2112+4058 23.4 –
32 J1210–6550 35.2 – 72 J1819–17 12.5 – 112 J2131–31 23.5 –
33 J1226–3223 33.8 – 73 J1824–0127 29.2 – 113 J2144–3933 62.9 –
34 J1236–0159 17.4 – 74 J1825–31 12 – 114 J2210+57 11.9 –
35 J1237–6725 55.9 – 75 J1826–1131 23.7 – 115 J2238+6021 42.4 –
36 J1245–6238 26.1 – 76 J1829+25 40 – 116 J2251–3711 66.9 –
37 J1303–6305 27.8 – 77 J1830–1135 17.3 – 117 J2321+6024 12.5 –
38 J1312–6400 43.3 – 78 J1831–1223 17.5 32.6 118 J2323+1241 28.2 –
39 J1314–6101 25.6 – 79 J1831–1329 23.5 – 119 J2324–6054 34.3 62
40 J1355–5747 34 – 80 J1835–0600 38 –        

Для выборки с $P > 2$ с:

(14)
$\lg ({{W}_{{10\min }}}\;[^\circ ]) = - 0.582\lg (P\;[{\text{с}}]) + 0.930,$
или

(15)
${{W}_{{10\min }}}\;[^\circ ]) = 8.5^\circ {{P}^{{ - 0.58}}}.$

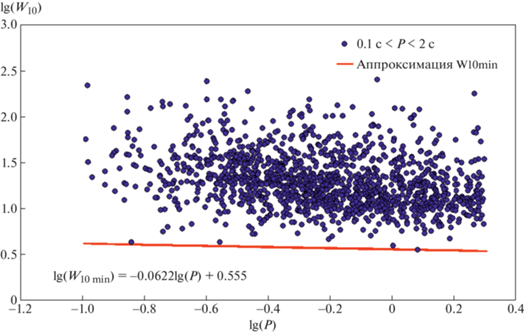
Нужно подчеркнуть, что зависимость ${{W}_{{10}}}(P)$ для различных выборок пульсаров может существенно отличаться, поэтому мы отдельно построили соответствующую диаграмму, аналогичную рис. 3, для исследуемых источников с $0.1{\text{ с}} < P < 2$ с (рис. 4). Нижняя граница для выборки с $0.1{\text{ с}} < P < 2$ с описывается уравнением

(16)
$\lg ({{W}_{{10\min }}}\;[^\circ ]) = - 0.062\lg (P\;[{\text{с}}]) + 0.555,$
откуда

(17)
${{W}_{{10\min }}}\;[^\circ ]) = 3.6^\circ {{P}^{{ - 0.06}}}.$
Рис. 4.

Зависимость ширин импульсов пульсаров от периода для выборки с $0.1{\text{ с}} < P < 2$ с.

Используя выражения (14) и (17) и каталожные значения ${{W}_{{10}}}$, мы вычислили углы ${{\beta }_{1}}$ для двух исследуемых групп пульсаров (см. табл. 1).

На рис. 5 показаны гистограммы распределения ${{\beta }_{1}}$ для двух выборок пульсаров, нормированные на полное число $N$ пульсаров в выборке.

Рис. 5.

Гистограммы распределения углов ${{\beta }_{1}}$ для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с и $P > 2$ с, нормированные на число $N$ пульсаров в выборке.

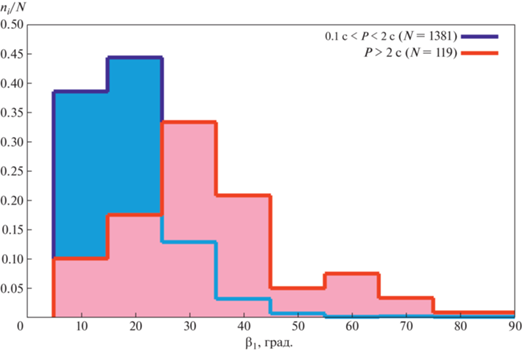
Для сопоставления статистического различия двух полученных распределений был использован критерий Колмогорова–Смирнова. Максимальная разность ${{d}_{{\max }}}$ отсчетов в двух гистограммах составила 0.285 (отсчеты нормированы на число $N$ пульсаров в выборках). Квантиль Колмогорова рассчитывался по формуле

(18)
$\lambda = {{d}_{{\max }}}\sqrt {\frac{{{{N}_{1}}{{N}_{2}}}}{{{{N}_{1}} + {{N}_{2}}}}} ,$
где ${{N}_{1}}$, ${{N}_{2}}$ – число пульсаров в первой и второй выборках. Рассчитанное согласно (18) значение квантиля Колмогорова $\lambda = 2.98$ означает, что выборки ${{\beta }_{1}}$ для пульсаров с $0.1{\text{ с}} < P < 2$ с и $P > 2$ с статистически различны с вероятностью $p = 0.99999$.

Полученные распределения могут быть аппроксимированы гауссианами (рис. 6, 7)

(19)
$\begin{gathered} \frac{n}{{N({{\beta }_{1}})}} = (0.492 \pm 0.010) \times \\ \times \;\exp \left\{ { - \frac{{{{{({{\beta }_{1}} - (16.0 \pm 0.2))}}^{2}}}}{{2(8.7 \pm {{{0.4)}}^{2}}}}} \right\} \\ \end{gathered} $
для выборки с $0.1{\text{ с}} < P < 2$ с и
(20)
$\begin{gathered} \frac{n}{{N({{\beta }_{1}})}} = (0.311 \pm 0.036) \times \\ \times \;\exp \left\{ { - \frac{{{{{({{\beta }_{1}} - (30.2 \pm 1.4))}}^{2}}}}{{2(11.7 \pm {{{3.1)}}^{2}}}}} \right\}. \\ \end{gathered} $
для пульсаров с $P > $ 2 с.

Рис. 6.

Гистограмма распределения углов ${{\beta }_{1}}$ для выборки пульсаров с $0.1{\text{ с}} < P < 2$ с, нормированная на число $N$ пульсаров в выборке.

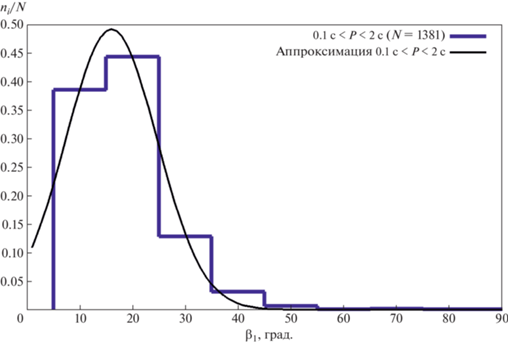
Рис. 7.

Гистограмма распределения углов ${{\beta }_{1}}$ для выборки пульсаров с $P > 2$ с, нормированная на число $N$ пульсаров в выборке.

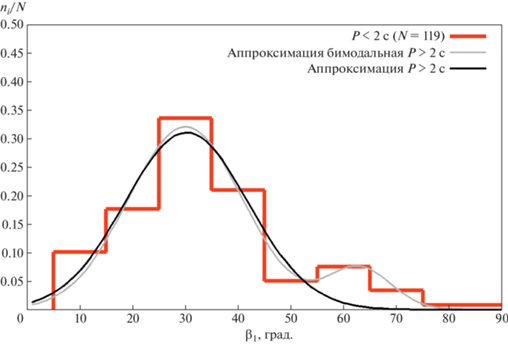
Для выборки с $P > 2$ с намечается бимодальность в распределении углов ${{\beta }_{1}}$. Статистическая достоверность наличия бимодальности также была оценена по критерию Колмогорова–Смирнова. Гистограмма сравнивалась с двумя гипотезами: 1) распределение может быть аппроксимировано единой функцией Гаусса (мономодальность); 2) распределение аппроксимировалось двумя функциями Гаусса (бимодальность). Сравнение гистограммы с гипотезой о мономодальности дает квантиль Колмогорова $\lambda = 0.49$, т.е. распределения значимо не отличаются с вероятностью $p = 0.97$. При сравнении гистограммы с бимодальной гипотезой мы получили $\lambda = 0.33$, что означает очень хорошее согласие с моделью. Визуально наблюдаемую бимодальность в распределении ${{\beta }_{1}}$ для $P > 2$ с следует еще раз проверить при увеличении числа пульсаров в этом интервале периодов. Следует подчеркнуть что наблюдаемые в настоящее время значения углов ${{\beta }_{1}}$ в двух максимумах ($30.0^\circ \pm 1.2^\circ $ и $62.9^\circ \pm 3.5^\circ $) не перекрываются с очень большой вероятностью (соответствующие дисперсии $\sigma $ равны $10.8^\circ \pm 0.4^\circ $ и $6.0^\circ \pm 0.3^\circ $). Кроме того, квантиль для бимодального представления существенно меньше, чем для мономодального. Это означает, что бимодальное распределение значительно лучше соответствует полученным значениям ${{\beta }_{1}}$. Для мономодального распределения с $P > 2$ с гауссиана описывается уравнением (20), а для бимодальной гипотезы можно использовать аппроксимацию:

$\begin{gathered} \frac{{n({{\beta }_{1}})}}{N} = {{A}_{1}}\exp \left( { - \frac{1}{2}{{{\left( {\frac{{{{\beta }_{1}} - {{m}_{1}}}}{{{{\sigma }_{1}}}}} \right)}}^{2}}} \right) + \\ + \;{{A}_{2}}\exp \left( { - \frac{1}{2}{{{\left( {\frac{{{{\beta }_{1}} - {{m}_{2}}}}{{{{\sigma }_{2}}}}} \right)}}^{2}}} \right), \\ \end{gathered} $
(21)
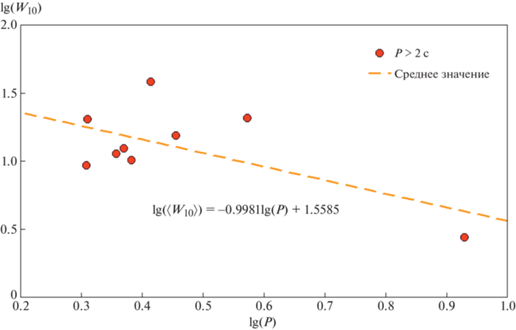
$\begin{gathered} {{A}_{1}} = 0.321 \pm 0.032,\quad {{m}_{1}} = 30.0 \pm 1.2, \\ {{\sigma }_{1}} = 10.8 \pm 0.4, \\ \end{gathered} $
$\begin{gathered} {{A}_{2}} = 0.073 \pm 0.003,\quad {{m}_{2}} = 62.9 \pm 3.5, \\ {{\sigma }_{1}} = 6.0 \pm 0.3. \\ \end{gathered} $

На рис. 8 и 9 показаны полученные зависимости $\langle {{W}_{{10}}}\rangle (P)$ для обеих выборок пульсаров (0.1  c < P < 2 с и P > c). Для выборки с $0.1{\text{ с}} < P < 2$ с

(22)
$\lg h(\langle {{W}_{{10}}}\;[^\circ ]\rangle (P)) = - 0.088\lg (P\;[{\text{с}}]) + 1.303,$
что соответствует

(23)
$\langle {{W}_{{10}}}\rangle = 20.1^\circ {{P}^{{ - 0.09}}}.$
Рис. 8.

Зависимость $\langle {{W}_{{10}}}\rangle $ от периода $P$ для выборки с $0.1{\text{ с}} < P < 2$ с.

Рис. 9.

Зависимость $\langle {{W}_{{10}}}\rangle $ от периода $P$ для выборки с $P > 2$ с.

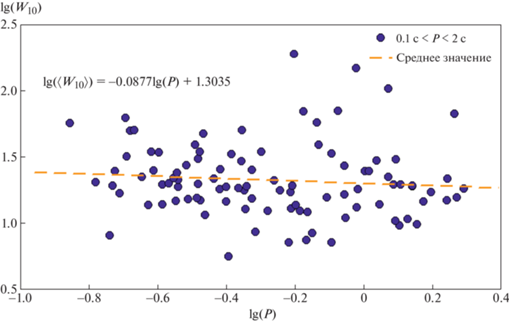
Для выборки с $P > 2$ с

(24)
$\lg (\langle {{W}_{{10}}}\;[^\circ ]\rangle (P)) = - 0.998\lg (P\;[{\text{с}}]) + 1.559,$
откуда:

(25)
$\langle {{W}_{{10}}}\rangle = 36.2^\circ {\text{/}}P.$

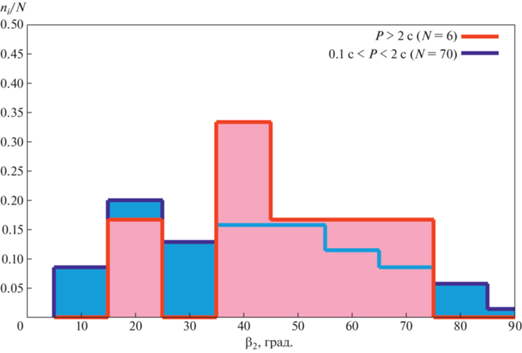
Так как число пульсаров в базе Джонстона и Керра [14] в несколько раз меньше объема базы ATNF, то кросс-сравнение каталогов привело к значительному сокращению объема анализируемых выборок. Дальнейший отсев поляризационных кривых в соответствии с упомянутыми выше критериями еще больше уменьшил объем выборок. В конечный анализ попали 93 пульсара для выборки с $0.1{\text{ с}} < P < 2$ с и 9 пульсаров для выборки с $P > 2$ с. Решение уравнения 4-й степени дает вещественные корни не при любых значениях $B$, $C$ и $D$, полученных из наблюдений, поэтому в конечный анализ вошли 70 пульсаров с $0.1{\text{ с}} < P < 2$ с и 6 пульсаров для выборки с $P > 2$ с. Вычисленные этим способом значения углов $\beta $, полученные из решения уравнения (10), обозначены как β2. Для двух указанных выборок были построены гистограммы распределения углов β2, показанные на рис. 10. Для сопоставления статистического различия двух полученных распределений был вновь использован критерий Колмогорова–Смирнова. Рассчитанное с помощью формулы (18) значение квантиля Колмогорова $\lambda = 0.41$ показывает, что выборки ${{\beta }_{2}}$ для пульсаров с $0.1{\text{ с}} < P < 2$ с и $P > 2$ с статистически не различимы с вероятностью $p = 0.996$. Возможно, что это связано с очень малым объемом выборки с $P > 2$ с.

Рис. 10.

Гистограммы распределения углов ${{\beta }_{2}}$ для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с и $P > 2$ с, нормированные на число $N$ пульсаров в выборках.

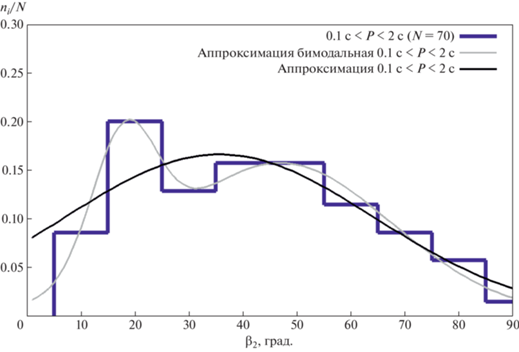
Для выборки с $0.1{\text{ с}} < P < 2$ с в распределении углов ${{\beta }_{2}}$ визуально намечается бимодальность (см. рис. 11). Статистический анализ достоверности наличия бимодальности проводился по методике, описанной в предыдущем разделе. Для случая сравнения гистограммы с гипотезой о мономодальности квантиль Колмогорова $\lambda = 0.34$, т.е. распределения значимо не отличаются. Таким образом, визуально наблюдаемая бимодальность в распределении ${{\beta }_{2}}$ для $0.1{\text{ с}} < P < 2$ с не подтверждается с точки зрения статистической значимости. Для мономодального распределения этой выборки $\langle {{\beta }_{2}}\rangle = 35.6^\circ \pm 4.3^\circ $ ($\sigma = 28.8^\circ \pm 4.1^\circ $).

Рис. 11.

Гистограмма распределения углов ${{\beta }_{2}}$ для выборки пульсаров с $0.1{\text{ с}} < P < 2$ с, нормированная на число $N$ пульсаров в выборке.

Аппроксимация функцией Гаусса распределения ${{\beta }_{2}}$ для выборки $P > $ 2 с дает среднее значение $\langle {{\beta }_{2}}\rangle = 47.6^\circ \pm 5.9^\circ $ ($\sigma = 17.8^\circ \pm 8.0^\circ $), что показано на рис. 12. На рис. 13 и 14 показаны распределения ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для двух групп выборок. Статистический анализ по критерию Колмогорова–Смирнова показал, что для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с распределения ${{\beta }_{1}}$ и ${{\beta }_{2}}$ значимо различаются ($\lambda = 2.45$, $p = 0.99999$), а распределения ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для объектов с $P > 2$ с статистическое различие невелико ($\lambda = 0.80$, $p = 0.4559$), что также может быть обусловлено малым объемом выборки источников с $P > 2$ с для ${{\beta }_{2}}$.

Рис. 12.

Гистограмма распределения углов ${{\beta }_{2}}$ для выборки пульсаров с $P > 2$ с, нормированная на число $N$ пульсаров в выборке.

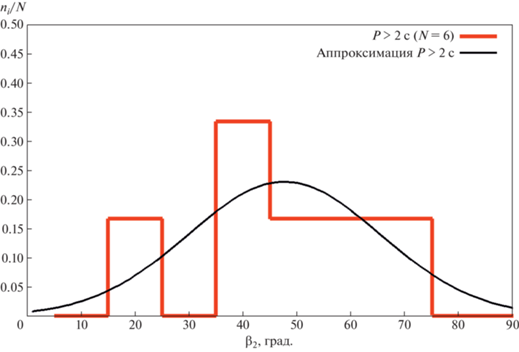
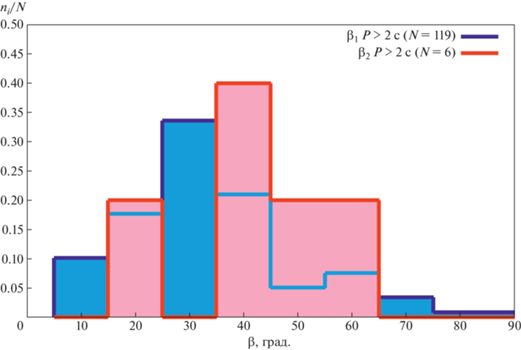
Рис. 13.

Гистограммы распределения углов ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с, нормированные на число $N$ пульсаров в выборке.

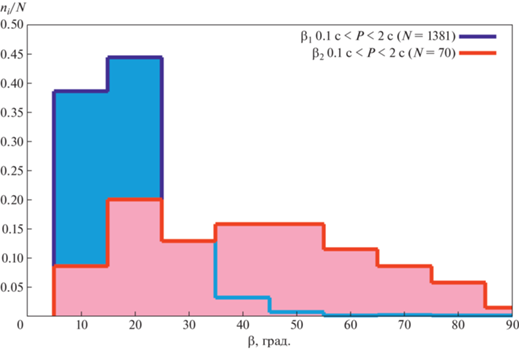
Рис. 14.

Гистограммы распределения углов ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для выборок пульсаров с $P > 2$ с, нормированные на число $N$ пульсаров в выборке.

На рис. 15 приведены диаграммы ${{\beta }_{1}} - {{\beta }_{2}}$ для обеих выборок. Биссектриса, показанная красной линией, определяет область на графике, где оба метода должны давать одинаковый результат. Как видно из полученных графиков, все значения ${{\beta }_{2}}$ больше соответствующих значений ${{\beta }_{1}}$ (за исключением четырех пульсаров, для которых в пределах ошибок их можно принять равными). Распределение ${{\beta }_{1}}$ заметно более узкое, чем ${{\beta }_{2}}$ (по величине $\sigma $ для пульсаров с $0.1{\text{ с}} < P < 2$ с почти в три раза).

Рис. 15.

Значения углов ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с и $P > 2$ с.

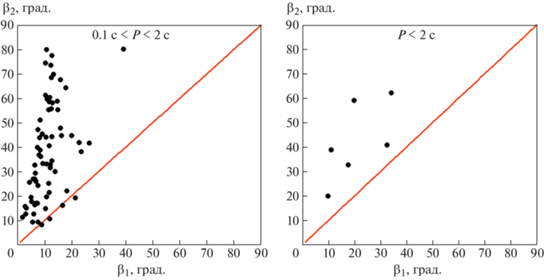
Полученные на основе формулы (6) значения ${{\beta }_{1}}$ следует рассматривать как нижние пределы угла между осью вращения и вектором магнитного момента пульсара.

4. ДИСКУССИЯ. ВЫВОДЫ

Основной целью нашей работы была проверка возможности объяснить различное поведение двух групп пульсаров с периодами $P > 2$ с и $0.1{\text{ с}} < P < 2$ с на диаграмме $(dP{\text{/}}dt) - (P)$ различием угла наклона их магнитного момента к оси вращения. Такая возможность предлагалась в работе [1]. Проведенный нами анализ показал, что такого различия не наблюдается. Средние значения нижних оценок угла $\langle {{\beta }_{1}}\rangle = 30.2^\circ $ для пульсаров с $P > 2$ с и $16.0^\circ $ для объектов с меньшими периодами перекрываются с учетом их дисперсий ($\sigma = 11.7^\circ $ и $8.7^\circ $ соответственно). То же можно сказать и о более точных оценках угла $\beta $ $\langle {{\beta }_{2}}\rangle = 47.6^\circ $ и $35.6^\circ $, $\sigma = 9.5^\circ $ и $10.2^\circ $). В обоих методах среднее значение угла $\beta $ для пульсаров с более длинными периодами оказывается больше, что в соответствии с уравнением (2) должно скорее свидетельствовать об усилении в них магнитодипольного излучения. Поэтому необходимо искать другие причины наблюдаемого различия.

Мы сравнили роль двух механизмов торможения, связанных с пульсарным ветром и магнитотормозным излучением. Соответствующие потери углового момента описываются приведенными выше уравнениями (1) и (2). Отношение эффективностей каждого из механизмов определяется следующим выражением:

(26)
$\xi = \frac{{{{{(6{{L}_{p}}{{c}^{3}})}}^{{1/2}}}{{P}^{2}}}}{{4{{\pi }^{2}}BR_{*}^{3}{{{\sin }}^{2}}\beta }}.$
Считая, что все характерные параметры пульсаров ($L,\;B,\;{{R}_{*}}$ и $\beta $) в двух рассматриваемых группах одинаковы, мы приходим к отношению:
(27)
$\frac{{{{\xi }_{2}}}}{{{{\xi }_{1}}}} = \frac{{P_{2}^{2}}}{{P_{1}^{2}}}.$
Средние значения периодов для двух исследуемых групп равны приблизительно 2.5 с и 0.5 с. Это означает, что в долгопериодических пульсарах мощность потерь за счет пульсарного ветра должна быть в 25 раз выше, чем мощность магнитодипольных потерь. Как было показано в работе [1], это действительно наблюдается.

1. Проведенный анализ показывает, что распределение углов $\beta $ по наблюдаемой ширине профиля импульса пульсара (${{\beta }_{1}}$) подтверждает наличие статистической значимости различий в распределениях для выборок пульсаров с $0.1{\text{ с}} < P < 2$ с (объем выборки $N = 1381$ пульсар) и $P > 2$ с ($N = 119$). При этом для выборки с $0.1{\text{ с}} < P < 2$ с среднее значение $\langle {{\beta }_{1}}\rangle = 16.0^\circ \pm 0.2^\circ $ ($\sigma = 8.7^\circ \pm 0.3^\circ $), а для $P > 2$ с $\langle {{\beta }_{1}}\rangle = 30.2^\circ \pm 1.4^\circ $ ($\sigma = 11.7^\circ \pm 3.1^\circ $).

Визуально наблюдаемая бимодальность в распределении ${{\beta }_{1}}$ для выборки с $P > 2$ с имеет невысокую статистическую значимость по критерию Колмогорова–Смирнова. Однако квантиль Колмогорова для бимодального представления существенно меньше, чем для мономодального. Это означает, что бимодальное распределение лучше соответствует полученным значениям ${{\beta }_{1}}$.

2. Анализ с использованием величины максимальной производной позиционного угла поляризации дает распределения углов ${{\beta }_{2}}$, заметно отличающиеся от соответствующих распределений для ${{\beta }_{1}}$: $\langle {{\beta }_{2}}\rangle = 35.6^\circ \pm 4.3^\circ $ ($\sigma = 28.8^\circ \pm 4.1^\circ $) для выборки пульсаров с $0.1{\text{ с}} < P < 2$ с ($Np$) и $\langle {{\beta }_{2}}\rangle = $ $ = 47.6^\circ \pm 5.9^\circ $ ($\sigma = 17.8^\circ \pm 8.0^\circ $) для выборки с $P > 2$ с ($N = 6$). Распределения ${{\beta }_{2}}$ в двух выборках статистически не отличимы по критерию Колмогорова–Смирнова, что может быть связано с малым объемом выборки для $P > 2$ с. Намечающаяся бимодальность в распределении ${{\beta }_{2}}$ для выборки с $0.1{\text{ с}} < P < 2$ с оказывается статистически незначимой по критерию Колмогорова–Смирнова.7

3. Для выборок с $0.1{\text{ с}} < P < 2$ с распределения ${{\beta }_{1}}$ и ${{\beta }_{2}}$ значимо различаются, а распределения ${{\beta }_{1}}$ и ${{\beta }_{2}}$ для выборок с $P > 2$ с статистически не различимы, что также может быть обусловлено малым объемом выборки с $P > 2$ с для ${{\beta }_{2}}$.

4. Все значения ${{\beta }_{2}}$ больше соответствующих значений ${{\beta }_{1}}$ или равны им (в пределах ошибок), подтверждая, что значения ${{\beta }_{1}}$ следует рассматривать как нижние пределы угла $\beta $ между осью вращения и вектором магнитного момента пульсара.

5. Обнаруженное ранее различное поведение радиопульсаров с периодами $P > 2$ с и $0.1{\text{ с}} < P < 2$ с на диаграмме $(dP{\text{/}}dt) - (P)$ объясняется разной зависимостью от периода мощности потерь для пульсарного ветра и магнитодипольного торможения и значительно более быстрым уносом углового момента релятивистскими частицами в долгопериодических пульсарах.

Для подтверждения полученных в работе результатов, в частности, более определенных суждениях о намечающихся бимодальностях в распределениях углов $\beta $ необходимо расширение выборки пульсаров с периодами $P > 2$ с.

Список литературы

  1. И. Ф. Малов, А. П. Морозова, Астрон. журн. 99(1), 29 (2022).

  2. A. K. Harding, L. Contopoulos, and D. Kazanas, Astrophys. J. Lett. 525, L125 (1999).

  3. J. P. Ostriker and J. E. Gunn, Astrophys. J. 157, 1395 (1969).

  4. А. Д. Кузьмин, И. М. Дагкесаманская, Письма в Астрон. журн. 9, 149 (1983).

  5. И. Ф. Малов, Астрофизика 24(3), 507 (1986).

  6. A. G. Lyne and R. N. Manchester, Monthly Not. Roy. Astron. Soc. 234, 477 (1988).

  7. J. M. Rankin, Astrophys. J. 352, 247 (1990).

  8. И. Ф. Малов, Е. Б. Никитина. Астрон. журн. 88(1), 22 (2011).

  9. В. С. Бескин, А. В. Гуревич, Я. Н. Истомин, ЖЭТФ 85(2), 401 (1983).

  10. A. Philippov, A. Tchekhovskoy, and J. G. Li, Monthly Not. Roy. Astron. Soc. 441, 1879 (2014).

  11. И. Ф. Малов, Радиопульсары (М.: Наука, 2004).

  12. R. N. Manchester, G. B. Hobbs, A. Teoh, and M. Hobbs, Astron. J. 129, 1993 (2005). https://www.atnf.csiro.au/research/pulsar/psrcat/

  13. Р. Манчестер, Дж. Тейлор, Пульсары (М.: Мир, 1980).

  14. S. Johnston and M. Kerr, Monthly Not. Roy. Astron. Soc. 474, 4629 (2018).

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал