Астрономический журнал, 2023, T. 100, № 1, стр. 32-40
Моделирование “центральной машины” астрофизических струйных выбросов на установке плазменного фокуса
1 Физический институт им. П.Н. Лебедева РАН
Москва, Россия
2 Московский физико-технический институт (национальный исследовательский университет)
Долгопрудный, Россия
* E-mail: beskin@lpi.ru
Поступила в редакцию 15.09.2022
После доработки 11.11.2022
Принята к публикации 11.11.2022
- EDN: NPMUQS
- DOI: 10.31857/S0004629923010012
Аннотация
Лабораторные плазменные выбросы на установках плазменного фокуса (структура их электрических токов, вращение, ударная волна, возникающая при взаимодействии с внешней средой) воспроизводят все основные элементы струйных выбросов из молодых звезд. С другой стороны, физические процессы, ответственные за запуск плазменного выброса, еще недостаточно поняты, и поэтому до сих пор нет однозначного ответа на вопрос о том, насколько лабораторный эксперимент адекватно воспроизводит механизм образования астрофизических джетов. В этой работе на основе анализа эффектов неидеальной магнитной гидродинамики сформулированы условия, при которых подобие физических процессов может иметь место и в самой “центральной машине” лабораторного эксперимента, приводящего к запуску плазменного выброса.
1. ВВЕДЕНИЕ
Проблема формирования и внутренней структуры астрофизических струйных выбросов, безусловно, находится на переднем крае современной астрофизики. Такие выбросы характерны для большинства активных галактичеких ядер [1, 2], молодых звезд [3] и микроквазаров [4]; по многим признакам они имеют место и в источниках гамма-всплесков [5]. Понятно, что из-за удаленности этих объектов трудно определить все детали физических процессов, ответственных за их наблюдаемую активность. Поэтому в последнее время большое внимание привлекают работы по лабораторному моделированию астрофизических джетов [6]. Прогресс же в этом направлении связан с развитием мощных установок, в которых достигается высокая плотность энергии. Прежде всего это мощные лазеры [7–9], быстрые Z-пинчи [10], плазменные ускорители [11], а также плазменный фокус (ПФ) [12].
Напомним, что основными образующими элементами астрофизических джетов, следующих из теории их внутреннего строения [13–15], являются регулярное полоидальное магнитное поле, продольный электрический ток, текущий вблизи оси и замыкающийся на периферии джета, а также их вращение. Поэтому адекватность лабораторного моделирования в значительной степени связана с тем, удается ли воспроизвести в лаборатории все эти ключевые свойства астрофизических струйных выбросов. Неудивительно поэтому, что подобная диагностика проводилась практически на всех установках. В частности, было проверено, что все эти элементы воспроизводятся на установке плазменного фокуса ПФ-3 в НИЦ “Курчатовский институт” [16–18]. При этом продольные токи в струйном выбросе составляли десятки килоампер, так что тороидальное магнитное поле на расстоянии ~1 см от оси выброса достигало нескольких килогаусс [19]. По-видимому, благодаря подобию физических процессов, все эти элементы реализуются и на других установках плазменного фокуса, таких как PF-1000 [20] (Институт физики плазмы и лазерного микросинтеза, Варшава) и КПФ-4 “Феникс” (Сухумский Физико-Технический Институт) [21]. Однако самом${\text{у}}\prime $ процессу образования плазменного выброса до сих пор не уделялось достаточного внимания. В частности, совершенно открытым остается вопрос о том, есть ли какое-нибудь подобие между механизмом формирования плазменного выброса в лабораторном эксперименте и запуском струйного выброса в астрофизических объектах.
Действительно, при обсуждении механизма запуска плазменного выброса в лабораторном эксперименте обычно говорят о кумулятивном эффекте, связанном либо со сжатием сходящейся токово-плазменной оболочки (ТПО) [22], либо со сжатием уже сформировавшегося плазменного жгута за счет “сосисочной” неустойчивости [23], т.е. о механизмах, которые заведомо не играют никакой роли в “центральных машинах” астрофизических объектов. При этом электродинамические процессы при анализе формирования плазменного выброса до сих пор практически не обсуждались. С другой стороны, подобие ключевых свойств астрофизических и лабораторных плазменных выбросов позволяет поставить вопрос о том, насколько похожими оказываются процессы их запуска. Иными словами, мы попробуем понять, насколько правдоподобной является электродинамическая гипотеза, согласно которой основную роль в механизме запуска плазменных выбросов на установках ПФ играют электромагнитные силы.
Прежде всего, мы обсудим вопрос о генерации полоидального магнитного поля. Понятно, что благодаря его системообразующей роли в большинстве лабораторных экспериментов такое полоидальное поле специально накладывалось [24, 25]. Подобные эксперименты проводились и на установках плазменного фокуса. Однако значительное полоидальное магнитное поле (порядка нескольких сот гаусс) возникало и в тех случаях, когда изначально полоидальное магнитное поле отсутствовало. Согласно работе [26], оно могло быть связано со сжатием геомагнитного магнитного поля хорошо проводящей токовой оболочкой.
Далее, нельзя обойти вниманием и вопрос о происхождении вращения. Несмотря на важность вращения при моделировании струйных выбросов, его удавалось уверенно воспроизвести лишь в немногих случаях. Это достигалось либо с помощью наложения радиального электрического поля в области основного разряда [25], либо путем неосесимметричного сходящегося потока при формировании токового жгута [27]. Что же касается экспериментов на установках ПФ, то никаких специальных условий для воспроизведения вращения в них не накладывались. Тем не менее ниже мы покажем, что и в установках ПФ вращение неизбежно возникает не только в уже сформировавшемся плазменном выбросе, но и в районе “центральной машины”. Поэтому не удивительно, что вращение плазменного выброса было в итоге подтверждено [28].
Наконец, еще одним важнейшим свойством астрофизических джетов, уверенно воспроизводимых в лабораторном эксперименте, является сверхзвуковой (сверхальфвеновский) характер течения. При этом в астрофизических источниках возникновение сверхзвукового режима (характерные скорости течения достигают сотен километров в секунду) связано с существенным увеличением поперечного размера замагниченного течения у его основания [3], в результате чего поток электромагнитной энергии перекачивается в поток энергии истекающей плазмы, что и приводит к ее ускорению. Природа же возникновения столь больших скоростей в лабораторном эксперименте остается неизвестной.
Таким образом, вопрос о генерации и структуре полоидального магнитного поля на установках ПФ становится центральным для объяснения природы образования плазменного выброса. Для его решения, как и для решения вопроса о запуске сверхзвукового потока, необходимо проанализировать все возможные диссипативные процессы, которые могут стать существенными в области формирования выброса. Действительно, в настоящее время не вызывает сомнения, что именно эффекты неидеальности (омическая и холловская проводимость, амбиполярная диффузия, турбулентность) играют определяющую роль в формировании астрофизических джетов [1, 3]. Этому кругу вопросов и будет посвящена настоящая работа.
В разделе 2 приведены основные результаты теории сильно замагниченных нерелятивистских струйных выбросов, которые понадобятся нам в дальнейшем. В разделе 3 обсуждаются основные параметры области формирования плазменного выброса на установке ПФ-3. Наконец, в разделе 4 исследована возможность электродинамического запуска плазменного выброса, подобного тому, как это имеет место в астрофизических источниках.
2. ОСНОВНЫЕ СВОЙСТВА СИЛЬНО ЗАМАГНИЧЕННЫХ СТРУЙНЫХ ВЫБРОСОВ
В этой части мы напомним основные соотношения теории сильно замагниченных нерелятивистских струйных выбросов, которые понадобятся нам в дальнейшем. Прежде всего, рассмотрим вопрос об угловой скорости вращения. В теории замагниченных течений благодаря вращению “центральной машины”, а также условию вмороженности неизбежно возникает электрическое поле ${\mathbf{E}}$, радиальную цилиндрическую компоненту которого удобно записать в виде [15]
т.е. выразить ее через угловую скорость ${{\Omega }_{{\text{F}}}}$, которая остается постоянной на магнитных поверхностях (закон изоротации Ферраро). При этом угловая скорость вращения вещества $\omega = {{V}_{\varphi }}{\text{/}}r$ в общем случае имеет вид(2)
$\omega = {{\Omega }_{{\text{F}}}}{\kern 1pt} \frac{{1 - k{{\mathcal{M}}^{2}}}}{{1 - {{\mathcal{M}}^{2}}}}{\kern 1pt} ,$(4)
${{\sigma }_{{\text{n}}}} = \frac{{\Omega _{{\text{F}}}^{2}{{\Psi }_{0}}}}{{8{{\pi }^{2}}V_{0}^{3}{{\eta }_{{\text{n}}}}}}$Таким образом, в сверхзвуковой области $\mathcal{M} > 1$ угловая скорость движения вещества $\omega $ оказывается меньше величины ${{\Omega }_{{\text{F}}}}$. Это связано с тем, что движение вещества слагается из вращения с угловой скоростью ${{\Omega }_{{\text{F}}}}$ и обратным скольжением вдоль магнитных силовых линий, имеющих тороидальную составляющую. Как мы видим, вопрос о существовании вращения оказался тесно связан с наличием полоидального магнитного поля, поскольку величина ${{\Omega }_{{\text{F}}}}$ зависит от величины ${{B}_{{\text{p}}}}$.
Далее, еще одним важнейшим свойством астрофизических джетов является трансзвуковой характер течения. При этом, как уже отмечалось, в астрофизических источниках возникновение сверхзвукового режима связано с существенным увеличением поперечного размера ${{r}_{{{\text{jet}}}}}$ замагниченного течения в основании струйного выброса. Поскольку в этом случае полоидальное магнитное поле, благодаря сохранению магнитного потока, будет вести себя как ${{B}_{{\text{p}}}} \propto r_{{{\text{jet}}}}^{{ - 2}}$, а плотность вещества как $\rho \propto r_{{{\text{jet}}}}^{{ - 2}}{{V}^{{ - 1}}}$, то в результате альфвеновское число Маха $\mathcal{M} = V{\text{/}}{{V}_{{\text{A}}}}$ будет вести себя как $\mathcal{M} \propto {{V}^{{1{\text{/}}2}}}{{r}_{{{\text{jet}}}}}$. Поскольку согласно теории замагниченных течений [15] скорость $V$ может только увеличиваться, мы приходим к заключению, что при достаточно большом увеличении поперечного сечения астрофизических струйных выбросов течение неизбежно должно стать сверхальфвеновским. Если такую же расходящуюся структуру полоидальное магнитное поле имело бы и в лабораторном эксперименте (в настоящее время никаких подтверждений этому мы, правда, не имеем), то и в этом элементе можно было бы говорить о подобии механизмов формирования джетов.
Принципиальная важность трансзвукового режима истечения связана еще и с тем, что именно критические условия на особых поверхностях определяют величину продольного тока ${{I}_{{{\text{eng}}}}}$, циркулирующего в “центральной машине”, а значит, и энергетику струйного выброса ${{W}_{{{\text{tot}}}}} = {{I}_{{{\text{eng}}}}}U$, где $U \sim ({{\Omega }_{{\text{F}}}}{{R}_{0}}{\text{/}}c){{B}_{z}}{{R}_{0}}$ (${{R}_{0}}$ –характерный размер “центральной машины”) – соответствующая разность потенциалов. При этом полный ток ${{I}_{{{\text{eng}}}}}$ удобно выразить через т.н. гольдрайховский ток ${{I}_{{{\text{GJ}}}}}$,
где При этом для сильно замагниченного течения ${{\sigma }_{{\text{n}}}} > 1$ имеем (см., напр., [15]) В итоге, получаем для полных потерь(8)
${{W}_{{{\text{tot}}}}} = {{i}_{0}}{{\left( {\frac{{{{\Omega }_{{\text{F}}}}{{R}_{0}}}}{c}} \right)}^{2}}B_{0}^{2}{\kern 1pt} R_{0}^{2}{\kern 1pt} c.$Как показано в [6], для уже сформировавшегося лабораторного плазменного выброса соответствующее согласование параметров действительно имеет место. Для анализа же условий в районе “центральной машины” приведем еще соответствующие соотношения для расширяющегося трансзвукового потока. В частности, радиус быстрой магнитозвуковой поверхности ${{r}_{{\text{F}}}}$ и скорости течения на этой поверхности $V({{r}_{{\text{F}}}})$ имеют вид
где(11)
${{\mu }_{l}} = \frac{{8{{\Omega }_{{\text{F}}}}{{r}_{{\text{c}}}}{{\eta }_{{\text{n}}}}}}{{{{B}_{z}}}}$3. ОСНОВНЫЕ ПАРАМЕТРЫ “ЦЕНТРАЛЬНОЙ МАШИНЫ” НА УСТАНОВКЕ ПФ-3
Обсудим теперь основные процессы, происходящие в области формирования плазменного выброса, обращая внимание прежде всего на те параметры, которые позволят нам сравнить динамику формирования лабораторного плазменного выброса с астрофизическими джетами. Как известно, приложенное напряжение между анодом и катодом порядка нескольких десятков кВ приводит к появлению токово-плазменной оболочки, сходящейся к оси установки (см. рис. 1). В момент наибольшего сжатия плотность тока достигает значений вплоть до ${{10}^{7}}$ А/см2 при радиусе токового жгута ${{r}_{{\text{c}}}}$ в несколько миллиметров (так что полный ток превышает 1 МА), а концентрация частиц вырастает до ${{10}^{{19}}}$ см–3. При этом тороидальное магнитное поле тока на масштабе ${{r}_{{\text{c}}}}$ должно достигать ${{10}^{5}}{\kern 1pt} - {\kern 1pt} {{10}^{6}}$ Гс.
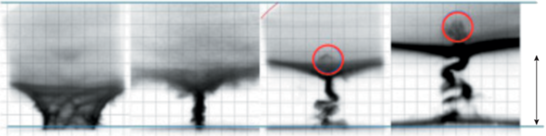
Рис. 1.
Кадровые фотографии пинчевания и формирования плазменного потока. Экспозиция 12 нс, масштаб 1 см. Интервал между кадрами 150 нс. Над ТПО видны образования, вытянутые вдоль оси установки в направлении от анода (выделено красной окружностью) [29].
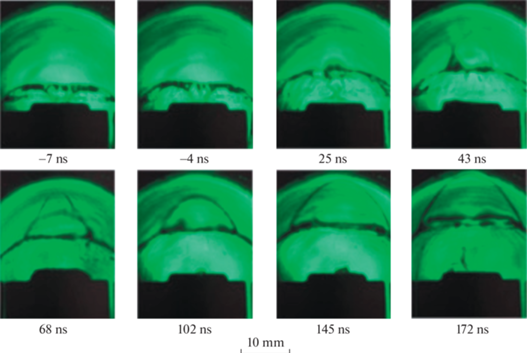
Отметим здесь сразу еще одно очень важное обстоятельство. Как показано на рис. 2, верхняя часть сходящейся плазменной оболочки действительно на время становится центром сферически расходящегося возмущения. Если это действительно так, то это может служить основанием для подтверждения гипотезы о воспроизведении в лабораторном эксперименте на установках ПФ расходящегося замагниченного потока, о котором говорилось выше.
Рис. 2.
Последовательность Шлирен-снимков, отражающая динамику плазмы ($t = 0$ соответствует времени минимального значения производной тока, т.е. близкому к времени пинча). Первые два снимка соответствуют стадии образования пинча. Последующие снимки соответствуют динамике после пинчевания [30].
Развитие турбулентности и, как следствие, включение аномального сопротивления приводит к резкому падению тока. При этом аномальный разогрев плазмы до температур $T \sim {{10}^{7}}$ K ($ \sim {\kern 1pt} 1$ кэВ) приводит к генерации рентгеновского излучения (до 100 кДж за времена порядка 200 нс) [16] и пучков заряженных частиц. Ионизация в этот момент достигает 100%. При этом сам ток течет, естественно, по направлению от анода (${{j}_{z}} > 0$), растекаясь радиально в верхней части сходящейся токовой оболочки.
Отметим, что при таких параметрах плазма в токовом жгуте должна быть сильно замагниченной. Действительно, даже в центральной части плазменного жгута (${{n}_{{\text{e}}}} \sim {{10}^{{19}}}$ см–3) известный плазменный параметр $b = {{\omega }_{B}}\tau $, где ${{\omega }_{B}} = eB{\text{/}}mc$ – гирочастота, а $\tau $ – время столкновений, составляет $b \sim {{10}^{2}}$ для ионов и $b \sim 1$ для электронов при значении магнитных полей $B \sim {{10}^{4}}$ Гс, т.е. для полей, значительно меньших, чем на границе плазменного жгута. В периферийной же области ($B \sim {{10}^{6}}$ Гс, ${{n}_{{\text{e}}}}{{ < 10}^{{16}}}$ см–3) можно ожидать значений $b{{ > 10}^{4}}$ для электронов и $b{{ > 10}^{2}}$ для ионов. При этом для магнитных полей $B \sim 1$ МГс ларморовский радиус электронов составляет ${{r}_{{{\text{L}},e}}} \sim {{10}^{{ - 4}}}$ см, а ларморовский радиус ионов ${{r}_{{{\text{L}},i}}} \sim {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}}$ см (в зависимости от заряда и атомного веса ионов). Так что можно считать, что во всех случаях ларморовский радиус меньше поперечного размера плазменного жгута. Что же касается длин пробега, то даже для концентраций ${{n}_{{\text{e}}}} \sim {{10}^{{18}}}$ см–3 они составляют несколько сантиметров как для электронов, так и для ионов.
Важным параметром также является токовая скорость частиц ${{v}_{{{\text{cur}}}}}$. Для плотности тока $ \sim {\kern 1pt} {{10}^{7}}$ А/см2 и концентрации электронов $ \sim {\kern 1pt} {{10}^{{18}}}$ см–3 получаем ${{v}_{{{\text{cur}}}}} \sim {{10}^{7}}$ см/c, что на несколько порядков меньше тепловой скорости электронов ${{v}_{{T,e}}} \sim {{10}^{9}}$ см/c для реализуемых температур $T \sim 1$ кэВ. Соответственно, тепловая скорость ионов ${{v}_{{T,i}}} \sim {{10}^{7}}$ см/c, т.е. сравнима со скоростью плазменного выброса.
С другой стороны, в самом плазменном выбросе положительная величина измеряемого тороидального магнитного поля (${{B}_{\varphi }} > 0$) говорит о том, что и вблизи оси выброса ток течет в том же направлении, т.е. по направлению движения выброса ${{{\mathbf{V}}}_{{{\text{jet}}}}}$. Соответственно, электрическое поле
связанное с тороидальным магнитным полем, будет направлено от оси (${{E}_{r}} > 0$), что, согласно (1), означает, что угловая скорость ${{\Omega }_{{\text{F}}}}$ и полоидальное магнитное поле должны быть направлены в противоположных направлениях.Наконец, отметим, что поскольку индуцируемое продольное электрическое поле значительно превосходит критическое поле Драйсера ${{E}_{{\text{D}}}} = 4\pi {{e}^{3}}{{n}_{{\text{e}}}}\Lambda {\text{/}}{{T}_{{\text{e}}}}$, то практически все электроны плазмы в области слабого магнитного поля вблизи оси токового жгута должны уйти в режим убегания. Однако вследствие того, что ускорение происходит в плотной плазме, максимальная величина тока пучка убегающих электронов определяется условием самоограничения тока собственным магнитным полем и она равна предельному току Альфвена $I = ({{m}_{{\text{e}}}}{{c}^{3}}{\text{/}}e)\beta \gamma $ [26].
4. КАК РАБОТАЕТ “ЦЕНТРАЛЬНАЯ МАШИНА”
Посмотрим теперь, может ли область воронки сходящейся ТПО в верхней части плазменного жгута действительно играть роль “центральной машины”. Начнем с обсуждения необходимого нам продольного магнитного поля. Его присутствие в эксперименте ПФ легко объяснить благодаря высокой степени ионизации ТПО и, как следствие, выполнению условия вмороженности. В результате по мере схлопывания токовой оболочки напряженность продольного магнитного поля может существенно возрасти. Действительно, при сжатии токовой оболочки с большого радиуса ${{r}_{0}} \sim 50$ см до размеров ${{r}_{{\text{c}}}} \sim 1$ см геомагнитное магнитное поле ${{B}_{0}} = 1$ Гс может дорасти до значений ${{B}_{z}} \sim 10$ кГс [26].
Еще одной причиной усиления продольного геомагнитного поля могут стать указанные выше эффекты неидеальности, связанные с эффектом Холла. Действительно, записав обобщенный закон Ома в стандартном виде [31], т.е. в пренебрежении инерционными членами
(13)
${\mathbf{E}} = \frac{{\mathbf{j}}}{\sigma } + \frac{{{\mathbf{V}} \times {\mathbf{B}}}}{c} + \frac{{{\mathbf{j}} \times {\mathbf{B}}}}{{{{n}_{{\text{e}}}}e{\kern 1pt} c}}{\kern 1pt} ,$(15)
$\delta B \sim \frac{{{{I}_{r}}}}{{c{{r}_{c}}}}{{\omega }_{B}}{\kern 1pt} \tau \sim {{10}^{6}}\left( {\frac{{{{I}_{r}}}}{{{{{10}}^{5}}\;{\text{А}}}}} \right){{\left( {\frac{{{{r}_{c}}}}{{1{\kern 1pt} \;{\text{см}}}}} \right)}^{{ - 1}}}\left( {\frac{{{{\omega }_{B}}\tau }}{{{{{10}}^{2}}}}} \right) \;{\text{Гс}}.$Напомним, что, как видно из соотношения (14), рассмотренное выше проявление эффекта Холла нечетно по отношению к направлению радиального тока. Для лабораторного эксперимента это свойство подробно исследовалось на установке COBRA [24], на которой можно было реализовать оба направления тока. Для астрофизических аккреционных дисков обсуждение этого вопроса можно найти в обзоре [3]. Для положительного же радиального тока (${{j}_{r}} > 0$), реализуемого на установке плазменного фокуса, дополнительное магнитное поле $\delta B$ (15) усиливает внешнее продольное магнитное поле.
Наконец, еще одной причиной сильного продольного магнитного поля могут служить неустойчивости в плазменном шнуре. К ним относятся т.н. “сосисочная” неустойчивость, связаная с возникновением перетяжек вдоль шнура, а также “кинковая” ($m = 1$) неустойчивость, которая хорошо видна на рис. 1. Согласно работе [23] во время фазы “сосисочной” неустойчивости энергия продольного магнитного поля увеличивается экспоненциально и потом еще продолжает расти на стадии “кинковой” неустойчивости благодаря тому, что в токовом шнуре возникает тороидальный ток ${{j}_{\varphi }} \sim {{j}_{z}}$. Оценка инкрементов дает значения $\gamma {\text{/}}{{\omega }_{{{\text{pe}}}}} = 0.049$ для “сосисочной” и 0.015 для “кинка”. Ссылаясь на работу [32], авторы приводят выражение для инкремента кинк-неустойчивости $\gamma {\text{/}}{{\omega }_{{{\text{pe}}}}} = (2{\kern 1pt} - {\kern 1pt} 3){{v}_{{Ti}}}{\text{/}}{{r}_{0}}{{\omega }_{{{\text{pe}}}}}$, где ${{r}_{0}}$ есть радиус токовой петли $\left( {{{r}_{0}} \sim c{\text{/}}{{\omega }_{{{\text{pe}}}}}} \right)$. В результате продольное магнитное поле действительно может дорасти до значений ${{B}_{z}} \approx 2I{\text{/}}(c{{r}_{{\text{c}}}}) \sim 10$ кГс.
Понятно, правда, что такие неустойчивости могут себя активно проявить лишь на последней стадии сжатия плазменного шнура, так что их влияние может быть не столь существенно. С другой стороны, оказалось, что уже на ранней стадии сжатия ТПО возникает волоконная спиралевидная структура (см. [33] и левый снимок на рис. 1), обусловленная, по-видимому, неустойчивостями с $m > 1$. Возникающие при этом тороидальные токи также должны приводить к генерации продольного магнитного поля.
Далее, напомним, что еще одним важнейшим свойством астрофизических джетов, уверенно воспроизводимых в лабораторном эксперименте, является сверхзвуковой (сверхальфвеновский) характер течения уже сформировавшегося плазменного выброса. При этом в астрофизических источниках возникновение сверхзвукового режима связано с существенным увеличением поперечного размера ${{r}_{{{\text{jet}}}}}$ замагниченного течения, поскольку, как уже отмечалось выше, при достаточно большом увеличении поперечного сечения течение неизбежно должно стать сверхальфвеновским. Предположим теперь, что и в лабораторном эксперименте на установках ПФ происходит трансзвуковое ускорение плазмы. В пользу этого, как уже отмечалось выше (см. рис. 2), говорит квазисферическое расширение возмущения в момент схождения ТПО. Если это действительно так, то можно оценить многие ключевые параметры течения в основании плазменного выброса.
Прежде всего отметим, что для оценки ключевого параметра замагниченности ${{\sigma }_{{\text{n}}}}$ (4) не нужно отдельно определять угловую скорость ${{\Omega }_{{\text{F}}}}$. Действительно, используя соотношение ${{\Psi }_{0}} \approx \pi {{r}^{2}}{{B}_{{\text{p}}}}$ и определение ${{\eta }_{{\text{n}}}} = \rho {{V}_{{{\text{jet}}}}}{\text{/}}{{B}_{{\text{p}}}}$ (эти две величины являются инвариантами течения), а также комбинируя соотношения (1) и (12) для электрического поля ${{E}_{r}}$ в области сформировавшегося плазменного выброса, получаем
(16)
${{\sigma }_{{\text{n}}}} \approx \frac{1}{{8\pi }}\frac{{{{V}_{{{\text{jet}}}}}B_{\varphi }^{2}}}{{{{\rho }_{{{\text{jet}}}}}V_{0}^{3}}}.$(17)
$\begin{gathered} {{\sigma }_{{\text{n}}}} \approx 10\left( {\frac{{{{V}_{{{\text{jet}}}}}}}{{{{{10}}^{7}} \;{\text{см/с}}}}} \right){{\left( {\frac{{{{V}_{0}}}}{{{{{10}}^{6}} \;{\text{см/c}}}}} \right)}^{{ - 3}}} \times \\ \, \times {{\left( {\frac{{{{B}_{\varphi }}}}{{{{{10}}^{3}} \;{\text{Гс}}}}} \right)}^{2}}{{\left( {\frac{{{{n}_{i}}}}{{{{{10}}^{{16}}} \;{\text{c}}{{{\text{м}}}^{{ - 3}}}}}} \right)}^{{ - 1}}}. \\ \end{gathered} $Здесь необходимо сделать одно существенное разъяснение, поскольку при оценке параметра замагниченности потока ${{\sigma }_{{\text{n}}}}$ (16) мы намеренно не учли тепловую энергию плазмы. Это связано с тем, что тепловая энергия быстро диссипирует за счет излучения, так что температура самого плазменного выброса составляет лишь несколько эВ. Кроме того, как хорошо известно, для гидродинамического ускорения плазмы до звуковых скоростей за счет тепловых эффектов необходимо сжатие плазменного потока, а не расширения, как это имеет место для областей над токовым шнуром.
В свою очередь, угловую скорость ${{\Omega }_{{\text{F}}}}$ можно оценить, комбинируя соотношения (9) и (10). Полагая ${{r}_{{\text{F}}}} \sim 1$ см и $V({{r}_{{\text{F}}}}) \sim {{10}^{7}}$ см/с (теория предсказывает, что скорость нерелятивистского течения на быстрой магнитозвуковой поверхности не сильно отличается от предельной скорости в струйном выбросе [15]), получаем ${{\Omega }_{{\text{F}}}} \sim {{10}^{7}}$ с–1. Tакое значение угловой скорости вращения ${{\Omega }_{{\text{F}}}}$ совпадает с оценкой, которая может быть сделана, опираясь на измеренную скорость вращения сверхзвукового плазменного выброса $\omega \approx {{10}^{6}}$ с–1 [28]. Поскольку согласно (3) $\omega = \sigma _{{\text{M}}}^{{ - 1{\text{/}}3}}{{\mathcal{M}}^{{ - 2}}}{{\Omega }_{{\text{F}}}}$, для ${{\sigma }_{{\text{n}}}} \sim 10$ и $\mathcal{M} \sim 3$ получаем вновь значение ${{\Omega }_{{\text{F}}}} \sim {{10}^{7}}$ с–1.
Наконец, нетрудно понять и механизм возникновения вращения. Действительно, в присутствии полоидального магнитного поля сила Ампера, связанная с радиально растекающимся электрическим током ${{j}_{r}}$ в верхней части сходящейся токовой оболочки, неизбежно приведет к возникновению вертикального момента сил ${{K}_{z}} \propto {{j}_{r}}{{B}_{z}}$. Подчеркнем, что этот процесс является обратным по сравнению со стандартным механизмом генерации электрического тока в униполярном индукторе, когда энергия, создающая ЭДС и выделяющаяся на внешней нагрузке, заключена в кинетической энергии вращающегося тела. При этом центральное тело будет, естественно, замедлять свое вращение. В нашем же случае, соответствующем замене внешней нагрузки на источник напряжения, будет происходить ускорение вращения до тех пор, пока внешний источник будет поддерживать токовую систему.
Посмотрим теперь, до какой угловой скорости может быть раскручена плазма в верхней части токового жгута за те несколько сотен наносекунд, пока еще не произошло его разрушение. Для этого запишем уравнение энергии для области с радиально расходящимся током в верхней части токового шнура в виде
Здесь ${{J}_{r}} \sim \rho r_{{\text{c}}}^{2}\mathcal{V}$ – момент инерции этой области ($\mathcal{V}$ – ее объем), а есть полный момент силы Ампера, связанный с расходящимся радиальным током ${{I}_{r}}$. При этом потери энергии ${{W}_{{{\text{tot}}}}}$, связанные с сильно замагниченным плазменным выбросом, задаются соотношением (8). Здесь как раз и используется наше основное предположение, что течение является трансзвуковым. При этом мы в дальнейшем в качестве характерного размера “центральной машины” ${{R}_{0}}$ будем выбирать радиус токового шнура ${{r}_{{\text{c}}}}$.Поскольку потери энергии ${{W}_{{{\text{tot}}}}}$ (8) пропорциональны квадрату угловой скорости вращения токового шнура $\omega $ (которая, как уже отмечалось выше, в этой области совпадает с величиной ${{\Omega }_{{\text{F}}}}$), то за время ${{\tau }_{{{\text{in}}}}} \approx {{J}_{r}}{{\Omega }_{{\text{F}}}}{\text{/}}K$ происходит переход в равновесное состояние с угловой скоростью вращения
(20)
${{\Omega }_{{\text{F}}}} \sim \frac{{{{I}_{r}}}}{{{{i}_{0}}r_{{\text{c}}}^{2}{{B}_{z}}}}{\kern 1pt} .$(21)
$\begin{gathered} {{\Omega }_{{\text{F}}}} \approx {{10}^{7}}\left( {\frac{{{{I}_{r}}}}{{100\;{\kern 1pt} {\text{кА}}}}} \right)\left( {\frac{{{{V}_{0}}}}{{{{{10}}^{6}}\;{\text{см/с}}}}} \right) \times \\ \times \;{{\left( {\frac{{{{B}_{z}}}}{{{{{10}}^{4}}\;{\text{Гс}}}}} \right)}^{{ - 1}}}{{\left( {\frac{{{{r}_{{\text{c}}}}}}{{3\;{\text{мм}}}}} \right)}^{{ - 2}}}\;{{{\text{с}}}^{{ - 1}}}. \\ \end{gathered} $Как мы видим, теоретическая оценка угловой скорости ${{\Omega }_{{\text{F}}}}$ находится в полном согласии с ее значением, оцененным по экспериментальным данным. При этом время раскрутки до такой угловой скорости,
(22)
${{\tau }_{{{\text{in}}}}} \approx \frac{{\rho c\mathcal{V}}}{{{{i}_{0}}r_{{\text{c}}}^{2}B_{z}^{2}}} \sim 0.1{\kern 1pt} \;{\text{мкс}},$5. ЗАКЛЮЧЕНИЕ
Таким образом, как показывают наши оценки, предположение о трансзвуковом характере течения у основания плазменного выброса на установке ПФ приводит к хорошему согласию предсказаний теории с измеряемыми величинами. Следовательно, гипотеза о том, что механизм запуска плазменного выброса в лабораторном эксперименте подобен механизму запуска струйных выбросов в молодых звездах, оказалась достаточно разумной.
Более того, удалось сформулировать и условия, при которых механизм запуска плазменного выброса на установках плазменного фокуса будет подобен механизму запуска астрофизических джетов. Как уже подчеркивалось, ключевую роль здесь должно сыграть наличие продольного магнитного поля и вращения плазмы, величины которых будут обеспечивать трансзвуковой характер истечения. Например, в качестве выполнения этого условия можно воспользоваться соотношением (9) для радиуса быстрой магнитозвуковой поверхности, потребовав, чтобы он был заключен между радиусом токового шнура и размером сформировавшегося плазменного выброса
Это условие может быть полезно при создании новых установок, нацеленных на лабораторное моделирование астрофизических струйных выбросов.Заметим прежде всего, что для уверенного выполнения условия (24) поперечный размер камеры должен быть достаточно большим. Иными словами, речь идет о поперечном размере камеры ${{r}_{{{\text{ch}}}}}$, содержащей плазменный выброс, до величин порядка одного метра. Далее, благодаря соотношениям (9) и (11), условие ${{r}_{{\text{c}}}} < {{r}_{{\text{F}}}}$, согласно которому быстрая магнитозвуковая поверхность находится за пределами “центральной машины”, можно записать как ${{\mu }_{l}} < 1$. С учетом определения ${{\eta }_{{\text{n}}}} = \rho V{\text{/}}{{B}_{z}}$ получаем окончательно
(25)
$\begin{gathered} {{B}_{z}} > 100{{\left( {\frac{{{{\Omega }_{{\text{F}}}}}}{{{{{10}}^{7}}{\kern 1pt} \;{{{\text{с}}}^{{ - 1}}}}}} \right)}^{{1{\text{/}}2}}}{{\left( {\frac{{{{V}_{0}}}}{{{{{10}}^{6}}\;{\text{см/с}}}}} \right)}^{{1{\text{/}}2}}} \times \\ \, \times {{\left( {\frac{{{{r}_{{\text{c}}}}}}{{3\;{\text{мм}}}}} \right)}^{{1{\text{/}}2}}}{{\left( {\frac{{{{n}_{i}}}}{{{{{10}}^{{16}}}\;{\text{c}}{{{\text{м}}}^{{ - 3}}}}}} \right)}^{{1{\text{/}}2}}}\;{\text{Гс}}. \\ \end{gathered} $Наконец, отметим, что для того, чтобы плазменный выброс мог свободно распространяться внутри камеры, необходимо выполнение условия ${{r}_{{{\text{jet}}}}} < {{r}_{{{\text{ch}}}}}$. Поскольку для сверхзвуковых джетов их поперечный размер определяется из баланса магнитного давления джета и внешнего газового давления ($B_{\varphi }^{2}{\text{/}}8\pi = {{P}_{{{\text{ext}}}}}$) [15], получаем в результате
Понятно, что при увеличении поперечного размера камеры в несколько раз характерное давление оказалось на один-два порядка меньше, чем в существующих экспериментах на установках ПФ.Список литературы
S. Komissarov and O. Porth, New Astron. Rev. 92, id. 101610 (2021).
S. W. Davis and A. Tchekhovskoy, Ann. Rev. Astron. Astrophys. 58, 407 (2020).
R. E. Pudritz and T. P. Ray, Frontiers in Astron. and Space Sci. 6, id. 54 (2019).
R. P. Fender, in Compact Stellar X-ray Sources, edited by W. Lewin and M. van der Klis (Cambridge: Cambridge Univ. Press, 2006), p. 381.
К. А. Постнов, Успехи физ. наук 169, 545 (1999).
В. С. Бескин, В. И. Крауз, С. А. Ламзин, Успехи физ. наук, в печати.
B. Albertazzi, A. Ciardi, M. Nakatsutsumi, T. Vinci, et al., Science 346, 325 (2014).
J. M. Stone, N. Turner, K. Estabrook, B. Remington, D. Farley, S. G. Glendinning, and S. Glenzer, Astrophys. J. Suppl. 127, 497 (2000).
В. С. Беляев, Г. С. Бисноватый-Коган, А. И. Громов, Б. В. Загреев, А. В. Лобанов, А. П. Матафонов, С. Г. Моисеенко, О. Д. Торопина, Астрон. журн. 95, 171 (2018).
S. V. Lebedev, A. Frank, and D. D. Ryutov, Rev. Modern Physics 91, id. 025002 (2019).
P. M. J. Bellan, J. Plasma Phys. 84, id. 755840501 (2018).
V. I. Krauz, V. S. Beskin, and E. P. Velikhov, Intern. J. Modern Physics D 27, id. 1844009 (2018).
G. Pelletier and R. E. Pudritz, Astrophys. J. 394, 117 (1992).
J. Heyvaerts and C. Norman, Astrophys. J. 347, 1055 (1989).
В. С. Бескин, Осесимметричные стационарные течения в астрофизике (М.: ФИЗМАТЛИТ, 2005).
N. V. Filippov, T. I. Filippova, I. V. Khutoretskaia, V. V. Mial-ton, and V. P. Vinogradov, Phys. Letters A 211, 168 (1996).
V. I. Krauz, K. N. Mitrofanov, V. V. Myalton, V. P. Vinogradov, et al., Plasma Phys. Rep. 36, 937 (2010).
В. С. Бескин, Я. Н. Истомин, А. М. Киселев, В. И. Крауз и др. Радиофизика 59, 1004 (2016).
В. И. Крауз, К. Н. Митрофанов, Д. А. Войтенко, Г. И. Астапенко, А. И. Марколия, А. П. Тимошенко, Астрон. журн. 96, 156, (2019).
M. Scholz, R. Miklaszewski, V. A. Gribkov, and F. Mezzetti, Nukleonika 45, 155 (2000).
E. A. Andreeshchev, D. A. Voitenko, V. I. Krauz, A. I. Mar-koliya, Yu. V. Matveev, N. G. Reshetnyak, and E. Yu. Khau-tiev, Plasma Phys. Rep. 33, 218 (2007).
С. С. Ананьев, С. В. Суслин, А. М. Харрасов, ВАНТ. Сер. Термоядерный синтез 39, 69 (2016).
T. Haruki, H. Reza Yousefi, K. Masugata, J.-I. Sakai, Y. Mizuguchi, N. Makino, and H. Ito, Phys. Plasmas 13, id. 082106 (2006).
T. Byvank, J. T. Banasek, W. M. Potter, J. B. Greenly, C. E. Seyler, and B. R. Kusse, Phys. Plasmas 24, id. 122701 (2017).
E. S. Lavine and S. You, Phys. Rev. Lett. 123, id. 145002 (2019).
Ю. Н. Жуков, А. И. Марколия, А. Ф. Попов, А. Ф. Чачаков, Журн. техн. физики 71, 32 (2001).
V. Valenzuela-Villaseca, L. G. Suttle, F. Suzuki-Vidal, J. W. D. Halliday, et al., Plasma Phys. Rep., in press.
В. И. Крауз, К. Н. Митрофанов, А. М. Харрасов, И. В. Ильичев, В. В. Мялтон, С. С. Ананьев, В. С. Бес-кин, Астрон. журн. 98, 29 (2021).
С. С. Ананьев, В. И. Крауз, В. В. Мялтон, А. М. Харрасов, ВАНТ. Сер. Термоядерный синтез 40, 21 (2017).
L. Soto, C. Pavez, J. Moreno, M. J. Inestrosa-Izurieta, et al., Phys. Plasmas 21, id. 122703 (2014).
С. И. Брагинский, в сб. Вопросы Теории Плазмы, под. ред. М. А. Леонтовича (М.: Атомиздат, 1963) 1, 183.
V. I. Sotnikov, B. S. Bauer, J. N. Leboeuf, P. Hellinger, P. Trávniček, and V. Fiala, Phys. Plasmas 11, 1897 (2004).
В. П. Виноградов, В. И. Крауз, А. Н. Мокеев, В. В. Мял-тон, А. М. Харрасов, Физика плазмы 42, 1033 (2016).
Д. Макдоналд, Р. Прайс, К. С. Торн, Черные дыры. Мембранный подход (М.: Мир, 1988).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


