Астрономический журнал, 2023, T. 100, № 1, стр. 6-18
Численное МГД моделирование лабораторных джетов в тороидальном магнитном поле
О. Д. Торопина 1, *, Г. С. Бисноватый-Коган 1, С. Г. Моисеенко 1
1 Институт космических исследований
Москва, Россия
* E-mail: toropina@iki.rssi.ru
Поступила в редакцию 20.10.2022
После доработки 11.11.2022
Принята к публикации 11.11.2022
- EDN: NQAPNB
- DOI: 10.31857/S0004629923010097
Аннотация
В работе представлены результаты МГД моделирования процесса образования и коллимации лабораторных джетов с тороидальным магнитным полем. Показано, что при отсутствии магнитного поля происходит существенное расширение джета в расчетной области. При наличии сильного тороидального магнитного поля джет расширяется незначительно, что подтверждает возможность магнитного механизма коллимации астрофизических джетов. Угол раствора конуса джета зависит от величины магнитной индукции поля. Чем больше ${{B}_{\phi }}$, тем меньше угол отклонения потока. При определенных значениях ${{B}_{\phi }}$ на детекторе возможно возникновение кольцевых структур в распределении плотности, характеристики которых зависят от величины поля. Выполнено сравнение результатов моделирования с лабораторными джетами, возникающими в эксперименте на лазерной установке “Неодим”, и с ранее полученными результатами МГД моделирования образования джетов в полоидальном магнитном поле.
1. ВВЕДЕНИЕ
Астрофизические джеты, или струйные выбросы плазмы, можно наблюдать в самых разных астрономических объектах. Например, многие квазары и активные ядра галактик (AGN) на радиокартах (в некоторых случаях и в оптическом, и рентгеновском диапазонах) представляют собой яркие компактные источники, из которых вылетают одиночные или двойные джеты. Наиболее известными объектами, в которых видны джеты, являются ядро гигантской эллиптической галактики М87 в созвездии Дева [1, 2] и первый из открытых квазаров 3С 273 [3]. Джеты наблюдаются и в компактных объектах в двойных системах, и в молодых звездах. Джеты могут возникать при взрыве коллапсирующих сверхновых. Формирование узконаправленного джета происходит при анизотропном взрыве, который считается возможной причиной происхождения космических гамма-всплесков. Процессы формирования и эволюции релятивистских джетов представляют собой одну из самых интересных задач современной астрофизики [4, 5].
Основными направлениями изучения релятивистских джетов являются наблюдения в оптическом, рентгеновском и радиодиапазонах и многомерное численное моделирование. В таком моделировании необходимо учитывать всю сложную природу релятивистских струйных выбросов, в том числе гравитационное поле и магнитное поле центрального объекта. Некоторое время назад к методам исследования джетов добавились методы лабораторной астрофизики, которые позволяют создавать релятивистские струи плазмы в лабораторных условиях при помощи лазеров и дают возможность исследовать структуру, эволюцию и особенности строения джетов. Сопоставить результаты лабораторных экспериментов с результатами астрофизических наблюдений и численных экспериментов можно с помощью методов подобия.
Лабораторные исследования струйных выбросов плазмы ведутся несколькими группами ученых. Фуа и др. [6] получили замагниченный сверхзвуковой джет в лаборатории. Они нагревали плоскую мишень лазерным пучком кольцевой формы и наблюдали выбросы вещества. Параллельно с лабораторным экспериментом было проведено численное моделирование эксперимента с помощью двумерного кода FLASH. Показано, что кольцеобразный лазерный пучок может вызывать сверхзвуковой выброс вещества с высокой плотностью, температурой, скоростью и высокой степенью коллимации. В истекающем джете наблюдалось сильное тороидальное магнитное поле.
В Курчатовском институте группой В.И. Крауза проводятся лабораторные эксперименты по созданию астрофизических джетов на установке плазменный фокус ПФ-3 [7]. Математическое моделирование этих экспериментов проводилось в работах [8–10].
В работе [10] показано, что многие свойства течений, полученных на экспериментальной установке, согласуются с основными характеристиками струйных выбросов, наблюдаемых в окрестности молодых звезд.
В статье [11] представлены результаты лабораторного лазерного эксперимента и численного моделирования замагниченного джета, истекающего из молодого звездного объекта. Коллимированный джет в этих расчетах получается благодаря наличию полоидального поля. Экспериментальному исследованию по моделированию астрофизических джетов, а также астрофизических ударных волн, получаемых при помощи лазеров на установке LULI (Laboratoire pour l’Utilisation des Lasers Intenses), посвящены работы [12–14].
В нашей группе несколько лет назад началась работа по исследованию лабораторных джетов, полученных в результате лазерного эксперимента на установке “Неодим” в ЦНИИМАШ. Было исследовано формирование струйного выброса в полоидальном магнитном поле и получено значительное сходство с результатами эксперимента [15].
Уравнения магнитной гидродинамики, с помощью которых исследуется формирование и эволюция джетов, являются нелинейными. Для теоретического описания происходящих в джетах процессов необходимо применять методы многомерного численного моделирования. Многомерные численные расчеты позволяют получить детальную картину течения вещества в джете и ударно-волновую структуру течения. Численное моделирование позволяет проводить расчеты как для начальных данных, соответствующих астрофизическим джетам, так и для набора параметров из лабораторного эксперимента.
2. МГД МОДЕЛИРОВАНИЕ ПРОЦЕССА ФОРМИРОВАНИЯ ДЖЕТОВ В МАГНИТНОМ ПОЛЕ
2.1. Постановка задачи
Основная цель нашего исследования – численное моделирование процессов формирования и эволюции джетов, анализ результатов и сравнение их с результатами лабораторных экспериментов, имитирующих образование астрофизических джетов.
Лабораторные эксперименты по исследованию пространственного распределения пучков ускоренных протонов проводились в Ц-НИИМАШ группой В.С. Беляева и А.П. Матафонова на созданной ими 10 ТВт пикосекундной лазерной установке “Неодим” [16]. Описание установки и результатов эксперимента, а также численного моделирования эксперимента в аксиально-симметричной МГД модели с полоидальным магнитным полем изложено в работе [15].
В данной работе, также как и в [15], мы не рассматривали детально процессы лазерного нагрева и испарения вещества мишени. Процессы лазерной абляции исследованы в значительном количестве работ. Например, Мажукин и др. изучали наносекундную лазерную абляцию в докритическом и транскритическом режимах [17, 18]. Также они моделировали лазерное взрывное вскипание металла [19]. В процессе исследования мы считаем, что процесс абляции уже произошел и вещество испарилось с поверхности мишени. Мы учитываем данный факт при определении начальных и граничных условий. Возможно, для более точного описания процессов, происходящих с веществом мишени в результате облучения мощным лазером, необходимо комбинировать разные подходы к решению задачи, сочетая уравнения магнитной гидродинамики и кинетический подход. В данной работе мы ограничиваемся системой МГД уравнений. Для численного моделирования эксперимента использовалась стандартная система уравнений магнитной гидродинамики [20].
Масштабы физических процессов в астрофизических джетах и масштабы в джетах, возникающих при воздействии лазерного импульса на мишень, сильно отличаются. Однако применение критериев подобия позволяет получить соответствие ряда характеристик астрофизического и лабораторного джета. Обоснование этого метода можно найти в работах [21, 22]. Ранее мы использовали методы подобия для исследования замагниченных джетов в полоидальном магнитном поле [15]. С помощью масштабирования и применения критериев подобия было получено удовлетворительное сходство ряда параметров джетов, истекающих из молодых звезд, и джета, наблюдаемого на установке “Неодим”. В настоящей работе мы моделируем образование и коллимацию джета с тороидальным магнитном полем.
2.2. Область моделирования
В ходе эксперимента было установлено, что образование джета связано с нагревом пластины, а форма и угол падения лазерного пучка не играют роли. Поэтому можно считать, что разогретое лазером пятно на мишени имеет форму круга и использовать осесимметричное приближение для построения математической модели джета.
Для моделирования задачи выбрана инерциальная цилиндрическая система координат $\left( {r,\phi ,z} \right)$ с центром в середине мишени, ось $z$ перпендикулярна мишени. В задаче предполагается осевая симметрия в распределении всех макроскопических величин $\rho $, $T$, $v$, $B$, $\partial {\text{/}}\partial \phi = 0$, однако вычисляются все три компонента скорости $v$ и магнитного поля $B$. Моделирование проводится в половине координатной плоскости $r - z$. В задаче используется равномерная разностная сетка, координаты узлов сетки лежат в пределах $0 \leqslant R \leqslant {{R}_{{\max }}}$, $0 \leqslant z \leqslant {{Z}_{{\max }}}$. Моделирование проводится на равномерной сетке $(r,z)$ с числом ячеек ${{N}_{R}} \times {{N}_{Z}} = 257 \times 513$, или ${{N}_{R}} \times {{N}_{Z}} = 513 \times 1026$.
Центральная область мишени, к которой однородно и мгновенно прикладывается энергия лазерного излучения, представляет собой однородный цилиндр с радиусом ${{R}_{d}}$ и толщиной ${{Z}_{d}}$. При этом ${{R}_{d}} \ll {{R}_{{\max }}}$, ${{Z}_{{\max }}}$ и ${{Z}_{d}} \ll {{R}_{{\max }}}$, ${{Z}_{{\max }}}$. Схема области моделирования приведена на рис. 1.
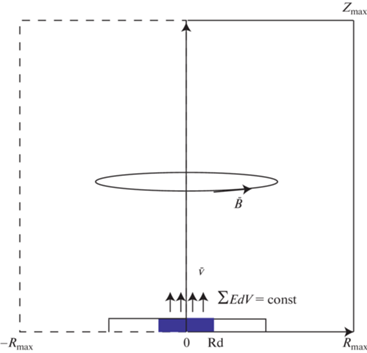
Рис. 1.
Схема области моделирования: используется инерциальная цилиндрическая система координат $(r,\phi ,z)$ с центром в середине мишени, ось $z$ перпендикулярна мишени. Задано тороидальное магнитное поле $B$. Центральная область мишени представляет собой однородный цилиндр с радиусом ${{R}_{d}} \ll {{R}_{{\max }}}$, ${{Z}_{{\max }}}$ и толщиной ${{Z}_{d}} \ll {{R}_{{\max }}}$, ${{Z}_{{\max }}}$.
2.3. Система уравнений
Для численного моделирования процессов образования и коллимации джетов в лабораторном эксперименте используется стандартная система уравнений магнитной гидродинамики с учетом конечной проводимости [20] в отсутствие гравитации.
(2)
$\rho \frac{{\partial {\mathbf{v}}}}{{\partial t}} + \rho \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{v}} = - \nabla p + \frac{1}{c}{\mathbf{J}} \times {\mathbf{B}},$(3)
$\frac{{\partial {\mathbf{B}}}}{{\partial t}} = \nabla \times \left( {{\mathbf{v}} \times {\mathbf{B}}} \right) + \frac{{{{c}^{2}}}}{{4\pi \sigma }}{{\nabla }^{2}}{\mathbf{B}},$(4)
$\frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \nabla \cdot \left( {\rho \varepsilon {\mathbf{v}}} \right) = - p\nabla \cdot {\mathbf{v}} + \frac{{{{{\mathbf{J}}}^{2}}}}{\sigma }.$В предыдущей серии расчетов [15] магнитное поле в области моделирования имело полоидальную конфигурацию (${{B}_{z}}$, ${{B}_{r}}$). Для точного выполнения условия равенства нулю дивергенции магнитного поля $\nabla \cdot {\mathbf{B}} = 0$ в расчетах вместо полоидального компонента магнитного поля ${{B}_{z}}$ и ${{B}_{r}}$ использовался тороидальный компонент ${{A}_{\phi }}$, вектор потенциала магнитного поля ${\mathbf{A}}$, ${\mathbf{B}} = \nabla \cdot {\mathbf{A}}$. В текущих расчетах в области задано тороидальное магнитное поле ${{B}_{\phi }}$, для которого в качестве наиболее подходящей модели выбрано поле проводника с током, направленного вдоль оси $Z$, как схематично показано на рис. 1.
После приведения системы уравнений (1)–(5) к безразмерному виду в ней возникают два характерных безразмерных параметра. Первый из них $\beta $,
(6)
$\beta = \frac{{8\pi {{P}_{{0jet}}}}}{{B_{0}^{2}}} = \frac{2}{\gamma }\frac{{c_{{s0}}^{2}}}{{V_{{A0}}^{2}}},$Второй параметр – характерная безразмерная магнитная вязкость (или обратное ей характерное магнитное число Рейнольдса ReM):
(7)
${{\tilde {\eta }}_{M}} = \frac{{{{\eta }_{M}}}}{{{{L}_{0}}{{V}_{{A0}}}}} = \frac{{{{c}^{2}}}}{{4\pi \sigma {{L}_{0}}{{V}_{{A0}}}}} = \frac{1}{{{\text{R}}{{{\text{e}}}_{M}}}},$Для решения системы уравнений использовалась осесимметричная разностная МГД схема с конечной проводимостью гибридного типа, основанная на методе локальных итераций [23], и методе коррекции потоков [24, 25]. Для решения астрофизических задач эта схема впервые была использована в работах [26, 27], и получила дальнейшее развитие в работах [28, 29].
2.4. Граничные и начальные условия
Система уравнений (1)–(5) численно решалась в цилиндрической области $(0 \leqslant z \leqslant {{Z}_{{\max }}}$, $0 \leqslant r \leqslant {{R}_{{\max }}})$. Предполагалось, что на внешних границах есть магнитное поле, но отсутствуют токи, и были заданы свободные граничные условия, т.е. для любой величины $f$ $\partial f{\text{/}}\partial n = 0$. Здесь $\partial f{\text{/}}\partial n$ – производная по нормали к поверхности, т.е. на внешней границе $f(r,z) = {\text{const}}$. В соответствии с предположением об осевой симметрии, граничные условия на оси $z$ ($r = 0$, $0 \leqslant z \leqslant {{Z}_{{\max }}}$) записываются как
На границе $(z = {{Z}_{{{\text{min}}}}},$ ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}})$ были заданы фиксированные граничные условия, $\rho = {{\rho }_{0}}$ и ${{v}_{0}} = 0$, чтобы запретить втекание вещества в область моделирования через эту границу. На противоположной границе $(z = {{Z}_{{\max }}},$ $0 \leqslant r \leqslant {{R}_{{\max }}})$, были заданы “свободные” граничные условия $\partial {\text{/}}\partial n = 0$, чтобы позволить веществу вытекать из области. Втекание вещества через эту границу в область моделирования также запрещено. На цилиндрической границе $({{Z}_{{\min }}} \leqslant z \leqslant {{Z}_{{\max }}},$ $r = {{R}_{{\max }}})$ также были заданы свободные граничные условия $\partial {\text{/}}\partial n = 0$. Для изучения влияния граничных условий была проведена серия расчетов с различными размерами области моделирования.Для расчетов с полоидальным магнитным полем использовался векторный потенциал магнитного поля $A = {{A}_{\phi }}$, который был определен и задан во всей области расчета. Для однородного магнитного поля $B$, сонаправленного с осью $z$, векторный потенциал записывается следующим образом: ${{A}_{\phi }} = rB$, ${{A}_{r}} = 0$, ${{A}_{z}} = 0$, тороидальный компонент поля ${{B}_{\phi }} = 0$. Для расчетов с тороидальным магнитным полем ${{B}_{\phi }}$ было задано по формуле поля проводника с током, направленного вдоль оси $Z$, как схематично показано на рис. 1 и 2. Таким образом, ${{A}_{\phi }} = 0$ во всей области, для $0 \leqslant r \leqslant {{R}_{d}}$ ${{B}_{\phi }} = {{B}_{0}}r{\text{/}}{{R}_{d}}$, для ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}}$ ${{B}_{\phi }} = {{B}_{0}}{\kern 1pt} {{R}_{d}}{\text{/}}r$, где ${{B}_{0}}$ – постоянная величина. При этом автоматически гарантировано, что поле на оси $Z$ ${{B}_{\phi }} = 0$.
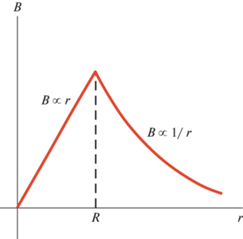
Рис. 2.
Тороидальное магнитное поле проводника с однородной плотностью тока внутри радиуса $R$, направленного вдоль оси $Z$.
В начальный момент времени $t = 0$ магнитное поле в области представляло собой “чистое” тороидальное поле. Начальная плотность вещества во всей области моделирования, за исключением мишени, была однородной и имела малое значение: $\rho = {{\rho }_{0}}$. Начальная скорость вещества во всей области моделирования, за исключением мишени, ${{v}_{z}} = {{v}_{r}} = 0$. Вещество не имело углового момента, ${{v}_{\phi }} = 0$.
В области мишени $0 \leqslant R \leqslant {{R}_{d}}$, $0 \leqslant z \leqslant {{Z}_{d}}$ было задано значение плотности $\rho \gg {{\rho }_{0}}$ и сверхзвуковая скорость вылетающего из мишени вещества. Большинство расчетов было проведено для $M = 3$, $M = 6$. Были исследованы случаи, когда вылетающее вещество не несет магнитное поле, и когда вылетаюшее вещество несет тороидальное магнитное поле, по величине и структуре аналогичное магнитному полю в области моделирования.
2.5. Джет в гидродинамическом случае
В качестве тестирования МГД модели традиционно использовалось гидродинамическое приближение, когда было выключено магнитное поле, и положено $B = 0$ во всей области. Это позволило оценить корректность выбора размеров области моделирования, гидродинамических параметров и граничных условий. В тестовом случае начальная плотность вещества во всей области моделирования была однородна и имела малое значение: $\rho = {{\rho }_{0}}$. Начальная скорость вещества во всей области моделирования, за исключением мишени, была нулевой ${{v}_{z}} = {{v}_{r}} = 0$. Вещество не имело углового момента, ${{v}_{\phi }} = 0$.
В области мишени $0 \leqslant R \leqslant {{R}_{d}}$, $0 \leqslant z \leqslant {{Z}_{d}}$ было задано значение плотности $\rho \approx 300{\kern 1pt} {{\rho }_{0}}$ и сверхзвуковая скорость вылетающих из мишени частиц $v = M{\kern 1pt} {{c}_{s}}$, ${{c}_{s}} = \gamma \frac{{{{P}_{0}}}}{{{{\rho }_{0}}}}$ – скорость звука в невозмущенной области, $M$ – число Маха. Для тестового гидродинамического случая $M = 3$. Для простоты тестовых расчетов скорость вылетающего вещества в начальный момент времени имела только $z$-компоненту ${{v}_{z}}$; ${{v}_{r}} = 0$.
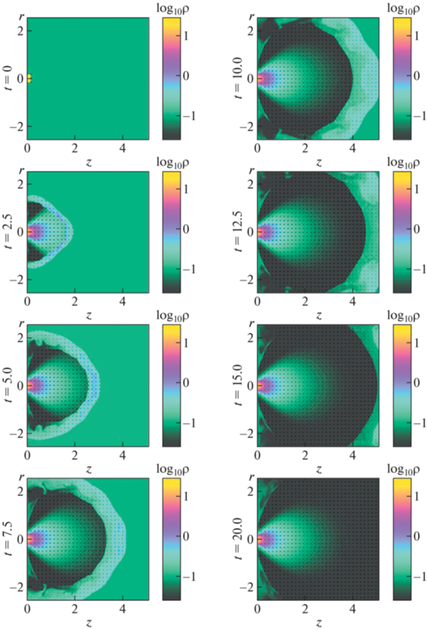
На рис. 3 показано начальное распределение плотности и скорости вещества, а также результаты моделирования выброса вещества в гидродинамическом случае. Цветной заливкой обозначен логарифм плотности вещества, стрелками показаны векторы скоростей, длина стрелки пропорциональна модулю скорости. Под воздействием тепловой энергии лазера вещество мишени начинает лететь вдоль оси $Z$ в направлении трекового детектора, попутно расширяясь в направлении оси $R$. Образуется ударная волна, которая движется к границе камеры, оставляя за собой небольшое устойчивое истечение конусовидной формы, параметры которого сохраняются с течением времени. Вблизи мишени наблюдается небольшая коллимация вещества, обусловленная наличием фонового газа. Остальное вещество рассеивается в области моделирования.
Рис. 3.
Картина течения вещества в гидродинамическом случае в различные моменты времени $t = 0.0$, 2.5, 5.0, 7.5, 10.0, 12.5, 15.0, 20.0. Цветной заливкой обозначен логарифм плотности вещества, стрелками показаны векторы скоростей.
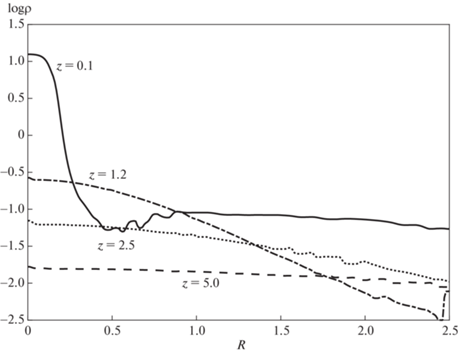
Форму истечения также можно увидеть на рис. 4, на котором показано распределение плотности вдоль оси $R$ на разных расстояниях $z$ от поверхности мишени в момент времени $t = 20$. Плотность потока вблизи мишени, $z = 0.1$ максимальна у оси $Z$ и распределена в узком конусе, ей соответствует тонкая сплошная линия. На расстоянии $z = 1.2$ распределение становится более широким, но еще сохраняет форму конуса, ей соответствует штрихпунктирная линия. Пунктирная линия соответствует плотности в середине камеры, $z = 2.5$. Вблизи детектора, $z = 5.0$ распределение плотности становится практически равномерным, что показывает штриховая линия.
Рис. 4.
Логарифм плотности вещества вдоль $R$ в зависимости от расстояния до мишени в гидродинамическом случае в момент времени $t = 20$ для значений $z = 0.1$ (сплошная линия), 1.2 (штрихпунктирная), 2.5 (пунктирная), и 5.0 (штриховая линия).
Таким образом, на трековом детекторе можно будет наблюдать либо равномерное распределение частиц, либо очень слабые и размытые кольцевые структуры, вызванные наличием фонового газа.
2.6. Джет в тороидальном магнитном поле
Проведенные тестовые расчеты для гидродинамического случая показали корректность выбора размеров области моделирования, гидродинамических параметров и граничных условий. На следующем этапе моделирования было включено тороидальное магнитное поле ${{B}_{\phi }}$, которое задавалось во всей области следующим образом: при $0 \leqslant r \leqslant {{R}_{d}}$ ${{B}_{\phi }} = {{B}_{0}}{\kern 1pt} r{\text{/}}{{R}_{d}}$, при ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}}$ ${{B}_{\phi }} = {{B}_{0}}{\kern 1pt} {{R}_{d}}{\text{/}}r$, где ${{B}_{0}}$ – постоянная величина. Были проведены расчеты для разных значений параметра $\beta = \frac{{8\pi {{P}_{\infty }}}}{{B_{0}^{2}}}$ и числа Маха $M$. Параметр магнитной вязкости был одинаковым во всех расчетах ${{\tilde {\eta }}_{M}} = \frac{1}{{{\text{R}}{{e}_{M}}}} = {{10}^{{ - 5}}}$. Остальные параметры соответствовали гидродинамическому случаю, т.е. начальная плотность вещества во всей области моделирования однородна и имеет малое значение: $\rho = {{\rho }_{0}}$. Начальная скорость вещества во всей области моделирования, за исключением мишени, нулевая ${{v}_{z}} = {{v}_{r}} = 0$. Вещество не имеет углового момента, ${{v}_{\phi }} = 0$.
В области мишени $0 \leqslant R \leqslant {{R}_{d}}$, $0 \leqslant z \leqslant {{Z}_{d}}$ задано значение плотности $\rho \approx 300{\kern 1pt} {{\rho }_{0}}$ и сверхзвуковая скорость вылетающих из мишени частиц $v = M{{c}_{s}}$, где ${{c}_{s}} = \gamma \frac{{{{P}_{0}}}}{{{{\rho }_{0}}}}$ – скорость звука в невозмущенной области, $M$ – число Маха. Скорость втекающего в расчетную область через границу мишени вещества в начальный момент времени имеет только $z$-компонету ${{v}_{z}}$; ${{v}_{r}} = 0$. Магнитное поле во втекающем веществе задано по такой же формуле, что и начальное поле в области: для $0 \leqslant r \leqslant {{R}_{d}}$ ${{B}_{\phi }} = {{B}_{0}}{\kern 1pt} r{\text{/}}{{R}_{d}}$, для ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}}$ ${{B}_{\phi }} = {{B}_{0}}{\kern 1pt} {{R}_{d}}{\text{/}}r$, где ${{B}_{0}}$ – постоянная величина.
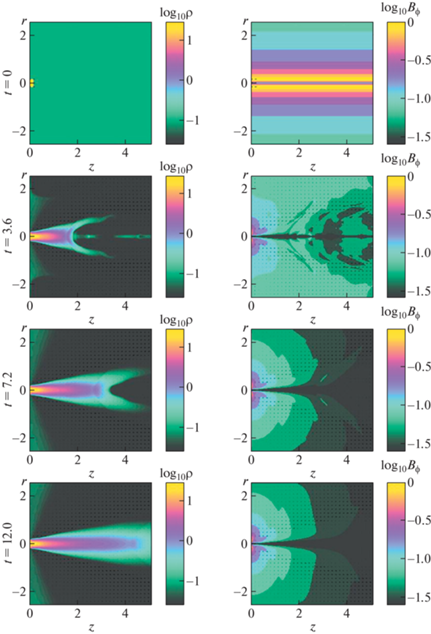
2.6.1. Тороидальное поле $\beta = {{10}^{{ - 4}}}$, $M = 3$. Результаты моделирования выброса вещества для параметра $\beta = {{10}^{{ - 4}}}$ представлены на рис. 5. На левой панели показана эволюция течения вещества. Цветная заливка соответствует логарифму плотности вещества, стрелками обозначены векторы скоростей. Можно видеть, что вещество мишени под воздействием энергии лазерного излучения начинает лететь вдоль оси $Z$. Сначала течение немного расширяется во всех направлениях, но затем коллимируется магнитным полем. Образуется ударная волна вытянутой формы, которая движется от мишени к границе камеры, оставляя за собой устойчивое истечение. Влияние внешнего газа на коллимацию потока в данном случае незначительно.
Рис. 5.
Формирование джета в тороидальном магнитном поле в моменты времени: $t = 0.0$, 3.6, 7.2, 12.0. Характерные параметры $\beta = {{10}^{{ - 4}}}$ и $M = 3$. Левая панель: картина течения вещества. Цветной заливкой обозначен логарифм плотности, стрелками показаны векторы скоростей. Правая панель: эволюция магнитного поля, цветная заливка соответствует логарифму ${{B}_{\phi }}$.
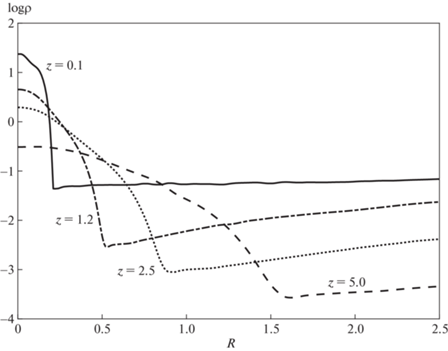
Форму течения также можно увидеть на рис. 6, где показано распределение плотности вдоль оси $R$ на разных расстояниях от поверхности мишени в момент времени $t = 12$. Тонкая сплошная линия соответствует плотности потока у границы мишени $z = 0.1$. Штрихпунктирная линия соответствует расстоянию $z = 1.2$, пунктирная соответствует плотности по середине камеры, $z = 2.5$, штриховая линия соответствует плотности вблизи границы камеры, $z = 5.0$. Можно видеть, что распределение плотности в потоке плазмы зависит от расстоянии от мишени. Плотность потока вблизи мишени максимальна у оси $z$ и распределена в узком конусе. По мере движения вещества к границе камеры поток сохраняет форму конуса, умеренно расширяясь к границе. С помощью рис. 5 и 6 можно оценить угол отклонения. Он приблизительно равен $ \approx {\kern 1pt} 11^\circ {\kern 1pt} - {\kern 1pt} 13^\circ $. И, соответственно, угол раствора конуса $\theta \approx 22^\circ {\kern 1pt} - {\kern 1pt} 26^\circ $. Таким образом, на трековом детекторе можно будет наблюдать четкое сплошное пятно джета.
Рис. 6.
Логарифм плотности вещества вдоль $R$ в зависимости от расстояния до мишени в случае с тороидальным магнитным полем, $\beta = {{10}^{{ - 4}}}$ и $M = 3$ в момент времени $t = 12.0$ для значений $z = 0.1$ (сплошная линия), 1.2 (штрихпунктирная), 2.5 (пунктирная), 5.0 (штриховая линия).
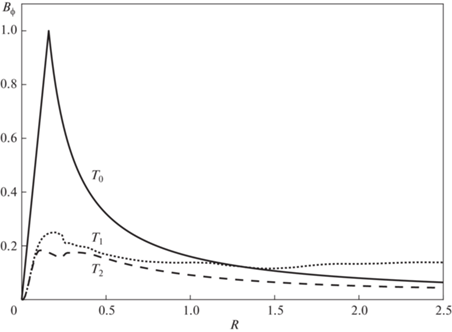
По правой панели рис. 5 можно проследить эволюцию магнитного поля в области моделирования. Цветная заливка соответствует логарифму ${{B}_{\phi }}$. В начальный момент времени поле в области увеличивается при значениях $0 \leqslant r \leqslant {{R}_{d}}$, а затем, при ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}}$ спадает к границе области. После выброса вещества первоначальное магнитное поле сначала деформируется, но остается достаточно сильным для коллимации вещества. По мере формирования джета поле начинает восстанавливаться. Начальное распределение индукции магнитного поля ${{B}_{\phi }}$ вдоль оси $R$ показано сплошной линией на рис. 7. Его структура в начальный момент времени ${{t}_{0}} = 0.0$ полностью соответствует полю проводника с током, направленного вдоль оси $Z$, схематично представленного на рис. 2. В момент времени ${{t}_{1}} = 1.2$ поле гораздо меньше по абсолютному значению и слабо спадает вдоль $R$ к границе области (пунктирная линия). В момент времени ${{t}_{2}} = 12.0$ структура ${{B}_{\phi }}$ снова возвращается к полю проводника с током, но с меньшими абсолютными значениями (штриховая линия). Таким образом, тороидальное магнитное поле сохраняется в области на протяжение всего расчета и играет главную роль в коллимации потока.
Рис. 7.
Распределение индукции магнитного поля ${{B}_{\phi }}$ вдоль оси $R$ на одном и том же расстоянии $z = 0.2$ в моменты времени ${{t}_{0}} = 0.0$ (сплошная линия), ${{t}_{1}} = 1.2$ (пунктирная линия), ${{t}_{2}} = 12.0$ (штриховая линия), для случая с параметрами $\beta = {{10}^{{ - 4}}}$ и $M = 3$.
2.6.2. Тороидальное поле $\beta = 1{{0}^{{ - {\mathbf{3}}}}}$, $M{\mathbf{ = 3}}$. В следующем расчете мы уменьшили магнитное поле. На рис. 8 представлены результаты моделирования для случая с параметрами $\beta = {{10}^{{ - 3}}}$, $M = 3$. Левая панель отображает эволюцию течения вещества, цветной заливкой показан логарифм плотности. Вещество мишени под воздействием тепловой энергии лазера летит вдоль оси $Z$ в направлении детектора. Сначала течение расширяется во всех направлениях, но затем коллимируется магнитным полем. Образуется конусообразная вытянутая ударная волна, которая движется от мишени к границе камеры, оставляя за собой устойчивое истечение. Влияние внешнего газа на коллимацию потока незначительно.
Рис. 8.
Формирование джета в тороидальном магнитном поле в моменты времени: $t = 0.0$, 1.5, 3.0, 6.0. Характерные параметры $\beta = {{10}^{{ - 3}}}$ и $M = 3$. Левая панель: картина течения вещества. Цветной заливкой обозначен логарифм плотности, стрелками показаны векторы скоростей. Правая панель: эволюция магнитного поля, цветная заливка соответствует логарифму ${{B}_{\phi }}$.
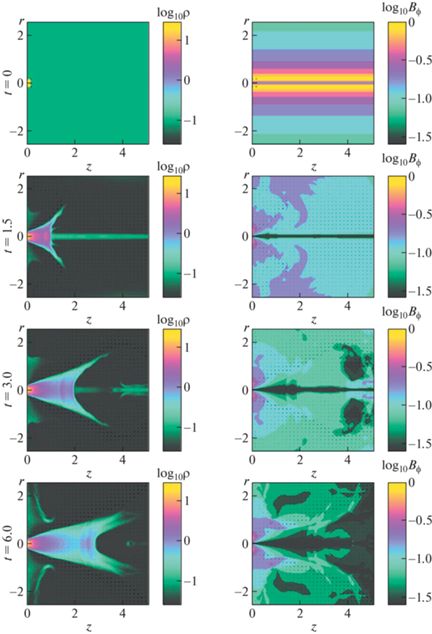
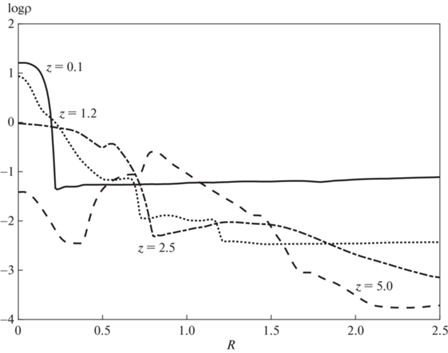
Рисунок 9 показывает распределение плотности вдоль оси $R$ на разных расстояниях от поверхности мишени в момент времени $t = 6$, по которому можно определить форму течения. Тонкая сплошная линия соответствует плотности потока у границы мишени $z = 0.1$. Штрих-пунктир соответствует расстоянию $z = 1.2$, пунктир соответствует плотности по середине камеры, $z = 2.5$, штриховая линия соответствует плотности вблизи границы камеры, $z = 5.0$. Видно, что распределение плотности в потоке плазмы зависит от расстоянии до мишени. Плотность потока вблизи мишени максимальна у оси $z$ и распределена в узком конусе. Если в середине камеры поток сохраняет форму конуса, умеренно расширяясь с увеличением $z$, то у границы $z = 5.0$ распределение плотности образует четкую кольцевую структуру. С помощью рис. 8 и 9 можно оценить угол отклонения. Он приблизительно равен $ \approx {\kern 1pt} 15^\circ {\kern 1pt} - {\kern 1pt} 18^\circ $. Соответственно, угол раствора конуса $\theta \approx 30^\circ {\kern 1pt} - {\kern 1pt} 36^\circ $. Таким образом, на трековом детекторе можно будет наблюдать джет в виде четкой кольцевой структуры.
Рис. 9.
Логарифм плотности вещества вдоль $R$ в зависимости от расстояния до мишени в случае с тороидальным магнитным полем, $\beta = {{10}^{{ - 3}}}$ и $M = 3$ в момент времени $t = 6.0$ для значений $z = 0.1$ (сплошная линия), 1.2 (штрихпунктирная), 2.5 (пунктирная), 5.0 (штриховая линия).
Правая панель рис. 8 отражает эволюцию магнитного поля в области моделирования. Цветная заливка соответствует логарифму ${{B}_{\phi }}$. В начальный момент времени поле в области увеличивается при значениях $0 \leqslant r \leqslant {{R}_{d}}$, а затем, при ${{R}_{d}} \leqslant r \leqslant {{R}_{{\max }}}$ спадает к границе области. После выброса вещества первоначальное магнитное поле деформируется, но остается достаточно сильным для коллимации вещества. По мере формирования джета поле так же начинает восстанавливаться, но остается неоднородным вдоль $Z$.
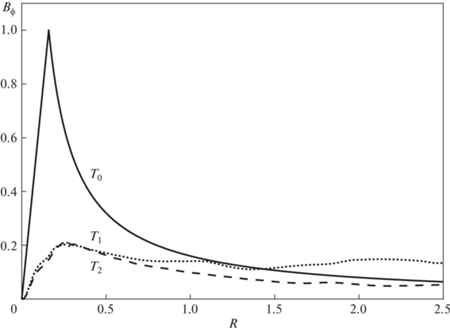
На рис. 10 показаны начальное распределение индукции магнитного поля ${{B}_{\phi }}$ вдоль оси $R$ и его эволюция во времени. Структура поля в начальный момент времени ${{t}_{0}} = 0.0$ полностью соответствует полю проводника с током, направленного вдоль оси $Z$, как схематично изображено на рис. 2. В момент времени ${{t}_{1}} = 1.5$ уменьшилось по абсолютному значению и слабо спадает вдоль $R$ к границе области (штриховая линия). В момент времени ${{t}_{2}} = 6.0$ структура ${{B}_{\phi }}$ снова возвращается к полю проводника с током, но с меньшими абсолютными значениями (штрихпунктирная линия). Таким образом, и в этом случае тороидальное магнитное поле сохраняется в области на протяжении всего расчета и играет главную роль в коллимации потока.
Рис. 10.
Распределение индукции магнитного поля ${{B}_{\phi }}$ вдоль оси $R$ на одном и том же расстоянии $z = 0.2$ в моменты времени ${{t}_{0}} = 0.0$ (сплошная линия), ${{t}_{1}} = 1.5$ (пунктирная линия), ${{t}_{2}} = 6.0$ (штриховая линия), для случая с параметрами $\beta = {{10}^{{ - 3}}}$ и $M = 3$.
3. ЗАКЛЮЧЕНИЕ
В работе представлены результаты МГД моделирования лабораторных сверхзвуковых джетов в тороидальном магнитном поле. Показано, что при отсутствии магнитного поля происходит существенное расширение джета в расчетной области. При наличии сильного тороидального магнитного поля джет расширяется незначительно, что подтверждает возможность магнитного механизма коллимации астрофизических джетов. Угол раствора конуса джета зависит от величины магнитной индукции поля. Чем больше ${{B}_{\phi }}$, тем меньше угол отклонения потока. Расчеты показали, что при определенных значениях индукции тороидального поля возможно возникновение кольцевых структур, характеристики которых зависят от величины поля. Полученные в расчетах значения угол раствора конуса $\theta \approx 22^\circ {\kern 1pt} - {\kern 1pt} 26^\circ $ и $\theta \approx 30^\circ {\kern 1pt} - {\kern 1pt} 36^\circ $ примерно соответствуют значениям, полученным в лазерном эксперименте. Эти результаты хорошо согласуются с ранее полученными результатами МГД моделирования образования джетов в полоидальном магнитном поле [15].
Формирование, развитие и коллимация джета как в астрофизике, так и в лабораторном лазерном эксперименте представляют собой сложное физическое явление и включают большое количество различных физических процессов. Численное моделирование эксперимента, который учитывал бы все возможные физические процессы, является крайне сложной математической задачей, и провести его в настоящее время не представляется возможным. Нами было предложено использовать приближение магнитной гидродинамики как один из первых шагов в исследовании данной проблемы. Результаты моделирования показали, что при использовании МГД приближения картина эксперимента качественно удовлетворительно воспроизводится.
Список литературы
A. S. Wilson and Y. Yang, Astrophys. J. 568, 133 (2002).
H. L. Marshall, B. P. Miller, D. S. Davis, E. S. Perlman, M. Wise, C. R. Canizares, and D. E. Harris, Astrophys. J. 564, 683 (2002).
H. L. Marshall, D. E. Harris, J. P. Grimes, J. J. Drake, et al., Astrophys. J. 549, L167 (2001).
G. S. Bisnovatyi-Kogan, B. V. Komberg, and A. M. Fridman, Soviet Astron. 13, 369 (1969).
G. S. Bisnovatyi-Kogan, Proc. 6th Int. Workshop of the Astronomical Observatory of Capodimonte (OAC 6), Capri, Italy, 1991 September 18–21, edited by L. Errico and A. A. Vittone (Dordrecht: Kluwer), Astrophys. Space Sci. Library 186, 369 (1993).
W. Fu, E. P. Liang, P. Tzeferacos, and D. Q. Lamb, High Energy Density Physics 17, 42 (2015).
K. N. Mitrofanov, V. I. Krauz, V. V. Myalton, V. P. Vinogradov, A. M. Kharrasov, and Yu. V. Vinogradova, Astron. Rep. 61, 138 (2017).
I. Yu. Kalashnikov, V. I. Krauz, and V. M. Chechetkin, J. Physics: Conference Series 798, id. 012008 (2017).
I. Yu. Kalashnikov, A. V. Dodin, I. V. Il’ichev, V. I. Krauz, and V. M. Chechetkin, Astron. Rep. 65, 477 (2021).
В. С. Бескин, Я. Н. Истомин, А. М. Киселев, В. И. Крауз и др., Изв. ВУЗов. Радиофизика 59, 1004 (2016).
B. Albertazzi, A. Ciardi, M. Nakatsutsumi, T. Vinci, et al. Science, 346, 325 (2014).
C. D. Gregory, B. Loupias, J. Waugh, P. Barroso, et al., Plasma Phys. Control. Fusion 50 (12), id. 124039 (2008).
C. D. Gregory, B. Loupias, J. Waugh, S. Dono, et al., Phys. Plasmas 17, id. 052708 (2010).
C. D. Gregory, A. Diziere, H. Aoki, H. Tanji, et al., High Energy Density Physics 11, 12 (2014).
V. S. Belyaev, G. S. Bisnovatyi-Kogan, A. I. Gromov, B. V. Zagreev, A. V. Lobanov, A. P. Matafonov, S.G. Moiseenko, and O. D. Toropina, Astron. Rep. 62, 162 (2018).
V. S. Belyaev, V. I. Vinogradov, A. P. Matafonov, A. M. Chekmarev, and A. G. Karabadzhak, Laser Phys. 16 (3), 477 (2006).
V. I. Mazhukin, A. V. Shapranov, M. M. Demin, A. A. Samokhin, and A. E. Zubko, Math. Montisnigri 37, 24 (2016).
V. I. Mazhukin, A. V. Shapranov, M. M. Demin, A. A. Sa-mokhin, and A. E. Zubko, Math. Montisnigri 38, 3 (2017).
V. I. Mazhukin, M. M. Demin, and A. V. Shapranov, A-ppl. Surface Sci. 302, 6 (2014).
Л. Д. Ландау, Е. М. Лившиц, Электродинамика сплошных сред (М.: Наука, 1982).
D. D. Ryutov, R. P. Drake, and B. A. Remington, Astrophys. J. Suppl. 127, 465 (2000).
S. Bouquet, E. Falize, C. Michaut, C. D. Gregory, B. Loupias, T. Vinci, and M. Koenig, High Energy Density Physics 6, 368, 2010.
V. T. Zhukov, A. V. Zabrodin, and O. B. Feodoritova, Comp. Math. and Math. Physics 33, 1099 (1993).
Э. Оран, Дж. Борис, Численное моделирование реагирующих потоков (М.: Мир, 1990).
J. P. Boris and D. L. Book, J. Comput. Phys. 11, 38 (1973).
V. V. Savelyev and V. M. Chechetkin, Astron. Rep. 39, 123 (1995).
V. V. Savelyev, Yu. M. Toropin, and V. M. Chechetkin, Astron. Rep. 40, 494 (1996).
O. D. Toropina, M. M. Romanova, Yu. M. Toropin, and R. V. E. Lovelace, Astrophys. J. 561, 964 (2001).
O. D. Toropina, M. M. Romanova, and R. V. E. Lovelace, Monthly Not. Roy. Astron. Soc. 420, 810 (2012).
Дополнительные материалы отсутствуют.
Инструменты
Астрономический журнал


