Астрономический вестник, 2019, T. 53, № 1, стр. 24-33
Поиск вековых резонансов в динамике нумерованных астероидов, проходящих через сферу тяготения Земли в ближайшие 200 лет
О. Н. Летнер a, *, Т. Ю. Галушина a
a НИИ прикладной математики и механики Томского госуниверситета
Томск, Россия
* E-mail: volna@sibmail.com
Поступила в редакцию 28.12.2017
После доработки 11.07.2018
Принята к публикации 04.07.2018
Аннотация
В работе представлены результаты исследования динамики нумерованных АСЗ (астероидов, сближающихся с Землей), проходящих через сферу тяготения Земли (256 000 км от геоцентра) в ближайшие 200 лет. Основной целью данной работы было выявление вековых резонансов и изучение взаимного влияния резонансных соотношений и тесных сближений. Для рассматриваемых АСЗ была построена орбитальная эволюция на интервале времени 400 лет, и выявлены все сближения астероидов с большими планетами. Так как динамика этих астероидов предсказуема только на коротких интервалах времени, а к проявлению хаотичности в движении АСЗ могут привести не только тесные и/или многократные сближения с большими планетами, но и наличие хотя бы одного неустойчивого резонанса, мы проследили их вековую резонансную динамику. Оценка хаотичности орбит АСЗ проводилась путем анализа поведения усредненного параметра MEGNO (Mean Exponential Growth factor of Nearby Orbits). Оказалось, что для исследуемых АСЗ (99942 Apophis, 153201 2000 WO107, 153814 2001 WN5, 456938 2007 YV56) наблюдается схожая картина с точки зрения поиска вековых резонансов. Все выявленные резонансы являются устойчивыми, а к проявлению хаотичности в движении астероидов приводят их тесные и/или многократные сближения с большими планетами.
ВВЕДЕНИЕ
Исследование особенностей динамики астероидов, сближающихся с Землей (АСЗ), является одной из важных задач небесной механики, так как полученные результаты могут внести вклад в решение проблемы астероидной опасности для Земли. К особенностям, существенно влияющим на динамику АСЗ, относятся тесные и многократные сближения с большими планетами, в том числе с Землей, резонансные взаимодействия с планетами, а также проявление хаотичности в их движении.
Тесные или многократные сближения АСЗ с большими планетами играют большую роль в движении астероидов и оказывают влияние на прогнозирование их динамики, так как сближения могут значительным образом изменить параметры орбит АСЗ и увеличить риск тесных сближений или столкновений с другими планетами, в том числе с Землей. Кроме того, значительные изменения параметров орбиты астероида создают трудности в дальнейшем численном исследовании динамики АСЗ.
Важной, но недостаточно изученной особенностью в движении АСЗ являются вековые резонансы (резонансы, обусловленные соизмеримостями между скоростями прецессий орбит астероида и планеты). Известно, что перекрытие резонансов, особенно при наличии среди них хотя бы одного неустойчивого резонанса, может привести к проявлению хаотичности в их движении (Чириков, 1977; Бордовицына, Томилова, 2016).
В научной литературе не так много работ, посвященных исследованию вековых резонансов в движении астероидов. При этом работ по выявлению вековых резонансов в динамике астероидов, сближающихся с Землей, нами вовсе не было обнаружено. Основная часть работ включает в себя результаты как аналитического, так и численного исследования вековых резонансов в динамике астероидов Главного пояса. Аналитическая теория J.G. Williams еще в 1969 г. показала, что в астероидном поясе были обнаружены основные вековые резонансы ν5, ν6 и ν16 (Williams, 1969). Немного позднее Nakai, Kinoshita и Yoshikawa смогли смоделировать основные свойства орбитального движения астероидов Главного пояса с учетом вековых резонансов ν16 и ν6 соответственно (Nakai, Kinoshita, 1985; Yoshikawa, 1987). Систематическим поиском вековых резонансов внутри резонансов по среднему движению занимались Moons и Morbidelli (1995). В результате проводимых численно-аналитических исследований были обнаружены два вековых резонанса (ν5 и ν6) в люках Кирквуда, соответствующих орбитальным резонансам 2/1, 3/1, 4/1, 5/2, 7/3 с Юпитером. Более того, вековой резонанс ν6 оказался в области влиянии резонанса ν5, в результате чего было найдено крупное перекрытие этих резонансов. Такое перекрытие было также обнаружено Froeschle и Scholl (1989). Когда во внимание принимаются оба вековых резонанса, большие регулярные колебания эксцентриситета заменяются огромной хаотической зоной. При этом переход к хаотичности может сопровождаться скачкообразным изменением эксцентриситета.
В работе (Nesvorny и др., 2003) представлены результаты численного исследования взаимодействия двух вековых резонансов ν5 и ν6 внутри орбитального резонанса 3/1 с Юпитером. Проведенные авторами исследования показали, что большую часть фазового пространства (при взаимодействии этих резонансов) покрывает хаотическая область. Только орбиты с маленькими эксцентриситетами e и небольшой амплитудой либраций большой полуоси а имеют регулярную динамику.
Среди современной литературы по исследованию вековых резонансов следует отметить работы (Smallwood и др., 2018; Carruba и др., 2018). В своей работе Smallwood и его соавторы моделируют в задаче N тел планетную систему с астероидным поясом и исследуют, как архитектура планетной системы влияет на скорость столкновения астероидов с Землей. Авторы показали, что вековой резонанс ν6 играет важную роль в скорости столкновения астероидов с планетой. В работе (Carruba и др., 2018) авторы рассматривают семейства астероидов, которые образуются в результате столкновения друг с другом и в процессе эволюции взаимодействуют с вековыми резонансами. В настоящее время существует более 100 таких семейств. Авторы отмечают, что среди вековых резонансов наиболее эффективным при увеличении эксцентриситета астероидов является резонанс ν6. Находясь под влиянием этого резонанса, объекты могут избежать быстрого роста эксцентриситета, что увеличит срок жизни этих объектов на устойчивой орбите.
Данная работа посвящена исследованию динамики нумерованных АСЗ, проходящих через сферу тяготения Земли (256 000 км от геоцентра) в ближайшие 200 лет. Основная цель проводимого исследования заключается в выявлении в движении астероидов вековых резонансов и сближений с большими планетами. Кроме того, весьма важным вопросом является взаимное влияние вековых резонансов и тесных сближений.
МЕТОДИКА ИССЛЕДОВАНИЯ
Исследование особенностей динамики астероидов проводилось путем построения их орбитальной эволюции. В качестве основного метода исследования использовалось численное интегрирование уравнений движения АСЗ в прямоугольной гелиоцентрической системе координат методом Эверхарта (Everhart, 1985; Авдюшев, 2010). В модель сил было включено влияние всех больших планет, Плутона и Луны, трех наиболее крупных астероидов (Цереры, Паллады и Весты) и сжатия Земли. Численная модель движения астероидов с учетом необходимых сил, действующих на него, реализована в виде программно-алгоритмического комплекса “ИДА”, разработанного коллективом НИИ ПММ ТГУ (Быкова и др., 2012; Раздымахина, 2011). Координаты больших планет, Плутона и Луны на заданный момент времени определялись из фонда координат больших планет DE406 (http://ssd.jpl.nasa.gov/horizons.html).
Используя результаты построения орбитальной эволюции астероидов, а именно кеплеровские элементы орбит АСЗ, выдаваемые с определенным шагом на рассматриваемом интервале времени, можно вычислить характеристики векового резонанса по аналитическим формулам. Подробно алгоритм выявления апсидально-нодальных вековых резонансов в динамике астероидов описан в работе (Galushina, Sambarov, 2017) и коротко состоит в следующем.
В работе (Мюррей, Дермотт, 2009) показано, что возмущающую функцию, описывающую влияние третьего тела на астероид, можно выразить через элементы орбиты следующим образом:
(1)
$\begin{gathered} R = \frac{{\mu {\text{'}}}}{{a{\text{'}}}}{\text{ }}\sum\limits_{l = 2}^\infty {{{\alpha }^{l}}} \sum\limits_{\bar {m} = 0}^l {{{{( - 1)}}^{{l - \bar {m}}}}{{\chi }_{{\bar {m}}}}\frac{{\left( {l - \bar {m}} \right)!}}{{\left( {l + \bar {m}} \right)!}}} \sum\limits_{p,p' = 0}^l {{{F}_{{l\bar {m}p}}}(i){{F}_{{l\bar {m}p}}}(i') \times } \\ \times \,\,\sum\limits_{q,q{\text{'}} = - \infty }^\infty {X_{{l - 2,p + q}}^{{l,l - 2p}}(e)X_{{l - 2,p' + q'}}^{{ - l - 1,l - 2p{\text{'}}}}(e{\text{'}})} \times \\ \times \,\,{\text{cos}}[(l - 2p{\text{'}} + q{\text{'}})\lambda {\text{'}} - (l - 2p + q)\lambda - \\ - \,\,q{\text{'}}\varpi {\text{'}} + q\varpi + (\bar {m} - l - 2p{\text{'}})\Omega {\text{'}} - (\bar {m} - l - 2p)\Omega ]. \\ \end{gathered} $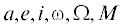 – кеплеровские элементы орбиты астероида (большая полуось, эксцентриситет, наклонение,
аргумент перигелия, долгота восходящего узла и средняя аномалия соответственно); $a{\text{'}},e{\text{'}},i',\omega {\text{'}},\Omega {\text{'}},M{\text{'}}$ – кеплеровские элементы орбиты возмущающего тела; $\lambda = {\bar {\omega }} + M$ и $\lambda {\text{'}} = {\bar {\omega }}' + M{\text{'}}$ – средние долготы астероида и третьего тела соответственно; ${\bar {\omega }} = {\omega } + {\Omega }$ и ${\bar {\omega }}' = {\omega '} + {\Omega '}$ – долготы перигелия астероида и возмущающего тела; $l,p,p',\bar {m}$ целые числа; $\alpha = {a \mathord{\left/ {\vphantom {a {a'}}} \right. \kern-0em} {a'}};$ ${{\chi }_{0}} = 2,$ ${{\chi }_{{\bar {m}}}} = 2,$ если $\bar {m} \ne 0.$
– кеплеровские элементы орбиты астероида (большая полуось, эксцентриситет, наклонение,
аргумент перигелия, долгота восходящего узла и средняя аномалия соответственно); $a{\text{'}},e{\text{'}},i',\omega {\text{'}},\Omega {\text{'}},M{\text{'}}$ – кеплеровские элементы орбиты возмущающего тела; $\lambda = {\bar {\omega }} + M$ и $\lambda {\text{'}} = {\bar {\omega }}' + M{\text{'}}$ – средние долготы астероида и третьего тела соответственно; ${\bar {\omega }} = {\omega } + {\Omega }$ и ${\bar {\omega }}' = {\omega '} + {\Omega '}$ – долготы перигелия астероида и возмущающего тела; $l,p,p',\bar {m}$ целые числа; $\alpha = {a \mathord{\left/ {\vphantom {a {a'}}} \right. \kern-0em} {a'}};$ ${{\chi }_{0}} = 2,$ ${{\chi }_{{\bar {m}}}} = 2,$ если $\bar {m} \ne 0.$
Аргумент возмущающей функции (1) для однократно и двукратно осредненной задачи будет иметь вид (2) и (3) соответственно:
(2)
$\begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } = (l - 2p{\text{'}} + q{\text{'}})M{\text{'}} - (l - 2p)\omega + \\ + \,\,(l - 2p{\text{'}})\omega {\text{'}} - \bar {m}(\Omega - \Omega {\text{'}}), \\ \end{gathered} $(3)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = (l - 2p{\text{'}})\omega {\text{'}} - (l - 2p)\omega - \bar {m}(\Omega - \Omega {\text{'}}),$(4)
$\begin{gathered} M{\text{'}} = M_{0}^{'} + \bar {n}{\text{'}}\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega {\text{'}} = \omega _{0}^{'} + \bar {\omega }{\text{'}}\left( {t - {{t}_{0}}} \right), \\ \Omega {\text{'}} = \Omega _{0}^{'} + \dot {\Omega }{\text{'}}\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega = {{\omega }_{0}} + \dot {\omega }\left( {t - {{t}_{0}}} \right), \\ \Omega = {{\Omega }_{0}} + \dot {\Omega }\left( {t - {{t}_{0}}} \right), \\ \end{gathered} $Величины $\dot {\omega }$ и $\dot {\Omega }$ определяются численно по производным от полинома Лагранжа.
Тогда условие возникновение резонанса можно представить в виде:
(5)
$\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } } \approx 0.$Явление, когда резонансное соотношение строго равно нулю, называется острым или точным резонансом.
В данной работе в качестве характеристик резонансного взаимодействия были рассмотрены критический (резонансный) аргумент (3) и его первая производная по времени (так называемое резонансное соотношение) (5). Перебирая значения целых чисел l, p, p', $\bar {m},$ получаем спектр значений резонансного аргумента и соответствующего ему резонансного соотношения. Если колебания критического аргумента всегда строго меньше 360°, имеет место либрация аргумента, а резонанс определяется как устойчивый. В противном же случае, когда резонансный аргумент изменяется от 0° до 360°, его поведение интерпретируется, как циркуляция, а резонанс вовсе отсутствует. При смене либрации критического аргумента на циркуляцию и наоборот резонанс определяется как неустойчивый.
В работах (Чириков, 1977; Бордовицына, Томилова, 2016) показано, что наложение резонансов разных типов, особенно, если среди них есть хотя бы один неустойчивый резонанс (когда резонансный аргумент меняет свое либрационное поведение на циркуляцию и наоборот), способно приводить к проявлению хаотичности в движении астероидов.
Для исследования регулярности или хаотичности движения астероидов нами использовался индикатор MEGNO (Mean Exponential Growth factor of Nearby Orbit) (Cinkotta и др., 2003).
Пусть $q = \left\{ {{\mathbf{x}},{\mathbf{\dot {x}}}} \right\}$ – есть вектор состояния исследуемого астероида, задающий траекторию в фазовом пространстве, а ${\mathbf{\delta }}({{t}_{0}}) = {{{\mathbf{\delta }}}_{0}}$ – начальное малое отклонение вектора состояния q. Эволюция вектора δ0 с точностью до бесконечно малых первого порядка можно описать вариационным уравнением следующего вида
(6)
${\mathbf{\dot {\delta }}} = {\mathbf{J}}({\mathbf{q}}){\mathbf{\delta }}(t),\,\,\,\,{\mathbf{J}}({\mathbf{q}}) = \frac{{\partial {\mathbf{f}}}}{{\partial {\mathbf{q}}}}({\mathbf{q}}),$Интегрируя совместно с уравнениями движения (7) и уравнениями в вариациях (6) уравнения вида
(8)
$\frac{d}{{dt}}y = \frac{{{\mathbf{\dot {\delta }}} \cdot {\mathbf{\delta }}}}{{{\mathbf{\delta }} \cdot {\mathbf{\delta }}}}t,\,\,\,\,\frac{d}{{dt}}w = 2\frac{y}{t},$(9)
$Y(t) = {{2y(t)} \mathord{\left/ {\vphantom {{2y(t)} t}} \right. \kern-0em} t},\,\,\,\,\bar {Y}(t) = {{w(t)} \mathord{\left/ {\vphantom {{w(t)} t}} \right. \kern-0em} t}.$Эволюция $\bar {Y}\left( t \right)$ во времени позволяет уверенно разделить регулярный и хаотический режимы движения (Cinkotta и др., 2003). Так, например, для хаотических орбит с экспоненциальным расхождением близких траекторий $\bar {Y}\left( t \right) > 2.$ Для квазипериодических (регулярных) орбит с линейным расхождением близких траекторий $\bar {Y}\left( t \right)$ осциллирует около 2, а для устойчивых орбит типа гармонического осциллятора $\bar {Y}\left( t \right) = 0$ (Галушина, Летнер, 2016).
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
На первом этапе исследования необходимо было выявить нумерованные АСЗ, проходящие через сферу тяготения Земли в ближайшие 200 лет. Эта задача решалась нами путем численного интегрирования уравнений движения всех АСЗ, известных на февраль 2017 года, на интервале времени 200 лет с начальными данными, взятыми из каталога Bowell и др. (1994). Орбиту, построенную на основании элементов из этого каталога, будем называть номинальной.
Проведенное исследование позволило выявить четыре нумерованных астероида (99942 Apophis, 153201 2000 WO107, 153814 2001 WN5, 456938 2007 YV56), которые в ближайшие 200 лет будут проходить на расстоянии меньше 256 000 км от геоцентра (радиус действия сферы тяготения Земли). В табл. 1 приведены кеплеровские элементы орбит АСЗ (большая полуось a, эксцентриситет e, наклонение плоскости орбиты к эклиптике i) на начальный момент времени, а также число имеющихся наблюдений N и интервал времени в годах ∆t, в течение которого были получены эти наблюдения.
Таблица 1.
Данные о наблюдениях и кеплеровские элементы орбит АСЗ на начальный момент времени 16.02.2017
| АСЗ | N | ∆t, годы | а, а. е. | e | i, град |
|---|---|---|---|---|---|
| 153814 2001 WN5 | 473 | 1996–2016 | 1.7119 | 0.4669 | 1.9195 |
| 99942 Apophis | 4469 | 2004–2015 | 0.9226 | 0.1915 | 3.3367 |
| 456938 2007 YV56 | 144 | 2007–2016 | 1.5757 | 0.6221 | 6.2434 |
| 153201 2000 WO107 | 431 | 2000–2017 | 0.9113 | 0.7806 | 7.7708 |
Из табл. 1 видно, что АСЗ имеют много наблюдений, полученных на большой дуге, то есть орбиты этих астероидов хорошо определены. Именно по этой причине мы ограничились исследованием номинальных орбит АСЗ. В табл. 2 приведены данные о прохождении астероидов через сферу тяготения Земли в ближайшие 200 лет. Здесь T – календарная дата, d – расстояние до геоцентра. Ближайшее тесное сближение с Землей произойдет в 2028 г. у астероида 153814 2001 WN5. Он подойдет на расстояние 248897.6 км от геоцентра. Самое тесное сближение с Землей в ближайшие 200 лет по-прежнему имеет широко известный астероид 99942 Apophis (Amato и др., 2017; Wlodarczyk, 2017). Его сближение с Землей порядка 38120.3 км состоится 13 апреля 2029 г.
Таблица 2.
Данные о прохождении АСЗ через сферу тяготения Земли
| АСЗ | Т | d, км |
|---|---|---|
| 153814 2001 WN5 | 26.06.2028 | 248897.6 |
| 99942 Apophis | 13.04.2029 | 38120.3 |
| 456938 2007 YV56 | 02.01.2101 | 237199.2 |
| 153201 2000 WO107 | 01.12.2140 | 243182.1 |
Выбрав объекты для эксперимента, мы продолжили исследование их динамики: построили орбитальную эволюцию этих четырех АСЗ на интервале времени (1817, 2217) гг. и выявили все сближения астероидов с большими планетами. Так как исследуемые астероиды имеют тесные сближения с Землей, которые способны привести к значительным изменениям орбит АСЗ, мы построили эволюцию усредненного параметра MEGNO и оценили время предсказуемости их движения. На рис. 1, 2 в качестве примера представлены результаты построения орбитальной эволюции астероидов 99942 Apophis и 153814 2001 WN5 и эволюция усредненного параметра MEGNO.
Рис. 1.
Сближения астероида 99942 Apophis с Землей (а) и Венерой (б), эволюция большой полуоси a (в), эксцентриситета e (г), наклонения плоскости орбиты к эклиптике i (д), долготы восходящего узла Ω (е), аргумента перицентра ω (ж) и усредненного параметра MEGNO (з).
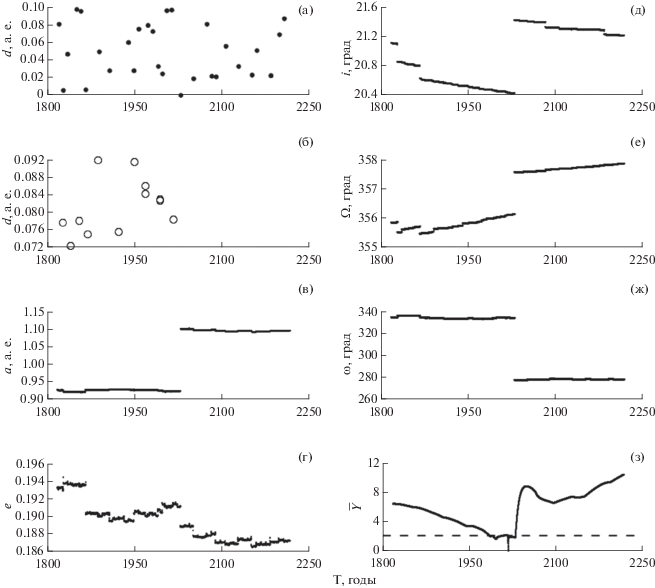
Рис. 2.
Сближения астероида 153814 2001 WN5 с Землей (а) и Марсом (б), эволюция большой полуоси a (в), эксцентриситета e (г), наклонения плоскости орбиты к эклиптике i (д), долготы восходящего узла Ω (е), аргумента перицентра ω (ж) и усредненного параметра MEGNO (з).
Из рис. 1 видно, что 99942 Apophis испытывает множественные сближения с Землей и Венерой (рис. 1а, 1б) на рассматриваемом интервале времени, а момент прохождения через сферу тяготения Земли в 2029 г. приводит к значительному изменению параметров орбиты астероида (рис. 1в–1ж). Анализируя поведение усредненного параметра MEGNO (рис. 1з), нетрудно заметить, что при интегрировании в прошлое движение является регулярным (параметр MEGNO колеблется около значения 2) на коротком интервале времени около 20 лет с 1997 г. до начального момента интегрирования. До 1997 г. в движении АСЗ проявляются признаки хаотичности. В этот период времени астероид испытывает множественные сближения с Землей и Венерой. При интегрировании в будущее под действием тесного сближения АСЗ с Землей порядка сферы тяготения параметр MEGNO скачкообразно меняет свое значение с 2 до 9, но затем падает до значения 7. Хаотичность начинает проявляться примерно с 2100 г. В этот период времени астероид испытывает множественные сближения с Землей. Таким образом, время предсказуемости движения 99942 Apophis можно оценить примерно в 100 лет.
Для астероида 153814 2001 WN5 наблюдается схожая картина в поведении элементов его орбиты (рис. 2), момент прохождения АСЗ через сферу тяготения Земли в 2028 г. приводит к значительному изменению всех параметров орбиты астероида (рис. 1в–1ж). Но, несмотря на многочисленные и тесные сближения астероида с Землей (рис. 2а) и Марсом (рис. 2б), движение астероида можно считать регулярным на рассматриваемом интервале времени. Из рис. 2з видно, при интегрировании в прошлое движение 153814 2001 WN5 остается регулярным, а при интегрировании в будущее под действием тесного сближения АСЗ с Землей порядка сферы тяготения параметр MEGNO начинает резко расти, достигая значения 7, затем падает, и стремится к постоянной величине примерно до 2180 г. В дальнейшем снова наблюдается тенденция к росту этого параметра.
Так как к проявлению хаотичности в движении АСЗ могут привести не только тесные и/или многократные сближения с большими планетами, но и наличие хотя бы одного неустойчивого резонанса, интересно было проследить их вековую резонансную динамику. На основании построенной орбитальной эволюции астероидов были выявлены вековые резонансы с планетами внутренней группы. Для каждого астероида был рассмотрен весь спектр апсидально-нодальных резонансов до 6-го порядка включительно с планетами внутренней группы (Меркурий, Венера, Земля и Марс). В качестве характеристик векового резонанса были рассмотрены критический аргумент (3) и резонансное соотношение (5). Варьируя значения целых чисел l, p, p', $\bar {m}$ в (3), мы получили 20 резонансных аргументов и соответствующих им 20 резонансных соотношений. В табл. 3 в виде формул представлены эти резонансные соотношения.
Таблица 3.
Типы апсидально-нодальных резонансных соотношений до 6-го порядка включительно
| № | Типы резонансных соотношений | № | Типы резонансных соотношений | № | Типы резонансных соотношений |
|---|---|---|---|---|---|
| 1 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + \dot {\omega } - \dot {\omega }_{i}^{'}$ | 8 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - 2{\dot {\omega }} - 2{\dot {\omega }}_{i}^{'}$ | 15 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - 2{\dot {\omega }}_{i}^{'}$ |
| 2 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - {\dot {\omega }} + {\dot {\omega }}_{i}^{'}$ | 9 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + 2{\dot {\omega }}$ | 16 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + 2{\dot {\omega }}_{i}^{'}$ |
| 3 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + 2{\dot {\omega }} - 2{\dot {\omega }}_{i}^{'}$ | 10 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - 2{\dot {\omega }}$ | 17 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right)$ |
| 4 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - 2{\dot {\omega }} + 2{\dot {\omega }}_{i}^{'}$ | 11 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + {\dot {\omega }}$ | 18 | ${\dot {\omega }} - {\dot {\omega }}_{i}^{'}$ |
| 5 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + {\dot {\omega }} + {\dot {\omega }}_{i}^{'}$ | 12 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - {\dot {\omega }}$ | 19 | $\dot {\omega } + \dot {\omega }_{i}^{'}$ |
| 6 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - {\dot {\omega }} - {\dot {\omega }}_{i}^{'}$ | 13 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + {\dot {\omega }}_{i}^{'}$ | 20 | ${\dot {\omega }}$ |
| 7 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) + 2{\dot {\omega }} + 2{\dot {\omega }}_{i}^{'}$ | 14 | $\left( {\dot {\Omega } - \dot {\Omega }_{i}^{'}} \right) - {\dot {\omega }}_{i}^{'}$ |
Соотношения 1–16 описывают смешанный вековой резонанс (апсидально-нодальный), соотношение 17 – чисто нодальный, а 18, 19 – апсидальные резонансы. Соотношение 20 представляет собой геометрический резонанс типа Лидова–Козаи. Этот резонанс интересен тем, что зависит только от взаимного расположения объектов и не связан с частотами движения возмущающих тел.
Поиск вековых резонансов в динамике опасных для Земли нумерованных астероидов дал весьма интересные результаты. Оказалось, что все исследуемые вековые резонансы являются устойчивыми на рассматриваемом интервале времени, их резонансные соотношения (5) регулярно проходят через значение точного резонанса, а критические аргументы (3) либрируют в пределах 360°.
Анализ эволюции резонансных соотношений показал, что все рассмотренные резонансы можно условно разделить на шесть групп в зависимости от изменения значений соотношений. В табл. 4 представлены границы изменения значений резонансных соотношений для рассматриваемых астероидов. Интересно, что для всех планет внутренней группы эти границы совпадают у каждого астероида. При этом эволюция соотношений может немного отличаться для разных планет, но границы изменения сохраняются.
Таблица 4.
Границы изменения резонансных соотношений
| Номер резонанса | 99 942 Apophis | 153 814 2001 WN5 |
153 201 2000 WO107 |
456 938 2007 YV56 |
|---|---|---|---|---|
| 1, 5, 11 | (–30; 10) | (–2; 4) | (–8; 0.5) | (–9; 12) |
| 18–20 | (–12; 2) | |||
| 2, 6, 12 | (–10; 30) | (–6; 2) | (–4; 15) | (–14; 10) |
| 3, 7, 9 | (–60; 20) | (–4; 8) | (–20; 2) | (–19; 25) |
| 4, 8, 10 | (–20; 60) | (–11; 4) | (–5; 25) | (–29; 19) |
| 13–17 | (–0.5; 4) | (–2; 0.5) | (–2; 4) | (–4.5; 2) |
Отдельно следует отметить астероид 99942 Apophis. Из табл. 4 видно, что амплитуда колебаний резонансных соотношений выше, чем у остальных астероидов, что, по-нашему мнению, обусловлено наиболее тесным сближением астероида с Землей среди исследуемых объектов. Кроме того, в момент тесного сближения для всех рассмотренных резонансов отмечается одномоментный скачок резонансного соотношения на несколько порядков выше границ, приведенных в табл. 4. При этом соотношение продолжает регулярно проходить через значение точного резонанса. Такое увеличение значения резонансного соотношения связано со скачкообразным изменением элементов орбиты астероида после тесного сближения, а именно, аргумент перицентра изменяется на 52°.
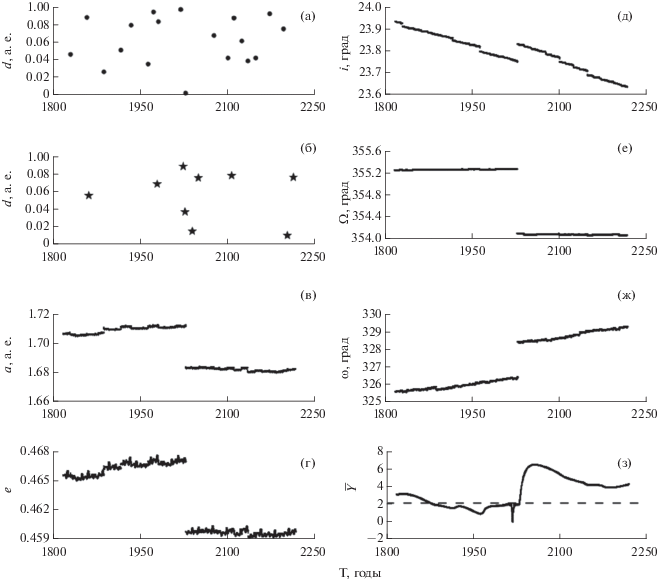
В качестве примера на рис. 3 и рис. 4 представлена эволюция резонансных характеристик для астероида 153814 2001 WN5. На рис. 3а и рис. 3в приведены графики эволюции резонансных аргументов и соотношений для резонансов № 8, 14 из табл. 3 с Венерой, а на рис. 3б и рис. 3г представлены так называемые фазовые портреты для этих резонансов.
Рис. 3.
Примеры эволюции резонансных соотношений $\dot {\Psi }$ и аргументов ψ (а, б) и фазовые портреты для некоторых апсидально-нодальных резонансов 153814 2001 WN5 с Венерой.
Рис. 4.
Примеры эволюции резонансных соотношений $\dot {\Psi }$ и аргументов ψ (а, б) и фазовые портреты для некоторых апсидально-нодальных резонансов 153814 2001 WN5 с Землей.
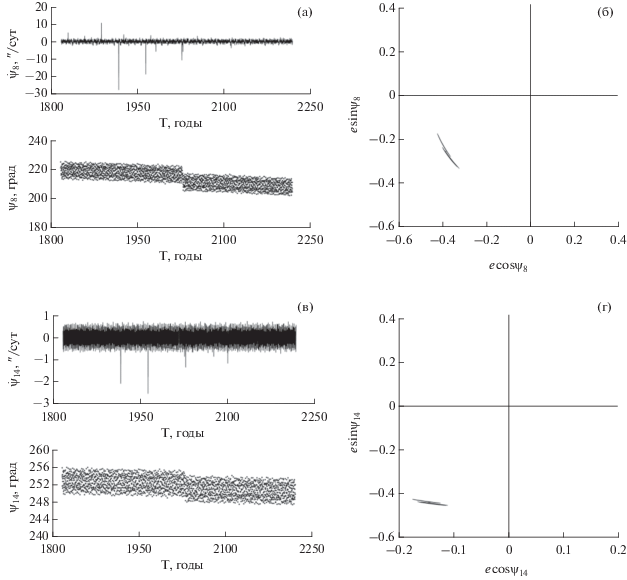
Фазовые портреты позволяют наглядно оценить поведение резонансного аргумента: если кривая покрывает начало координат, при этом замыкаясь, то имеет место циркуляция. В противном случае, когда кривая не охватывает начало координат, можно говорить о либрации резонансного аргумента. На рис. 4 представлено поведение тех же характеристик, но для резонансов № 8, 14 астероида 153814 2001 WN5 с Землей.
Из рис. 3 и рис. 4 видно, что критические аргументы либрируют, т.е. резонансы являются устойчивыми на рассматриваемом интервале времени. Если обратиться к рис. 2, нетрудно заметить, что прохождение астероида 153814 2001 WN5 через сферу тяготения Земли приводит к смещению центра либрации критических аргументов.
ЗАКЛЮЧЕНИЕ
Таким образом, в данной работе представлены результаты исследования динамики нумерованных астероидов, проходящих через сферу тяготения Земли в ближайшие 200 лет (99942 Apophis, 153201 2000 WO107, 153814 2001 WN5 и 456938 2007 YV56). Основной целью данного исследования было выявление в движении АСЗ вековых резонансов и изучение взаимного влияния резонансных соотношений и тесных сближений.
Исследуемые астероиды не только проходят через сферу тяготения Земли, но и имеют тесные и/или многократные сближения с большими планетами, которые значительным образом изменяют параметры орбит АСЗ. По этой причине мы оценили время предсказуемости движения астероидов с помощью параметра MEGNO и выявили причины проявления хаотичности. Как и ожидалось, времена предсказуемости движения астероидов оказались очень маленькими (не превышают интервал времени интегрирования), а тесные и/или многократные сближения с большими планетами привели к проявлению хаотичности в движении АСЗ.
Так как к проявлению хаотичности могут привести не только тесные и/или многократные сближения с большими планетами, но и наличие хотя бы одного неустойчивого резонанса, мы проследили их вековую резонансную динамику.
Для всех АСЗ наблюдается схожая картина с точки зрения поиска вековых резонансов с планетами внутренней группы. Резонансные аргументы для всех групп соотношений либрируют на рассматриваемом интервале времени, что позволяет сделать вывод об устойчивости вековых резонансов для данных объектов. Таким образом, к проявлению хаотичности в динамике исследуемых астероидов приводят только описанные в этой работе сближения астероидов с планетами.
Тем не менее нам удалось выявить влияние тесных сближений на эволюцию характеристик векового резонанса. Исследования показали, что прохождение АСЗ через сферу тяготения Земли приводит к скачкообразному изменению центров либрации критических аргументов и одномоментному возрастанию резонансного соотношения, но при этом резонанс сохраняет свою устойчивость.
Работа выполнена при финансовой поддержке гранта РФФИ № 15-02-02868а.
Список литературы
Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычисл. технологии. 2010. Т. 15. № 4. С. 31–47.
Бордовицына Т.В., Томилова И.В. Особенности структуры вековых резонансов в динамике околоземных космических объектов // Изв. вузов. Физика. 2016. Т. 59. № 3. С. 41–48.
Быкова Л.Е., Галушина Т.Ю., Батурин А.П. Прикладной программный комплекс “ИДА” для исследования динамики астероидов // Изв. вузов. Физика. 2012. № 10/2. С. 89–96.
Галушина Т.Ю., Летнер О.Н. Исследование эффективности использования быстрых индикаторов хаотичности MEGNO и OMEGNO в задачах астероидной динамики // Изв. вузов. Физика. 2016. № 10/2. С. 32–37.
Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2009. 588 с.
Раздымахина О.Н. Алгоритмическое и программное обеспечение для определения параметра хаотичности MEGNO в задачах динамики астероидов // Изв. вузов. Физика. 2011. № 6/2. С. 31–38.
Чириков В.В. Нелинейный резонанс. Учебное пособие. Изд-во НГУ, 1977. 82 с.
Amato D., Baù G., Bombardelli C. Accurate orbit propagation in the presence of planetary close encounters // Mon. Notic. Roy. Astron. Soc. 2017. V. 470. Iss. 2. P. 2079–2099.
Bowell E., Muinonen K., Wasserman L.H. A public-domain asteroid data base // Asteroids, Comets, Meteors. Dordrecht, Netherlands: Kluwer, 1994. P. 477–481.
Carruba V., Vokrouhlický D., Novaković B. Asteroid families interacting with secular resonances // Planet. and Space Sci. 2018. V. 157. P. 72–81.
Cincotta P.M., Girdano C.M., Simo C. Phase space structure of multi-dimensional systems by means of the mean exponential growth factor of nearby orbits // Physica D: Nonlinear Phenomena. 2003. V. 182. № 3–4. P. 151–178.
Everhart E. An efficient integrator that uses Gauss–Radau Spacings // Dynamics of Comets: Their Origin and Evolution (Proc. IAU Colloq. 83. Rome, Italy, June 11–15, 1984) / Eds Carusi A., Valsecchi G.B. Dordrecht: Reidel, 1985. P. 185–202.
Froeschle Ch., Scholl H. The three principal resonances ν5, ν6 and ν16 in the asteroidal belt // Celest. Mech. 1989. V. 46. P. 231–251.
Galushina T.Yu., Sambarov G.E. The dynamical evolution and the force model for asteroid (196256) 2003 EH1 // Planet. and Space Sci. 2017. V. 142. P. 38–47.
Moons M., Morbidelli A. Secular resonances inside mean-motion commensurabilities: the 4/1, 3/1, 5/2 and 7/3 cases // Icarus. 1995. V. 114. P. 33–50.
Nakai H., Kinoshita H. Secular perturbations of asteroids in secular resonance // Celest. Mech. 1985. V. 36. P. 391–407.
Nesvorny D., Ferraz-Mello S., Holman M., Morbidelli A. Regular and chaotic dynamics in the mean-motion resonances: Implications for the structure and evolution of the asteroid belt // Asteroids III / Eds Bottke W.F., Cellino A., Paolicchi P., Binzel R.P. Tucson: Univ. Arizona Press, 2003. P. 379–394.
Smallwood J.L., Martin R.G., Lepp S., Livio M. Asteroid impacts on terrestrial planets: The effects of super-Earths and the role of the ν6 resonance // Mon. Notic. Roy. Astron. Soc. 2018. V. 473. Iss. 1. P. 295–305. https://doi.org/10.1093/mnras/stx2384.
Williams J.G. Secular perturbations in the Solar System // Ph.D. Dissertation, Univ. California, Los Angeles, 1969.
Wlodarczyk I. Possible impact solutions of asteroid (99942) Apophis // Bulgarian Astron. J. 2017. V. 27. P. 89.
Yoshikawa M. A simple analytical model for the secular resonance ν6 in the asteroidal belt // Celest. Mech. 1987. V. 40. № 3–4. P. 233–272.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник


