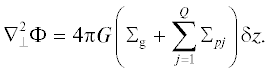Астрономический вестник, 2019, T. 53, № 3, стр. 195-213
Механизм потоковой неустойчивости в газопылевой среде протопланетного диска и формирование пылевых фрактальных кластеров
А. В. Колесниченко a, *, М. Я. Маров b, **
a Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
b Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия
* E-mail: kolesn@keldysh.ru
** E-mail: marovmail@yandex.ru
Поступила в редакцию 26.11.2018
После доработки 28.12.2018
Принята к публикации 15.01.2019
Аннотация
Последовательность эволюции протопланетного газопылевого диска вокруг родительской звезды включает, по современным представлениям, его уплотнение в центральной плоскости и распад на отдельные пылевые сгущения (кластеры) вследствие возникновения различного типа неустойчивостей. Взаимодействие пылевых кластеров фрактальной структуры при их соударениях рассматривается в качестве ключевого механизма образования и роста первичных твердых тел, служащих основой последующего формирования планетезималей и зародышей планет. Среди механизмов, способствующих формированию планетезималей, важное место принадлежит, наряду с гравитационной неустойчивостью, гидродинамическим неустойчивостям, в частности, так называемой потоковой неустойчивости двухфазного газопылевого слоя из-за ее способности концентрировать дисперсные частицы в плотные сгустки. В отличие от ряда существующих моделей потоковой неустойчивости, в которых пылевые частиц считаются структурно компактными и монодисперсными, в данной работе предложена более реалистичная модель полидисперсных частиц фрактальной природы, образующих пылевые кластеры в результате коагуляции. Рассмотрена неустойчивость пылевого слоя в центральной плоскости протопланетного диска при линейных осесимметричных возмущениях его параметров. Можно сделать предварительный вывод о том, что предложенная модель пылевых фрактальных агрегатов разного масштаба повышает эффективность линейного роста гидродинамических неустойчивостей, в том числе, потоковой неустойчивости, связанной с различием между скоростями пылевой и газовой фаз.
ВВЕДЕНИЕ
Реконструкция процессов, лежащих в основе формирования планетных систем, находится на передовом рубеже современной астрофизики. Значительный прогресс достигнут благодаря данным наблюдений структуры и состава околозвездных дисков с высоким пространственным разрешением, таких, как данные, полученные с телескопов ALMA (Atacama Large Millimeter Array), измерениям их свойств с космических аппаратов и, конечно, открытию экзопланет, число которых достигло многих тысяч, и этот процесс непрерывно нарастает. Все большее значение приобретает математическое моделирование физических и химических механизмов, ответственных за формирование и эволюцию протопланетных газопылевых дисков, образование в них первичных твердых тел и их прогрессивный рост до размеров планетезималей/зародышей планет, включая многообразные процессы термической и динамической эволюции.
Вещество протопланетного газопылевого диска представляет собой сложную систему различного фазового состава, плотности, температуры и степени ионизации, которые изменяются с радиальным расстоянием. В основном это неоднородная среда, состоящая из частиц газа и пыли различных размеров и происхождения. Эта среда представляет собой намагниченную пылевую плазму, находящуюся в состоянии турбулентности, свойства которой зависят от радиального и азимутального положения в диске (см. Колесниченко, Маров, 2009; Lissauer, de Pater, 2013; Marov, Kolesnichenko, 2013; Armitage, 2015). Когда основные динамические силы, управляющие состоянием вращающегося диска (гравитационные и центробежные) находятся в равновесии, более слабые факторы, такие как тепловые/вязкие процессы, турбулентность и электромагнитные явления, являются доминирующими. Они влияют на конденсацию летучих и оказывают существенное влияние на относительное содержание и обилие газа и твердых частиц, а также на перенос энергии и углового момента в диске.
В пренебрежении плазменными эффектами движение газопылевой дисковой среды наиболее адекватно моделируется в рамках механики гетерогенных турбулизованных сред с учетом физико-химических свойств фаз, тепло-массопереноса, вариаций непрозрачности среды для приходящего излучения, вязкости, химических реакций, фазовых переходов, коагуляции, фрагментации и др. Строгое математическое рассмотрение проблемы представлено, в частности, в работах (Сhavanis, 1999; Kolesnichenko, Marov, 2006; Колесниченко, Маров, 2009; Marov, Kolesnichenko, 2013), в которых проанализирован характер динамического взаимодействия турбулентного газа и пыли, включая влияние изменения энергии турбулентности несущей фазы на поведение твердых частиц и обратное влияние пылевой компоненты на динамический и тепловой режимы газовой фазы, а также влияние турбулентных вихрей на фазовые превращений в среде (испарение, конденсация). С этими процессами связаны также аккумуляция частиц вследствие коагуляции и фрагментация при взаимных соударениях твердых частиц в потоке газа и оседании частиц через газ к средней плоскости диска, где они образуют геометрически тонкий уплощенный слой – пылевой субдиск (Mizuno, 1989; Dominik, Tielens, 1997). Как видим, наличие полидисперсной примеси частиц в турбулентной среде существенно усложняет гидродинамику диска, способствуя появлению дополнительных режимов течения. Отметим, что синергетические процессы коллективной самоорганизации в термодинамически открытой системе протопланетного диска на фоне крупномасштабного сдвигового течения вещества, связанные с его дифференциальным вращением и наличием касательных напряжений в пограничных слоях, представляют собой важные механизмы, формирующие свойства вязкого аккреционного диска на различных этапах его эволюции (Cuzzi, Dobrovolskis, Champney, 1993; Колесниченко, 2004; Колесниченко, Маров, 2006; Blum, Wurm, 2008).
Континуальная модель гетерогенной дисковой среды должна учитывать влияние турбулентности на динамику и процессы тепло- и массопереноса в дифференциально вращающемся веществе с учетом инерционных свойств полидисперсной примеси твердых частиц и эффектов на границе между газовой и конденсированной фазами (Hodgson, Brandenburg, 1998). Последние соответствуют параметрам на границе экмановского слоя и существенно влияют на динамику диска, включая неустойчивость Кельвина–Гельмгольца (Johansen и др., 2006a). Формирование и поддержание сдвиговой турбулентности в двухфазной среде с дифференциальной угловой скоростью вращения и различным относительным содержанием пылевых частиц разного размера значительно усложняет картину явлений, включая эффективность процессов коагуляции. Также предполагается, что на эволюцию турбулентности во вращающемся аккреционном диске влияет гидродинамическая спиральность, ответственная за каскадный процесс обратного переноса энергии от малых к большим вихрям и появление отрицательной вязкости в среде (Колесниченко, 2014; Колесниченко, Маров, 2007).
Очевидно, каким бы ни был характер рассматриваемых событий, ясно, что сложные физико-химические процессы, сопровождающие эволюцию гетерогенной среды, в которой происходят активные процессы столкновений частиц пыли, ответственны за возникновение первичных твердых тел и их последующую эволюцию. Разработанные в литературе модели включают последовательность изменения агрегатного состояния основных компонентов протопланетного вещества; расположение фронтов конденсации-испарения в зависимости от термодинамических параметров диска (особенно в окрестности снеговой линии), роль сублимации и коагуляции частиц в двухфазной среде с учетом их распределения по размерам, с чем связаны механизмы развития гидродинамической и гравитационной неустойчивостей (см., например, Armitage, 2007; Marov, Kolesnichenko, 2013). Заметим, что поскольку планеты земной группы формируются вблизи Солнца и большое число открытых экзопланет находится в непосредственной окрестности родительской звезды, фокус моделирования сужается до слабо разрешимых областей внутреннего диска в пределах долей астрономической единицы, где материя активно аккретирует на молодую звезду. Это приводит к изменению соотношения пыль/газ, оптической непрозрачности и теплового режима, а также значительному вкладу фотохимических процессов в преобразование состава и перенос вещества.
В процессе формирования пылевого субдиска вещество испытывает сжатие/уплощение за счет оседания частиц в средней плоскости в сочетании с радиальным дрейфом на ранней стадии его эволюции. В субдиске внутреннее давление газа недостаточно для предотвращения гравитационного коллапса достаточно крупных пылевых частиц в области, заполненной газопылевым веществом. Если хаотические турбулентные скорости пылевых частиц не слишком велики, а поверхностная плотность массивного пылевого слоя достаточно велика, то развивается гравитационная (джинсовая) неустойчивость, соответствующая классическому сценарию Гольдрейха–Уорда формирования планетезималей (Goldreich, Ward, 1973). Гравитационная неустойчивость, как считается, ответственна за появление первичных пылевых кластеров в преобладающей кольцеобразной конфигурации субдиска (Зиглина, Макалкин, 2016; Nakamoto, Nakagawa, 1994; Toomre, 1964; Youdin, Shu, 2002). Недавно нами в работе (Kolesnichenko, Marov, 2014) была предложена модификация критерия джинсовской неустойчивости для астрофизических дисков на основе неэкстенсивной статистики Тсаллиса (Tsallis, 1988). Этот критерий выведен из модифицированного кинетического уравнения со специальной формой интеграла столкновений применительно к однородной дисковой среде, имеющей фрактальную структуру в фазовом пространстве.
Альтернативный (или, скорее, комплиментарный) подход к развитию неустойчивости в диске носит гидродинамический характер. Основной концепцией является дисбаланс между поверхностной газопылевой плотностью и массопереносом. Предложены два основных сценария такой нестабильности. Первый связан с идеей о том, что турбулентность в диске/субдиске может создавать локальные области с высоким отношением пыль/газ, которые растут, достигая, в конечном итоге, размера крупных тел (Cuzzi и др., 2008). Предполагается, что происходит либо пассивная концентрация частиц турбулентностью на больших масштабах, сравнимых с диссипативным интервалом турбулентности, либо концентрация частиц внутри турбулентных вихрей, играющих роль своего рода ловушки, на что указывалось также в работе (Marov, Kolesnichenko, 2013). Допускается возможность возникновения подобных образований в зональных потоках (Johansen и др., 2009), включая аэродинамически возникающие области между вихрями (Cuzzi и др., 2008; Pan и др., 2011). Второй сценарий предполагает наличие обратной связи между газом и конденсированными частицами в двухфазном потоке, то есть обратную реакцию частиц на поток газа. Такую связь между газом и пылью обычно называют линейной неустойчивостью потока (Youdin, Goodman, 2005), ответственной за генерацию исходных зародышей прото-планетезималей. При численном моделировании выявлены плотности пыль/газ и некоторые другие параметры, необходимые для реализации такого механизма. Большие “комки” пыли, особенно содержащие зерна cантиметровых размеров, образовавшиеся в предшествующих процессах столкновения и коагуляции/коалесценции, могут оказывать существенное влияние на стабильность течения газопылевой среды. Было также показано, что нелинейная эволюция потоковой неустойчивости может сопровождаться гравитационной неустойчивостью при меньших отношениях пыль/газ (см. Armitage, 2007; 2011; Bai, Stone, 2010a; 2010b; 2010c; Chiang, Youdin, 2010; Drazkowska, Dullemond, 2014; Jacquet и др., 2011; Johansen и др., 2007; 2009; Yang, Johansen, 2014). Потоковая неустойчивость развивается при металличности выше протосолнечной (Bai, Stone, 2010a; Morbidelli, Raymond, 2016). Если это условие не выполняется в диске на стадии образования планетезималей, дальнейшее оседание комков может приводить к гравитационной неустойчивости при меньшем отношении пыль/газ, чем в однофазной модели (Сафронов, 1987; Макалкин, Зиглина, 2018). Кроме того, сдвиговая турбулентность, вызванная различными скоростями газа и пыли в неоднородном веществе диска, ответственна за возникновение неустойчивости Кельвина–Гельмгольца (Garaud, Lin, 2004; Marov, Kolesnichenko, 2013).
Кластеры, возникающие в результате потоковой и гравитационной неустойчивости, предположительно, содержат частицы субмикронного размера, включая небулярную пыль и конденсаты дисковой среды. Последние образуются при различных температурах в зависимости от радиального расстояния: от тугоплавких соединений в непосредственной близости к протосолнцу до льдов за снеговой линией. Очевидно, помимо взаимодействия пылевых кластеров в дальнейшем росте важную роль играют процессы коагуляции/коалесценции, с чем связано образование более плотных структур. Сами кластеры могут содержать как плотные, так и рыхлые (пористые) частицы (Kataoka и др., 2013). Пористой (fluffy) структурой, предположительно, обладают и сами кластеры, подобно тенденции ледяных частиц сформировывать очень рыхлые (“пушистые”) образования фрактальной природы. Это значительно облегчает режим роста тел в диске за счет столкновительного взаимодействия кластеров и частиц внутри них. Действительно, такие пушистые агрегаты, благодаря их чрезвычайно высокой пористости, являются стойкими к разрушительным столкновениям при высоких скоростях соударений, а их радиальный дрейф в диске является очень медленным. Для типичных ворсистых агрегатов, имеющих по сравнению с компактными пылевыми частицами относительно большие геометрические поперечные сечения, меняется весь режим движения в газовом несущем потоке, в частности, изменяются условия возникновения потоковой неустойчивости в диске из-за значительной модификации аэродинамической силы трения пыли и газа. Кроме этого, может существенно измениться эффективность отталкивания при столкновении пористых структур (Колесниченко, Маров, 2014; Маров, Русол, 2018).
Последующий процесс включает в себя непрерывный рост формирующихся тел, наиболее крупные из которых поглощают меньшие тела и пыль в результате столкновений и гравитационного притяжения, в то время как газ из внутренних областей диска постепенно теряется. В конечном итоге процесс приводит к образованию многочисленных более плотных планетезималей размером от десятков до сотен километров в поперечнике, а затем планетарных эмбрионов, из которых в конечном итоге формируются планеты (см., например, Kolesnichenko, Marov, 2013; Маров, 2005; Weidenschilling, 2000; Wetherill, Stewart, 1989).
Протосолнечный аккреционный диск, вероятно, был полностью рассеян в первые 4–5 миллионов лет после рождения Солнечной системы. В последующий период происходило накопление первичных твердых тел, унаследованных от начальной фазы эволюции, за счет необратимого (олигархического) роста остаточных планетезималей из области их аккумуляции, а также аккреция основной массы газа на планетах-гигантах (Lissauer, de Pater, 2013). Подобные процессы, по-видимому, происходят и при формировании планетных систем вокруг как одиночных, так и двойных звезд со своеобразной динамикой такой бинарной системы (Маров, Шевченко, 2017).
В данной работе мы не будем касаться турбулентного механизма, сопровождающего образования планетезималей, а сосредоточимся на рассмотрении различных гидродинамических неустойчивостей двухфазного газопылевого потока, которые могут способствовать локальной концентрации пылевых агрегатов, преодолевающих барьеры отталкивания и разрушения. Потоковая неустойчивость дисковой двухфазной газопылевой среды является, по мнению ряда исследователей, перспективным механизмом образования планетезималей, из-за ее способности концентрировать твердые частицы в плотные структуры, способные вызвать гравитационный коллапс в протопланетном диске (Bai, Stone, 2010a; 2010b; Yang и др., 2017; Umurhan и др., 2018). Степень сгущения сильно зависит от интегрированного по высоте отношения массы тела к газу в протопланетных дисках. Как уже отмечалось, оседание частиц является ключевым процессом их концентрации в окрестности центральной плоскости диска. Получаемая при этом высокая массовая нагрузка на газ является основным фактором, необходимым для достижения высоких удельных весов пылевых агрегатов, в то время как турбулентная диффузия газовой фазы способствует выметанию подобных сгущений из пылевого субдиска (Johansen и др., 2007). Когда отношение плотности пылевой составляющей диска к плотности газа приближается к единице, влияние пыли на движение несущей фазы становится достаточно сильным, для того чтобы убыстрить этот поток и вместе с ним двигаться по круговой орбите со скоростью, близкой к кеплеровской. В результате радиального дрейфа пылевых частиц возникает не связанная с силой тяжести неустойчивость газопылевого потока, вследствие которой возникают локальные флуктуации плотности частиц и формируются фрактальные пылевые агломераты в центральной плоскости диска.
СТРУКТУРНЫЕ ПАРАМЕТРЫ ФРАКТАЛЬНОЙ ГАЗОПЫЛЕВОЙ СРЕДЫ
Перенос пыли газовым потоком и рост пылевых частиц формируют глобальную структуру протопланетного диска. Перенос пылевых частиц зависит от размера частиц (который меняется в течение долгого времени), тогда как масштабная эволюция частиц, в свою очередь, зависит от локальных условий в диске (температуры, газовой плотности, плотности пыли и т.п.). Таким образом, рост частиц и их перенос несущим потоком происходит одновременно и для того чтобы понять глобальные тенденции эволюции, оба эти эффекта должны быть приняты во внимание.
Основные допущения задачи
Огромное разнообразие, взаимовлияние и сложность физико-химических и гидродинамических эффектов, происходящих в допланетном газопылевом облаке, с необходимостью требует разумной схематизации описания эволюции дисковой гетерогенной среды. В связи с этим далее будем предполагать, что эволюция газовой и пылевой составляющих протопланетного диска может быть адекватно описано при следующих допущениях.
i) Первичные пылевые частицы (мономеры) – однородные по составу, твердые и недеформируемые, сферичные по форме и монодисперсны.
ii) Предполагается несжимаемость материала мономеров, ${{\rho }_{0}} = {\text{const}}.$
iii) Истинная плотность материала мономеров много больше истинной плотности газовой составляющей дисковой системы, ${{\rho }_{0}} \gg {{\tilde {\rho }}_{g}}.$
iv) Вкладом от приповерхностного слоя кластеров (на которых терпят разрыв непрерывности поля различных гидродинамических параметров) в динамику дисковой гетерогенной системы в целом можно пренебречь.
v) Несущая фаза – сжимаемый совершенный газ.
vi) Вязкостными эффектами для несущей и дисперсной фазы можно пренебречь.
vii) Предполагается условие термического равновесия газовой и дисперсной фаз, ${{T}_{\operatorname{g} }} = {{T}_{{\text{p}}}} = T.$
viii) Предполагается, что фрактальная среда пылевых кластеров внутри элементарного (совокупного) макрообъема $\delta V$ имеет фрактальную размерность D, а размерность на его границе $\delta W$ равна d (в общем случае размерность d не равна ни 2, ни D – 1).
ix) При исследовании гидродинамической устойчивости газопылевого слоя можно пренебречь турбулентной диффузией пыли, вызванной турбулентностью газовой фазы11.
Основные параметры фрактальных структур
Далее все первичные мелкодисперсные компактные частицы газопылевого протопланетного облака вне зависимости от их реальной формы, размера и материала будем считать твердыми сферами, имеющими один и тот же радиус ${{r}_{0}}$ и массу ${{m}_{0}},$ поскольку форма мономера (сферическая, эллипсоидальная и т.п.) оказывает незначительное влияние (≲2%) на фрактальную размерность образующихся кластеров (см., например, Bertini и др., 2009). На первоначальном этапе роста (на основе механизма “частица–частица”) пылевые образования состоят из небольшого числа первичных мономеров и по этой причине не могут, вообще говоря, считаться фракталами. Но, по мере дальнейшего слипания мономеров в кластеры, механизмом “кластер–кластер” формируются фрактальные пылевые агрегаты относительно крупных размеров. При этом число ${{n}_{0}}$ первичных пылевых частиц (ядер), входящих в состав изотропного фрактального пылевого агрегата (ФПА) и масса кластера ${{m}^{{{\text{cl}}}}}$ определяются следующими асимптотическими формулами (см., например, Смирнов, 2011)
(1)
$\begin{gathered} {{n}_{{\text{0}}}} = {{\left( {{R \mathord{\left/ {\vphantom {R {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right)}^{D}}{\text{,}}\,\,\,\,{{m}^{{{\text{cl}}}}} = {{m}_{0}}{{n}_{0}} = {{m}_{0}}{{\left( {{R \mathord{\left/ {\vphantom {R {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right)}^{D}}, \\ {R \mathord{\left/ {\vphantom {R {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}} \gg 1, \\ \end{gathered} $(2)
$D = {{\ln {{n}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{\ln {{n}_{{\text{0}}}}} {{\text{ln}}}}} \right. \kern-0em} {{\text{ln}}}}({R \mathord{\left/ {\vphantom {R {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}),\,\,\,\,\left( {1 < D < n} \right)$При объединении большого числа малых пылевых кластеров (в результате процесса кластер-кластерной ассоциации) образуются обладающие самоподобными свойствами на малых расстояниях22однородные ворсистые агрегаты, в которых по мере увеличения их радиуса гирации увеличиваются размеры пустот, а средняя плотность (средняя массовая плотность вещества в объеме, занимаемом кластером) убывает по закону ${{\bar {\rho }}^{{{\text{cl}}}}} = {{\rho }_{0}}\left( {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R}} \right){{\,}^{{3 - D}}},$ где ${{\rho }_{0}} = {{3{{m}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{3{{m}_{{\text{0}}}}} {4\pi r_{0}^{3}}}} \right. \kern-0em} {4\pi r_{0}^{3}}}$ – массовая плотность материала первичных ядер. Отсюда следует вывод, что чем больший объем занимают части фрактального агрегата, тем больше пустот всех размеров он содержит. Таким образом, одним из характерных свойств фрактального агрегата является его способность захватывать большое пространство (за счет создания ажурной, сильно разветвленной структуры) при использовании меньшего по сравнению с плотным (компактным) агрегатом количества вещества, необходимого для его образования. Компактность и физические свойства отдельного кластера зависят как от характера движения первичных мономеров и кластеров (прямолинейное или броуновское) до столкновения, так и от вероятности слипания мономеров и кластеров при их соприкосновении. В зависимости от числовой плотности ${{N}_{1}}(r,t)$ мономеров (не входящих в состав кластеров) в единице объема $\delta V \equiv \delta r( = \delta x\delta y\delta z)$ дисковой среды возможны два механизма роста кластеров с фрактальной структурой: в результате прилипания к кластеру мономеров или благодаря процессу кластер-кластерной агрегации. При этом в первом случае процесс роста кластера может происходить либо в результате присоединения к нему единичных ядер, двигающихся прямолинейно (кинетический режим), либо когда много первичных пылевых мономеров, двигающихся диффузионно, одновременно объединяются с кластером (диффузионный или гидродинамический режим).
Далее эволюционирующее газопылевое протопланетное ламинарное облако будем рассматривать как гетерогенный термодинамический комплекс, состоящий из двух взаимопроникающих континуумов, которые заполняют одновременно один и тот же объем евклидова пространства непрерывно − газовой фазы солнечного состава и полидисперсной фазы пылевых частиц (фрактальная среда с нецелой массовой размерностью $D,$ меньшей размерности $n$ координатного пространства задачи), которые находятся при общей абсолютной температуре $T(r,t)$ и давлении $P(r,t).$ Газовую фазу, являющуюся несущей средой, будем описывать моделью идеальной жидкости. В свою очередь, полидисперсную пылевую фазу будем считать фрактальной средой, состоящей из нескольких фракций: фракции первичных пылевых конденсированных мономеров и внедренного в них большого числа фракций фрактальных агрегатов, отличающихся друг от друга размерами. Другими словами, элементарный макрообъем $\delta V$ дисковой среды, помимо несущей газовой фазы, описываемой обычными структурными параметрами, такими как числовая ${{n}_{{\text{g}}}}(r,t)$ и массовая ${{\rho }_{{\text{g}}}}(r,t) = {{n}_{{\text{g}}}}{{m}_{{\text{g}}}}$ плотности (“размазанные” по совокупному элементарному объему смеси), давление ${{P}_{{\text{g}}}}(r,t),$ температура ${{T}_{{\text{g}}}}(r,t),$ гидродинамическая скорость ${{\text{v}}_{{\text{g}}}}(r,t)$ и др., содержит еще множество пылевых фрактальных образований (кластеров), которое можно разбить на $j$ ($j = 1,2,...,Q$) фракций с разными размерами кластеров33. Если пронумеровать эти фракции в порядке возрастания размеров кластеров, то 1-фракция будет содержать первичные мономеры, 2-фракция содержит ассоциации двух мономеров и т.д. В результате мы получим $Q$ фракций со следующими характеристиками:
(3)
$\begin{gathered} m_{j}^{{{\text{с l}}}} = {{n}_{{0j}}}{{m}_{0}},\,\,\,\,{{R}_{j}} = {{r}_{0}}n_{{{\text{0}}j}}^{{1/D}},\,\,\,\,V_{j}^{{{\text{с l}}}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\pi R_{j}^{3}, \\ N_{j}^{{{\text{с l}}}}(r,t),\,\,\,\,\rho _{j}^{{{\text{с l}}}}(r,t) = {{m}_{0}}{{n}_{{0j}}}N_{j}^{{{\text{с l}}}}, \\ \tilde {\rho }_{j}^{{{\text{cl}}}} = {{m_{j}^{{{\text{cl}}}}} \mathord{\left/ {\vphantom {{m_{j}^{{{\text{cl}}}}} {V_{j}^{{{\text{с l}}}}}}} \right. \kern-0em} {V_{j}^{{{\text{с l}}}}}},\,\,\,\,s_{j}^{{{\text{с l}}}}(r,t) = V_{j}^{{{\text{с l}}}}N_{j}^{{{\text{с l}}}}. \\ \end{gathered} $Здесь $D$ – фрактальная размерность отдельного кластера и фрактальной среды в целом; ${{r}_{0}}$ и ${{m}_{0}}$ – радиус и масса первичных мономеров, из которых составлен фрактальный кластер; ${{\rho }_{0}} = {{3{{m}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{3{{m}_{{\text{0}}}}} {4\pi \,r_{0}^{3}}}} \right. \kern-0em} {4\pi \,r_{0}^{3}}}$ – массовая плотность материала первичных ядер; ${{n}_{{{\text{0}}j}}} = {{({{{{R}_{j}}} \mathord{\left/ {\vphantom {{{{R}_{j}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})}^{D}}$ – число первичных мономеров, входящих в состав $j$-го ФПА; ${{R}_{j}},$ $V_{j}^{{{\text{с l}}}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\pi r_{0}^{3}n_{{0j}}^{{3/D}},$ $m_{j}^{{{\text{с l}}}} = {{m}_{0}}{{({{{{R}_{j}}} \mathord{\left/ {\vphantom {{{{R}_{j}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})}^{D}},$ ${{\text{v}}_{{pj}}}(r,t)$ – соответственно радиус гирации, объем, масса и гидродинамическая скорость ФПА $j$-го сорта; $\rho _{j}^{{{\text{с l}}}}(r,t) = m_{j}^{{{\text{с l}}}}N_{j}^{{{\text{с l}}}},$ $\tilde {\rho }_{j}^{{{\text{с l}}}}(r,t) = {{\rho }_{0}}{{\left( {{{R}_{j}}/{{r}_{0}}} \right)}^{{D - 3}}}$ – соответственно массовая плотность и истинная массовая плотность ФПА $j$-го сорта. $N_{j}^{{{\text{с l}}}}(r,t)$ – числовая плотность ФПА $j$-го сорта (число кластеров в единице объема дисковой среды).
В табл. 1 приведены характерные структурные параметры газовой составляющей диска.
Таблица 1.
Структурные параметры газовой фазы диска
| ${{\Sigma }_{{\text{g}}}} = 152{{({r \mathord{\left/ {\vphantom {r 5}} \right. \kern-0em} 5}\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.}})}^{{ - 3/2}}}$ г см–2 | поверхностная плотность газа |
| $T = 125{{(r{\text{/}}5\,\,{\text{a}}{\text{.}}\,{\text{e}}.{\text{)}}}^{{ - 1/2}}}$ К | температура |
| $r$ | расстояние до центра звезды |
| ${{\rho }_{{\text{g}}}} = {{{{\Sigma }_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{{\text{g}}}}} {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}\,{{H}_{{\text{g}}}}$ | массовая плотность газа |
| ${{H}_{{\text{g}}}} = {{c}_{{\text{g}}}}{\text{/}}{{\Omega }_{K}}$ | газовая шкала высот |
| ${{c}_{{\text{g}}}} = \sqrt {{{kT} \mathord{\left/ {\vphantom {{kT} {{{m}_{{\text{g}}}}}}} \right. \kern-0em} {{{m}_{{\text{g}}}}}}} = 6.7 \times {{10}^{4}}{{({r \mathord{\left/ {\vphantom {r 5}} \right. \kern-0em} 5}\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.)}}}^{{ - 1/4}}}$ см с–1 | изотермическая скорость звука |
| ${{m}_{{\text{g}}}} = 3.9 \times {{10}^{{ - 24}}}$ г | средняя молекулярная масса |
| ${{\Omega }_{K}} = \sqrt {G{{M}_{{{\text{star}}}}}/{{r}^{3}}} = 1.8 \times {{10}^{{ - 8}}}{{(r/5\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.}})}^{{ - 3/2}}}$ рад. с–1 | кеплеровская частота |
| ${{{{H}_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{H}_{{\text{g}}}}} r}} \right. \kern-0em} r} = 0.05{{({r \mathord{\left/ {\vphantom {r 5}} \right. \kern-0em} 5}\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.)}}}^{{1/4}}}$ | |
| $Q = {{{{c}_{{\text{g}}}}{{\Omega }_{K}}} \mathord{\left/ {\vphantom {{{{c}_{{\text{g}}}}{{\Omega }_{K}}} {\pi G{{\Sigma }_{{\text{g}}}}}}} \right. \kern-0em} {\pi G{{\Sigma }_{{\text{g}}}}}}$ | параметр Тумре, описывающий стабильность газового диска |
ДИНАМИЧЕСКИЕ УРАВНЕНИЯ ДЛЯ МОДЕЛИРОВАНИЯ ЭВОЛЮЦИИ ФРАКТАЛЬНОГО ГАЗОПЫЛЕВОГО ДИСКА
Рассмотрим дисковую модель, в которой будем пренебрегать турбулентной диффузией пылевой фазы в газе. Газ и пылевые фрактальные агрегаты образуют $(Q + 1)$ континуумов, которые взаимодействуют друг с другом через аэродинамическое сопротивление. В общем случае пылевые кластеры разных сортов двигаются с разными скоростями, что приводит к столкновительной фрагментации, сопровождаемой взаимным обменом массой, импульсом, моментом импульса и энергией. Однако далее мы будем пренебрегать процессами фрагментации (предполагая малыми относительные скорости (${{\text{v}}_{{pj}}} - {{\text{v}}_{{pk}}}$) столкновения пылевых кластеров) и их воздействием на неустойчивость диска. Тогда система уравнений гетерогенной механики (в системе координат, связанной с центральной плоскостью диска, вращающейся с угловой скоростью ${{\Omega }_{K}} = {{\Omega }_{K}}{{i}_{z}}$ вокруг протоcолнца), описывающая ламинарное движение газа и разномасштабных фрактальных агрегатов пыли в протопланетном диске, имеет вид:
(4)
$\frac{{{{d}_{g}}{{\rho }_{{\text{g}}}}}}{{d{\kern 1pt} t}} + {{\rho }_{{\text{g}}}}\nabla \cdot {{\text{v}}_{{\text{g}}}} = 0,$(5)
$\frac{{{{d}_{j}}{{\rho }_{{pj}}}}}{{d{\kern 1pt} t}} + {{\rho }_{{pj}}}\nabla \cdot {{\text{v}}_{{pj}}} = 0,\,\,\,\,\left( {j = 1,2,...,Q} \right),$(6)
$\begin{gathered} \frac{{{{d}_{{\text{g}}}}{{\text{v}}_{{\text{g}}}}}}{{dt}} + 2{{\Omega }_{K}}({{i}_{z}} \times {{\text{v}}_{{\text{g}}}}) - \Omega _{k}^{2}r = \\ = - \frac{1}{{{{\rho }_{{\text{g}}}}}}\nabla {{P}_{{\text{g}}}} + \nabla \left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{{\left| r \right|}}} \right) - \frac{1}{{{{\rho }_{{\text{g}}}}}}{{F}_{{{\text{gp}}}}}, \\ \end{gathered} $(7)
$\begin{gathered} \frac{{{{d}_{j}}{{\text{v}}_{{pj}}}}}{{dt}} + 2{{\Omega }_{K}}({{{\mathbf{i}}}_{z}} \times {{{\mathbf{v}}}_{{pj}}}) - \Omega _{K}^{2}r = \\ = - \frac{1}{{{{\rho }_{{pj}}}}}\nabla {{P}_{{pj}}} + \nabla \left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{{\left| r \right|}}} \right) + \frac{1}{{{{\rho }_{{pj}}}}}{{F}_{{{\text{g}},pj}}}, \\ (j = 1,2,...,Q), \\ \end{gathered} $(8)
${{\nabla }^{2}}\Phi = 4\pi G\left( {{{\rho }_{{\text{g}}}} + \sum\limits_{j = 1}^Q {{{\rho }_{{pj}}}} } \right).$Здесь ${{{{d}_{l}}(..)} \mathord{\left/ {\vphantom {{{{d}_{l}}(..)} {dt}}} \right. \kern-0em} {dt}} = {{\partial (..)} \mathord{\left/ {\vphantom {{\partial (..)} {\partial t}}} \right. \kern-0em} {\partial t}} + {{\text{v}}_{l}} \cdot \nabla (..)$ – субстанциональная производная для континуума $l;$ $\Phi $ – потенциал самогравитации для газопылевого диска, удовлетворяющий уравнению Пуассона (8); $G$ и ${{M}_{{{\text{star}}}}}$ – гравитационная постоянная и масса протозвезды; $r = {{i}_{x}}x + {{i}_{y}}y + {{i}_{z}}z;$ через x, $y$ и $z$ обозначены соответственно локальные радиальные, азимутальные и высотные координаты;
(9)
${{F}_{{{\text{g,}}p}}} = \sum\limits_{j = 1}^Q {{{F}_{{{\text{g}},pj}}}} \cong - {\kern 1pt} \sum\limits_{j = 1}^Q {k{{T}_{g}}\left[ {\frac{{{\kern 1pt} N_{j}^{{{\text{cl}}}}}}{{{{D}_{{{\text{g}},pj}}}}}({{\text{v}}_{{pj}}} - {{\text{v}}_{{\text{g}}}})} \right]} $Диффузия пылевых фрактальных агрегатов в газе
Перенос ФПА в газопылевом диске определяется их взаимодействием с молекулами несущего газа и двигающимися вместе с ними мелкодисперсными пылевыми частицами, и это взаимодействие имеет различный характер в зависимости от радиуса гирации кластеров и массовой плотности ${{\rho }_{{\text{g}}}}$ газа. В разреженной аэродисперсной среде, когда ${{l}_{{\text{g}}}} \gg {{R}_{j}}$ (где ${{l}_{{\text{g}}}}$ – длина свободного пробега атомов или молекул в газе), сила торможения движущегося пылевого агрегата создается в результате однократных столкновений с ним газовых частиц, что соответствует кинетическому режиму переноса этого агрегата в газовом потоке. В плотном газе, когда ${{l}_{{\text{g}}}} \ll {{R}_{j}},$ в каждый момент времени большое число частиц газа одновременно взаимодействует с кластером, и движение кластера соответствует диффузионному (гидродинамическому) режиму. В случае кинетического режима движения коэффициент диффузии $D_{{{\text{g}},pj}}^{{{\text{kin}}}}$ фрактальных кластеров в газе определяется формулой
(10)
$D_{{{\text{g}},pj}}^{{{\text{kin}}}} = \frac{3}{{8\sqrt {2\pi } }}\frac{{\sqrt {k{{T}_{{\text{g}}}}{{m}_{{\text{g}}}}} }}{{{{\rho }_{{\text{g}}}}}}\frac{1}{{R_{j}^{2}}} = \frac{3}{{8\sqrt {2\pi } }}\frac{{{{c}_{{{\text{g}}s}}}}}{{{{n}_{{\text{g}}}}}}\frac{1}{{R_{j}^{2}}},\,\,\,\,{{l}_{{\text{g}}}} > {{R}_{j}},$(11)
$\begin{gathered} F_{{{\text{g,}}p}}^{{{\text{kin}}}} = \sum\limits_{j = 1}^Q {F_{{{\text{g}},pj}}^{{{\text{kin}}}}} \cong \\ \cong - \frac{{8\sqrt {2\pi } }}{3}{{c}_{{{\text{g}}s}}}{{\rho }_{{\text{g}}}}\sum\limits_{j = 1}^Q {\left[ {R_{j}^{2}N_{j}^{{{\text{cl}}}}({{\text{v}}_{{pj}}} - {{\text{v}}_{{\text{g}}}})} \right]} , \\ {{l}_{{\text{g}}}} > {{R}_{j}} \\ \end{gathered} $В другом предельном случае (в диффузионном режиме движения) коэффициент диффузии фрактальных агрегатов в плотном газе определяется формулой
(12)
$\begin{gathered} D_{{{\text{g}},pj}}^{{{\text{dif}}}} = \frac{{2k{\kern 1pt} {{T}_{{\text{g}}}}}}{{\pi {\kern 1pt} R_{j}^{2}{{\rho }_{{\text{g}}}}{{C}_{{{\text{g}},j}}}\left| {{{w}_{{{\text{g,}}\,p}}}} \right|}} = \frac{{4k{\kern 1pt} {{T}_{{\text{g}}}}}}{{\pi {\kern 1pt} {{R}_{j}}{{\eta }_{{\text{g}}}}{{C}_{{{\text{g}},j}}}{\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}}}, \\ {{l}_{{\text{g}}}} \ll {{R}_{j}}, \\ \end{gathered} $(13)
$\begin{gathered} {{C}_{{{\text{g}},j}}}({\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}) = \frac{{24}}{{{\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}}}{{(1 + 0.27{\text{R}}{{{\text{e}}}_{{{\text{g}},j}}})}^{{0.43}}} + \\ + \,\,0.47\left[ {1 - \exp ( - 0.04{\text{Re}}_{{{\text{g}},j}}^{{0.38}})} \right]. \\ \end{gathered} $В данной работе, как указывалось выше, мы не будем учитывать процессы фрагментации ФПА при столкновениях, поэтому вполне естественно предположить, что относительные скорости ${{w}_{{gj}}}$ столкновения малы (столкновения кластеров с большими относительными скоростями сопровождаются, как известно, их разрушением). Тогда, при малых числах Рейнольдса ${{C}_{{{\text{g}},j}}}({\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}) \cong {{24} \mathord{\left/ {\vphantom {{24} {{\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}_{{{\text{g}},j}}}}},$ коэффициент диффузии кластеров (при гидродинамическом режиме движения) принимает вид:
(14)
$D_{{{\text{g}},pj}}^{{{\text{dif}}}} = \frac{{k{\kern 1pt} {{T}_{{\text{g}}}}}}{{6\pi {\kern 1pt} {{R}_{j}}{{\eta }_{{\text{g}}}}}} = \left( {\frac{{k{\kern 1pt} {{T}_{{\text{g}}}}m_{0}^{{1/D}}}}{{6\pi {\kern 1pt} {{r}_{0}}{{\eta }_{{\text{g}}}}}}} \right){{\left( {m_{j}^{{{\text{cl}}}}} \right)}^{{ - 1/D}}},\,\,\,\,{{l}_{{\text{g}}}} \ll {{R}_{j}},$(15)
$\begin{gathered} F_{{{\text{g}},p}}^{{{\text{dif}}}} = \sum\limits_{j = 1}^Q {F_{{{\text{g}},pj}}^{{{\text{dif}}}}} = 6\pi {{\eta }_{{\text{g}}}}\sum\limits_{j = 1}^Q {\left[ {N_{j}^{{{\text{cl}}}}{{R}_{{{\text{g}}j}}}({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}})} \right]} {\kern 1pt} \, = \\ = \frac{{6\pi {{\eta }_{{\text{g}}}}{{r}_{0}}}}{{m_{0}^{{1/D}}}}\sum\limits_{j = 1}^Q {\left[ {N_{j}^{{{\text{cl}}}}{{{\left( {m_{j}^{{{\text{cl}}}}} \right)}}^{{1/D}}}{\kern 1pt} ({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}})} \right]} . \\ \end{gathered} $Заметим, что в протопланетном диске на расстоянии $r = 1\,\,{\text{а }}{\text{.}}\,{\text{е }}{\text{.}}$ длина свободного пробега частиц газа ${{l}_{{\text{g}}}} \approx 1\,\,{\text{с м }},$ а на расстоянии $r = 10\,\,{\text{а }}{\text{.}}\,{\text{е }}.$ ${{l}_{{\text{g}}}} \approx 1\,\,{\text{м }}.$ По этой причине пылевые агрегаты с размерами $1 - 100\,\,{\text{с м }}$ находятся в стоксовом режиме торможения на $1\,\,{\text{а }}{\text{.}}\,{\text{е }}.$ и в режиме Эпстейна на $10\,\,{\text{а }}{\text{.}}\,{\text{е }}.$
Формулы (10) и (12) для коэффициентов диффузии кластеров в диффузионном и кинетическом режимах удобно объединить и использовать для коэффициента диффузии пылевых образований в газовом потоке следующее соотношение:
(16)
$\begin{gathered} {{D}_{{{\text{g}},pj}}} = D_{{{\text{g}},pj}}^{{{\text{dif}}}} + D_{{{\text{g}},pj}}^{{{\text{kin}}}} = \frac{{k{{T}_{{\text{g}}}}}}{{6\pi {\kern 1pt} {{\eta }_{{\text{g}}}}{{R}_{j}}}}\left( {1 + \frac{{15\pi }}{{32\sqrt 2 }}\frac{{{{l}_{{\text{g}}}}}}{{{{R}_{j}}}}} \right) \cong \\ \cong \frac{{k{\kern 1pt} {{T}_{{\text{g}}}}}}{{4\sqrt {2\pi } {{с }_{{s{\text{g}}}}}{{\rho }_{{\text{g}}}}\,R_{j}^{2}}}\left( {\frac{1}{{K{{n}_{j}}}}\, + 1.5} \right), \\ \end{gathered} $(17)
$\begin{gathered} {{F}_{{{\text{g,}}p}}} = \sum\limits_{j = 1}^Q {{{F}_{{{\text{g}},pj}}}} \cong - k{{T}_{{\text{g}}}}{\kern 1pt} \sum\limits_{j = 1}^Q {\left[ {\frac{{{\kern 1pt} N_{j}^{{{\text{cl}}}}}}{{{{D}_{{{\text{g}},pj}}}}}({{\text{v}}_{{pj}}} - {{\text{v}}_{{\text{g}}}})} \right]} \cong \\ \cong - \,4\sqrt {2\pi } {{c}_{{{\text{g}}s}}}{{\rho }_{{\text{g}}}}\sum\limits_{j = 1}^Q {\left[ {\frac{{{\kern 1pt} \,R_{j}^{2}N_{j}^{{{\text{cl}}}}}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {K{{n}_{j}}}}} \right. \kern-0em} {K{{n}_{j}}}} + 1.5} \right)}}({{\text{v}}_{{pj}}} - {{\text{v}}_{{\text{g}}}})} \right]} . \\ \end{gathered} $Важно отметить, что формула (17) при численном моделировании эволюции протопланетного облака позволяет учитывать плавный переход от кинетического режима к диффузионному режиму взаимодействия пылевых агрегатов с газом по мере увеличения как плотности газовых частиц ${{n}_{{\text{g}}}},$ так и радиусов гирации ${{R}_{j}}$ ФПА при их оседании к центральной плоскости диска, причем этот переход управляется параметром ${{n}_{{\text{g}}}}{{R}_{j}}.$
Ограничения на размеры пылевых фрактальных агрегатов, при которых справедлив закон Стокса
При написании формул (12) и (13) мы предположили, что соответствующие числа Рейнольдса малы. Выясним, при каких максимальных размерах пылевых агрегатов это допущение справедливо, на примере их свободного квазистационарного оседания в газе к центральной плоскости диска под влиянием $z$-компоненты силы тяготения Солнца ${{g}_{z}} = \Omega _{k}^{2}\,z$ (здесь ${{\Omega }_{k}}$ – кеплеровская угловая скорость на экваториальной плоскости диска). При указанных условиях уравнение движение $j$-кластера (7) сводится к виду
(18)
$6\pi {\kern 1pt} {{R}_{j}}{{\eta }_{{\text{g}}}}{{\left. {{{w}_{{{\text{g}}p}}}} \right|}_{z}} = {{g}_{z}}m_{j}^{{{\text{cl}}}} = {{g}_{z}}\left( {{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\pi {{\rho }_{{\text{0}}}}r_{0}^{{3 - D}}} \right)R_{j}^{D}.$Отсюда для скорости гравитационного оседания (вдоль оси $z$) одиночного ФПА $j$-го сорта в газопылевом диске будем иметь
(19)
$\begin{gathered} {{\left. {{{w}_{{{\text{g}}j}}}} \right|}_{z}} \equiv - {{u}_{{zj}}} = \Omega _{k}^{2}\,z\left( {\frac{{2{{\rho }_{0}}}}{{9{{\eta }_{{\text{g}}}}}}r_{0}^{{3 - D}}} \right){\kern 1pt} R_{j}^{{D - 1}} = \\ = \Omega _{K}^{2}\,z\left( {\frac{{m_{0}^{{1/D}}}}{{6\pi {\kern 1pt} {{r}_{0}}{{\eta }_{{\text{g}}}}}}} \right){{(m_{j}^{{{\text{с l}}}})}^{{1 - 1/D}}}. \\ \end{gathered} $Определим число Рейнольдса формулой ${{\operatorname{Re} }_{{{\text{g}},j}}} = \;2{{R}_{j}}{{{{u}_{{zj}}}} \mathord{\left/ {\vphantom {{{{u}_{{zj}}}} {{{\nu }_{{\text{g}}}}}}} \right. \kern-0em} {{{\nu }_{{\text{g}}}}}};$ тогда условие на радиус гирации ФПА, при выполнении которого число Рейнольдса мало (${{\operatorname{Re} }_{{{\text{g}},j}}} \ll 1$), имеет вид: $1 \gg {\text{R}}{{{\text{e}}}_{{{\text{g}},j}}} = {{g}_{z}}\left( {4{{\rho }_{0}}{{r_{0}^{{3 - D}}} \mathord{\left/ {\vphantom {{r_{0}^{{3 - D}}} {9\eta _{{\text{g}}}^{2}}}} \right. \kern-0em} {9\eta _{{\text{g}}}^{2}}}} \right)R_{j}^{D},$ откуда
(20)
${{R}_{j}} \ll r_{0}^{{1 - 3/D}}{{\left( {{{9\eta _{{\text{g}}}^{2}} \mathord{\left/ {\vphantom {{9\eta _{{\text{g}}}^{2}} {4{{\rho }_{0}}}}} \right. \kern-0em} {4{{\rho }_{0}}}}{{g}_{z}}{{\rho }_{{\text{g}}}}} \right)}^{{1/D}}}.$Это неравенство позволяет оценить максимальный размер стоксовских пылевых агрегатов. Из этой оценки (менее жесткой по сравнению с оценкой ${{R}_{j}} \ll {{\left( {{{9\eta _{{\text{g}}}^{2}} \mathord{\left/ {\vphantom {{9\eta _{{\text{g}}}^{2}} {4{{g}_{z}}{{\rho }_{{\text{g}}}}{{\rho }_{0}}}}} \right. \kern-0em} {4{{g}_{z}}{{\rho }_{{\text{g}}}}{{\rho }_{0}}}}} \right)}^{{1/3}}}$ для компактных тел) следует, в частности, что в гравитационном поле пушистые фрактальные агрегаты оседают значительно медленнее, чем компактные частицы той же массы.
Следует отметить, что в силу структурных особенностей кластеров сила сопротивления газовой среды более точно определяется рассеянием ее частиц на первичных ядрах фрактальных агрегатов (см. Михайлов, Власенко, 1995). Соответственно этому механизму рассеяния длина свободного пробега мономеров ${{\lambda }_{{\text{0}}}}$ внутри кластера (при средней плотности числа мономеров входящих в кластер ${{\langle n\rangle }_{{0,j}}} = {{{{n}_{{0,j}}}} \mathord{\left/ {\vphantom {{{{n}_{{0,j}}}} {V_{j}^{{{\text{с l}}}}}}} \right. \kern-0em} {V_{j}^{{{\text{с l}}}}}} = {{3R_{j}^{{D - 3}}} \mathord{\left/ {\vphantom {{3R_{j}^{{D - 3}}} {4\pi \,r_{0}^{D}}}} \right. \kern-0em} {4\pi \,r_{0}^{D}}}$) определяется соотношением
(21)
${{l}_{{j0}}} = {1 \mathord{\left/ {\vphantom {1 \pi }} \right. \kern-0em} \pi }r_{0}^{2}{{n}_{{0,j}}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}{{R}_{j}}{{\left( {\,{{r}_{0}}/{{R}_{j}}} \right)}^{{\,D - 2}}},$Массовую размерность $D$ определяют, как правило, на основе численного моделирования поведения кластера в гравитационном (или электрическом) поле с помощью “in situ”-методов процесса его сборки. Эти методы различаются специфическими деталями кластер-кластерной агрегации, к которым, в частности, относятся: характер движения кластеров (прямолинейное или броуновское), характер объединения кластеров в зависимости от вероятности слипания ${{\kappa }^{{\text{P}}}}$ при их взаимном касании, наличие или отсутствие полного реструктуринга (при котором кластеры связываются в трех точках), нарушение изотропии объединяемых кластеров, связанное с наведенным электрическим диполем во внешнем электрическом поле или наведенным магнитным моментом во внешнем магнитном поле, несферичность сталкивающихся кластеров, наличие вращательной диффузии ФПА, приводящей к захвату налетающего кластера краями образуемого пылевого агрегата (что способствует уменьшению его фрактальной размерности) и т.п. В табл. 2 представлены значения фрактальной размерности кластеров, образующихся в трехмерном пространстве при различных механизмах роста.
Таблица 2.
Фрактальная размерность кластера, образующегося при ассоциации твердых частиц (Смирнов, 1991)
| Модель агрегации | Вероятность прилипания, ${{\kappa }^{{\text{P}}}}$ |
Фрактальная размерность |
|---|---|---|
| Прямолинейная траектория, кластер–частица | 1 | 2.97 ± 0.08 |
| Броуновское движение, кластер–частица | 1 0.25 | 2.51 ± 0.06 2.48 ± 0.12 |
| Прямолинейная траектория, кластер–кластер | 1 | 2.00 ± 0.05 |
| Броуновское движение, кластер–кластер | 1 | 1.78 ± 0.05 |
| Кластер–кластер, малая вероятность прилипания (RLCA-модель) | ${{\kappa }^{{\text{P}}}} < 1$ | 2.11 ± 0.03 |
Итак, с учетом формулы (15), уравнения движения (6) и (7) для газа и совокупности пылевых гранул могут быть переписаны следующим образом:
(22)
$\begin{gathered} \frac{{\partial {{\text{v}}_{{\text{g}}}}}}{{\partial t}} + {{\text{v}}_{{\text{g}}}} \cdot \nabla {{\text{v}}_{{\text{g}}}} + 2{{\Omega }_{K}}({{i}_{z}} \times {{\text{v}}_{{\text{g}}}}) - \Omega _{k}^{2}r = \\ = - \frac{{\nabla {{P}_{{\text{g}}}}}}{{{{\rho }_{{\text{g}}}}}} + \frac{1}{{{{\rho }_{{\text{g}}}}}}\sum\limits_{j = 1}^Q {\frac{{{{\rho }_{{pj}}}({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}})}}{{{{\tau }_{{{\text{stop}},j}}}}}} + \nabla \left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{r}} \right), \\ \end{gathered} $(23)
$\begin{gathered} \frac{{\partial {{\text{v}}_{{pj}}}}}{{\partial t}} + {{\text{v}}_{{pj}}} \cdot \nabla {{\text{v}}_{{pj}}} + 2{{\text{v}}_{{pj}}} \times {{\Omega }_{K}} - \Omega _{K}^{2}r = \\ = - \frac{{\nabla {{P}_{{pj}}}}}{{{{\rho }_{{pj}}}}}\, + \,\,\frac{{{{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}}}}{{{{\tau }_{{{\text{stop}},j}}}}} + \nabla \left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{{\left| r \right|}}} \right), \\ \end{gathered} $Здесь
(24)
$\begin{gathered} {{\tau }_{{{\text{stop}},j}}}{\kern 1pt} \equiv \frac{{{{\rho }_{{\text{p}}}}\left| {{{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}}} \right|}}{{\left| {{{F}_{{{\text{g}},pj}}}} \right|}} = \frac{{{{\rho }_{{pj}}}}}{{6\pi {{\eta }_{{\text{g}}}}}}{{\left[ {N_{j}^{{{\text{cl}}}}{{R}_{j}}} \right]}^{{ - 1}}} = \\ = \frac{1}{{4\sqrt {2\pi } {{с }_{{s{\text{g}}}}}}}\frac{{{{\rho }_{{pj}}}}}{{{{\rho }_{{\text{g}}}}}}{{\left[ {\frac{{{\kern 1pt} \,R_{j}^{2}N_{j}^{{{\text{cl}}}}}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {K{{n}_{j}}}}} \right. \kern-0em} {K{{n}_{j}}}} + 1.5} \right)}}} \right]}^{{ - 1}}} \\ \end{gathered} $На основе этой системы уравнений проанализируем далее дисперсионные свойства осесимметричных возмущений в плоскости тонкого газопылевого слоя протопланетного диска.
ДИНАМИКА ВОЗМУЩЕНИЙ В ПЛОСКОСТИ ДИСКА
Основные безразмерные параметры гидродинамической неустойчивости в плоском газопылевом слое
Гидродинамическая неустойчивость газопылевой среды в плоскости диска и способность твердых пылевых образований (кластеров, гранул, комков) гравитационно уплотняться управляются некоторым числом безразмерных параметров, среди которых ключевое значение имеет параметр металличности $\Gamma = \sum\nolimits_{j = 1}^Q {{{\Gamma }_{j}}} \,$ = = $\sum\nolimits_{j = 1}^Q {{{{{\Sigma }_{{pj}}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{{pj}}}} {{{\Sigma }_{{\text{g}}}}}}} \right. \kern-0em} {{{\Sigma }_{{\text{g}}}}}}} = {{{{\Sigma }_{p}}} \mathord{\left/ {\vphantom {{{{\Sigma }_{p}}} {{{\Sigma }_{{\text{g}}}}}}} \right. \kern-0em} {{{\Sigma }_{{\text{g}}}}}},$ являющийся суммой отношений поверхностных плотностей пылевых фракций ${{\Sigma }_{{pj{\text{/g}}}}} = \sqrt {2\pi } {{\rho }_{{pj{\text{/g}}}}}{{H}_{{pj{\text{/g}}}}}$ и газовой ${{\Sigma }_{{\text{g}}}}$ компоненты дисковой среды. При значении параметра $\Gamma $ в протопланетном диске порядка ${{10}^{{ - 2}}},$ совокупная пылевая фаза динамически не влияет на движение газовой фазы, в то время как газ сильно воздействует на гидродинамику пыли. Здесь ${{H}_{{pj{\text{/g}}}}} = {{{{c}_{{pj{\text{/g}}}}}} \mathord{\left/ {\vphantom {{{{c}_{{pj{\text{/g}}}}}} {{{\Omega }_{K}}}}} \right. \kern-0em} {{{\Omega }_{K}}}}$ – высоты однородной атмосферы для отдельных пылевых фракций и газовой фазы, причем согласно (Youdin, Lithwick, 2007)
В эту формулу входит второй из ключевых параметров – безразмерное число Стокса для $j$-й пылевой фракции
где ${{\Omega }_{k}} = \sqrt {{{G{{M}_{{{\text{star}}}}}} \mathord{\left/ {\vphantom {{G{{M}_{{{\text{star}}}}}} {{{{\left| r \right|}}^{3}}}}} \right. \kern-0em} {{{{\left| r \right|}}^{3}}}}} $ – кеплеровская угловая скорость (равная характерной частоте колебаний звезды поперек плоскости диска), $r$ – центральный радиус-вектор,${{\tau }_{{{\text{stop}},j}}}$ – время торможения пылевых агрегатов $j$-й фракции в газовом потоке55. Точное значение параметра ${\text{S}}{{{\text{t}}}_{j}}$ зависит как от размеров пылевых агрегатов, так и от их радиального местоположения (Chiang, Youdin, 2010). Время торможения ${{\tau }_{{{\text{stop}},j}}}$ пылевых агрегатов определяется формулой (24), а для плоского слоя (см. (29)).В случае, если число Стокса для $j$-й пылевой фракции $1 \ll {\text{St}} \ll {\alpha }_{{\text{g}}}^{{ - {\text{1}}}},$ то
Здесь
В работе (Pinte и др., 2016) показано, что численное значение параметра ${{\alpha }_{p}}$ для пылевого слоя, вычисленное с учетом шкалы высот для пыли в субдиске, отличается от стандартной альфа-параметризации интенсивности αg при глобальной турбулентности, имеющей место во всем протопланетном диске, равной ${{{\alpha }}_{{\text{g}}}} \approx {{10}^{{ - 2}}},$ тогда как ${{{\alpha }}_{p}} \approx 3 \times {{10}^{{ - 4}}}.$
Третий важный параметр ${{\zeta }_{j}} = {{c_{{pj}}^{2}} \mathord{\left/ {\vphantom {{c_{{pj}}^{2}} {c_{{s{\text{g}}}}^{2}}}} \right. \kern-0em} {c_{{s{\text{g}}}}^{2}}}$ – отношение дисперсий скоростей пылевой и газовой составляющих гетерогенного потока. Заметим, что в первом приближении, пульсации скоростей пылевых частиц связаны со свойствами турбулентности несущей газовой фазы, а не с межагрегатными столкновениями
Четвертый параметр
Базовые уравнения гетерогенной механики в плоскости тонкого диска
Будем далее считать, что исходные уравнения двухфазной газопылевой гидродинамики осреднены по вертикальной толщине газопылевого диска. Будем также пренебрегать возможными осложнениями (например, сдвиговой неустойчивостью и турбулентностью), возникающими на масштабах, меньших шкалы высот для пыли ${{H}_{{pj}}} = {{{{c}_{{pj}}}} \mathord{\left/ {\vphantom {{{{c}_{{pj}}}} {{{\Omega }_{K}}.}}} \right. \kern-0em} {{{\Omega }_{K}}.}}$ Кроме этого будем предполагать, что дисперсия скорости газа ${{c}_{{\text{g}}}}$ и соответствующая шкала высот ${{H}_{{\text{g}}}} = {{c}_{{s{\text{g}}}}}/{{\Omega }_{K}}$ конечны, а слои пылевых фракций в субдиске находятся внутри газовой оболочки, так что $c_{{pj}}^{{}} < {{c}_{{sg}}}$ и ${{H}_{{pj}}} < {{H}_{{\text{g}}}}.$
Принимая локальную модель “обрезанной” коробки для диска (см. Goldreich, Lynden-Bell, 1965), мы сосредоточимся на рассмотрении окрестности точки $(r,\theta ) = ({{r}_{0}},{{\Omega }_{K}}t)$ в цилиндрических координатах. При этом радиальная и азимутальная координаты имеют вид: $(x,y) = (r - {{r}_{0}},\,\,{{r}_{0}}(\theta - {{\Omega }_{K}}t)),$ а кеплеровская частота ${{\Omega }_{K}} = \sqrt {{{G{{M}_{ \odot }}} \mathord{\left/ {\vphantom {{G{{M}_{ \odot }}} {r_{0}^{3}}}} \right. \kern-0em} {r_{0}^{3}}}} .$ Ограничимся стационарным фоном газопылевой среды с равномерным распределением плотностей пыли и газа (${{\Sigma }_{{pj0}}} = {\text{const}},$ ${{\Sigma }_{{{\text{g}}0}}} = {\text{const}}$). Тогда осредненные по высоте $z$ уравнения гетерогенной механики (5), (6), (22) и (23), используемые далее для изучения дисперсионных свойств возмущений в плоскости тонкого диска, принимают вид:
(25)
$\frac{{\partial {{\Sigma }_{{\text{g}}}}}}{{\partial {\kern 1pt} t}} + {{\nabla }_{ \bot }} \cdot ({{\Sigma }_{{\text{g}}}}{{\text{v}}_{{\text{g}}}}) = 0,$(26)
$\begin{gathered} \frac{{\partial {{\text{v}}_{{\text{g}}}}}}{{\partial t}} + {{\text{v}}_{{\text{g}}}} \cdot {{\nabla }_{ \bot }}{{\text{v}}_{{\text{g}}}} + 2{{\Omega }_{K}}({{\text{v}}_{{\text{g}}}} \times {{i}_{z}}) - \Omega _{K}^{2}r = \\ = - \frac{{c_{{s{\text{g}}}}^{2}}}{{{{\Sigma }_{{\text{g}}}}}}{{\nabla }_{ \bot }}{{\Sigma }_{{\text{g}}}} + {{\nabla }_{ \bot }}\left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{{\left| r \right|}}} \right) + \\ + \,\,\sum\limits_{j = 1}^Q {\frac{{{{\Gamma }_{{pj}}}({{\text{v}}_{{pj}}} - {{\text{v}}_{{\text{g}}}})}}{{\tau _{{{\text{stop}},j}}^{{2d}}}},} \\ \end{gathered} $(27)
$\frac{{\partial {{\Sigma }_{p}}}}{{\partial {\kern 1pt} t}} + {{\nabla }_{ \bot }} \cdot ({{\Sigma }_{p}}{{\text{v}}_{p}}) = 0,$(28)
$\begin{gathered} \frac{{\partial {{\text{v}}_{{pj}}}}}{{\partial t}} + ({{\text{v}}_{{pj}}} \cdot {{\nabla }_{ \bot }}){{\text{v}}_{{pj}}} + 2{{\Omega }_{K}}({{\text{v}}_{{pj}}} \times {{i}_{z}}) - \Omega _{k}^{2}r = \\ = - \frac{{c_{{pj}}^{2}}}{{{{\Sigma }_{{pj}}}}}{{\nabla }_{ \bot }}{{\Sigma }_{{pj}}} + {{\nabla }_{ \bot }}\left( {\Phi - \frac{{G{{M}_{{{\text{star}}}}}}}{{\left| r \right|}}} \right) + \frac{{({{\text{v}}_{{\text{g}}}} - {{\text{v}}_{{pj}}})}}{{\tau _{{{\text{stop}},j}}^{{2d}}}}, \\ \end{gathered} $(29)
$\tau _{{{\text{stop}},j}}^{{2d}} = \frac{\pi }{{2{{\Sigma }_{{\text{g}}}}{{\Omega }_{K}}}}{{\left[ {\frac{{{\kern 1pt} \,{{\rho }_{{pj}}}R_{j}^{2}N_{j}^{{{\text{cl}}}}}}{{\left( {{1 \mathord{\left/ {\vphantom {1 {K{{n}_{j}}}}} \right. \kern-0em} {K{{n}_{j}}}} + 1.5} \right)}}} \right]}^{{ - 1}}}$Система уравнений (25)–(28) должна быть дополнена осредненным по высоте уравнением Пуассона
Здесь $\delta z$ – дельта-функция.Линейные возмущения движения дисковой газопылевой среды
Для изучения динамики малых возмущений линеаризуем систему (25)–(28), для чего представим входящие в нее переменные в виде сумм равновесных и возмущенных величин:
В случае пренебрежения нелинейными членами (квадратичными по амплитуде) и всеми пространственными производными от стационарных величин, малыми по сравнению с производными от возмущенных величин в системе (25)–(28), можно получить систему линеаризованных уравнений гетерогенной механики для описания малых колебаний вращающегося газопылевого диска. Будем далее считать, что радиальные возмущения осесимметричного газопылевого слоя имеют вид монохроматической волны, т.е. зависимость возмущенных величин $\delta \chi $ от радиальной координаты $x$ и времени $t$ пропорциональна $\exp ( - i\omega t + ikx),$ где $\omega $ – круговая частота монохроматической волны с длиной волны $\lambda = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {\left| k \right|}}} \right. \kern-0em} {\left| k \right|}};$ $k$ – волновое число; $\left| k \right| = \sqrt {k_{x}^{2} + k_{y}^{2}} $ (частота $\omega $ и волновое число $k$ могут быть комплексными величинами). В этом случае линеаризованная указанным выше способом система (25)–(29) перейдет в следующую систему алгебраических уравнений:
(31)
$ - i\omega \delta {{\Sigma }_{{\text{g}}}} + ik{{\Sigma }_{{{\text{g}}0}}}{\kern 1pt} {\kern 1pt} \delta {{\text{v}}_{{{\text{g}}x}}} = 0,$(32)
$\begin{gathered} - i\omega \,\delta {{\text{v}}_{{{\text{g}}x}}} - 2{{\Omega }_{K}}\delta {{\text{v}}_{{{\text{g}}y}}} = - c_{{s{\text{g}}}}^{2}\frac{{i{\kern 1pt} k\delta {{\Sigma }_{{\text{g}}}}}}{{{{\Sigma }_{{{\text{g}}0}}}}} - \\ - \,\,ik\delta \Phi + \sum\limits_{j = 1}^Q {{{\Gamma }_{{j0}}}} \frac{{\delta {{\text{v}}_{{px}}} - \delta \text{v}_{{{\text{g}}x}}^{'}}}{{\tau _{{{\text{stop}},j}}^{{2d}}}}, \\ \end{gathered} $(33)
$ - i\omega \,\delta {{\text{v}}_{{{\text{g}}y}}} + \frac{1}{2}{{\Omega }_{K}}\delta {{\text{v}}_{{{\text{g}}x}}} = \sum\limits_{j = 1}^Q {{{\Gamma }_{{j0}}}} \frac{{\delta {{\text{v}}_{{{\text{g}}x}}} - \delta {{\text{v}}_{{px}}}}}{{\tau _{{{\text{stop}},j}}^{{2d}}}},$(34)
$ - i\omega {\kern 1pt} \,\delta {{\Sigma }_{{pj}}} + i\,k{{\Sigma }_{{pj}}}_{0}\delta {\kern 1pt} {{\text{v}}_{{pjx}}} = 0,\,\,\,\,\left( {j = 1,2,...Q} \right),$(35)
$\begin{gathered} - i\omega \,\delta {{\text{v}}_{{pj,x}}} - 2{{\Omega }_{K}}\delta {{\text{v}}_{{pj,y}}} = - c_{{pj}}^{2}\frac{{ik\delta {{\Sigma }_{{pj}}}}}{{{{\Sigma }_{{pj,0}}}}} - \\ - \,\,ik\delta \Phi + \frac{{\delta {{\text{v}}_{{{\text{g}}x}}} - \delta {{\text{v}}_{{pj,x}}}}}{{\tau _{{{\text{stop}},j}}^{{2d}}}},\,\,\,\,\left( {j = 1,2,...Q} \right), \\ \end{gathered} $(36)
$\begin{gathered} - i\omega \delta {{\text{v}}_{{pj,y}}} + \frac{{{{\Omega }_{K}}}}{2}\delta {{\text{v}}_{{pj,x}}} = \frac{{\delta {{\text{v}}_{{{\text{g}}x}}} - \delta {{\text{v}}_{{pj,x}}}}}{{\tau _{{{\text{stop}},j}}^{{2d}}}}, \\ \left( {j = 1,2,...Q} \right), \\ \end{gathered} $(37)
$\delta \Phi = - \,\frac{{2\pi G}}{{\left| k \right|}}\left( {\delta {{\Sigma }_{{\text{g}}}} + \sum\limits_{j = 1}^Q {\delta {{\Sigma }_{{pj}}}} } \right).$Заметим, что если учитывать влияние на гравитационный потенциал $\Phi $ толщин пылевого и газового слоев, то уравнение (37) следует переписать в виде (Shu, 1984):
(37a)
$\delta \Phi = - \,\frac{{2\pi G}}{{\left| k \right|}}\left( {\frac{{\delta {{\Sigma }_{{\text{g}}}}}}{{1 + \left| k \right|{{H}_{{\text{g}}}}}} + \sum\limits_{j = 1}^Q {\frac{{\delta {{\Sigma }_{{pj}}}}}{{1 + \left| k \right|{{H}_{{pj}}}}}} } \right),$Система (31)–(37) является исходной для дальнейшего анализа динамики малых линейных возмущений в рассматриваемой модели газопылевого диска с произвольным распределением величин ${{\Sigma }_{{pj,0}}},$ ${{\Sigma }_{{{\text{g0}}}}},$ ${{c}_{{pj{\text{/g}}}}},$ ${{\Phi }_{0}}.$ На основе этой системы уравнений возможно, вообще говоря, получить в явном виде дисперсионное соотношение для изучения неустойчивости тонкого слоя. Однако вывод этого соотношения в общем случае – процедура чрезвычайно трудоемкая. По этой причине ограничимся здесь (для простоты) рассмотрением двухжидкостной дисковой среды, состоящей из газа и совокупной пылевой фазы, полагая, что все пылевые фракции двигаются с одинаковой скоростью, ${{\text{v}}_{{pj}}} = {{\text{v}}_{p}}.$
Дисперсионное соотношение
Далее будем использовать обозначение $n = - i\omega .$ Очевидно, что неустойчивость возникает (возмущения растут), если величина $\operatorname{Re} [n]$ становится положительной. Приравнивая к нулю определитель системы алгебраических уравнений (31)–(37), после несложных преобразований получим следующее дисперсионное уравнение 5-го порядка по $n{\text{:}}$
которое описывает линейные возмущения гидродинамических параметров в плоскости вращающегося газопылевого диска с учетом влияния на его структуру давлений в фазах и эффекта аэродинамического трения. Здесь(40)
${{A}_{3}} = \frac{{A_{4}^{2}}}{4} + 2\left[ {\Omega _{K}^{2} + kc_{{s{\text{g}}}}^{2} - \pi G(2{{\Sigma }_{{{\text{g}}0}}} + {{\Sigma }_{p}})\left| k \right|} \right],$(41)
$\begin{gathered} {{A}_{2}} = \frac{{{{A}_{4}}}}{2}\left\{ {2\left[ {\Omega _{K}^{2} - 2\pi {{\Gamma }_{0}}G({{\Sigma }_{{{\text{g}}0}}} + {{\Sigma }_{{p0}}})} \right.} \right. \times \\ \times \,\,\left. {\left. {\left| k \right| + {{k}^{2}}(c_{{s{\text{g}}}}^{2} + c_{p}^{2})} \right] - c_{p}^{2}{{k}^{2}}} \right\}, \\ \end{gathered} $(42)
$\begin{gathered} {{A}_{1}} = {{k}^{2}}c_{p}^{2}\left( {\Omega _{K}^{2} + c_{{s{\text{g}}}}^{2}{{k}^{2}}} \right) + \\ + \,\,{{\Omega }_{K}}\left( {\Omega _{K}^{2} - 2\pi G{{\Sigma }_{{{\text{g}}0}}}\left| k \right| + c_{{s{\text{g}}}}^{2}{{k}^{2}}} \right) - \\ - \,\,2\left( {c_{{s{\text{g}}}}^{2} + c_{p}^{2}} \right){{k}^{2}}\pi G{{\Sigma }_{{{\text{g}}0}}}\left| k \right| + \frac{{A_{4}^{2}}}{{4(1 + {{\gamma }_{0}})}} \times \\ \times \,\,\left[ {(1 + {{\Gamma }_{0}})\left( {\Omega _{K}^{2} - 2\pi G{{\Sigma }_{{{\text{g}}0}}}\left| k \right| + c_{{s{\text{g}}}}^{2}{{k}^{2}}} \right)} \right. + \\ + \,\,\left. {{{\Gamma }_{0}}{{k}^{2}}\left( {c_{p}^{2} - c_{{s{\text{g}}}}^{2}} \right)} \right], \\ \end{gathered} $(43)
$\begin{gathered} {{A}_{0}} = {{k}^{2}}{{\Omega }_{K}}{\text{St}}\left\{ {{{\Gamma }_{0}}\left[ {c_{{s{\text{g}}}}^{2}\Omega _{K}^{2} - 2\pi G({{\Sigma }_{{{\text{g}}0}}} + {{\Sigma }_{{p{\text{0}}}}})\left| k \right|} \right]} \right. + \hfill \\ + \,\,c_{p}^{2}\left. {\left[ {\Omega _{K}^{2} - 2\pi G({{\Sigma }_{{{\text{g0}}}}} + {{\Sigma }_{{p{\text{0}}}}})\left| k \right| + (1 + {{\Gamma }_{0}})c_{{s{\text{g}}}}^{2}{{k}^{2}}} \right]} \right\}, \hfill \\ \end{gathered} $С помощью уравнений, полученных на основании системы (25)–(30), возможно изучение как классических неустойчивостей (таких как гравитационная неустойчивость (GI), вековая гравитационная неустойчивость (SGI), потоковая неустойчивость (SI)), так и ряда новых неустойчивостей двухфазного газопылевого потока, например, резонансных неустойчивостей сопротивления (Resonant Drag Instabilities), некоторые из них могут иметь важное значение для образования планетезималей (Squire, Hopkins, 2018a; 2018b). При этом нахождение критериев возникновения тех или других гидродинамических неустойчивостей в газопылевом слое основано на существенном упрощении дисперсионного уравнения (38), возможного при использовании численных значений безразмерных параметров (таких, как ${\text{St}},$ ${{\Gamma }_{0}},$ $\zeta ,$ ${{Q}_{{p{\text{/g}}}}},$ ${{\alpha }_{{p{\text{/g}}}}},$ ${{H}_{{p{\text{/g}}}}}$ и др.), характерных для той или иной области протопланетного диска (см., например, Youdin, 2005а; 2005b; 2011; Youdin, Lithwick, 2007; Takahashi, Inutsuka, 2014; 2016; Carrera и др., 2015; 2017; Зиглина, Макалкин, 2016).
Оставляя строгий количественный анализ системы (38)–(43) на будущее численное моделирование, проиллюстрируем возможности этого подхода на простом примере аналитического определения условий возникновения гидродинамических неустойчивостей в тонком субдиске в случае, когда нет заметного обратного влияния пыли на орбитальное движение газа.
ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ ТОНКОГО ГАЗОПЫЛЕВОГО СЛОЯ
По современным представлениям гидродинамическая неустойчивость двухфазной газопылевой дисковой среды, связанная с ростом возмущений плотности макроскопических пылевых агрегатов, является естественным механизмом формирования планетезималей в областях протопланетного диска с высокой металличностью $\Gamma $ (Youdin, Goodman, 2005). Эта неустойчивость вызвана различием в скоростях пылевой и газовой фаз в диске, благодаря чему пылевые частицы быстро концентрируются в умеренно плотном пылевом слое (субдиске) в виде локализованных плотных глыб, перестающих дрейфовать к Солнцу. В результате возникающей потоковой неустойчивости в субдиске создаются необходимые условия для генерации растущих возмущений плотности макроскопических пылевых агрегатов (и последующего разрушения субдиска), в отличие от более мелких пылевых частиц (${\text{St}} \gg 1$) (с плохой обратной связью с газом по аэродинамическому сопротивлению ($\Gamma \ll 1$)), для которых характерны низкие темпы роста линейных возмущений66. В работах (Carrera и др., 2015; 2017) найдены зависящие от параметров $\Gamma $ и ${\text{St}}$ условия возникновения потоковой неустойчивости и указана область значений этих параметров, где она особенно активна.
Линейные возмущения движения пыли в субдиске
Рассмотрим плоский пылевой субдиск, в котором возникает гидродинамическая неустойчивость. Характерная шкала расстояний в субдиске составляет приблизительно 5% от газовой шкалы высот ${{H}_{{\text{g}}}}.$ Будем далее предполагать, что ${{{{H}_{p}}} \mathord{\left/ {\vphantom {{{{H}_{p}}} {{{H}_{{\text{g}}}} < 1}}} \right. \kern-0em} {{{H}_{{\text{g}}}} < 1}}$ и газ движется устойчивым образом по круговой орбите с кеплеровой скоростью ${{\text{v}}_{{\text{g}}}} = - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}{{\Omega }_{K}}x{{i}_{y}}.$ Заметим, что в реальных дисках из-за турбулентности газовой компоненты имеется пульсирующая компонента скорости газа, которая приводит к дисперсии скорости пыли ${{c}_{p}}$. Поскольку целью этого пункта является качественное объяснение гидродинамической неустойчивости, скорее, чем подробное моделирование динамики возмущений пылевой фазы в плоскости субдиска, будем для простоты предполагать, что жидкостной пылевой континуум является изотермическим, и таким образом, для пылевого давления справедливо соотношение ${{p}_{p}} = c_{p}^{2}{{\Sigma }_{p}},$ где дисперсия скорости пыли ${{c}_{p}}$ постоянна. В принятых предположениях система уравнений, описывающая возмущение гидродинамических параметров пылевого континуума, включает в себя линеаризованные указанным выше способом уравнения (26), (28) и (29):
(45)
$(n + {\text{St}}{{\Omega }_{K}})\delta {{v}_{{px}}} - 2{{\Omega }_{K}}\delta {{\text{v}}_{{py}}} = - c_{p}^{2}\frac{{ik\delta {{\Sigma }_{p}}}}{{{{\Sigma }_{{p0}}}}} - ik\delta \Phi ,$(46)
$(n + {\text{St}}{{\Omega }_{K}})\delta {{\text{v}}_{{py}}} + \frac{{{{\Omega }_{K}}\delta {{\text{v}}_{{px}}}}}{2} = 0,$(48)
$\begin{gathered} {{n}^{3}} + 2{\text{St}}{{\Omega }_{K}}{{n}^{2}} + \Omega _{K}^{2}\left[ {{\text{S}}{{{\text{t}}}^{2}} + {{F}_{W}}(k)} \right]n + \\ + \,\,{\text{St}}\Omega _{K}^{3}\left[ {{{F}_{W}}(k) - 1} \right] = 0, \\ \end{gathered} $Методом Кардана можно получить точное решение этого кубического уравнения. Однако это решение не приводит к простым формулам для различных показателей роста. Вместе с тем качественный анализ соотношения (48) возможен на основе рациональной аппроксимации отдельных его членов с учетом их предварительной оценки.
Вводя с этой целью безразмерные переменные (см. Youdin, 2005a)
(49)
$\begin{gathered} s = n{\text{/}}{{\Omega }_{K}},\,\,\,\,\kappa = \pi G{{\Sigma }_{p}}{k \mathord{\left/ {\vphantom {k {\Omega _{K}^{2}}}} \right. \kern-0em} {\Omega _{K}^{2}}}, \\ {{Q}_{p}} = {{{{c}_{p}}{{\Omega }_{K}}} \mathord{\left/ {\vphantom {{{{c}_{p}}{{\Omega }_{K}}} {\pi G{{\Sigma }_{p}}}}} \right. \kern-0em} {\pi G{{\Sigma }_{p}}}},\,\,\,\,{{Q}_{R}} = {{{{H}_{p}}\Omega _{K}^{2}} \mathord{\left/ {\vphantom {{{{H}_{p}}\Omega _{K}^{2}} {\pi G{{\Sigma }_{p}}}}} \right. \kern-0em} {\pi G{{\Sigma }_{p}}}}, \\ \end{gathered} $(50)
${{s}^{3}} + 2{\text{St}}{{s}^{2}} + ({\text{S}}{{{\text{t}}}^{2}} + {{F}_{W}})s + {\text{St}}({{F}_{W}} - 1) = 0,$(51)
${{F}_{W}}(\kappa ) \equiv {{1 - 2\kappa } \mathord{\left/ {\vphantom {{1 - 2\kappa } {(1 + \kappa {{Q}_{R}})}}} \right. \kern-0em} {(1 + \kappa {{Q}_{R}})}} + Q_{p}^{2}{{\kappa }^{2}}.$Ясно, что в случае ${{s}^{2}} < 0$ имеет место устойчивость решения (если частота $\omega $ – действительное число, то это означает, что волна распространяется по диску – система устойчива); в случае ${{s}^{2}} = 0$ имеет место нейтральность; для случая ${{s}^{2}} > 0$ имеем неустойчивость, если $Re\,\left[ s \right] > 0.$
Поскольку анализ корней дисперсионного уравнения (50) (особенно определение его неустойчивых мод) для “классического” случая компактности и одноразмерности пылевых агрегатов выполнен для всей области образования планетезималей в целом ряде работ (см., например, Youdin, 2005; 2011; Youdin, Lithwick, 2007; Chiang, Youdin, 2010; Shariff, Cuzzi, 2011; Takahashi, Inutsuka, 2014; 2016; Carrera и др., 2015; 2017), то мы не будем воспроизводить его здесь. Заметим только, что даже при массовом разнообразии параметров ${{c}_{p}},{{\alpha }_{p}},\Gamma $ и ${\text{St}}$ всегда можно найти волновое число κ такое, что система (44)–(47) будет неустойчива (Chiang, Youdin, 2010; Youdin, 2011).
Предварительный качественный анализ точного решения (найденного методом Кардана) кубического дисперсионного уравнения (50), выполненного для ряда комбинаций параметров кольцевых областей околосолнечного протопланетного диска (с радиальными расстояниями $r \in \left\{ {0.1\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.}},\,\;1\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.}},\;10\,\,{\text{a}}{\text{.}}\,{\text{e}}{\text{.}}} \right\},$ значениями параметров металличности $\Gamma \in $ {0.01, 0.05, 10} и турбулентной интенсивности $\alpha \in $ {${{10}^{{ - 2}}},{{10}^{{ - 4}}},{{10}^{{ - 5}}}$}), показал, что учет фрактальной размерности ($D \in $ {2, 2.11, 2.9}) и неодинаковости геометрических размеров (радиусов гирации $R \in $ {0.1 см, 10 см, 100 см}) пылевых агрегатов оказывает существенное влияние на условия, при которых возникают различные гидродинамические неустойчивости в пылевом слое. В последующих публикациях предполагается определение критических условий возникновения гидродинамических неустойчивостей на основе численной реализации уравнений (38)–(43), описывающих линейные возмущения гидродинамических параметров в плоскости вращающегося газопылевого диска.
ЗАКЛЮЧЕНИЕ
Формирование и эволюция нашей Солнечной системы и планетных систем вокруг других звезд (звездно-планетная космогония) – одна из наиболее сложных и интригующих областей современной астрофизики. Данные наблюдений образования и эволюции околозвездных дисков и открытие экзопланет положили начало новому этапу в развитии космогонии. В самых общих чертах последовательность процессов образования планетных систем включает фрагментацию исходного межзвездного молекулярного облака, формирование протопланетного аккреционного газопылевого диска вокруг родительской звезды, его распад на первичные сгущения, из которых образуются твердые тела, зародыши планет и, в конечном итоге, сами планеты. Ключевую роль в этой последовательности играют неустойчивость диска и его фрагментация, служащие основой образования твердых тел и их последующей эволюции.
Среди механизмов, способствующих формированию планетезималей, важное место принадлежит различным гидродинамическим неустойчивостям пылевого слоя в центральной плоскости протопланетного диска из-за их способности концентрировать пылевые частицы в плотные сгустки, которые могут вызывать гравитационный коллапс и создавать зародыши планетезималей. Среди них особо выделяют так называемую потоковую неустойчивость.
До недавнего времени основным механизмом, обусловливающим распад диска и начало роста пылевых частиц, считалась гравитационная неустойчивость. Вместе с тем, существуют и другие механизмы роста возмущений плотности макроскопических пылевых агрегатов в диске. К ним относится, в частности, различие между скоростями пылевой и газовой фаз, в результате которого частицы пыли быстро концентрируются в компактные структуры (“глыбы”), вызывая коллапс плотного пылевого слоя в средней плоскости диска даже в условиях слабой самогравитации. Такой механизм был назван потоковой неустойчивостью, имеющей гидродинамическую природу. Его эффективность сильно зависит от численного значения интегрированного по высоте отношения масс пыли и газа и от числа Стокса пылевых частиц, определяющих критические условия возникновения неустойчивости.
Другим важным обстоятельством при рассмотрении эволюции диска является представление о пористой (“пушистой”) структуре пылевых агрегатов (fluffy particles), возникающих при коагуляции мелких мономеров, приобретающих в процессе роста фрактальную структуру. Подобные пушистые агрегаты обладают также низкими относительными скоростями (и следовательно, меньшей вероятностью разрушения и отталкивания при соударениях). Это позволяет им, в частности, преодолевать барьер радиального дрейфа в направлении к протосолнцу быстрее их скорости роста, особенно внутри снеговой линии, способствуя образованию более крупных тел. Кроме этого, фрактальные агрегаты двигаются медленнее, чем окружающие их мелкие частицы, благодаря чему на них продолжают оседать пылевые мономеры, образуя все более массивные пылевые кластеры. Плотность подобных пылевых образований при возникновении потоковой неустойчивости может превышать локальную плотность газа по крайней мере в несколько сот раз, что превышает критическое значение для гравитационной неустойчивости, и потому потоковая неустойчивость может наступить раньше гравитационной неустойчивости и быть более эффективной.
В статье предложен новый подход к изучению ряда гидродинамических неустойчивостей двухфазного газопылевого слоя, учитывающий фрактальную природу и многомасштабность образующихся в результате процессов коагуляции пылевых агрегатов. Этот подход представляется наиболее адекватным при изучении гидродинамической неустойчивости газопылевых протопланетных дисков, позволяя учесть при этом также фрактальную природу и многомасштабность коагулированных пылевых агрегатов. Он позволяет выйти за рамки классического аналитического исследования линейных возмущений движения пылевой и газовой фаз, когда принимается компактная структура возникающих пылевых агрегатов и одинаковость их размеров.
ПРИЛОЖЕНИЕ: ГИДРОДИНАМИКА ФРАКТАЛЬНЫХ СРЕД
Плотность состояний и обобщенные дифференциальные операторы для фрактальных сред
В общем случае фрактальные среды не могут рассматриваться как сплошные среды. Поскольку в любой фрактальной среде существуют пустоты, которые не заполнены веществом, то и дисковая среда пылевых фрактальных агрегатов не может в общем случае описываться как традиционная сплошная среда, но должна рассматриваться как особый тип сплошной среды, для моделирования которой необходимо привлекать модели, использующие интегрирование дробного порядка по области евклидового пространства, вместо интегрирования по фрактальному множеству (см. Roy, Ray, 2009).
Для описания фрактальных сред с помощью дробно-интегральных моделей обычно используется так называемая функция плотности разрешенных состояний77${{c}_{n}}(D,R),$ описывающая, как плотно упакованы разрешенные состояния в $n$‑мерном ($n = 1,2,3$) евклидовом пространстве (см., например, Tarasov, 2005; 2010). При этом выражение ${{c}_{n}}(D,R)d{{V}_{n}}$ представляет собой число разрешенных мест в элементарном объеме $d{{V}_{n}}.$ Здесь $R = {r \mathord{\left/ {\vphantom {r {{{L}_{{{\text{hydr}}}}}}}} \right. \kern-0em} {{{L}_{{{\text{hydr}}}}}}}$ − безразмерная координата. Вид и свойства функции ${{c}_{n}}(D,R)$ определяются свойствами и симметриями фрактального распределения. Далее мы будем предполагать, что дисковая фрактальная среда обладает сферически симметричным распределением вещества в ней; в этом случае можно использовать следующее выражение для плотности состояний:
(52)
$\begin{gathered} {{c}_{{\text{3}}}}(D,R) = \frac{{{{2}^{{2 - D}}}\sqrt \pi }}{{{\Gamma (}{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}{\text{)}}}}{{\left| R \right|}^{{D - 3}}}, \\ {{c}_{{\text{2}}}}(d,R) = \frac{{{{2}^{{2 - d}}}}}{{{\Gamma (}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}{\text{)}}}}{{\left| R \right|}^{{d - 2}}},\,\,\,\,{{c}_{{\text{1}}}}(D,R) = \frac{{{{{\left| R \right|}}^{{D - 1}}}}}{{{\Gamma (}D{\text{)}}}}, \\ \end{gathered} $Отметим также, что в случае иных симметрий среды с дробной размерностью, для функции плотности разрешенных состояний ${{c}_{n}}(D,R)$ нужно использовать выражения для ядер интегралов дробного порядка, отвечающих этой симметрии, т.е. фигурирующих в дробно-интегральной модели данной фрактальной среды (в частности, в случае распределения вещества с фрактальной размерностью, соответствующей симметрии параллелепипеда, нужно использовать плотность состояний по Риману–Лиувиллю) (см., например, Самко и др., 1987).
Введем обобщенный дифференциальный оператор ${{\nabla }^{D}},$ с помощью которого удобно записать обобщенные гидродинамические уравнения для фрактальных сред. Используемый далее обобщенный оператор ${{\nabla }^{D}}$ в форме Рисса (см. Самко и др., 1987) имеет вид
(53)
$\begin{gathered} {{\nabla }^{D}}a \equiv c_{3}^{{ - 1}}(D,R)\nabla \left\{ {{{c}_{{\text{2}}}}(d,R)a} \right\} = \\ = \frac{{{{2}^{{D - d}}}}}{{\sqrt \pi }}\frac{{{\Gamma (}{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}{\text{)}}}}{{{\Gamma (}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}{\text{)}}}}{{\left| R \right|}^{{3 - D}}}\nabla \left\{ {{{{\left| R \right|}}^{{d - 2}}}a} \right\}. \\ \end{gathered} $Заметим, что правило почленного дифференцирования ${{\nabla }^{D}}(ab) = a{{\nabla }^{D}}b + \,b{{\nabla }^{D}}a$ для оператора набла ${{\nabla }^{D}}$ не справедливо; этот оператор удовлетворяет следующему правилу:
где(55)
$\begin{gathered} \Theta (D,d,R) \equiv c_{3}^{{ - 1}}(D,R)\,{{c}_{{\text{2}}}}(d,R) = \\ = \frac{{{{2}^{{D - d}}}}}{{\sqrt \pi }}\frac{{{\Gamma (}{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}{\text{)}}}}{{{\Gamma (}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}{\text{)}}}}{{\left| R \right|}^{{1 - D + d}}}. \\ \end{gathered} $С помощью оператора ${{\nabla }^{D}}$ обобщенная дивергенция записывается в виде
(56)
$\begin{gathered} {{\nabla }^{D}} \cdot a \equiv c_{3}^{{ - 1}}(D,R)\,\nabla \cdot \left\{ {{{c}_{{\text{2}}}}(d,R)a} \right\} = \\ = \frac{{{{2}^{{D - d}}}}}{{\sqrt \pi }}\frac{{{\Gamma (}{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}{\text{)}}}}{{{\Gamma (}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}{\text{)}}}}{{\left| R \right|}^{{3 - D}}}\nabla \cdot \left\{ {{{{\left| R \right|}}^{{d - 2}}}a} \right\}, \\ \end{gathered} $(57)
${{\left( {\frac{{da}}{{d{\kern 1pt} t}}} \right)}_{D}} \equiv \frac{{\partial a}}{{\partial t}} + c(D,d,R){{\text{v}}_{{\text{d}}}} \cdot \nabla a.$Если обозначить $\Xi (D,d) \equiv \frac{{{{2}^{{D - d}}}}}{{\sqrt \pi }}\frac{{{\Gamma (}{D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0em} 2}{\text{)}}}}{{{\Gamma (}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}{\text{)}}}}$ и учесть, что $\nabla {{\left| R \right|}^{{d - 2}}} = (d - 2){{\left| R \right|}^{{d - 4}}}R,$ то
Базовые уравнения для моделирования эволюции фрактального газопылевого диска
Пусть газ и твердые частицы образуют два континуума, которые взаимодействуют друг с другом через аэродинамическое сопротивление. В общем случае необходимо вводить в рассмотрение объемные содержания отдельных фаз s, поскольку в отличие от гомогенной смеси, где каждая компонента может рассматриваться как занимающая весь элементарный объем пространства непрерывно и равномерно с другими компонентами, в гетерогенной системе каждая фракция занимает лишь часть элементарного объема. В частности, ${{s}_{{\text{g}}}} \equiv {{{{\rho }_{{\text{g}}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{\text{g}}}}} {{{{\tilde {\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{\tilde {\rho }}}_{{\text{g}}}}}},$ где ${{\tilde {\rho }}_{{\text{g}}}}$ – истинная плотность газа, равная отношению массы газа в элементарном объеме $\delta V$ к части этого объема $\delta {{V}_{{\text{g}}}},$ которую занимает масса газа. Объемное содержание ФПА $j$-го сорта определяется аналогично: $s_{j}^{{{\text{с l}}}}(r,t) = {{\rho _{j}^{{{\text{с l}}}}} \mathord{\left/ {\vphantom {{\rho _{j}^{{{\text{с l}}}}} {\tilde {\rho }_{j}^{{{\text{с l}}}}}}} \right. \kern-0em} {\tilde {\rho }_{j}^{{{\text{с l}}}}}},$ где ${{\rho _{j}^{{{\text{с l}}}}} \mathord{\left/ {\vphantom {{\rho _{j}^{{{\text{с l}}}}} {\tilde {\rho }_{j}^{{{\text{с l}}}}}}} \right. \kern-0em} {\tilde {\rho }_{j}^{{{\text{с l}}}}}}$ – соответственно массовая плотность и истинная массовая плотность. Тогда объемное содержание ${{s}_{{\text{g}}}}$ несущей фазы выражается в виде ${{s}_{{\text{g}}}} = 1 - s_{p}^{{{\text{с l}}}},$ где
В случае если суммарный гетерогенный континуум рассматривать в однодавленческом приближении, ${{P}_{\operatorname{g} }} = {{P}_{p}} = P({{\rho }_{g}},T),$ то система уравнений Эйлера, описывающая движение газа и фрактальной пылевой среды, имеет вид (см. Нигматулин, 1987; Tarasov, 2010):
(59)
$\frac{{d{{\rho }_{{\text{g}}}}}}{{d{\kern 1pt} t}} + {{\rho }_{{\text{g}}}}\nabla \cdot {{\text{v}}_{{\text{g}}}} = 0,\,\,\,\,{{\rho }_{{\text{g}}}} = {{\tilde {\rho }}_{{\text{g}}}}s,$(60)
${{\left( {\frac{{d{{\rho }_{p}}}}{{d{\kern 1pt} t}}} \right)}_{D}} + {{\rho }_{p}}{{\nabla }^{D}} \cdot {{\text{v}}_{d}} = \;0,\,\,\,\,{{\rho }_{d}} = {{\tilde {\rho }}_{d}}(1 - s),$(61)
$\begin{gathered} {{\rho }_{g}}\frac{{d{{\text{v}}_{{\text{g}}}}}}{{dt}} = - {{\rho }_{{\text{g}}}}\Omega _{k}^{2}r + 2{{\rho }_{{\text{g}}}}{{\text{v}}_{{\text{g}}}} \times {{\Omega }_{K}} - \\ - \,\,(1 - s)\nabla P + \nabla {{\Phi }_{{{\text{g}}r}}} - {{F}_{{{\text{g}}p}}}, \\ \end{gathered} $(62)
$\begin{gathered} {{\rho }_{p}}{{\left( {\frac{{d{{\text{v}}_{p}}}}{{dt}}} \right)}_{D}} = - {{\rho }_{p}}\Omega _{K}^{2}r + 2{{\rho }_{p}}{{\text{v}}_{p}} \times {{\Omega }_{K}} - \\ - \,\,s{{\nabla }^{D}}P + {{\nabla }^{D}}{{\Phi }_{{{\text{g}}r}}} + {{F}_{{{\text{g}},p}}}. \\ \end{gathered} $Важно при этом отметить, что для исчерпывающего решения заявленной в этой статье проблемы необходимо в общем случае моделировать процессы коагуляции пылевых частиц и потоковую неустойчивость одновременно. Поэтому строгое решение задачи образования протопланетозималей в рамках рассматриваемого механизма включает, наряду с оценкой скоростей газопылевых кластеров, также и нахождение функции распределения (спектра) кластеров по размерам (массам) в произвольный момент времени $t$ в точке $r.$ Другими словами, необходимо совместное решение уравнений движения для фрактальной пылевой среды и обобщенного кинетического уравнения Смолуховского для пространственно неоднородной коагуляции. Заметим, что указанный подход использовался ранее в работах (Kolesnichenko, Marov, 2013; Колесниченко, 2017), в которых моделирование эволюции допланетного облака проводилось в рамках фрактальной газопылевой среды, использующей для учета фрактальности пылевого континуума дробные интегралы, порядок которых определялся массовой размерностью $D$ пылевых кластеров.
Работа выполнена в рамках госзаданий ИПМ им. М.В. Келдыша и ГЕОХИ им. В.И. Вернадского РАН при частичной поддержке грантами РФФИ № 17-02-00507, 18-01-00064 и Программы Президиума РАН № 12.
Список литературы
Зиглина И.Н., Макалкин А.Б. Гравитационная неустойчивость в пылевом слое протопланетного диска: взаимодействие твердых частиц с турбулентным газом в слое // Астрон. вестн. 2016. Т. 50. № 6. С. 431–449. (Ziglina I.N., Makalkin A.B. Gravitational instability in the dust layer of a protoplanetary disk: Interaction of solid particles with turbulent gas in the layer // Sol. Syst. Res. 2016. V. 50. № 6. P. 408–425.)
Колесниченко А.В. О синергетическом механизме возникновения когерентных структур в континуальной теории развитой турбулентности // Астрон. вестн. 2004. Т. 38. № 5. С. 405–427. (Kolesnichenko A.V. Synergetic mechanism of the development of coherent structures in the continual theory of developed turbulence // Sol. Syst. Res. 2004. V. 38. № 5. P. 351–371.)
Колесниченко А.В. К теории инверсного каскада энергии в спиральной турбулентности астрофизического диска // Препр. ИПМ им. М.В. Келдыша. 2014. № 70. 36 с.
Колесниченко А.В., Маров М.Я. Основы механики гетерогенных сред в околосолнечном допланетном облаке: Влияние твердых частиц на турбулентность в диске // Астрон. вестн. 2006. Т. 40. № 1. С. 3–64. (Kolesnichenko A.V., Marov M.Ya. Fundamentals of the mechanics of heterogeneous media in the circumsolar protoplanetary cloud: The effects of solid particles on disk turbulence // Sol. Syst. Res. 2006. V. 40. № 1. P. 1–56.)
Колесниченко А.В., Маров М.Я. О влиянии спиральности на эволюцию турбулентности в солнечном протопланетном облаке // Астрон. вестн. 2007. Т. 41. № 1. С. 3–23. (Kolesnichenko A.V., Marov M.Ya. The effect of spirality on the evolution of turbulence in the solar protoplanetary cloud // Sol. Syst. Res. 2007. V. 41. № 1. P. 1–18.)
Колесниченко А.В., Маров М.Я. Турбулентность и самоорганизация. Проблемы моделирвания космических и природных сред. М.: БИНОМ. Лаборатория знаний, 2009. 632 с.
Колесниченко А.В., Маров М.Я. Моделирование процессов образования пылевых фрактальных кластеров как основы рыхлых протопланетезималей в солнечном допланетном облаке // Препр. ИПМ им. М.В. Келдыша. 2014. № 75. 44 с.
Колесниченко А.В. Некоторые проблемы конструирования космических сплошных сред: Моделирование аккреционных протопланетных дисков. М.: ИПМ им. М.В. Келдыша, 2017. 372 с.
Макалкин А.Б., Зиглина И.Н. Гравитационная неустойчивость в пылевом слое протопланетного диска с учетом взаимодействия слоя и окружающего газа в диске // Астрон. вестн. 2018. Т. 52. С. 534–551. (Makalkin A.B., Ziglina I.N. Gravitational instability in the dust layer of a protoplanetary disk with interaction between the layer and the surrounding gas // Sol. Syst. Res. 2018. V. 52. № 6. P. 518–533.)
Маров М.Я. Малые тела Солнечной системы и некоторые проблемы космогонии // УФН. 2005. Т. 175. № 6. С. 668–678.
Маров М.Я., Шевченко И.И. Экзопланеты. Экзопланетология. М.–Ижевск: Институт компьютерных исследований, 2017. 138 с.
Маров М.Я., Русол А.В. Оценка параметров столкновений пылевых фрактальных кластеров в газопылевом протопланетном диске // Письма в Астрон. журн. 2018. Т. 44. № 7. С. 517–524.
Михайлов Е.Ф., Власенко С.С. Образование фрактальных структур в газовой фазе // УФН. 1995. Т. 165. № 3. С. 263–283.
Нигматулин Р.И. Динамика многофазных сред. Ч. I. М.: Наука, 1987. 464 с.
Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. Минск: Наука и техника, 1987. 688 с.
Сафронов В.С. Эволюция пылевой компоненты околосолнечного допланетного диска // Астрон. вестн. 1987. Т. 21. № 3. С. 216–220.
Смирнов Б.М. Физика фрактальных кластеров. М.: Наука, 1991. 134 с.
Смирнов Б.М. Процессы с участием кластеров и малых частиц в буферном газе // УФН. 2011. Т. 181. № 7. С. 713–745.
Чепмен C., Каулинг Т. Математическая теория неоднородных газов. М.: ИЛ, 1960. 510 с.
Armitage P.J. Lecture notes on the formation and early evolution of planetary systems. 2007. Eprint arXiv:astro-ph/0701485.
Armitage P.J. Dynamics of protoplanetary disks // Ann. Rev. Astron. and Astrophys. 2011. V. 49. P. 195–236.
Armitage P.J. Physical processes in protoplanetary disks // arXiv: 1509.06382v1 [astro-ph.SR] 21 Sep. 2015. P. 1–127.
Bai X.-N., Stone J.M. Dynamics of solids in the midplane of protoplanetary disks: Implications for planetesimal formation // Astrophys. J. 2010a. V. 722. № 2. P. 1437–1459.
Bai X.-N., Stone J.M. Particle-gas dynamics with Athena: Method and convergence // Astrophys. J. Suppl. 2010c. V. 190. № 2. P. 297–310.
Bai X.-N., Stone J.M. The effect of the radial pressure gradient in protoplanetary disks on planetesimal formation // Astrophys. J. 2010b. V. 722. № 2. P. L220–L223.
Bertini I., Gutierrez P.J., Sabolo W. The influence of the monomer shape in the first stage of dust growth in the protoplanetary disk // Astron. and Astrophys. 2009. V. 504. P. 625–633.
Blum J., Wurm G. The growth mechanisms of macroscopic bodies in protoplanetary disks // Ann. Rev. Astron. and Astrophys. 2008. V. 46. P. 21–56.
Carrera D., Johansen A., Davies M. How to form planetesimals from mm-sized chondrules and chondrule aggregates // Astron. and Astrophys. 2015. V. 579. id. A43. 20 p.
Carrera D., Gorti U., Johansen A., Davies M. Planetesimal formation by the streaming instability in a photoevaporating disk // Astrophys. J. 2017. V. 839. № 1. article id. 16. 17 p.
Chavanis P.-H. Trapping of dust by coherent vortices in the solar nebula // arXiv:astro-ph/9912087. 1999. V. 16. P. 1–54.
Chen Z.-Y., Meakin P., Deutch J.M. Comment on “Hydrodinamic Behavior of Fractal Aggregates”// Phys. Rev. Lett. 1987. 59. № 18. P. 2121.
Chiang E., Youdin A.N. Forming planetesimals in solar and extrasolar nebulae // Ann. Rev. Earth and Planet. Sci. 2010. V. 38. P. 493–522.
Cuzzi J.N., Dobrovolskis A.R., Champney J.M. Particle-gas dynamics in the midplane of a protoplanetary nebulae // Icarus. 1993. V. 106. P. 102–134.
Cuzzi J.N., Hogan R.C., Shariff K. Toward planetesimals: Dense chondrule clumps in the protoplanetary nebula // Astrophys. J. 2008. V. 687. P. 1432–1447.
Hodgson L.S. Brandenburg A. Turbulence effects in planetesimal formation // Astron. and Astrophys. 1998. V. 330. P. 1169–1174.
Jacquet E., Balbus S., Latter H. On linear dust-gas streaming instabilities in protoplanetary discs // Mon. Notic. Roy. Astron. Soc. 2011. V. 415. P. 3591–3598.
Johansen A., Oishi J.S., Mac Low M.-M., Klahr H., Henning T., Youdin A. Rapid planetesimal formation in turbulent circumstellar disks // Nature. 2007. V. 448. P. 1022–1025.
Johansen A., Henning T., Klahr H. Dust sedimentation and self-sustained Kelvin-Helmholtz turbulence in protoplanetary disk midplanes // Astrophys. J. 2006a. V. 643. P. 1219–1232.
Johansen A., Youdin A., Klahr H. Zonal flows and long-lived axisymmetric pressure bumps in magnetorotational turbulence // Astrophys. J. 2009. V. 697. P. 1269–1289.
Dominik C., Tielens A.G. The physics of dust coagulation and the structure of dust aggregates in space // Astrophys. J. 1997. V. 480. P. 647–673.
Drążkowska J., Dullemond C.P. Can dust coagulation trigger streaming instability? // Astron. and Astrophys. 2014. V. 572. A78. 12 p.
Garaud P., Lin D.N.C. On the evolution and stability of a protoplanetary disk dust layer // Astrophys. J. 2004. V. 608. № 2. P. 1050–1075.
Goldreich P., Ward W.R. The formation of planetesimals // Astrophys. J. 1973. V. 183. № 3. P. 1051–1061.
Goldreich P., Lynden-Bell D.I. Gravitational stability of uniformly rotating disks // Mon. Notic. Roy. Astron. Soc. 1965. V. 130. P. 97–124.
Kataoka A., Tanaka H., Okuzumi S., Wada K. Fluffy dust forms icy planetesimals by static compression // Astron. and Astrophys. 2013. V. 557. P. L4.
Kolesnichenko A.V., Marov M.Ya. Modeling of aggregation of fractal dust clusters in a laminar protoplanetary disk // Sol. Syst. Res. 2013. V. 47. № 2. P. 80–98.
Kolesnichenko A.V., Marov M.Ya. Modification of the jeans instability criterion for fractal-structure astrophysical objects in the framework of non-extensive statistics // Sol. Syst. Res. 2014. V. 48. № 5. P. 354–365.
Lissauer J.J., de Pater I. Fundamental Planetary Science. Physics, Chemistry and Habitability. New York: Cambridge Univ. Press, 2013. 583 p.
Marov M.Ya., Kolesnichenko A.V. Turbulence and Self-Organization. Modeling Astrophysical Objects. Springer, 2013. 657 p.
Mizuno H. Grain growth in the turbulent accretion disk solar nebula // Icarus. 1989. V. 80. P. 189–201.
Morbidelli A., Raymond S.N. Challenges in planet formation // J. Geophys. Res. Planets. 2016. V. 121. Iss. 10. P. 1962–1980.
Nakagawa Y., Sekiya M., Hayashi C. Settling and growth of dust particles in a laminar phase of a low-mass olar nebula // Icarus. 1986. V. 67. P. 375–390.
Nakamoto T., Nakagawa Y. Formation, early evolution, and gravitational stability of protoplanetary disks // Astrophys. J. 1994. V. 421. P. 640–651.
Okuzumi S., Tanaka H., Sakagami M.-A. Numerical modeling of the coagulation and porosity evolution of dust aggregates // Astrophys. J. 2009. V. 707. P 1247–1264.
Pan L., Padoan P., Scalo J., Kritsuk A.G., Norman M.L. Turbulent clustering of protoplanetary dust and planetesimal formation // Astrophys. J. 2011. V. 740. № 1. article id. 6. 21 p.
Perets H.B., Murray-Clay R. Wind-shearing in gaseous protoplanetary disks // Astrophys. of Planet. Systems: Formation, Structure, and Dynamical Evolution, Proc. Int. Astron. Union, IAU Symp. 2011. V. 276. P. 453–454.
Pinte C., Dent W. R. F., Ménard F., Hales A., Hill T., Cortes P., de Gregorio-Monsalvo I. Dust and gas in the disk of HL Tauri: Surface density, dust settling, and dust-to-gas ratio // Astrophys. J. 2016. V. 816. № 1. article id. 25. 12 p.
Roy N., Ray A.K. Fractal features in accretion discs // Mon. Notic. Roy. Astron. Soc. 2009. V. 397. № 3. P. 1374–1385.
Shakura N.I., Sunyaev R.A. Black holes in binary systems. Observational appearance // Astron. and Astrophys.1973. V. 24. P. 337–355.
Shariff K., Cuzzi J.N. Gravitational instability of solid assisted by gas drag: slowing by turbulent mass diffusivity // Astrophys. J. 2011. V. 738. № 1. article id. 73. 9 p.
Shu F.H. Waves in planetary rings // Planetary rings (A85-34401 15-88). Tucson, AZ. Univ. Arizona Press, 1984. P. 513–561.
Squire J., Hopkins P.F. Resonant drag instabilities in protoplanetary discs: the streaming instability and new, faster growing instabilities // Mon. Notic. Roy. Astron. Soc. 2018a. V. 477. № 4. P. 5011–5040.
Squire J., Hopkins P.F. Resonant drag instability of grains streaming in fluids // Astrophys. J. Lett. 2018b. V. 856. № 1. article id. L15. 5 p.
Tarasov V.E. Fractional hydrodynamic equations for fractal media // Ann. Phys. 2005. V. 318. № 2. P. 286–307.
Tarasov V.E. Fractional dynamics: Applicationsof fractional calculus to dynamics of particles, fields and media. Springer. Higher Education Press, 2010. 516 p.
Takahashi S.Z., Inutsuka S. Two-component secular gravitational instability in a protoplanetary disk: A possible mechanism for creating ring-like structures // Astrophys. J. 2014. V. 794. Iss. 1. Article id. 55. 7 p.
Takahashi S.Z., Inutsuka S. An origin of multiple ring structure and hidden planets in Hl Tau: A unified picture by secular gravitational instability // Arxiv: 1604.054 50v3[astro-ph.SR]. 2016.
Toomre A. On the gravitational stability of a disk of stars // Astrophys. J. 1964. V. 139. P. 1217–1238.
Tsallis C. Possible generalization of Boltzmann-Gibbs statistics // J. Statistical Phys. 1988. V. 52. P. 479–487.
Ward W.R. On Planetesimal Formation: The Role of Collective Particle Behavior // Origin of the Earth and Moon / Eds Canup R.M., Righter K. Tucson: Univ. Arizona Press, 2000. P. 75–84.
Weidenschilling S.J. Formation of planetesimals and accretion of the terrestrial planets // Space Sci. Rev. 2000. V. 92. P. 295–310.
Wiltzius P. Hydrodinamic behavior of fractal aggregates // Phys. Rev. Lett. 1987. V. 58. № 7. P. 710–713.
Wetherill G.W., Stewart G.R. Accumulation of a swarm of small planetesimals // Icarus. 1989. V. 77. P. 330–357.
Umurhan O.M., Estrada P.R., Cuzzil J.N., Hartlep T. Streaming instability in turbulent protoplanetary disks: Theoretical predictions // 49th Lunar and Planet. Sci. Conf. 2018. LPI Contrib. № 2083.
Yang C.-C., Johansen A. On the feeding zone of planetesimal formation by the streaming instability // Astrophys. J. 2014. V. 792. № 2. P. 86.
Yang C.-C., Johansen A., Carrera D. Concentrating small particles in protoplanetary disks through the streaming instability // Astron. and Astrophys. 2017. V. 606. id. A80.
Youdin A.N., Shu F. Planetesimal formation by gravitational instability // Astrophys. J. 2002. V. 580. P. 494–505.
Youdin A.N., Goodman J. Streaming instabilities in protoplanetary disks // Astrophys. J. 2005. V. 620. P. 459–469.
Youdin A.N. Planetesimal formation without thresholds. I. Dissipative gravitational instabilities and particle stirring by turbulence // arXiv:astro-ph/0508659. 2005a.
Youdin A.N. Planetesimal formation without thresholds. II. Gravitational instability of solids in turbulent protoplanetary disks // arXiv:astro-ph/0508662. 2005b.
Youdin A.N., Lithwick Y. Particle stirring in turbulent gas disks: Including orbital oscillations // Icarus. 2007. V. 192. P. 588–604.
Youdin A.N. On the formation of planetesimals via secular gravitational instabilities with turbulent stirring // Astrophys. J. 2011. V. 731 P. 99–117.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник