Астрономический вестник, 2019, T. 53, № 4, стр. 256-264
Гравитационные маневры около Венеры для выхода на внеэклиптические положения. Резонансная асимптотическая скорость
Ю. Ф. Голубев a, *, А. В. Грушевский a, **, В. В. Корянов a, ***, А. Г. Тучин a, ****, Д. А. Тучин a, *****
a ИПМ им. М.В. Келдыша РАН
Москва, Россия
* E-mail: golubev@keldysh.ru
** E-mail: alexgrush@rambler.ru
*** E-mail: korianov@keldysh.ru
**** E-mail: tag@kiam1.rssi.ru
***** E-mail: den@kiam1.rssi.ru
Поступила в редакцию 15.01.2019
После доработки 18.02.2019
Принята к публикации 21.02.2019
Аннотация
Планета Венера, ближайший сосед Земли в Солнечной системе, в первую очередь подходит для совершения гравитационных маневров космическим аппаратом (КА) с целью малозатратного изменения наклонения его орбиты относительно эклиптики. В работе вычислены “резонансные” значения асимптотической скорости КА относительно планеты, такие, что орбитальный период КА после каждого гравитационного маневра был соизмерим с периодом обращения Венеры и обеспечивал новую встречу с нею, что позволяет производить увеличение наклонения орбиты КА с помощью гравитационных маневров без переходов на соседние резонансы по инвариантной линии основного на ${{\operatorname{V} }_{\infty }}$-сфере с достижением максимума наклонения. Получен венерианский инвариант, не меняющийся при совершении гравитационных маневров с Венерой. Представлен адаптивный полуаналитический метод и его геометрическая интерпретация для синтеза цепочек гравитационных маневров около Венеры для малозатратного изменения наклонения орбиты КА.
ВВЕДЕНИЕ
Для осуществления ряда перспективных космических проектов (миссия Solar Orbiter ЕSА, отечественный проект Интергелиозонд и др.), предполагающих изучение внутренней гелиосферы из внеэклиптических положений, требуются орбиты с большим наклонением к плоскости эклиптики. Например, для проекта Интергелиозонд требуются наклонения не менее 30°. Маневры, связанные с активным изменением наклонения орбиты в ходе полета, являются в астродинамике особенно энергозатратными. Эффективность гравитационного маневра около небесного тела была теоретически обоснована (Келдыш и др., 1988) и впервые практически продемонстрирована проектом Луна-3 в октябре 1959 г.
Планета Венера, являясь ближайшим соседом Земли в Солнечной системе, в первую очередь подходит для совершения гравитационных маневров КА с целью малозатратного изменения своих орбитальных характеристик. Внешний сосед Земли, Марс, уже не столь эффективен для этих целей в силу отдаленности от Солнца и более слабого гравитационного поля. Применение гравитационных маневров (ГМ) около Венеры с целью формирования орбит с большим наклонением позволяет существенно сэкономить необходимые для полета запасы топлива.
Технология построения полуаналитических высокоточных алгоритмов, синтезирующих сценарии проведения последовательности ГМ, которые обеспечивают значительное изменение наклонения орбиты исследовательского КА (Голубев и др., 2016; 2017a; 2017б), осложняется необходимостью их 3D-проектирования с учетом точных эфемеридных моделей. Рассмотрим отдельно различные случаи синтеза последовательности ГМ около Венеры.
При баллистическом проектировании орбит с высоким наклонением i, как показано в (Голубев и др., 2017б; 2016), помимо стандартных ограничений на расход ресурса и длительность космической миссии необходимо учитывать следующие базовые ограничения:
– геометрические ограничения на максимально возможное наклонение орбиты КА, которое достижимо в зависимости от величины его асимптотической скорости относительно Венеры при любой последовательности ГМ с ней;
– динамические ограничения на максимальный угол $\varphi $ поворота вектора асимптотической скорости КА относительно Венеры при совершении ГМ, зависящие от величины ${{V}_{\infty }}$ асимптотической скорости.
Совместный анализ указанных ограничений позволяет сформировать основной динамический облик планируемой космической миссии (Голубев и др., 2017a; 2017б; 2016).
ОБОБЩЕННЫЙ “КОМЕТНЫЙ” ИНВАРИАНТ ПЛАНЕТЫ
Как известно, в круговой ограниченной задаче трех тел (ОЗТТ) (“первое тело–второе тело–бесконечно малое тело”) остается инвариантным интеграл Якоби с постоянной Якоби $J$ (Субботин, 1968), не меняющийся, в частности, при совершении ГМ бесконечно малым телом около малого (второго) тела. Следствием этой инвариантности является сохранение также и параметра Тиссерана $\Gamma $ (Tisserand, 1896) (“кометного инварианта”), впервые введенного французским астрономом Феликсом Тиссераном в 1889 г. для определения тождественности комет. Параметр $\Gamma $ используется при идентификации разнесенных по времени астрономических наблюдений, поскольку сами элементы орбиты кометы могут неоднократно меняться при прохождении ею сферы действия планеты Юпитер. Для ОЗТТ системы Солнце–Юпитер–комета (ОЗТТ “S–J–comet”) условие инвариантности юпитерианского параметра Тиссерана $\Gamma _{{{\text{S}} - {\text{J}}}}^{{{\text{au}}}}$ может быть записано в виде (Субботин, 1968):
(1)
$\begin{gathered} \Gamma _{{{\text{S}} - {\text{J}}}}^{{{\text{au}}}} \approx \frac{1}{{({{{{a}_{{{\text{sc}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{{\text{sc}}}}}} {{{r}_{{{\text{oЕ }}}}}}}} \right. \kern-0em} {{{r}_{{{\text{oЕ }}}}}}})}} + \\ + \,\,0.16860\sqrt {({{{{a}_{{{\text{sc}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{{\text{sc}}}}}} {{{r}_{{{\text{oЕ }}}}}}}} \right. \kern-0em} {{{r}_{{{\text{oЕ }}}}}}})\left( {1 - {{e}^{2}}} \right)} \cos i\; = {\text{const}}, \\ \end{gathered} $Таким образом, можно выписать обобщенный безразмерный инвариант кометы $\Gamma _{{{\text{S - p}}}}^{{\text{u}}}$ для произвольной ОЗТТ “${\text{S}}{\kern 1pt} - {\kern 1pt} {\text{p}}{\kern 1pt} - {\kern 1pt} {\text{sc}}$” (Solar–planet–spacecraft) (Голубев и др., 2014) в произвольных u-единицах измерения расстояния:
С целью нахождения инварианта прохождения бесконечно малого тела (КА) через сферу действия Венеры (иными словами – для совершения ГМ около нее) получим аналогично венерианский инвариант кометы $\Gamma _{{{\text{S}} - {\text{Ven}}}}^{{{\text{au}}}}{\text{:}}$
(2)
$\Gamma _{{{\text{S}} - {\text{Ven}}}}^{{{\text{au}}}} \approx \;\frac{1}{{({{{{a}_{{{\text{sc}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{{\text{sc}}}}}} {{{r}_{{{\text{oЕ }}}}}}}} \right. \kern-0em} {{{r}_{{{\text{oЕ }}}}}}})}} + 3.25105\sqrt {({{{{a}_{{{\text{sc}}}}}} \mathord{\left/ {\vphantom {{{{a}_{{{\text{sc}}}}}} {{{r}_{{{\text{oЕ }}}}}}}} \right. \kern-0em} {{{r}_{{{\text{oЕ }}}}}}})(1 - {{e}^{2}})} \cos i.$Для случая прохождения сферы действия Земли, аналогично (1), получим
При совершении гравитационных маневров КА с Венерой остается неизменным именно “венерианский кометный инвариант” $\Gamma _{{{\text{S - Ven}}}}^{{{\text{au}}}}.$
УСЛОВИЯ ФОРМИРОВАНИЯ БОЛЬШИХ НАКЛОНЕНИЙ С ПОМОЩЬЮ ГРАВИТАЦИОННЫХ МАНЕВРОВ
В результате анализа пространственной геометрии проведения ГМ (Голубев и др., 2016) выводится следующее утверждение (Голубев и др., 2017б; 2016). Пусть величина ${{V}_{\infty }}$ асимптотической скорости КА (инвариантная до и после маневра) не превосходит модуля вектора средней орбитальной скорости ${{V}_{{{\text{Ven}}}}} \approx 35$ км/с Венеры. Тогда для максимального наклонения ${{i}_{{\max }}}$ орбиты КА при проведении любой последовательности ГМ около Венеры верна оценка (Голубев и др., 2017б; 2016; Labunsky и др., 1998; Kawakatsu, 2009):
Левая часть (3) не превосходит величины $90^\circ $ и является точной верхней гранью множества возможных наклонений КА. Из полученной оценки следует, что для повышения наклонения орбиты КА относительно эклиптики более чем на $30^\circ $ необходимо до совершения ГМ увеличить асимптотическую скорость КА относительно Венеры до величины не менее 17.5 км/с. Такой разгон КА можно осуществить с помощью двигателя малой тяги и (или) последовательностью ГМ около других планет. В дальнейшем предполагается, что ${{V}_{\infty }} \geqslant 17.5$ км/с. Несмотря на это, однократного гравитационного маневра около Венеры для увеличения наклонения орбиты до требуемой величины может оказаться недостаточно из-за наличия ограничений. В таком случае необходимо синтезировать возрастающую по наклонению последовательность “резонансных” ГМ (то есть таких, чтобы орбитальный период КА после каждого ГМ был соизмерим с периодом обращения Венеры и обеспечивал новую встречу с нею). Выполнение резонансных ГМ есть основное необходимое условие для построения подобных миссий.
Как уже указывалось выше, при совершении КА ГМ с Венерой справедлив именно “венерианский кометный инвариант” $\Gamma _{{{\text{S}} - {\text{Ven}}}}^{{{\text{au}}}}.$ Поскольку величина ${{V}_{\infty }}$ асимптотической скорости КА относительно малого тела (планеты) связана с параметром Тиссерана как $\Gamma = 3 - {{({{{{V}_{\infty }}} \mathord{\left/ {\vphantom {{{{V}_{\infty }}} {{{V}_{{{\text{pl}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{pl}}}}}}})}^{2}}$ (Miller и др., 2002), постольку факт инвариантности величины асимптотической скорости КА относительно планеты ${{V}_{\infty }}$ при совершении ГМ можно рассматривать как следствие существования критерия Тиссерана (Субботин, 1968; Tisserand, 1896; Голубев и др., 2014; Labunsky и др., 1998). Иными словами, конец всевозможных положений вектора ${{{\mathbf{V}}}_{\infty }}$ до и после совершения ГМ лежит на поверхности сферы, построенной с центром на конце вектора ${{{\mathbf{V}}}_{{{\text{pl}}}}}$ в месте совершения ГМ.
Проанализируем достаточные условия для построения рассматриваемого класса миссий. Это условия, позволяющие обеспечить динамическую реализуемость указанных “резонансных” ГМ (“резонансных переходов”). Рассмотрим сферу, радиус которой равен модулю ${{{\mathbf{V}}}_{\infty }},$ а центр находится на конце вектора скорости ${{{\mathbf{V}}}_{{{\text{pl}}}}}$ планеты (${{{\mathbf{V}}}_{\infty }}$-сфера) (Labunsky и др., 1998; Kawakatsu, 2009; Strange и др., 2007). При совершении КА гравитационного маневра конец вектора асимптотической скорости всегда будет оставаться на этой сфере.
Возможности ГМ будем исследовать, исходя из предположения о том, что имеется трубка допустимых траекторий с одним и тем же вектором ${{{\mathbf{V}}}_{\infty }}.$ Для каждой траектории из этой трубки отклонение вектора скорости из-за гравитационного маневра будет происходить в зависимости от места траектории в трубке (которое определяет соответствующую точку на картинной плоскости при входе в сферу действия планеты). Рассмотрим область, образованную концами возможных векторов асимптотической скорости после совершения гравитационного маневра при заданном векторе входной асимптотической скорости. Эта область представляет собой пересечение ${{{\mathbf{V}}}_{\infty }}$-сферы и телесного угла с раствором, равным удвоенному максимальному углу поворота вектора асимптотической скорости КА на одинарном ГМ (сферической шапочкой).
Ограничимся рассмотрением случая тангенциальных ГМ, когда ГМ совершается на линии апсид орбиты КА. Заметим, что ${{{\mathbf{V}}}_{{{\text{sc}}}}} = {{{\mathbf{V}}}_{\infty }} + {{{\mathbf{V}}}_{{{\text{pl}}}}}$ есть скорость КА относительно Солнца. Изменение угла между векторами ${{{\mathbf{V}}}_{\infty }}$ и ${{{\mathbf{V}}}_{{{\text{pl}}}}}$ влечет изменение скорости ${{{\mathbf{V}}}_{{{\text{sc}}}}}.$ При этом можно получить скорость, соответствующую той или иной резонансной траектории. Нанесем на ${{{\mathbf{V}}}_{\infty }}$-сферу указанные сферические шапочки и концы векторов асимптотической скорости, которые отвечают основным резонансам между периодами обращения КА и Венеры вокруг Солнца: 3 : 4, 1 : 1, 4 : 3. Возможность новой встречи с Венерой обеспечивается одним из двух вариантов проведения ГМ (рис. 1).
Рис. 1.
Резонансные изолинии на поверхности ${{{\mathbf{V}}}_{\infty }}$-сферы для основных резонансов 3 : 4, 1 : 1 и 4 : 3 (слева направо).

1. ГМ проводится вдоль фиксированной резонансной линии на ${{{\mathbf{V}}}_{\infty }}$-сфере (“монорезонанс”– “резонансный переход”–переход по резонансу).
2. Сферическая шапочка на ${{{\mathbf{V}}}_{\infty }}$-сфере, соответствующая ГМ, должна покрывать соседние резонансные линии (“переход”).
Для проектирования обоих вариантов необходимо иметь оценки допустимых вариаций наклонения орбиты КА при совершении одного ГМ. При этом они должны быть максимально точными.
УТОЧНЯЮЩИЕ ОЦЕНКИ ИЗМЕНЕНИЯ НАКЛОНЕНИЯ ПРИ СОВЕРШЕНИИ ОДНОГО ГМ
Для оценки изменения наклонения $\Delta i$ на одном ГМ часто используется приближение Лабунского ($\Pi \Lambda $) (Labunsky и др., 1998, с. 4):
В (Голубев и др., 2017a; 2017б; 2016) показано, что, будучи приблизительной, оценка $\Pi \Lambda $ и соответствующие графики допустимых вариаций наклонения на однократном ГМ (Labunsky и др., 1998) несколько отличаются от более точных расчетов (рис. 2). В (Голубев и др., 2017a; 2017б) получено аналитическое выражение для максимальной допустимой вариации наклонения при однократном ГМ, уточняющее $\Pi \Lambda $. Вводится безразмерный параметр ${{\Theta }_{{{\text{pl}}}}},$ равный отношению орбитальной скорости планеты и ее первой космической скорости ${{V}_{{{\text{Fpl}}}}}{\text{:}}$ ${{\Theta }_{{{\text{pl}}}}} = {{{{V}_{{{\text{pl}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{\text{pl}}}}}} {\sqrt {{\mu \mathord{\left/ {\vphantom {\mu {{{R}_{\pi }}}}} \right. \kern-0em} {{{R}_{\pi }}}}} }}} \right. \kern-0em} {\sqrt {{\mu \mathord{\left/ {\vphantom {\mu {{{R}_{\pi }}}}} \right. \kern-0em} {{{R}_{\pi }}}}} }} \approx {{{{V}_{{{\text{pl}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{\text{pl}}}}}} {{{V}_{{{\text{Fpl}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{Fpl}}}}}}}{\kern 1pt} .$ В (Голубев и др., 2016) доказано, что в случае, когда выполнено условие ${{\Theta }_{{{\text{pl}}}}} \geqslant \Theta _{{{\text{pl}}}}^{*} \equiv \frac{{\sqrt {102\sqrt {17} - 214} }}{{16}} \approx 0.898255,$ максимальная добавка по наклонению достигается при значениях (Голубев и др., 2016, Утв. 1) ${{\text{v}}_{\infty }} = \text{v}_{\infty }^{*} \equiv \Theta _{{{\text{pl}}}}^{{ - 1}}\sqrt {\frac{{\sqrt {17} - 1}}{2}} $ и составляет величину
Рис. 2.
Максимальные изменения наклонений при совершении ГМ с планетами земной группы в зависимости от ${{V}_{\infty }}$, (а) уточненные авторами в (Голубев и др., 2016) по приближению Лабунского (Labunsky и др., 1998) и (б) воспроизведенные из книги (Labunsky и др., 1998): 1 – Меркурий, 2 – Венера, 3 – Земля, 4 – Марс.
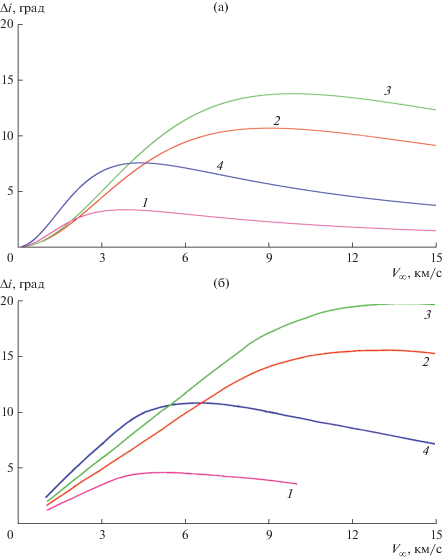
Проведя вычисления, можно убедиться, что для Венеры, ${{\Theta }_{{{\text{Ven}}}}} = {{{{V}_{{{\text{Ven}}}}}} \mathord{\left/ {\vphantom {{{{V}_{{{\text{Ven}}}}}} {{{V}_{{{\text{FVen}}}}}}}} \right. \kern-0em} {{{V}_{{{\text{FVen}}}}}}} = {{35.02} \mathord{\left/ {\vphantom {{35.02} {7.23}}} \right. \kern-0em} {7.23}}$ = = $4.841 > \Theta _{{{\text{pl}}}}^{*} \equiv 0.898,$ и условия Утв. 1 (Голубев и др., 2016) выполняются. При этом максимальное приращение наклонения достигается при $\frac{{{{V}_{\infty }}}}{{{{V}_{{{\text{Ven}}}}}}} = \frac{{V_{\infty }^{*}}}{{{{V}_{{{\text{Ven}}}}}}} \equiv \Theta _{{{\text{Ven}}}}^{{ - 1}}\sqrt {\frac{{\sqrt {17} - 1}}{2}} = 0.258$ (так что $V_{\infty }^{*} \equiv 9.04$ (км/с)) и составляет величину $\Delta {{i}_{{{\text{Ven}}}}} = 10.87^\circ $ (рис. 2), не совпадающую с оценкой Лабунского: $\Delta i_{{{\text{Ven}}}}^{\Lambda } \approx 16^\circ .$
ПОЛЮС НАКЛОНЕНИЯ НА ${{{\mathbf{V}}}_{\infty }}$-СФЕРЕ
В (Голубев и др., 2017б; 2016) представлена более понятная геометрически, чем в (Labunsky и др., 1998), формула для итогового наклонения орбиты КА при совершении ГМ около планеты в сферических координатах $\rho ,\psi $ (рис. 3) в виде:
(5)
$i = {\text{arctg}}\frac{{{{V}_{\infty }}\sin \rho }}{{{{V}_{{{\text{pl}}}}} + {{V}_{\infty }}\cos \rho \cos \psi }}.$Рис. 3.
Сферические координаты $(\psi ,\rho )$ на ${{V}_{\infty }}$-сфере и положение “полюса наклонения” ${{T}_{{Pole}}}$ – точки экстремума наклонения $i = {{i}_{{max}}}$ на ${{{\mathbf{V}}}_{\infty }}$-сфере в случае $\sin \psi = 0.$
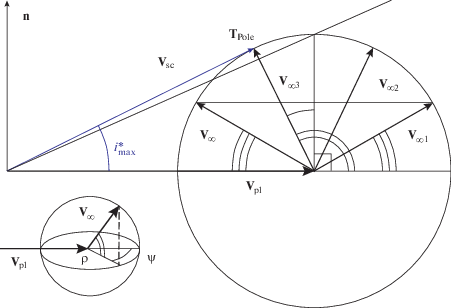
Там же найдены координаты “полюса наклонения” – экстремума наклонения на ${{{\mathbf{V}}}_{\infty }}$-сфере после выполнения любой последовательности ГМ:
(6)
${{T}_{{{\text{Pole}}}}}{\text{ }}\left\{ {{{\psi }_{{{\text{Pole}}}}} = \pi ;{\text{ }}{{\rho }_{{{\text{Pole}}}}} \equiv {{\varphi }_{{{\text{Pole}}}}} = \pi - \arccos {{\text{v}}_{\infty }}} \right\}.$Графики изменения наклонения при совершении одного ГМ для планет Венера и Земля в зависимости от ${{V}_{\infty }},$ посчитанные согласно (5), представлены на рис. 4.
Рис. 4.
Максимальные возможные вариации наклонения при однократном ГМ для $(\psi = 0^\circ - 1,\;\psi = 90^\circ - 2,\;\psi = 180^\circ - 3),$ (а) около Венеры, (б) около Земли.
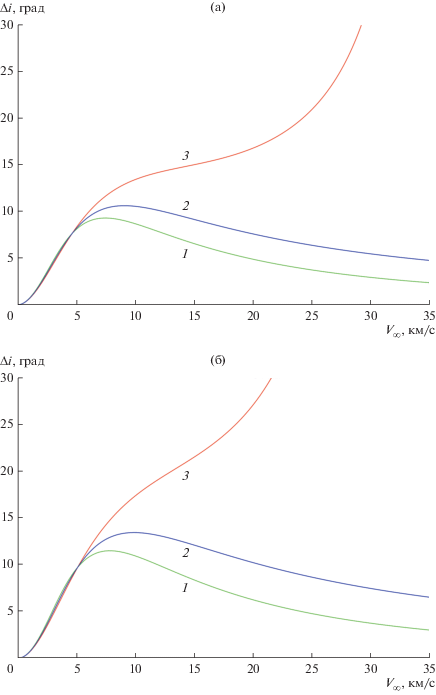
Квазиоптимальный гомановский перелет приводит КА от Земли на ГМ с Венерой так, что вектор асимптотической скорости КА относительно Венеры почти коллинеарен вектору орбитальной скорости Венеры: $(\psi = 0,\pi ).$
Рассмотрим последовательность ${{N}_{\gamma }}$ гравитационных маневров, таких что перемещение конца вектора ${{{\mathbf{V}}}_{\infty }}$ к “полюсу наклонения” на ${{\operatorname{V} }_{\infty }}$-сфере происходит в результате ГМ строго по меридиану $(\psi = 0,\pi ).$ В этом случае угол $\rho $ “накапливает” углы ${{\varphi }_{{j,j\, = \,1,\,...,\,N}}}{\kern 1pt} :$
${{\rho }_{k}}{\text{ = }}{{\rho }_{0}} + \sum\limits_{j = 1}^{{{N}_{\gamma }}} {{{\varphi }_{j}}} ,$ а итоговое наклонение определяется по формуле
(7)
${\text{tg}}i = \frac{{{{V}_{\infty }}\sin \rho }}{{{{V}_{{{\text{pl}}}}} + {{V}_{\infty }}\cos \rho }} = \frac{{{{V}_{\infty }}\sin \left( {{{\rho }_{0}} + \sum\limits_{j = 1}^{{{N}_{\gamma }}} {{{\varphi }_{j}}} } \right)}}{{{{V}_{{{\text{pl}}}}} + {{V}_{\infty }}\cos \left( {{{\rho }_{0}} + \sum\limits_{j = 1}^{{{N}_{\gamma }}} {{{\varphi }_{j}}} } \right)}}.$СОВМЕСТНЫЙ АНАЛИЗ ДИНАМИЧЕСКИХ И ГЕОМЕТРИЧЕСКИХ ОГРАНИЧЕНИЙ
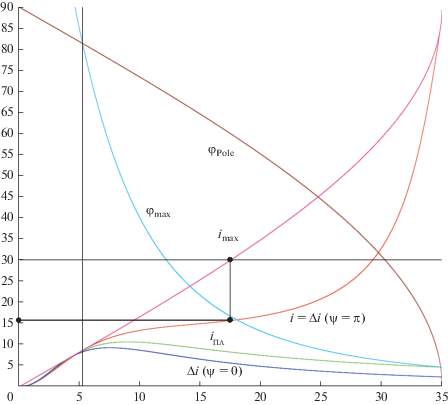
Сопоставим с выражением (3) зависимость (4) от величины ${{V}_{\infty }}$ угла $\varphi $ поворота вектора асимптотической скорости ${{{\mathbf{V}}}_{\infty }}$ КА относительно Венеры. Графики зависимости ${{\varphi }_{{\max }}}$ от величины ${{V}_{\infty }}$ для Венеры представлены на рис. 5. Они показывают, что максимальные углы разворота достигаются при близких к нулю значениях ${{V}_{\infty }}.$ Однако и величина ${{i}_{{\max }}}$ при этом, согласно (3), близка к нулю. На графике видно, что “эффективность” ГМ появляется только при увеличении ${{V}_{\infty }}$ до значений, обеспечивающих требуемую для космической миссии величину ${{i}_{{\max }}}.$ При этом уменьшается значение ${{\varphi }_{{\max }}}.$ Горизонтальной линией обозначено модельное значение ${{i}_{{\max }}} = 30^\circ $ проектного угла наклонения. Вертикаль, опущенная из точки пересечения этой линии с графиком функции максимального наклонения планеты, показывает соответствующее значение угла ${{\varphi }_{{\max }}}$ поворота вектора асимптотической скорости на одном ГМ. Одновременно, в случае осуществления переходов по резонансам, должно обеспечиваться условие поставки такой величины ${{\varphi }_{{\max }}},$ сферическая шапочка которой перекрывает на ${{{\mathbf{V}}}_{\infty }}$-сфере смежные резонансные линии при переходе. Таким способом можно получить характерный размер “рабочего” телесного угла области элементарного ГМ на поверхности ${{\operatorname{V} }_{\infty }}$-сферы.
Рис. 5.
Базовые углы в зависимости от величины ${{V}_{\infty }}$ для планеты Венера. По оси абсцисс отложена величина ${{V}_{\infty }}$ относительно Венеры в км/c, по оси ординат – углы ${{\varphi }_{{\max }}},$ ${{\rho }_{{{\text{Pole}}}}} = {{\varphi }_{{{\text{Pole}}}}},$ ${{i}_{{\max }}},$ $\Delta i$ и ${{i}_{{\Pi \Lambda }}}$ в град ($\Pi \Lambda $ – приближение Лабунского).
УСЛОВИЕ ФОРМИРОВАНИЯ БОЛЬШОГО НАКЛОНЕНИЯ С ПОМОЩЬЮ ПЕРЕХОДА ВДОЛЬ МОНОРЕЗОНАНСА
Согласно (5) и (Голубев и др., 2017б; 2016), для произвольных миссий с наклонением ${{i}_{{\max }}} = i{\text{*}}$ полюс наклонения ${{T}_{{Pole}}}$ будет находиться на широте $\rho = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} - i* = \arccos \frac{{{{V}_{\infty }}}}{{{{V}_{{{\text{Ven}}}}}}}.$ В табл. 1 приведены координаты ${{T}_{{Pole}}}$ для различных значений ${{i}_{{max}}}.$
Таблица 1.
Координаты $\rho *,\psi {\text{*}}$ стационарной точки ${{T}_{{Pole}}}$ в зависимости от величины максимального наклонения ${{i}_{{\max }}}$
| ${{i}_{{max}}},$ град | $\rho *,{\text{г р а д }}$ | $\psi *,\;{\text{г р а д }}$ |
|---|---|---|
| 10 | 80 | 180 |
| 20 | 70 | 180 |
| 30 | 60 | 180 |
| 40 | 50 | 180 |
| 45 | 45 | 180 |
| 50 | 40 | 180 |
| 60 | 30 | 180 |
| 70 | 20 | 180 |
| 80 | 10 | 180 |
Координаты $\rho *,\psi {\text{*}}$ точки ${{T}_{{{\text{Res}}}}},$ по определению отвечающей экстремуму угла наклонения $i$ на линии фиксированного резонанса, приведены для конкретных основных резонансов в модельном случае ${{\text{v}}_{\infty }} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}$ в табл. 2.
Таблица 2.
Координаты $\rho *,\sigma {\text{*}}$ точки ${{T}_{{{\text{Res}}}}}$ максимума наклонения на фиксированной линии резонанса в случае ${{\text{v}}_{\infty }} = 1{\text{/}}2$
| Резонанс | $\rho *,\,\,{\text{г р а д }}$ | $\psi *,\;{\text{г р а д }}$ |
|---|---|---|
| 1 : 1 | 75.5 | 180 |
| 3 : 4 | 62.5 | 180 |
| 4 : 3 | 85.7 | 180 |
| 5 : 4 | 83.6 | 180 |
| 3 : 2 | 89.3 | 180 |
| 1 : 2 | 34.0 | 180 |
| 2 : 1 | 83.0 | 0 |
| 3 : 1 | 75.5 | 0 |
Для произвольных значений ${{\text{v}}_{\infty }}$ широта $\rho {\text{*}}$ точки ${{T}_{{{\text{Res}}}}}$ максимума наклонения главного резонанса $1:1$ может быть вычислена аналитически (Голубев и др., 2017б):
(8)
$\cos \rho * = \frac{{{{V}_{\infty }}}}{{2{{V}_{{{\text{Ven}}}}}}} = \frac{{{{\text{v}}_{\infty }}}}{2},$так что, например, для космических проектов с “рабочей” скоростью ${{V}_{\infty }} = \frac{{{{V}_{{{\text{Ven}}}}}}}{2}$ верно:
В табл. 3 приведены значения широты $\rho {\text{*}}$ точки ${{T}_{{{\text{Res}}}}},$ по определению отвечающей экстремуму угла наклонения $i$ на линиях главных резонансов.
Таблица 3.
Широта $\rho {\text{*}}$ точки ${{T}_{{{\text{Res}}}}},$ отвечающей экстремуму угла наклонения $i$ на линиях главных резонансов
| Резонанс | $\rho {\text{*}}$ для ${{i}_{{\max }}} = 20^\circ ,$ град |
$\rho {\text{*}}$ для ${{i}_{{\max }}} = 30^\circ ,$ град |
$\rho {\text{*}}$ для ${{i}_{{\max }}} = 45^\circ ,$ град |
|---|---|---|---|
| 3 : 4 | 61.34 | 62.54 | 59.81 |
| 1 : 1 | 80.15 | 75.52 | 69.30 |
| 4 : 3 | 85.13 ($\psi * = 0^\circ $) |
85.69 ($\psi * = 180^\circ $) |
76.71 ($\psi * = 180^\circ $) |
В табл. 4 представлены ресурсы углов поворота на одном ГМ около планет земной группы, соответствующие требуемой величине наклонения орбиты КА.
Таблица 4.
Максимально возможные углы поворота вектора асимптотической скорости КА при однократном пролете планет земной группы для миссий, различающихся требуемой величиной наклонения орбиты
| Планета | Первая космическая скорость ${{V}_{{{\text{Fpl}}}}},$ км/c | ${{V}_{{{\text{pl}}}}},$ км/c |
${{\varphi }_{{\max }}}$ для ${{i}_{{\max }}} = 20^\circ ,$ град |
${{\varphi }_{{\max }}}$ для ${{i}_{{\max }}} = 30^\circ ,$ град |
${{\varphi }_{{\max }}}$ для ${{i}_{{\max }}} = 45^\circ ,$ град |
|---|---|---|---|---|---|
| Меркурий | 3.10 | 47.36 | 4.05 | 1.93 | 1.17 |
| Венера | 7.23 | 35.02 | 31.01 | 16.75 | 9.02 |
| Земля | 7.92 | 29.78 | 44.12 | 25.37 | 14.17 |
| Марс | 3.55 | 24.13 | 17.97 | 9.14 | 5.71 |
Анализ таблиц показывает, что переходы между основными резонансами при совершении ГМ около Венеры (которые, согласно табл. 2, требуют изменения текущего $\rho $ на 9.8–13.3 град) эффективны вплоть до значений ${{i}_{{max}}} = 40^\circ .$ В противном случае необходимо проектировать последовательность ГМ по монорезонансу. Как показывает табл. 4, любые ГМ около Меркурия неэффективны для осуществления переходов между резонансами (ячейки отмечены темным). Таким же свойством обладают ГМ около Венеры при ${{i}_{{\max }}}\; > \;40^\circ $ и ГМ около планеты Марс при ${{i}_{{\max }}}\; \geqslant \;30^\circ .$
Практически, величина наклонения, обеспечивающая выполнение основной задачи полета, принадлежит некоторому диапазону значений. Используя это свойство, с помощью представленных таблиц можно проводить уточнение проектной величины ${{V}_{\infty }},$ варьируя полюс наклонения ${{T}_{{Pole}}}$ по ${{{\mathbf{V}}}_{\infty }}$-сфере с тем, чтобы достичь точки максимума наклонения ${{T}_{{{\text{Res}}}}}$ на линии выбранного резонанса.
ЗАКЛЮЧЕНИЕ
Для проведения многократных гравитационных маневров необходимо использовать такие орбиты КА, период обращения которых вокруг Солнца кратен периоду обращения планеты-партнера. Эти орбиты называются резонансными. Использование орбит, соответствующих различным резонансам, в общем случае оказывается проблематичным. В работе получено значение асимптотической скорости КА относительно планеты, позволяющее производить увеличение наклонения орбиты КА по ${{{\mathbf{V}}}_{\infty }}$-сфере без перехода на соседние резонансы и достичь максимума наклонения.
Получен венерианский инвариант, не меняющийся при совершении гравитационных маневров. Представлен адаптивный полуаналитический метод и его геометрическая интерпретация для синтеза цепочек гравитационных маневров около Венеры для малозатратного изменения наклонения орбиты КА.
Список литературы
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г. Синтез сценариев космических миссий в системе Юпитера с использованием гравитационных маневров // Докл. Академии наук. 2014. Т. 456. № 1. С. 39–41.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г., Тучин Д.А. О вариации наклонения орбит небесных тел при совершении гравитационного маневра в Солнечной системе // Препр. ИПМ им. М.В. Келдыша. 2016. № 15. 36 с.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г., Тучин Д.А. Методика формирования больших наклонений орбит космических аппаратов с использованием гравитационных маневров // Докл. Академии наук. 2017a. Т. 472. № 4. С. 403–406.
Голубев Ю.Ф., Грушевский А.В., Корянов В.В., Тучин А.Г., Тучин Д.А. Формирование орбит космического аппарата с большим наклонением к эклиптике посредством многократных гравитационных маневров // Изв. РАН. Теория и системы управления. 2017б. № 2. С. 108–132.
Келдыш М.В., Власова З.П., Лидов М.Л., Охоцимский Д.Е., Платонов А.К. Исследование траекторий облета Луны и анализ условий фотографирования и передачи информации // Келдыш М.В. Избранные труды. Ракетная техника и космонавтика. М.: Наука, 1988. С. 261–309.
Субботин М.Ф. Введение в теоретическую астрономию. М.: Наука, 1968. 800 с.
Kawakatsu Y. V∞ Direction Diagram and its Application to Swingby Design // 21st ISSFD, Toulouse, France, September 28-October 2, 2009. P. 1–14.
Labunsky A.V., Papkov O.V., Sukhanov K.G. Multiple Gravity Assist Interplanetary Trajectories // ESI Book Series. L.: Gordon and Breach Publishers, 1998. P. 9–266.
Miller J.K., Weeks C.J. Application of Tisserand’s Criterion to the Design of Gravity Assist Trajectories // AIAA/AAS Astrodyn. Specialist Conf. and Exhibit, Monterey, AIAA Paper 2002-4717, 2002. P. 1–7.
Strange N.J., Russell R., Buffington B. Mapping the V-infinity Globe // AIAA/AAS Space Flight Mechanics Meeting, AAS Paper 07-277, 2007.
Tisserand F.F. Traité de Mecanique céléste. V. 4. Gauthier-Villars et fils. Paris, 1896. P. 203–205.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник


