Астрономический вестник, 2019, T. 53, № 5, стр. 323-338
Особенности динамики объектов, движущихся в окрестности резонанса 1 : 3 с вращением Земли
И. В. Томилова a, *, Е. В. Блинкова a, **, Т. В. Бордовицына a, ***
a Томский государственный университет
Томск, Россия
* E-mail: irisha_tom@mail.ru
** E-mail: zbizk322@mail.ru
*** E-mail: tvbord@sibmail.com
Поступила в редакцию 05.03.2019
После доработки 22.03.2019
Принята к публикации 26.03.2019
Аннотация
В работе представлены результаты исследования динамической структуры околоземного орбитального пространства в области резонанса 1 : 3 со скорость вращения Земли. Приведены результаты обширного численно-аналитического эксперимента по исследованию орбитальной эволюции объектов, движущихся в диапазоне больших полуосей от 20250 до 20280 км, с наклонениями от 0 до 90 градусов. Выявлены зоны действия в ней пяти компонент орбитального резонанса и апсидально-нодальных вековых резонансов низких порядков. Даны карты распределения выявленных резонансов. Представлен анализ динамической структуры орбитального пространства, полученный с использованием быстрой ляпуновской характеристики MEGNO и дана MEGNO-карта области в сечении плоскостью (наклонение орбиты, большая полуось). Показано, что особенностью динамической эволюции большинства исследованных орбит является хаотичность, возникающая под действием наложения резонансов различных типов.
ВВЕДЕНИЕ
Исследование динамической структуры околоземного орбитального пространства актуальная задача, поскольку знание динамических особенностей различных областей этого пространства необходимо и при разработке новых спутниковых систем и при определении областей паркинга отработавших объектов. Авторы настоящей работы планируют построить динамическую структуру всего околоземного орбитального пространства и это только вторая работа из запланированной серии. Первая работа (Томилова и др., 2018) посвящена исследованию динамической структуры области функционирования глобальных навигационных спутниковых систем (ГНСС).
Самой интересной в динамическом плане является структура областей, где действуют резонансы низких порядков между средним движением спутника и скоростью вращения Земли. К таким областям относится рассматриваемая здесь область резонанса 1 : 3 с вращением Земли. Эта область околоземного космического пространства мало изучена. В работе Кузнецова и др. (2012) посвященной исследованию влияния светового давления на эволюции объектов, движущихся в окрестности резонансов низких порядков, для резонанса 1 : 3 со скоростью вращения Земли была определена область действия этого резонанса по большой полуоси. Правда, при этом не было указано, для каких наклонений эти оценки были получены. Кроме того отмечалось, что зона резонанса является очень узкой и при большой парусности (т.е. большом отношении миделевого сечения к массе) объект может покидать область данного резонанса. Никакие другие динамические характеристики области не рассматривались.
Целью данной работы является детальное исследование динамической структуры области резонанса 1 : 3 со скоростью вращения Земли и особенностей долговременной орбитальной эволюции объектов, движущихся в этой области. При этом мы не рассматриваем влияние светового давления на объекты, поскольку это возмущение не имеет прямого отношения к динамической структуре пространства, а связано с параметрами исследуемого объекта. Мы не рассматриваем также влияние на динамическую эволюцию параметров вывода объекта в точку стояния.
Для реализации поставленной цели были решены следующие задачи:
– исследована динамическая структура орбитального пространства с использованием быстрой ляпуновской характеристики MEGNO (Mean Exponential Growthof Nearby Orbits) (Cincotta и др., 2003) и построена соответствующая динамическая карта области;
– произведен анализ резонансных возмущений, действующих на движение объектов в рассматриваемой орбитальной области;
– выявлены особенности динамической эволюции орбит под действием резонансов.
МЕТОДИКА ИССЛЕДОВАНИЯ
Для исследования динамической структуры движения объектов, находящихся в окрестности резонанса 1 : 3 со скоростью вращения Земли, применялась методика, изложенная в (Томилова и др., 2018). Методика состоит из нескольких этапов:
– построение динамической карты области с использованием быстрой ляпуновской характеристики MEGNO (Cincotta, Simo, 2000; Cincotta и др., 2003; Valk и др., 2009);
– анализ структуры всех резонансных возмущений, действующих на движение объектов рассматриваемой орбитальной области;
– изучение особенностей долговременной эволюции орбит.
Численное моделирование движения объектов осуществлялось на кластере “СКИФ Cyberia” ТГУ с использованием программного комплекса “Численная модель движения систем ИСЗ” (Александрова и др., 2017), построенного с использованием высокоточного интегратор Гаусса–Эверхарта (Авдюшев, 2010). В процессе моделирования учитывались возмущения от гармоник геопотенциала до 10 порядка и степени, а также возмущения от Луны и Солнца. Совместно с уравнениями движения интегрировались уравнения для вычисления параметров MEGNO (Бордовицына и др., 2010).
Выявление орбитальных резонансов производилось по методике предложенной Allan (1967a; 1967b) и уточненной Кузнецовым (Кузнецов и др., 2012).
Резонансные (критические) аргументы ищутся в виде
(1)
$\begin{gathered} {{\Phi }_{1}} = u(M + \Omega + \omega ) - {v}\theta , \\ {{\Phi }_{2}} = u(M + \omega ) + {v}(\Omega - \theta ), \\ {{\Phi }_{3}} = uM + {v}(\Omega + \omega - \theta ), \\ {{\Phi }_{4}} = {{\Phi }_{1}} - \nu \Omega ,\,\,\,\,{{\Phi }_{5}} = {{\Phi }_{3}} + \nu \Omega - 2\nu \omega , \\ \end{gathered} $(2)
$\begin{gathered} {{{\dot {\Phi }}}_{1}} = u(\dot {M} + \dot {\Omega } + \dot {\omega }) - {v}\dot {\theta }, \\ {{{\dot {\Phi }}}_{2}} = u(\dot {M} + \dot {\omega }) + {v}(\dot {\Omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{3}} = u\dot {M} + {v}(\dot {\Omega } + \dot {\omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{4}} = {{{\dot {\Phi }}}_{1}} - \nu \dot {\Omega },\,\,\,\,{{{\dot {\Phi }}}_{5}} = {{{\dot {\Phi }}}_{3}} + \nu \dot {\Omega } - 2\nu \dot {\omega }, \\ \end{gathered} $Для рассматриваемого в данной работе резонанса 1 : 3 со скоростью вращения Земли соотношения (1) примут вид
(3)
$\begin{gathered} {{\Phi }_{1}} = (M + \Omega + \omega ) - 3\theta , \\ {{\Phi }_{2}} = (M + \omega ) + 3(\Omega - \theta ), \\ {{\Phi }_{3}} = M + 3(\Omega + \omega - \theta ), \\ {{\Phi }_{4}} = M - 2\Omega + \omega - 3\theta , \\ {{\Phi }_{5}} = M + 3( - \omega + 2\Omega - \theta ), \\ \end{gathered} $(4)
$\begin{gathered} {{{\dot {\Phi }}}_{1}} = (\dot {M} + \dot {\Omega } + \dot {\omega }) - 3\dot {\theta }, \\ {{{\dot {\Phi }}}_{2}} = (\dot {M} + \dot {\omega }) + 3(\dot {\Omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{3}} = \dot {M} + 3(\dot {\Omega } + \dot {\omega } - \dot {\theta }), \\ {{{\dot {\Phi }}}_{4}} = \dot {M} - 2\dot {\Omega } + \dot {\omega } - 3\dot {\theta }, \\ {{{\dot {\Phi }}}_{5}} = \dot {M} + 3( - \dot {\omega } + 2\dot {\Omega } - \dot {\theta }). \\ \end{gathered} $Исследование структуры вековых резонансов осуществлялось при помощи методики, которая была изложена в работе (Бордовицына и др., 2012), и дополнена в (Бордовицына, Томилова, 2016).
Также, как и в случае с орбитальным резонансом, изучается эволюция во времени резонансных аргументов, полученных из аргументов возмущающей функции для однократно (5) и двукратно (6) осредненной ограниченной задачи трех тел
(5)
$\begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } = (l - 2p{\text{'}} + q{\text{'}})M{\text{'}} + (l - 2p)\omega - \\ - \,\,(l - 2p{\text{'}})\omega {\text{'}} + \bar {m}(\Omega - \Omega {\text{'}}), \\ \end{gathered} $(6)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = (l - 2p)\omega - (l - 2p{\text{'}})\omega {\text{'}} + \bar {m}(\Omega - \Omega {\text{'}}),$(7)
$\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } \approx 0,\,\,\,\,\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } } \approx 0,$(8)
$\begin{gathered} M{\text{'}} = M_{0}^{'} + \overline {n{\text{'}}} \left( {t - {{t}_{0}}} \right),\,\,\,\,\omega {\text{'}} = \omega _{0}^{'} + \dot {\omega }{\text{'}}\left( {t - {{t}_{0}}} \right), \\ \Omega {\text{'}} = \Omega _{0}^{'} + \dot {\Omega }{\text{'}}\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega = {{\omega }_{0}} + \dot {\omega }\left( {t - {{t}_{0}}} \right), \\ \Omega = {{\Omega }_{0}} + \dot {\Omega }\left( {t - {{t}_{0}}} \right). \\ \end{gathered} $(9)
$\begin{gathered} {{{\dot {\Omega }}}_{{{{J}_{2}}}}} = - \frac{3}{2}{{J}_{2}}\bar {n}{{\left( {\frac{{{{r}_{0}}}}{a}} \right)}^{2}}\cos i{{(1 - {{e}^{2}})}^{{ - 2}}}, \\ {{{\dot {\omega }}}_{{{{J}_{2}}}}} = \frac{3}{4}{{J}_{2}}\bar {n}{{\left( {\frac{{{{r}_{0}}}}{a}} \right)}^{2}}\frac{{5{{{\cos }}^{2}}i - 1}}{{{{{(1 - {{e}^{2}})}}^{2}}}}, \\ \end{gathered} $(10)
$\begin{gathered} {{{\dot {\Omega }}}_{{L,S}}} = - \frac{3}{{16}}\bar {n}\frac{{m_{{L,S}}^{'}}}{{{{m}_{ \oplus }}}}{{\left( {\frac{a}{{a{\text{'}}}}} \right)}^{3}}\frac{{2 + 3{{e}^{2}}}}{{\sqrt {1 - {{e}^{2}}} }}(2 - 3{{\sin }^{2}}i{\text{'}})\cos i, \\ {{{\dot {\omega }}}_{{L,S}}} = \frac{3}{{16}}\bar {n}\frac{{m_{{L,S}}^{'}}}{{{{m}_{ \oplus }}}}{{\left( {\frac{a}{{a{\text{'}}}}} \right)}^{3}}\frac{{4 - 5{{{\sin }}^{2}}i + {{e}^{2}}}}{{\sqrt {1 - {{e}^{2}}} }}(2 - 3{{\sin }^{2}}i{\text{'}}). \\ \end{gathered} $Если резонансный аргумент испытывает либрационное изменение во времени, то резонанс считается устойчивым, а при циркуляционном изменении – неустойчивым (Мюррей, Дермотт, 2010).
Полагая в формуле (6) индексы, равными l = = 2, p, p', $\bar {m}$ = 0, 1, 2, q' = –1, 0, 1, можно получить все вековые резонансные соотношения низких порядков. Эти соотношения можно разделить на 4 группы или класса: резонансные соотношения, связанные со средним движением Солнца, резонансные соотношения, связанные со средним движением Луны, апсидально-нодальные резонансы, связанные с Солнцем, и аналогичные резонансы, связанные с Луной, причем геометрический резонанс Лидова (1961)–Козаи (1962) $\dot {\omega } = 0,$ является частным случаем апсидально-нодальных резонансов и представляет собой вековой резонанс первого порядка. В табл. 1 приведен набор апсидально-нодальных резонансов до четвертого порядка включительно. В табл. 2. приведена группа связанных со средним движением возмущающего тела резонансных соотношений второго–пятого порядков. Поскольку величины $\dot {\omega }_{S}^{'}$ и $\dot {\Omega }_{S}^{'},$ связанные с прецессией орбиты Земли, пренебрежимо малы, формулы, приведенные в табл. 1 для апсидально-нодальных резонансов, связанных с Солнцем, существенно упрощаются. Эти резонансы практически превращаются в геометрические резонансы, связывающие только собственные вековые частоты, возникающие в движении спутника под действием возмущений от Солнца.
Таблица 1.
Типы вековых апсидально-нодальных резонансов до четвертого порядка
| № | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
|---|---|---|---|---|---|---|---|
| 1 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ | 5 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }_{{S,L}}^{'}$ | 9 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }$ | 13 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right)$ |
| 2 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ | 6 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }_{{S,L}}^{'}$ | 10 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }$ | 14 | $\dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ |
| 3 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ | 7 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }$ | 11 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }_{{S,L}}^{'}$ | 15 | $\dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ |
| 4 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ | 8 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }$ | 12 | $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }_{{S,L}}^{'}$ | 16 | $\dot {\omega }$ |
Таблица 2.
Типы вековых резонансов со скоростью движения возмущающего тела второго–пятого порядков
| № | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
№ | Тип резонансного соотношения |
|---|---|---|---|---|---|---|---|
| 1 | $\bar {n}_{{S,L}}^{'} - \dot {\omega }$ | 5 | $\bar {n}_{{S,L}}^{'} - (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 9 | $\bar {n}_{{S,L}}^{'} - \dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 13 | $\bar {n}_{{S,L}}^{'} - 2\dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\text{'}})$ |
| 2 | $\bar {n}_{{S,L}}^{'} + \dot {\omega }$ | 6 | $\bar {n}_{{S,L}}^{'} + (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 10 | $\bar {n}_{{S,L}}^{'} + \dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 14 | $\bar {n}_{{S,L}}^{'} + 2\dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\text{'}})$ |
| 3 | $\bar {n}_{{S,L}}^{'} - 2\dot {\omega }$ | 7 | $\bar {n}_{{S,L}}^{'} + \dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 11 | $\bar {n}_{{S,L}}^{'} - 2(\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 15 | $\bar {n}_{{S,L}}^{'} - 2\dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\text{'}})$ |
| 4 | $\bar {n}_{{S,L}}^{'} + 2\dot {\omega }$ | 8 | $\bar {n}_{{S,L}}^{'} - \dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 12 | $\bar {n}_{{S,L}}^{'} + 2(\dot {\Omega } - \dot {\Omega }{\text{'}})$ | 16 | $\bar {n}_{{S,L}}^{'} + 2\dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\text{'}})$ |
Следует отметить, что классификация основной части вековых резонансов, действующих на движение ИСЗ, была впервые дана Дж. Куком (Cook, 1962), а аналитическая теория вековых спутниковых резонансов представлена в работах (Breiter, 2001a; 2001b; Daquin et al., 2016). Hughes (1980; 1981) был первым, кто предложил использовать численное моделирование в исследовании влияния вековых резонансов, а в работах (Chao, Gick, 2004; Rossi, 2008) были впервые применены совместно аналитический и численный подходы к исследованию проблемы.
Кроме формул (1)–(10), в применяемой здесь методике для более надежного определения устойчивости резонанса используются динамические портреты резонансов, которые строятся в фазовой плоскости (Мюррей, Дермотт, 2010; Морбиделли, 2002)
где е – эксцентриситет орбиты спутника, ψ – критический аргумент.ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ СТРУКТУРЫ ОРБИТАЛЬНОГО ПРОСТРАНСТВА
Общая оценка динамической структуры области резонанса 1 : 3 со скоростью вращения Земли осуществлялась на основе результатов численного эксперимента, который проводился по методике, изложенной в предыдущем разделе. Принимались во внимание только гравитационные возмущения, определяемые влиянием несферичности гравитационного поля Земли, а также притяжением Луны и Солнца.
Все исследования проводились на модельных объектах, которые были распределены равномерно в интервале больших полуосей от 20 250 до 20 280 км с шагом в 200 м, в диапазоне наклонений от 0° до 90° с шагом 10° и начальным эксцентриситетом, равным 0.01. Расчет орбитальной эволюции проводился на интервале 100 лет.
Первоначально был проведен MEGNO-анализ динамической структуры рассматриваемой области.
На рис. 1 приведена MEGNO-карта области резонанса 1 : 3 со скоростью вращения Земли.
Рис. 1.
MEGNO-карта области резонанса 1 : 3 со скоростью вращения Земли. Пунктирной линией обозначена область, где усредненный параметр MEGNO равен двум.
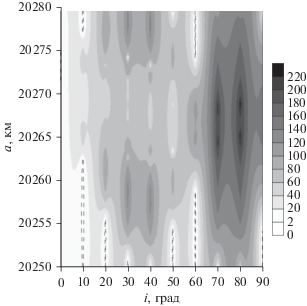
Пунктирной линией на рис. 1 обозначена область, где усредненный параметр MEGNO равен двум.
Данные, приведенные на рис. 1, показывают, что область резонанса 1 : 3 со скоростью вращения Земли отличается высокой хаотичностью движения объектов. Причем наиболее хаотична приполярная область.
Как известно (Бордовицына и др., 2012), хаотичность в движении объектов возникает вследствие одновременного действия на движение объектов резонансов различных типов, поэтому был проведен детальный анализ по выявлению всех действующих на объекты резонансов.
Прежде всего, был выполнен поиск орбитальных резонансов. Для этого исследовалась близость к нулю резонансных соотношений (4), затем определялось наличие либрации в поведении критических аргументов (3) на столетнем интервале времени. Кроме того, для каждого объекта были построены фазовые портретыв плоскости (11) для оценки устойчивости резонанса.
Поведение критического аргумента можно разделить на 3 типа: циркуляция (рис. 2), циркуляция-либрация (рис. 3) и либрация (рис. 4). Как известно (Мюррей, Дермотт, 2010) либрация критического аргумента и незамкнутость фазового портрета говорят об устойчивости резонанса. Состояние “циркуляция-либрация” свидетельствует о неустойчивости резонанса, а наличие циркуляции считается отсутствием резонанса.
Рис. 2.
Пример циркуляции: динамика резонансного соотношения ${{\dot {\Phi }}_{2}}$, критического аргумента Φ2 и фазовый портрет при a = 20 264,6 км, i = 0°.
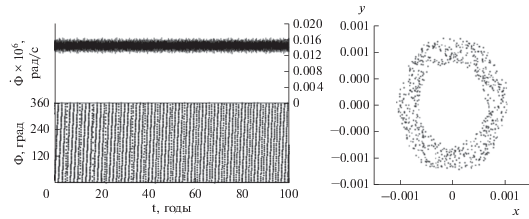
Рис. 3.
Пример циркуляции-либрации: динамика резонансного соотношения ${{\dot {\Phi }}_{1}}$, критического аргумента Φ1 и фазовый портрет при a = 20 268 км, i = 70°.
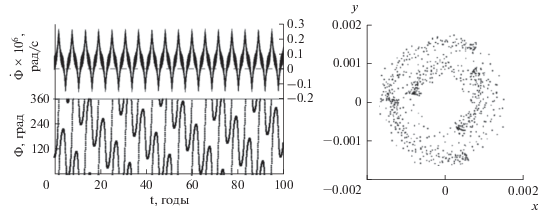
Рис. 4.
Пример либрации: динамика резонансного соотношения ${{\dot {\Phi }}_{5}}$, критического аргумента Φ5 и фазовый портрет при a = 20264,6 км, i = 60°.
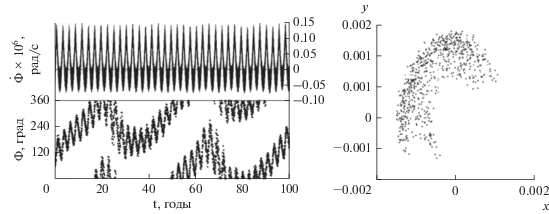
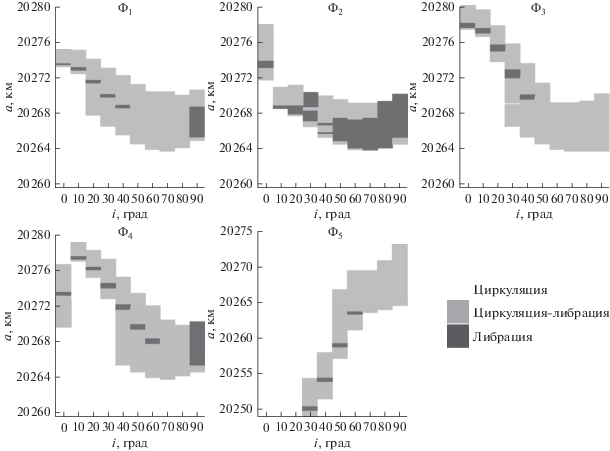
На основе этого были определены зоны действия мультиплетов (2) для всей рассматриваемой области (рис. 5). При построении рисунка, однако, из графиков были исключены области, где наблюдается только циркуляция. Это область в интервале от 20 250 до 20 260 км по большой полуоси для ${{\Phi }_{1}}$–${{\Phi }_{4}}$ и от 20 275 до 20 280 км для ${{\Phi }_{5}}.$
Приведенные на рис. 5 оценки показывают, что зоной действия резонанса 1 : 3 со скоростью вращения Земли следует считать область, простирающуюся по большой полуоси от 20 250 до 20 280 км, а по наклонению от 0° до 90°.
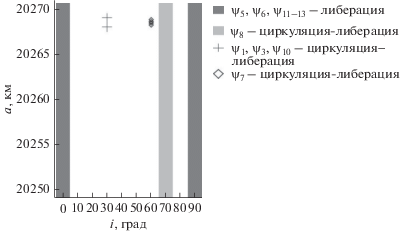
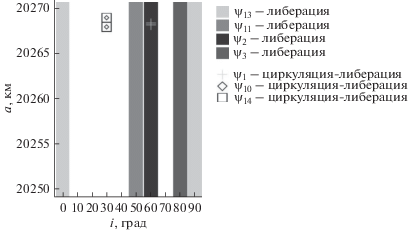
На рис. 6 показано распределение апсидально-нодальных вековых резонансов, связанных с Солнцем, а на рис. 7 – связанных с Луной. На рисунках для краткости введены такие обозначения: ψ – критический аргумент векового резонанса, а приписанный ему номер есть номер типа резонанса из табл. 1.
Как показывают приведенные на рис. 6 и 7 данные, в рассматриваемой области орбитального пространства действуют 5 устойчивых апсидально-нодальных резонансов, связанных с Солнцем, и четыре устойчивых резонанса, связанных с Луной. В области от 10° до 40° по наклонению вообще не обнаружено вековых резонансов. В области больших полуосей от 20 268 до 20 269 км проявляют свое действие несколько неустойчивых резонансов, связанных как с Луной, так и с Солнцем, но только для наклонений 30° и 60°.
Кроме того, исследования показали, что в рассматриваемой области орбитального пространства нет устойчивых резонансов с движением возмущающих тел.
Полученные сведения о распределении резонансов были сопоставлены с орбитальной эволюцией объектов. Общие данные о вековых и долгопериодических возмущениях объектов рассматриваемой резонансной зоны приведены на рис. 8 и 9.
Рис. 8.
Размеры амплитуд долгопериодических колебаний больших полуосей в зависимости от величин параметров a и i.
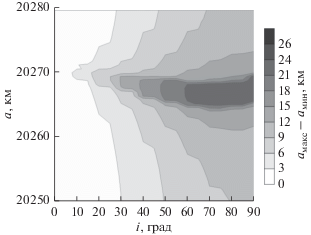
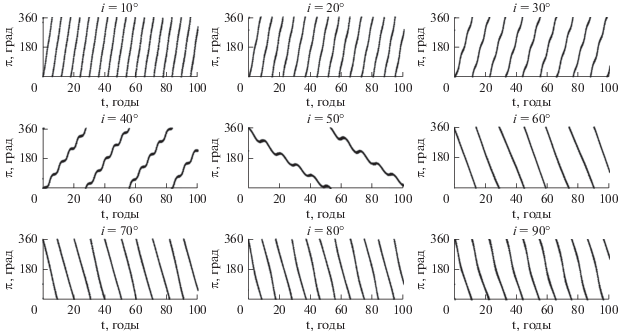
Рис. 9.
Вековые и долгопериодические колебания долготы перицентра от узла в зависимости от наклонения орбиты.
На рис. 8 показана зависимость величин амплитуд долгопериодических колебаний больших полуосей от величин основных параметров орбит: большой полуоси a объекта и наклонения его орбиты i.
Данные, приведенные на рис. 9, выявляют зависимость скорости прецессии орбиты от ее наклонения. Зависимость прецессии от большой полуоси внутри рассматриваемой области не обнаружена.
Представленные на рис. 8 и 9 данные хорошо коррелируют с данными о распределении мультиплетов орбитального резонанса и вековых резонансов, приведенных на рис. 5–7.
Сопоставляя эти данные, можно сделать вывод, что существенную роль в увеличении амплитуды долгопериодических колебаний играет орбитальный резонанс, поскольку амплитуды растут по всей области изменения наклонений от 10° и до 90°. Особенно большие значения амплитуд приходятся на область наложения резонансных мультиплетов и вековых резонансов при наклонениях от 50° до 90°. Существенное уменьшение скорости прецессии орбиты приходится на зону действия вековых апсидально-нодальных резонансов $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }_{{S,L}}^{'}$ и $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } + \dot {\omega }_{{S,L}}^{'}.$
Рассмотрим орбитальную эволюцию конкретных объектов исследуемой области орбитального пространства в зависимости от действия на движение объектов резонансов различных типов.
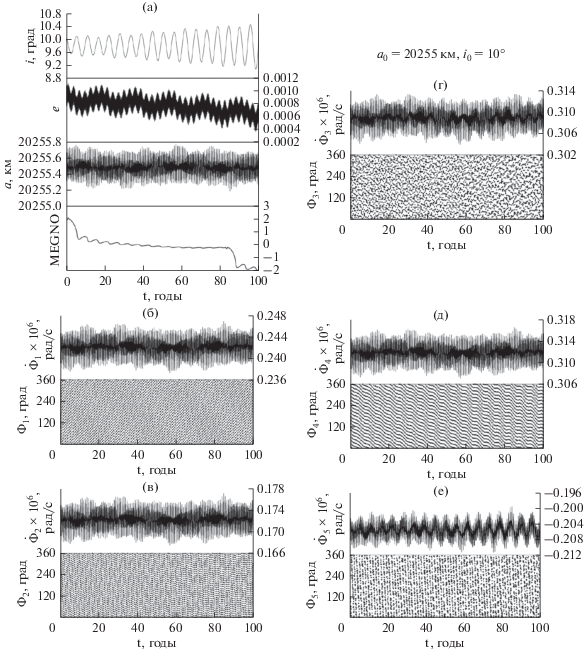
Для начала, приведем пример объекта, который движется в области отсутствия резонансов (рис. 10). Все компоненты мультиплета циркулируют, что говорит об отсутствии орбитальных резонансов. Вековых резонансов в данной области также не было обнаружено. На объект не действуют факторы, которые могли бы существенно изменить его движение. Об этом свидетельствует и параметр MEGNO, который на протяжении всего столетнего интервала времени осциллирует около нуля.
Рис. 10.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$ ${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$ ${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$ ${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$ ${{\Phi }_{5}}.$
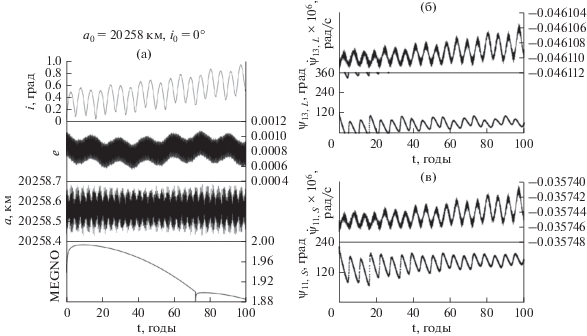
На рис. 11 показана эволюция орбиты объекта, на который действуют два устойчивых вековых резонанса связанные с Солнцем и Луной. Несмотря на их присутствие, параметр MEGNO близок к 2.
Рис. 11.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{13}}},\,\,{{\psi }_{{13}}},$ связанного с Луной; (в) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{11}}},\,\,{{\psi }_{{11}}},$ связанного с Солнцем.
Далее следует интересный пример движения в области устойчивого орбитального резонанса и трех неустойчивых вековых резонансов, связанных с Луной и Солнцем (рис. 12).
Рис. 12.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$${{\Phi }_{5}};$ (ж) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{10}}},\,\,{{\psi }_{{10}}},$ связанного с Луной; (з) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{14}}},\,\,{{\psi }_{{14}}},$ связанного с Луной; (и)- эволюция параметров векового резонанса ${{\dot {\psi }}_{1}},\,\,{{\psi }_{1}},$ связанного с Солнцем.
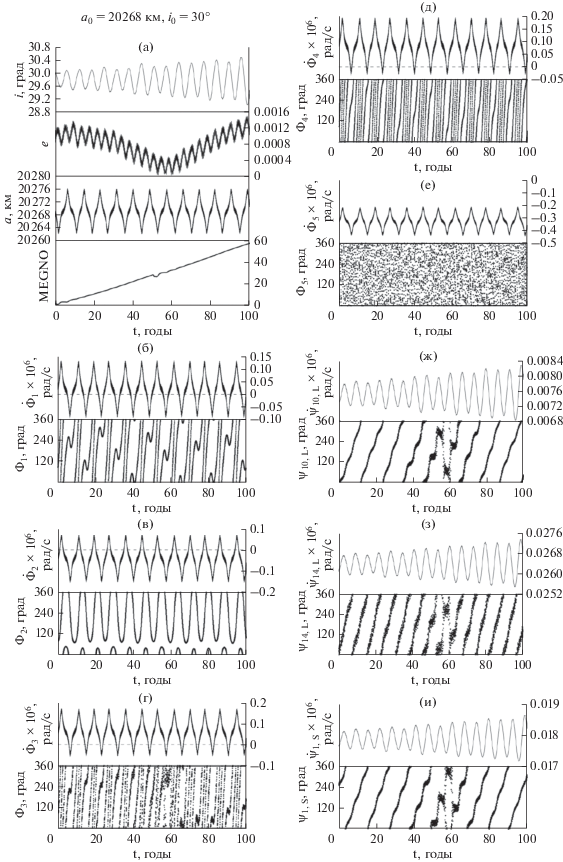
На рис. 12 объект находится в зоне острого орбитального резонанса, резонансные аргументы четырех компонент мультиплета переходят через нулевые значения, критический аргумент второй компоненты уверенно либрирует, а критический аргумент первой компоненты многократно меняет циркуляционные колебания на либрационные и обратно. Параметр MEGNO растет быстро.
На интервале времени от 50 до 70 лет начинают проявлять свое действие одновременно три вековых резонанса, в результате чего значение эксцентриситета, которое за первые 50 лет практически опустилось до нуля, начинает расти.
Следующий пример демонстрирует орбитальную эволюцию объекта, на который действует устойчивый вековой резонанс, связанный с Луной (рис. 13). Движение происходит в области острого орбитального резонанса. Все резонансные соотношения компонентов мультиплета проходят через нулевые значения. Критический аргумент второго типа вначале временного интервала имеет либрационные колебания, но под действием векового резонанса начинает менять свое поведение на циркуляцию. В тот же момент, все остальные критические аргументы начинают испытывать некоторые изменения, оставаясь в состоянии “циркуляция-либрация”. В результате такого действия резонансов, показатель MEGNO стремительно растет.
Рис. 13.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$ ${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$ ${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$ ${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$ ${{\Phi }_{5}};$ (ж) – эволюция параметров векового резонанса ${{\dot {\psi }}_{3}},\,\,{{\psi }_{3}},$ связанного с Луной.
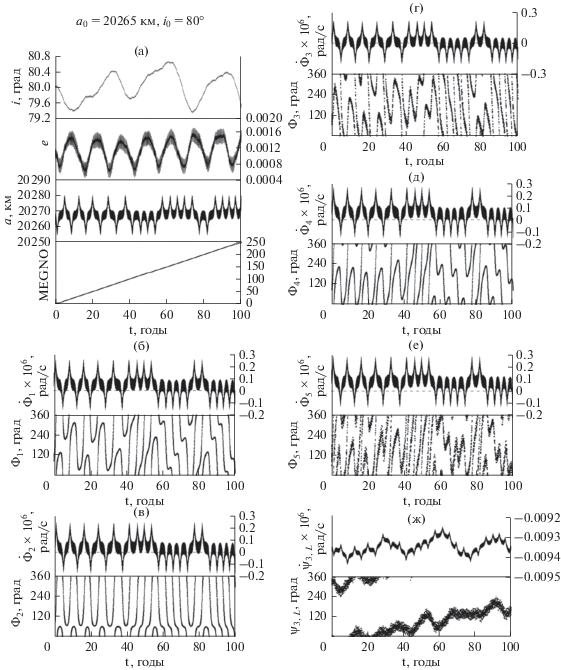
Приведем два характерных примера для объектов, имеющих одинаковое наклонение и близкие значения большой полуоси (рис. 14 и 15). И в том, и в другом случаях оба объекта находятся в зоне острого резонанса, резонансные аргументы всех компонент мультиплета переходят через нулевые значения. Вековые резонансы у объектов одни и те же. Но на более низкой орбите (рис. 14) критические аргументы циркулируют первую половину временного интервала и примерно через 50 лет на объект начинают действовать устойчивые орбитальные резонансы первого, второго и четвертого типов. В результате этого объект на рис. 14 переходит на более высокую орбиту. На второй объект (рис. 15) три орбитальных резонанса действуют на всем столетнем интервале, поэтому большая полуось не подверглась изменениям.
Рис. 14.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$ ${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$ ${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$ ${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$ ${{\Phi }_{5}};$ (ж) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{13}}},\,\,{{\psi }_{{13}}},$ связанного с Луной; (з) – эволюция параметров векового резонанса ${{\dot {\psi }}_{5}},\,\,{{\psi }_{5}},$ связанного с Солнцем.
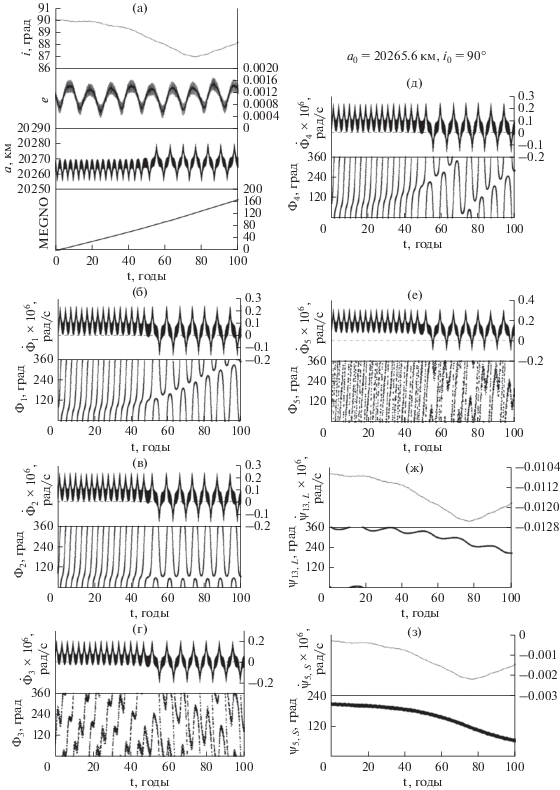
Рис. 15.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$ ${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$ ${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$ ${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$ ${{\Phi }_{5}};$ (ж) – эволюция параметров векового резонанса ${{\dot {\psi }}_{{13}}},\,\,{{\psi }_{{13}}},$ связанного с Луной; (з) – эволюция параметров векового резонанса ${{\dot {\psi }}_{5}},\,\,{{\psi }_{5}},$ связанного с Солнцем.
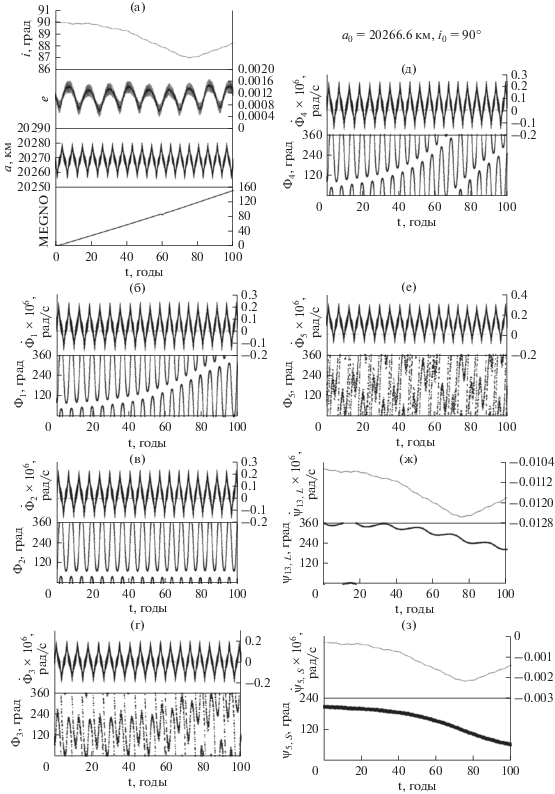
Комплексное действие всех выявленных резонансов влечет быстрый рост MEGNO параметра.
Далее приведем пример объекта, движущегося в зоне действия неустойчивого орбитального резонанса (рис. 16). В этой области все резонансные соотношения компонентов мультиплета проходят через нулевые значения, а все критические аргументы имеют состояние “циркуляция-либрация”. В то же время на объект действует устойчивый апсидально-нодальный резонанс ${{\dot {\psi }}_{2}} = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right) - \dot {\omega } + \dot {\omega }_{L}^{'}$ с Луной.
Рис. 16.
(а) – эволюция основных орбитальных элементов и параметров MEGNO; (б) – эволюция ${{\dot {\Phi }}_{1}},$ ${{\Phi }_{1}};$ (в) – эволюция ${{\dot {\Phi }}_{2}},$ ${{\Phi }_{2}};$ (г) – эволюция ${{\dot {\Phi }}_{3}},$ ${{\Phi }_{3}};$ (д) – эволюция ${{\dot {\Phi }}_{4}},$ ${{\Phi }_{4}};$ (е) – эволюция ${{\dot {\Phi }}_{5}},$ ${{\Phi }_{5}};$ (ж) – эволюция параметров векового резонанса ${{\dot {\psi }}_{2}},\,\,{{\psi }_{2}},$ связанного с Луной; (з) – эволюция параметров векового резонанса ${{\dot {\psi }}_{7}},\,\,{{\psi }_{7}},$ связанного с Луной.
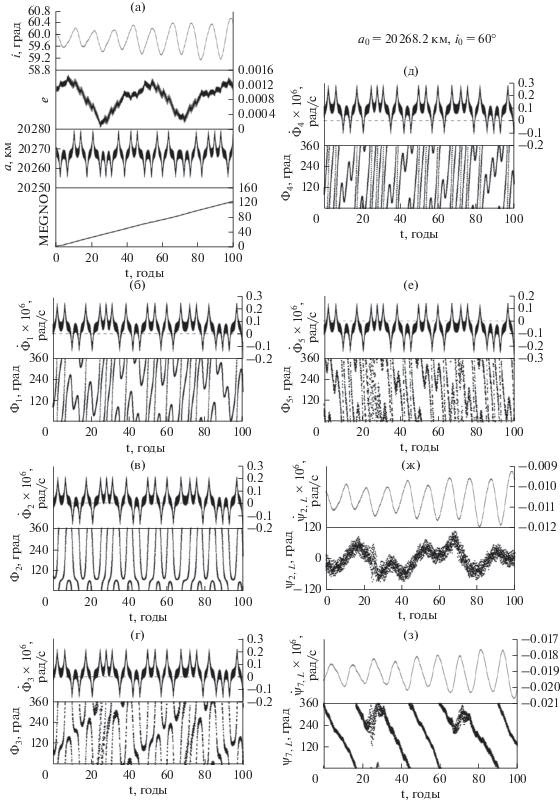
В результате такого влияния, значение эксцентриситета начинает стремительно уменьшаться. В момент, когда эксцентриситет становится близок к нулю, на объект начинает действовать другой вековой резонанс ${{\dot {\psi }}_{7}} = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right) + 2\dot {\omega }$ с Луной, который вытягивает орбиту и эксцентриситет начинает стремительно расти. Такое действие неустойчивого векового резонанса наблюдается дважды на протяжении столетнего интервала.
Таким образом, в рамках проведенных исследований можно утверждать, что в области действия резонанса 1 : 3 со скоростью вращения Земли большинство объектов показывают высокую хаотичность движения. Причем это можно объяснить наложением резонансов различных типов.
ЗАКЛЮЧЕНИЕ
В данной работе представлены результаты анализа динамики околоземных объектов, движущихся в резонансе 1 : 3 со скоростью вращения Земли. Для выявления особенностей динамики в этой области были решены следующие задачи.
– Исследована динамическая структура орбитального пространства с использованием быстрой ляпуновской характеристики MEGNO (Cincotta, Simo, 2000; Cincotta и др., 2003; Valk и др., 2009) и построена соответствующая динамическая карта области.
– Произведен анализ резонансных возмущений, действующих на движение объектов, населяющих рассматриваемую орбитальную область; во внимание принимались только орбитальные резонансы пяти типов и вековые апсидально-нодальные резонансы. Были построены карты распределения резонансов;
– Выявлены особенности динамической эволюции орбит под действием рассмотренных резонансов.
Общий анализ орбитальной эволюции всех рассмотренных объектов говорит о том, что хаотичность возникает во всех случаях, когда хотя бы один из действующих резонансов неустойчив.
При использовании данной области околоземного космического пространства для развертывания спутниковых сетей или паркинга отработавших объектов нужно учитывать сложность динамической структуры области.
Работа выполнена по гранту РФФИ 18-32-00735мол_а “Исследование особенностей динамики околоземных космических объектов в условиях наложения резонансов различных типов”.
Список литературы
Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычисл. технологии. 2010. Т. 15. № 4. С. 31–47.
Александрова А.Г., Бордовицына Т.В., Чувашов И.Н. Численное моделирование в задачах динамики околоземных объектов // Изв. вузов. Физика. 2017. Т. 60. С. 69–76.
Бордовицына Т.В., Александрова А.Г., Чувашов И.Н. Комплекс алгоритмов и программ для исследования хаотичности в динамике искусственных спутников Земли // Изв. вузов. Физика. 2010. Т. 53. № 8/2. С. 14–21.
Бордовицына Т.В., Томилова И.В., Чувашов И.Н. Влияние вековых резонансов на долговременную орбитальную эволюцию неуправляемых объектов спутниковых радионавигационных систем в области МЕО // Астрон. вестн. 2012. Т. 46. № 5. С. 356–368. (Bordovitsyna T.V., Tomilova I.V., Chuvashov I.N. The effect of secular resonances on the long-term orbital evolution of uncontrollable objects on satellite radionavigation systems in the MEO region // Sol. Syst. Res. 2012. V. 46. Is. 5. P. 329–340.)
Бордовицына Т.В., Томилова И.В. Особенности структуры вековых резонансов в динамике околоземных космических объектов // Изв. вузов. Физика. 2016. Т. 59. № 3. С. 41–48.
Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Шагабутдинов А.И., Кудрявцев С.О. О влиянии светового давления на орбитальную эволюцию объектов, движущихся в окрестности резонансов низких порядков // Астрон. вестн. 2012. Т. 46. № 6. С. 480–488. (Kuznetsov E.D., Zakharova P.E., Glamazda D.V., Shagabutdinov A.I., Kudryavtsev S.O. Light pressure effect on the orbital evolution of objects moving in the neighborhood of low-order resonances // Sol. Syst. Res. 2012. V. 46. Is 6. P. 442–449.)
Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2010. 588 с.
Томилова И.В., Бордовицына Т.В., Красавин Д.С. Динамическая структура орбитального пространства ГЛОНАСС и GPS. Проблема утилизации отработавших объектов // Астрон. вестн. 2018. Т. 52. № 5. С. 463–478. (Bordovitsyna T.V., Tomilova I.V., Krasavin D.S. Dynamic Structure of the GLONASS and GPS Orbital Space: Problem of Disposal of Retired Objects // Sol. Syst. Res. 2018. V. 52. № 5. P. 450–465.)
Allan R.R. Resonance effects due to the longitude dependence of the gravitational field of a rotating primary // Planet. and Space Sci. 1967a. V. 15. P. 53–76.
Allan R.R. Satellites resonance with the longitude dependent gravity. II. Effects involving the eccentricity // Planet. and Space Sci. 1967b. V. 15. P. 1829–1845.
Breiter S. On the coupling of lunisolar resonances for Earth satellite orbits // Celest. Mech. Dyn. Astr.2001a. V. 80. P. 1–20.
Breiter S. Lunisolar resonances revisited // Celest. Mech. Dyn. Astr. 2001b. V. 81. P. 81–91.
Chao C., Gick R., Long-term evolution of navigation satellite orbits // Adv. Space Res. 2004. V. 34. P. 1221–1226.
Cincotta P.M., Simó C. Simple tools to study global dynamics in non-axisymmetric galactic potentials – I // Astron. and Astrophys. Suppl. 2000. V. 147. P. 205–228.
Cincotta P.M., Girdano C.M., Simo C. Phase space structure of multi-dimensional systems by means of the mean exponential growth factor of nearby orbits // Physica D. 2003. V. 182. P. 151–178.
Daquin J., Rosengren A.J., Alessi E.M., Deleflie F., Valsecchi G.B., Rossi A. The dynamical structure of the MEO region: long-term stability, chaos, and transport // CelestMechDynAstr. 2016. V. 124(4). P. 335–366.
Hughes S. Earth satellite orbits with resonant lunisolar perturbations, I. Resonances dependent only on inclination // Proc. Roy. Soc. Lond. 1980. A 372. P. 243–264.
Hughes S. Earth satellite orbits with resonant lunisolar perturbations, II. Some resonances dependent on the semi-major axis, eccentricity and inclination // Proc. Roy. Soc. Lond. 1981. A 375. P. 379–396.
Rossi A. Resonant dynamics of Medium Earth Orbits: space debris // Celest. Mech. and Dyn. Astron. 2008. V. 100 P. 267–286.
Valk S., Delsate N., Lemaitre A., Carletti T. Global dynamics of high area-to-mass ratios GEO space debris by means of the MEGNO indicator // Adv. Space Res. 2009. V. 43. P. 1509–1526.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник