Астрономический вестник, 2019, T. 53, № 6, стр. 436-455
Термодинамика Реньи как обязательный опорный базис при моделировании эволюции протопланетного газопылевого диска с фрактальной структурой
А. В. Колесниченко a, *, М. Я. Маров b, **
a Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
b Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия
* E-mail: kolesn@keldysh.ru
** E-mail: marovmail@yandex.ru
Поступила в редакцию 12.03.2019
После доработки 26.04.2019
Принята к публикации 13.06.2019
Аннотация
В рамках проблемы математического моделирования процессов формирования протопланетезималей в солнечном допланетном диске, с учетом фрактальных представлений о свойствах дисперсных пылевых агрегатов в дисковой среде, в работена основе параметрической энтропии Реньи сконструирована статистическая термодинамика для неэкстенсивных фрактальных систем и определены ее свойства. Установлено, что между термодинамикой Реньи неэкстенсивной систем, с одной стороны, и техникой получения фрактальных и мультифрактальных размерностей, опирающейся на геометрию и стохастику, существует тесная взаимосвязь. Показано, что временная эволюция замкнутой термодинамической системы к равновесному состоянию зависит от знака параметра деформации, являющегося мерой неэкстенсивности фрактальной системы. Обсуждаются различные варианты построения фрактальных размерностей разных порядков для фракталов и мультифракталов и проанализированы их особенности. Развитый подход позволяет с единых позиций на основе обобщенной гидродинамики с производными дробного порядка и термодинамики для фрактальных сред моделировать эволюцию космологических и космогонических объектов от галактик и газопылевых астрофизических дисков до космической пыли, специфической чертой которых является отдаленность и глобальность силовых взаимодействий между элементами системы, иерархичность (обычно мультифрактальность) геометрического и фазового пространств, большая дальность пространственно-временных корреляций, а также наличие асимптотически степенных статистических распределений.
ВВЕДЕНИЕ
Реконструкция процессов, лежащих в основе формирования планетных систем, находится на передовом рубеже современной астрофизики. Все большее значение приобретает математическое моделирование физических и химических механизмов, ответственных за формирование и эволюцию протопланетных газопылевых дисков, образование в них первичных твердых тел и их прогрессивный рост до размеров планетезималей/зародышей планет, включая многообразные процессы термической и динамической эволюции. Вещество протопланетного газопылевого диска представляет собой сложную систему различного фазового состава, плотности, температуры и степени ионизации, которые изменяются с радиальным расстоянием. В основном это неоднородная среда, состоящая из частиц газа и пыли различных размеров и происхождения. В общем случае эта среда представляет собой намагниченную пылевую плазму, находящуюся в состоянии турбулентности, свойства которой зависят от радиального иазимутального положения в диске (см. Колесниченко, Маров, 2009; Lissauer, de Pater, 2013; Marov, Kolesnichenko, 2013; Armitage, 2015).
В пренебрежении плазменными эффектами движение газопылевой дисковой среды наиболее адекватно моделируется в рамках механики гетерогенных турбулизованных сред с учетом физико-химических свойств фаз, тепло-массопереноса, вязкости, вариаций химических реакций, фазовых переходов, коагуляции, фрагментации, непрозрачности среды для приходящего излучения и др. Строгое математическое рассмотрение проблемы представлено, в частности, в работах (Сhavanis, 1999; Колесниченко, Маров, 2006; 2009; Marov, Kolesnichenko, 2013), в которых проанализирован характер динамического взаимодействия турбулентного газа и пыли, включая влияние изменения энергии турбулентности несущей фазы на поведение твердых частиц и обратное влияние пылевой компоненты надинамический и тепловой режимы газовой фазы, а также влияние турбулентных вихрей на фазовые превращения в среде (испарение, конденсация). С этими процессами связаны также аккумуляция частиц вследствие коагуляции и фрагментацияпри взаимных соударениях твердых частиц в потоке газа и оседании частиц через газ к средней плоскости диска, где они образуют геометрически тонкий уплощенный слой – пылевой субдиск (см. Mizuno, 1989; Dominik, Tielens, 1997; Cuzzi и др., 1993; Колесниченко, 2004; Колесниченко, Маров, 2006; Blum, Wurm, 2008). Последовательность эволюции протопланетного газопылевого диска вокруг родительской звезды включает, по современным представлениям, его уплотнение в центральной плоскости и распад на отдельные пылевые агрегаты (кластеры) вследствие возникновения различного типа неустойчивостей. Взаимодействие пылевых кластеров при их соударениях рассматриваетсяв качестве ключевого механизма образования и роста первичных твердых тел, служащих основой последующего формирования планетезималей и зародышей планет. Среди механизмов, способствующих формированию планетезималей, важное место принадлежит, наряду с гравитационной неустойчивостью, различным гидродинамическим неустойчивостям, в частности, так называемой потоковой неустойчивости двух фазного газопылевого слоя из-за ее способности концентрировать дисперсные частицы в плотные пылевые кластеры (Youdin, Goodman, 2005; Youdin, 2011; Shariff, Cuzzi, 2011; Yang, Johansen, 2014; Yang и др., 2017; Макалкин, Зиглина, 2018; Колесниченко, Маров, 2019).
Пылевые кластеры содержат частицы субмикронного размера, включая небулярную пыль и конденсаты дисковой среды. Последние образуются при различных температурах в зависимости от радиального расстояния: от тугоплавких соединений внепосредственной близости к протосолнцу до льдов за снеговой линией. Очевидно, помимо взаимодействия пылевых кластеров в дальнейшем росте важную роль играют процессы коагуляции/коалесценции, с чем связано образование более плотных структур. Сами кластеры могут содержать как плотные, так и рыхлые (пористые) частицы (Cuzzi и др., 1998; Kataoka и др., 2013). Пористой (fluffy) структурой, предположительно, обладают и самикластеры, подобно тенденции ледяных частиц сформировывать очень рыхлые (“пушистые”) образования фрактальной природы. Это значительно облегчает режим роста тел в диске за счет столкновительного взаимодействия кластеров и частиц внутри них. Процесс коагуляции малых (суб-) миллиметровых пылевых частиц протопланетного диска начинается с формирования разветвленных цепочечных структур – фрактальных нитей с размерами, значительно превышающими размер кластеров, которые, в конечном счете, и формируются из подобных цепочечных структур (Jullien, 1986). Затем в условиях эволюции дисковой системы такие нити перепутываются11 и образуют клубки – первичные фрактальные кластеры (ФК). В дальнейшем в процессе кластер-кластерной коагуляции происходит частичное их слияние с образованием крупных фрактальных агрегатов, являющихся основным структурообразующим элементом рыхлых протопланетезималей, возникающих в результате протекания физико-химических и динамических процессов, сходных с процессами роста ФК.
Важно отметить, что до последнего времени в большинстве теоретических моделей объединения пылевых частиц в допланетном диске изначально принималась компактная структура возникающих пылевых агрегатов (см., например, Ossenkopf, 1993; Ormel и др., 2007; Suyama и др., 2008; Wada и др., 2008; Okuzumi и др., 2011; Suyama и др., 2012). Однако, как теперь стало ясно, растущие благодаря взаимным столкновениям частиц пылевые образования могут иметь весьма ажурную структуру и чрезвычайно низкую объемную плотность (см., например, Cuzzi и др., 1998; Blum, 2004; Blum, Wurm, 2008; Estrada, Cuzzi, 2016). Подобные пушистые агрегаты, благодаря их чрезвычайно высокой пористости, являются стойкими к разрушительным столкновениям при высоких скоростях соударений, а их радиальный дрейф в диске является очень медленным. Для типичных ворсистых пылевых агрегатов, имеющих по сравнению с компактными пылевыми образованиями относительно большие геометрические поперечные сечения, меняется весь режим движения в несущем газовом потоке, в частности, изменяются условия возникновения потоковой неустойчивости в диске из-за значительной модификации аэродинамической силы трения пыли и газа. Кроме этого, может существенно измениться эффективность отталкивания при столкновении пористых структур (Колесниченко, Маров, 2009; 2014; Маров, Русол, 2018). Последующий процесс включает в себя непрерывный рост формирующихся тел, наиболее крупные из которых поглощают меньшие тела и пыль в результате столкновений и гравитационного притяжения, в то время как газ из внутренних областей диска постепенно теряется. В конечном итоге процесс взаимодействия пылевых кластеров приводит к образованию многочисленных более плотных планетезималей размером от десятков до сотен километров в поперечнике, а затем планетарных эмбрионов, изкоторых в конечном итоге формируются планеты (см., например, Wetherill, Stewart, 1989; Weidenschilling, 2000; Маров, 2005; Kolesnichenko, Marov, 2013).
Таким образом, для адекватного описания эволюции пылевых агрегатов в диске и, в конечном счете, механизма образования рыхлых протопланетезималей необходимо, в общем случае, привлекать к рассмотрению их фрактальные свойства и внутреннюю структуру. Однако в целом ряде классических работ (см., например, Сафронов, 1969; Weidenschilling, 1980; Nakagawa и др., 1981, Nakagawa и др., 1986; Wada и др., 2008; Suyama и др., 2012) моделирование велось в рамках “обычной” сплошной среды и зачастую не принимались во внимание много фракционность пылевой составляющей первичного протопланетного облака, а также фрактальная природа формирующихся в процессе его эволюции пылевых кластеров (изучались в основном компактные пылевые образования с постоянной плотностью или пористые тела). В отличие от этих исследований, нами в серии работ (Kolesnichenko, Cheverushkin, 2013; Колесниченко, 2016; 2017; Колесниченко, Маров, 2009; 2014; 2019; Kolesnichenko, Marov, 2013; Kolesnichenko, 2017) предлагалось рассматривать совокупность пылевых агрегатов, как особый тип сплошной среды − фрактальной среды22, для которой существуют точки и области, не заполненные ее частицами. Заметим, что дробный векторный анализ на фрактальных множествах, как обобщение математического анализа на гладких многообразиях, в настоящее время активно разрабатывается (см., например, Kilbas и др., 2003, 2006; Strichartz, 1999). В частности, разрабатываются различные варианты гидродинамического моделирования фрактальных сред, обладающих нецелой массовой размерностью33, что существенно облегчает их применение для различных прикладных задач (Tarasov, 2005; 2010).
Идея изучения сред фрактальной природы на основе меры Хаусдорфа принадлежит (Mandelbrot, 1975; 1977; 1982; Мандельброт, 2002). Им были получены нетривиальные результаты и построена соответствующая математическая теория. При этом центральная роль в определении фрактальной размерности была отведена энтропии Реньи (Renyi, 1961; 1970). В настоящее время интерес к изучению свойств фрактальных множеств на основе энтропии Реньи продолжает расти (см. Johal, Rai, 2000; Tsallis, 1995). Обзор уже полученных важных результатов можно найти, в частности, в работах (Шредер, 2001; Божокин, Паршин, 2001; Tsallis, 2002).
В отличие от классической статистики и теории информации, основанных на энтропии Больцмана−Гиббса−Шеннона, в цитируемых выше работах, А. Реньи впервые ввел в рассмотрение параметрическую $q$-энтропию и соответствующую ей различающую информацию44. Тем самым, А. Реньи предложил ясную формулу связи между энтропией и континуумом мультифрактальных размерностей, указав достаточно универсальный путь к решению проблемы фрактальной параметризации (Mandelbrot, 1974; 1975; 1977; 1982; Beck, Schlögl, 1993; Grassberger, 1981; 1985; Grassberger, Procaccia, 1984; Halsey и др., 1986; Hentschel, Procaccia, 1983; Федер, 1991; Смирнов, 1991; Beck, Schlogl, 1993; Кроновер, 2000; Шредер, 2001; Божокин, Паршин, 2001; Потапов, 2002; Jizba, Arimitsu, 2004). В дальнейшем функционалы Реньи сыграли важнейшую роль не только в физике фракталов и в теории информации, но и в различных областях статистической механики, описывающих динамические свойства нелинейных сложных систем. Последнее связано с тем, что между теорией фракталов, опирающейся на геометрию и теорию размерности, с одной стороны, и теорией хаоса, являющейся развитием теории динамических систем, существует тесная связь (Зарипов, 2002; 2010).
Отметим также, что важным преимуществом неэкстенсивной статистики Реньи является наличие степенной функции распределения вероятностей, появляющейся (при максимизации энтропии) вместо экспоненциальной функции распределения классической статистики Гиббса. Ее использование привело к значительному прогрессу, связанному с исследованиями ряда аномальных физических процессов, например, в ядерной физике (Nagy, Romera, 2009), в теории черных дыр (Bialas, Czyz, 2008), при изучении фрактальных и мультифрактальных систем в космологии (Peebles, 1980; Колесниченко, 2016), при производстве частиц высоких энергий (Kropivnitskaya, Rostovtsev, 2003) и т.п.
Вместе с тем, обобщенная термодинамика, основанная на энтропии Реньи, в отличие от термодинамики Тсаллиса (см., например, Kolesnichenko, Marov, 2014; Колесниченко, 2013; 2016; 2018a; 2018б; 2018в), все еще не нашла достойного применения при феноменологическом моделировании ряда космогонических явлений. В частности, при моделировании формирования протопланетезималей в солнечном допланетном облаке с учетом фрактальных представлений о свойствах пылевых кластеров в космической аэродисперсной среде в наших работах (Kolesnichenko, Marov, 2013; Колесниченко, Маров, 2014) была использована гидродинамическая модель для фрактальной среды (Tarasov, 2005; 2010), для которой существуют точки и области, не заполненные ее частицами. Однако, моделирование подобной среды, обладающей нецелой фрактальной размерностью, было проведено только в рамках дробно-интегральной гидродинамической модели (ее дифференциальной формы), использующей для учета фрактальности дробные интегралы, порядок которых определяется массовой размерностью фрактальных пылевых кластеров. К сожалению, универсальные законы термодинамики, основанной на энтропии Реньи (как меры хаоса) и взаимодополняющие ее методы фрактального анализа, обосновывающие технику построения дробных мер (мер структурной упорядоченности) фракталов для сложных нелинейных систем, не были привлечены к замыканию системы уравнений Навье−Стокса для фрактальных сред. Это упущение связано с тем, что эти, на первый взгляд, столь противоположные научные направления, совокупно описывающие процессы эволюции фрактальных сред, не разработаны в достаточно близком соотнесении между собой.
В связи с указанным обстоятельством, данная работа посвящена конструированию (на основе параметрических энтропии и различающей информации Реньи) статистической термодинамики фрактальных систем и разработке техники получения мультифрактальных размерностей (с определением их свойств), выполненных с учетом их взаимосвязи. Предложенный подход базируется на негиббсовом равновесном распределении состояний, полученном из условия экстремума энтропии Реньи при заданности осредненных динамических параметров, характеризующих аномальную систему, а также на осреднении этих параметров по эскортному (нормированному) распределению, удобному при рассмотрении фрактальных и мультифрактальных сред. Обсуждаются различные варианты построения мер (разных порядков) фракталов и мультифракталов на основе энтропии и информации различия Реньи и основные неравенства для полученных фрактальных размерностей. На базе двухпараметрической различающей информации рассмотрен перспективный подход к моделированию мультифрактальных мер с двумя характерными масштабами длины.
НЕКОТОРЫЕ СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭНТРОПИИ И ИНФОРМАЦИИ РАЗЛИЧИЯ РЕНЬИ
При аксиоматическом подходе теории вероятностей (Фадеев, 1956), для объекта (системы, процесса), который имеет дискретные случайные состояния, в работах (Havrda, Charvat, 1967; Daroczy, 1970; Rathie, Kannappan, 1972) на базе основополагающих работ (Renyi, 1961; 1970) дается строгий вывод следующих функционалов: однопараметрической $q$-энтропии Реньи $S_{q}^{R}(p)$ для дискретного распределения вероятностей ${{p}_{i}} \geqslant 0$
(1)
$\Sigma _{q}^{R}(p) = \left\{ {\begin{array}{*{20}{c}} {\frac{k}{{1 - q}}\ln \sum\limits_i^N {p_{i}^{q},\,\,\,\,q \ne 1;} } \\ { - k\sum\limits_i^N {{{p}_{i}}\ln {{p}_{i}},\,\,\,\,q = 1,} } \end{array}} \right.$(2)
$K_{q}^{R}(p:f) = \left\{ {\begin{array}{*{20}{c}} {\frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}f_{i}^{{1 - q}}} ,\,\,\,\,q \ne 1;} \\ {k\sum\limits_i^N {\left( {\ln \frac{{{{p}_{i}}}}{{{{f}_{i}}}}} \right){{p}_{i}},\,\,\,\,q = 1,} } \end{array}} \right.$Покажем, что в пределе слабой связи $q \to 1$ энтропия Реньи $S_{q}^{R}(p)$ совпадает с энтропией Больцмана−Гиббса−Шеннона $S_{1}^{R} = S(p) \equiv $ $ \equiv - k\sum\nolimits_i^N {{{p}_{i}}\ln {{p}_{i}}} $ (Зубарев, 1971), а функционал $K_{q}^{R}(p:f)$ совпадает с различающей информацией Кульбака–Лейблера $K_{1}^{R}(p:f) = {{K}^{{KL}}}(p:f) \equiv $ $ \equiv k\sum\nolimits_i^N {{{p}_{i}}\ln \left( {{{{{p}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{i}}} {{{f}_{i}}}}} \right. \kern-0em} {{{f}_{i}}}}} \right)} $ (Kullback, Leibler, 1951; Кульбак, 1967). Действительно, разложение суммы ${{\Gamma }_{q}}(p) \equiv \sum\nolimits_i^N {p_{i}^{q}} $ по параметру $\varepsilon \equiv q - 1$ показывает, что при $\varepsilon \to 0$ имеет место следующее приближенное равенство
Аналогично, для различающей информации Реньи имеем
Пусть рассматриваемая статистическая система с мерой Реньи реализуется двумя множествами: множеством всех состояний системы, описываемых распределением вероятностей $p = \left\{ {{{p}_{1}},...,{{p}_{N}}} \right\},$ и множеством случайных параметров $A(p) = \left\{ {{{A}_{1}},...{{,}_{N}}A} \right\},$ характеризующих систему. Будем далее считать, что средневзвешенное каждой случайной величины A в состоянии с распределением $p$ определяется по формуле55
(3)
${{\langle A\rangle }_{q}} \equiv \sum\limits_i^N {{{A}_{i}}{{P}_{i}}(q)} = {\Gamma }_{q}^{{{\kern 1pt} {\kern 1pt} - 1}}(p)\sum\limits_i^N {{{A}_{i}}p_{i}^{q}} ,$(4)
${{\Gamma }_{q}}(p) \equiv \sum\limits_i^N {p_{i}^{q}} = \exp \left\{ {{{k}^{{ - 1}}}(1 - q)S_{q}^{R}} \right\}$Приведем теперь необходимые для дальнейшего и наиболее важные свойства функционалов (1) и (2), подробно рассмотренных в основополагающих работах (Renyi, 1961; 1970; Kullback, Leibler, 1951; Кульбак, 1967), а также в монографиях (Beck, Schlogl, 1993; Зарипов, 2010).
Основные свойства энтропии Реньи
Положительность и выпуклость. Энтропия Реньи является вещественным, неотрицательным и выпуклым функционалом с максимумом (минимумом) при $q > 0\,\,(q < 0),$ т.е. для произвольных распределений ${{p}_{1}}$ и ${{p}_{2}}$ имеем следующие неравенства (Харди и др., 1948):
(5)
$\begin{gathered} S_{q}^{R}(p) \geqslant 0,\,\,\,\,S_{q}^{R}\left( {{{a}_{1}}{{p}^{{(1)}}} + {{a}_{2}}{{p}^{{(2)}}}} \right) \leqslant \\ \leqslant {{a}_{1}}S_{q}^{R}({{p}^{{(1)}}}) + {{a}_{2}}S_{q}^{R}({{p}^{{(2)}}}), \\ \end{gathered} $Покажем, что $S_{q}^{R}(p) \geqslant 0.$ Пусть $\alpha > 1$ и $\beta < 1.$ Поскольку $0 < {{p}_{i}} \leqslant 1,$ то справедливо $\sum\nolimits_i {p_{i}^{\alpha }} \leqslant \sum\nolimits_i {{{p}_{i}}} \leqslant \sum\nolimits_i {p_{i}^{\beta }} ,$ или $\ln \sum\nolimits_i {p_{i}^{\alpha }} \leqslant 0 \leqslant $ $ \leqslant \ln \sum\nolimits_i {p_{i}^{\beta }} ;$ отсюда следует, что $S_{\alpha }^{R} \geqslant 0$ при $\alpha > 1$ и $S_{\beta }^{R} \geqslant 0$ при $\beta < 1,$ т.е. $S_{q}^{R}(p) \geqslant 0,$ $\forall q \in \mathbb{R},$ что и требовалось доказать.
Аддитивность для независимых объектов. Для суммарного случайного объекта (с энтропией $S_{q}^{R}({{p}^{{(12)}}}) = k{{(1 - q)}^{{ - 1}}}\ln \left( {\sum\nolimits_{i,j}^N {p_{{ij}}^{q}} } \right)$ и нормированным распределением $\sum\nolimits_{i,j}^N {{{p}_{{ij}}} = 1} $), описываемого совместным мультипликативным распределением вероятностей ${{p}_{{ij}}} = {{p}_{i}}{{p}_{j}},$ где ${{p}_{i}}$ и ${{p}_{j}}$ относятся к разным независимым объектам, справедливо свойство аддитивности для энтропий
где энтропии $S_{q}^{R}({{p}^{{(n)}}}) \equiv k{{(1 - q)}^{{ - 1}}}\ln {{\Gamma }_{q}}({{p}^{{(n)}}}),$ ($n = 1,\,\,2$), с соответствующими нормированными распределениями.Энтропия равновероятного состояния. Согласно Jaynes (1963), равновесные вероятностные распределения Гиббса для стохастической системы могут быть выведены из условия экстремума ее энтропии при дополнительных условиях нормировки вероятностного распределения и заданности средневзвешенных значений некоторых случайных параметров $A = \left\{ {{{A}_{1}},...,{{A}_{N}}} \right\},$ характеризующих систему. Этот вариационный метод оказался особенно полезным как в классической статистике (Зубарев, 1971), так и в неэкстенсивной статистической механике (Tsallis, 1999; Зарипов, 2002).
Рассмотрим здесь экстремум энтропии Реньи $S_{q}^{R}(p)$ только при сохранении нормировки распределения $p.$ Для этого вычислим безусловный экстремум функционала $L(p) \equiv \frac{k}{{1 - q}}\ln \sum\nolimits_i^N {p_{i}^{q} - \alpha } \sum\nolimits_i^N {{{p}_{i}}} ,$ где $\alpha $ есть множитель Лагранжа. Из равенства $\delta {\kern 1pt} L = 0,$ получим ${{p}_{i}} = {\text{сonst}}.$ Из условия нормировки следует равновероятное распределение ${{p}_{i}} = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}.$ Таким образом, экстремальное значение энтропии Реньи $S_{q}^{R}(p) = S(p) = k\ln N$ не зависит от параметра экстенсивности $q$ и совпадает с соответствующим значением энтропии Больцмана−Гиббса−Шеннона. Для второй вариации удлиненной энтропии Реньи $L(p)$ имеет место неравенство ${{\delta }^{2}}L > 0$ при $q < 0$ (или ${{\delta }^{2}}L < 0$ при $q > 0$), что и доказывает утверждение о максимуме (минимуме) энтропии $S_{q}^{R}(p).$
Неравенства. Получим теперь некоторые важные для дальнейших целей неравенства, которым удовлетворяет энтропия Реньи. При использовании приведенных выше определений классической энтропии Больцмана−Гиббса−Шеннона S и различающей информации Кульбака−Лейблера ${{K}^{{KL}}}$ легко получить соотношения:
(7)
$S(P) \equiv - k\sum\limits_i^N {{{P}_{i}}\ln {{P}_{i}} = - kq\sum\limits_i^N {{{P}_{i}}\ln {{p}_{i}} - (1 - q)S_{q}^{R},} } $(8)
$\begin{gathered} K_{{}}^{{KL}}(P:p) \equiv \\ \equiv k\sum\limits_i^N {{{P}_{i}}\ln ({{{{P}_{i}}} \mathord{\left/ {\vphantom {{{{P}_{i}}} {{{p}_{i}}}}} \right. \kern-0em} {{{p}_{i}}}}) = k(q - 1)\sum\limits_i^N {{{P}_{i}}\ln {{p}_{i}} - (1 - q)S_{q}^{R}} } , \\ \end{gathered} $(9)
$\begin{gathered} {{K}^{{KL}}}(p:P) \equiv k\sum\limits_i^N {{{p}_{i}}\ln \left( {{{{{p}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{i}}} {{{P}_{i}}}}} \right. \kern-0em} {{{P}_{i}}}}} \right)} = \\ = - (1 - q)S(p) + (1 - q{\text{)}}S_{q}^{R}, \\ \end{gathered} $(10*)
$\frac{q}{{q - 1}}{{K}^{{KL}}}\left( {P:p} \right) = - \left[ {S\left( P \right) - S_{q}^{R}\left( p \right)} \right],$(10**)
${{(1 - q)}^{{ - 1}}}{{K}^{{KL}}}\left( {p:P} \right) = - \left[ {S_{q}^{R}\left( p \right) - S\left( p \right)} \right],$(10***)
$\begin{gathered} q{{(1 - q)}^{{ - 1}}}{{K}^{{KL}}}\left( {P:p} \right) + \\ + \,\,{{(1 - q)}^{{ - 1}}}{{K}^{{KL}}}\left( {p:P} \right) = - \left[ {S\left( P \right) - S\left( p \right)} \right]. \\ \end{gathered} $Учитывая теперь условие ${{K}^{{KL}}} \geqslant 0$ выпуклости для информации различия Кульбака−Лейблера (см., например, Зарипов, 2002), из соотношений (10) получим неравенства
справедливые в области $0 < q < 1.$ При $q > 1$ знаки в (11) меняются на противоположныеСоответственно, в области $q < 0$ справедливы неравенства
(13)
$S_{q}^{R}\left( p \right) > S\left( P \right)\,\,\,\,{\text{и }}S_{q}^{R}\left( p \right) > S\left( p \right).$Используем теперь неравенство (теорема № 16 в монографии (Харди и др., 1948))
(14)
${{\left( {\sum {{{p}_{i}}a_{i}^{r}} } \right)}^{{1/r}}} \leqslant {{\left( {\sum {{{p}_{i}}a_{i}^{{r{\kern 1pt} '}}} } \right)}^{{1/r{\kern 1pt} '}}},\,\,\,\,r{\kern 1pt} ' > r,$Предположим теперь, что $q{\kern 1pt} ' > q$ и что $q{\kern 1pt} '$ и $q$ имеют один и тот же знак, и примем во внимание стандартные неравенства (теорема № 27 в монографии (Харди и др., 1948))
(16)
$\begin{gathered} {{\left( {\sum {{{a}_{i}}} } \right)}^{r}} \geqslant \sum {a_{i}^{r}} ,\,\,\,\,(r \geqslant 1); \\ {{\left( {\sum {{{a}_{i}}} } \right)}^{r}} \leqslant \sum {a_{i}^{r}} ,\,\,\,\,(0 \leqslant r \leqslant 1), \\ \end{gathered} $справедливые для произвольных значений ${{a}_{i}} > 0$ и положительных $r \in \mathbb{R}.$ Для того, чтобы отсюда получить еще одно важное неравенство для энтропии Реньи, положим ${{a}_{i}} = p_{i}^{q},$ $r = {{q{\kern 1pt} '} \mathord{\left/ {\vphantom {{q{\kern 1pt} '} q}} \right. \kern-0em} q}.$ Пусть теперь $q{\kern 1pt} ' > q > 0,$ тогда $r > 1$ и из (16) следует
(16*)
${{\left( {\sum {p_{i}^{q}} } \right)}^{{q{\kern 1pt} '/q}}} \geqslant \sum {p_{i}^{{q'}}} ,\,\,\,\,(q{\kern 1pt} ' > q > 0).$Если $0 > q{\kern 1pt} ' > q,$ то имеем $0 \leqslant r = {{q{\kern 1pt} '} \mathord{\left/ {\vphantom {{q{\kern 1pt} '} q}} \right. \kern-0em} q} < 1$ и, следовательно,
(16**)
${{\left( {\sum {p_{i}^{q}} } \right)}^{{q{\kern 1pt} '/q}}} \leqslant \sum {p_{i}^{{q'}}} ,\,\,\,\,(0 > q{\kern 1pt} ' > q).$Если возвести неравенства (16*) и (16**) в степень ${1 \mathord{\left/ {\vphantom {1 {q{\kern 1pt} '}}} \right. \kern-0em} {q{\kern 1pt} '}},$ то для обоих случаев справедливо неравенство
(16***)
${{\left( {\sum {p_{i}^{q}} } \right)}^{{1/q}}} \geqslant {{\left( {\sum {p_{i}^{{q'}}} } \right)}^{{1/q{\kern 1pt} '}}},\,\,\,\,(q{\kern 1pt} ' > q,\,\,\,\,q{\kern 1pt} 'q > 0).$Наконец, с учетом (16***) и формулы $\ln {{\Gamma }_{q}}(p){\kern 1pt} = \ln \sum\nolimits_i^N {p_{i}^{q}} = {{k}^{{ - 1}}}(1 - q)S_{q}^{R},$ окончательно получим (применяемое далее) неравенство для энтропии Реньи
(17)
$\frac{{(1 - q)}}{q}S_{q}^{R} \geqslant \frac{{(1 - q{\kern 1pt} ')}}{{q{\kern 1pt} '}}S_{{q{\kern 1pt} '}}^{R},\,\,\,\,(q{\kern 1pt} ' > q,\,\,\,\,q{\kern 1pt} 'q > 0).$Помимо полученных выше неравенств для энтропии Реньи, справедливы также следующие неравенства:
а также и некоторые другие, которые можно найти, например, в работах (Beck, 1990; Beck, Schlögl, 1993; Зарипов, 2002).Основные свойства различающей информации Реньи
Наряду с энтропией Реньи (1), информация различия Реньи (2)
Рассмотрим здесь некоторые наиболее важные свойства информации различия Реньи (Beck, Schlögl, 1993; Tsallis, 2009; Зарипов, 2002).
Выпуклость. Различающая информация есть вещественный, выпуклый и положительный (или отрицательный) функционал с минимумом (максимумом) при $q > 0$ $\left( {q < 0} \right).$ Покажем это. Для действительного числа $r > 0$ имеем
(21)
$\begin{gathered} \frac{{{{r}^{{q - 1}}} - 1}}{{q - 1}} \geqslant 1 - \frac{1}{r},\,\,\,\,{\text{если}}\,\,q > 0, \\ = \,1 - \frac{1}{r},\,\,\,\,{\text{если}}\,\,q = 0, \\ \leqslant \,1 - \frac{1}{r},\,\,\,\,{\text{если}}\,\,q < 0. \\ \end{gathered} $Поэтому, например, для $q < 0$ справедливо ${{(p{{f}^{{ - 1}}})}^{{q - 1}}} \geqslant q + (1 - q)(f{{p}^{{ - 1}}}).$ Отсюда следует, что
(22)
$\begin{gathered} K_{q}^{R}(p{\kern 1pt} :{\kern 1pt} f) \leqslant 0,\,\,\,\,\left( {q < 0} \right); \\ K_{q}^{R}(p{\kern 1pt} {\kern 1pt} :{\kern 1pt} f) \geqslant 0,\,\,\,\,\left( {q > 0} \right). \\ \end{gathered} $Заметим, что поскольку при $p = f$ имеет место равенство $K_{q}^{R}\left( {p:p} \right) = 0,$ то различающая информация Реньи является функцией Ляпунова66.
Справедливо также неравенство
(23)
$\begin{gathered} K_{q}^{R}\left[ {\left( {{{a}_{1}}{{p}_{1}} + {{a}_{2}}{{p}_{2}}} \right):f} \right] \leqslant {{a}_{1}}K_{q}^{R}\left( {{{p}_{1}}:f} \right) + \\ + \,\,{{a}_{2}}K_{q}^{R}\left( {{{p}_{2}}:f} \right), \\ \end{gathered} $Аддитивность для двух независимых объектов. Пусть состояние суммарного случайного объекта описывается нормированными совместными распределениями ${{p}^{{(12)}}}$ и ${{f}^{{(12)}}}$. Тогда различающая информация совокупной и отдельных систем определяются выражениями
(24)
$K_{q}^{R}\left( {{{p}^{{(12)}}}:{{f}^{{(12)}}}} \right) = \frac{k}{{q - 1}}\ln \sum\limits_{i,j}^N {p_{{ij}}^{q}f_{{i,j}}^{{1 - q}}} ,$(25)
$\begin{gathered} K_{q}^{R}\left( {{{p}^{{(1)}}}:{{f}^{{(1)}}}} \right) = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}f_{i}^{{1 - q}}} , \\ K_{q}^{R}\left( {{{p}^{{(2)}}}:{{u}^{{(2)}}}} \right) = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{j}^{q}u_{j}^{{1 - q}}} . \\ \end{gathered} $В случае статистической независимости состояний имеет место условие мультипликативности ${{p}_{{ij}}} = {{p}_{i}}{{p}_{j}}$ и ${{f}_{{ij}}} = {{f}_{i}}{{f}_{j}}.$ Отсюда, при использовании (24) и (25) легко получить равенство
(26)
$\begin{gathered} K_{q}^{R}\left( {{{p}^{{(12)}}}:{{f}^{{(12)}}}} \right) = \\ = \,\,K_{q}^{R}\left( {{{p}^{{(1)}}}:{{f}^{{(1)}}}} \right) + K_{q}^{R}\left( {{{p}^{{(2)}}}:{{f}^{{(2)}}}} \right), \\ \end{gathered} $Следствие различающей информации Реньи c равновероятным распределением для $f = \left\{ {{{f}_{{1,}}}{{f}_{{2,}}}...,{{f}_{N}}} \right\}.$ Покажем, что энтропия Реньи $S_{q}^{R}(p)$ произвольного состояния $p$ меньше (больше), чем энтропия равновероятного состояния системы при $q > 0$ $(q < 0).$ Подставляя распределение ${{f}_{i}} = {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}$ в (21), получим
(27)
$\begin{gathered} K_{q}^{R}({{p}_{1}}:{{f}_{1}}) = \\ = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}{{N}^{{q - 1}}} = - \left( {S_{q}^{R} - k\ln N} \right)} . \\ \end{gathered} $Используя (27) и условия выпуклости (22) функционала $K_{q}^{R},$ получим неравенства (18), означающие, что энтропия Реньи меньше (больше), чем энтропия равновероятного состояния при $q > 0$ ($q < 0$).
Неравенства. Для различающей информации Реньи справедливы также следующие неравенства:
(28)
$\begin{gathered} K_{q}^{R}\left( {{{p}^{{(12)}}}:{{f}^{{(12)}}}} \right) \leqslant K_{q}^{R}\left( {{{p}^{{(1)}}}:{{f}^{{(1)}}}} \right) + \\ + \,\,K_{q}^{R}\left( {{{p}^{{(2)}}}:{{f}^{{(2)}}}} \right), \\ \end{gathered} $(29)
$\begin{gathered} K_{q}^{R}(p:f) > {{K}^{{KL}}}(P:f), \\ K_{q}^{R}(p:f) > {{K}^{{KL}}}(p:f),\,\,\,\,(q < 0), \\ \end{gathered} $(31)
$\begin{gathered} {{K}^{{KL}}}(P:f) > K_{q}^{R}(p:f) > {{K}^{{KL}}}(p:f), \\ (0 < q < 1). \\ \end{gathered} $Мера неточности. Наряду с информацией различия Реньи, функционал
(32)
$\begin{gathered} {{H}_{q}}\left( {p:f} \right) = S_{q}^{R}\left( p \right) + K_{q}^{R}\left( {p:f} \right) = \\ = \frac{k}{{1 - q}}\ln \left[ {{{\sum\limits_i^N {p_{i}^{q}} } \mathord{\left/ {\vphantom {{\sum\limits_i^N {p_{i}^{q}} } {\sum\limits_i^N {{{p}_{i}}} {{{\left( {\frac{{{{p}_{i}}}}{{{{f}_{i}}}}} \right)}}^{{q - 1}}}}}} \right. \kern-0em} {\sum\limits_i^N {{{p}_{i}}} {{{\left( {\frac{{{{p}_{i}}}}{{{{f}_{i}}}}} \right)}}^{{q - 1}}}}}} \right], \\ \end{gathered} $ЭКСТРЕМУМ ЭНТРОПИИ РЕНЬИ И НЕГИББСОВОЕ РАСПРЕДЕЛЕНИЕ. ТЕРМОДИНАМИЧЕСКИЕ СООТНОШЕНИЯ
Пусть случайными объектами неэкстенсивной системы являются рассматриваемые в статистической физике дискретные частицы с энергией ${{H}_{i}}.$ Рассмотрим равновесное состояние системы. Далее будем использовать нормированное эскортное распределение ${{P}_{i}}(q),$ поскольку осреднение с ним приводит к аддитивности средних энергий ${{E}_{q}}$ (46). Для определения равновесного распределения найдем безусловный экстремум энтропии Реньи $S_{q}^{R}(p)$ при сохранении нормировки и заданности средней энергии частиц
(33)
${{E}_{q}} = \sum\limits_i^N {{{P}_{i}}(q){{H}_{i}}} ,\,\,\,\,\sum\limits_i^N {{{p}_{i}} = 1} .$Согласно вариационному принципу Jaynes, определим функционал
(34)
$L(p) \equiv \frac{k}{{1 - q}}\ln \sum\limits_i^N {p_{i}^{q}} - \beta \sum\limits_i^N {{{H}_{i}}} {{P}_{i}} - k\lambda \sum\limits_i^N {{{p}_{i}}} ,$(35)
$\Gamma _{q}^{{ - 1}}p_{i}^{{q - 1}}\left[ {1 - {{k}^{{ - 1}}}\left( {1 - q} \right)\beta \left( {{{H}_{i}} - {{E}_{q}}} \right)} \right] = {{q}^{{ - 1}}}\left( {1 - q} \right)\lambda ,$(36)
${{p}_{{i0}}}(\beta ) = Z_{q}^{{{\kern 1pt} - 1}}{{\left\{ {1 - {{k}^{{ - 1}}}\beta \left( {1 - q} \right)\Delta \left[ {{{H}_{i}}} \right]} \right\}}^{{1/\left( {1 - q} \right)}}}.$(37)
$\begin{gathered} {{{\Gamma }}_{q}}(p) \equiv \sum\limits_i^N {p_{i}^{q}} , \\ {{Z}_{q}}(\beta ) \equiv {\Gamma }_{q}^{{1/(1 - q)}} = \\ = \sum\limits_i^N {{{{\left\{ {1 - {{k}^{{ - 1}}}\left( {1 - q} \right)\beta \Delta \left[ {{{H}_{i}}} \right]} \right\}}}^{{1/\left( {1 - q} \right)}}}} > 0, \\ \end{gathered} $− статистический интеграл; $\beta = 1{\text{/}}T$ − обратная температура (изменяющаяся в пределах допустимых значений); $\Delta \left[ {{{H}_{i}}} \right] \equiv ({{H}_{i}} - {{E}_{{q0}}})$ − флуктуация энергии частиц. Таким образом, распределение вероятностей состояния статистического ансамбля неэкстенсивных систем с мерой Реньи, которые находятся в тепловом равновесии с внешней средой (термостатом) и могут обмениваться с ней энергией при постоянном объеме и постоянном числе частиц, соответствует обобщенному каноническому ансамблю Гиббса (36).
Равновесное распределение (36) можно переписать в виде
(38)
$\begin{gathered} {{p}_{{i0}}}({{\beta }_{0}}) = {{\left[ {\frac{{1 - {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]}}{{{{\Gamma }_{q}}({{\beta }_{0}})}}} \right]}^{{1/(1 - q)}}} = \\ = \frac{{{{{\exp }}_{q}}\left\{ {{{ - \Delta \left[ {{{H}_{i}}} \right]} \mathord{\left/ {\vphantom {{ - \Delta \left[ {{{H}_{i}}} \right]} {k{{T}_{0}}}}} \right. \kern-0em} {k{{T}_{0}}}}} \right\}}}{{\exp \left( {{{S_{{q0}}^{R}} \mathord{\left/ {\vphantom {{S_{{q0}}^{R}} k}} \right. \kern-0em} k}} \right)}}, \\ \end{gathered} $(39)
$\begin{gathered} {{\exp }_{q}}(x) \equiv [1 + (1 - q)x]_{ + }^{{\tfrac{1}{{1 - q}}}} = \\ = \left\{ {\begin{array}{*{20}{c}} {0,\,\,\,\,{\text{если}}\,\,q < 1\,\,и\,\,x < - 1{\text{/}}1 - q;} \\ {{{{[1 + (1 - q)x]}}^{{1/1 - q}}}{\text{,}}\,\,\,\,{\text{если}}\;q < 1\,\,и\;x \geqslant - 1{\text{/}}1 - q;} \\ {{{{[1 + (1 - q)x]}}^{{1/1 - q}}}{\text{,}}\,\,\,\,{\text{если}}\;q > 1\,\,и\;x < - 1{\text{/}}1 - q,} \end{array}} \right. \\ \end{gathered} $Обобщенные термодинамические соотношения. Подстановка распределения (36) в (1) дает следующее экстремальное значение энтропии
Реньи при равновесном распределении 
(40)
$\begin{gathered} S_{{q0}}^{R} \equiv S_{q}^{R}({{p}_{0}}) = \frac{k}{{1 - q}}\ln \left( {\sum\limits_i^N {p_{{i0}}^{q}} } \right) = \frac{k}{{1 - q}}\ln \left\{ {\sum\limits_i^N {{{p}_{{i0}}}\frac{{{{\Gamma }_{q}}({{\beta }_{0}})}}{{1 - {{k}^{{ - 1}}}(1 - q){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]}}} } \right\} = \\ = \frac{k}{{1 - q}}\ln \left\{ {\sum\limits_i^N {{{\Gamma }_{q}}} ({{\beta }_{0}}){{p}_{{i0}}}\left[ {1 + \frac{{{{k}^{{ - 1}}}{{\beta }_{0}}(1 - q)\Delta \left[ {{{H}_{i}}} \right]}}{{1 - {{k}^{{ - 1}}}{{\beta }_{0}}(1 - q)\Delta \left[ {{{H}_{i}}} \right]}}} \right]} \right\} = \frac{k}{{1 - q}}\ln \left\{ {{{\Gamma }_{q}}({{\beta }_{0}}) + \sum\limits_i^N {{{p}_{{i0}}}\frac{{{{\Gamma }_{q}}({{\beta }_{0}}){{k}^{{ - 1}}}{{\beta }_{0}}(1 - q)\Delta \left[ {{{H}_{i}}} \right]}}{{1 - {{k}^{{ - 1}}}{{\beta }_{0}}(1 - q)\Delta \left[ {{{H}_{i}}} \right]}}} } \right\} = \\ = \frac{k}{{1 - q}}\ln \left\{ {{{\Gamma }_{q}}({{\beta }_{0}}) + {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\sum\limits_i^N {\Delta \left[ {{{H}_{i}}} \right]p_{{i0}}^{q}} } \right\} = \frac{k}{{1 - q}}\ln {{\Gamma }_{q}}({{\beta }_{0}}) = k\ln {{Z}_{q}}({{\beta }_{0}}). \\ \end{gathered} $Тогда свободная энергия ${{F}_{q}}$ для равновесной неэкстенсивной системы в термостате с температурой $T = 1{\text{/}}\beta $ и статистический интеграл задаются соотношениями (далее индекс “0” будем опускать)
(41)
$S_{q}^{R} = k\ln {{Z}_{q}}(T),\,\,{{F}_{q}} = {{E}_{q}} - TS_{q}^{R} = {{E}_{q}} - kT\ln {{Z}_{q}},$(42)
${{E}_{q}} = \sum\limits_i^N {{{P}_{i}}(q){{H}_{i}}} = \frac{1}{{{{\Gamma }_{q}}(T)}}\sum\limits_i^N {p_{i}^{q}{{H}_{i}}} ,$(43)
${{Z}_{q}}(T) = {{\left[ {{{\Gamma }_{q}}(T)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {1 - q} \right)}}} \right. \kern-0em} {\left( {1 - q} \right)}}}}} = {{\left( {\sum\limits_i^N {p_{i}^{q}} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 {\left( {1 - q} \right)}}} \right. \kern-0em} {\left( {1 - q} \right)}}}}}.$При дифференцировании энтропии Реньи для равновесного состояния, заданной выражением (40), получим следующие соотношения
(44)
$\begin{gathered} \frac{{\partial S_{q}^{R}}}{{\partial E_{q}^{R}}} = \frac{1}{T},\,\,\,\,{{E}_{q}} = {{F}_{q}} - T\frac{{\partial ({{F}_{q}})}}{{\partial T}}, \\ \frac{{\partial {{E}_{q}}}}{{\partial T}} = - T\frac{{{{\partial }^{2}}{{F}_{q}}}}{{\partial T}} = {{C}_{{qv}}}, \\ \end{gathered} $Термодинамическое равновесие. Рассмотрим термодинамическое равновесие двух независимых $q$-систем с энтропиями $S_{{q1}}^{R} = S_{q}^{R}({{p}^{{(1)}}})$ и $S_{{q2}}^{R} = S_{q}^{R}({{p}^{{(2)}}}),$ представляющих собой общую замкнутую систему с энтропией $S_{q}^{R} = S_{q}^{R}({{p}^{{(12)}}})$ при ${{p}^{{(12)}}} = {{p}^{{(1)}}}{{p}^{{(2)}}}$ и энергии ${{E}_{{q12}}}.$ Согласно свойству аддитивности (6) энтропии Реньи (1), для энтропии суммарной системы имеем $S_{{q12}}^{R} = S_{{q1}}^{R} + S_{{q2}}^{R}.$
Для нахождения осредненной энергии $E_{{q12}}^{R}$ суммарной системы воспользуемся распределением (36). Тогда, используя условие мультипликативности ${{p}_{{12}}} = {{p}_{1}}{{p}_{2}},$ будем иметь
(45)
$\begin{gathered} {{\Delta }_{{12}}}\left[ {{{H}_{i}}} \right] = {{\Delta }_{1}}\left[ {{{H}_{i}}} \right] + {{\Delta }_{2}}\left[ {{{H}_{i}}} \right] - \\ - \,\,(1 - q){{k}^{{ - 1}}}\beta {{\Delta }_{1}}\left[ {{{H}_{i}}} \right]{{\Delta }_{2}}\left[ {{{H}_{i}}} \right]. \\ \end{gathered} $В этом соотношении необходимо использовать условие аддитивности осредненных энергий
поскольку без этого предположения осредненные величины будут зависеть от микроскопических величин, что является неприемлемым (Zaripov, 2005). Тогда из (46) для микроскопических энергий получим следующее условие квазиаддитивности микроскопических энергий
(47)
${{H}_{i}}_{{12}} = {{H}_{i}}_{1} + {{H}_{i}}_{2} - (1 - q){{k}^{{ - 1}}}\beta {{\Delta }_{1}}\left[ {{{H}_{i}}} \right]{{\Delta }_{2}}\left[ {{{H}_{i}}} \right].$Заметим, что именно наличие этого равенства является той причиной, благодаря которой статистику на мере Реньи относят к неэкстенсивной статистической механике.
При варьировании соотношений (6) и (46) получатся следующие равенства $\delta S_{{q12}}^{R} = \delta S_{{q1}}^{R} + \delta S_{{q2}}^{R},$ $\delta {{E}_{{q12}}} = \delta {{E}_{{q1}}} + \delta {{E}_{{q2}}},$ из которых следует
(48)
${{\delta S_{{q1}}^{R}} \mathord{\left/ {\vphantom {{\delta S_{{q1}}^{R}} {\delta {{E}_{{q1}}}}}} \right. \kern-0em} {\delta {{E}_{{q1}}}}} = {{\delta S_{{q2}}^{R}} \mathord{\left/ {\vphantom {{\delta S_{{q2}}^{R}} {\delta {{E}_{{q2}}}}}} \right. \kern-0em} {\delta {{E}_{{q2}}}}} = \beta $Н-теорема в статистике Реньи. Рассмотрим теперь замкнутую систему, для которой распределение ${{p}_{i}}$ является произвольным, а распределение ${{p}_{{i0}}}$ − равновесным
(49)
${{p}_{{i0}}} = {{\left[ {\frac{{1 - {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]}}{{{{\Gamma }_{q}}({{p}_{0}})}}} \right]}^{{1/(1 - q)}}}.$Тогда спонтанный переход между этими состояниями описывается следующей различающей информацией Реньи (Zaripov, 2005)
(50)
$\begin{gathered} K_{q}^{R}(p:{{p}_{0}}) = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}p_{{i0}}^{{1 - q}}} = \\ = \frac{k}{{q - 1}}\ln \left\{ {{{\Gamma }_{q}}(p)\sum\limits_i^N {{{P}_{i}}(q)p_{{i0}}^{{1 - q}}} } \right\} = \\ = \frac{k}{{q - 1}}\ln {{\Gamma }_{q}}(p) + \frac{k}{{q - 1}}\ln \,\, \times \\ \times \,\,\sum\limits_i^N {{{P}_{i}}(q)\frac{{1 - {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]}}{{{{\Gamma }_{q}}({{p}_{0}})}}} = \\ = - \left[ {S_{q}^{R}(p) - S_{q}^{R}({{p}_{0}})} \right] + \\ + \,\,\frac{k}{{q - 1}}\ln \sum\limits_i^N {{{P}_{i}}(q)\left\{ {1 - {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]} \right\} = } \\ = - \left( {S_{q}^{R} - S_{{q0}}^{R}} \right) + \frac{k}{{q - 1}}\ln \left\{ {1 - \frac{{(1 - q)}}{{k{{T}_{0}}}}({{E}_{q}} - {{E}_{{q0}}})} \right\}, \\ \end{gathered} $Если $q = 1,$ то из (50) следует известное выражение для информации различия Кульбака–Лейблера неэкстенсивной статистической механики (Зарипов, 2002; Колесниченко, 2018в)
характеризующее степень отклонения хаотической системы от полного равновесия.При выполнении условия Гиббса ${{E}_{q}} = {{E}_{{q0}}}$ (Климонтович, 1990) и с учетом свойства (22) знакоопределенности информации различия $K_{q}^{R}(p:{{p}_{0}})$ из (51) следуют два неравенства
которые обобщают теорему Гиббса на неэкстенсивную статистику Реньи. Согласно этой теореме для замкнутой системы энтропия Реньи $S_{q}^{R} = S_{{q0}}^{R} - K_{q}^{R}(p:{{p}_{0}})$ возрастает (убывает) до экстремального ее значения $S_{{q0}}^{R}$ при $q > 0\,\,\,\left( {q < 0} \right)$ одновременно с уменьшением (увеличением) положительной (отрицательной) информации $K_{q}^{R}(p:{{p}_{0}}).$ Таким образом, различающая информация представлена здесь в виде отрицательного вклада в текущую энтропию Реньи $S_{q}^{R}$ и потому может быть названа негэнтропией (Шредингер, 1947).Поскольку информация различия Реньи является знакоопределенной функцией Ляпунова, то для того, чтобы состояние равновесия ${{S}_{{q0}}}$ было устойчивым, необходимо выполнение следующих неравенств
(53)
$\begin{gathered} {{dK_{q}^{R}} \mathord{\left/ {\vphantom {{dK_{q}^{R}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{ - d\left( {S_{q}^{R} - S_{{q0}}^{R}} \right)} \mathord{\left/ {\vphantom {{ - d\left( {S_{q}^{R} - S_{{q0}}^{R}} \right)} {dt}}} \right. \kern-0em} {dt}} < 0\,\,\,\,{\text{при}}\,\,q > 0; \\ {{dK_{q}^{R}} \mathord{\left/ {\vphantom {{dK_{q}^{R}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = - d{{\left( {S_{q}^{R} - S_{{q0}}^{R}} \right)} \mathord{\left/ {\vphantom {{\left( {S_{q}^{R} - S_{{q0}}^{R}} \right)} {dt}}} \right. \kern-0em} {dt}} > 0\,\,\,\,{\text{при }}q < 0. \\ \end{gathered} $Из соотношений (53) следует неравенство для энтропии Реньи: ${{d{{S}_{q}}} \mathord{\left/ {\vphantom {{d{{S}_{q}}} {dt}}} \right. \kern-0em} {dt}} > 0$ при $q > 0$ и ${{d{{S}_{q}}} \mathord{\left/ {\vphantom {{d{{S}_{q}}} {dt}}} \right. \kern-0em} {dt}} < 0$ при $q < 0,$ которые выражают H-теорему для рассматриваемой стохастической $q$-системы: при временной эволюции к равновесному состоянию энтропия Реньи замкнутой системы возрастает (убывает) до экстремального ее значения $S_{{q0}}^{R}$ при $q > 0\,\,\,\,\left( {q < 0} \right).$
Рассмотрим теперь открытые системы, находящиеся в окружении с температурой ${{Т}_{0}}.$ Согласно равенству (50) они характеризуются физической различающей информацией Реньи
(50*)
$\begin{gathered} K_{q}^{R}(p:{{f}_{0}}) = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}f_{{i0}}^{{1 - q}}} = - \left( {S_{q}^{R} - S_{{q0}}^{R}} \right) + \\ + \,\,\frac{k}{{q - 1}}\ln \left\{ {1 - \frac{{(1 - q)}}{{k{{T}_{0}}}}({{E}_{q}} - {{E}_{{q0}}})} \right\} \\ \end{gathered} $(49*)
${{f}_{{i0}}} = {{\left[ {\frac{{1 - {{k}^{{ - 1}}}\left( {1 - q} \right){{\beta }_{0}}\Delta \left[ {{{H}_{i}}} \right]}}{{{{\Gamma }_{q}}({{f}_{0}})}}} \right]}^{{1/(1 - q)}}}.$Дифференцируя (50*) по времени, получим следующее соотношение для открытых неэкстенсивных $q$-систем с мерой Реньи
(54)
$dK_{q}^{R} \geqslant - dS_{q}^{R} + \frac{{d{{E}_{q}}}}{{{{Т}_{0}}\left[ {1 - (1 - q){{k}^{{ - 1}}}{{\beta }_{0}}({{E}_{q}} - {{E}_{{q0}}})} \right]}},$Покажем теперь, что между неэкстенсивной термодинамикой Реньи сложных стохастических систем, с одной стороны, и теорией фракталов, опирающейся на геометрию и статистику, существует тесная взаимосвязь.
ФРАКТАЛ И ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ
Фракталы появляются во множестве физических приложений (Mandelbrot, 1977). Фрактальные объекты в пространстве или фрактальные процессы во времени являются самоподобными (или самоафинными) и обнаруживают скейлинговое поведение на разных пространственно-временных масштабах. В частности, их широко используют в космологии (см., например, Bialas, Czyz, 2008; Kolesnichenko, Marov, 2013; 2014; Kolesnichenko, 2017), космогонии звездных и планетных систем (см. Пиблс, 1983; Мандельброт, 2002; Колесниченко, Маров, 2014), в физике Солнца (Могилевский, 2001), а также для понимания динамического поведения хаотических систем (Lorenz, 1963), когда фракталами являются все “странные” аттракторы, связанные с непрерывными потоками (Ruelle, Takens, 1971). Основной характеристикой фрактала является его размерность.
Регулярный фрактал. Мера Хаусдорфа−Безиковича. Напомним теперь некоторые точные определения. Регулярными фракталами называют геометрические объекты в евклидовом пространстве (с мерой $d$), которые обладают свойством самоподобия77 (т.е. неизменности основных геометрических особенностей при изменении масштаба) и имеют дробную метрическую меру (в смысле Минковского или Хаусдорфа) либо меру, отличную от топологической. При этом мера (размерность) регулярного фрактала определяется следующим образом. Предположим, что для полного покрытия фрактала $d$-мерными гипершарами88 радиуса $\Delta $ необходимо не менее чем $N(\Delta )$ шаров. Тогда, если при достаточно малых $\Delta $ величина $N(\Delta )$ меняется с $\Delta $ по степенному закону $N(\Delta ) \sim 1{\text{/}}{{\Delta }^{{{{D}_{H}}}}},$ то показатель скейлинга ${{D}_{H}}$ называется хаусдорфовой или фрактальной мерой этого объекта. Это определение может быть представлено в виде (Hausdorff, 1919; Besicovitch, 1934)
(55)
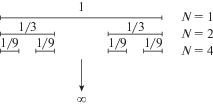
${{D}_{H}} = - \mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln N(\Delta )}}{{\ln \Delta }} = \mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln N(\Delta )}}{{\ln (1{\text{/}}\Delta )}}.$В качестве примера вычислим фрактальную размерность канторового множества, схема построения которого приведена на рис. 1.
Начнем с отрезка единичной длины. На первом шаге построения фрактала заменим его двумя отрезками с длинами $1{\text{/}}3,$ примыкающими соответственно к его левому и правому концам. Очевидно, что на $n$-м шаге рекуррентного построения имеется ${{2}^{n}}$ отрезков генератора длиной $1{\text{/}}{{3}^{n}}$ каждый.
Предел $\Delta \to 0$ соответствует пределу $n \to \infty .$ Поэтому фрактальная размерность равна
Размерность Хаусдорфа ${{D}_{H}},$ рассчитанная с использованием формулы (55) для некоторых известных фрактальных множеств, приведена в табл. 1 (Шредер, 2001; Мандельброт, 2002). Более сложные объекты – мультифракталы – являются суперпозицией нескольких регулярных фракталов различных размерностей и имеют более сложные свойства, чем непосредственно монофракталы (Mandelbrot, 1977; 1982; Шредер, 2001; Божокин, Паршин, 2001).
Таблица 1.
Размерность Хаусдорфа для некоторых фрактальных множеств
| Фрактальное множество | ${{D}_{H}}$ |
|---|---|
| Канторовское множество | 0.63 |
| Триадная кривая Коха | 1.26 |
| Кривая Мандельброта–Гивена | 1.89 |
| Салфетка Серпинского | 1.58 |
| Ковер Серпинского | 1.89 |
| Кривая Госпера | 1.13 |
| Универсальная кривая Менгера | 2.73 |
Континуум мультифрактальных размерностей Реньи
Мультифракталы. Обобщенная фрактальная размерность. К мультифракталам относятся неоднородные фрактальные объекты, для характеристики которых недостаточно одной размерности Хаусдорфа ${{D}_{H}},$ а необходим целый спектр таких размерностей, число которых, вообще говоря, бесконечно. Причина этого заключается в том, что в отличие от регулярных фракталов (геометрически подобных объектов) мультифракталы (точнее их фрагменты), наряду с чисто геометрическими характеристиками, определяемыми величиной ${{D}_{H}},$ являются статистически подобными копиями целого, т.е. обладают некоторым набором статистических свойств. Для характеристики таких структур вводятся в рассмотрение различные информационные размерности, которые чувствительны к неоднородностям подобных множеств (Grassberger, Procaccia, 1983; Бадии, Полити, 1988). Одним из наиболее содержательных описаний фрактальных размерностей служат обобщенные размерности Реньи $D(q),$ разных порядков.
Пусть часть пространства $G,$ занятая фрактальным объектом покрыта равными (гипер) кубическими ячейками с ребром $\Delta > 0$ и объемом ${{\Delta }^{d}}.$ Обозначим через ${{n}_{i}}(\Delta )$ число точек (элементов системы), в гиперкубе с номером $i = 1,2,...,N(\Delta ),$ где $N(\Delta )$ − полное число элементов выбранного $\Delta $-покрытия. Тогда вероятность, характеризующая относительную заселенность ячейки i, равна ${{p}_{i}}(\Delta ) = {{{{n}_{i}}(\Delta )} \mathord{\left/ {\vphantom {{{{n}_{i}}(\Delta )} {\sum\nolimits_i^{N(\Delta )} {{{n}_{i}}} }}} \right. \kern-0em} {\sum\nolimits_i^{N(\Delta )} {{{n}_{i}}} }}.$ Ясно, что $\sum\nolimits_i^{N(\Delta )} {p_{i}^{q}} = 1.$ Реньи в работе (Renyi, 1961) ввел энтропию $S_{q}^{R} = \frac{k}{{1 - q}}\ln \sum\nolimits_i^{N(\Delta )} {p_{i}^{q}} ,$ как $q$-момент меры $\Delta $-покрытия. Рассмотрим обобщенную статистическую сумму
которая характеризуется показателем степени q, принимающим любые значения в интервале $ - \infty < q < + \infty .$ Тогда спектр обобщенных фрактальных размерностей $D(q),$ характеризующих распределение вероятностей ${{p}_{i}}(\Delta )$ в области $G,$ определяется соотношением (Hentschel, Procaccia, 1983)(57)
$\begin{gathered} D(q) \equiv \mathop {\lim }\limits_{\Delta \to 0} \frac{1}{{q - 1}}\frac{{\ln \Gamma (q,\Delta )}}{{\ln \Delta }} = \\ = \mathop {\lim }\limits_{\Delta \to 0} \frac{1}{{(q - 1)\ln \Delta }}\ln \sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} (\Delta ) = \\ = - \frac{1}{k}\mathop {\lim }\limits_{\Delta \to 0} \frac{{S_{q}^{R}(p)}}{{\ln \Delta }} = \frac{1}{{q - 1}}\tau (q), \\ \end{gathered} $(58)
$\begin{gathered} \tau = \tau (q) = - \mathop {\lim }\limits_{\Delta \to 0} \left\{ {\frac{1}{{\ln \Delta }}\ln \sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} (\Delta )} \right\}, \\ \tau (q) = (q - 1)D(q). \\ \end{gathered} $Легко показать, что если $D(q) = D = {\text{const}},$ то данный фрактальный объект представляет собой регулярный монофрактал. Действительно, в случае регулярного фрактала во всех занятых ячейках содержится одинаковое количество элементов ${{n}_{i}}(\Delta ) = N{\text{/}}N(\Delta ),$ т.е. фрактал является однородным. Тогда очевидно, что относительные населенности всех ячеек, ${{p}_{i}}(\Delta ) = 1{\text{/}}N(\Delta ),$ тоже одинаковы, и обобщенная статистическая сумма (56) принимает вид $\Gamma (q,\Delta ) = {{N}^{{1 - q}}}(\Delta ).$ Поскольку, согласно определению фрактальной размерности D, число занятых ячеек при достаточно малом $\Delta $ равно $N(\Delta ) \approx {{\Delta }^{{ - D}}},$ то $\Gamma (q,\Delta ) = {{\Delta }^{{(q - 1)D}}} \approx {{\Delta }^{{\tau (q)}}}.$ Отсюда следует, что в случае обычного фрактала функция $\tau (q) = (q - 1)D,$ т.е. является линейной. Тогда все обобщенные фрактальные размерности $D(q) = D$ совпадают при всех значениях q.
Наиболее широкое распространение получили три совершенно разные меры фрактала: хаусдорфова размерность ${{D}_{H}} \equiv D(q \to 0),$ информационная размерность $D(q \to 1)$ и корреляционная размерность $D(q \to 2)$ (Grassberger, 1981; 1985; Grassberger, Procaccia, 1984).
Фрактальная и информационная размерности. При $q = 0$ из выражения (56) следует, что $\Gamma (0,\Delta ) = N(\Delta ).$ С другой стороны, для этого случая имеем $\Gamma (0,\Delta ) \approx {{\Delta }^{{\tau (0)}}} = {{\Delta }^{{D(0)}}}.$ Из сопоставления этих равенств следует, что $N(\Delta ) \approx {{\Delta }^{{D(0)}}}.$ Это означает, что величина $D(0)$, представляющая собой обычную хаусдорфову размерность ${{D}_{H}}$ множества $G,$ является наиболее грубой характеристикой мультифрактала и не несет информации о его статистических свойствах.
При $q = 1,$ в силу условия нормировки вероятности ${{p}_{i}},$ статистическая сумма равна $\Gamma (1,\Delta ) = 1,$ а $\tau (1) = 0.$ Таким образом, мы имеем неопределенность в выражении (57) для $D(1),$ которая раскрывается с помощью очевидного равенства
(59)
$\begin{gathered} D(1) = \mathop {\lim }\limits_{q \to 1} \left\{ {\frac{1}{{q - 1}}\mathop {\lim }\limits_{\Delta \to 0} \left[ {\ln {{\sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} (\Delta )} \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} (\Delta )} {\ln \Delta }}} \right. \kern-0em} {\ln \Delta }}} \right]} \right\} = \\ = \mathop {\lim }\limits_{q \to 1} \left\{ {\frac{1}{{q - 1}}\mathop {\lim }\limits_{\Delta \to 0} \left[ {\ln \left( {\sum\limits_{i = 1}^{N(\Delta )} {{{p}_{i}}\exp } } \right.} \right.} \right. \times \\ \times \left. {\left. {{{{{{\left. {\left[ {(q - 1)} \right]\ln {{p}_{i}}} \right)} \mathord{\left/ {\vphantom {{\left. {\left[ {(q - 1)} \right]\ln {{p}_{i}}} \right)} {\ln \Delta }}} \right. \kern-0em} {\ln \Delta }}}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}} \right]} \right\} = \\ = \mathop {\lim }\limits_{q \to 1} \left\{ {\frac{1}{{q - 1}}\mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln 1 + (q - 1)\sum\limits_{i = 1}^{N(\Delta )} {{{p}_{i}}} \ln {{p}_{i}}}}{{\ln \Delta }}} \right\} = \\ = \mathop {\lim }\limits_{\Delta \to 0} \frac{1}{{\ln \Delta }}\sum\limits_{i = 1}^{N(\Delta )} {{{p}_{i}}} \ln {{p}_{i}}. \\ \end{gathered} $В результате величина обобщенной фрактальной размерности $D(1)$ связана с энтропией Больцмана−Гиббса99$S(p) = - k\sum\nolimits_{i = 1}^{N(\Delta )} {{{p}_{i}}} \ln {{p}_{i}}$ соотношением
(60)
$D\left( 1 \right) = - \frac{1}{k}\mathop {\lim }\limits_{\Delta \to 0} \frac{{S(\Delta )}}{{\ln \Delta }}.$Таким образом, поскольку $S \approx {{\Delta }^{{ - kD(1)}}},$ то величина $D(1)$ характеризует информацию, необходимую для определения местоположения элемента фрактального объекта в некоторой ячейке. В связи с этим обобщенную фрактальную размерность $D(1)$ часто называют информационной размерностью. Она показывает, как информация, необходимая для определения местоположения элемента фрактала, возрастает при стремлении размера ячейки к нулю.
Корреляционная размерность. Важную роль в различных приложениях играет так называемая корреляционная размерность, которая следует из (57) при $q = 2$
(61)
$D(2) = \mathop {\lim }\limits_{\Delta \to 0} \frac{{\sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{2}} (\Delta )}}{{\ln \Delta }} \approx \mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln I(\Delta )}}{{\ln \Delta }},$Заметим, что при $q$ = 3,4,… имеют место обобщенные размерности, связанные с корреляционными интегралами $I$-триплетов, квадруплетов и т.д. точек на фрактальном множестве.
Свойства размерностей Реньи. Из свойств энтропии Реньи, приведенных в “Некоторые…”, следует, что для размерностей фракталов Реньи (57) выполняются следующие неравенства:
Во-первых, размерность $D(q),$ согласно свойству неотрицательности (5) энтропии Реньи, удовлетворяет неравенству
(62)
$D(q) = - \frac{1}{k}\mathop {\lim }\limits_{\Delta \to 0} \left\{ {\frac{1}{{\ln \Delta }}S_{q}^{R}(p)} \right\} \geqslant 0.$Во-вторых, размерности Реньи, согласно свойству (15) для $S_{q}^{R}$ и определению (57), подчиняются неравенству (Mandelbrot, 1974)
из которого следует, что обобщенная фрактальная размерность $D(q)$ всегда монотонно убывает (или, в крайнем случае, остается постоянной) с ростом $q.$ Знак равенства имеет место, например, для однородных фракталов, в которых вероятность ${{p}_{i}}$ удовлетворяет закону подобия ${{p}_{i}} \approx {{\Delta }^{D}},$ где $D$ – любая размерность. Максимальное значения ${{D}_{{\max }}} = D( - \infty )$ величина $D(q)$ достигает при $q \to - \infty ,$ а минимальное значение ${{D}_{{\min }}} = D(\infty )$ при $q \to + \infty .$В-третьих, вследствие свойства (17) для энтропии Реньи, имеют место общие неравенства
(64)
$\frac{{(q{\kern 1pt} ' - 1)}}{{q'}}D(q{\kern 1pt} ') \geqslant \frac{{(q - 1)}}{q}D(q),\,\,{\text{если }}q{\kern 1pt} ' > q,\,\,\,\,q{\kern 1pt} 'q > 0,$(65)
$(q{\kern 1pt} ' - 1)D(q{\kern 1pt} ') \geqslant (q - 1)D(q),\,\,\,\,{\text{если }}q{\kern 1pt} ' > q > 0.$В случае, когда $q{\kern 1pt} ' \to + \infty $ и $q > 1,$ из (64) вытекает неравенство
аналогично, когда $q \to - \infty $ и $q < 0,$ для размерности $D(q)$ справедливоПолезными частными случаями выражений (63) и (64) являются неравенства
(68)
$\begin{gathered} {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}D(2) \leqslant D(\infty ) \leqslant D(2)\,\,\,\,и \\ D( - 1) \leqslant D( - \infty ) \leqslant 2D( - 1), \\ \end{gathered} $Наконец, согласно неравенству (62) информационная $D(1)$ и корреляционная $D(2)$ размерности мультифрактала ограничивают хаусдорфову размерность ${{D}_{H}}$ снизу, т.е.
Мультифракталы с двумя характерными масштабами длины
В качестве примера рассмотрим неоднородное канторовское множество, где причиной неоднородности является наличие нескольких пространственных масштабов, при том, что все вероятности ${{p}_{i}}$ совпадают.
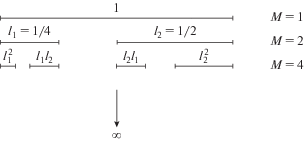
Пусть в начале процедуры (нулевой шаг) у нас имеется множество с мерой 1 и размером 1 (например, единичный отрезок, по которому как-то распределены N точек нашего фрактального множества. На первом шаге заменим его двумя отрезками с длинами l1 = 1/4 и l2 = 1/2, примыкающими соответственно к его левому и правому концам. Обоим отрезкам припишем одинаковую меру р = 1/2. Затем повторим ту же процедуру с каждым из этих двух отрезков. В результате получится уже четыре отрезка с длинами (l1)2, l1l2, l2l1 и (l2)2 и одинаковыми мерами, равными 1/4. Продолжая этот процесс до бесконечности, мы получим в конце концов неоднородное канторовское множество, т.е. мультифрактал. Первые шаги этого процесса изображены на рис. 2. Чтобы определить спектр обобщенных фрактальных размерностей в этом случае, необходимо видоизменить соотношение (58), определяющее функцию $\tau (q),$ так как теперь мультифрактал характеризуется не одним масштабом, а многими.
Рис. 2.
Неоднородное канторовское множество с двумя характерными масштабами длины l1 = 1/4, l 2 = 1/2 и p1 = р2 = 1/2.
Введем более общее определение фрактальной размерности $D(q)$. Предположим, что множество $S$ (мультифрактальный объект) покрыто счетным числом $N$ непересекающихся подмножеств ${{S}_{i}}$ (гиперкубов) с диаметрами ${{\Delta }_{i}} < \Delta $$(\Delta > 0).$ Допустим теперь, что подмножества ${{S}_{i}}$ имеют размерность $( - \tau ).$ Пусть вероятность того, что элемент множества $S$ находится в ${{S}_{i}}$ есть ${{p}_{i}}.$ Тогда, вводимая в теории мультифракталов так называемая обобщенная статистическая сумма (Halsey и др., 1986)
(70)
$\Gamma \left( {q,\tau ,\left\{ {{{S}_{i}}} \right\},\Delta } \right) = \sum\limits_{i = 1}^{N = N\left( \Delta \right)} {p_{i}^{q}\Delta {\kern 1pt} _{i}^{{ - \tau }}} ,$(71)
$\Gamma \left( {q,\tau } \right) = \mathop {\lim }\limits_{\Delta \to 0} \sum\limits_{i = 1}^{N\left( \Delta \right)} {p_{i}^{q}} \Delta _{i}^{{ - \tau }} = \mathop {\lim }\limits_{\Delta \to 0} \sum\limits_{i = 1}^{N\left( \Delta \right)} {{{p}_{i}}} {{\left( {\frac{{{{p}_{i}}}}{{\Delta _{i}^{{D(q)}}}}} \right)}^{{q - 1}}}.$Для каждого $q$ существует одно значение $\tau = \tau (q),$ и мера (71) имеет конечное значение (порядка единицы) при достаточно большом $N$ лишь в случае выполнения условия $\tau (q) = (q - 1)D(q)$ (см. Halsey и др., 1986). Тогда обобщенная размерность Реньи, вводимая соотношением
(72)
$D(q) = {{\tau (q)} \mathord{\left/ {\vphantom {{\tau (q)} {(q - 1)}}} \right. \kern-0em} {(q - 1)}} \geqslant 0,$(73)
$\Gamma \left( {0,1} \right) = \mathop {\lim }\limits_{\Delta \to 0} \sum\limits_{i = 1}^{N\left( \Delta \right)} {\Delta {\kern 1pt} _{i}^{{D(0)}}} .$Расчет мультифрактальных спектров размерностей. Следует заметить, что формула (57) мало пригодна для практических расчетов размерностей мультифракталов в силу ряда трудностей, связанных с предельным переходом к бесконечно малым объемам $\Delta \to 0.$ Однако задача создания алгоритма для определения фрактальной размерности Реньи существенно упрощается, если наложить некоторые ограничения на процедуру выбора иерархии покрытий (Meisel и др., 1992). Точные формулировки этого метода определения фрактальных размерностей − метода подсчета ячеек, покрывающих фрактальное множество, − можно найти, например, в работах (Meisel и др., 1992; Шредер, 2001). Размерность фрактальных сред может быть эмпирически получена методом поклеточного счета (box-countingmethod). Простой и быстрый алгоритм для оценки корреляционной размерности аттракторов динамической системы предложен в работе (Grassberger, Procaccia, 1983).
Покажем теперь, что между приведенными здесь мультифрактальными мерами и так называемой двухпараметрической информацией различия существует глубокая связь.
ДВУХПАРАМЕТРИЧЕСКАЯ РАЗЛИЧАЮЩАЯ ИНФОРМАЦИЯ И МУЛЬТИФРАКТАЛЬНЫЕ МЕРЫ
Вывод двухпараметрической информации различия. С целью получения двухпараметрического аналога различающей информации Реньи $K_{q}^{R}(p:f)$ найдем минимум информации Кульбака−Лейблера
(74)
${{K}^{{KL}}}(u:p) \equiv k\sum\limits_i^N {{{u}_{i}}\ln \left( {{{{{u}_{i}}} \mathord{\left/ {\vphantom {{{{u}_{i}}} {{{p}_{i}}}}} \right. \kern-0em} {{{p}_{i}}}}} \right)} ,$(75)
$H(u:p) \equiv \sum\limits_i^N {{{u}_{i}}\ln {{p}_{i}}} ,\,\,\,\,H(u:f) \equiv \sum\limits_i^N {{{u}_{i}}\ln {{f}_{i}}} ,$Согласно вариационному принципу Jaynes, найдем безусловный экстремум функционала
(76)
$\begin{gathered} L(u) = k\sum\limits_i^N {{{p}_{i}}} \ln \left( {\frac{{{{u}_{i}}}}{{{{p}_{i}}}}} \right) + k(1 - q)\sum\limits_i^N {{{u}_{i}}\ln {{p}_{i}}} - \\ - \,\,k\tau \sum\limits_i^N {{{u}_{i}}\ln {{f}_{i}}} + k(\alpha - 1)\sum\limits_i^N {{{u}_{i}}} , \\ \end{gathered} $(77)
$\begin{gathered} \delta L = k\sum\limits_i^N {\delta {{u}_{i}}} \times \\ \times \,\,\left[ {\ln \left( {{{{{u}_{i}}} \mathord{\left/ {\vphantom {{{{u}_{i}}} {{{p}_{i}}}}} \right. \kern-0em} {{{p}_{i}}}}} \right) + (1 - q)\ln {{p}_{i}} + \tau \ln {{f}_{i}} + \alpha } \right] = 0, \\ \end{gathered} $(78)
${{u}_{i}} = {{p}_{i}}\exp \left[ { - (1 - q)\ln {{p}_{i}} - \tau \ln {{f}_{i}} - \alpha } \right],$(79)
${{u}_{i}} = {{p_{i}^{q}f_{i}^{{ - \tau }}} \mathord{\left/ {\vphantom {{p_{i}^{q}f_{i}^{{ - \tau }}} {{{\Gamma }_{{q\tau }}}(p,f)}}} \right. \kern-0em} {{{\Gamma }_{{q\tau }}}(p,f)}}.$Здесь введены обобщенная статистическая сумма
(80)
${{\Gamma }_{{q\tau }}}(p,f) \equiv \sum\limits_i^N {p_{i}^{q}} f_{i}^{{ - \tau }} = {{\sum\limits_i^N {{{p}_{i}}\left( {{{{{p}_{i}}} \mathord{\left/ {\vphantom {{{{p}_{i}}} {f_{i}^{{D(q)}}}}} \right. \kern-0em} {f_{i}^{{D(q)}}}}} \right)} }^{{q - 1}}}$Подставляя распределение (79) в выражения для информаций различия Кульбака, получим следующие соотношения (Зарипов, 2002):
(81)
$\begin{gathered} {{K}^{{KL}}}\left( {u:p} \right) = k\sum\limits_i^N {{{u}_{i}}\left( {\ln \frac{{{{u}_{i}}}}{{{{p}_{i}}}}} \right)} = \\ = k\left( {q - 1} \right)\sum\limits_i^N {{{u}_{i}}\left( {\ln \frac{{{{p}_{i}}}}{{f_{i}^{{D(q)}}}}} \right)} - k\ln {{\Gamma }_{{q\tau }}}, \\ \end{gathered} $(82)
$\begin{gathered} {{K}^{{KL}}}\left( {p:u} \right) = k\sum\limits_i^N {{{p}_{i}}\left( {\ln \frac{{{{p}_{i}}}}{{{{u}_{i}}}}} \right)} = \\ = k\left( {q - 1} \right)\sum\limits_i^N {{{p}_{i}}\left( {\ln \frac{{{{p}_{i}}}}{{f_{i}^{{D(q)}}}}} \right)} + k\ln {{\Gamma }_{{q\tau }}}, \\ \end{gathered} $(83)
$\frac{q}{{q - 1}}{{K}^{{KL}}}\left( {u:p} \right) = {{K}_{{{{D}_{q}}}}}\left( {u:f} \right) - {{K}_{{q,\tau }}}\left( {p:f} \right),$(84)
$\frac{1}{{q - 1}}{{K}^{{KL}}}\left( {p:u} \right) = {{K}_{{q,\tau }}}\left( {p:f} \right) - {{K}_{{{{D}_{q}}}}}\left( {p:f} \right).$В выражениях (83)–(84) введены специфические различающие информации
(85)
$\begin{gathered} {{K}_{{{{D}_{q}}}}}(u:f) = k\sum\limits_i^N {{{u}_{i}}\ln \left( {\frac{{{{u}_{i}}}}{{f_{i}^{{{{D}_{q}}}}}}} \right)} \,\,\,\,{\text{и}} \\ {{K}_{{{{D}_{q}}}}}\left( {p:f} \right) = k\sum\limits_i^N {{{p}_{i}}} \ln \left( {\frac{{{{p}_{i}}}}{{f_{i}^{{{{D}_{q}}}}}}} \right), \\ \end{gathered} $(86)
$\begin{gathered} {{K}_{{q\tau }}}(p:f) \equiv \frac{k}{{q - 1}}\ln {{\Gamma }_{{q\tau }}} = \frac{k}{{q - 1}}\ln \left( {\sum\limits_i^N {p_{i}^{q}f_{i}^{{ - \tau }}} } \right) = \\ = \frac{k}{{q - 1}}\ln \left\{ {\sum\limits_i^N {{{p}_{i}}{{{\left( {\frac{{{{p}_{i}}}}{{f_{i}^{{D(q)}}}}} \right)}}^{{q - 1}}}} } \right\}. \\ \end{gathered} $Заметим, что при $D(q) = 1$ функционалы (85) и (86) совпадают с различающими информациями Кульбака−Лейблера и Реньи:
(87)
${{K}_{1}}(u:f) = {{K}^{{KL}}}(u:f) \equiv k\sum\limits_i^N {{{u}_{i}}\ln \left( {{{{{u}_{i}}} \mathord{\left/ {\vphantom {{{{u}_{i}}} {{{f}_{i}}}}} \right. \kern-0em} {{{f}_{i}}}}} \right)} ,$(88)
${{K}_{{q,1}}}\left( {p:f} \right) = K_{q}^{R}\left( {p:f} \right) \equiv \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}f_{i}^{{1 - q}}} .$Основные свойства двухпараметрической информации различия можно найти в работе (Зарипов, 2010). В частности, там показано, что величина ${{K}_{{q\tau }}}(p:f)$ является выпуклым аддитивным функционалом для независимых объектов,
(89)
${{K}_{{q,\tau }}}\left( {{{p}_{{12}}}:{{f}_{{12}}}} \right) = {{K}_{{q,\tau }}}\left( {{{p}_{1}}:{{f}_{1}}} \right) + {{K}_{{q,\tau }}}\left( {{{p}_{2}}:{{f}_{2}}} \right),$(90)
$\begin{gathered} {{K}_{{q,\tau }}}\left( {p{\kern 1pt} {\kern 1pt} :f} \right) = \frac{k}{{q - 1}}\ln \sum\limits_i^N {p_{i}^{q}f_{i}^{{{{D}_{q}}(1 - q)}}} = \\ = {{S}_{N}} - {{S}_{q}}\left( p \right), \\ \end{gathered} $Связь с мультифрактальными размерностями. Покажем теперь, что приведенные выше результаты позволяют по-новому переосмыслить и интерпретировать сведения о мультифрактальных спектрах размерностей.
Во-первых, из формул (71) и (80) следует, что обобщенная размерность Хаусдорфа $\Gamma \left( {q,\tau } \right)$ связана c обобщенной статистической суммой ${{\Gamma }_{{q\tau }}}(p,f),$ записанной при ${{f}_{i}} \equiv {{{{\Delta }_{i}}} \mathord{\left/ {\vphantom {{{{\Delta }_{i}}} \Delta }} \right. \kern-0em} \Delta },$ следующим соотношением
(91)
$\begin{gathered} \Gamma \left( {q,\tau } \right) \equiv \mathop {\lim }\limits_{\Delta \to 0} \sum\limits_{i = 1}^{N\left( \Delta \right)} {p_{i}^{q}} \Delta _{i}^{{ - \tau }} = \\ = \mathop {\lim }\limits_{\Delta \to 0} {{\Delta }^{{ - \tau }}}\sum\limits_{i = 1}^{N\left( \Delta \right)} {p_{i}^{q}} {{\left( {\frac{{\Delta {{{\kern 1pt} }_{i}}}}{\Delta }} \right)}^{{ - \tau }}} = \mathop {\lim }\limits_{\Delta \to 0} {{\Delta }^{{ - \tau }}}{{\Gamma }_{{q\tau }}}\left( {p,\frac{{\Delta {{{\kern 1pt} }_{i}}}}{\Delta }} \right). \\ \end{gathered} $Во-вторых, в случае равновозможного распределения ${{f}_{i}} = {1 \mathord{\left/ {\vphantom {1 \Delta }} \right. \kern-0em} \Delta }$ из (86) вытекает соотношение:
(92)
$\begin{gathered} {{K}_{{q\tau }}}(p:f) = \frac{k}{{q - 1}}\ln {{\Delta }^{\tau }}\left( {\sum\limits_i^N {p_{i}^{q}} } \right) = \\ = \frac{{k\tau }}{{q - 1}}\ln \Delta - S_{q}^{R}(p). \\ \end{gathered} $Тогда так называемая информационная размерность мультифракталов, определяемая соотношением (Halsey и др., 1986)
(93)
${{D}_{K}} = \frac{1}{k}\mathop {\lim }\limits_{\Delta \to 0} \frac{{{{K}_{{q\tau }}}(p:f)}}{{\ln \Delta }},$(94)
$\begin{gathered} {{D}_{K}} = \frac{\tau }{{q - 1}} - \frac{1}{k}\mathop {\lim }\limits_{\Delta \to 0} \frac{{S_{q}^{R}(p)}}{{\ln \Delta }} = D(q) + \\ + \,\,\mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln \sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} (\Delta )}}{{(q - 1)\ln \Delta }} = D(q) + {{D}^{{HP}}}. \\ \end{gathered} $Здесь второе слагаемое совпадает с размерностью мультифракталов ${{D}^{{HP}}},$ впервые введенной в рассмотрение в работе (Hentschel, Procaccia, 1983).
При ${{f}_{i}} \equiv {{\Delta {{{\kern 1pt} }_{i}}} \mathord{\left/ {\vphantom {{\Delta {{{\kern 1pt} }_{i}}} \Delta }} \right. \kern-0em} \Delta }$ имеет место обобщение формулы (94)
(95)
$\begin{gathered} {{D}_{K}} = D(q) + \mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln \sum\limits_{i = 1}^{N(\Delta )} {p_{i}^{q}} \Delta {\kern 1pt} _{i}^{{ - \tau }}}}{{(q - 1)\ln \Delta }} = \\ = D(q) + \mathop {\lim }\limits_{\Delta \to 0} \frac{{\ln \Gamma \left( {q,\tau ,\left\{ {{{S}_{i}}} \right\},\Delta } \right)}}{{(q - 1)\ln \Delta }}, \\ \end{gathered} $ЗАКЛЮЧЕНИЕ
В настоящее время вопрос о построении усложненных моделей материальных средc учетом новых и дополнительных свойств и эффектов поставлен в порядок дня. Как известно, нередко учет малых эффектов, едва уловимых на первоначальной стадии исследования, впоследствии при более глубоком проникновении в сущность природы явлений и при расширении поля приложений становится основой возникновения прогресса, т.е. такого рода эффекты представляет собой самую квинтэссенцию проблемы и обязательно должны учитываться. В представленной работе на основе параметрических энтропии и различающей информации Реньи выполнены в их взаимосвязи и взаимодополняемости конструирование статистической термодинамики фрактальных систем и разработка техники получения мультифрактальных размерностей. Развитый здесь подход предназначен, в частности, для математического моделирования (на основе системы гидродинамических уравнений для фрактальных сред и замыкающих ее обобщенных термодинамических соотношений)процессов эволюции различных космических сред, отличительной чертой которых является наличие динамических структур (фракталов) с нецелой топологической размерностью, глобальность силовых взаимодействий между элементами системы, а также наличие асимптотически степенных статистических распределений.
Список литературы
Башкиров А.Г. Энтропия Реньи как статистическая энтропия для сложных систем // Теор. и мат. физика. 2006. Т. 149. № 2. С. 299–317.
Бадии Р., Полити А. Численное исследование неоднородных фракталов // Фракталы в физике / Ред. Синая Я.Г. и Халатников И.М. М.: Мир, 1988. С. 632–637.
Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. Москва–Ижевск: РХД, 2001. 128 с.
Зарипов Р.Г. Самоорганизация и необратимость в неэкстенсивных системах. Казань: Фэн, 2002. 251 с.
Зарипов Р.Г. Принципы неэкстенсивной статистической механики и геометрия мер беспорядка и порядка. Казань: Изд-во Казан. гос. техн. ун-та, 2010. 404 с.
Зубарев Д.П. Неравновесная статистическая механика. М.: Наука, 1971. 416 с.
Климонтович Ю.Л. Турбулентное движение и структура хаоса. Новый подход к статистической теории открытых систем. М.: Наука, 1990. 320 с.
Колесниченко А.В. О синергетическом механизме возникновения когерентных структур в континуальной теории развитой турбулентности // Астрон. вестн. 2004. Т. 38. № 5. С. 405–427. (Kolesnichenko A.V. Synergetic mechanism of the development of coherent structures in the continual theory of developed turbulence // Sol. Syst. Res. 2004. V. 38. № 5. P. 351–371.)
Колесниченко А.В. К построению неаддитивной термодинамики сложных систем на основе статистики Курадо-Тсаллиса // Препр. ИПМ им. М.В. Келдыша. 2018a. № 25. 40 с.
Колесниченко А.В. К конструированию термодинамики неаддитивных сред на основе статистики Тсаллиса−Мендеса−Пластино // Препр. ИПМ им. М.В. Келдыша. 2018б. № 23. 28 с.
Колесниченко А.В. Модификация фундаментального уравнения Гиббса классической термодинамики на основе различающей информации Кульбака–Лейблера // Препр. ИПМ им. М.В. Келдыша. 2018в. № 36. 32 с.
Колесниченко А.В., Маров М.Я. Моделирование процессов образования пылевых фрактальных кластеров как основы рыхлых протопланетезималей в солнечном допланетном облаке // Препр. ИПМ им. М.В. Келдыша. 2014. № 75. 44 с.
Колесниченко А.В. Конструирование энтропийной транспортной модели на основе статистики Тсаллиса // Препр. ИПМ им. М. В. Келдыша. 2013. № 33. 23 с.
Колесниченко А.В. Критерий термической устойчивости и закон распределения частиц для самогравитирующих астрофизических систем в рамках статистики Тсаллиса // Mathematica Montisnigri. 2016. Т. 37. С. 45–75.
Колесниченко А.В. Некоторые проблемы конструирования космических сплошных сред: Моделирование аккреционных протопланетных дисков. М.: ИПМ им. М.В. Келдыша, 2017. 372 с.
Колесниченко А.В. Статистическая механика и термодинамика Тсаллиса неаддитивных систем. Введение в теорию и приложения. М.: ЛЕНАНД, 2019. 360 с.
Колесниченко А.В., Маров М.Я. Основы механики гетерогенных сред в околосолнечном допланетном облаке: Влияние твердых частиц на турбулентность в диске // Астрон. вестн. 2006. Т. 40. № 1. С. 3–64. (Kolesnichenko A.V., Marov M.Ya. Fundamentals of the mechanics of heterogeneous media in the circumsolar protoplanetary cloud: The effects of solid particles ondisk turbulence // Sol. Syst. Res. 2006. V. 40. № 1. P. 1–56.)
Колесниченко А.В., Маров М.Я. Турбулентность и самоорганизация. Проблемы моделирования космических и природных сред. М.: БИНОМ. Лаборатория знаний, 2009. 632 с.
Колесниченко А.В., Маров М.Я. Механизм потоковой неустойчивости в газопылевой среде протопланетного диска и формирование пылевых фрактальных кластеров // Астрон. вестн. 2019. Т. 53. № 3. С. 195–213. (Kolesnichenko A.V., Marov M.Ya. Streaming instability in the gas–dust medium of the protoplanetary disc and the formation of fractal dust clusters // Sol. Syst. Res.2019. V. 53. № 3. P. 181–198.)
Кроновер P.M. Фракталы и хаос в динамических системах. М.: Лостмаркет, 2000. 352 с.
Кульбак С. Теория информации и статистика. М.: Наука, 1967. 408 с.
Мандельброт Б. Фрактальная геометрия природы. М.: Институт компьютерных исследований. 2002. 656 с.
Макалкин А.Б., Зиглина И.Н. Гравитационная неустойчивость в пылевом слое протопланетного диска с учетом взаимодействия слоя и окружающего газа в диске // Астрон. вестн. 2018. Т. 52. С. 534–551. (Makalkin A.B., Ziglina I.N. Gravitational instability inthe dust layer of a protoplanetary disk with interaction between the layer and the surrounding gas // Sol. Syst. Res. 2018. V. 52. № 6. P. 518–533.)
Маров М.Я. Малые тела Солнечной системы и некоторые проблемы космогонии // УФН. 2005. Т. 175. № 6. С. 668–678.
Маров М.Я., Русол А.В. Оценка параметров столкновений пылевых фрактальных кластеров в газопылевом протопланетном диске // Письма в Астрон. журн. 2018. Т. 44. № 7. С. 517–524.
Могилевский Э.И. Фракталы на Солнце. М.: Физматлит, 2001. 152 с.
Пиблс Ф.Дж.Э. Структура Вселенной в больших масштабах. М.: Мир, 1983. 408 с.
Потапов А.А. Фракталы в радиотехнике и радиолокации: Топология выборки. М.: Университетская книга, 2002. 848 с.
Сафронов В.С. Эволюция допланетного облака и образование Земли и планет. М.: Наука, 1969. 244 с.
Смирнов Б. М. Физика фрактальных кластеров. М.: Наука, 1991.136 с.
Учайкин В.В. Метод дробных производных. Ульяновск: Изд-во “Артишок”, 2008. 512 с.
Федер Е. Фракталы. М.: Мир, 1991. 260 с.
Харди Г.Г., Литтльвуд Дж.Е., Полиа Г. Неравенства. М.: Ин.-Лит, 1948. 456 с.
Шредингер Э. Что такое жизнь с точки зрения физики? М.: Ин. Лит, 1947. 147 с.
Шредер М. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001. 527 с.
Abe S. Remark on the escort distribution representation of nonextensive statistical mechanics // Phys. Lett. A. 2000. V. 275. № 4. P. 250–253.
Armitage P.J. Physical processes in protoplanetary disks // arXiv: 1509.06382v1 [astro-ph.SR] 21 Sep. 2015. P. 1–127.
Beck C. Upper and lower bounds on the Renyi dimensions and the uniformity of multifractals // Physica D. 1990. V. 41. P. 67–78.
Beck C., Schlogl F. Thermodynamics of chaotic systems: an introduction. Cambridge: Cambridge University Press, 1993. 286 p.
Besicovitch A.S. On the sum of digits of real numbers represented in the dyadic system // Math. Annal. 1934. B. 110. № 3. P. 321–330.
Bialas A., Czyz W. Renyi entropies of a black hole from Hawking radiation // EPL (Europhysics Letters). 2008. V. 83. № 6. P. 60009.
Blum J. Grain growth and coagulation// ASP Conf. Ser. 2004. V. 309. Astrophysics of Dust / Eds Witt A.N., Clayton G.C., Draine B.T. (San Francisco: ASP). P. 369.
Blum J., Wurm G. The growth mechanisms of macroscopic bodies in protoplanetary disks // Ann. Rev. Astron. and Astrophys. 2008. V. 46. P. 21–56.
Chavanis P.-H. Trapping of dust by coherent vortices in the solar nebula // arXiv:astroph/9912087. 1999. V. 16. P. 1–54.
Cuzzi J.N., Dobrovolskis A.R., Champney J.M. Particle-gas dynamics in the midplane of a protoplanetary nebulae // Icarus. 1993. V. 106. P. 102–134.
Cuzzi J.N., Hogan R.C., Dobrovolskis A.R.Turbulent concentration: Fractal description, scaling laws, and ceneralized applications to planetesimal accretion // 29th Ann. Lunar and Planet. Sci. Conf. March 16–20, 1998, Houston, TX, abstract № 1443.
Dominik C., Tielens A.G. The physics of dust coagulation and the structure of dust aggregates in space // Astrophys. J. 1997. V. 480. P. 647–673.
Daroczy Z. Generalized information function // Inform. Control. 1970. V. 16. P. 36–51.
Estrada P.R., Cuzzi J.N. Fractal growth and radial migration of solids: The role of porosity and compaction inan evolving nebula// 47th Lunar and Planet. Sci. Conf. held March 21–25, 2016 at the Woodlands, Texas. LPI Contribution № 1903. P. 285.
Grassberger P. On the Hausdorff dimension of fractal attractors // J. Statist. Phys. 1981. V. 26. № 1. P. 173–179.
Grassberger P. Generalizations of the Hausdorff dimension of fractal measures // Phys. Lett. A. 1985. V. 107. № 3. P. 101–105.
Grassberger P., Procaccia I. Characterization of strange attractors // Phys. Rev. Lett. 1983. V. 50. № 5. P. 346–349.
Grassberger P., Procaccia I. Dimensions and entropies of strange attractors from a fluctuating dynamics approach // Physica D: Nonlinear Phenomena. 1984. V. 13. № 1–2. P. 34–54.
Halsey T.C., Jensen M.H., Kadanoff L.P., Procaccia I., Shraiman B.I. Fractal measures and their singularities: The characterization of strange sets // Phys. Rev. A. 1986. V. 33. P. 1141–1151.
Hausdorff F. Dimension und Ausseres Mass // Math. Annal. 1919. B. 79. S. 157–179.
Havrda J., Charvat F. Quantification method of classification processes // Kybernetika. 1967. V. 3. P. 30–35.
Hentschel H.G.E., Procaccia I. The infinite number of generalized dimensions of fractals and strange attractors // Physica D: Nonlinear Phenomena. 1983. V. 8. № 3. P. 435–444.
Jaynes E.T. Information theory and statistical mechanics // Statistical Physics. Brandeis Lectures. 1963. V. 3. P. 160.
Jizba P., Arimitsu T. Observability of Renyi’s entropy // Phys. Rev. E. 2004. V. 69. № 2. id. 026128.
Johal R.S., Rai R. Nonextensive thermodynamic formalism for chaotic dynamical systems // Physica A. 2000. V. 282. P. 525–535.
Jullien R. A new model of cluster aggregation // J. Phys. A. 1986. V. 19. № 11. P. 2129–2136
Kataoka A., Tanaka H., Okuzumi S., Wada K. Fluffy dust forms icy planetesimals by static compression // Astron. and Astrophys. 2013. V. 557. P. L4.
Kilbas A.A., Srivastava H.M., Trujillo J.J. Fractional differential equations: An emergent field in applied and mathematical sciences // Factorization, Singular Operators and Related Problems // Eds Samko S., Lebre A., Dos Santos A.F. London: Kluwer Acad. Publ., 2003. P. 151–73.
Kilbas A.A., Srivastava H.M., Trujillo J.J. Theory and Appllications of Fractional Differential Equations. Amsterdam: Elsevier, 2006.
Kolesnichenko A.V., Cheverushkin B.N. Kinetic derivation of a quasi-hydrodinamic system of equations on the base of nonextensive statistics // Russian J. Numerical Analys. and Mathemat. Modell. 2013. V. 28. № 6. P. 547–576.
Kolesnichenko A.V., Marov M.Ya. Modeling of aggregation of fractal dust clusters in a laminar protoplanetary disk // Sol. Syst. Res. 2013. V. 47. № 2. P. 80–98.
Kolesnichenko A.V., Marov M.Ya. Modification of the jeans instability criterion for fractal-structure astrophysical objects in the framework of nonextensive statistics // Sol. Syst. Res. 2014. V. 48. № 5. P. 354–365.
Kolesnichenko A.V. Power distributions for self-gravitating astrophysical systems based on nonextensive tsallis kinetics // Sol. Syst. Res. 2017. V. 51. № 2. P. 127–144.
Kropivnitskaya A., Rostovtsev A. R’enyi statistics in high energy particle production // 2003. /eprintarXiv:hep-ph/0309287.
Kullback S., Leibler R.A. On information and sufficiency // Ann. Math. Statist. 1951. V. 22. P. 79–86.
Lissauer J.J., de Pater I. Fundamental Planetary Science. Physics, Chemistry and Habitability. New York: Cambridge Univ. Press, 2013. 583 p.
Lorenz E.N. Deterministic Nonperiodic Flow // J. Atmosph. Sci. 1963. V. 20. № 2. P. 130–148.
Mandelbrot B.B. Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier // J. Fluid. Mech. 1974. V. 62. P. 331–358.
Mandelbrot B.B. Les Objects Fractals. Forms, Hazard et Dimension. Paris: Flammarion, 1975. 195 p.
Mandelbrot B.B. Fractals: Form, Change and Dimension. San Francisco: Freeman, 1977. 365 p.
Mandelbrot B.B.The Fractals Geometry of Nature. New York: Freeman, 1982. 460 p.
Martinez S., Nicolas F., Pennini F., Plastino A. Tsallis’entropy maximization procedure revisited // Physica A. 2000. V. 286. P. 489–502.
Marov M.Ya., Kolesnichenko A.V. Turbulence and Self-Organization.Modeling Astrophysical Objects. Springer, 2013. 657 p.
Meisel L., Johnson M., Cote P.J. Box-counting multifractal analysis // Phys. Rev. A 45. 1992. P. 6989–6996.
Mizuno H. Grain growth in the turbulent accretion disk solar nebula // Icarus. 1989. V. 80. P. 189–201.
Moon F.C., Li G.-X. The fractal dimension of the two-well potential strange attractors // Physica D. 1985. V. 17. № 1. P. 99–108.
Nagy Á., Romera E. Maximum Rényi entropy principle and the generalized Thomas-Fermi model // Phys. Lett. A. 2009. V. 373. № 8–9. P. 844–846.
Nakagawa Y., Sekiya M., Hayashi C. Settling and growth of dust particles in a laminar phase of a low-mass Solar nebula // Icarus. 1986. V. 67. P. 375–390.
Nakagawa Y., Nakazawa K., Hayashi C. Growth and sedimentation of dust grains in the primordial solar nebula // Icarus. 1981. V. 45. P. 517–528
Nath P. On Coding Theorem Connected with Rényi’s Entropy // Inform. and Contr. 1975. V. 29. P. 234–242.
Nonextensive statistical mechanics and thermodynamics: Bibliography/ http:// tsallis.cat.cbpf.br/biblio.htm.
Okuzumi S., Tanaka H., Takeuchu T., Sakagami M.-A. Electrostatic barrier against dust growth in protoplanetary disks. 1. Classifying the evolution of size distribution // Astrophys. J. 2011. V. 731. P. 95.
Ormel C.W., Spaans M., Tielens A.G.G.M. Dust coagulation in protoplanetary disks: Porosity matters // Astron. and Astrophys. 2007. V. 461. P. 215–236.
Ossenkopf V. Dust coagulation in dense molecular clouds: the formation of fluffy aggregates // Astron. and Astrophys. 1993. V. 280. P. 617–646.
Parvan A.S., Biro T.S. Ther modynamical limit in non-extensive Renyi statistics // Phys. Lett. A. 2005. V. 340. № 5–6. P. 375–387.
Peebles P.J.E. The Large-Scale Structure of the Universe. Princeton: Princeton Univ. Press, 1980. 435 p.
Rathie P.N., Kannappan Pl. A directed-divergence function of type β // Inform. and Contr. 1972. V. 20. P. 38–45.
Renyi A. On measures of entropy and information // Proc. 4th Berkeley Symp. on Math. Stat. Prob. 1960. V. 1. Berkeley, Los Angeles: Univ. California Press, 1961. P. 547–561.
Renyi A. Probability Theory. Amsterdam: North-Holland Publ. Co., 1970. 573 p.
Ruelle D., Takens F. On the nature of turbulence // Commun. in Math. Phys. 1971. V. 20. № 3. P. 167–192.
Shariff K., Cuzzi J.N. Gravitational instability of solids assisted by gas drag: slowing by turbulent mass diffusivity // Astroph. J. 2011. V. 738. № 1. article id. 73. 9 p.
Strichartz R.S. Analysis on fractals// not. Ame. Math. Soc. 1999. V. 46. № 10. P. 1199–1208.
Suyama T., Wada K., Tanaka H. Numerical simulation of density evolution of dust aggregates in protoplanetary disks. I. Head-on collisions // Astrophys. J. 2008. V. 684. P. 1310–1322.
Suyama T., Wada K., Tanaka H., Okuzumi S. Geometrical cross sections of dust aggregates and a compression model for aggregate collisions//arxiv:1205.1894vl [astro-ph. EP]. 2012. 28 p.
Tarasov V.E. Fractional hydrodynamic equations for fractal media // Ann. Phys. 2005. V. 318. № 2. P. 286–307.
Tarasov V.E. Fractional dynamics: Applications of fractional calculus to dynamics of particles, fields and media. Springer: Higher Education Press, 2010. 516 p.
Tsallis C. Nonextensive ther mostatistics and fractal // Fractals. 1995. V. 3. P. 541–554.
Tsallis C. Nonextensive Statistic: Theoretical, Experimental and Computational Evidences and Connections // Brazilian J. Phys. 1999. V. 29. № 1. P. 1–35.
Tsallis C. Nonextensive statistical mechanics and thermodynamics: Historical back groud and present status // Nonextensive Statistical Mechanics and Its Applications / Ed. S. Abe S. Classical and quantum complexity and nonextensive thermodynamics // Chaos, Solitons and Fractals. 2002. V. 13. P. 371–391.
Tsallis C. Introduction to Nonextensive Statistical Mechanics. Approaching a Complex World. New York: Springer, 2009. 382 p.
Tsallis C., Mendes R.S., Plastino A.R. The role of containts within generalized nonextensive statistics // Physica A. 1998. V. 261. P. 534–554.
Wada K., Tanaka H., Suyama T., Kimura H., Yamamoto T. Simulation of dust aggregate collisions. II. Compression and disruption of three-dimensional aggregates in head-on collisions // Astrophys. J. 2008. V. 677. P. 1296–1308.
Weidenschilling S.J. Dust to planetesimals: Settling and coagulation in the solar nebula // Icarus. 1980. V. 44. P. 172–189.
Weidenschilling S.J. Formation of planetesimals and accretion of the terrestrial planets // Space Sci. Rev. 2000. V. 92. P. 295–310.
Wetherill G.W., Stewart G.R. Accumulation of a swarm of small planetesimals // Icarus. 1989. V. 77. P. 330–357.
Yang C.-C., Johansen A. On the feeding zone of planetesimal formation by the streaming instability // Astrophys. J. 2014. V. 792. № 2. P. 86.
Yang C.-C., Johansen A., Carrera D. Concentrating small particles in protoplanetary disks through the streaming instability // Astron. and Astrophys. 2017. V. 606. id. A80.
Youdin A.N., Goodman J. Streaming instabilities in protoplanetary disks // Astrophys. J. 2005. V. 620. P. 459–469.
Youdin A.N. On the formation of planetesimals via secular gravitational instabilities with turbulent stirring // Astrophys. J. 2011. V. 731. № 2. article id. 99.18 p. arXiv:astro-ph/0508662
Zaripov R. Evolution of the entropy and Renyi difference information during self-organization of open additive systems // Russian Phys. J. 2005. V. 48. № 3. P. 267–274.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник