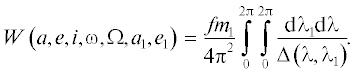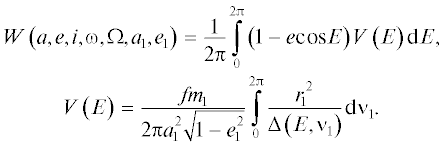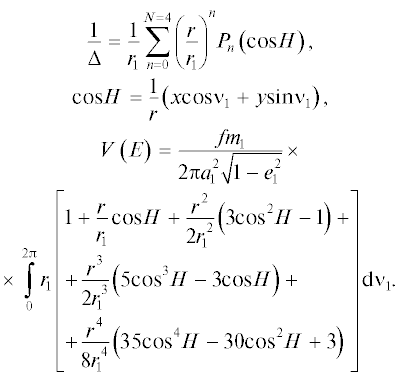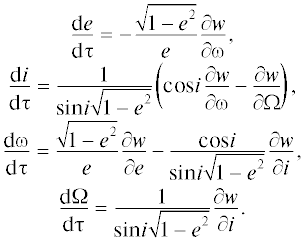Астрономический вестник, 2020, T. 54, № 1, стр. 57-73
Некоторые особенности эволюции орбит в спутниковой ограниченной эллиптической двукратно осредненной задаче трех тел
М. А. Вашковьяк *
Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: vashkov@keldysh.ru
Поступила в редакцию 10.06.2019
После доработки 20.06.2019
Принята к публикации 01.07.2019
Аннотация
Рассмотрен внутренний (или спутниковый) вариант ограниченной эллиптической задачи трех тел. В разложении возмущающей функции задачи сохранены слагаемые до четвертой степени включительно относительно малого параметра. Отношение больших полуосей орбит возмущаемого и возмущающего тел является таким параметром, а их средние долготы – наиболее быстрыми переменными. Для анализа эволюции орбиты тела пренебрежимо малой массы использована схема Гаусса независимого двойного осреднения по быстрым переменным. Приведены явные аналитические выражения двукратно осредненной возмущающей функции и ее производных по элементам, входящих в правые части эволюционных уравнений. Детально исследованы интегрируемые случаи двукратно осредненной задачи: плоские и ортогонально-апсидальные орбиты. В общем (неинтегрируемом) случае проведено численное интегрирование эволюционной системы для некоторых специальных значений параметров задачи и начальных условий, в частности, для совокупности орбитальных элементов, в которой проявляются так называемые “флипы” – переходы орбиты из прямого типа к обратному и наоборот. В модели Солнце–Юпитер–астероид на примере некоторых особенных астероидных орбит показано влияние на их эволюцию учтенных в работе слагаемых четвертой степени и эллиптичности орбиты Юпитера.
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ
Осредненные задачи небесной механики являются как предметом самостоятельного аналитического и численного исследования, так и одной из методических основ для изучения динамики реальных астрономических объектов на длительных промежутках времени. Специальный интерес представляют различные осредненные схемы задачи трех тел как общей, так и ограниченной. Особо выделяется так называемая схема Гаусса независимого осреднения силовой функции задачи по двум наиболее быстрым переменным – средним долготам возмущающего и возмущаемого тел, когда их средние движения несоизмеримы. В ограниченной задаче для круговой орбиты возмущающего тела относительно центрального Н.Д. Моисеев получил полную систему независимых первых интегралов осредненных (эволюционных) уравнений в элементах (Моисеев, 1945). Качественное и аналитическое исследование эволюционных уравнений было впервые проведено М.Л. Лидовым для спутникового варианта задачи, когда в разложении возмущающей функции по степеням малого параметра α (отношения больших полуосей возмущаемого и возмущающего тел) сохранены лишь слагаемые второй степени (Лидов, 1961). Практически одновременно Y. Kozai выполнил исследование астероидного варианта задачи с учетом слагаемых порядка α8, включительно (Kozai, 1962). Наряду с приложениями к динамике спутников планет и астероидов, в указанных работах был выявлен эффект падения на центральное тело тела бесконечно малой массы, если его орбита сильно наклонена к плоскости орбиты возмущающего тела. Описанию этого эффекта, получившего название “эффект Лидова–Козаи”, вместе с его астрофизическими приложениями посвящена монография И.И. Шевченко (Shevchenko, 2017). Развитием исследования (Kozai, 1962) послужила работа (Ito, 2016), в которой получено разложение двукратно осредненной возмущающей функции ограниченной круговой задачи трех тел с точностью до α14, включительно, для внутреннего варианта (α < 1) и до α–15, включительно, для внешнего варианта (α > 1). Необходимо отметить, несомненно, полиграфическую опечатку в последней строке формулы (33) последней работы.
Естественным обобщением эволюционной задачи трех тел является ее развитие на случай, более близкий к реальности, когда орбита возмущающего тела отличается от круговой. Соответствующая двукратно осредненная ограниченная эллиптическая задача имеет лишь несколько интегрируемых случаев (Вашковьяк, 1984), а в общем случае не интегрируема. Тем не менее в ней также проявляется эффект Лидова–Козаи и, как следствие, возникает новая качественная особенность – сильно эксцентрические орбиты, изменяющие в процессе эволюции свой тип с прямого на обратный и наоборот. Это явление, связанное с прохождением орбитального наклонения через 90° и открытое исследованиями (Katz и др., 2011; Naoz и др., 2011), получило название “флип”. Указанному явлению в двукратно осредненной эллиптической задаче трех тел (как общей, так и ограниченной) с приложениями к динамике экзопланет, тройных звездных систем и малых тел Солнечной системы посвящено достаточно большое количество работ. Их обширная библиография содержится в уже упомянутой книге (Shevchenko, 2017). Из относительно недавних работ укажем статьи (Naoz, 2016; Sidorenko, 2018), посвященные “эксцентрическому эффекту Козаи–Лидова”.
В данной работе получена специальная форма разложения двукратно осредненной возмущающей функции ограниченной эллиптической задачи трех тел с точностью до α4, включительно (слагаемые порядка α4 содержат, в частности, квадрат эксцентриситета орбиты возмущающего тела). Проведено более детальное рассмотрение интегрируемых случаев задачи, выполнено численное интегрирование эволюционной системы с начальными данными, отвечающими как флип-орбите, так и устойчивому равновесному решению соответствующей плоской эллиптической задачи. Кроме того, проведены численные расчеты, показывающие, что учет слагаемых порядка α4 является необходимым при анализе эволюции особых астероидных орбит, в частности, ряда орбит нумерованных астероидов с либрационным изменением аргумента перигелия: № 143 219, 159 518, 417 444 и 1866.
Рассмотрим движение материальной точки Р пренебрежимо малой массы под действием притяжения центральной точки S массы m и возмущающей точки J массы m1 $ \ll $ m, движущейся относительно S по эллиптической орбите с большой полуосью а1 и эксцентриситетом е1. Введем прямоугольную систему координат Oxyz с началом в точке S, основная плоскость xOy которой совпадает с плоскостью орбиты точки J. Ось Ox пусть направлена в перицентр орбиты точки J, ось Oy – в сторону ее движения от перицентра в основной плоскости, а ось Oz дополняет систему координат до правой. Возмущенная орбита точки Р характеризуется оскулирующими кеплеровскими элементами: большой полуосью а, эксцентриситетом е, наклонением i, аргументом перицентра ω и долготой восходящего узла Ω. Внутренний вариант задачи предполагает, что расстояние апоцентра орбиты точки Р в процессе ее эволюции не превосходит расстояния перицентра орбиты возмущающей точки J, т.е.
Для исследования эволюции орбиты точки Р, как правило, используется вековая часть W полной возмущающей функции
Здесь, кроме уже введенных обозначений элементов орбит, f – гравитационная постоянная, Δ – расстояние между возмущаемой и возмущающей точками Р и J, λ и λ1 – суть средние долготы этих точек, соответственно. Процедура подобного (независимого) двукратного осреднения по быстрым переменным носит название схемы Гаусса, в которой предполагается отсутствие соизмеримостей низких порядков между средними движениями точек J и Р. Как следствие, в двукратно осредненной задаче появляются первые интегралы уравнений возмущенного движения в элементах (Моисеев, 1945) а в случае е1 = 0 существует еще один первый интеграл (1 – e2)cos2i = const. В функции W а1 и е1 вместе с а играют роль параметров эволюционной задачи.СПЕЦИАЛЬНОЕ ВЫРАЖЕНИЕ ОСРЕДНЕННОЙ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ СПУТНИКОВОГО ВАРИАНТА ЗАДАЧИ И ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ
В аналитических исследованиях нередко используется и другое равносильное выражение функции W с помощью известных формул
Здесь Е – эксцентрическая аномалия возмущаемой точки, ν1 – истинная аномалия возмущающей точки, r1 = a1 (1 – $e_{1}^{2}$)/(1 + e1cos ν1), а V представляет собой силовую функцию эллиптического гауссова кольца, моделирующего осредненное влияние точки J. В дальнейшем будет рассматриваться так называемый внутренний или спутниковый вариант задачи, в предположении r $ \ll $ r1, а в разложении функции 1/Δ по полиномам Лежандра Pn (или по степеням отношения r/r1) будут сохранены слагаемые до четвертой степени, включительно, так что
Выполняя стандартную процедуру интегрирования в (3), получим явное выражение функции V
(4)
$\begin{gathered} V\left( E \right) = \frac{{3f{{m}_{1}}}}{{2a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left\{ {\frac{1}{2}\left( {{{x}^{2}} + {{y}^{2}}} \right) - \frac{1}{3}{{r}^{2}} + _{{}}^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}} \right. \\ + \frac{{{{e}_{1}}x}}{{4{{a}_{1}}\left( {1 - e_{1}^{2}} \right)}}\left[ {5\left( {{{x}^{2}} + {{y}^{2}}} \right) - 4{{r}^{2}}} \right] + \frac{1}{{64a_{1}^{2}{\kern 1pt} {{{\left( {1\, - \,e_{1}^{2}} \right)}}^{2}}}}{\kern 1pt} \times \\ \times \,\left. {\,\left[ \begin{gathered} 35\left( {2 + 5e_{1}^{2}} \right){{x}^{4}} + 70{\kern 1pt} \left( {2 + 3e_{1}^{2}} \right){{x}^{2}}{{y}^{2}} + \hfill \\ + \,\,35{\kern 1pt} \left( {2 + 5e_{1}^{2}} \right){\kern 1pt} {{y}^{4}} - 20{\kern 1pt} \left( {4 + 9e_{1}^{2}} \right){\kern 1pt} {{r}^{2}}{{x}^{2}} - \hfill \\ - \,\,20\left( {4 + 9e_{1}^{2}} \right){{r}^{2}}{{y}^{2}} + 8\left( {2 + 3e_{1}^{2}} \right){{r}^{4}} \hfill \\ \end{gathered} \right]} \right\}{\kern 1pt} , \\ \end{gathered} $Отметим, что в принятом приближении относительно α выражение для функции W приведено в работе (Yokoyama и др., 2003). Однако все последующие результаты, относящиеся к устойчивости внешних спутников Юпитера, получены для резонансной части функции W, содержащей лишь слагаемые ∼cos(Ω ± ω) и ∼cos 2(Ω ± ω). В отличие от выражения, приводимого в указанной работе, в нижеследующих более компактных формулах непосредственно выделена зависимость W от долготы $1$восходящего узла Ω (именно эта зависимость является препятствием для интегрируемости двукратно осредненной ограниченной эллиптической задачи трех тел)
(5)
$\begin{gathered} W\left( {e,i,\omega ,\Omega ,\alpha ,{{e}_{1}}} \right) = \frac{{3f{{m}_{1}}{{\alpha }^{2}}}}{{8{{a}_{1}}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}w, \\ w = {{w}_{0}} - A{{w}_{1}} + B{{w}_{2}},\,\,\,\,{{w}_{0}} = {{e}^{2}} - {\text{si}}{{{\text{n}}}^{2}}i + \\ + \,\,{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}i\left( {1 - 5{\text{si}}{{{\text{n}}}^{2}}\omega } \right),\,\,\,\,{{w}_{1}} = {{A}_{1}}{\text{cos}}\Omega + {{B}_{1}}{\text{sin}}\Omega , \\ {{w}_{2}} = \left( {1 + \frac{3}{2}e_{1}^{2}} \right){{A}_{0}} + e_{1}^{2}\left( {{{A}_{2}}{\text{cos2}}\Omega + {{B}_{2}}{\text{sin2}}\Omega } \right), \\ \alpha = \frac{a}{{{{a}_{1}}}},\,\,\,\,A = \frac{{5\alpha {{e}_{1}}}}{{8\left( {1 - e_{1}^{2}} \right)}},\,\,\,\,B = \frac{{15{{\alpha }^{2}}}}{{64{{{\left( {1 - e_{1}^{2}} \right)}}^{2}}}}, \\ \alpha \left( {1 + e} \right) < 1 - {{e}_{1}}. \\ \end{gathered} $Здесь коэффициенты А0, 1, 2 и В1, 2, зависящие от элементов e, i, ω и не зависящие от Ω, определяются формулами
(6)
$\begin{gathered} {{A}_{1}} = {{C}_{1}}e{\text{cos}}\omega ,\,\,\,\,{{B}_{1}}{\text{ = }}\left[ {10\left( {1 - {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}i - {{C}_{1}}} \right] \times \\ \times \,\,e{\text{cos}}i{\text{sin}}\omega ,\,\,\,\,{{C}_{1}} = 4 + 3{{e}^{2}} - 5{\text{si}}{{{\text{n}}}^{2}}i \times \\ \times \,\,\left( {1 - {{e}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right),\,\,\,\,{{A}_{0}} = {{e}^{2}}\left( {8 + 3{{e}^{2}}} \right) - \\ - \,\,2{\text{si}}{{{\text{n}}}^{2}}i\left[ {\left( {1 - {{e}^{2}}} \right)\left( {4 + 3{{e}^{2}}} \right) + 21{{e}^{2}} \times } \right. \\ \left. { \times \,\,\left( {2 + {{e}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\omega } \right] + {{C}_{2}},\,\,\,\,{{A}_{2}} = 7{{e}^{2}}\left( {2 + {{e}^{2}}} \right) \times \\ \times \,\,{\text{cos}}2\omega + 2{\text{si}}{{{\text{n}}}^{2}}i\left[ {\left( {1 - {{e}^{2}}} \right)\left( {3 - 10{{e}^{2}}} \right) + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega \times } \right. \\ \left. { \times \,\,\left( {8 - 17{{e}^{2}} + 21{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right)} \right] - {{C}_{2}}, \\ {{B}_{2}} = 7{{e}^{2}}{\text{cos}}i{\text{sin2}}\omega \times \\ \times \,\,\left[ {7{\text{si}}{{{\text{n}}}^{2}}i\left( {1 - {{e}^{2}} + 3{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right) - \left( {2 + {{e}^{2}}} \right)} \right], \\ {{C}_{2}} = 7{\text{si}}{{{\text{n}}}^{4}}i\left\{ {{{{\left( {1 - {{e}^{2}}} \right)}}^{2}} + 7{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega \times } \right. \\ \left. { \times \,\,\left[ {2\left( {1 - {{e}^{2}}} \right) + 3{{e}^{2}}{\text{si}}{{{\text{n}}}^{2}}\omega } \right]} \right\}. \\ \end{gathered} $Функция w1 содержит множителем е и умножается на величину, пропорциональную е1, а функция w2 содержит слагаемые нулевой и второй степени относительно е1.
Далее удобно ввести новую независимую переменную – “безразмерное время” τ, согласно формуле
(7)
$\tau = \frac{{3f{{m}_{1}}}}{{8a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}n}}\left( {t - {{t}_{0}}} \right),$Для описания эволюции орбит будут использованы уравнения Лагранжа в элементах с функцией w, являющейся их первым (и в общем случае единственным) интегралом
Для произвольных орбит точки Р и е1 > 0 строгое решение уравнений (8) может быть найдено, по-видимому, лишь численным методом для заданных начальных условий, а процесс вычислений может контролироваться постоянством функции w вдоль этого решения. Для полноты совокупности формул мы приводим выражения для производных функций w0, w1 и w2 по элементам. Они необходимы для вычисления правых частей эволюционных уравнений.
Производные функции w0
Производные функции w1
Производные функции w2
ИНТЕГРИРУЕМЫЕ СЛУЧАИ ЭЛЛИПТИЧЕСКОЙ ЗАДАЧИ
Плоские орбиты
Если sin i = 0, орбита точки Р постоянно располагается в основной координатной плоскости $\left( {\frac{{{\text{d}}i}}{{{\text{d}}\tau }} = 0} \right),$ а эволюционные уравнения упрощаются. С введением долготы перицентра орбиты точки Р
где δ = sign(cosi), эволюционная система принимает вид(10)
$\frac{1}{\delta }\frac{{{\text{d}}e}}{{{\text{d}}\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial g}},\,\,\,\,\frac{1}{\delta }\frac{{{\text{d}}g}}{{{\text{d}}\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$При этом очевидно, что эволюция прямых (δ = 1) и обратных (δ = –1) орбит происходит одинаковым образом с инверсией времени, а наличие первого интеграла
делает плоскую эволюционную задачу интегрируемой как систему с одной степенью свободы.Интегрируемость данного (плоского) случая двукратно осредненной ограниченной эллиптической задачи была впервые установлена Е.П. Аксеновым для B = 0, когда в разложении функции W не учитываются слагаемые порядка α4 и выше. В работе (Аксенов, 1979а) проведено качественное исследование задачи, а в работе (Аксенов, 1979б) выполнено аналитическое обращение квадратур и получены зависимости элементов орбиты от времени. Исследования Е.П. Аксенова получили свое развитие в работах Ф. Вереша (Вереш, 1980а; 1980б; 1980в) как в плане качественного анализа задачи, так и в плане построения ее приближенного аналитического решения для α < 1. Позднее в работе (Вашковьяк, 1982) исследование плоского случая задачи для произвольных значений α было выполнено с помощью численно-аналитического метода, который предусматривал численное нахождение функции W и аналитическое определение функции V в формулах (2). В дальнейшем изложении результаты указанных работ будут использованы, а также, по возможности, сохранены введенные в них обозначения.
Нашей целью будет получение количественных характеристик эволюции, уточненных по сравнению со случаем B = 0, а также качественное исследование задачи для B > 0, более детальное, чем проведенное в работе (Вереш, 1980а).
Из формул (5) при sin i = 0 получим
(12)
$\begin{gathered} w\left( {e,g,\alpha ,{{e}_{1}}} \right) = {{e}^{2}} - Ae\left( {4 + 3{{e}^{2}}} \right){\text{cos}}g + B{{e}^{2}} \times \\ \times \,\,\left[ {\left( {1 + \frac{3}{2}e_{1}^{2}} \right)\left( {8 + 3{{e}^{2}}} \right) + 7e_{1}^{2}\left( {2 + {{e}^{2}}} \right){\text{cos}}2g} \right] = h, \\ \end{gathered} $(13)
$\begin{gathered} \frac{1}{\delta }\frac{{{\text{d}}e}}{{{\text{d}}\tau }} = - \sqrt {1 - {{e}^{2}}} \times \\ \times \,\,\left[ {A\left( {4 + 3{{e}^{2}}} \right) - 28Be_{1}^{2}e\left( {2 + {{e}^{2}}} \right){\text{cos}}g} \right]{\text{sin}}g, \\ \frac{1}{\delta }\frac{{{\text{d}}g}}{{{\text{d}}\tau }} = \sqrt {1 - {{e}^{2}}} \left\{ {2 - \frac{A}{e}\left( {4 + 9{{e}^{2}}} \right){\text{cos}}g + 2B \times } \right. \\ \left. { \times \,\,\left[ {\left( {2 + 3e_{1}^{2}} \right)\left( {4 + 3{{e}^{2}}} \right) + 14e_{1}^{2}\left( {1 + {{e}^{2}}} \right){\text{cos}}2g} \right]} \right\}. \\ \end{gathered} $При фиксированных значениях параметров α и е1 интеграл (12) определяет h-семейство интегральных кривых в плоскости (g, e). Для А = 0.1 и В = 0 в работе (Аксенов, 1979а) построено такое семейство, подробно исследована его качественная структура, найдены стационарные значения переменных e*, g* = 0, а также выявлены три возможных типа фазовых траекторий: I – либрация обеих переменных е и g, II – либрация е и циркуляция g, III – вырождение траекторий, когда при монотонном изменении g фазовая точка достигает граничного значения е = 1 за конечное время, что при a =const отвечает соударению точки Р с центральной точкой S. В работе (Вереш, 1980a) для α = 0.5 и е1 = 0.3 аналогичные семейства построены как при В = 0 (решение Е.П. Аксенова), так и при В > 0. При этом установлено, что учет слагаемых высших степеней относительно α не изменяет качественной структуры семейств интегральных кривых, не приводит к появлению каких-либо новых типов фазовых траекторий, а влияет только на их количественные характеристики.
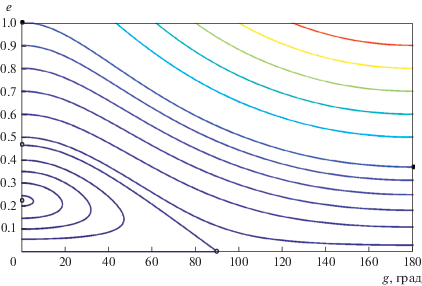
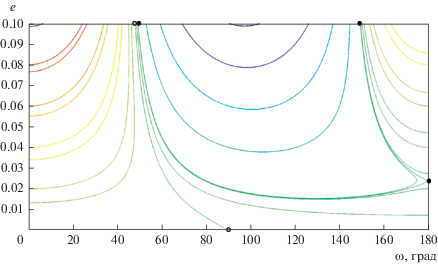
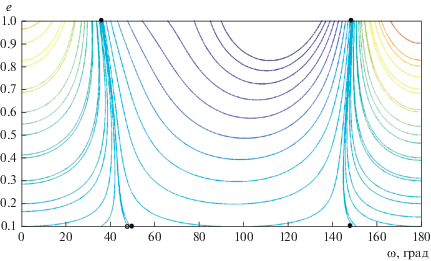
Для полноты изложения мы приведем здесь h‑семейства интегральных кривых (12) для α = 0.24, e1 = 0.5, A = 0.1, B = 0.024 (рис. 1) и B = 0 (рис. 2).
Рис. 1.
Семейство интегральных кривых (12) в плоскости (g, е) для α = 0.24, e1 = 0.5, A = 0.1, B = 0.024 (решение Ф. Вереша).
В силу имеющейся симметрии фазовых траекторий, показаны лишь области 0° < g < 180°. Светлыми кружками на рисунках отмечены стационарные точки (g = 0, e = e*), а также точки (g = 0, e = es) и (g = 90°, e = 0) на интегральных кривых, ограничивающих зоны либрации аргумента перицентра. Черными кружками отмечены точки (g = 0, e = 1) и (g = 90°, e = ес) на сепаратрисах, отделяющих области циркуляции от областей, отвечающих вырожденным траекториям. Движение фазовой точки по этим кривым происходит так, что е → 1 при t → ±∞. Сопоставление рис. 1 и 2, как это отмечено и в работе (Вереш, 1980a), дает возможность оценить влияние фактора В на количественные характеристики семейства фазовых траекторий задачи. Далее подобные характеристики будут представлены для достаточно широкой области значений параметров α, е1.
Стационарные решения системы (13) находятся приравниванием нулю правых частей обоих уравнений. Из первого уравнения (13) имеем
(14)
$\begin{gathered} g{\text{ }} = {\text{ }}0,\,\,\,\,{\text{или}}\,\,\,\,g = \pi ,~ \\ {\text{или}}\,\,\,\,g = {\text{arccos}}\left[ {\frac{{A\left( {4 + 3{{e}^{2}}} \right)}}{{28Be_{1}^{2}e\left( {2 + {{e}^{2}}} \right)}}} \right]. \\ \end{gathered} $Можно показать, что для двух последних равенств правая часть второго уравнения (13) положительна при любых значениях α, е1 и е ≠ 1. Поэтому при е < 1 единственным стационарным значением переменной g является
Стационарное значение эксцентриситета 0 < < е* < 1 находится как соответствующий действительный корень кубического уравнения
в котором(17)
$\begin{gathered} {{c}_{3}} = 2B\left( {6 + 23e_{1}^{2}} \right),\,\,\,\,{{c}_{2}} = - 9A, \\ {{c}_{1}} = 2\left[ {1 + 2B\left( {4 + 13e_{1}^{2}} \right)} \right],\,\,\,\,{{c}_{0}} = - 4A. \\ \end{gathered} $Заметим, что при В = 0 уравнение (16) становится квадратным, а стационарное значение эксцентриситета определяется одним из его корней формулой (Аксенов, 1979а)
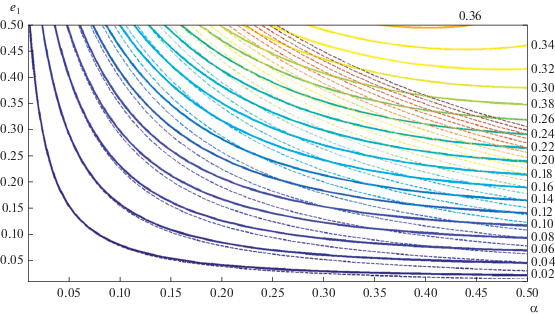
Поскольку А и В зависят от параметров задачи α и е1, то для наглядности естественно представить результаты решения уравнения (16) в виде семейства изолиний е*(α, е1) = const (рис. 3). Численные значения е* нанесены по вертикали у правых концов жирных линий. Соответствующие штриховые линии (В = 0) практически совпадают с жирными при малых значениях α. При α, заметно отличающихся от нуля, сплошные и штриховые линии расходятся, что дает оценку влияния на величину е* слагаемых порядка α4 в разложении осредненной возмущающей функции. В частности, для значений параметров α = 0.24, e1 = 0.5, принятых при построении семейств на рис. 1 и 2, величины е* ≈ 0.155 и 0.230 соответственно.
Рис. 3.
Семейство изолиний стационарных значений эксцентриситета е*(α, е1) = const (решение для В > 0 – жирные линии, решение для В = 0 – штриховые линии).
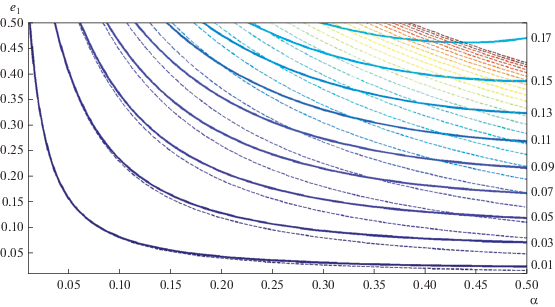
Отметим, что в рассматриваемой области значений параметров α, е1 величины е* относительно невелики и не превышают примерно 0.2.
Замечание. Выходя за рамки плоского интегрируемого случая, укажем недавнюю работу (Neishtadt и др., 2018), в которой выполнено исследование пространственной устойчивости стационарных решений в линейном приближении относительно i. Отмечено также, что КАМ-теория гарантирует устойчивость стационарных решений по Ляпунову для всех значений параметров в плоскости α, e1, за исключением, возможно, параметров, принадлежащих некоторому конечному множеству аналитических кривых.
Аналогично семейству изолиний для е*, строятся семейства еs(α, е1) = const (рис. 4) и ес(α, е1) = = const (рис. 5), характеризующие размеры либрационной и циркуляционной зон.
Для определения еs и ес, соответственно, служат уравнения
(19)
$\frac{1}{4}{{c}_{3}}e_{s}^{3} + \frac{1}{3}{{c}_{2}}e_{s}^{2} + \frac{1}{2}{{c}_{1}}{{e}_{s}} + {{c}_{0}} = 0,$(20)
$\frac{1}{4}{{c}_{3}}e_{c}^{4} - \frac{1}{3}{{c}_{2}}e_{c}^{3} + \frac{1}{2}{{c}_{1}}e_{c}^{2} - {{c}_{0}}{{e}_{c}} - {{h}_{c}} = 0.$В уравнении (20) величина hc определяется формулой
(21)
${{h}_{c}} = {\text{1}}--{\text{7}}A + {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} \mathord{\left/ {\vphantom {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} {\text{2}}}} \right. \kern-0em} {\text{2}}}.$Для значений параметров α = 0.24, e1 = 0.5, принятых при построении семейств на рис. 1 и 2, величины еs ≈ 0.32 и 0.48 соответственно, а величины ес ≈ 0.595 и 0.370 соответственно.
Кроме вышеуказанных специальных значений эксцентриситета, представляет интерес нахождение его экстремальных значений для каждого из характерных диапазонов изменения постоянной интеграла (12) h. Как показывает анализ, величина h может изменяться в пределах
(22)
$\begin{gathered} \min h = h{\kern 1pt} * = h(e*,0) \leqslant {{h}_{s}} = h({{e}_{s}},0) = h\left( {0, - } \right) \leqslant {{h}_{c}} = \\ = h({{e}_{c}},\pi ) \leqslant h{\kern 1pt} *{\kern 1pt} * = h(1,\pi ) = \max h. \\ \end{gathered} $По известному значению е* при В > 0 нетрудно найти значение
(23)
$h* = e{\text{*}}\left( {\frac{1}{4}{{c}_{3}}{{e}^{{*3}}} + \frac{1}{3}{{c}_{2}}{{e}^{{*2}}} + \frac{1}{2}{{c}_{1}}e{\text{*}} + {{c}_{0}}} \right),$(24)
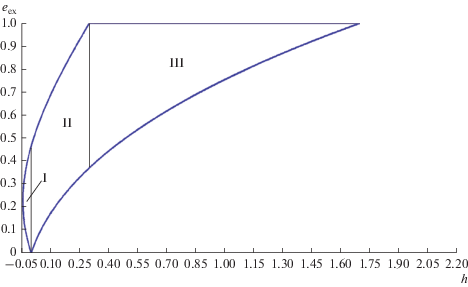
${{h}_{s}} = 0,\,\,h{\text{**}} = {\text{1}} + {\text{7}}A + {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} \mathord{\left/ {\vphantom {{B\left( {{\text{22}} + {\text{75}}e_{{\text{1}}}^{{\text{2}}}} \right)} {\text{2}}}} \right. \kern-0em} {\text{2}}}$Типы фазовых траекторий, выявленные Е.П. Аксеновым при В = 0 (Аксенов, 1979б), сохраняются и при B > 0, однако их экстремальные характеристики претерпевают изменения. На рис. 6 и 7 представлены зависимости от h экстремальных значений эксцентриситета, построенные при α = 0.24, e1 = 0.5, А = 0.1 соответственно, для В = 0.024 и В = 0. Римскими цифрами отмечены три области с различными типами изменения элементов
Рис. 6.
Зависимости экстремальных значений эксцентриситета от h для α = 0.24, e1 = 0.5, А = 0.1, В = 0.024.
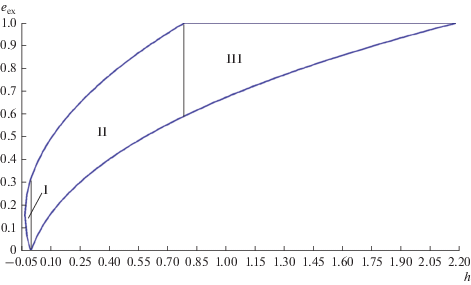
Для области I (h* ≤ h < 0, либрация е, g) экстремальные значения эксцентриситета 0 < еex < 1 определяются двумя положительными корнями полинома 4-й степени
(25)
$\frac{1}{4}{{c}_{3}}e_{{{\text{ex}}}}^{4} + \frac{1}{3}{{c}_{2}}e_{{{\text{ex}}}}^{3} + \frac{1}{2}{{c}_{1}}e_{{{\text{ex}}}}^{2} + {{c}_{0}}{{e}_{{{\text{ex}}}}} - h = 0.$Для области II (0 < h < hc, либрация е, циркуляция g) минимальное значение 0 < еmin < 1 определяется положительным корнем полинома
(26)
$\frac{1}{4}{{c}_{3}}e_{{{\text{ex}}}}^{4} - \frac{1}{3}{{c}_{2}}e_{{{\text{ex}}}}^{3} + \frac{1}{2}{{c}_{1}}e_{{{\text{ex}}}}^{2} - {{c}_{0}}{{e}_{{{\text{ex}}}}} - h = 0,$Наконец, для области III (вырожденные траектории, hc < h ≤ h**) минимальное значение эксцентриситета 0 < еmin < 1 определяется положительным корнем полинома (26).
Заметим, что процедура вычисления корней полиномов является одной из стандартных во многих вычислительных системах, в частности, в системе Matlab, а выбор нужных корней не представляет особого труда. Кроме того, приведенные алгебраические уравнения позволяют при необходимости строить зависимости, аналогичные рис. 1 и 6, для любых допустимых значений параметров задачи α и е1.
Из сравнения рис. 6 и 7, представленных в одном масштабе, можно видеть, что выполненный в данной работе учет слагаемых ∼α4 приводит к уменьшению экстремальных значений эксцентриситета и позволяет получить их более точные значения, заметно отличающиеся от случая В = 0.
Ортогонально-апсидальные орбиты
Если cos i = 0 и sin Ω = 0, то орбита точки Р постоянно располагается ортогонально орбитальной плоскости возмущающей точки J $\left( {{{{\text{d}}i} \mathord{\left/ {\vphantom {{{\text{d}}i} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = 0,\,\,{{{\text{d}}\Omega } \mathord{\left/ {\vphantom {{{\text{d}}\Omega } {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = 0} \right).$ Общее качественное исследование этого случая с учетом возможных пересечений орбит точек Р и J было проведено с помощью численно-аналитического метода в работе (Вашковьяк, 1984) для произвольных значений α. Здесь спутниковый вариант задачи исследуется с получением более детальных количественных характеристик эволюции.
В рассматриваемом приближении эволюционные уравнения (8) также упрощаются и принимают вид
(27)
$\frac{{{\text{d}}e}}{{{\text{d}}\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{{\text{d}}\omega }}{{{\text{d}}\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$(28)
$\begin{gathered} w\left( {e,\omega ,\alpha ,{{e}_{1}}} \right) = {{e}^{2}}\left( {5{\text{co}}{{{\text{s}}}^{2}}\omega - 3} \right) + A{{\delta }_{1}}e{\text{cos}}\omega \times \\ \times \,\,\left[ {1 + {{e}^{2}}\left( {27 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right)} \right] + B \times \\ \times \,\,\left\{ \begin{gathered} \left( {10 + 3e_{1}^{2}} \right){{e}^{2}} + \frac{1}{2}\left( {46 + 95e_{1}^{2}} \right){{e}^{4}} - 7{{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega \times \hfill \\ \times \,\,\left[ {2\, + \,e_{1}^{2}\, + \,\left( {22\, + \,53e_{1}^{2}} \right){{e}^{2}}\, - \,\frac{{21}}{2}\left( {2\, + \,5e_{1}^{2}} \right){\kern 1pt} {{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega } \right] \hfill \\ \end{gathered} \right\} = \\ = h = {\text{const}}, \\ \end{gathered} $δ1 = sign(cosΩ), так что
(29)
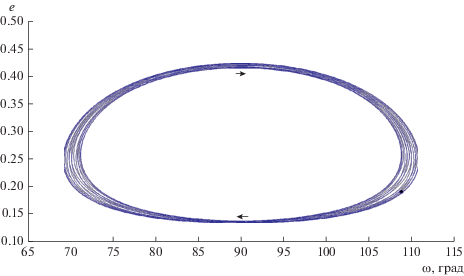
$\begin{gathered} \frac{{{\text{d}}e}}{{{\text{d}}\tau }} = \sqrt {1 - {{e}^{2}}} {\text{sin}}\omega \left\{ \begin{gathered} 10e{\text{cos}}\omega + A{{\delta }_{1}}\left[ {1 + 3\left( {9 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right){{e}^{2}}} \right] + \hfill \\ + 14Be{\text{cos}}\omega \left[ {21\left( {2 + 5e_{1}^{2}} \right){{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega - \left( {22 + 53e_{1}^{2}} \right){{e}^{2}} - 2 - e_{1}^{2}} \right] \hfill \\ \end{gathered} \right\}, \\ \frac{{{\text{d}}\omega }}{{{\text{d}}\tau }} = \sqrt {1 - {{e}^{2}}} \left\{ \begin{gathered} 2\left( {5{\text{co}}{{{\text{s}}}^{2}}\omega - 3} \right) + \hfill \\ + 2B\left[ \begin{gathered} 10 + 3e_{1}^{2} + \left( {46 + 95e_{1}^{2}} \right){{e}^{2}} - \hfill \\ - \,7\left( {2 + e_{1}^{2} + 2\left( {22 + 53e_{1}^{2}} \right){{e}^{2}} - 21\left( {2 + 5e_{1}^{2}} \right){{e}^{2}}{\text{co}}{{{\text{s}}}^{2}}\omega } \right){\text{co}}{{{\text{s}}}^{2}}\omega \hfill \\ \end{gathered} \right] + \hfill \\ + A{{\delta }_{1}}\frac{{{\text{cos}}\omega }}{e}\left[ {1 + 3\left( {27 - 35{\text{co}}{{{\text{s}}}^{2}}\omega } \right){{e}^{2}}} \right] \hfill \\ \end{gathered} \right\}. \\ \end{gathered} $При фиксированных значениях параметров α и е1 интеграл (28) определяет h-семейство интегральных кривых в плоскости (ω, e). Одно из таких семейств для α = 0.3, е1 = 0.4 представлено на рис. 8 и 9 (для двух диапазонов изменения эксцентриситета). На рис. 8 с целью большей детализации показана область 0 < e < 0.1, а на рис. 9 – область 0.1 < e < 1. Как и в известном случае ортогональных орбит двукратно осредненной задачи Хилла, когда е1 = 0, α → 0 (В = 0) (Лидов, 1961; Lidov, 1962), все фазовые траектории, кроме сепаратрис, выходят за конечное время на пересечение с граничной прямой е = 1, и происходит соударение точки Р с центральной точкой S. Небольшое качественное изменение состоит в появлении седловой стационарной точки на границе ω = 180°.
В силу имеющейся симметрии фазовых траекторий, на рис. 8 и рис. 9 также показаны лишь области 0° < ω < 180°. Светлыми кружками на рисунках отмечены граничные точки особых интегральных кривых (ω = 90°, e = 0). Черными кружками отмечены точки (ω = 180°, e = е*) на сепаратрисах. Движение фазовой точки по этим кривым происходит так, что е → 1 при t → ±∞.
Стационарные решения системы (29), или особые точки в фазовой плоскости (ω, е), находятся приравниванием нулю правых частей обоих уравнений. При произвольных значениях постоянных А и В, вообще говоря, не исключено существование особых точек внутри рассматриваемой прямоугольной области. Их координаты могут удовлетворять системе двух уравнений, получающихся приравниванием нулю выражений в двух фигурных скобках (29). Однако здесь рассмотрены лишь решения sin ω = 0, следующие из первого уравнения (29), т.е.
(30)
$\omega * = 0,\,\,\,{\text{или}}\,\,\omega * = \pi ,\,\,\,\,{{\delta }_{2}} = {\text{sign}}(\cos \omega *).$Стационарное значение эксцентриситета 0 < < е* < 1 находится как соответствующий действительный корень кубического уравнения
(31)
${{p}_{3}}e{\kern 1pt} {{*}^{3}} + {{p}_{2}}e{{{\text{*}}}^{2}} + {{p}_{1}}e{\text{*}} + {{p}_{0}} = 0,$в котором
(32)
$\begin{gathered} {{p}_{3}} = 16B\left( {4 + 11e_{1}^{2}} \right),\,\,\,\,{{p}_{2}} = - 24A{{\delta }_{1}}{{\delta }_{2}}, \\ {{p}_{1}} = 4\left[ {1 - 2B\left( {1 + e_{1}^{2}} \right)} \right],\,\,\,\,{{p}_{0}} = A{{\delta }_{1}}{{\delta }_{2}}. \\ \end{gathered} $При В = 0 уравнение (31) становится квадратным, а в работе (Вашковьяк, 1984) приведено его решение
Отметим, что решение, удовлетворяющее условию 0 < e* < 1, существует только при δ1δ2 < 0, т.е.
(34)
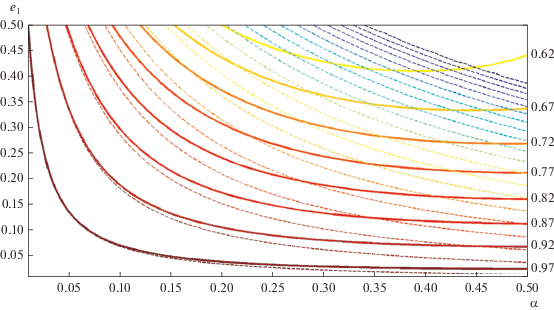
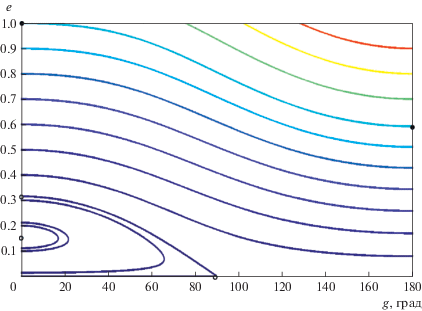
$\begin{gathered} {\text{либо при }}(\Omega = 0{\text{ и}}\,\omega * = \pi ),{\text{ }} \\ {\text{либо при }}(\Omega = \pi {\text{ и}}\,\omega * = 0). \\ \end{gathered} $Для общего случая В > 0 изолинии е*(α, е1) = = const показаны на рис. 10. Численные значения е* нанесены по вертикали у правых концов жирных линий. Соответствующие штриховые линии практически совпадают с жирными при малых значениях α. При α, заметно отличающихся от нуля, жирные и штриховые линии расходятся. Это дает оценку влияния на величину е* слагаемых порядка α4 в разложении осредненной возмущающей функции, учет которых выполнен в данной работе.
Рис. 10.
Семейство изолиний стационарных значений эксцентриситета е*(α, е1) = const (решение для В > 0 – жирные линии, решение для В = 0 – штриховые линии).
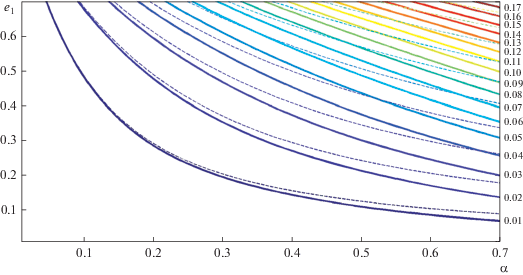
Отметим, что в рассматриваемой области значений параметров α, е1 величины е* относительно невелики и не превышают примерно 0.2.
ЧИСЛЕННОЕ РЕШЕНИЕ ЭВОЛЮЦИОННОЙ СИСТЕМЫ
Модельные примеры
В данном разделе представлены результаты численного решения уравнений (8) в модели системы, включающей в себя Солнце – центральную притягивающую точку и одну главную возмущающую точку – Юпитер (а1 = 5.2 а. е., е1= 0.048). Расчеты проведены с различными начальными данными для ряда эволюционирующих орбит гипотетических и реальных астероидов.
В качестве одного из тестовых модельных примеров для демонстрации “флипа” (известного явления, имеющего место в ограниченной эллиптической двукратно осредненной задаче трех тел и заключающегося в переходе орбиты астероида в процессе эволюции из прямой в обратную и наоборот) рассмотрена орбита с большой полуосью а =2.2 а. е. и начальными элементами е0 = 0.15, i0 = = 75°, ω0 = 0. Эта орбита, сильно наклоненная к основной плоскости, в известной степени близка к приведенной в работе (Naoz и др., 2013), в которой, однако, не указано начальное значение долготы восходящего узла. Известно, что “флипы” могут существовать лишь в некоторой области значений начальных элементов орбиты. В работе (Lithwick, Naoz, 2011) для фиксированных значений малого параметра ε = 8A/5 границы этих областей в плоскости (е0, cos i0) построены численным способом. В работе (Sidorenko, 2018), в частности, предложено достаточно хорошее асимптотическое приближение для аналитической аппроксимации этих границ в случае ε ≤ 0.1.
В приведенном здесь примере Ω0 = 120° подобрано специальным образом, а на рис. 11 показаны зависимости от времени наклонения и (удобной для графического изображения вместо е) величины lg(1 – e) на интервале 3 млн лет.
Рис. 11.
Изменение со временем наклонения и эксцентриситета орбиты с начальными элементами а = 2.2 а. е., е0 = 0.15, i0= 75°, ω0 = 0, Ω0 = 120°.
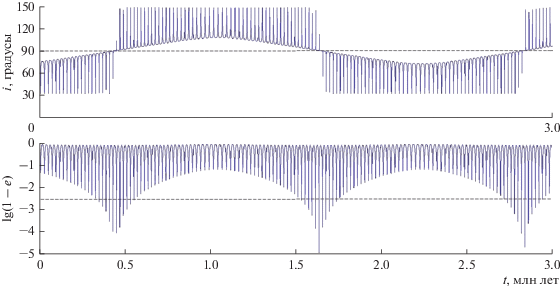
С приближением орбитального наклонения к значению 90° (штриховая прямая на верхнем фрагменте рис. 11) эксцентриситет становится весьма близким к единице. В реальности, с учетом ненулевого радиуса Солнца это, конечно, привело бы к падению астероида на его “поверхность” уже при t ≈ 0.4 млн лет (первое пересечение штриховой прямой с графиком на нижнем фрагменте рис. 11). Интересно отметить, что достаточно тонкий флип-эффект обнаруживается даже при использовании одного из простейших методов численного интегрирования (в данной работе – метода Рунге–Кутты 4-го порядка).
Другим модельным примером служит прослеживание трансформации устойчивого стационарного решения плоского интегрируемого случая задачи c начальными условиями е0= е*(α, е1), i0= 0, g0= g* = 0, при увеличении i0. Для этого было выполнено численное интегрирование системы (8) для принятых значений постоянных параметров а1, е1, а = 2.2 а. е. (α = 0.423), е0 = 0.019 и начальных угловых элементов ω0 = Ω0 = 0. Результаты этих расчетов иллюстрирует табл. 1, в которой представлены экстремальные значения элементов на интервале времени 1 млн лет. При начальных наклонениях, не превосходящих величину примерно 32°.7, изменение аргумента перицентра и долготы восходящего узла носит циркуляционный характер, а элементы e, i, g изменяются либрационным образом, хотя амплитуда колебаний g может приближаться к 180°, причем минимальные значения эксцентриситета и максимальные значения наклонения достаточно близки к начальным. При i0 ≥ 33° обе переменные g и ω изменяются монотонно со временем, но амплитуды колебаний эксцентриситета и наклонения существенно возрастают. Подобные закономерности характерны и для круговой двукратно осредненной задачи (Лидов, 1961; Lidov, 1962; Kozai, 1962). Они сохраняются при наклонениях, не слишком близких к 90°. В эллиптической задаче для данного примера, начиная с i0 = 76°, начинают проявляться “флипы” с переходом наклонения через 90° (его максимальные значения составляют примерно 147°) и с достижением эксцентриситета величины, весьма близкой к единице. Интересно отметить, что, как показывают расчеты, для незначительно меньшего значения i0 = 75° “флипы” отсутствуют, по крайней мере на интервале 5 млн лет.
Таблица 1.
Экстремальные на интервале времени 1 млн лет значения элементов эволюционирующих орбит для а = 2.2 а. е., е0 = е* = 0.019, ω0 = Ω0 = 0 и для различных начальных наклонений i0
| i0, град | emin | emax | imin, град | imax, град | gmin, град | gmax, град |
|---|---|---|---|---|---|---|
| 1 | 0.019 | 0.020 | 0.999 | 1.000 | –0.016 | 0.015 |
| 10 | 0.019 | 0.020 | 9.99 | 10.00 | –1.72 | 1.73 |
| 20 | 0.018 | 0.022 | 19.99 | 20.00 | –6.38 | 6.38 |
| 30 | 0.019 | 0.075 | 29.89 | 30.07 | –40.10 | 40.17 |
| 32 | 0.019 | 0.252 | 30.695 | 32.996 | –104.09 | 104.01 |
| 32.7 | 0.019 | 0.328 | 30.555 | 34.494 | –165.52 | 165.04 |
| 33 | 0.019 | 0.121 | 32.547 | 33.195 | 0 | 360 |
| 40 | 0.0097 | 0.363 | 34.97 | 40.01 | 0 | 360 |
| 50 | 0.0086 | 0.639 | 34.26 | 50.25 | 0 | 360 |
| 60 | 0.0012 | 0.812 | 33.66 | 60.61 | 0 | 360 |
| 70 | 0.0072 | 0.946 | 33.10 | 73.87 | 0 | 360 |
| 75 | 0.0119 | 0.998 | 32.77 | 86.66 | 0 | 360 |
| 76 | 0.0096 | 0.9999 | 32.82 | 147.15 | 0 | 360 |
| 80 | 0.0023 | 0.9999 | 32.87 | 147.17 | 0 | 360 |
| 89 | 0.0055 | 0.9999 | 33.37 | 146.67 | 0 | 360 |
Таким образом, для выбранных значений параметров а1, е1 данные табл. 1 позволяют проследить за качественными изменениями “астероидной” орбиты при изменении ее начального наклонения. Начиная от стационарного положения в плоскости движения возмущающего тела при небольшом значении эксцентриситета, эта орбита в конечном счете превращается в сильно эволюционирующую по эксцентриситету и наклонению с его переходом через 90°.
Об эволюции некоторых особых астероидных орбит
В задаче об эволюции астероидных орбит влияние эксцентричности орбиты Юпитера, обычно, является одним из второстепенных факторов, так же как и влияние слагаемых возмущающей функции порядка выше, чем α2. Тем не менее существуют орбиты реальных астероидов, которые требуют безусловного учета вышеназванных факторов для адекватного описания их эволюции. К таковым относятся астероиды с элементами орбит, удовлетворяющими некоторым специальным условиям. Это, в первую очередь, орбиты, для которых постоянные первых интегралов двукратно осредненной задачи Хилла (Лидов, 1961; Lidov, 1962)
(35)
${{с}_{1}} = \left( {1 - {{e}^{2}}} \right){\text{co}}{{{\text{s}}}^{2}}i,\,\,\,\,{{c}_{2}} = {{e}^{2}}\left( {\frac{2}{5} - {\text{si}}{{{\text{n}}}^{2}}i{\text{si}}{{{\text{n}}}^{2}}\omega } \right)$В табл. 2 приводятся характеристики эволюции указанных орбит (вместе с орбитой астероида 1866), полученные численным интегрированием системы (8) на интервале времени 1 млн лет для двух основных вариантов: В = 0 (модель ∼α3) и В > 0 (модель ∼α4). Вместе с экстремальными значениями эксцентриситета приведены символы, характеризующие тип эволюции аргумента перигелия: С – циркуляция, L – либрация. Для астероида 143219 учет слагаемых ∼α4 уточняет лишь диапазон изменения эксцентриситета по сравнению с моделью ∼α3. Однако для остальных астероидов пренебрежение слагаемыми ∼α4 дополнительно приводит и к качественным изменениям в характере эволюции ω.
Таблица 2.
Качественные и количественные характеристики эволюции особых астероидных орбит в двух различных моделях: В = 0 (модель ∼α3), В > 0 (модель ∼α4)
| Номер астероида | В = 0 | В > 0 | ||||
|---|---|---|---|---|---|---|
| тип эволюции ω | emin | emax | тип эволюции ω | emin | emax | |
| 1866 | C | 0.10 | 0.60 | L | 0.16 | 0.61 |
| 143 219 | L | 0.02 | 0.67 | L | 0.03 | 0.72 |
| 159 518 | L – C | 0.02 | 0.67 | L | 0.21 | 0.67 |
| 417 444 | L – C – L | 0.03 | 0.35 | L | 0.13 | 0.42 |
На рис. 12 и 13 для иллюстрации показано изменение эксцентриситета и аргумента перигелия орбиты последнего астероида 417 444, соответственно, в модели ∼α3 и в модели ∼α4.
Рис. 12.
Изменение эксцентриситета и аргумента перигелия орбиты астероида 417 444 в упрощенной модели ∼α3.
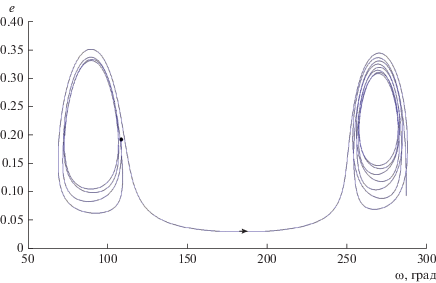
В плоскости указанных элементов на рис. 12 начальная точка, отмеченная на рисунке черным кружком, с течением времени сначала переходит из режима либрации ω относительно 90° в режим циркуляции (по стрелке), а затем возвращается в режим либрации, но уже относительно 270°. В более точной модели (рис. 13) изменение ω носит либрационный характер относительно 90° на всем рассматриваемом интервале времени.
В заключение отметим некоторые возможности развития данной работы. Наряду с прослеживанием пространственной трансформации плоских равновесных спутниковых орбит, интерес мог бы представить численный поиск так называемых периодически-эволюционирующих орбит с равными (соизмеримыми) периодами изменения всех элементов. Дополнением данного исследования послужит также рассмотрение внешнего варианта ограниченной эллиптической двукратно осредненной задачи трех тел.
Список литературы
Аксенов Е.П. Двукратно осредненная эллиптическая ограниченная задача трех тел // Астрон. журн. 1979а. Т. 56. № 2. С. 419–426.
Аксенов Е.П. Траектории в двукратно-осредненной эллиптической ограниченной задаче трех тел // Астрон. журн. 1979б. Т. 56. № 3. С. 623–631.
Вашковьяк М.А. Эволюция орбит в плоской ограниченной эллиптической двукратно осредненной задаче трех тел // Космич. исслед. 1982. Т. 20. Вып. 3. С. 332–341.
Вашковьяк М.А. Об интегрируемых случаях ограниченной двукратно осредненной задачи трех тел // Космич. исслед. 1984. Т. 22. Вып. 3. С. 327–334.
Вереш Ф. Качественный анализ плоской осредненной ограниченной задачи трех тел // Астрон. журн. 1980а. Т. 57. С. 182–189.
Вереш Ф. Аналитическое решение плоской осредненной ограниченной задачи трех тел в случае циркуляции перицентра орбиты частицы // Астрон. журн. 1980б. Т. 57. С. 824–832.
Вереш Ф. Два частных типа решения плоской осредненной ограниченной задачи трех тел // Астрон. журн. 1980в. Т. 57. С. 1070–1077.
Лидов М.Л. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел // Искусственные спутники Земли. 1961. Вып. 8. С. 5–45.
Моисеев Н.Д. О некоторых основных упрощенных схемах небесной механики, получаемых при помощи осреднения ограниченной круговой проблемы трех точек. 2. Об осредненных вариантах пространственной ограниченной круговой проблемы трех точек // Тр. Гос. астрон. ин-та им. П.К. Штернберга. 1945. Т. 15. Вып. 1. С. 100–117.
Скрипниченко П.В., Кузнецов Э.Д. Исследование динамической эволюции астероидов, испытывающих влияние эффекта Лидова–Козаи // Изв. Главной астрон. обсерв. в Пулкове. 2018. № 225. (Тр. Всероссийской астрометрической конференции “ПУЛКОВО – 2018”.) С. 217–222.
Ito T. High-order analytic expansion of disturbing function for doubly averaged circular restricted three-body problem // Adv. Astron. V. 2016. Article ID 8945090. 23 p.
Katz B., Dong S., Malhotra R. Long-term cycling of Kozai-Lidov cycles: Extreme eccentricities and inclinations excited by a distant eccentric perturber // Phys. Rev. Lett. 2011. V. 107. 181 101. 5 p.
Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.
Lidov M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies // Planet. and Space Sci. 1962. № 9. P. 719–759.
Lithwick Y., Naos S. The eccentric Kozai mechanism for a test particle // Astrophys. J. 2011. V. 742. 94. 8 p.
Naoz S., Farr W.M., Lithwick Y., Rasio F.A., Teyssandier J. Hot Jupiter fromsecular planet-planet interaction // Nature. 2011. V. 473. P. 187–189.
Naoz S., Farr W. M., Lithwick Y., Rasio F.A., Teyssandier J. Secular dynamics in hierarchical three-body systems // Mon. Notic. Roy. Astron. Soc. 2013. V. 431. 2155–2171. https://doi.org/10.1093/mnras/stt302
Naoz S. The eccentric Kozai-Lidov effect and its applications // Annu. Rev. Astron. and Astrophys. 2016. AA. P. 1–59.
Neishtadt A.I., Sheng K., Sidorenko V.V. On stability of planar solution of double averaged restricted elliptic three-body problem// arXiv:1803.08847v2 [math.DS] 4 Apr 2018. 7 p.
Shevchenko I. The Lidov-Kozai effect – applications in exoplanet research and dynamical astronomy // Astrophys. and Space Science Library. 2017. V. 441. Dordrecht: Springer, Int. Publ. Switzeland, 2017. V. 441. 194 p.
Sidorenko V.V. The eccentric Kozai–Lidov effect as a resonance phenomenon // Celest. Mech. and Dyn. Astron. 2018. 130:4. P. 2–23.
Yokoyama T., Santos M.T., Cardini G., Winter O.C. On the orbits of the outer satellites of Jupiter // Astron. and Astrophys. 2003.V. 401. P. 763–772.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник