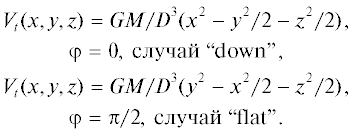Астрономический вестник, 2020, T. 54, № 2, стр. 171-182
Разрыв вытянутого малого тела приливными силами Земли при подлете: возможные сценарии
С. А. Воропаев a, *, Ян Джианго b, **, Жан-Пьер Барриот c, ***
a Институт геохимии и аналитической химии РАН
Москва, Россия
b Государственная лаборатория по геодезии и удаленному зондированию, Университет Ухань
Ухань, Китай
c Обсерватория геодезии Таити, Университет Французской Полинезии
Фаа, Французская Полинезия
* E-mail: voropaev@geokhi.ru
** E-mail: jgyan@whu.edu.cn
*** E-mail: jpbarriot@yahoo.fr
Поступила в редакцию 05.03.2019
После доработки 25.09.2019
Принята к публикации 30.09.2019
Аннотация
В данной статье изучается возможный разрыв вытянутого эллипсоидального малого тела приливными силами Земли при подлете. С помощью аналитического решения упругой задачи получено точное выражение для тензора напряжений под действием сил гравитации, вращения и приливных воздействий. Выведены ограничения на предельное расстояние с учетом размера, формы, плотности, механических свойств (прочность, коэффициент Пуассона), вращения и двух вариантов ориентации тела. В качестве примера рассмотрен астероид 433 Эрос. Полученные результаты имеют важное значение для методов оценки астероидной опасности околоземных (NEO) объектов и эволюции планет земной группы.
ВВЕДЕНИЕ
Изучение ранней истории Луны привело к формированию концепции “поздней массивной бомбардировки” (ПМБ), что позволяло объяснить пик возникновения ряда крупных бассейнов и кратеров, размером более 300 км, в узком временном интервале ~3.7–3.8 млрд лет назад. Предполагалось, что ПМБ завершился формированием моря Восточное (Gomes и др., 2005), но недавние исследования соотношения изотопов содержания Ar в образцах лунного реголита, доставленные миссиями Аpollo раздвинули эти границы (Boehnke и др., 2016). Теоретические и численные расчеты, проведенные для объяснения этого факта, показали решающую роль ранней динамики газовых гигантов Юпитера и Сатурна (Haisch и др., 2001). Смещение их орбит к Солнцу и обратное движение дестабилизировало астроидный пояс из-за возникновения ряда орбитальных резонансов (Morbidelli и др., 2007). Как показывают данные изотопии вольфрама, к этому моменту аккреция планет земной группы в целом уже завершилась (Pierens и др., 2008), и они оказались мишенями практически постоянного потока малых тел различных размеров из зоны Е астроидного пояса (Bottke и др., 2012).
Следы ПМБ на Земле прослеживаются до Архея и раннего Протерозоя в виде глобальных планетарных слоев, содержащих ударные сферулы-импактиты (Johnson и др., 2012). По меньшей мере, семь таких слоев были сформированы между 3.23 и 3.47, четыре между 2.49 и 2.63, и один между 1.7 и 2.1 млрд лет назад (Lowe и др., 2003). Сравнительно недавно по геологической шкале времени, в позднем Эоцене, был сформирован кластер значительных ударных структур: Ашмор (Тиморское море, D ~ 90 км, 35.4 ± 0.1 млн лет назад), Попигай (Восточная Сибирь, D ~ 100 км, 35.7 ± 0.2 млн лет назад) и Чесапик (Северная Америка, D ~ 85 км, 35.3 ± 0.1 млн лет назад) (Glikson и др., 2010). Возможно, причиной послужило разрушение огромного астероида размером 30–40 км на обломки размером до 10 км вблизи Земли приливными силами. В любом случае, механическая прочность ударников, очевидно, оказалась достаточной для преодоления аэродинамического сопротивления атмосферы, что является дополнительным аргументом для применения методов теории упругости.
Представители семейств околоземных астероидов регулярно пересекают орбиту Земли и, в среднем один раз в сто лет, происходит падение тела размером около 20 м, такого как метеорит Челябинск в феврале 2013 г., LL5 обыкновенный хондрит (Галимов и др., 2013). Вероятность падения большего метеорита, размером около 1 км, значительно меньше, но такая возможность реализуется раз в несколько миллионов лет (Bottke и др., 1994). Катастрофические последствия такого падения для всей земной биосферы заставляют, как можно более детально рассмотреть возможные сценарии приближения подобного объекта к Земле, с распадом на части и без. Для правильной оценки опасности в общем случае, важно понимать роль как механических свойств малого тела (прочность, упругие и реологические характеристики), так и геометрических параметров его фигуры на скорость распада под действием приливных сил со стороны Земли.
Удобным частным примером является околоземный астероид 433 Эрос. В настоящее время, благодаря миссии аппарата NEAR-Shoemaker в феврале 2001 г., собран большой объем информации о его топографии, структуре и гравитационном поле (Veverka и др., 2000). Фигура Эроса может быть представлена трехосным эллипсоидом с главными полуосями: a = 17200 м, b = 5771 м и c = = 5332 м, или вытянутым двухосным эллипсоидом с полуосями b = c = 5600 м и a = 17 200 м. По современным представлениям, Эрос – это единое сплошное тело, хотя и с системой значительных трещин (Flynn и др., 1999). Средняя плотность ρ0 = 2.67 г/см3 указывает на силикатный состав, близкий обыкновенным хондритам, но со значительной пористостью. Вращение с периодом 5.2 ч, и приливные силы при близком прохождении Земли или Марса могут вызывать значительные растягивающие напряжения в его теле.
Одним из важнейших вопросов в контексте приливного разрушения является предельное расстояние пролета малого тела до планеты, после которого может начаться его распад. Этот вопрос обсуждался со времен Roche (1983), который первым оценил такое расстояние, D, через безразмерную величину δ с помощью выражения
(1)
$\begin{gathered} D = {\text{2}}.{\text{45}}{{\left( {{{\rho }_{{\text{p}}}}{\text{/}}{{\rho }_{0}}} \right)}^{{{\text{1}}/{\text{3}}}}}{{R}_{{{\text{p }}}}} \\ {\text{or }}\delta = D{\text{/}}{{R}_{{\text{p}}}}{{\left( {{{\rho }_{0}}{\text{/}}{{\rho }_{{\text{p}}}}} \right)}^{{{\text{1}}/{\text{3}}}}} = {\text{2}}.{\text{45}},~ \\ \end{gathered} $Сжимаемое упругое тело с фигурой трехосного эллипсоида было рассмотрено (Dobrovolskis, 1990) для случая синхронного вращения с большой осью постоянно направленной на планету. Хотя Dobrovolskis’ и получил общее выражение для тензора напряжений, он использовал упрощенный сферический случай при анализе результатов для пластичного и хрупкого материалов. В реальной ситуации, форма, свойства вещества и вращение являются независимыми от орбиты тела параметрами и расчеты должны учитывать это обстоятельство. Общий анализ условий разрушения эллипсоидального твердого тела из слабосвязанного материала с использованием критерия прочности Мора-Кулона был сделан (Hollsaple, 2008). Были получены выражения для напряжений, возникающих при действии центробежных и приливных сил, причем критерием разрушения являлось возникновение в произвольном месте тела растягивающего напряжения. Показано, что при нулевой величине сцепления вещества данный критерий распада выполняется одновременно во всем теле. Позже Hollsaple сделал попытку учесть ненулевую величину сцепления вещества и ее зависимость от давления по критерию Мора-Кулона. Добавление конечной величины сцепления усложнило рассмотрение Hollsaple настолько, что точные результаты получить не удалось и был применен усредняющий подход с интегрированием по объему тела. Подход с нулевым сцеплением был также использован при численном моделировании приливного распада (Richardson и др., 1998) с помощью гидродинамического кода для различных комбинаций скорости вращения и ориентации оси вращения. Было показано, что Земля, начиная с дистанции D ≈ 1.5REarth, разорвет любой приближающийся астероид размером 1 км и более, если он имеет слабосвязанную структуру. В таком случае, рыхлые объекты не могли быть источниками значительных по размеру ударных структур на Земле и кратерообразующие тела для вышеприведенных примеров были монолитными.
Целью данной статьи является устранение ограничений модели слабо связанного малого тела и упрощающего предположения о несжимаемости вещества. Мы решаем в общем виде пространственную задачу распределения напряжений для однородного вращающегося упругого астероида с конечной прочностью вещества на разрыв и сдвиг. При этом на него действуют приливные силы со стороны Земли, а также центробежные силы из-за вращения и силы собственной гравитации. Получены точные аналитические выражения деформации жесткого вытянутого эллипсоидального тела с полуосями a > b = c, однородной структурой и изотропным распределением таких упругих параметров, как модуль Юнга и коэффициент Пуассона. Безусловно, это тоже сильно упрощенная модель, но она позволяет получить более реалистичные асимптотические оценки для последующих детальных расчетов методами механики разрушений. В частности, для рассмотрения условий роста трещин в малом теле под нагрузкой необходимо знать величину высвобождаемой при этом энергии упругой деформации. Астероид 433 Эрос использован как базовый пример для проверки расчетов.
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
Для расчета упругих деформаций малых тел применена хорошо разработанная теория гравитационного и приливного потенциала. Результирующая сила F в объеме тела может быть определена с помощью градиента полного потенциала
(2)
$F = {{\rho }_{{0{\text{ }}}}}{\text{grad}}\left[ {V(r)} \right],\,\,\,\,V(r) = {{V}_{{\text{g}}}}\left( r \right) + {{V}_{\omega }}\left( r \right) + {{V}_{{\text{t}}}}\left( r \right),$Условия равновесия вещества в объеме изотропного тела под действием общей силы (суммы гравитационной, центробежной и приливной сил) имеют вид
где μ, λ – это постоянные Ламэ(6)
$\mu = E{\text{/2}}\left( {{\text{1}} + \nu } \right);\,\,\,\,\lambda = \nu E{\text{/}}\left( {{\text{1}} + \nu } \right)\left( {1 - 2\nu } \right),$Также, для вычисления деформации тела важно правильно учесть граничные условия нагрузки на его поверхность. Эти условия для компонент поверхностной силы в общем виде можно представить как
(7)
$\begin{gathered} {\text{2}}\mu \left[ {{{e}_{{{\text{11}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{x}}} \right) + 1{\text{/}}2{{e}_{{{\text{12}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{y}}}}} \right) + } \right. \\ \left. { + \,\,1{\text{/}}2{{e}_{{{\text{13}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{z}}}}} \right)} \right] + \lambda e{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{x}}}}} \right) = {{f}_{{\text{1}}}}, \\ {\text{2}}\mu \left[ {{{e}_{{{\text{22}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{y}}}}} \right) + 1{\text{/}}2{{e}_{{{\text{12}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{x}}}}} \right) + } \right. \\ + \,\,1{\text{/}}2{{e}_{{{\text{23}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{z}}}}} \right) + \lambda e{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{y}}}}} \right) = {{f}_{{\text{2}}}}, \\ {\text{2}}\mu \left[ {{{e}_{{{\text{33}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{z}}}}} \right) + 1{\text{/}}2{{e}_{{{\text{13}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{x}}}}} \right) + } \right. \\ + \,\,1{\text{/}}2{{e}_{{{\text{23}}}}}{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{y}}}}} \right) + ~{\text{ }}\lambda e{\text{cos}}\left( {{\mathbf{n}},{{{\mathbf{e}}}_{{\mathbf{z}}}}} \right) = {{f}_{{\text{3}}}}, \\ \end{gathered} $Суммарное напряжение в теле определяется композицией растягивающих и сжимающих сил. Их величины зависят в свою очередь от соотношений интенсивностей соответствующих потенциалов:
(9)
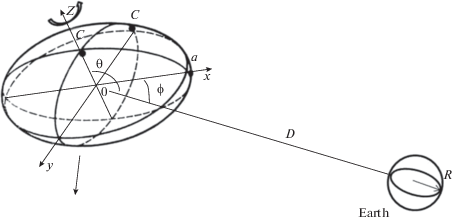
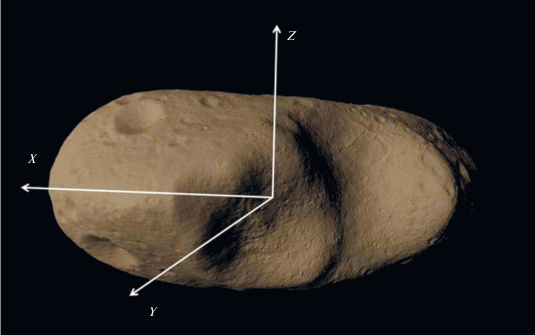
$\begin{gathered} {{I}_{\omega }} = \pi {\text{/}}{{T}^{{\text{2}}}}G{{\rho }_{0}},\,\,\,\,\omega = {\text{2}}\pi {\text{/}}T; \\ {{I}_{t}} = {\text{ }}M{{D}^{{\text{3}}}}{\text{/2}}\pi {{\rho }_{0}}~ = {\text{2/3}} \times {\text{1/}}{{\delta }^{{\text{3}}}}, \\ \end{gathered} $Рис. 1.
433 Эрос: фигура и ось вращения. Размер 17200 × 5711 × 5332 м, средняя плотность ~2.67 г/см3. Период вращения 5.2 ч вокруг Z-оси.
В этом случае, гравитационный потенциал Vg имеет простой вид, и для однородного тела с постоянной плотностью ρ0 записывается в виде
(10)
$\begin{gathered} {{V}_{{\text{g}}}}(x,y,z) = \\ = {{\rho }_{0}}G \times {\text{2}}\pi [{{f}_{0}}\left( \varepsilon \right) - {{x}^{{\text{2}}}}{{f}_{{\text{1}}}}\left( \varepsilon \right) - ({{y}^{{\text{2}}}} + {{z}^{{\text{2}}}}){\text{ }}{{f}_{{\text{2}}}}\left( \varepsilon \right)], \\ \end{gathered} $Аналогично, центробежный потенциал, Vω(x, y, z), имеет квадратичную форму
(11)
${{V}_{\omega }}(x,y,z) = {{\omega }^{{\text{2}}}}({{x}^{{\text{2}}}} + {{y}^{{\text{2}}}}){\text{/2}}{\text{.}}$Сила приливного воздействия, Ft(x, y, z), в общем случае (см. рис. 2) описывается выражением
(12)
${{{\mathbf{F}}}_{{\text{t}}}}\left( {\mathbf{r}} \right) = - GM{\text{/}}{{D}^{{\text{3}}}}\left[ {{\mathbf{r}} - {\text{3}}{\mathbf{R}}\left( {{\mathbf{R}}{\kern 1pt} *{\kern 1pt} {\mathbf{r}}} \right){\text{/}}{{R}^{{\text{2}}}}} \right],$В этих особых случаях, большая ось либо указывает на планету (случай “down”) или перпендикулярна соединяющей линии (случай “flat”).
Для указанных случаев φ = 0 и φ = π/2 (θ = π/2) мы можем представить компоненты вектора смещения в простой форме, наиболее отвечающей симметрии задачи, как
(14)
$\begin{gathered} {{u}_{{x~}}} = x\left( {{{A}_{0}} + {{A}_{{\text{1}}}}{{x}^{{\text{2}}}} + {{A}_{{\text{2}}}}{{y}^{{\text{2}}}} + {{A}_{{\text{3}}}}{{z}^{{\text{2}}}}} \right),{\text{ смещение вдоль }}x{\text{ - оси}}; \hfill \\ {{u}_{{y~}}} = y\left( {{{B}_{{0{\text{ }}}}}~ + {\text{ }}{{B}_{{\text{1}}}}{{x}^{{\text{2}}}} + {{B}_{{\text{2}}}}{{y}^{{\text{2}}}} + {{B}_{{\text{3}}}}{{z}^{{\text{2}}}}} \right),{\text{ смещение вдоль }}y{\text{ - оси}}; \hfill \\ {{u}_{z}} = z\left( {{{C}_{{0{\text{ }}}}} + {{C}_{{\text{1}}}}{{x}^{{\text{2}}}} + {{C}_{{\text{2}}}}{{y}^{{\text{2}}}} + {{C}_{{\text{3}}}}{{z}^{{\text{2}}}}} \right),{\text{ смещение}}\,\,{\text{вдоль }}z{\text{ - оси}}{\text{.}} \hfill \\ \end{gathered} $Тензор деформации определяется выражением
(15)
${{\sigma }_{{ij}}} = {\text{2}}\mu {{e}_{{ij}}}_{{\text{ }}} + \lambda e{{\delta }_{{ij}}},\,\,\,\,{{\delta }_{{ij}}} - {\text{символ Кронекера,}}$Напряжения для вытянутого двухосного эллипсоида выражены в квадратичной форме, где компоненты являются функциями коэффициента Пуассона (ν), величины t = c2/a2 или ε = $\sqrt {(1 - t)} $ и соотношениями интенсивностей потенциалов Iω и It:
(16)
$\begin{gathered} {{e}_{{ij}}} = E_{{ij}}^{{\left( 0 \right)}}(\nu ,t,{{I}_{k}}) + {{x}^{{\text{2}}}}E_{{ij}}^{{\left( {\text{1}} \right)}}(\nu ,t,{{I}_{k}}) + \\ + \,\,{{y}^{{\text{2}}}}E_{{ij}}^{{\left( 2 \right)}}(\nu ,t,{{I}_{k}}) + {{z}^{{\text{2}}}}E_{{ij}}^{{\left( 3 \right)}}(\nu ,t,{{I}_{k}}), \\ {{s}_{{ij}}} = {\text{1/2}}\mu {{\sigma }_{{ij}}} = S_{{ij}}^{{\left( 0 \right)}}(\nu ,t,{{I}_{k}}) + {{x}^{{\text{2}}}}S_{{ij}}^{{\left( {\text{1}} \right)}}(\nu ,t,{{I}_{k}}) + \\ + \,\,{{y}^{{\text{2}}}}S_{{ij}}^{{\left( 2 \right)}}(\nu ,t,{{I}_{k}}) + {{z}^{{\text{2}}}}S_{{ij}}^{{\left( 3 \right)}}(\nu ,t,{{I}_{k}}). \\ \end{gathered} $После решения уравнения (5) при граничных условиях (7) и (8) можно получить точные значения для коэффициентов $E_{{ij}}^{{(p)}}$и $S_{{ij}}^{{(p)}},$ p = 0, 1, 2, 3. Итак,
(17)
$\begin{gathered} {{e}_{{{\text{11}}}}}\left( {x,y,z} \right) = \partial {{u}_{x}}{\text{/}}\partial x = {{A}_{0}} + {\text{3}}{{A}_{{\text{1}}}}{{x}^{{\text{2}}}} + {{A}_{{\text{2}}}}{{y}^{{\text{2}}}} + {{A}_{{\text{3}}}}{{z}^{{\text{2}}}}, \\ {{e}_{{{\text{22}}}}}\left( {x,y,z} \right) = \partial {{u}_{y}}{\text{/}}\partial y = {{B}_{{0{\text{ }}}}}~ + {\text{ }}{{B}_{{\text{1}}}}{{x}^{{\text{2}}}} + {\text{3}}{{B}_{{\text{2}}}}{{y}^{{\text{2}}}} + {{B}_{{\text{3}}}}{{z}^{{\text{2}}}}, \\ {{e}_{{{\text{33}}}}}\left( {x,y,z} \right) = {\text{ }}\partial {{u}_{z}}{\text{/}}\partial z = {{C}_{{0{\text{ }}}}} + {{C}_{{\text{1}}}}{{x}^{{\text{2}}}} + {{C}_{{\text{2}}}}{{y}^{{\text{2}}}} + {\text{3}}{{C}_{{\text{3}}}}{{z}^{{\text{2}}}}, \\ e\left( {x,y,z} \right) = {{e}_{{{\text{11}}}}} + {{e}_{{{\text{22}}}}} + {{e}_{{{\text{33}}}}} = \\ = {{A}_{0}} + {{B}_{0}} + {{C}_{0}} + ({\text{3}}{{A}_{{\text{1}}}} + {{B}_{{\text{1}}}} + {{С}_{{\text{1}}}}){{x}^{{\text{2}}}} + \\ + \,\,\left( {{{A}_{{\text{2}}}} + {\text{3}}{{B}_{{\text{2}}}} + {{C}_{{\text{2}}}}} \right){{y}^{{\text{2}}}} + \left( {{{A}_{{\text{3}}}} + {{B}_{{\text{3}}}} + {\text{3}}{{C}_{{\text{3}}}}} \right){{z}^{{\text{2}}}}. \\ \end{gathered} $Компоненты $S_{{ij}}^{{(p)}}$тензора напряжений σij определяются выражением (15) как линейная комбинация Am, Bm и Сm. Например, для s11(x, y, z) = 1/2μσ11(x, y, z)
Условие равновесия Эроса как изотропного тела (5) обеспечивает первый набор условий для коэффициентов разложения
(18)
$\begin{gathered} {\text{6}}{{A}_{{\text{1}}}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + {{A}_{{\text{2}}}} + {{A}_{{\text{3}}}} + {{B}_{{\text{1}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) + \\ + \;{{C}_{{\text{1}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) = {{P}_{0}}( - {{f}_{{\text{1}}}}\left( \varepsilon \right) + {\text{ }}{{I}_{t}}{{V}_{{{\text{1}}~}}} + {{I}_{\omega }}), \\ {{A}_{{\text{2}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) + {{B}_{{\text{1}}}} + {{B}_{{\text{3}}}} + {\text{6}}{{B}_{{\text{2}}}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + \\ + \;{{C}_{{\text{2}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) = {{P}_{0}}( - {{f}_{{\text{2}}}}\left( \varepsilon \right) + {{I}_{t}}{{V}_{{\text{2}}}} + {{I}_{\omega }}), \\ {{A}_{{\text{3}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) + {{C}_{{\text{1}}}} + {{C}_{{\text{2}}}} + {{B}_{{\text{3}}}}\left( {{\text{1}} + \lambda {\text{/}}\mu } \right) + \\ + \,\,{\text{6}}{{C}_{{\text{3}}}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) = {{P}_{0}}( - {{f}_{{\text{2}}}}\left( \varepsilon \right)--{\text{1/2}}{{I}_{t}}), \\ \end{gathered} $Каждое из трех граничных условий на поверхности Эроса (7) обеспечивает дополнительный набор условий для базисных коэффициентов. Например, из первого условия – f1 = 0:
(19.1)
$\begin{gathered} {\text{3}}{{A}_{{\text{1}}}}({\text{1}}\, + \,\lambda {\text{/2}}\mu )\, - \,{{A}_{{\text{2}}}}[t({\text{1}}\, + \,\lambda {\text{/2}}\mu )\, + \,{\text{1}}]\, + \,{{B}_{{\text{1}}}}(\lambda {\text{/2}}\mu \, - \,{\text{1}}) - \\ - \,\,{\text{3}}t(\lambda {\text{/2}}\mu ){{B}_{{\text{2}}}} + {{C}_{{\text{1}}}}(\lambda {\text{/2}}\mu ) - t(\lambda {\text{/2}}\mu ){{C}_{{\text{2}}}} = 0, \\ {\text{3}}{{A}_{{\text{1}}}}({\text{1}} + \lambda {\text{/2}}\mu ) - {{A}_{{\text{3}}}}[t({\text{1}} + \lambda {\text{/2}}\mu ) + {\text{1}}] + {{B}_{{\text{1}}}}(\lambda {\text{/2}}\mu ) - \\ - \,\,t(\lambda {\text{/2}}\mu ){{B}_{{\text{3}}}} + {{C}_{{\text{1}}}}(\lambda {\text{/2}}\mu - {\text{1}}) - {\text{3}}t(\lambda {\text{/2}}\mu ){{C}_{{\text{3}}}} = 0, \\ {\text{3}}{{A}_{{\text{1}}}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + \lambda {\text{/2}}\mu \left( {{{B}_{{\text{1}}}} + {{C}_{{\text{1}}}}} \right) = \\ = - \left[ {{{A}_{0}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + \lambda {\text{/2}}\mu \left( {{{B}_{0}} + {{C}_{0}}} \right)} \right]{\text{/}}{{a}^{{\text{2}}}}. \\ \end{gathered} $Из второго уравнения – f2 = 0:
(19.2)
$\begin{gathered} {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) + {{A}_{{\text{2}}}}t\left( {{\text{1}} - \lambda {\text{/2}}\mu } \right) + {{B}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu + {\text{1}} + t} \right) - \\ - \,\,{\text{3}}t\left( {\lambda {\text{/2}}\mu + {\text{1}}} \right){{B}_{{\text{2}}}} + {{C}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) - t\left( {\lambda {\text{/2}}\mu } \right){{C}_{{\text{2}}}} = 0, \\ {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) + {{A}_{{\text{2}}}}t - t\lambda {\text{/2}}\mu {{A}_{{\text{3}}}} + \\ + \,\,{{B}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu + t + {\text{1}}} \right) - t\left( {\lambda {\text{/2}}\mu + {\text{2}}} \right){{B}_{{\text{3}}}} + \\ + \,\,{{C}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right)--t{{C}_{{\text{2}}}} - {\text{3}}t\left( {\lambda {\text{/2}}\mu } \right){{C}_{{\text{3}}}} = 0, \\ {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right)\, + t{{A}_{{\text{2}}}}\, + \,{{B}_{{\text{1}}}}{\kern 1pt} \left( {{\text{1}}\, + \,t\, + \,\lambda {\text{/2}}\mu } \right) + \left( {\lambda {\text{/2}}\mu } \right){{C}_{{\text{1}}}} = \\ = - \left[ {{{B}_{0}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + \lambda {\text{/2}}\mu \left( {{{A}_{0}} + {{C}_{0}}} \right)} \right]{\text{/}}{{a}^{{\text{2}}}}. \\ \end{gathered} $Из третьего уравнения – f3 = 0:
(19.3)
$\begin{gathered} {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) + {{A}_{{\text{3}}}}t - t\lambda {\text{/2}}\mu {{A}_{{\text{2}}}} + \\ + \,\,{{B}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) - {\text{3}}t\left( {\lambda {\text{/2}}\mu } \right){{B}_{{\text{2}}}}--t{{B}_{{\text{3}}}} + \\ + \,\,{{C}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu + t + {\text{1}}} \right)--t\left( {{\text{2}} + \lambda {\text{/2}}\mu } \right){{C}_{{\text{2}}}} = 0, \\ {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) + {{A}_{{\text{3}}}}t\left( {{\text{1}} - \lambda {\text{/2}}\mu } \right) + {{B}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right) - \\ - \,\,t\left( {\lambda {\text{/2}}\mu } \right){{B}_{{\text{3}}}} + {{C}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu + t + {\text{1}}} \right) - \\ - \,\,{\text{3}}t\left( {\lambda {\text{/2}}\mu + {\text{1}}} \right){{C}_{{\text{3}}}}{\text{ }} = {\text{ }}0, \\ {\text{3}}{{A}_{{\text{1}}}}\left( {\lambda {\text{/2}}\mu } \right)\, + \,t{{A}_{{\text{3}}}}\, + \,{{B}_{{\text{1}}}}\left( {\lambda {\text{/}}{\text{2}}\mu } \right)\, + \,\left( {\lambda {\text{/2}}\mu \, + \,t + {\text{1}}} \right){{C}_{{\text{1}}}} = \\ = - \left[ {{{C}_{0}}\left( {{\text{1}} + \lambda {\text{/2}}\mu } \right) + \lambda {\text{/2}}\mu \left( {{{A}_{0}} + {{B}_{0}}} \right)} \right]{\text{/}}{{a}^{{\text{2}}}}.~~~~{\text{ }} \\ \end{gathered} $Решение системы линейных уравнений (18) и (19.1), (19.2), (19.3) позволяет получить явные выражения для Am, Bm и Сm от f1(ε), f2(ε), It и Iω. Например, A1 для случая “down”
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Итоговое решение для диагональных компонент тензора напряжений для последующего анализа удобно представить в нормированном виде
(20)
$\begin{gathered} {{\sigma }_{{{\text{11}}}}}\left( {x,y,z} \right) = {{\sigma }_{0}}[S_{{11}}^{{({\text{1}})}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right)\left( {{{{\left( {x{\text{/}}a} \right)}}^{{\text{2}}}} - {\text{1}}} \right) + \\ + \,\,S_{{11}}^{{(2)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {y{\text{/}}c} \right)}^{{\text{2}}}} + S_{{11}}^{{(3)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {z{\text{/}}c} \right)}^{{\text{2}}}}, \\ {{\sigma }_{{{\text{22}}}}}\left( {x,y,z} \right) = {{\sigma }_{0}}[S_{{22}}^{{(2)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right)\left( {{{{\left( {y{\text{/}}c} \right)}}^{{\text{2}}}} - {\text{1}}} \right) + \\ + \,\,S_{{22}}^{{(1)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {x{\text{/}}a} \right)}^{{\text{2}}}} + S_{{22}}^{{(3)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {z{\text{/}}c} \right)}^{{\text{2}}}}], \\ {{\sigma }_{{{\text{33}}}}}\left( {x,y,z} \right) = {{\sigma }_{0}}[S_{{33}}^{{(3)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right)\left( {{{{\left( {z{\text{/}}c} \right)}}^{{\text{2}}}} - {\text{1}}} \right) + \\ + \,\,S_{{33}}^{{(1)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {x{\text{/}}a} \right)}^{{\text{2}}}} + S_{{22}}^{{(2)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\left( {y{\text{/}}c} \right)}^{{\text{2}}}}], \\ \end{gathered} $Так, для Эроса растягивающее (положительное) напряжение возникает начиная с некоторого расстояния до Земли вдоль оси, направленной на планету: для ориентации “down” – это ось ОХ (см. рис. 3), для ориентации “flat” – это ось ОY (см. рис. 4). Причем для последнего случая, данное расстояние существенно меньше. При умеренном вращении, по остальным осям тело испытывает только сжатие.
Рис. 3.
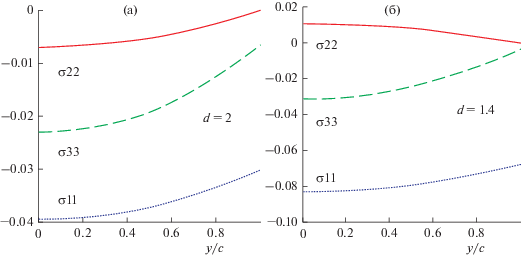
Компоненты тензора напряжений (в σ0) вдоль оси ОХ (y = z = 0) при ориентации “down”: σ11 – сплошная, σ22 – пунктирная, σ33 – штриховая линии (а) d = D/RE = 3; (б) d = D/RE = 2.
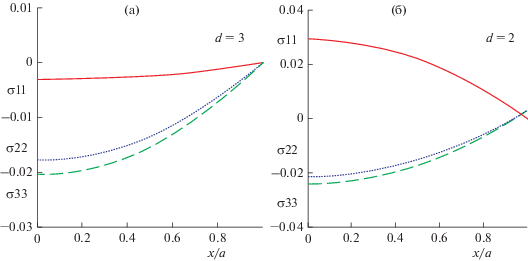
Рис. 4.
Компоненты тензора напряжений (в σ0) вдоль оси ОY (x = z = 0) при ориентации “flat”: σ22 – сплошная, σ11 – пунктирная, σ33 – штриховая линии. (а) d = D/RE = 2; (б) d = D/RE = 1.4.
При достаточно малом сближении астероида и Земли для ориентации “down” σ11 растягивающее (положительное) напряжение возникает вначале в центральном сечении тела на боковой поверхности. Проще всего это показать с помощью (20), введя угол θ от оси OZ и эффективное расстояние от центра – ρ. Для сечения x = 0
(21)
$\begin{gathered} {{\sigma }_{{{\text{11}}}}}\left( {\rho ,\theta } \right) = {{\sigma }_{0}}[ - S_{{11}}^{{(1)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right) + \\ + \,\,S_{{11}}^{{(2{\text{d}})}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\rho }^{{\text{2}}}} + S_{{11}}^{{(3{\text{d}})}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){\text{cos}}\left( {{\text{2}}\theta } \right){{\rho }^{{\text{2}}}}], \\ \end{gathered} $Рис. 5.
Компоненты (в σ0) тензора напряжений σ11 и σ22 на различных расстояниях от планеты: ρ = 0 (центр) – сплошная; ρ = 1, θ = π/2 (поверхность экватор) – пунктирная; ρ = 1, θ = 0 (поверхность полюс) – штриховая линии. (а) “down”; (б) “flat” ориентации.
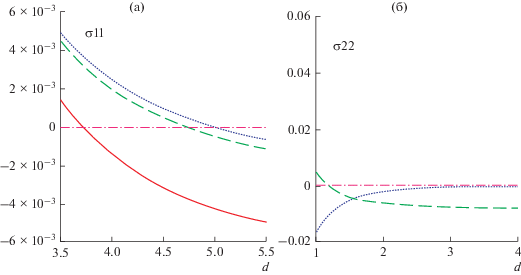
Другой случай представляет ориентация “flat”. σ22 выражение для сечения y = 0
(22)
$\begin{gathered} {{\sigma }_{{{\text{22}}}}}\left( {\rho ,\theta } \right) = {{\sigma }_{0}}[ - S_{{22}}^{{(2)}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right) + \\ + \,\,S_{{22}}^{{1{\text{f}}}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right){{\rho }^{{\text{2}}}} + S_{{22}}^{{3{\text{f}}}}\left( {\nu ,\varepsilon ,{{I}_{\omega }},{{I}_{{\text{t}}}}} \right)~{\text{cos}}\left( {{\text{2}}\theta } \right){{\rho }^{{\text{2}}}}], \\ \end{gathered} $Пространственная плотность потенциальной энергии упругой деформации выражается в виде суммы запасенных работ внутренних напряжений (Папкович, 1939)
(23)
${{U}_{0}}\left( {x,y,z} \right) = 1{\text{/}}2\sum {{{\sigma }_{{ij}}} \cdot {{\varepsilon }_{{ij }}}} ;\,\,\,\,i,j = {\text{1}},{\text{2}},{\text{3}}{\text{. }}$Полная величина потенциальной энергии упругой деформации U = U(D, T, ν, ε) определяется интегралом от U0(x, y, z) по всему объему тела
и складывается из энергии объемного сжатия (расширения) и энергии изменения формы тела. Важным параметром при анализе является величина (и знак) полного относительного изменения объема всего тела E = E(D, T, ν, ε) , который можно получить в явном виде, интегрируя e(x, y, z) из (17) аналогично U. Например, для случая “down”(25)
$\begin{gathered} E \times {\text{3}}({\text{1}} + \lambda {\text{/2}}\mu )({\text{1}} + {\text{3}}\lambda {\text{/2}}\mu )Z\left( {\nu ,\varepsilon } \right) = {{I}_{{\text{t}}}} \times {\text{8}}{{T}_{{\text{e}}}}(\nu ,\varepsilon ){\text{ }} + \\ + \,\,{{I}_{\omega }} \times {\text{8}}{{R}_{{\text{e}}}}(\nu ,\varepsilon )--{\text{16}}{\kern 1pt} \text{[}{{f}_{{\text{1}}}}(\varepsilon ){{F}_{{{\text{1e}}}}}(\nu ,\varepsilon ) + {{f}_{{\text{2}}}}(\varepsilon )t{{F}_{{{\text{2e}}}}}(\nu ,\varepsilon )]; \\ {{T}_{{\text{e}}}}(\nu ,\varepsilon ) = ({\text{1}} - t)({\text{1}} + \lambda {\text{/2}}\mu )[{{t}^{{\text{2}}}}({\text{5}} + {\text{9}}\lambda {\text{/2}}\mu ) + \\ + \,\,{\text{2}}({\text{1}} + {\text{3}}\lambda {\text{/2}}\mu )({\text{5}}t + {\text{4}})], \\ {{R}_{{\text{e}}}}(\nu ,\varepsilon ) = {{t}^{{\text{2}}}}({\text{5}} + {\text{9}}\lambda {\text{/2}}\mu )[t({\text{1}} + \lambda {\text{/2}}\mu ) - \lambda {\text{/}}\mu ] + \\ + \,\,({\text{1}} + {\text{3}}\lambda {\text{/2}}\mu )[{{t}^{{\text{2}}}}({\text{5}} + \lambda {\text{/2}}\mu ) + \\ + \,\,{\text{2}}t({\text{5}} - {\text{3}}\lambda {\text{/2}}\mu ) + {\text{8}}({\text{1}} + \lambda {\text{/2}}\mu )], \\ {{F}_{{\text{1}}}}_{{\text{e}}}(\nu ,\varepsilon ) = {\text{4}}({\text{1}} + \lambda {\text{/2}}\mu )({\text{1}} + {\text{3}}\lambda {\text{/2}}\mu ) - \\ - \,\,{{t}^{{\text{2}}}}({\text{5}} + {\text{9}}\lambda {\text{/2}}\mu )\lambda {\text{/2}}\mu --t(\lambda {\text{/2}}\mu - {\text{3}})({\text{3}}\lambda {\text{/2}}\mu - {\text{1}}), \\ {{F}_{{\text{2}}}}_{{\text{e}}}(\nu ,\varepsilon ) = {{t}^{{\text{2}}}}({\text{5}} + {\text{9}}\lambda {\text{/2}}\mu )(\lambda {\text{/2}}\mu + {\text{1}}) + \\ + \,\,t({\text{5}} + \lambda {\text{/2}}\mu )({\text{1}} + {\text{3}}\lambda {\text{/2}}\mu ) - {\text{4}}(\lambda {\text{/2}}\mu - {\text{1}})({\text{3}}\lambda {\text{/2}}\mu + {\text{1}}).{\text{ }} \\ \end{gathered} $Обращает на себя внимание коэффициент (1 – t), t = c2/a2 в выражении для функции Te(ν, ε). Он означает, что для сферы, при t = 1, полный вклад приливного воздействия в изменение объема тела равен нулю. Сфера сжимается “с боков” (оси OY и OZ) и одновременно удлиняется по оси OX таким образом, что эти вклады полностью компенсируют друг друга.
Для Эроса объемное сжатие (расширение) при различных коэффициентах Пуассона вещества показано на рис. 6.
Рис. 6.
E(D, ν) в зависимости от расстояния до Земли для астероида с различным упругим поведением пород: ν = 0.05 – сплошная; ν = 0.2 – пунктирная; ν = 0.33 – штриховая линии. (а) “down”; (б) “flat” ориентации.
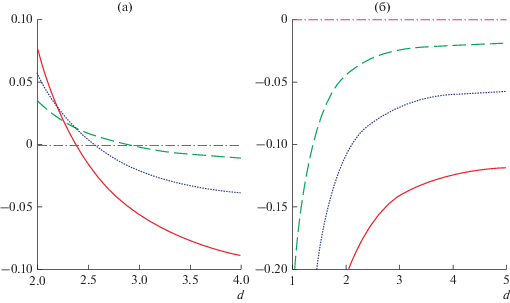
Для случая “down”, при приближении астероида к Земле, на определенном расстоянии происходит смена сжатия тела на его расширение (в целом). Это делает астероид неустойчивым и становится возможным его распад. В случае “flat” такого не происходит: тело остается сжатым (в целом) вплоть до столкновения с Землей.
Таким образом, только для ориентации “down” реализуется возможность полного распада малого тела под действием приливных сил при приближении к планете. Необходимым условием для этого является наличие растягивающих напряжений, по какому либо сечению целиком. Предыдущий анализ напряжений (21) показал, что для нижней оценки критического расстояния Dc до планеты лучше всего использовать значение σ11 в центре тела (x = y = z = 0). Величина $\sigma _{{11}}^{{({\text{c}})}}$ может быть определена как
(26)
$\begin{gathered} \sigma _{{11}}^{{({\text{c}})}}(D,T,\nu ,\varepsilon )Z\left( {\nu ,\varepsilon } \right){\text{/}}{{\sigma }_{0}}_{~} = {{I}_{{\text{t}}}} \times T(\nu ,\varepsilon ) + \\ + \,\,{{I}_{\omega }} \times R(\nu ,\varepsilon )--({{f}_{{\text{1}}}}(\varepsilon ) \times {{F}_{{\text{1}}}}(\nu ,\varepsilon ) + {{f}_{{\text{2}}}}(\varepsilon ) \times {{F}_{{\text{2}}}}(\nu ,\varepsilon )).{\text{ }} \\ \end{gathered} $Расстояние Dc может быть определено в общем виде с помощью выражения (23) условием
или, при T = 0, через безразмерную величину δс = = Dс/Rp(ρ0/ρp)1/3. Но, в отличие от выражения Роше (1), δс = δ(ν, ε) является функцией формы тела и его упругих свойств (см. рис. 7a). Альтернативно, можно воспользоваться условием возникновения нестабильности тела при расширении (в целом) после приближения к Земле на определенное расстояние De (см. рис. 7б). Оно может быть определено в общем виде с помощью выражения (25) условиемРис. 7.
Критическое расстояние в безразмерной форме для астероидов различного состава и формы: ν = 0.05 – сплошная; ν = 0.2 – пунктирная; ν = 0.33 – штриховая линии. (а) δc – “силовой” критерий; (б) δe – “объемный” критерий.
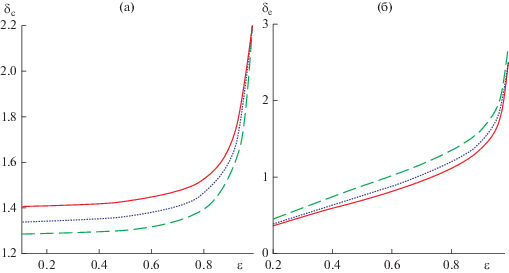
Анализ обеих зависимостей показывает, что твердые тела сферической формы существенно более устойчивы к приливному воздействию, чем вытянутые двухосные эллипсоиды с ориентацией осей “down”. Коэффициент Пуассона вещества для вытянутых тел играет при определении критического расстояния незначительную роль, но важен для точного расчета компонент тензора напряжений (20).
При плотности, размерах и периоде вращения Эроса, интенсивности вовлеченных потенциалов (9) имеют величины
Рис. 8.
Растягивающее напряжение на боковой поверхности Эроса вблизи Земли (ρ0 = 2.67 г/см3, ε = = 0.946, T = 5.2 ч, a = 17 км, ν = 0.2). Уровни прочности на растяжение: 10 КПа – пунктирная, 100 КПа – штриховая линии.
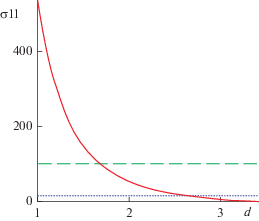
Оценим приблизительно влияние поврежденности и размеров малого тела на его стабильность при близком пролете с помощью выражения (20). Горизонтальные линии на рис. 8 представляет различные уровни прочности: 10 кПa (слабо связанный материал) и 100 кПa (значительная трещиноватость). При этом 1000 кПa – типичная прочность на растяжение консолидированного тела хондритового состава. Рис. 8 показывает, что если бы Эрос имел прочность на растяжение 100 кПa, приливные силы Земли разорвали бы его на дистанции D ~ 1.7REarth. Но, как консолидированный хондрит с прочностью пород на растяжение ~ 1 МПа, он был бы разорван вблизи Земли только если бы имел размер не менее a ~ 25 км. Более точные оценки возможны при явном рассмотрении поведения существующих на поверхности малого тела трещин. Использование метода А. Гриффитса (баланс выделяемой при разрыве тела энергии деформации, и энергии, поступающей в вершину растущей трещины), позволило бы определить критической размер магистральной трещины при данной растягивающей нагрузке (Griffith, 1921). Развитию данного подхода механики разрушений к проблеме приливного распада астероидов и комет будут посвящены последующие работы.
ЗАКЛЮЧЕНИЕ
В данной статье получены дополнительные ограничивающие факторы на критическое расстояние для приливного распада малого тела с фигурой двухосного эллипсоида вращения, учитывая его размер, форму, плотность, сжимаемость, прочность слагающих пород и ориентации большой полуоси относительно планеты. Мы не рассматривали случай рыхлых малых тел, когда в силу большой поврежденности, прочность на растяжение близка к нулю. Были изучены консолидированные тела, хотя и ослабленные ударными процессами, но с конечной величиной прочности пород. Показано, что сжимаемость, форма и ориентация малого тела при подлете к планете оказывает значительное влияние на испытываемые приливные напряжения и оценен вклад вращения. Несмотря на то, что были использованы осредненные величины пределов прочности для малых тел, полученные значения тензоров деформаций и напряжения имеют самостоятельную ценность в качестве асимптотических выражений для более точных методов механики разрушений.
Применение результатов расчетов к случаю пролета тела возле планеты возможно только при соблюдении ряда ограничений. Главное из них – это постоянное пространственное положение оси вращения и ориентации тела относительно направления на Землю, что, строго говоря, не выполняется. При характерных скоростях движения околоземных объектов порядка 20 км/с, расстояние 2REarth будет пройдено за время порядка 600 с, что составит 1/30 периода вращения 5 ч. За это время ось OX повернется от выбранного направления примерно на 12°, в случае сохранения постоянного направления оси вращения перпендикулярно направлению на Землю. Таким образом, необходимо более строгое рассмотрение напряжений и деформаций в несферическом астероиде, возникающих при близком пролете массивной планеты, в общем случае изменения его состояния вращения под действием приливных сил (Scheeres, 2000).
Показано, что наибольшая нагрузка возникает, когда вытянутое тело направлено при подлете большой полуосью на планету, а наименьшая, - когда оно развернуто к планете своей малой полуосью. Методами теории упругости было получено точное аналитическое выражение для компонент тензора деформаций и напряжений в малом теле под действием гравитации, вращения и приливного воздействия. В качестве примера взят астероид Эрос, который имеет фигуру сильно вытянутого эллипсоида с размерами ~34 × 12 × 12 км. Наш анализ показывает, что в худшем сценарии эволюции его орбиты, Эрос может оказаться вблизи Земли и пережить ее приливное воздействие. Это означает, что он может не распасться при подлете на части и войти как целое тело в атмосферу Земли.
Рассмотрение вопроса, как далеко могут разойтись обломки родительского тела в случае его разрыва при падении на Землю, выходит за рамки представленной модели. Это связано с тем, что после разрушения необходимо рассматривать уже бинарную систему разделенных и взаимодействующих между собой фрагментов в гравитационном поле планеты (Melosh, Stansmerry, 1991). Выражение (24) позволяет только оценить условия начала перехода консолидированного астероида в состояние роя фрагментов. Подчеркнем еще раз, что наша упрощенная оценка не учитывает изменение орбиты астероида и состояния его вращения при его взаимодействии с Землей, поскольку рассмотрен случай прямого падения. Реальная картина распределения ударных кратеров на Земле (и Луне), их форма и статистика по размерам весьма сложны (Ivanov, 2007). Вместе с тем, полученные результаты, после необходимого расширения модели, могут быть полезны для рассмотрения актуальной проблемы формирования семейств за счет приливного разрушения астероидов при пролете мимо Земли (Schunová и др., 2014).
Как у члена семейства NEO, типа Амура, орбита Эроса регулярно пересекает орбиту Марса, но, пока, не пересекается с земной. Астероид следует по слабо эллиптической траектории, обращаясь вокруг Солнца за 1.76 лет с наклоном 10.8° к эклиптике. Из-за регулярных появлений вблизи Земли Эрос стал важным астрономическим объектом для уточнения орбит системы Земля–Луна и больших астероидов. С помощью прибора мультиспектральный анализатор (MSI), установленного на космическом аппарате NEAR, в 2000–2001 гг. были получены десятки тысяч изображений высокого разрешения. В частности, были детально описаны глобальные линеаменты на его поверхности (Buczkowski, 2006). Сеть разломов, видимо, возникла в результате сильных ударов и предполагает наличие значительной прочности пород Эроса, несмотря на его низкую общую плотность. Большинство линейных структур привязано к ударным кратерам и нет никаких видимых следов приливного разрушения от Марса, что косвенно подтверждает наши результаты.
Авторы благодарны проектной команде миссии NEAR за предоставленные данные, а также Иванову Б.А. за материалы по ударным кратерам и критическому анализу текста.
Аналитические исследования были выполнены С.А. Воропаевым за счет гранта Российского научного фонда (проект № 17-17-01279). Jean-Pierre Barriot был поддержан грантом Французского космического агенства (CNES) проект “Decision d’aide a la Recherche, Planetary Sciences”. Ян Джинго был поддержан Открытым фондом Университета Макао по науке и технологиям (проект FDCT 119/2017/A3).
Список литературы
Воропаев С.А., Кочеров А.В., Лоренц К.А., Нугманов И.Р., Джингао Я. Особенности построения паспорта прочности внеземного вещества на примере метеорита Челябинск // ДАН. 2017. Т. 476. № 6. С. 635.
Галимов Э.М., Колотов В.П., Назаров М.А., Костицын Ю.А. Результаты вещественного анализа метеорита Челябинск // Геохимия. 2013. № 7. С. 580.
Папкович П.Ф. Теория упругости. М.: Наука, 1939. С. 633.
Чандрасекхар С. Эллипсоидальные фигуры равновесия. М.: Мир, 1971. С. 289.
Aggarwal H.R., Oberbeck V.R. Roche limit of a solid body // Astrophys. J. 1974. V. 191. P. 577.
Bottke W.F. Hazards due to Comets and Asteroids / Ed. Gehreis T. Tucson: Univ. Arizona Press, 1994. P. 337.
Bottke W.F., Minton D., Morbidelli A. An Archaean heavy bombardment from a destabilized extension of the asteroid belt // Nature. 2012. V. 485. P. 78.
Boehnke P., Harrison T. Illusory Late Heavy Bombardments // Proc. Nat. Acad. Sci. USA. 2016. V. 113. № 39. P. 10 802.
Buczkowski D.L. Linear Structures on Eros and Other Small Bodies. Johns Hopkins APL Technical Digest. 2006. V. 27. № 2. P. 100.
Davidsson B.J. Tidal Splitting and Rotational Breakup of Solid Biaxial Ellipsoids // Icarus. 2001. V. 149. P. 375.
Dobrovolskis A.R. Tidal disruption of solid bodies // Icarus. 1990. V. 88. P. 24.
Flynn G.J., Moore L.B., Kloeck W. Density and Porosity of Stone Meteorites: Implications for the Density, Porosity, Cratering, and Collisional Disruption of Asteroids // Icarus. 1999. V. 142. P. 97.
Glikson A.Y., Jablonski D., Westlake S. Origin of the Mt Ashmore structural dome, west Bonaparte Basin, Timor Sea // Austral. J. Earth Sci. 2010. V. 57 № 4. P. 411.
Griffith A.A. The phenomena of rupture and flow in solids // Phil. Trans. Roy. Soc. A. 1921. V. 221. № 2. P. 163.
Gomes R., Levison H.F., Tsiganis K., Morbidelli A. Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets // Nature. 2005. V. 435. P. 466.
Haisch K.E., Jr., Lada E.A., Lada C.J. Disk frequencies and lifetimes in young clusters // Astrophys. J. 2001. V. 553. P. 153.
Holsapple K.A., Michel P. Tidal disruptions II. A continuum theory for solid bodies with strength, with applications to the Solar System // Icarus. 2008. V. 193. P. 283.
Ivanov B.A., Hartmann W.K. Exogenic Dynamics, Cratering and Surface Ages. Treatise on Geophysics / Ed. Schubert G. Amsterdam: Elsevier, 2007. P. 207.
Johnson B.C., Melosh H.J. Impact spherules as a record of ancient heavy bombardment of Earth // Nature. 2012. V. 485. P. 75.
Lowe D.R. Spherule beds 3.47–3.24 billion years old in the Barberton Greenstone belt, South Africa: a record of large meteorite impacts and their influence on early crustal and biological evolution. Astrobiology. 2003. V. 3. P. 7.
Melchior P. Physique et Dynamique Planetaries. Royal de Belgique. 1971. V. 2. P. 484.
Melosh H.J., Stansberry J.A. Doublet craters and the tidal disruption of binary asteroids// Icarus. 1991. V. 94. P. 171.
Michel P., Farinella P., Froeschle Ch. The orbital evolution of the asteroid Eros and implications for collision with the Earth // Nature. 1996. V. 380. P. 689.
Morbidelli A., Crida A. The dynamics of Jupiter and Saturn in the gaseous protoplanetary disk // Icarus. 2007. V. 191. P. 158.
Pierens A., Nelson R.P. Constraints on resonant-trapping for two planets embedded in a protoplanetary disc// Astron. and Astrophys. 2008. V. 482. P. 333.
Pravec P., Harris W., Concalves R. Spin rate distribution of small asteroids. P. 497. // Icarus. 2008. V. 197
Richardson D., Bottke W., Love S. Tidal Distortion and Disruption of Earh-Crossing asteroids // Icarus. 1998. V. 134. P. 47.
Roche Edouard Albert (1820–1883). Astrophysics and Space Science. 1983. V. 97. № 2. P. 223.
Scheeres D.J., Ostro S.J., Hudson R.S. Effects of Gravitational Interactions on Asteroid Spin States // Icarus. 2000. V. 147. P. 106.
Schunová E., Jedicke R., Granvik M. Properties and evolution of NEO families created by tidal disruption at Earth // Icarus. 2014. V. 238. P. 156.
Veverka J., Robinson M., Thomas P. NEAR at Eros: Imaging and Spectral Results // Science. 2000. V. 289. P. 2088.
Watters T.R., Thomas P.C., Robinson M.S. Thrust faults and the near-surface strength of asteroid 433 Eros // Geophys. Res. Lett. 2011. V. 38. P. L02202.
Wilkison S.L., Robinson M., Yeomans D. An Estimate of Eros’s Porosity and Implications for Internal Structure // Icarus. 2002. V. 155. P. 94.
Yomogida K., Matsui T. Physical Properties of Ordinary Chondrites // J. Geophys. Res. 1983. V. 88. P. 9513.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник