Астрономический вестник, 2020, T. 54, № 4, стр. 376-384
Оцифровка астронегативов пулковской стеклотеки: положения главных спутников Сатурна в период 1972–1982 годов в системе Gaia DR2
М. Ю. Ховричев a, *, Н. В. Нарижная a, Т. А. Васильева a, И. С. Измайлов a, А. М. Куликова a, Д. А. Бикулова a
a Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия
* E-mail: deimos@gaoran.ru
Поступила в редакцию 19.11.2019
После доработки 11.12.2019
Принята к публикации 13.12.2019
Аннотация
Мы представляем результаты повторной редукции пулковских фотографических пластинок с изображениями главных спутников Сатурна в системе каталога Gaia DR2 (169 пластинок, 3007 отдельных положений). Астронегативы были сняты с помощью 26-дюймового рефрактора Пулковской обсерватории в период с 1972 по 1982 гг. Внутренняя точность измерения астронегативов с помощью пулковской системы MDD составила 1 мкм (20 угл. мс в масштабе 26-дюймового рефрактора). Средние значения разностей О–С при сравнении с самыми современными эфемеридами варьируются в пределах ±20 угл. мс. Ошибки среднегодовых значений разностей обычно лучше 20 угл. мс. Имеет место хорошее согласие между представленным пулковским рядом и результатами повторной редукции аналогичных наблюдений USNO (среднесезонные разности меньше 50 угл. мс по модулю). Учитывая, что разные реализации современных эфемерид дают положения спутников, различающиеся в пределах ±50 угл. мс для рассматриваемого интервала времени, можно сделать вывод о высокой информативности пулковского ряда для совершенствования моделей движения главных спутников Сатурна.
ВВЕДЕНИЕ
В последнее десятилетие отмечается качественное изменение в использовании результатов астрометрических наблюдений спутников планет-гигантов. Еще недавно ряды экваториальных и относительных координат спутников прежде всего служили для совершенствования теорий движения данных небесных тел и планет, вокруг которых они обращаются. В наши дни, в связи с ростом точности наземных астрометрических наблюдений и публикацией высокоточных измерений, выполненных в ходе космических миссий, проводятся исследования, сфокусированные на изучении динамических эффектов, проявляющихся в движении спутников. Особый интерес вызывает изучение влияния приливов в телах планет и их спутников на орбитальное движение. Поскольку возмущения, вызванные этой причиной, зависят от вязко-упругих свойств планет и их спутников, можно говорить о том, что астрометрические наблюдения рассматриваемых небесных тел обеспечивают дополнительную возможность исследовать их физическое строение. Подробное описание физической стороны этого вопроса можно найти, например, в статье (Emelyanov, 2018).
Работы, отражающие указанную тенденцию, касаются обнаружения вековых изменений величин среднего движения для Ио (Lainey и др., 2009) и Мимаса (Lainey и др., 2012), вызванных приливными явлениями. В этих работах широко используются результаты фотографических наблюдений спутников планет, выполненных на протяжении XX века. Таким образом, переработка старых наблюдений с помощью современных технических средств приобретает дополнительную актуальность: помимо уточнения эфемерид, эти данные обеспечивают возможность продвижения в изучении приливной динамики в системах спутников планет-гигантов.
Второй релиз данных, полученных на космическом телескопе Gaia (Brown и др., 2018) обеспечил астрометристов, выполняющих наземные наблюдения в относительно широких полях, опорной системой небывалого качества: более чем для миллиарда звезд точность координат составляет от десятков микросекунд до нескольких миллисекунд, а собственных движений – от десятых долей до нескольких миллисекунд дуги в год. Даже при разности эпох между наблюдениями на Gaia и моментом получения астронегатива в целое столетие, ошибка координат опорных звезд будет порядка 1 угл. мс и лучше. Важно отметить, что Gaia DR2 обеспечивает наименьший уровень систематических ошибок. Поэтому естественно ожидать, что использование данных из Gaia DR2 даст возможность повысить точность повторной редукции астронегативов, содержащих изображения спутников планет.
Данная работа посвящена переработке пулковских фотографических наблюдений спутников Сатурна в системе GaiaCRF2. Фотографические наблюдения системы Сатурна начались в Пулковской обсерватории с 1966 г. и продолжились до 2007 г. За этот период снято 443 астронегатива с помощью Нормального астрографа и 511 – на 26-дюймовом рефракторе. Основной массив пластинок получен в периоды с 1972 по 1982 гг. и с 2001 по 2007 гг. Планируя обработку этих наблюдений, пулковские астрометристы ориентировались на стандартную астрометрическую редукцию с опорными звездами для астронегативов, снятых на Нормальном астрографе. Фотопластинки 26-дюймового рефрактора снимали с разными экспозициями, подразумевая применение метода “след–масштаб” (Пэску, 1980; Киселева и др., 2008). Поэтому далеко не все пластинки содержат изображения достаточного числа опорных звезд.
Первый опыт оцифровки данных пластинок и их обработка в системе каталогов Tycho-2, UCAC2/3 описан в работах Е.А. Рощиной и Т.П. Киселевой (Киселева и др., 2015; 2016). В этих исследованиях анализируются наблюдения, выполненные в 1972–1974 гг. Сравнительно высокое качество результатов (Киселева и др., 2016) и появление новой опорной системы побудило нас продолжить оцифровку и повторную редукцию пулковских астронегативов, полученных по данной программе исследований. Астронегативы, использованные в представленной работе, были получены в период с 1972 по 1982 гг. посредством 26-дюймового рефрактора Пулковской обсерватории. Достаточное количество опорных звезд представлено на 169 пластинках. Для контроля точности измерений в данной работе использовано 25 астронегативов, полученных на Нормальном астрографе с октября 1972 г. по апрель 1973 г.
АНАЛИЗ ОЦИФРОВАННЫХ АСТРОНЕГАТИВОВ
MDD – Пулковская система для быстрой оцифровки астронегативов
MDD (Mobile Digitizing Device – мобильная система оцифровки) создавалась в Пулковской обсерватории с целью многократно повысить скорость сканирования астронегативов при сохранении точности определения координат на уровне 1 мкм. Логика построения MDD вытекает из истории становления современных подходов к оцифровке старого астрономического материала.
С появлением доступных и относительно качественных планшетных сканеров в 1990-е годы в разных обсерваториях предпринимались попытки вести оцифровку астронегативов. Однако нерегулярность движения линейки сканера (невоспроизводимость картины искажений от скана к скану) предопределила трудности астрометрической обработки такого материала (Бережной, 2013). Специализированные комплексы для оцифровки оказались штучным товаром. Они дают высокую точность пространственной привязки цифровых кадров (на уровне 10 нм). Но массовая доставка фотопластинок в институты, располагающие подобными машинами, чаще всего затруднена. В Пулковской обсерватории сделана ставка на комбинацию возможностей лучших машин для оцифровки и измерения астронегативов (ROB-digitizer и NAROO) и относительной простоты массовой съемки пластинок с помощью современных камер.
Система MDD представляет собой неподвижный стол (плоскопараллельная пластина), над которым закреплена камера с качественным объективом (Canon EF 100 mm f/2.8L Macro IS USM). Вся пластинка помещается в рабочее поле, и производится съемка на просвет. В итоге получается скан с масштабом 0.026 мм/пиксель. При фокусном расстоянии Нормального астрографа это дает около 1.6 угл. с/пиксель, а для 26-дюймового рефрактора примерно 0.5 угл. с/пиксель, что при пулковских атмосферных условиях и использованных экспозициях обеспечивает приемлемое качество оцифрованных изображений звездообразных объектов. Наглядное представление об этом дает рис. 1.
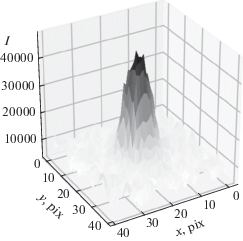
Рис. 1.
Типичное распределение интенсивностей для изображения звезды 11m на сканах пулковских астронегативов, используемых в данной работе. Характерная величина FWHM ≈ 10 пикселей ≈ 5 угл. с (в масштабе 26-дюймового рефрактора).
Совершенно естественно, что прямая астрометрическая редукция полученных снимков не дает хороших результатов, так как объективы, доступные для такого рода работ, имеют сложную картину геометрических искажений. Их учет возможен благодаря высокой стабильности системы “объектив–стол” в течение съемки серии из нескольких десятков пластинок. Для калибровки оказалось возможным использовать высокоточный шаблон с регулярными звездообразными метками, оцифрованный и измеренный с помощью ROB-Digitizer (de Cuyper и др., 2011). Для уплотнения сетки шаблона использовалась пластинка со звездным скоплением, измеренная с помощью машины NAROO. Эта аббревиатура расшифровывается как New Astrometric Reduction of Old Observations (новая астрометрическая редукция старых наблюдений). NAROO это целый научный проект, реализуемый Парижской обсерваторией и IMCCE, в рамках которого создан измерительный комплекс нового поколения. Описание установки и первых научных результатов, полученных с ее помощью, можно найти в серии публикаций (например, Arlot, Robert, 2019). Главная идея, отличающая NAROO от ROB-digitizer – изготовление сложного объектива, дающего геометрические искажения, меньшие, чем ошибки позиционирования каретки с фотопластинкой. Это в значительной мере избавляет результаты от систематических ошибок.
Таким образом, используя измерения шаблонов и пластинок со звездными скоплениями, выполненные на современных машинах для оцифровки, несложно было вычислить постоянные перехода от пиксельных координат текущей пластинки к положениям в системе шаблона. Анализ показал, что такой подход гарантирует точность определения измеренных координат на уровне 1 мкм.
Сканы астронегативов представлены в виде стандартных для астрономии fits-файлов, в блок метаданных которых занесена вся необходимая информация, включая wcs-параметры (постоянные для перехода от пиксельных координат к экваториальным и обратно). Как правило, во время наблюдений на одну пластинку делалось несколько экспозиций, поэтому в файл включено соответствующее количество HDU (модулей “описание–данные”). Для дальнейшего удобства каждый HDU содержит эфемеридные положения спутников Сатурна и добавлен HDU с данными каталога Gaia DR2. Полностью избежать “ручной работы” на этапе первичной обработки сканов оказалось невозможным по двум причинам: во-первых, необходимо было ввести в файлы метаданные из журналов наблюдений (это весьма долгая и утомительная процедура), во-вторых, нередко встречались ошибки распознавания звездных изображений и отождествления звездных полей из-за многочисленных артефактов фотоэмульсии.
Не для всех сканов удалось провести стандартную астрометрическую редукцию с общей системой опорных звезд. Всем необходимым условиям удовлетворили 169 сканов астронегативов, полученных на 26-дюймовом рефракторе, и 25 тестовых сканов пластинок Нормального астрографа. Благодаря описанной выше предварительной обработке сканов появилась возможность автоматизации процесса астрометрической редукции, что обеспечило быстрый и многократный анализ всего материала. При таком подходе удалось за короткое время подобрать оптимальные параметры аппроксимации изображений и учета градиентов фона. В этом (кроме количества пластинок) состоят преимущества данной работы перед выполненной ранее (Киселева и др., 2015).
Анализ изображений звездообразных объектов на оцифрованных астронегативах
Благодаря наличию wcs-параметров в HDU соответствующих файлов несложно выделить область оцифрованного астронегатива, в которой располагается изображение звезды или спутника Сатурна. Поэтому мы не испытывали сложностей с формированием массивов, отвечающих изображениям звезд и спутников, для дальнейшей аппроксимации и измерения положений их фотоцентров.
Ожидаемая трудность, с которой сталкиваются почти все специалисты, занимающиеся определением положений спутников планет на основе ПЗС-наблюдений или оцифрованных астронегативов, связана с проблемой учета ореола от яркой планеты, который искажает положения спутников и опорных звезд, расположенных сравнительно близко от планеты (Khovritchev, 2009). При анализе ПЗС-кадров с изображениями спутников Юпитера (Нарижная и др., 2019) это достигалось путем аппроксимации фона с помощью модели
Как видно из рис. 2, при наличии нескольких снимков на одной пластинке ореолы от разных экспозиций накладываются друг на друга, создавая значительные трудности при учете фона. По этой причине мы предпочли использовать кратномасштабную медианную фильтрацию участка изображения (Прэтт, 1982), размером 10 · FWHM × × 10 · FWHM, центрированного относительно изображения объекта. Рис. 3 свидетельствует о том, что этот способ позволяет корректно учесть влияние градиента фона, обусловленного засветкой от планеты.
Рис. 2.
Фрагмент типичного астронегатива с изображениями Сатурна и его главных спутников (пластинка 6128, 19 февраля 1973 г.).
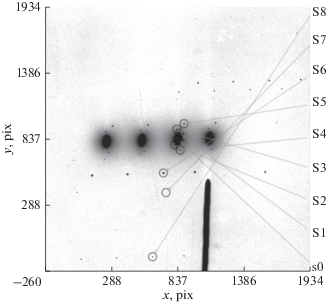
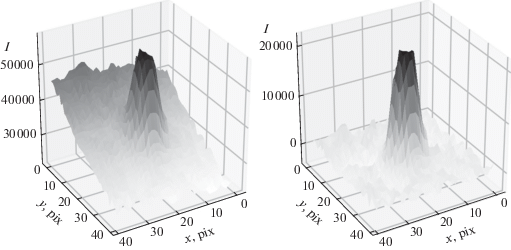
Рис. 3.
Учет влияния засветки от Сатурна на изображение спутника S03 Тефия. Слева показано распределение интенсивностей до учета ореола, справа – после коррекции (вычитания ореола).
В дальнейшем применялся алгоритм шейплет-разложения изображения звездообразного объекта (Massey, Refregier, 2005). Коэффициенты данного разложения однозначно определяют пиксельные координаты фотоцентра изображения. Подробно применение этого подхода к анализу изображений спутников планет продемонстрировано в серии работ по определению координат галилеевых спутников Юпитера (Нарижная и др., 2018).
От пиксельных координат к экваториальным
Как уже отмечалось в первой части данного раздела, объектив, используемый при оцифровке, обладает остаточными аберрациями. Поэтому была необходима соответствующая коррекция. Каждая серия измерений начиналась и заканчивалась оцифровкой шаблона – специального негатива, на котором фотографическим способом нанесены регулярно расположенные метки. Свойства изображений меток соответствуют свойствам изображений реальных звезд. Шаблоны ранее измерялись с помощью машины ROB-digitizer (Бережной, 2013).
Уравнения связи измеренных координат меток u, v (в миллиметрах) с их пиксельными координатами x, y можно представить в виде:
Постоянные ai,j, bi,j позволяли преобразовать пиксельные координаты в системе оцифрованного астронегатива к “системе шаблона”, свободного от систематических ошибок на уровне точности 1 мкм.
На каждой пластинке присутствуют изображения, относящиеся к серии экспозиций. Совершенно естественно было пытаться получить положения спутников, относящиеся к разным экспозициям, в единой системе опорных звезд. Поэтому проводился отбор звезд поля с условием, чтобы сходимость положений этих звезд в системе центральной экспозиции была лучше 2 мкм. В дальнейшем выполнялась астрометрическая редукция методом шести постоянных. В итоге, для центральных моментов каждой экспозиции вычислялись экваториальные и относительные (“спутник–спутник”) координаты главных спутников Сатурна, которые являются основным результатом данной работы.
В качестве опорного каталога использовался Gaia DR2. Положения опорных звезд для центральных моментов экспозиций вычислялись с учетом собственных движений (точность экваториальных координат опорных звезд оказалась лучше 1 угл. мс). Продолжительность экспозиций лежит в пределах от 30 с до 3 мин. Поэтому самые слабые звезды, изображения которых надежно измеряются на оцифрованных астронегативах, имеют блеск около 12.5m – 13.0m. В начале 1970-х Сатурн пересекал область вблизи Млечного Пути, поэтому число опорных звезд на снимках достигало сотни. К началу 1980-х количество опорных звезд снизилось до десяти и даже меньше. Величины ошибок единицы веса в большинстве случаев составляют 40–80 угл. мс.
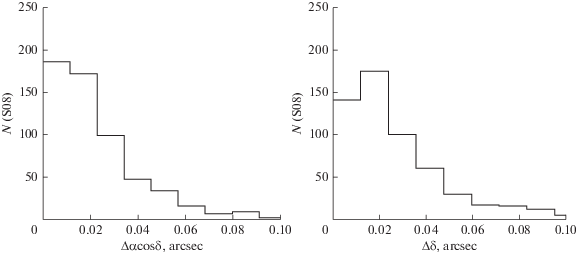
Как видно из описания процедуры получения экваториальных координат главных спутников Сатурна, алгоритм включает в себя несколько стадий, качество реализации которых контролируется на основе анализа внутренней сходимости результатов. Точность измерений положений звезд характеризуется величинами ошибок единицы веса. Из предыдущего абзаца следует, что значения данных величин соответствуют ожиданиям для фотографического материала. Для контроля качества измерений каждая пластинка оцифровывалась 4 раза при последовательных поворотах на 90°. Далее экваториальные координаты для соответствующего спутника и центрального момента экспозиции сравнивались между собой. Сходимость результатов при разных положениях пластинки на столе MDD дает представление о внутренней точности финальных координат спутников. Данные рис. 4 свидетельствуют о том, что по всему материалу для подавляющего большинства измерений стандартная ошибка в среднем близка к 20 угл. мс, что отвечает точности измерений 1 мкм.
Рис. 4.
Гистограммы разностей координат Δαcosδ и Δδ для Япета (S08) для одних и тех же экспозиций, но полученных при разных положениях пластинки относительно стола MDD (N – число разностей).
Финальный результат представляет собой таблицу в формате NSDB11. Мы приводим экваториальные координаты, вычисляя средние значения по всем измерениям для центральных моментов времени каждой экспозиции. Файлы доступны на сайте ЛАЗА ГАО РАН puldb.ru22.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Анализ полученных координат спутников Сатурна имеет целью оценить качество рядов наблюдений, выяснить насколько они полезны для дальнейшего применения в контексте совершенствования теорий движения и выявления тонких динамических эффектов.
В первую очередь целесообразно вычислить величины О–С (выполнить сравнение с самой совершенной на текущий момент эфемеридой). Полученные экваториальные координаты сопоставлялись с эфемеридами (комбинация теорий EPM2017 и S01–S08 Lainey и др. (2017)) с помощью сервиса MULTI-SAT (Emel’yanov, Arlot, 2008; http://nsdb.imcce.fr/multisat/nssephmr.htm). Табл. 1 содержит сводную информацию о результатах сравнения. В этой таблице для каждого спутника указаны число наблюдений (N), средние значения O–С по всему материалу ((O–C)αcosδ и (О–С)δ) и величины ошибок одного наблюдения (σαcos δ и σδ). Величина ошибки одного наблюдения вычислялась согласно соотношению:
Как видно из табл. 1, количество наблюдений (N) растет по мере увеличения расстояния от Сатурна до спутника (оно увеличивается вместе с номером спутника), так как более далекий спутник проводит большее время на достаточном угловом удалении от планеты, чем обеспечиваются условия, необходимые для качественных измерений. Исключение составляет S07 Гиперион – это сравнительно слабый спутник и нужны исключительные условия наблюдений и качество фотоматериала, чтобы адекватно измерить его изображение. Логично, что и величины ошибок координат одного наблюдения для этого спутника значимо больше, чем для других. В целом можно заключить, что средние значения О–С по обеим координатам обычно меньше 20 угл. мс при ошибке одного наблюдения порядка 100 угл. мс для всего материала.
Таблица 1.
Средние значения О–С и ошибки одного наблюдения для экваториальных координат главных спутников Сатурна по результатам фотографических наблюдений, выполненных с помощью пулковского 26-дюймового рефрактора в период с 1972 по 1982 гг.
| Спутник | N | (O–C)αcosδ | (O–C)δ | σαcosδ | σδ |
|---|---|---|---|---|---|
| Угл. с | |||||
| S01 | 39 | 0.012 | –0.019 | 0.148 | 0.128 |
| S02 | 283 | 0.003 | 0.017 | 0.128 | 0.108 |
| S03 | 406 | 0.009 | 0.013 | 0.111 | 0.099 |
| S04 | 500 | 0.007 | 0.011 | 0.092 | 0.099 |
| S05 | 527 | –0.003 | 0.021 | 0.089 | 0.089 |
| S06 | 568 | –0.005 | 0.009 | 0.094 | 0.095 |
| S07 | 102 | 0.001 | 0.013 | 0.178 | 0.137 |
| S08 | 582 | –0.003 | 0.004 | 0.090 | 0.082 |
СОВМЕСТНЫЙ АНАЛИЗ РЕЗУЛЬТАТОВ, ПОЛУЧЕННЫХ С ПОМОЩЬЮ НОРМАЛЬНОГО АСТРОГРАФА И 26-ДЮЙМОВОГО РЕФРАКТОРА
Как было указано выше, основную часть результатов представляют положения спутников, полученные с помощью 26-дюймового рефрактора. Мы с осторожностью отнеслись к необходимости оцифровки аналогичного ряда наблюдений Нормального астрографа, которые охватывают несколько сезонов. Для сравнения и принятия решения относительно целесообразности дальнейшей оцифровки пластинок данного инструмента обработано только 25 из них, снятых в период с октября 1972 г. по апрель 1973 г.
Фокусное расстояние Нормального астрографа примерно втрое меньше, чем у 26-дюймового рефрактора. Следовательно, при той же точности измерений экваториальные и относительные координаты спутников будут определяться с меньшей точностью – примерно 60 угл. мс по внутренней сходимости. Правда Нормальный астрограф обеспечивает большее рабочее поле и, соответственно, больше опорных звезд, что повышает качество привязки к опорному каталогу.
Прямое сравнение О–С спутников Сатурна, полученных с помощью двух инструментов в близкие моменты времени, дает возможность оценить, насколько различаются результаты наблюдений, являются ли тренды в поведении О–С следствием особенностей телескопов. На рис. 5 представлен пример хода разностей О–С для относительных координат S06–S08 по прямому восхождению. Нетрудно видеть, что вариации О–С со временем примерно одинаковы для обоих инструментов. Это убеждает в том, что стоит продолжить оцифровку всех доступных пластинок Нормального астрографа, содержащих спутники планет, так как ряд наблюдений на этом инструменте иногда плотнее, чем на 26-дюймовом рефракторе. Кроме того, несмотря на менее высокую точность результатов, получаемых с помощью Нормального астрографа, появится возможность объединить ряды и повысить шансы на выявление систематических трендов в О–С, обусловленных несовершенством эфемерид.
ПРИМЕНИМОСТЬ ПОЛУЧЕННЫХ РЯДОВ НАБЛЮДЕНИЙ ДЛЯ ДИНАМИЧЕСКИХ ИССЛЕДОВАНИЙ
Вопрос о наличии в представленных рядах наблюдений информации, полезной для изучения динамики спутников Сатурна, рационально решать посредством изучения поведения О–С со временем. В нашем случае интервал наблюдений достаточно большой – почти 10 лет наблюдений. С точки зрения построения эфемерид экваториальные координаты спутников есть результат объединения численной теории движения самой планеты с моделью движения спутников. Поэтому для нас наиболее интересно анализировать поведение О–С не для экваториальных координат, а для относительных положений. Это позволяет исключить эффекты, обусловленные несовершенством планетной теории.
В качестве примера рассмотрим вариации О–С для пары спутников Титан–Япет (S06–S08), показанные на рис. 6. На этих графиках показаны средние значения для О–С за соответствующий сезон наблюдений. Левая часть данного рисунка дает представление о вариациях О–С обсуждаемого пулковского ряда, правая – то же самое для большого ряда фотографических наблюдений главных спутников Сатурна, полученного в период с 1974 по 1998 гг. с помощью 26-дюймового рефрактора USNO. Эти пластинки были оцифрованы в Королевской обсерватории Бельгии с помощью машины ROB-digitizer. Результаты переизмерения данных астронегативов и привязки к системе каталога UCAC4 представлены в статье Robert (2016). Совершенно естественно было выполнить сравнение нашего ряда и данных из цитированной работы.
Рис. 6.
Поведение О–С по склонению для разностей S06–S08 со временем. Слева обсуждаемый пулковский ряд, справа – О–С, полученные для ряда наблюдений Вашингтонской обсерватории (USNO), представленного в работе Robert и др., 2016.
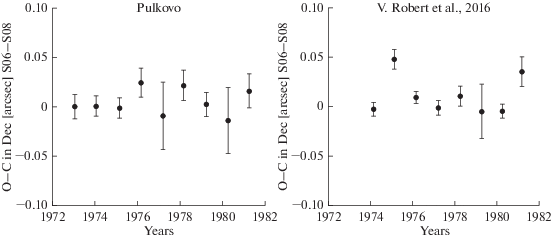
Рис. 6 показывает, что внутренняя точность вашингтонского ряда примерно в 1.5 раза выше пулковского. Это обусловлено в первую очередь тем, что MDD заметно уступает ROB-digitizer по качеству оцифровки. Этого следовало ожидать. ROB-digitizer – машина, специально изготовленная для оцифровки и прецизионного измерения астронегативов. Пулковская система MDD использует шаблоны, оцифрованные ROB-digitizer, но основное устройство – обычная промышленная камера с объективом среднего качества.
Все вариации О–С для обоих рядов не превосходят 50 угл. мс по модулю. Среднее значение О–С для пулковского ряда составило 5 ± 13 угл. мс, для вашингтонского: 11 ± 19 угл. мс. Разности обсуждаемых рядов представлены на левом графике рис. 7 (среднее значение: –5 ± 20 угл. мс). С учетом оценок точности можно заключить, что почти для всех моментов времени пулковский и вашингтонский ряды согласуются между собой в пределах стандартной ошибки.
Рис. 7.
Разности пулковского и вашингтонского рядов наблюдений (слева) на фоне различия двух вариантов моделей движения (справа) для разностей склонений спутников S06–S08. Использовались модели Lainey (2012) и Lainey и др. (2017) (ссылки на модели даны согласно сервису MULTI-SAT).
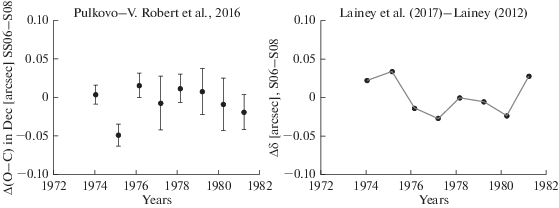
Правая половина рис. 7 дает пример сравнения двух свежих теорий движения главных спутников Сатурна (на сервере MULTI-SAT они представлены как Lainey (2012) и Lainey и др. (2017)). Вариации разностей теорий лежат в пределах ±50 угл. мс. Характер изменения разностей год от года аналогичен соответствующим вариациям, присущим разностям пулковского и вашингтонского рядов. То есть неопределенности в моделях движения для рассматриваемого десятилетия могут достигать десятков миллисекунд. Это можно интерпретировать как свидетельство в пользу высокой информативности обсуждаемых рядов наблюдений для дальнейшего совершенствования моделей движения главных спутников Сатурна.
ВЫВОДЫ
В ходе данной работы из всех оцифрованных астронегативов с изображениями главных спутников Сатурна, снятых с помощью 26-дюймового рефрактора Пулковской обсерватории в период с 1972 по 1982 гг., было измерено 169. Проведена астрометрическая привязка положений спутников к системе, заданной звездами каталога Gaia DR2. В общей сложности это 3007 отдельных положений спутников Сатурна.
Серьезное внимание уделено процедуре учета влияния ореола на координаты спутников, что позволило корректно определить положения S01–S04, изображения которых чаще всего погружены в ореол.
Внутренняя точность измерений спутников составляет 20 угл. мс (или 1 мкм на астронегативе). Тестовая оцифровка пластинок, полученных по той же программе с помощью Нормального астрографа, показала отсутствие значимых систематических разностей, обусловленных различием систем инструментов – 26-дюймового рефрактора и Нормального астрографа.
Выполнено сравнение пулковского ряда наблюдений спутников Сатурна с эфемеридой (Lainey и др., 2017). Показано, что вариации О–С редко достигают 50 угл. мс по модулю и в среднем составляют 5 ± 13 угл. мс для пары S06–S08. Сравнение с аналогичным рядом наблюдений, полученном в USNO, демонстрирует более высокую плотность пулковского ряда (в период 1972–1982 гг. пулковских наблюдений почти в 1.5 раза больше). Вариации разностей рядов и разностей эфемерид (Lainey, 2012; Lainey и др., 2017) для рассматриваемого периода имеют сходные амплитуды. Поэтому можно говорить о том, что пулковский ряд будет полезен для совершенствования эфемерид главных спутников Сатурна.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-02-00843 А.
Список литературы
Бережной А.А. Новая редукция оцифрованных фотографических пластинок с избранными астероидами, полученных на нормальном астрографе пулковской обсерватории в период с 1948 по 1990 гг. // Астрон. вестн. 2013. Т. 47. № 3. С. 220–229. (Berezhnoi A.A. A new reduction of digitized photographic plates with selected asteroids obtained with the normal astrograph of the Pulkovo Observatory from 1948 to 1990 // Sol. Syst. Res. 2013. V. 47. Iss. 3. Р. 203–212.)
Киселева Т.П., Киселев А.А., Калиниченко О.А., Васильева Т.А., Ховричева М.Л. Результаты астрометрических наблюдений галилеевых спутников Юпитера в Пулковсвкой обсерватории в 1986–2005 гг. // Астрон. вестн. 2008. Т. 42. № 5. С. 444–463. (Kiseleva T.P., Kiselev A.A., Kalinichenko O.A., Vasil’eva T.A., Khovricheva M.L. Results of Astrometric Observations of Jupiter’s Galilean Satellites at the Pulkovo Observatory from 1986 to 2005. // Sol. Syst. Res. 2008. V. 42. Iss. 5. Р. 414–433.)
Киселева Т.П., Васильева Т.А., Измайлов И.С., Рощина Е.А. Новая астрометрическая редукция старых фотографических наблюдений спутников Сатурна на основе оцифровки астронегативов // Астрон. вестн. 2015. Т. 49. № 1. С. 76–78. (Kiseleva T.P., Vasil’eva T.A., Izmailov I.S., Roshchina E.A. New astrometric reduction of old photographic observations of Saturn’s moons based on digitizing of astronegatives // Sol. Syst. Res. 2015. V. 49. Iss. 1. Р. 72–74.)
Киселева Т.П., Васильева Т.А., Рощина Е.А., Измайлов И.С. Новая астрометрическая редукция старых фотографических наблюдений спутников Сатурна на основе оцифровки астронегативов // Астрон. вестн. 2016. Т. 50. № 6. С. 425–430. (Kiseleva T.P., Vasil’eva T.A., Izmailov I.S., Roshchina E.A. Astrometric studies of the results of a new reduction of old photographic observations of the Saturnian System based on the comparison with the modern theories of satellite motion // Sol. Syst. Res. 2016. V. 50. Iss. 6. Р. 402–407.)
Нарижная Н.В., Ховричев М.Ю., Апетян А.А., Бикулова Д.А., Ершова А.П., Баляев И.А., Куликова А.М., Оськина К.И., Максимова Л.А. Астрометрические наблюдения галилеевых спутников Юпитера на пулковском Нормальном астрографе в 2016–2017 гг. // Астрон. вестн. 2018. Т. 52. № 4. С. 316–323. (Narizhnaya N.V., Khovrichev M.Yu., Apetyan A.A., Bikulova D.A., Ershova A.P., Balyaev I.A., Kulikova A.M., O’skina K.I., Maksimova L.A. Astrometric Observations of the Galilean Moons of Jupiter at the Pulkovo Normal Astrograph in 2016–2017 // Sol. Syst. Res. 2018. V. 52. Iss. 4. Р. 312–319.)
Нарижная Н.В., Ховричев М.Ю., Бикулова Д.А. Наблюдения галилеевых спутников Юпитера в 2018 г. в Пулкове // Астрон. вестн. 2019. Т. 53. № 5. С. 386–393. (Narizhnaya N.V., Khovrichev M.Yu., Bikulova D.A. Observations of the Galilean Moons of Jupiter at Pulkovo in 2018 // Sol. Syst. Res. 2019. V. 53. Iss. 5. Р. 363–375.)
Прэтт У. Цифровая обработка изображений. М.: Мир, 1982. (Pratt W. Digital Image Processing: PIKS Inside 3rd John Wiley & Sons, Inc. New York, N.Y., USA, 2001.)
Пэску Д. Методы астрономических наблюдений // Спутники планет / Ред. Бернс Дж. М.: Мир, 1980. С. 75–105. (Pascu D. Methods of Astrometric Observations // Planetary Satellites / Ed. Burns J. Tucson: Univ. Arizona Press, 1976.)
Arlot J.-E., Robert V. New tools for reducing old observations: Project NAROO // EPSC-DPS Joint Meeting 2019, held 15–20 September 2019 in Geneva, Switzerland, id. EPSC-DPS2019-1961.
de Cuyper J.-P., de Decker G., Winter L., Zacharias N. The Archive and Digitizer Facility at the ROB // Astronomical Data Analysis Software and Systems XX. ASP Conference Proceedings, Vol. 442, proceedings of a Conference held at Seaport World Trade Center, Boston, Massachusetts, USA on 7–11 November 2010. Edited by Ian N. Evans, Alberto Accomazzi, Douglas J. Mink, and Arnold H. Rots. San Francisco: Astronomical Society of the Pacific, 2011. P. 301.
Emel’yanov N.V., Arlot J.-E. The natural satellites ephemerides facility MULTI-SAT // Astron. and Astrophys. 2008. V. 487. P. 759–765.
Emelyanov N.V. Influence of tides in viscoelastic bodies of planet and satellite on the satellite’s orbital motion // Mon. Notic. Roy. Astron. Soc. 2018. V. 479. Iss. 1. P. 1278–1286.
Gaia Collaboration; Brown A.G.A., Vallenari A., Prusti T., de Bruijne J.H.J., Babusiaux C., Bailer-Jones C.A.L., Biermann M., Evans D.W., Eyer L., Jansen F., Jordi C., Klioner S.A., Lammers U., Lindegren L., Luri X., Mignard F., Panem C., Pourbaix D., Randich S. Gaia Data Release 2. Summary of the contents and survey properties // Astron. and Astrophys. 2018. V. 616. A1. P. 1–22.
Khovritchev M.Yu. Astrometric observations of the Uranian satellites with the Faulkes Telescope North in 2007 September // Mon. Notic. Roy. Astron. Soc. 2009. V. 393. Iss. 4. P. 1353–1358.
Lainey V., Arlot J.-E., Karatekin Ö., van Hoolst T. Strong tidal dissipation in Io and Jupiter from astrometric observations // Nature. 2009. V. 459. Iss. 7249. P. 957–959.
Massey R., Refregier A. Polar Shapelets // Mon. Notic. Roy. Astron. Soc. 2005. V. 363. Iss. 1. P. 197–210.
Lainey V., Karatekin Ö., Desmars J., Charnoz S., Arlot J.-E., Emelyanov N., Le Poncin-Lafitte Ch., Mathis S., Remus Franзoise, Tobie Gabriel, Zahn Jean-Paul. Strong Tidal Dissipation in Saturn and Constraints on Enceladus’ Thermal State from Astrometry // Astrophys. J. 2012. V. 752. Iss. 1. article id. 14. P. 19.
Lainey V., Jacobson R.A., Tajeddine R., Cooper N.J., Murray C., Robert V., Tobie G., Guillot T., Mathis S., Remus F., Desmars J., Arlot J.-E., De Cuyper J.-P., Dehant V., Pascu D., Thuillot W., Le Poncin-Lafitte Ch., Zahn J.-P. New constraints on Saturn’s interior from Cassini astrometric data // Icarus. 2017. V. 281. P. 286–296.
Robert V., Pascu D., Lainey V., Arlot J.-E., De Cuyper J.-P., Dehant V., Thuillot W. New astrometric measurement and reduction of USNO photographic observations of the main Saturnian satellites: 1974–1998 // Astron. and Astrophys. 2016. V. 596. A37. P. 1–10.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник



