Астрономический вестник, 2020, T. 54, № 5, стр. 446-457

ВВЕДЕНИЕ

Как теперь стало понятно, статистическая механика Больцмана–Гиббса и стандартная термодинамика не являются вполне универсальными теориями, поскольку они имеют ограниченные области применимости. В качестве примера можно привести невозможность в рамках статистики БГ объяснить спектр космических лучей – одной из наиболее важных систем релятивистских частиц.

В физике и в других естественных науках, использующих методы статистической механики, известны многочисленные примеры сложных (аномальных) систем, которым присущи эффекты сильного дальнодействия, нелокальные корреляции между отдельными элементами системы (помнящей свое прошлое), фрактальный характер фазового пространства, немарковское поведение. Сложная пространственно-временная структура подобных систем приводит к нарушению принципа аддитивности для таких важнейших термодинамических характеристик, как энтропия или внутренняя энергия.

В связи с этим, исследования в области механики неэкстенсивных (неаддитивных) систем стали в последнее время предметом значительного интереса, что объясняется как новизной возникающих здесь общетеоретических проблем, так и важностью практических приложений. Начало систематического изучения в этом направлении связано с работой К. Тсаллиса (Tsallis, 1988), в которой был введен функционал энтропии ${{{\text{S}}}_{q}}(p)$ := ${\text{k}}{{(q - 1)}^{{ - 1}}}\left[ {1 - \int {{{p}^{q}}d\Gamma {\kern 1pt} '} } \right],$ зависящей от некоторого действительного числа $q$ (так называемого параметра деформации) и обладающей неаддитивностью для совокупности независимых аномальных систем. Важно, что в пределе слабой связи $q \to 1$ энтропия Тсаллиса переходит в энтропию БГ. Наиболее существенным преимуществом, основанной на энтропии Тсаллиса¹¹ статистической механики, по сравнению со статистикой БГ является то, что она приводит к асимптотическому степенному закону распределения вероятностей, который отличен от экспоненциального поведения, порожденного классическим распределением Гиббса.

Неэкстенсивная статистика, в настоящее время интенсивно развивается. Возникают многочисленные новые математические проблемы, требующие своего решения. В научной литературе доступны многочисленные коллекции миниобзоров (см., например, Tsallis, 1999; Abe, Okamoto, 2001; Grigolini и др., 2002; Kaniadakis и др., 2002, 2006; Kaniadakis, Lissia, 2004; Gell-Mann, Tsallis, 2004; Herrmann и др., 2004; Колесниченко, 2019). Эта статистика успешно применяется ко многим природным системам, в частности, к ранней вселенной (Pessah и др., 2001), к космической плазме (Lima и др., 2000), к космологическим проблемам (к трехмерной гравитационной проблеме N-тел), к астрофизическим проблемам (например, при толковании черных дыр, суперструн, темной материи (Leubner, 2005)) и так далее. Моделированию Бозе-газа и чернотельному излучению в рамках неэкстенсивной статистики также посвящено большое число публикаций (см., например, Tsallis и др., 1995; Plastino и др., 1995; Tirnakli и др., 1997; Lenzi, Mendes, 1998; Wang, Le Méhauté, 1998; Wang и др., 1998; Büyükkilic., Demirhan, 2000; Anchrordoqui, Torres, 2001; Martinez и др., 2001, 2002; Chamati и др., 2006; Zaripov, 2009; Rovenchak, 2018; Ma и др., 2019; Kolesniсhenko, 2020).

Тем не менее, в настоящей работе предлагается вновь вернуться к обсуждению в рамках формализма Тсаллиса механизма чернотельного излучения применительно к задачам космологии. Исходным основанием подобного рассмотрения является утверждение, согласно которому существующее космическое фоновое излучение (находящееся по предположению в тепловом равновесии) может несколько отличаться от классического закона излучения черного тела Планка из-за влияния дальнодействующего гравитационного воздействия на больших расстояниях (Mather и др., 1994). Это влияние может быть отражением того отдаленного во времени факта, когда материя и свет были сильно связаны между собой, или же оно является результатом еще более изощренных природных явлений (Sistema, Vucetich, 2005).

Правомерность нового обсуждения данной проблемы, по мнению автора статьи, связана со следующим обстоятельством. В статистической механике Тсаллиса возможно осреднение микроскопических физических величин с помощью трех распределений: $p({\mathbf{r}}),$ ${{p}^{q}}({\mathbf{r}}),$ ${{{{p}^{q}}({\mathbf{r}})} \mathord{\left/ {\vphantom {{{{p}^{q}}({\mathbf{r}})} {\int {{{p}^{q}}({\mathbf{r}})} d\Gamma {\kern 1pt} '}}} \right. \kern-0em} {\int {{{p}^{q}}({\mathbf{r}})} d\Gamma {\kern 1pt} '}}.$ Первое осреднение соответствует первоначальной статистике Тсаллиса (Tsallis, 1988), второе (ненормированное) осреднение – статистике Курадо–Тсаллиса (Curado, Tsallis, 1991; Зарипов, 2002; Колесниченко, 2018), третье осреднение – статистике Тсаллиса–Мендеса–Пластино (Tsallis и др., 1998). Эти способы осреднения, каждый из которых имеет, вообще говоря, свои преимущества и недостатки, предопределяют совершенно разные $q$-термодинамики. По этой причине вопрос об использовании того или иного способа осреднения в физических приложениях носит принципиальный характер, поскольку различия в определении средних значений могут оказаться существенными при обработке экспериментальных данных.

Вместе с тем, получаемые при этом существенные несоответствия могут быть, по мысли ряда авторов, благополучно устранены путем использования осреднения Тсаллиса–Мендеса–Пластино, когда осреднение производится по так называемому нормированному эскортному распределению вероятности ${{{\text{P}}}_{q}}({\mathbf{r}})$ := ${{{{p}^{q}}} \mathord{\left/ {\vphantom {{{{p}^{q}}} {\int {{{p}^{q}}d\Gamma {\kern 1pt} '} }}} \right. \kern-0em} {\int {{{p}^{q}}d\Gamma {\kern 1pt} '} }}$ (см, например, Tsallis и др., 1998; Tsallis, 1999; Martinez и др., 2000). Однако существует и иная точка зрения (которой автор придерживается в данной работе), согласно которой единственно правильным осреднением является осреднение с ненормированным распределением $p{{({\mathbf{r}})}^{q}},$ используемое в аксиоматическом обосновании рассматриваемой неэкстенсивной статистики (см. Havrda, Charvat, 1967; Daroczy, 1970). Она обуславливается, в частности, и тем, что только распределение $p{{({\mathbf{r}})}^{q}}$ не приводит к переопределению понятия температуры неаддитивной $q$-системы, которая в этой статистике является интенсивным параметром (абсолютной температурой $T$), а не функционалом (так называемой физической температурой ${{T}_{{ph}}},$ зависящей от энтропии ${{{\text{S}}}_{q}}$), как это происходит при иных определениях взвешенного среднего. Отметим, что это и некоторые другие убедительные соображения в пользу осреднения Курадо–Тсаллиса приведены в монографии (Зарипов, 2002).

Возвращаясь к своевременности появления данной работы, заметим, что во многих цитируемых выше публикациях по заявленной тематике авторы (см., например, Tirnakli и др., 1997; Wang и др., 1998; Rovenchak, 2018) в качестве отправной точки использовали обобщенное распределение Планка собственных частот излучения в виде: ${{\bar {n}}_{j}}(T,q)$ = ${1 \mathord{\left/ {\vphantom {1 {\left\{ {{{{\left[ {1 + (q - 1)\tfrac{{\hbar {{\omega }_{j}}}}{{\operatorname{k} T}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 {(1 - q)}}} \right. \kern-0em} {(1 - q)}}}}} - 1} \right\}}}} \right. \kern-0em} {\left\{ {{{{\left[ {1 + (q - 1)\tfrac{{\hbar {{\omega }_{j}}}}{{\operatorname{k} T}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 {(1 - q)}}} \right. \kern-0em} {(1 - q)}}}}} - 1} \right\}}}.$ Легко можно убедиться в том, что к этому распределению приводит условие максимальности модифицированной в статистике Тсаллиса энтропии Бозе-газа только при условии, что осреднение физических величин производится с помощью распределения ${{p}^{q}}({\mathbf{r}})$ (Büyükkilic, Demirhan, 2000; Зарипов, 2010). Тем не менее эти авторы в своих работах использовали осреднение с распределением $p({\mathbf{r}}),$ соответствующее оригинальной статистике Тсаллиса. В ряде других публикаций (см., например, Martinez и др., 2002; Ma и др. 2019) за исходное распределение неэкстенсивного фотонного газа принималось обобщенное распределение Планка ${{\bar {n}}_{j}}({{T}_{{ph}}},q)$ с физической температурой ${{T}_{{ph}}},$ что представляется совершенно не практичным, поскольку измерение физической температуры ${{T}_{{ph}}}$ нереально, что связано с ее зависимостью от энтропии системы ${{{\text{S}}}_{q}}.$ В недавней работе автора (Kolesniсhenko, 2020), посвященной рассмотрению Джинсовой неустойчивости протопланетного газового облака с радиацией в рамках неэкстенсивной кинетики Тсаллиса, термодинамика чернотельного излучения использовалась в классической форме.

В связи с высказанными выше критическими соображениями в представленной работе нами с единых позиций кинетики Тсаллиса изложен круг вопросов, связанных с конструированием деформированной термодинамики чернотельного излучения на основе модифицированных энтропии Бозе-газа и дивергенции Брэгмана. При этом при получении всех термодинамических величин систематически использовано осреднение Курадо–Тсаллиса. Проведенное исследование базируется на свойствах негиббсового канонического ансамбля бозонных систем, полученного из принципа Джейнса (Jaynes, 1963) максимума $q$‑энтропии при заданности усредненной внутренней энергии и полного числа частиц бозонного газа. Получены обобщенные выражения для термодинамического потенциала, полной и свободной энергии, энтропии, удельной теплоты, давления и теплоемкости, а также дифференциальные термодинамические уравнения для бозонных газовых систем. Показано, что сохраняются принцип максимума равновесной энтропии Тсаллиса, лежандрова структура теории и H-теорема статистики БГ. Получено статистическое распределение для массивных бозонов, а также обобщение классического закона Планка для черного излучения в рамках статистики Тсаллиса. Показано, что все характеристики неэкстенсивного Бозе-газа восстанавливают свои стандартные выражения в пределе $q \to 1.$

Результаты работы могут быть использованы, в частности, в качестве теоретического обоснования экспериментальных исследований чернотельной радиации, таких как исследование космического микроволнового фонового излучения.

ЭЛЕМЕНТЫ НЕАДДИТИВНОЙ СТАТИСТИКИ ТСАЛЛИСА

В статистической механике Тсаллиса для непрерывных величин при вероятностной нормировке

для фазовой функции распределения $p({\mathbf{r}})$ (в общем случае эта функция может зависеть от времени $t$ и от внешних параметров $\{ {{a}_{k}}\} $) энтропия Тсаллиса для вещества задается следующим функционалом (Tsallis, 1988):

Здесь и далее везде область интегрирования совпадает со всем 6N-мерным фазовым пространством ${\mathbf{r}}$ := $\left\{ {{{{\mathbf{q}}}_{1}},...,{{{\mathbf{q}}}_{N}};\,\,{{{\mathbf{p}}}_{1}},...,{{{\mathbf{p}}}_{N}}} \right\},$ безразмерный элемент которого записывается в следующей современной форме $d\Gamma {\kern 1pt} '$ := ${{(2\pi \hbar )}^{{ - s}}}d{\mathbf{r}}$ (где $d{\mathbf{r}}$ := $\prod\nolimits_j {d{{{\mathbf{q}}}_{j}}d{{{\mathbf{p}}}_{j}}} ;$ ${\text{k}} \simeq 1.380662$ × ${{10}^{{ - 16}}}\,\,{{{\text{эрг}}} \mathord{\left/ {\vphantom {{{\text{эрг}}} {\text{К}}}} \right. \kern-0em} {\text{К}}}$ – постоянная Больцмана; $\hbar = {h \mathord{\left/ {\vphantom {h {2\pi }}} \right. \kern-0em} {2\pi }};$ $h \simeq 6.626117$ × ${{10}^{{ - 27}}}\,\,{\text{эрг}} \cdot {\text{с}}$ – постоянная Планка). Энтропийный индекс $q$ представляет собой вещественное число, принадлежащее области $q \in {\text{R}}{\text{.}}$ Такая деформированная энтропия позволяет учитывать важную особенность поведения аномальных материальных систем с длинной памятью и/или дальнодействующими силовыми взаимодействиями, при которых вероятность реализации $p({\mathbf{r}})$ больших значений состояний убывает (при $q > 1$) не экспоненциально, а степенным образом.

Можно показать, что в пределе слабой связи энтропия Тсаллиса (2) переходит в классическую формулу для энтропии ${{{\text{S}}}_{{{\text{BG}}}}}$ в статистике Больцмана–Гиббса. Действительно, в пределе $q \to 1$ имеем: ${{p}^{{q - 1}}} = \exp \left\{ {(q - 1)\ln p} \right\}$ → $1 + (q - 1)\ln p,$ и энтропия ${{{\text{S}}}_{q}}$ сводится к ${\text{S}}(p) = \mathop {\lim }\limits_{q \to 1} {{{\text{S}}}_{q}}(p)$ = = $ - {\text{k}}\int {p\ln pd\Gamma {\kern 1pt} '} = {{{\text{S}}}_{{{\text{BG}}}}}.$

Если состояние физической двухкомпонентной системы описывается совместным мультипликативным распределением ${{p}_{{12}}} = {{p}_{1}}{{p}_{2}}$ с ${{p}_{{12}}} = {{p}_{{12}}}({{{\mathbf{r}}}_{1}},{{{\mathbf{r}}}_{2}}),$ ${{p}_{1}} = {{p}_{1}}({{{\mathbf{r}}}_{1}}),$ ${{p}_{2}} = {{p}_{2}}({{{\mathbf{r}}}_{2}}),$ которое может зависеть от времени $t,$ а ${{{\mathbf{r}}}_{1}}$ и ${{{\mathbf{r}}}_{2}}$ относятся к двум независимым $q$-системам, то общая энтропия дается выражением

Соотношение (3) выражает свойство неаддитивности для энтропии совокупной системы в статистике Тсаллиса.

Энтропия Тсаллиса (2) может быть представлена в следующей эквивалентной форме:

при написании которой использовано осреднение с ненормированным распределением ${{p}^{q}}$ (свойственным статистике Курадо–Тсаллиса (Curado, Tsallis, 1991)) для произвольной физической величины ${\text{A}}({\mathbf{r}}),$ а также, так называемый, “деформированный логарифм”

Экстремальное значение энтропии Тсаллиса. Аналог равновесного распределения Гиббса в статистике Курадо–Тсаллиса может быть получен, как и в классическом случае, из экстремума энтропии (2) при выполнении условия сохранения нормировки (1) и заданном значении средней энергии системы

где функция Гамильтона ${\text{H}}({\mathbf{r}})$ задается математической моделью изучаемых физических процессов. В соответствии с теоремой Лагранжа вероятное распределение $p({\mathbf{r}}),$ “экстремизирующее” энтропию Тсаллиса ${{{\text{S}}}_{q}}(p)$ при указанных ограничениях имеет вид (см., например, Колесниченко, 2019): где – обобщенный статистический интеграл, определяемый из условия нормировки (1); множитель Лагранжа $\beta $ (обратная эффективная температура, $\beta = {1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}$) определяется из уравнения, получаемого подстановкой (8) в (7).

Распределение (8) удобно записать в виде, аналогичном классической форме Гиббса

выражая стоящую в (8) степенную функцию ${{[..]}^{{{1 \mathord{\left/ {\vphantom {1 {1 - q}}} \right. \kern-0em} {1 - q}}}}}$ через так называемую экспоненту Тсаллиса, которая определяется следующим образом (Тсаллис, 2009): Здесь выражение, стоящее в квадратных скобках, либо положительно, либо равно нулю, ${{[y]}_{ + }} \equiv \max (y,0).$ Легко проверить, что в пределе $q \to 1$ эта функция принимает стандартный вид: $\mathop {{{{\exp }}_{q}}(x)}\limits_{q \to 1} $ = $\exp (x).$

Используя определения деформированных функций ${{\ln }_{q}}x$ и ${{\exp }_{q}}(x),$ легко можно убедиться в том, что имеют место следующие соотношения:

Далее эти соотношения будут широко использованы.

ЭНТРОПИЯ БОЗЕ-ГАЗА В СТАТИСТИКЕ БОЛЬЦМАНА–ГИББСА

Бозе-газ состоит из бозонов – частиц, имеющих целый спин и подчиняющихся статистике Бозе–Эйнштейна. Бозе создал статистическую механику для газа фотонов, а Эйнштейн развил ее для описания массивных частиц.

Напомним классический вероятностно-статистический способ вычисления энтропии Бозе-газа. С этой целью рассматриваются различные равновероятные группы квантовых состояний $j = 1,2,...,$ которыми может быть реализовано изучаемое макроскопическое состояние ансамбля из ${\text{N}}$ газовых частиц. $6{\text{N}}$-мерное фазовое пространство делится на ${\text{M}}$ ячеек безразмерного объема ${{g}_{j}}: = {{(2\pi \hbar )}^{{ - s}}}(\Delta {{{\mathbf{q}}}_{j}}\Delta {{{\mathbf{p}}}_{j}}),$ который характеризует максимально возможное число микросостояний в $j$-ой ячейке, содержащей ${{n}_{j}}$ Бозе-частиц (здесь $s$ – число степеней свободы элементарной частицы). Далее определяется число всех возможных способов заполнения ${\text{N}} = \sum\nolimits_j {{{n}_{j}}} $ частиц по ${\text{M}}$ ячейкам. Данное число является по определению статистическим весом $\Delta \Gamma ,$ характеризующим вероятность макроскопического состояния системы. Если теперь каждую группу из ${{n}_{j}}$ частиц рассматривать как независимую подсистему и обозначить посредством $\Delta {{\Gamma }_{{{{n}_{j}}}}}$ ее статистический вес, то можно написать: $\Delta \Gamma = \prod\nolimits_j {\Delta {{\Gamma }_{{{{n}_{j}}}}}} .$ В классической статистике энтропия выражается логарифмической мерой статистического веса ${\text{S}}: = \operatorname{k} \ln \Delta \Gamma $ = = $\operatorname{k} \ln \prod\nolimits_j {\Delta {{\Gamma }_{{{{n}_{j}}}}}} .$ В случае статистики Бозе–Эйнштейна в каждом квантовом состоянии может находиться любое число частиц, так что статистический вес $\Delta {{\Gamma }_{{{{n}_{j}}}}}$ есть число всех способов, которыми можно распределить ${{n}_{j}}$ частиц по ${{g}_{j}}$ состояниям. Статистический вес в статистике Бозе имеет вид $\Delta {{\Gamma }_{{{{n}_{j}}}}} = \frac{{({{g}_{j}} + {{n}_{j}} - 1)!}}{{{{n}_{j}}!({{g}_{j}} - 1)!}},$ вытекающий из условия, что в ячейке может находиться любое количество частиц. Логарифмируя это выражение и воспользовавшись для логарифмов всех трех факториалов приближенной формулой Стирлинга $\ln x! = x\ln (x{\text{/}}e),$ найдем:

Если записать эту формулу, используя среднее число ${{\bar {n}}_{j}} = {{{{n}_{j}}} \mathord{\left/ {\vphantom {{{{n}_{j}}} {{{g}_{j}}}}} \right. \kern-0em} {{{g}_{j}}}}$ частиц в каждом из квантовых состояний $j$-й группы, то получим известное выражение для энтропии неравновесного Бозе-газа в классическом случае (см. Ландау, Лифшиц, 1964):

Легко убедиться в том, что условие экстремальности энтропии ${{{\text{S}}}_{{\text{N}}}}$ приводит к дискретному распределению Бозе–Эйнштейна:

Заметим, что величина ${{\bar {n}}_{j}}$ есть дискретный аналог непрерывной функции распределения $D({\mathbf{r}},t)$ по фазовому пространству ${\mathbf{r}}: = \left\{ {{\mathbf{q}};{\mathbf{p}}} \right\}.$ Переход от дискретного распределения ${{\bar {n}}_{j}}$ к плотности распределения Бозе частиц в фазовом пространстве $D({\mathbf{r}},t)$ осуществляется заменой суммирования по $j$ интегрированием по всему фазовому пространству, безразмерный элемент которого определяется соотношением $d\Gamma : = g{{(2\pi \hbar )}^{{ - s}}}d{\mathbf{r}}$ (здесь $g = 2S + 1,$ $S$ – спин частицы; $d{\mathbf{r}}: = d{\mathbf{q}}d{\mathbf{p}} = d{\mathbf{p}}d{{V}_{{\text{N}}}}$)²². В итоге получим следующее выражение для энтропии неравновесного Бозе-газа в случае непрерывных распределений:

Приведем также выражение для так называемой физической информации различия Бозе-газа ${{{\mathbf{I}}}_{{12}}},$ характеризующей переходы между двумя состояниями неравновесной системы. Величина ${{{\mathbf{I}}}_{{12}}},$ являющаяся знакоопределенным функционалом (функцией Ляпунова), определяет меру статистической упорядоченности в микросостояниях системы с распределением ${{\bar {n}}_{{1j}}}$ относительно ее состояния с распределением ${{\bar {n}}_{{2j}}}.$

В дискретном случае эта величина имеет вид (см. Зарипов, 2010):

а для непрерывного аналога имеем:

ЭНТРОПИЯ БОЗЕ-ГАЗА В СТАТИСТИКЕ ТСАЛЛИСА

Обобщенное выражение квантовой энтропии (20) для Бозе-газа, полученное в рамках неэкстенсивной статистики Тсаллиса в работах (Büyükkilic, Demirhan, 1993, 2004), имеет вид:

Энтропию (25) удобно представить в следующих эквивалентных двух формах:

При $q \to 1$ из (26) вытекает выражение (20) для энтропии неравновесного Бозе-газа для аддитивных систем.

Совершая переход от суммирования к интегрированию в формуле (25), получим выражение для квантовой энтропии в случае непрерывных распределений

Здесь $D({\mathbf{r}})$ – плотность распределения квантовых частиц в фазовом пространстве ${\mathbf{r}}.$ Используя (27), легко показать, что в статистике Тсаллиса энтропия Бозе-газа двух независимых систем не обладает свойством аддитивности.

Экстремум энтропии и равновесные состояния. Равновесные состояния неэкстенсивных систем характеризуются распределениями, которые не меняются с течением времени. В состоянии равновесия энтропия должна иметь максимальное значение. Покажем, каким образом из этого требования можно найти функцию распределения частиц Бозе-газа в состоянии статистического равновесия. Задача заключается в нахождении таких ${{\bar {n}}_{j}},$ при которых квантовая энтропия (25) имеет максимальное значение, возможное при дополнительных условиях

выражающих постоянство полного числа частиц ${{{\text{N}}}_{q}}$ и полной энергии ${{{\text{E}}}_{q}}$ газа. Следуя известному методу неопределенных множителей Лагранжа, надо приравнять нулю первую вариацию функционала где $\beta $ и $\mu $ – некоторые постоянные. Произведя дифференцирование, найдем: откуда или, Это есть не что иное, как обобщенное распределение Бозе–Энштейна в статистике Тсаллиса. Здесь ${{T}_{0}} = {1 \mathord{\left/ {\vphantom {1 {{{\beta }_{0}}}}} \right. \kern-0em} {{{\beta }_{0}}}}$ – равновесная температура и ${{\mu }_{0}}$– равновесный химический потенциал Бозе-газа $({{\mu }_{0}} < 0).$

С помощью распределения (32) могут быть вычислены равновесные значения полного число частиц и полной энергии системы:

Заметим, что формула (33) определяет в неявном виде химический потенциал ${{\mu }_{0}}({{T}_{0}},{{{\text{N}}}_{{q0}}})$ Бозе-газа как функцию от температуры T₀ и полного числа частиц ${{{\text{N}}}_{{q0}}}.$

Термодинамические соотношения. Получим теперь экстремальное значение ${{{\text{S}}}_{{q0}}}$ энтропии и основные термодинамические соотношения. Подставляя распределение (31) в выражение (26) для энтропии и используя формулы (14), получим:

Здесь – термодинамический потенциал полного числа частиц бозонного газа; ${{\Omega }_{{qj}}}$– термодинамический потенциал частиц в $j$-ом квантовом состоянии, определяемый соотношением

Используя производные по ${{\beta }_{0}},{{\mu }_{0}}$ и ${{\varepsilon }_{j}}$ от распределения ${{\bar {n}}_{{j0}}}$

и формулы (18), легко получить следующие уравнения равновесной термодинамики для систем с переменным числом частиц: Найдем теперь вторую вариацию функционала (29) ${\text{L}}({{\bar {n}}_{j}});$ в результате получим:

Из (43) следует, что при $q > 0$ экстремум соответствует максимуму функционала, ${{\delta }^{2}}{\text{L}} < 0.$ Таким образом, распределение (32) максимизирует обобщенную энтропию (25) для бозонного газа.

Дивергенция Брэгмана. Рассмотрим теперь спонтанный переход между произвольным неравновесным состоянием ${{\bar {n}}_{j}}(t)$ и равновесным состоянием ${{\bar {n}}_{{j0}}}.$ открытой неэкстенсивной квантовой системы. В качестве информации различия далее будем использовать обобщенную меру Брэгмана, порожденную отрицательной функцией $\left( { - {{{\text{S}}}_{q}}} \right)$ (см. Bregman, 1967; Cichocki, Amari, 2010)

где первый член – это разность квантовых энтропий (сравни с (23)). Дивергенция Брэгмана (44), являясь знакоопределенным функционалом, определяет меру статистической упорядоченности в микросостояниях системы с распределением ${{\bar {n}}_{j}}(t)$ относительно равновесного состояния c распределением ${{\bar {n}}_{{j0}}}.$ Основные свойства дивергенции Брегмана можно найти в фундаментальной работе (Cichocki, Amari, 2010). Здесь же мы отметим лишь то, что величина ${{I}_{q}}\left[ {\bar {n}:{{{\bar {n}}}_{0}}} \right]$ является вещественным, положительным, выпуклым (в первом аргументе) функционалом. Кроме этого, поскольку при ${{\bar {n}}_{j}} = {{\bar {n}}_{{j0}}}$ имеет место равенство ${{I}_{q}}\left[ {{{{\bar {n}}}_{0}}:{{{\bar {n}}}_{0}}} \right] = 0,$ то дивергенция Брегмана является функцией Ляпунова³³.

Принцип максимум энтропии равновесного распределения Бозе–Эйнштейна в статистике Тсаллиса. Подставляя в формулу (44) равновесное распределение ${{\bar {n}}_{{j0}}}$ (32), в результате получим

Отсюда вытекает следующее дифференциальное уравнение

Если теперь предположить, что для обоих состояний системы справедливы соотношения ${{{\text{E}}}_{q}} = {{{\text{E}}}_{{q0}}}$ и ${{{\text{N}}}_{q}} = {{{\text{N}}}_{{q0}}}$ (так называемое, условие Гиббса), то из (45) следует неравенство

в котором информация различия представлена в виде отрицательного вклада в энтропию и называется негэнтропией. Понятие негэнтропии, т.е. изменения энтропии с обратным знаком, было предложено Э. Шредингером (Шредингер, 1947). В общем случае и для Бозе-газа выполняется негэнтропийный принцип Л. Бриллюэна (Бриллюэн, 1960). Из соотношения (47) следует, что энтропия равновесного состояния ${{{\text{S}}}_{{q0}}}$ больше, чем энтропия произвольного состояния ${{{\text{S}}}_{q}},$ ${{{\text{S}}}_{q}} \leqslant {{{\text{S}}}_{{q0}}}.$

Сравнивая значения энтропий при условии Гиббса, получим из уравнения (46) теорему Гиббса в виде неравенства (47). Таким образом, увеличение энтропии к ее максимальному равновесному значению происходит с потерей информации различия, то есть увеличивается статистическое разупорядочение и понижается статистическое упорядочение микросостояний неэкстенсивной системы. Поскольку информация различия является функцией Ляпунова с фиксированным знаком, то равновесие будет устойчивым, если выполняется неравенство

Таким образом, при стремлении $q$-системы, состоящей из элементарных частиц Бозе-газа, к равновесному состоянию во временной эволюции информация различия уменьшается. Из (48) следует $H$-теорема для открытых неравновесных неэкстенсивных $q$-систем (неравенство для энтропии Тсаллиса)

которое справедливо при приближении к состоянию полного статистического равновесия. Эта теорема утверждает, что $q$-энтропия системы непрерывно растет в направлении равновесия, где энтропия становится максимальной и достигает конечного значения. Таким образом, происходит хаотизация макроскопической системыаллиса при спонтанных переходах.

Заметим, что тот факт, что $q$-энтропия квазиаддитивна, и энтропия совокупной системы больше, чем сумма энтропий отдельных подсистем, указывает на то, что совокупная система термодинамически более стабильна (Landsberg, Vedral, 1998).

ЭНТРОПИЯ СВЕТОВЫХ КВАНТОВ БОЗЕ. ЧЕРНОЕ ИЗЛУЧЕНИЕ

Электромагнитное излучение, находящееся в тепловом равновесии (так называемое черное излучение) можно рассматривать как фотонный газ. В силу целочисленности момента импульса фотонов этот газ подчиняется статистике Бозе–Эйнштейна. Поскольку фотоны не взаимодействуют друг с другом (принцип суперпозиции для электромагнитного поля), то состоящий из фотонов газ можно считать идеальным. Для возможности установления теплового равновесия в излучении необходимо наличие хотя бы небольшого количества материальной среды (например, газа). Механизм, обеспечивающий установление равновесия, заключается при этом в поглощении и испускании фотонов веществом. Это обстоятельство приводит к существенной специфической особенности фотонного газа – число частиц ${\text{N}}$ в нем является переменной величиной и само должно определиться из условий теплового равновесия, что приводит к равенству нулю химического потенциала $\mu $ фотонного газа (см. Ландау, Лифшиц, 1964).

Следовательно, распределение фотонов по различным квантовым состояниям $j$ (уровням энергии) с определенными энергиями ${{\varepsilon }_{j}}: = \hbar {{\omega }_{j}}$ (где ${{\omega }_{j}}$ – собственная частота излучения в данном объеме ${{V}_{{\text{N}}}}$) определяется формулой (32) с $\mu = 0{\text{:}}$

Это есть так называемое обобщенное распределение Планка в статистике Тсаллиса. Считая далее объем системы ${{V}_{{\text{N}}}}$ достаточно большим, перейдем указанным выше способом от дискретного к непрерывному распределению собственных частот излучения.

Заметим, что в силу определения (11) экспоненты Тсаллиса, второе представление распределения ${{D}_{{\omega }}}$ в формуле (51) справедливо в том случае, когда при $q < 1$ имеет место неравенство ${{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\operatorname{k} T}}} \right. \kern-0em} {\operatorname{k} T}} < {{(1 - q)}^{{ - 1}}},$ или когда при $q > 1$ и ${{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\operatorname{k} T}}} \right. \kern-0em} {\operatorname{k} T}} \geqslant {{(1 - q)}^{{ - 1}}}.$

Учитывая непрерывное распределение энергии фотонов, плотность квантовых состояний фотонов с частотами собственных колебаний в интервале между $\omega $ и $\omega + d\omega $ может быть задана как (см. Ландау, Лифшиц, 1964)

где $с = 2.99792458 \times {{10}^{{10}}}\,\,{{{\text{см}}} \mathord{\left/ {\vphantom {{{\text{см}}} {\text{с}}}} \right. \kern-0em} {\text{с}}}$ – скорость света в вакууме, а $\omega $ – угловая частота. Умножив распределение (51) на эту величину, найдем число фотонов в данном интервале частот: а умножив еще на $\hbar \omega ,$ получим энергию излучения, заключенную в этом же участке спектра:

Формула (54) для спектрального распределения энергии черного излучения является обобщенной формулой Планка в статистике Тсаллиса. Будучи выражена через длины волн $\lambda = {{2\pi с} \mathord{\left/ {\vphantom {{2\pi с} \omega }} \right. \kern-0em} \omega },$ она принимает вид:

Обобщенный закон Планка (51) описывает распределение электромагнитной энергии (или распределение плотности фотонов), излучаемой черным телом при данной температуре $T.$ Закон Планка может быть представлен в различных вариантах, включающих такие параметры, как плотность потока или спектральное распределение. Два предельных случая, а именно, $\hbar \omega \ll \operatorname{k} T$ и $\hbar \omega \gg \operatorname{k} T,$ заслуживают особого внимания. В низкочастотном или высокотемпературном пределе ($\hbar \omega \ll \operatorname{k} T$) из соотношения (54), при учете свойства (17) функции $\mathop {{{{\exp }}_{{2 - q}}}(x}\limits_{x \to 0} ) \cong 1 + x + ...,$ получим:

Эту формулу можно считать аналогом ($q$-обобщением) классической формулы Рэлея–Джинса $d{\text{E}}(\omega )$ = ${{V}_{{\text{N}}}}{{({{\pi }^{2}}{{c}^{3}})}^{{ - 1}}}\operatorname{k} T{{\omega }^{2}}d\omega $ в статистике Тсаллиса. Она справедлива, если $1 > q \to - \infty .$ Из (56) видно, что с уменьшением $q$ излучение черного тела излучает меньше энергии по сравнению со стандартным излучением закона Рэлея–Джинса.

В обратном предельном случае больших частот ($\hbar \omega \gg {{k}_{{\text{B}}}}T$) соотношение (54), при учете формулы ${{\exp }_{{2 - q}}}(x)$ = ${1 \mathord{\left/ {\vphantom {1 {{{{\exp }}_{q}}( - x)}}} \right. \kern-0em} {{{{\exp }}_{q}}( - x)}}$ дает:

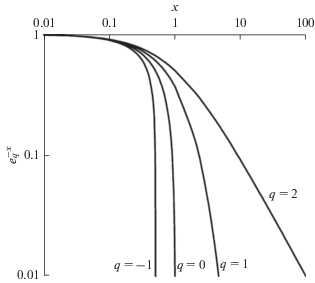
При написании (57) использовано свойство $\mathop {{{{\exp }}_{q}}( - x)}\limits_{x \to \infty } = 0$ деформированной экспоненты Тсаллиса (см. рис. 1). Выражение (57) можно рассматривать как $q$-обобщение классического закона Вина.

Заметим, что в пределе слабой связи $q \to 1$ формулы (56) и (57) восстанавливают свои стандартные выражения.

Термодинамика черного излучения. Вычислим теперь термодинамические характеристики чернотельного излучения. Интегрируя (54) по всем частотам, получим полную энергию фотонного газа (черного излучения)

Используя обозначение $x: = {{\hbar \omega } \mathord{\left/ {\vphantom {{\hbar \omega } {\operatorname{k} T}}} \right. \kern-0em} {\operatorname{k} T}}$ перепишем формулу (58) в виде:

В выражение (59) входит интеграл вида $\int_0^\infty {{{x}^{3}}{{{\left[ {{{{\exp }}_{{2 - q}}}(x) - 1} \right]}}^{{ - q}}}dx} ,$ который при $q \to 1$ равен ${{{{\pi }^{4}}} \mathord{\left/ {\vphantom {{{{\pi }^{4}}} {15}}} \right. \kern-0em} {15}} \simeq 6.49394$ (см. Ландау, Лифшиц, 1964).

Обозначим интеграл через

(см. формулу (П.6) для его вычисления в Приложении). Тогда для полной энергии излучения будем иметь: где ${{a}_{q}}: = aJ_{q}^{{(3)}};$ $a = \frac{1}{{15}}\frac{{{{\pi }^{5}}{{\operatorname{k} }^{4}}}}{{{{c}^{3}}{{\hbar }^{3}}}}$ = 7.56566(7) × $ \times \,\,{{10}^{{ - 15}}}\,\,\frac{{{\text{эрг}}}}{{{\text{c}}{{{\text{м}}}^{{\text{3}}}}\,{{{\text{К}}}^{{\text{4}}}}}}$ – постоянная давления излучения.

Как известно при $\mu = 0$ термодинамический потенциал ${{\Omega }_{{rad}}}({{V}_{{\text{N}}}},T,q)$ совпадает со свободной энергией ${{{\text{F}}}_{{rad}}}({{V}_{{\text{N}}}},T,q).$ При использовании формулы (41), в которой положим $\mu = 0$ и перейдем обычным образом от суммирования к интегрированию, для величины ${{{\text{F}}}_{{rad}}}$ получим:

Отсюда

Энтропия чернотельного излучения в статистике Тсаллиса равна

Она пропорциональна кубу температуры.

Полная энергия излучения, согласно (35), равна

Таким образом, полная энергия черного излучения пропорциональна четвертой степени температуры (закон Больцмана).

Для теплоемкости чернотельного излучения ${{C}_{{rad,V}}}: = {{\left( {{{\partial {{{\text{E}}}_{{rad}}}} \mathord{\left/ {\vphantom {{\partial {{{\text{E}}}_{{rad}}}} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{V}}$ имеем:

Наконец, давление и уравнения состояния определяются соотношениями: Таким образом, несмотря на зависимость термодинамических величин от параметра деформации $q,$ уравнение для полной энергии излучения (64) и уравнение состояния (67) остаются неизменными и в формализме Тсаллиса.

Наконец, для полного число фотонов в черном излучении согласно (53) и (60), имеем:

ЗАКЛЮЧЕНИЕ

В представленной работе дается логическая схема построения модифицированной термодинамики для неэкстенсивных бозонных систем, основанная на модифицированных энтропии Бозе-газа и соответствующей дивергенции Брэгмана. Показано, что обобщенная энтропия бозонного газа подчиняется псевдоаддитивному закону для двух статистически независимых подсистем. Положительность энтропии совокупной системы указывает на существование силы притяжения между отдельными подсистемами, и это взаимодействие явно происходит от взаимодействия между их составными бозонными частицами. Найдено универсальное распределение степенного закона на основе максимизации модифицированной энтропии Бозе-газа при заданных ограничениях на усредненные значения энергии и числа частиц системы, полученные по ненормированному распределению вероятностей Курадо–Тсаллиса. Используя модифицированное распределения Бозе–Эйнштейна, получены обобщенные выражения для термодинамического потенциала, полной и свободной энергии, энтропии, удельной теплоты, давления и удельной теплоемкости, а также дифференциальные термодинамические уравнения для бозонного газа. Обсуждаются обобщенные законы Планка, Рэлея–Джинса и Вина для фотонов, которые могут быть применимы к различным физическим задачам, в частности, к описанию космического черного излучения. Результаты деформированной статистики бозонного газа, как показано, более заметны при высоких температурах. Было также показано, что, несмотря на высокую $q$-чувствительность обобщенных термодинамических величин, уравнение состояния остается инвариантным и для фотонного газа. На основе так называемой дивергенции Брэгмана сформулированы и доказаны Н‑теорема и теорема Гиббса, описывающие хаотизацию макроскопической бозонной системы при спонтанных переходах.

Результаты работы могут быть использованы в качестве теоретического обоснования экспериментальных исследований чернотельного излучения, таких как исследование космиического микроволнового фонового излучения.