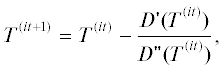Астрономический вестник, 2020, T. 54, № 6, стр. 560-566
Выявление столкновительных орбит астероидов с помощью условной минимизации расстояния до Земли
А. П. Батурин *
* E-mail: alexbaturin@sibmail.com
Поступила в редакцию 14.04.2020
После доработки 10.07.2020
Принята к публикации 20.07.2020
Аннотация
Разработан метод выявления столкновительных орбит астероидов в доверительном эллипсоиде начальных параметров движения. Метод заключается в условной минимизации расстояния от астероида до Земли в каком-либо его рассматриваемом сближении с Землей. В методе накладывается ограничение на так называемый “доверительный коэффициент”, т.е. коэффициент увеличения размеров доверительного эллипсоида. Ограничение заключается в задании для этого коэффициента некоторого постоянного значения, которое определяет некоторое нормированное расстояние от центра эллипсоида в шестимерном пространстве начальных параметров движения. Разработанный метод состоит в нахождении начальных параметров движения, соответствующих этому расстоянию и приводящих к столкновению астероида с Землей. Варьирование доверительного коэффициента с достаточно мелким шагом позволяет выявить такие параметры на всех соответствующих расстояниях, т.е. получить картину расположения столкновительных начальных параметров движения во всем доверительном эллипсоиде. Метод был апробирован для трех потенциально опасных астероидов (2001 VB, 2005 WG57 и 2008 JL3) в их предстоящих сближениях с Землей.
Задача выявления столкновительных орбит потенциально опасных астероидов в настоящее время является актуальной, ей посвящено много работ, среди которых можно отметить работы Milani, 2006; Ivashkin, Stikhno, 2007; 2019; Milani и др., 2009; Ивашкин, Стихно, 2009; Железнов, 2010; Прохоренко, 2010; Соколов и др., 2010; Черницов и др., 2016; Батурин, 2017.
Рассматриваемый в настоящей работе метод предназначен для выявления начальных параметров движения, приводящих к столкновению какого-либо астероида с Землей, в доверительном эллипсоиде, определяемом в результате улучшения орбиты астероида по данным его наблюдений. Метод заключается в условной минимизации квадрата расстояния от астероида до Земли в каком-либо его рассматриваемом сближении, причем в качестве “условия” применяется ограничение расстояния до центра эллипсоида в задаваемой им эллипсоидальной системе координат. Такое “расстояние” можно также назвать “доверительным коэффициентом”, представляющим собой коэффициент увеличения размеров доверительного эллипсоида. Таким образом, в рассматриваемом методе выполняется поиск столкновительных орбит, имеющих один и тот же доверительный коэффициент, т.е. расположенных на одной и той же эллипсоидальной гиперповерхности в пространстве начальных параметров движения.
Опишем рассматриваемый метод. Задачу поиска столкновительных начальных параметров движения, соответствующих определенному значению доверительного коэффициента, можно представить в виде
где ${\mathbf{q}} = {{(x,y,z,\dot {x},\dot {y},\dot {z})}^{T}}$ – искомый вектор начальных параметров движения; T – момент наибольшего сближения с Землей; D – квадрат расстояния до Земли в момент T; r – доверительный коэффициент; K – заданное постоянное значение этого коэффициента; λ – множитель Лагранжа.Описываемый метод функционально является развитием методов, основанных на условной оптимизации, применяемых, например, в работе (Батурин, Черницов, 2001), а также в работах В.В. Ивашкина и К.А. Стихно (2007; 2019).
Параметр D определяется выражением
где $\Delta x = x({\mathbf{q}},T) - {{x}_{ \oplus }}(T),$ $\Delta y = y({\mathbf{q}},T) - {{y}_{ \oplus }}(T),$ $\Delta z = z({\mathbf{q}},T) - {{z}_{ \oplus }}(T).$ Здесь $x,y,z$ – гелиоцентрические координаты астероида и ${{x}_{ \oplus }},{{y}_{ \oplus }},{{z}_{ \oplus }}$ – гелиоцентрические координаты Земли.Доверительный коэффициент r определяется как
где $l_{1}^{2},...,l_{6}^{2}$ – собственные значения ковариационной матрицы вектора оценки ${\mathbf{\hat {q}}},$ получаемой вместе с ним в результате улучшения орбиты методом наименьших квадратов; ${{\xi }_{1}}, \ldots ,{{\xi }_{6}}$ – координаты некоторой точки в системе координат, определяемой доверительным эллипсоидом: оси этой системы совпадают с осями эллипсоида, а начало координат расположено в его центре (вектор ${\mathbf{\hat {q}}}$). Связь между этой системой координат и исходной гелиоцентрической системой может быть выражена как где вектор ${\mathbf{s}} = {{({{\xi }_{1}},...,{{\xi }_{6}})}^{T}};$ U – матрица поворота, столбцами которой являются единичные собственные вектора ковариационной матрицы вектора ${\mathbf{\hat {q}}}.$Условия минимума (1) можно записать в виде:
(2)
$\begin{gathered} {{F}_{i}} = \frac{1}{2}\frac{{\partial \Phi }}{{\partial {{q}_{i}}}} = \Delta x\frac{{\partial x}}{{\partial {{q}_{i}}}} + \Delta y\frac{{\partial y}}{{\partial {{q}_{i}}}} + \Delta z\frac{{\partial z}}{{\partial {{q}_{i}}}} + \\ + \,\,\lambda \sum\limits_{k = 1}^6 {\frac{{{{\xi }_{k}}}}{{l_{k}^{2}}}{{u}_{{ki}}}} = 0\,\,\,\,(i = 1,...,6), \\ {{F}_{7}} = \frac{1}{2}\frac{{\partial \Phi }}{{\partial \lambda }} = \frac{1}{2}({{K}^{2}} - {{C}^{2}}) = 0, \\ \end{gathered} $Систему уравнений (2) можно решить, например, с помощью метода Ньютона или каких-либо его модификаций. Автор использовал для решения известную модификацию метода Ньютона, называемую “методом дифференциальных поправок” и заключающуюся. в том, что в выражениях производных от левых частей системы (2) по определяемым параметрам отбрасываются слагаемые со вторыми изохронными производными. Итерации метода дифференциальных поправок можно, как и в случае метода Ньютона, записать в виде
(3)
${{{\mathbf{g}}}^{{(it + 1)}}} = {{{\mathbf{g}}}^{{(it)}}} - {{\left( {\frac{{\partial {\mathbf{F}}}}{{\partial {\mathbf{g}}}}} \right)}^{{ - 1}}}{\mathbf{F}},$Изохронные производные $\frac{{\partial x}}{{\partial {{q}_{i}}}},\frac{{\partial y}}{{\partial {{q}_{i}}}},\frac{{\partial z}}{{\partial {{q}_{i}}}}\,\,(i = 1,...,6)$ вычисляются методом Мультона совместного интегрирования системы уравнений движения и уравнений в вариациях.
Поскольку расстояние в задаче (1) минимизируется для фиксированного момента сближения T, то в окрестности этого момента оно может быть еще меньшим. Поэтому далее квадрат расстояния до Земли минимизируется при фиксированном векторе g, найденном при решении задачи (1). В этом случае расстояние до Земли зависит только от времени $(D = D(T))$; поэтому для определения момента наибольшего сближения применяется метод Ньютона для нахождения нуля функции одной переменной:
где “it” – номер итерации; $D{\kern 1pt} '(T)$ = $ = 2(\Delta x\Delta \dot {x} + \Delta y\Delta \dot {y} + \Delta z\Delta \dot {z})$ и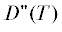 = $2(\Delta {{\dot {x}}^{2}} + $ $ + \,\,\Delta {{\dot {y}}^{2}} + \Delta {{\dot {z}}^{2}}$ $[ + \Delta x\Delta \ddot {x} + \Delta y\Delta \ddot {y} + \Delta z\Delta \ddot {z}]).$ Здесь выражение, взятое в квадратные скобки, при расчетах может не учитываться. Момент
сближения может исправляться по формуле (4) после каждой итерации процесса (3). В настоящей работе итерации процессов (3) и (4)
выполняются поочередно.
= $2(\Delta {{\dot {x}}^{2}} + $ $ + \,\,\Delta {{\dot {y}}^{2}} + \Delta {{\dot {z}}^{2}}$ $[ + \Delta x\Delta \ddot {x} + \Delta y\Delta \ddot {y} + \Delta z\Delta \ddot {z}]).$ Здесь выражение, взятое в квадратные скобки, при расчетах может не учитываться. Момент
сближения может исправляться по формуле (4) после каждой итерации процесса (3). В настоящей работе итерации процессов (3) и (4)
выполняются поочередно.
ПРИМЕНЕНИЕ МЕТОДА
Описанный метод был апробирован при выявлении столкновительных орбит астероидов 2001 VB, 2005 WG57 и 2008 JL3 в их предстоящих сближениях с Землей. Эти объекты были выбраны из таблицы потенциально опасных астероидов на сайте (https://cneos.jpl.nasa.gov/sentry/). Выбор объектов подчинялся двум требованиям: наличия достаточного числа наблюдений и наличия не слишком удаленного в будущем сближения с Землей. Наблюдения астероидов были взяты с сайта Центра малых планет (https://minorplanetcenter.net/db_search). Для объекта 2001 VB имеется 53 наблюдения, охватывающих дугу в 7 сут, для объекта 2005 WG57 – 75 наблюдений, охватывающих дугу в 30 сут, и для объекта 2008 JL3 – 39 наблюдений, охватывающих 7 сут.
Для этих астероидов было выполнено улучшение орбиты с сопутствующей отбраковкой ряда наблюдений. Благодаря отбраковке (без сокращения дуги наблюдаемости) остаточная среднеквадратическая ошибка представления наблюдений была уменьшена с 0.75″ до 0.25″ для объекта 2001 VB, с 0.48″ до 0.19″ для объекта 2005 WG57 и с 0.80″ до 0.38″ для объекта 2008 JL3. Оставшееся число наблюдений составило 19 для 2001 VB, 47 для 2005 WG57 и 35 для 2008 JL3. Затем на основе улучшенных элементов орбиты были вычислены сближения с Землей, среди которых для каждого астероида было выбрано одно сближение, отстоящее не слишком далеко в будущее, а именно: 6 августа 2023 г. (0.33 а. е.) для 2001 VB, 9 августа 2034 г. (0.11 а .е.) для 2005 WG57 и 8 апреля 2027 г. (0.013 а .е.) для 2008 JL3.
В качестве модели движения астероидов была использована возмущенная задача двух тел с учетом возмущений от восьми планет, Плутона и Луны, координаты которых при выполнении вычислений извлекались из последних на момент данной публикации эфемерид DE438 (ftp://ssd.jpl.nasa.gov/pub/eph/planets). Такой упрощенной модели вполне достаточно для демонстрации возможностей рассматриваемого способа выявления столкновительных орбит. При необходимости возможно более точного их выявления в модель движения следует включить учет более тонких эффектов, таких как возмущения от несферичности Земли, светового давления и т.п. Все вычисления выполнялись с использованием стандартных для ПЭВМ 80-битовых чисел с плавающей точкой, соответствующих 19-значной десятичной разрядности. Для компиляции вычислительных программ был использован свободно распространяемый компилятор GNU-Fortran (https://gcc.gnu.org/wiki/GFortranBinaries). Для численного интегрирования уравнений движения был использован метод Эверхарта (1984) 19-го порядка с переменным шагом интегрирования.
Описанный метод был применен для выявления столкновительных орбит в выбранных сближениях астероидов с Землей. Поскольку метод позволяет получать столкновительные или близкие к ним орбиты с начальными параметрами движения, расположенными на какой-то гиперповерхности, соответствующей заданному значению K доверительного коэффициента, то весь доверительный эллипсоид был представлен как набор таких вложенных эллипсоидальных гиперповерхностей, соответствующих значению доверительного коэффициента, пробегающему с мелким шагом определенный интервал, а именно, интервал [0.1; 4.5] с шагом 0.1.
В качестве конечного значения коэффициента K было задано число “4.5”, поскольку это число соответствует доверительной вероятности 0.997 в шестимерном случае (как число “3” в одномерном случае). Формулы вычисления доверительной вероятности в пространстве произвольной размерности были получены в работах (Черницов и др., 2007; Сюсина и др., 2012). Далее приводится еще один способ вычисления этой вероятности.
Уравнение доверительного эллипсоида в n-мерном пространстве может быть записано в виде
где ${{\xi }_{1}},...,{{\xi }_{n}}$ – координаты некоторой точки поверхности эллипсоида в системе координат, определяемой этим эллипсоидом (оси координат совпадают с осями эллипсоида, начало координат – с его центром); ${{l}_{1}},...,{{l}_{n}}$ – полуоси эллипсоида; r – “доверительный коэффициент”, т.е. коэффициент увеличения эллипсоида.Можно записать и параметрические уравнения эллипсоида по аналогии с уравнениями в трехмерном случае, используя определение сферической системы координат для n-мерного пространства (Розенфельд, 1966). Эти уравнения имеют вид
(6)
$\begin{gathered} {{\xi }_{1}} = r{{l}_{1}}\cos {{\varphi }_{1}}\cos {{\varphi }_{2}}\cos {{\varphi }_{3}}...\cos {{\varphi }_{{n - 1}}}, \hfill \\ {{\xi }_{2}} = r{{l}_{2}}\sin {{\varphi }_{1}}\cos {{\varphi }_{2}}\cos {{\varphi }_{3}}...\cos {{\varphi }_{{n - 1}}}, \hfill \\ {{\xi }_{3}} = r{{l}_{3}}\sin {{\varphi }_{2}}\cos {{\varphi }_{3}}...\cos {{\varphi }_{{n - 1}}}, \hfill \\ ................................................. \hfill \\ {{\xi }_{{n - 1}}} = r{{l}_{{n - 1}}}\sin {{\varphi }_{{n - 2}}}\cos {{\varphi }_{{n - 1}}}, \hfill \\ {{\xi }_{n}} = r{{l}_{n}}\sin {{\varphi }_{{n - 1}}}, \hfill \\ \end{gathered} $Как известно, плотность вероятности нормального распределения в n-мерном пространстве имеет вид
(7)
$f({\mathbf{s}}) = \frac{1}{{\sqrt {{{{(2\pi )}}^{n}}\det {\mathbf{C}}} }}\exp \left[ { - \frac{1}{2}{{{({\mathbf{s}} - {\mathbf{\hat {s}}})}}^{T}}{{{\mathbf{C}}}^{{ - 1}}}({\mathbf{s}} - {\mathbf{\hat {s}}})} \right],$(8)
${\mathbf{C}} = \left( {\begin{array}{*{20}{c}} {l_{1}^{2}}&{}&0 \\ {}&.&{} \\ 0&{}&{l_{n}^{2}} \end{array}} \right).$Поэтому определитель матрицы: $\det {\mathbf{C}} = l_{1}^{2}...l_{n}^{2}.$
Таким образом, учитывая выражения (5)–(8), функцию f можно записать как
(9)
$f({\mathbf{s}}) = \frac{1}{{{{l}_{1}}...{{l}_{n}}\sqrt {{{{(2\pi )}}^{n}}} }}\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right),$(10)
$P(r,n) = \frac{1}{{{{l}_{1}}...{{l}_{n}}\sqrt {{{{(2\pi )}}^{n}}} }}\int\limits_V {\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right)} \,dV,$Якобиан преобразования координат (6), как это легко вывести, имеет следующий вид:
(11)
$\begin{gathered} \frac{{\partial ({{\xi }_{1}},...,{{\xi }_{n}})}}{{\partial (r,{{\varphi }_{1}},...,{{\varphi }_{{n - 1}}})}} = \\ = {{r}^{{n - 1}}}{{l}_{1}}...{{l}_{n}}\cos {{\varphi }_{2}}{{\cos }^{2}}{{\varphi }_{3}}...{{\cos }^{{n - 2}}}{{\varphi }_{{n - 1}}}. \\ \end{gathered} $Учитывая это, можно переписать выражение (10) с интегралом, записанным в переменных $r,{{\varphi }_{1}},...,{{\varphi }_{{n - 1}}}.$ Тогда оно будет выглядеть как произведение независимых “одномерных” интегралов:
(12)
$\begin{gathered} P(r,n) = {{(2\pi )}^{{\frac{{2 - n}}{2}}}}\int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\cos {{\varphi }_{2}}d{{\varphi }_{2}}} \int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{{\cos }}^{2}}{{\varphi }_{3}}d{{\varphi }_{3}}} {\kern 1pt} ... \\ \ldots \int\limits_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{{\cos }}^{{n - 2}}}{{\varphi }_{{n - 1}}}d{{\varphi }_{{n - 1}}}} \int\limits_0^r {{{r}^{{n - 1}}}\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right)dr} . \\ \end{gathered} $Введя обозначения ${{J}_{i}} = \int_{{{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}}^\pi {{{{\cos }}^{i}}\varphi d\varphi } $ и ${{R}_{i}} = \int_0^r {{{r}^{i}}\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right)dr} ,$ выражение (12) можно записать в более компактном виде:
(13)
$P(r,n) = {{(2\pi )}^{{\frac{{2 - n}}{2}}}}{{J}_{1}}{\kern 1pt} ...{\kern 1pt} {{J}_{{n - 2}}}{{R}_{{n - 1}}}.$Интегралы Ji в (13) могут быть вычислены по рекуррентной формуле:
(14)
${{J}_{0}} = \pi ,\,\,\,{{J}_{1}} = 2,\,\,\,\,{{J}_{i}} = \frac{{i - 1}}{i}{{J}_{{i - 2}}}\,\,\,\,\,\,(i = 2,...,n - 2).$Интеграл ${{R}_{{n - 1}}}$ также может вычисляться с помощью рекуррентного соотношения:
(15)
$\begin{gathered} {{R}_{0}} = \int\limits_0^r {\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right)dr} = \sqrt {\frac{\pi }{2}} {\text{erf}}\left( {\frac{r}{{\sqrt 2 }}} \right), \\ {{R}_{1}} = 1 - \exp \left( { - \frac{{{{r}^{2}}}}{2}} \right), \\ {{R}_{i}} = - {{r}^{{i - 1}}}\exp \left( { - \frac{{{{r}^{2}}}}{2}} \right) + (i - 1){{R}_{{i - 2}}} \\ \left( \begin{gathered} i = 2,...,n - 1\,{\text{ с шагом 2 при нечетном }}n{\text{,}} \hfill \\ i = 3,...,n - 1\,{\text{ с шагом 2 при четном }}n \hfill \\ \end{gathered} \right), \\ \end{gathered} $Заметим еще, что в одномерном случае (n = 1) доверительная вероятность вычисляется как
(16)
$P(r,1) = {\text{erf}}({r \mathord{\left/ {\vphantom {r {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}).$В табл. 1 приведены некоторые значения доверительной вероятности $P(r,n),$ рассчитанной по формулам (13)–(16).
Талица 1. Доверительная вероятность, соответствующая некоторым значениям коэффициента увеличения r в n-мерном пространстве
| r | n = 1 | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 |
|---|---|---|---|---|---|---|---|---|
| 3.0 | 0.997300 | 0.988891 | 0.970709 | 0.938901 | 0.890936 | 0.826422 | 0.747344 | 0.657704 |
| 3.1 | 0.998065 | 0.991811 | 0.977811 | 0.952465 | 0.912929 | 0.857934 | 0.788228 | 0.706528 |
| 3.2 | 0.998626 | 0.994024 | 0.983368 | 0.963427 | 0.931286 | 0.885098 | 0.824624 | 0.751416 |
| 3.3 | 0.999033 | 0.995682 | 0.987664 | 0.972172 | 0.946395 | 0.908164 | 0.856510 | 0.791990 |
| 3.4 | 0.999326 | 0.996911 | 0.990947 | 0.979059 | 0.958660 | 0.927464 | 0.884011 | 0.828059 |
| 3.5 | 0.999535 | 0.997813 | 0.993426 | 0.984414 | 0.968482 | 0.943382 | 0.907369 | 0.859607 |
| 3.6 | 0.999682 | 0.998466 | 0.995276 | 0.988527 | 0.976243 | 0.956324 | 0.926911 | 0.886767 |
| 3.7 | 0.999784 | 0.998935 | 0.996641 | 0.991647 | 0.982297 | 0.966703 | 0.943022 | 0.909788 |
| 3.8 | 0.999855 | 0.999268 | 0.997637 | 0.993985 | 0.986957 | 0.974911 | 0.956113 | 0.929006 |
| 3.9 | 0.999904 | 0.999502 | 0.998354 | 0.995715 | 0.990498 | 0.981315 | 0.966600 | 0.944812 |
| 4.0 | 0.999937 | 0.999665 | 0.998866 | 0.996981 | 0.993156 | 0.986246 | 0.974884 | 0.957620 |
| 4.1 | 0.999959 | 0.999776 | 0.999227 | 0.997896 | 0.995125 | 0.989993 | 0.981337 | 0.967851 |
| 4.2 | 0.999973 | 0.999852 | 0.999478 | 0.998549 | 0.996567 | 0.992802 | 0.986296 | 0.975907 |
| 4.3 | 0.999983 | 0.999903 | 0.999652 | 0.999010 | 0.997609 | 0.994882 | 0.990056 | 0.982162 |
| 4.4 | 0.999989 | 0.999937 | 0.999770 | 0.999332 | 0.998353 | 0.996403 | 0.992869 | 0.986951 |
| 4.5 | 0.999993 | 0.999960 | 0.999849 | 0.999554 | 0.998878 | 0.997501 | 0.994946 | 0.990570 |
| 4.6 | 0.999996 | 0.999975 | 0.999902 | 0.999706 | 0.999244 | 0.998283 | 0.996460 | 0.993266 |
| 4.7 | 0.999997 | 0.999984 | 0.999938 | 0.999808 | 0.999497 | 0.998834 | 0.997549 | 0.995248 |
| 4.8 | 0.999998 | 0.999990 | 0.999960 | 0.999876 | 0.999668 | 0.999217 | 0.998323 | 0.996687 |
| 4.9 | 0.999999 | 0.999994 | 0.999975 | 0.999920 | 0.999784 | 0.999480 | 0.998865 | 0.997717 |
| 5.0 | 0.999999 | 0.999996 | 0.999985 | 0.999950 | 0.999861 | 0.999659 | 0.999241 | 0.998445 |
Сравнение этих значений со значениями доверительной вероятности, полученными в работах (Черницов и др., 2007; Сюсина и др., 2012) показывает их полное совпадение. Поэтому можно сделать вывод, что описанный здесь еще один способ вычисления этой вероятности с помощью выражений (13)–(15) дает верные результаты. Кроме того, напомним, что доверительная вероятность 0.997 соответствует коэффициенту r = 3 (табл. 1 ) только в случае одномерного пространства (n = 1) – это хорошо известное так называемое “правило трех сигм”. В случае большего числа измерений доверительный коэффициент должен быть больше трех. Так, в шестимерном пространстве вероятность 0.997 имеет место при значении коэффициента r, приблизительно равного 4.5 (табл. 1 ), следовательно, это значение можно принять в качестве границы доверительного эллипсоида.
Возвращаясь к задаче выявления столкновительных начальных параметров движения в доверительном эллипсоиде, коснемся вопроса задания начального приближения для итерационных процессов (3) и (4). Начальные приближения задавались путем равномерного заполнения гиперповерхности, соответствующей заданному значению K, множеством точек способом, описанным в работе (Батурин, 2016). Способ заключается в равномерном заполнении объема эллипсоида множеством точек и в последующем их перенесении на поверхность эллипсоида с использованием формул перехода между сферическими и прямоугольными координатами в шестимерном пространстве. Число точек, заполняющих эллипсоидальные гиперповерхности, задавалось различным, так как гиперповерхности, соответствующие различным значениям доверительного коэффициента, имеют разный размер. Для заполнения “крайних” гиперповерхностей, соответствующих значениям K = 4.5 и K = 0.1, было использовано 1000 и 100 точек; число точек, заполняющих остальные гиперповерхности (для K от 4.4 до 0.2 с шагом 0.1), изменялось по линейному закону между этими крайними значениями.
Результаты минимизации приводятся далее: на рис. 1 – для объекта 2001 VB; на рис. 2 – для объекта 2005 WG57 и на рис. 3 – для объекта 2008 JL3. На этих рисунках для каждого значения K из интервала [0.1; 4.5] приводятся значения минимального расстояния dmin до центра Земли в рассматриваемых сближениях. Эти значения соответствуют всем начальным приближениям, задаваемым описанным выше способом. Пунктирная линия на рисунках соответствует радиусу Земли, равному 4.26 × 10–5 а. е.
Рис. 1.
Результаты условной минимизации расстояния до Земли объекта 2001 VB вблизи его сближения с Землей 6 августа 2023 г.
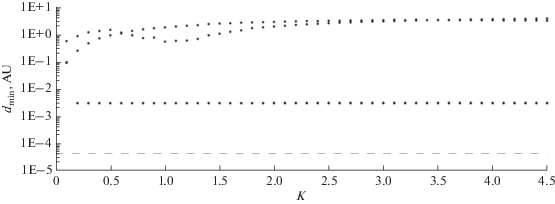
Рис. 2.
Результаты условной минимизации расстояния до Земли объекта 2005 WG57 вблизи его сближения с Землей 9 августа 2034 г.
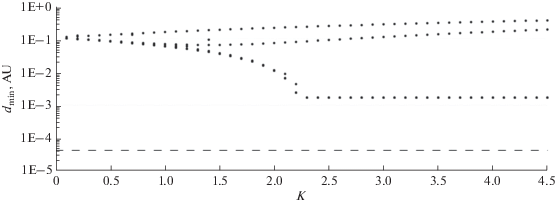
Рис. 3.
Результаты условной минимизации расстояния до Земли объекта 2008 JL3 вблизи его сближения с Землей 8 апреля 2027 г.
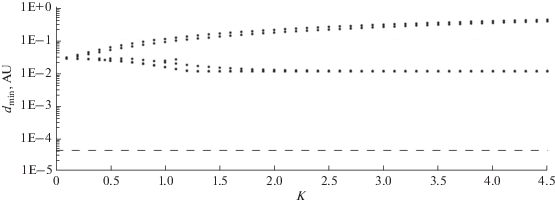
Как видно из рис. 1–3, процессы минимизации (3), (4) для всех точек каждой гиперповерхности сходятся лишь к двум-трем точкам, соответствующим экстремальному расстоянию до Земли. Так, для объекта 2001 VB (рис. 1) минимальное значение этого расстояния для всех 45 рассмотренных значений доверительного коэффициента практически одинаково: около 3 × × 10–3 а.е. Поэтому можно заключить, что это значение, вероятнее всего, и является минимальным для всего доверительного эллипсоида и этот эллипсоид не содержит каких-либо столкновительных начальных параметров. Верхние точки на рис. 1–3, по-видимому, представляют собой максимальные значения расстояния до Земли. Очевидно, что эти точки появляются в случае, когда итерационные процессы (3), (4) сходятся не к минимальному расстоянию, а к максимальному.
На рис. 2–3 есть небольшое отличие от рис. 1, а именно, в начале графиков (для K ~ 1.5–2) минимальное расстояние до Земли убывает, а затем становится практически постоянным. Для 2005 WG57 (рис. 2) это конечное постоянное значение составляет около 1.7 × 10–3 а. е., а для 2008 JL3 (рис. 3) – около 10–2 а. е. Поэтому можно заключить, что эти значения в каждом случае являются минимальными для соответствующих доверительных эллипсоидов и эти эллипсоиды, как и в случае астероида 2001 VB, не содержат столкновительных начальных параметров движения.
В заключение заметим, что рассмотренный метод выявления столкновительных параметров в начальном доверительном эллипсоиде прежде всего может быть использован как предварительная процедура в задаче оценивания вероятности столкновения. Как было показано выше, метод позволяет выявлять столкновительные параметры на каждой эллипсоидальной гиперповерхности, и шаг перебора гиперповерхностей (расстояние между соседними гиперповерхностями) может быть сколь угодно малым. Если минимальное расстояние от астероида до Земли для всех гиперповерхностей заметно превышает ее радиус, то можно сделать вывод, что весь доверительный эллипсоид не содержит приводящих к столкновению начальных параметров движения. Если же это минимальное расстояние на некоторых гиперповерхностях окажется меньше радиуса Земли, то в окрестности найденных точек может быть выполнено более детальное исследование с целью построения картины распределения таких точек с последующим оцениванием вероятности столкновения.
Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № 0721-2020-0049).
Список литературы
Батурин А.П., Черницов А.М. Два алгоритма определения областей возможных движений космических объектов // Исследования по баллистике и смежным вопросам механики: Сборник статей. Томск: Изд-во Том. ун-та, 2001. С. 86–88.
Батурин А.П. Выявление столкновительных орбит астероидов с помощью представления начальной доверительной области в виде последовательности эллипсоидальных гиперповерхностей // Изв. вузов. Физика. 2016. Т. 59. № 10. С. 145–150.
Ивашкин В.В., Стихно К.А. О предотвращении возможного столкновения астероида Апофис с Землей // Астрон. вестн. 2009. Т. 43. № 6. С. 502–516.
Железнов Н.Б. Влияние корреляционных связей между орбитальными параметрами астероида на определение вероятности его столконовения с планетой методом Монте-Карло // Астрон. вестн. 2010. Т. 44. № 2. С. 150–157.
Прохоренко В.И. Об анализе тесных сближений двух космических тел на близких почти круговых орбитах // Космич. исслед. 2010. Т. 48. № 6. С. 541–548.
Соколов Л.Л., Башаков А.А., Борисова Т.П., Петров Н.А., Питьев Н.П., Шайдулин В.Ш. Траектории соударения астероида Апофис с Землей в XXI веке // Астрон. вестн. 2012. Т. 46. № 4. С. 311–320.
Черницов А.М., Тамаров В.А., Баранников Е.А. Оценивание вероятности столкновения астероида с Землей методом Монте-Карло // Изв. вузов. Физика. 2016. Т. 59. № 5. С. 84–91.
Черницов А.М., Тамаров В.А., Авдюшев В.А., Баньщикова М.А., Дубас О.М. Особенности определения доверительных областей в пространстве начальных параметров движения Солнечной системы // Изв. вузов. Физика. 2007. Т. 50. № 12/2. С. 33–43.
Сюсина О.М., Черницов А.М., Тамаров В.А. Построение доверительных областей в задаче вероятностного исследования движения малых тел Солнечной системы // Астрон. вестн. 2012. Т. 46. № 3. С. 209–222. (Syusina O.M., Chernitsov A.M., Tamarov V.A. Construction of confidence regions in problem on probabilistic study into motion of minor bodies of the Solar system // Sol. Syst. Res. 2012. V. 46. № 3. P. 195–207.)
Розенфельд Б. А. Многомерные пространства. М.: Наука, 1966. 648 с.
Ivashkin V.V., Stikhno C.A. A problem of the orbit correction for the near-Earth asteroid Apophis // 58th Int. Astronautical Congress-2007, Hyderabad, India, September 24–28, 2007. Proc. ISSN 1995-6258), Paper IAC-07-C1.7.08.
Ivashkin V.V., Stikhno C.A. Analysis of correction of asteroid Apophis’ orbit providing its collision with the Moon // Int. Meeting “Fundamental and applied problems of mechanics – 2018”. IOP Conf. Series: Journal of Physics: Conf. Series 1301 (2019) 012003 IOP Publishing, 2019. https://doi.org/10.1088/1742-6596/1301/1/012003.
Milani A. Asteroid impact monitoring // Serb. Astron. J. 2006. V. 172. P. 1–11.
Milani A., Chesley S.R., Sansaturio M.E., Bernardi F., Valsecchi G.B., Arratia O. Long term impact risk for (101955) 1999RQ36 // Icarus. 2009. V. 203. Iss. 2. P. 460–471.
Everhart E. An efficient integrator that uses Gauss–Radau spacings // Proc. 83rd Colloquium of the Int. Astron. Union “Dynamics of Comets: Their Origin and Evolution,” Rome, June 11–15, 1984, Carusi, A. and Valsecchi, G.B., Eds., Dordrecht: D. Reidel, 1985, pp. 185–202.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник