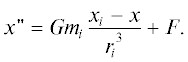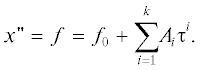Астрономический вестник, 2020, T. 54, № 6, стр. 567-576
Об ускорении численного интегрирования уравнений движения астероидов
И. А. Баляев *
Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
* E-mail: balasteravan@yandex.ru
Поступила в редакцию 03.06.2020
После доработки 17.08.2020
Принята к публикации 04.09.2020
Аннотация
Поиск и изучение возможных соударений астероидов, сближающихся с Землей, требуют значительного объема вычислений. В настоящей работе описывается программа R0, созданная для расчета траекторий большого числа виртуальных астероидов и параметров сближений с телами Солнечной системы: планетами, Луной и Солнцем. Программа использует эфемериды DE430 и метод интегрирования Гаусса–Эверхарта. Сравнение с разработанным ранее программным комплексом v19 в разных тестах показало прирост производительности на порядок и более. При интегрировании движения одного астероида достигнуто меньшее ускорение, однако данная задача уже решалась за приемлемое время. Оптимизация выполнялась в расчете на большое количество астероидов. С использованием новой программы произведена оценка вероятности соударения 200 астероидов методом Монте‒Карло, результаты сравниваются с полученными NASA.
ВВЕДЕНИЕ
В 2004 г. в обсерватории Китт‒Пик в Аризоне был открыт астероид 2004 MN4, впоследствии получивший имя Апофис и номер 99942. Крупный размер, около 300 м, и существенная вероятность соударения с Землей вызвали интерес многих исследователей, в том числе в СПбГУ. Особенностью данного астероида является тесное сближение с Землей в 2029 г., порождающее множество резонансных возвратов и затрудняющее точное предсказание дальнейшей траектории (Соколов и др., 2008). Хотя к настоящему моменту соударения вскоре после 2029 г. исключены, сохраняется вероятность соударения во второй половине XXI века. https://cneos.jpl.nasa.gov/sentry/ – результаты расчета вероятности соударения, полученные NASA.
Для поиска и изучения возможных соударений на кафедре небесной механики СПбГУ был разработан программный комплекс v19. С его помощью для ряда астероидов был получен существенно более полный список возможных соударений, чем приводится на сайте NASA, в том числе для астероида Апофис (Соколов и др., 2013). Поиск соударений осуществляется путем одномерного варьирования начальных данных. Типичное время работы над одним астероидом составляет от нескольких часов до нескольких суток. Расширение исследований на большее количество астероидов и переход к многомерному варьированию потребовали бы колоссальных затрат вычислительных ресурсов.
Основное время занимает вычисление траектории астероида и параметров сближений с Землей. Для этой задачи было решено создать с нуля новую программу. Программа R0 предназначена для расчета траекторий и сближений с планетами, Луной и Солнцем большого числа виртуальных астероидов. Модель движения учитывает притяжение больших планет, координаты которых берутся из эфемерид DE430. Для интегрирования уравнений выбран метод Гаусса–Эверхарта (Авдюшев, 2010). Создание с нуля позволило провести существенную оптимизацию. Ускорение по сравнению с программным комплексом v19 составило более 10 раз. Точное число зависит от конкретного теста. Новая программа опробована на задаче определения вероятности соударения методом Монте‒Карло. Полученные результаты близки к приведенным на сайте NASA.
УРАВНЕНИЕ ДВИЖЕНИЯ АСТЕРОИДА
Пусть $x$ – вектор положения астероида, ${{x}_{i}}$ – вектор положения массивного тела Солнечной системы, ${{r}_{i}}$ – расстояние между массивным телом и астероидом, $G$ – гравитационная постоянная, ${{m}_{i}}$ – масса тела. Тогда уравнение движения можно записать в следующем виде:
Слагаемое $F$ – позволяющее учесть различные возмущения, принято равным нулю в рамках данной работы. Преобразовав уравнение движения, для трехмерного пространства можно получить систему из 6 обыкновенных дифференциальных уравнений первого порядка. Начальными данными будут координаты и скорости в стартовый момент времени. Для реального астероида начальные данные определены с погрешностями, так что существует область неопределенности ненулевого размера, где может быть астероид. Интерес представляют области начальных данных, точки из которых ведут к соударению с Землей или другими телами. Пересечение таких областей с областью неопределенности означает ненулевую вероятность соударения.
МЕТОД ГАУССА–ЭВЕРХАРТА
Подробное описание метода можно найти в работе (Авдюшев, 2010), здесь же будут изложены основные формулы и алгоритм интегрирования на шаге. Рассмотрим следующую задачу:
Здесь $t$ – независимая переменная, $x$ – интегрируемая переменная, $f$ – заданная функция. На шаге интегрирования $h$ введем переменную $\tau = {{\left( {t - {{t}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {t - {{t}_{0}}} \right)} h}} \right. \kern-0em} h}$, а правую часть аппроксимируем многочленом степени $k$:
Интегрируя многочлен, получаем:
(4)
$x = {{x}_{0}} + h\left( {{{f}_{0}}\tau + \sum\limits_{i = 1}^k {{{A}_{i}}\frac{{{{\tau }^{{i + 1}}}}}{{i + 1}}} } \right).$Перепишем правую часть в виде интерполяционного многочлена Ньютона на сетке ${{\tau }_{0}},{{\tau }_{1}}, \ldots ,{{\tau }_{k}},{{\tau }_{0}} = 0$:
(5)
$f = {{f}_{0}} + \sum\limits_{i = 1}^k {{{\alpha }_{i}}} \prod\limits_{j = 0}^{i - 1} {\left( {\tau - {{\tau }_{j}}} \right){\kern 1pt} {\kern 1pt} } .$Если известны коэффициенты $A$ на предыдущем шаге, начальным приближением на новом шаге будет:
r – отношение нового шага интегрирования к предыдущему; чаще всего r = 1.
Коэффициенты $e$ вычисляются по рекуррентным формулам:
(7)
$\begin{gathered} {{e}_{{ii}}} = {{e}_{{i0}}} = 1, \\ {{e}_{{ij}}} = {{e}_{{i - 1,j - 1}}} + {{e}_{{i - 1,j}}}\left( {i > j > 0} \right). \\ \end{gathered} $Прибавив полученную на предыдущем шаге разницу $\Delta A$ между $A$ в конце итерационного процесса и начальным приближением $\bar {A}$, оценку можно улучшить. В начале интегрирования за начальное приближение принимаются нулевые значения.
Итерация производится следующим образом. Для каждого $i = 1,2, \ldots ,k$ последовательно выполняется цикл $A \to {{x}_{i}} \to {{f}_{i}} \to {{\alpha }_{i}} \to A$. Первое действие $A \to {{x}_{i}}$ производится по формуле (4); второе действие ${{x}_{i}} \to {{f}_{i}}$ – в соответствии с уравнением (1). Для третьего действия ${{f}_{i}} \to {{\alpha }_{i}}$ преобразуем формулу (5):
(8)
$\begin{gathered} {{\alpha }_{1}} = {{\left( {{{f}_{1}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{1}} - {{f}_{0}}} \right)} {{{\tau }_{1}}}}} \right. \kern-0em} {{{\tau }_{1}}}}, \\ {{\alpha }_{2}} = {{\left( {{{\left( {{{f}_{2}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{2}} - {{f}_{0}}} \right)} {{{\tau }_{2}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{2}} - {{\alpha }_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\left( {{{f}_{2}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{2}} - {{f}_{0}}} \right)} {{{\tau }_{2}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{2}} - {{\alpha }_{1}}}}} \right)} {\left( {{{\tau }_{2}} - {{\tau }_{1}}} \right)}}} \right. \kern-0em} {\left( {{{\tau }_{2}} - {{\tau }_{1}}} \right)}}, \\ {{\alpha }_{3}} = {{\left( {{{\left( {{{\left( {{{f}_{3}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{3}} - {{f}_{0}}} \right)} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\left( {{{f}_{3}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{3}} - {{f}_{0}}} \right)} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right)} {\left( {{{\tau }_{3}} - {{\tau }_{1}}} \right) - {{\alpha }_{2}}}}} \right. \kern-0em} {\left( {{{\tau }_{3}} - {{\tau }_{1}}} \right) - {{\alpha }_{2}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\left( {{{\left( {{{f}_{3}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{3}} - {{f}_{0}}} \right)} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\left( {{{f}_{3}} - {{f}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{f}_{3}} - {{f}_{0}}} \right)} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right. \kern-0em} {{{\tau }_{3}} - {{\alpha }_{1}}}}} \right)} {\left( {{{\tau }_{3}} - {{\tau }_{1}}} \right) - {{\alpha }_{2}}}}} \right. \kern-0em} {\left( {{{\tau }_{3}} - {{\tau }_{1}}} \right) - {{\alpha }_{2}}}}} \right)} {\left( {{{\tau }_{3}} - {{\tau }_{2}}} \right)}}} \right. \kern-0em} {\left( {{{\tau }_{3}} - {{\tau }_{2}}} \right)}}, \\ \ldots \\ \end{gathered} $За одно прохождение цикла вычисляется одно значение ${{\alpha }_{i}}$. Начальное приближение $\alpha $ выводится из начального приближения $A$:
Четвертое действие $\alpha \to A$ будет обратным к (9):
Коэффициенты $c$ и $d$ вычисляются по рекуррентным формулам:
(11)
${{c}_{{ij}}} = {{c}_{{i - 1,j - 1}}} - {{\tau }_{{i - 1}}}{{c}_{{i - 1,j}}}\left( {i > j > 0} \right),$(12)
${{d}_{{ij}}} = {{d}_{{i - 1,j - 1}}} + {{\tau }_{j}}{{d}_{{i - 1,j}}}\left( {i > j > 0} \right).$В последней формуле в исходной статье была допущена опечатка.
Для повышения порядка метода узлы ${{\tau }_{i}}$ следует выбирать из разбиений Гаусса–Лежандра, Гаусса–Радо или Гаусса–Лобатто. В программе R0 использовано разбиение Гаусса–Лобатто, узловые значения для которого являются корнями уравнения:
(13)
$\left( {{{\tau }^{k}}{{{\left( {\tau - 1} \right)}}^{k}}} \right)_{\tau }^{{\left( {k - 1} \right)}} = 0.$Порядок метода в этом случае равен $2k$, ${{\tau }_{0}} = 0,{{\tau }_{k}} = 1$.
ОПТИМИЗАЦИЯ МЕТОДА ДЛЯ КОНКРЕТНОЙ ЗАДАЧИ
Задача – расчет траектории и параметров тесных сближений с телами Солнечной системы большого количества виртуальных астероидов. Как правило, самой затратной частью является вычисление правых частей уравнений. Для самого простого вида уравнений движения (1) большую часть времени занимает вычисление положений массивных тел. Между тем, поскольку узловые значения времени не меняются от итерации к итерации, достаточно вычислить положения на несколько моментов времени один раз за шаг. Более того, если множество виртуальных астероидов интегрировать параллельно с одинаковым шагом, достаточно вычислить положения планет один раз за шаг для всех астероидов. Благодаря этому при достаточно большом числе виртуальных астероидов затраты на вычисление эфемерид можно сделать пренебрежимо малыми. Алгоритм выбора шага, позволяющий эффективно группировать астероиды в процессе интегрирования, описан в следующем разделе.
Оценим количество арифметических операций, затрачиваемое на каждое из четырех действий в течение одной итерации при $k = 6$. Для одного астероида интегрируемая переменная представляет собой 6-вектор, но, например, при вычислении правых частей существенны только 3 компоненты из 6, а расстояние до планеты достаточно вычислить один раз, как и величину ${{G{{m}_{i}}} \mathord{\left/ {\vphantom {{G{{m}_{i}}} {{{r}_{i}}^{3}}}} \right. \kern-0em} {{{r}_{i}}^{3}}}$. Для первого действия $A \to {{x}_{i}}$ величины ${{\tau _{i}^{{j + 1}}} \mathord{\left/ {\vphantom {{\tau _{i}^{{j + 1}}} {\left( {j + 1} \right)}}} \right. \kern-0em} {\left( {j + 1} \right)}}$ лучше вычислить заранее, тогда будет затрачено $6k\left( {k + 1} \right) = 252$ сложения и $6k\left( {k + 1} \right) = 252$ умножения. Второе действие ${{x}_{i}} \to {{f}_{i}}$ для 10 массивных тел потребует $30k = 180$ вычитаний, $10k = 60$ делений, $10k = 60$ извлечений квадратного корня, $30k = 180$ сложений и $80k = 480$ умножений. Для третьего действия ${{f}_{i}} \to {{\alpha }_{i}}$, поскольку операция деления дороже умножения, имеет смысл вычислить величины ${1 \mathord{\left/ {\vphantom {1 {\left( {{{\tau }_{i}} - {{\tau }_{j}}} \right)}}} \right. \kern-0em} {\left( {{{\tau }_{i}} - {{\tau }_{j}}} \right)}}$. Тогда третье действие потребует всего $6k{{\left( {k + 1} \right)} \mathord{\left/ {\vphantom {{\left( {k + 1} \right)} 2}} \right. \kern-0em} 2} = 126$ вычитаний и $6k{{\left( {k + 1} \right)} \mathord{\left/ {\vphantom {{\left( {k + 1} \right)} 2}} \right. \kern-0em} 2} = 126$ умножений. Четвертое действие $\alpha \to A$ выполняется за $6{{k}^{2}}{{\left( {k + 1} \right)} \mathord{\left/ {\vphantom {{\left( {k + 1} \right)} 2}} \right. \kern-0em} 2} = 756$ умножений и $6{{k}^{2}}{{\left( {k - 1} \right)} \mathord{\left/ {\vphantom {{\left( {k - 1} \right)} 2}} \right. \kern-0em} 2} = 540$ сложений. Последнее действие, как можно заметить, сопоставимо по затратам с вычислением правых частей. При учете дополнительных сил соотношение изменится в пользу правых частей, но при повышении порядка разбиения $k$ затраты на четвертое действие растут очень быстро. Например, при $k = 8$ потребуется уже 1728 умножений и 1344 сложения на одну итерацию. Можно было бы оптимизировать это действие, но можно объединить с первым в сокращенной схеме $\alpha \to {{x}_{i}} \to {{f}_{i}} \to {{\alpha }_{i}}$. Тогда получение начального приближения будет осуществляться по схеме $\alpha \to A \to \bar {A} \to \bar {\alpha }$, а вместо поправки $\Delta A$ можно использовать аналогичную $\Delta \alpha $. Объединенное действие $\alpha \to {{x}_{i}}$ выполняется по формуле:
(14)
${{x}_{i}} = {{x}_{0}} + h\left( {{{f}_{0}}{{\tau }_{i}} + \mathop \sum \limits_{j = 1}^k {{B}_{{ij}}}{{\alpha }_{j}}} \right),$(15)
${{B}_{{ij}}} = \mathop \sum \limits_{l = 1}^j {{c}_{{jl}}}\frac{{{{\tau }_{i}}^{{l + 1}}}}{{l + 1}}.$Количество арифметических операций такое же, как и для действия $A \to {{x}_{i}}$, при этом четвертое действие полностью отсутствует. Аналогичным образом упрощается получение начального приближения:
(17)
${{H}_{{ij}}} = \mathop \sum \limits_{l = i}^j \mathop \sum \limits_{m = i}^l {{d}_{{mi}}}{{r}^{m}}{{e}_{{lm}}}{{c}_{{jl}}}.$В подавляющем большинстве случаев шаг будет равен предыдущему, в остальных случаях проще в качестве начального приближения взять нулевые значения, как в начале интегрирования.
Наконец, поскольку исходная система уравнений имеет второй порядок, можно использовать другой вариант аппроксимации решения (Everhart, 1974) и таким образом избавиться от необходимости вычислять скорости в течение итерации:
Тогда действие $\alpha \to {{x}_{i}}$ примет вид:
(19)
${{x}_{i}} = {{x}_{0}} + h\left( {x{{'}_{0}}{{\tau }_{i}} + h\left( {{{f}_{0}}\frac{{{{\tau }_{i}}^{2}}}{2} + \mathop \sum \limits_{j = 1}^k {{W}_{{ij}}}{{\alpha }_{j}}} \right)} \right),$(20)
${{W}_{{ij}}} = \mathop \sum \limits_{l = 1}^j {{c}_{{jl}}}\frac{{\tau _{i}^{{l + 2}}}}{{\left( {l + 1} \right)\left( {l + 2} \right)}}.$Основной идеей оптимизации является параллельное интегрирование большого числа астероидов, поэтому информация о них всех занимает много места в памяти. При тестировании оказалось, что поправка $\Delta \alpha $ не приводит к существенному росту производительности, зато повышает расход памяти почти в два раза. Начальное приближение $\bar {\alpha }$ уже без поправки позволяет делать всего 2–3 итерации на шаге. В связи с этим программа R0 эту поправку не использует.
Итерации производятся до полной сходимости положения и скорости на конце шага. Критерий выбран с учетом машинной точности, составляющей 52 двоичных порядка для типа double.
АЛГОРИТМ ВЫБОРА ШАГА И ГРУППИРОВКИ ВИРТУАЛЬНЫХ АСТЕРОИДОВ
Даже если изначально множество виртуальных астероидов было компактным, тесные сближения с планетами легко разрывают первоначально компактный пучок траекторий на широкий веер. Из-за этого очень часто небольшое количество виртуальных астероидов сближается с некоторой планетой, что требует уменьшение шага интегрирования, но для остальных астероидов уменьшение шага не нужно и только поспособствует накоплению ошибок округления. Необходим алгоритм, который бы позволил эффективно группировать астероиды по величине шага.
В качестве базового шага выбрана величина ${{h}_{0}} = {{4}^{d}}$, обеспечивающая наиболее удобное использование эфемерид DE430. В течение базового шага сохраняется аппроксимация положений планет, Луны и Солнца. Ни один шаг интегрирования не превышает этой величины, а большинство равны ей. Критерий уменьшения шага – эвристический, направленный прежде всего на обнаружение сближений. Для уменьшения шага хотя бы одно отношение планетоцентрической скорости к планетоцентрическому расстоянию должно вырасти до некоторой регулируемой величины $2M$. Если отношение превышает ${{2}^{i}}M$, шаг уменьшается до ${{2}^{{ - i}}}{{h}_{0}}$. В итоге шаг подбирается из расчета, чтобы изменение планетоцентрического радиус-вектора не превысило четверти величины этого радиус-вектора (или 1/25 длины окружности). Порядок разбиения $k$ подобран для достижения наилучшей точности и равен 5. Точность контролировалась параллельным интегрированием с меньшим шагом.
В ходе интегрирования на базовом шаге производятся следующие итерации: определяется множество астероидов с наименьшим значением времени, до которого рассчитана траектория; для каждого из них определяется шаг; затем для каждого шага выполняется расчет эфемерид и собственно интегрирование на шаге. Если шаг можно увеличить по сравнению с предыдущим, проверяется текущая степень дробления шага. Например, если астероид был рассчитан на 5/8 базового шага, новый шаг выбирается не более 1/8, чтобы в следующий раз он смог войти в группу, интегрируемую с шагом 1/4.
АЛГОРИТМ ПОИСКА И УТОЧНЕНИЯ СБЛИЖЕНИЙ
Для каждой планеты задается расстояние ${{R}_{{{\text{min}}}}}$, при сближении до которого нужно вычислить параметры сближения. После каждого шага интегрирования проверяется наличие сближения в пределах шага. Для этого вычисляется скалярное произведение планетоцентрических скорости и положения астероида в начале и в конце шага. Если в начале произведение отрицательно, а в конце положительно, произошло сближение. Если расстояние на конце шага меньше $2{{R}_{{{\text{min}}}}}$, производится уточнение сближения. Если полученное минимальное расстояние оказывается меньше ${{R}_{{{\text{min}}}}}$, параметры сближения записываются в файл: номер виртуального астероида, дата сближения, номер тела, минимальное расстояние. Если минимальное расстояние меньше радиуса тела, то сближение является соударением, расчет траектории в этом случае останавливается.
Уточнение сближения производится с помощью бинарного поиска. Интервал, на котором произошло сближение, делится пополам, после чего проверяется скалярное произведение планетоцентрических положения и скорости. При уточнении сближений для интегрируемого астероида используется многочлен $A$, вычисленный на текущем шаге, положения и скорости планет берутся из эфемерид.
СРАВНЕНИЕ РЕЗУЛЬТАТОВ R0 И v19
Первое требование к программе – точность результата. Как бы быстро программа не считала, если результат отличается от контрольного больше, чем на радиус Земли, для предсказания соударений такая программа не годится по меньшей мере в условиях данного теста. Для программы R0 контрольный результат предоставила старая программа v19, использующая ту же модель движения, но другой интегратор. Основным тестом стал расчет астероида (1036) Ганимед на 320 000 суток. Большое время интегрирования (в 10 раз больше обычного) и наличие тесного сближения (с Марсом) делали задачу сложнее или сопоставимой с предположительными задачами для большинства АСЗ. Расхождение положения астероида в течение всего времени интегрирования оставалось менее 10–6 а. е.
Второе требование к программе – скорость работы. Вообще говоря, старая программа не может одновременно рассчитывать сближения с разными планетами и должна быть запущена отдельно для каждой из планет. Уже поэтому она заведомо в 10 раз медленнее новой. Однако в задаче поиска сближений и соударений конкретно с Землей этот недостаток не имеет значения. Для теста была взята тысяча виртуальных астероидов в окрестности номинальной орбиты Апофиса и процессор Intel Pentium G3260. Расчет велся на 20 000 суток вперед (около 55 лет). Среднее время, затраченное на один астероид, составило у программы v19 – 300 мс, у программы R0 – 13 мс.
ВЫЧИСЛЕНИЕ ВЕРОЯТНОСТИ СОУДАРЕНИЯ МЕТОДОМ МОНТЕ‒КАРЛО
Данная задача требует расчета траекторий большого числа виртуальных астероидов, что позволит максимально использовать преимущества новой программы. С помощью программы R0 был произведен расчет траектории до 2132 года 107 виртуальных астероидов из области неопределенности, выбранных случайно в соответствии с нормальным распределением, задаваемым математическим ожиданием и матрицей ковариаций элементов орбиты. https://ssd.jpl.nasa.gov/sbdb.cgi – база данных малых тел Солнечной системы. Для генерации случайных чисел использован вихрь Мерсенна. Астероиды выбраны из числа имеющих размер более 30 м и вероятность соударения с Землей более 10–8 по данным NASA, с которыми и сравниваются результаты.
В табл. 1 приведены вероятность соударения с Землей по данным NASA и количество попавших в тела Солнечной системы виртуальных астероидов из 107 по расчетам программой R0. Для удобства сравнения вероятность NASA умножена на 107. Всего было исследовано 200 астероидов.
Таблица 1.
Число соударений с планетами и Луной из 10 млн виртуальных астероидов и ожидаемое число соударений с Землей по данным NASA
| Астероид | Земля (NASA) | Земля | Луна | Венера | Меркурий | Марс | Юпитер |
|---|---|---|---|---|---|---|---|
| 2000 SG344 | 26014.4 | 36 034 | 110 | 0 | 0 | 0 | 0 |
| 2019 WG2 | 1645.2 | 1793 | 0 | 0 | 0 | 0 | 0 |
| 2000 SB45 | 1553.8 | 1676 | 8 | 0 | 0 | 0 | 0 |
| 2019 QS8 | 49.8 | 1158 | 7 | 8 | 0 | 1 | 80 |
| 2017 VJ | 18.6 | 846 | 0 | 0 | 0 | 0 | 0 |
| 2010 DG77 | 73.8 | 828 | 8 | 35 | 0 | 0 | 27 |
| 2014 JU15 | 562.7 | 808 | 15 | 0 | 0 | 0 | 0 |
| 2010 GM23 | 630.7 | 730 | 2 | 0 | 0 | 0 | 0 |
| 2005 QK76 | 681.0 | 703 | 0 | 0 | 0 | 0 | 0 |
| 2007 DX40 | 617.6 | 688 | 10 | 43 | 0 | 0 | 0 |
| 1994 GK | 690.7 | 662 | 1 | 0 | 0 | 0 | 0 |
| 2008 CC71 | 585.3 | 653 | 8 | 0 | 0 | 0 | 0 |
| 2008 UB7 | 347.5 | 571 | 25 | 0 | 0 | 0 | 0 |
| 2008 EX5 | 471.9 | 502 | 91 | 0 | 0 | 0 | 0 |
| 2006 BC8 | 95.0 | 350 | 5 | 0 | 0 | 0 | 0 |
| 2017 YM1 | 276.4 | 342 | 28 | 0 | 0 | 0 | 0 |
| 2009 FJ | 93.9 | 327 | 1 | 0 | 0 | 0 | 0 |
| 2011 UM169 | 332.3 | 311 | 1 | 0 | 0 | 0 | 0 |
| 2008 VS4 | 5.8 | 295 | 3 | 8 | 0 | 0 | 319 |
| 2008 ST7 | 270.0 | 276 | 19 | 0 | 0 | 0 | 0 |
| 2008 YO2 | 75.8 | 269 | 10 | 0 | 0 | 0 | 0 |
| 2019 BE5 | 123.5 | 250 | 25 | 2 | 4 | 0 | 0 |
| 2014 GN1 | 207.4 | 212 | 0 | 0 | 0 | 0 | 0 |
| 2016 CY135 | 13.7 | 208 | 9 | 0 | 0 | 0 | 0 |
| 2019 YV1 | 83.2 | 195 | 1 | 0 | 0 | 0 | 0 |
| 2019 DP | 59.5 | 189 | 7 | 0 | 0 | 0 | 0 |
| 2009 HC | 28.7 | 174 | 0 | 0 | 0 | 0 | 0 |
| 2007 KE4 | 139.9 | 158 | 0 | 0 | 0 | 0 | 0 |
| 2019 XS | 51.6 | 157 | 6 | 0 | 0 | 0 | 0 |
| 2006 HF6 | 107.9 | 138 | 5 | 0 | 0 | 0 | 0 |
| 2009 FZ4 | 23.8 | 136 | 1 | 10 | 0 | 2 | 14 |
| 2019 WU2 | 109.2 | 133 | 3 | 0 | 0 | 0 | 0 |
| 2002 VU17 | 137.8 | 133 | 13 | 0 | 0 | 0 | 0 |
| 2009 TH8 | 88.5 | 121 | 0 | 0 | 0 | 0 | 0 |
| 2010 QG2 | 106.0 | 114 | 8 | 0 | 0 | 0 | 0 |
| 443104 | 14.3 | 107 | 0 | 0 | 0 | 0 | 0 |
| 2012 PB20 | 28.3 | 106 | 10 | 0 | 0 | 0 | 0 |
| 2007 EV | 87.9 | 100 | 0 | 0 | 0 | 0 | 0 |
| 2002 MN | 27.9 | 98 | 8 | 0 | 0 | 0 | 0 |
| 2017 AE21 | 46.4 | 98 | 0 | 77 | 0 | 0 | 0 |
| 2002 RB182 | 60.9 | 92 | 0 | 0 | 0 | 0 | 2 |
| 2007 WP3 | 76.9 | 88 | 0 | 0 | 0 | 0 | 0 |
| 2000 WJ107 | 28.9 | 87 | 0 | 0 | 0 | 0 | 0 |
| 2016 WG | 58.0 | 80 | 8 | 0 | 0 | 0 | 0 |
| 2012 QD8 | 64.9 | 79 | 1 | 70 | 0 | 0 | 0 |
| 2019 YX1 | 86.9 | 76 | 1 | 0 | 0 | 0 | 0 |
| 2004 ME6 | 1.0 | 74 | 1 | 0 | 0 | 0 | 522 |
| 2018 NF15 | 0.3 | 74 | 0 | 4 | 0 | 21 | 8 |
| 2010 MZ112 | 46.8 | 63 | 2 | 8 | 1 | 0 | 0 |
| 2006 SC | 64.2 | 62 | 0 | 0 | 0 | 0 | 0 |
| 2010 UB | 36.5 | 61 | 0 | 0 | 0 | 0 | 0 |
| 2015 HQ182 | 1.6 | 61 | 2 | 15 | 0 | 1 | 0 |
| 2019 FE | 49.0 | 58 | 0 | 0 | 0 | 0 | 0 |
| 2007 KO4 | 43.0 | 55 | 4 | 0 | 0 | 0 | 0 |
| 2004 VZ14 | 18.6 | 52 | 2 | 0 | 0 | 0 | 0 |
| 2019 LU1 | 46.5 | 52 | 5 | 0 | 0 | 0 | 0 |
| 2018 JN | 16.5 | 50 | 0 | 0 | 0 | 0 | 0 |
| 2019 RT3 | 20.1 | 48 | 4 | 0 | 0 | 0 | 0 |
| 2019 ND7 | 31.8 | 46 | 1 | 0 | 0 | 0 | 0 |
| 2017 UQ7 | 0.4 | 40 | 2 | 0 | 0 | 0 | 0 |
| 2008 PK9 | 5.2 | 40 | 3 | 0 | 0 | 0 | 0 |
| 2016 GU2 | 0.1 | 39 | 0 | 0 | 0 | 0 | 0 |
| 2014 JV79 | 2.9 | 37 | 0 | 0 | 0 | 0 | 0 |
| 2004 GE2 | 0.7 | 33 | 0 | 0 | 0 | 101 | 0 |
| 2011 AK37 | 27.7 | 32 | 6 | 0 | 0 | 0 | 0 |
| 2012 TV | 30.6 | 31 | 4 | 0 | 0 | 0 | 0 |
| 2010 UC7 | 5.1 | 31 | 2 | 0 | 0 | 0 | 0 |
| 2019 UH9 | 29.5 | 30 | 5 | 0 | 0 | 0 | 0 |
| 2002 EM7 | 0.6 | 29 | 0 | 0 | 0 | 0 | 0 |
| 2006 DN | 3.6 | 28 | 1 | 0 | 0 | 0 | 0 |
| 2011 VG9 | 7.7 | 28 | 0 | 0 | 0 | 0 | 0 |
| 2018 LM | 11.5 | 28 | 0 | 40 | 0 | 0 | 0 |
| 2019 QS | 2.2 | 26 | 1 | 1 | 0 | 0 | 0 |
| 2006 HX57 | 30.8 | 24 | 0 | 0 | 0 | 0 | 0 |
| 2005 WG57 | 7.2 | 24 | 0 | 0 | 0 | 0 | 0 |
| 2009 CZ1 | 7.5 | 23 | 1 | 7 | 0 | 0 | 0 |
| 2006 QN111 | 18.9 | 23 | 0 | 0 | 0 | 0 | 0 |
| 1997 TC25 | 2.6 | 22 | 0 | 0 | 0 | 0 | 0 |
| 2007 FT3 | 13.6 | 22 | 4 | 0 | 0 | 0 | 0 |
| 2017 QC36 | 4.8 | 22 | 1 | 14 | 0 | 0 | 0 |
| 2007 XZ9 | 10.8 | 21 | 0 | 0 | 0 | 0 | 0 |
| 2018 FE4 | 15.1 | 20 | 3 | 0 | 0 | 0 | 0 |
| 2007 CS5 | 3.1 | 20 | 0 | 0 | 0 | 0 | 0 |
| 2018 GG | 19.1 | 20 | 0 | 0 | 0 | 0 | 0 |
| 2005 CC37 | 13.0 | 18 | 0 | 0 | 0 | 0 | 0 |
| 2006 JE | 17.6 | 18 | 0 | 0 | 0 | 0 | 0 |
| 2015 MN11 | 5.1 | 15 | 0 | 0 | 0 | 0 | 0 |
| 2017 PY26 | 12.4 | 15 | 11 | 0 | 0 | 0 | 0 |
| 2008 FF5 | 4.8 | 15 | 0 | 0 | 0 | 0 | 0 |
| 1979 XB | 7.4 | 15 | 0 | 0 | 0 | 0 | 0 |
| 2015 ME131 | 0.3 | 15 | 0 | 9 | 0 | 0 | 0 |
| 2011 BF40 | 11.5 | 14 | 0 | 0 | 0 | 0 | 0 |
| 2017 NT5 | 5.8 | 13 | 0 | 0 | 0 | 0 | 0 |
| 2016 AB166 | 3.1 | 13 | 0 | 0 | 0 | 0 | 0 |
| 2011 BH40 | 1.4 | 13 | 0 | 27 | 0 | 0 | 44 |
| 2013 BR15 | 1.6 | 12 | 1 | 0 | 0 | 0 | 0 |
| 2011 XC2 | 6.7 | 12 | 0 | 0 | 0 | 0 | 0 |
| 2012 ES10 | 16.4 | 12 | 3 | 0 | 0 | 0 | 0 |
| 1999 RZ31 | 15.9 | 12 | 0 | 0 | 0 | 0 | 0 |
| 2002 XV90 | 4.8 | 11 | 0 | 0 | 0 | 0 | 0 |
| 2007 EH26 | 0.1 | 11 | 0 | 0 | 0 | 0 | 0 |
| 2018 PA25 | 0.3 | 11 | 0 | 13 | 0 | 0 | 0 |
| 2016 WN55 | 1.2 | 11 | 1 | 39 | 0 | 1 | 0 |
| 1996 TC1 | 13.2 | 10 | 0 | 0 | 0 | 0 | 0 |
| 2008 KO | 7.8 | 10 | 0 | 0 | 0 | 0 | 0 |
| 2016 NL56 | 7.2 | 10 | 0 | 5 | 0 | 1 | 1 |
| 2004 FY3 | 0.8 | 9 | 0 | 0 | 0 | 0 | 0 |
| 2005 NX55 | 0.4 | 9 | 0 | 0 | 0 | 0 | 0 |
| 2017 UC52 | 4.0 | 9 | 0 | 1 | 0 | 0 | 0 |
| 2011 CW46 | 5.0 | 8 | 1 | 0 | 0 | 0 | 0 |
| 2016 JT38 | 1.8 | 8 | 0 | 0 | 0 | 0 | 0 |
| 2010 XB73 | 2.8 | 8 | 0 | 1 | 0 | 1 | 371 |
| 2010 XQ | 2.1 | 8 | 0 | 0 | 0 | 0 | 260 |
| 2014 FX32 | 11.2 | 7 | 0 | 0 | 0 | 0 | 0 |
| 2017 KB3 | 0.4 | 7 | 0 | 0 | 0 | 0 | 0 |
| 2019 YA2 | 1.8 | 7 | 1 | 0 | 0 | 0 | 0 |
| 2005 TM173 | 9.4 | 7 | 0 | 0 | 0 | 0 | 271 |
| 2018 EL4 | 0.8 | 6 | 0 | 0 | 0 | 0 | 0 |
| 2006 UC64 | 0.9 | 5 | 0 | 0 | 0 | 0 | 0 |
| 2018 BP6 | 0.7 | 5 | 0 | 0 | 0 | 0 | 0 |
| 2017 UL7 | 3.5 | 5 | 0 | 0 | 0 | 0 | 0 |
| 2005 ED224 | 26.1 | 5 | 0 | 0 | 0 | 0 | 0 |
| 2001 HJ31 | 1.9 | 5 | 1 | 0 | 0 | 0 | 0 |
| 2017 FB1 | 2.9 | 5 | 0 | 2 | 0 | 0 | 0 |
| 2011 SE191 | 0.2 | 5 | 0 | 0 | 0 | 0 | 0 |
| 2017 UE52 | 0.3 | 5 | 0 | 2 | 0 | 3 | 443 |
| 2017 RZ17 | 0.2 | 5 | 0 | 49 | 1 | 0 | 9 |
| 2017 MZ8 | 0.4 | 5 | 0 | 0 | 0 | 4 | 122 |
| 2005 UL6 | 1.1 | 4 | 7 | 0 | 0 | 0 | 0 |
| 2008 OO1 | 2.3 | 4 | 189 | 0 | 0 | 0 | 0 |
| 2014 MO68 | 6.3 | 4 | 0 | 0 | 0 | 0 | 0 |
| 2011 BT59 | 1.4 | 4 | 0 | 0 | 3 | 2 | 32 |
| 2014 ML67 | 4.3 | 4 | 1 | 2 | 0 | 0 | 510 |
| 1998 DK36 | 5.6 | 4 | 0 | 136 | 6 | 0 | 0 |
| 2010 MY112 | 0.1 | 4 | 0 | 4 | 3 | 0 | 0 |
| 2018 YH2 | 3.3 | 4 | 0 | 0 | 0 | 0 | 0 |
| 2014 UX34 | 0.1 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2018 YW2 | 2.2 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2008 DA4 | 3.4 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2007 PR25 | 0.2 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2006 CM10 | 1.8 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2008 UY91 | 0.6 | 3 | 0 | 5 | 0 | 0 | 0 |
| 2003 UQ25 | 0.9 | 3 | 0 | 0 | 0 | 1 | 0 |
| 2014 CH13 | 1.3 | 3 | 0 | 0 | 0 | 0 | 0 |
| 2016 PR66 | 0.1 | 3 | 1 | 0 | 0 | 0 | 49 |
| 2014 HN197 | 0.6 | 3 | 0 | 1 | 0 | 0 | 633 |
| 2016 JB29 | 1.7 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2016 BQ15 | 0.4 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2001 SB170 | 0.3 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2013 WM | 4.3 | 2 | 0 | 0 | 0 | 0 | 0 |
| 1997 UA11 | 2.9 | 2 | 0 | 0 | 0 | 0 | 12 |
| 2016 AU193 | 0.9 | 2 | 1 | 0 | 0 | 0 | 0 |
| 2011 QF48 | 3.1 | 2 | 0 | 0 | 0 | 1 | 0 |
| 2017 OO1 | 0.3 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2019 DF2 | 0.1 | 2 | 0 | 5 | 0 | 0 | 10 |
| 2018 LT5 | 1.3 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2009 BR5 | 1.7 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2009 MU | 0.2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2009 WQ25 | 0.9 | 1 | 1 | 7 | 0 | 0 | 0 |
| 2010 CR5 | 0.8 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2001 SD286 | 0.6 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2015 FA345 | 1.6 | 1 | 0 | 0 | 0 | 0 | 652 |
| 2010 JA43 | 0.8 | 1 | 2 | 2 | 0 | 0 | 0 |
| 2010 LJ68 | 0.2 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2006 CD | 0.2 | 1 | 0 | 1 | 0 | 0 | 37 |
| 2004 FM4 | 0.1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2018 LF16 | 0.3 | 1 | 0 | 0 | 0 | 0 | 3 |
| 2005 GQ33 | 0.3 | 1 | 0 | 1 | 0 | 13 | 38 |
| 2017 DC120 | 0.5 | 1 | 0 | 0 | 0 | 1 | 7 |
| 2010 HV20 | 1.3 | 1 | 0 | 1 | 0 | 0 | 0 |
| 2016 PA79 | 0.1 | 0 | 0 | 0 | 0 | 5 | 256 |
| 2009 WZ53 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2017 DB120 | 0.1 | 0 | 0 | 0 | 0 | 0 | 12 |
| 2016 UB26 | 0.1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2001 CA21 | 0.1 | 0 | 0 | 155 | 0 | 3 | 1 |
| 410 777 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2016 RP41 | 0.2 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2015 RD36 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2017 SH33 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2014 HE199 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2018 HJ2 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2014 MR26 | 0.3 | 0 | 0 | 49 | 1 | 0 | 0 |
| 2007 VH189 | 0.3 | 0 | 0 | 1 | 0 | 8 | 0 |
| 2019 XQ2 | 0.3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2015 HV182 | 0.3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2008 KN11 | 0.4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2014 XM7 | 0.4 | 0 | 2 | 0 | 0 | 0 | 0 |
| 2001 UD5 | 0.4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2006 QK33 | 0.6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2006 WM3 | 0.6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2010 JH80 | 0.6 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2007 SN6 | 1.1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2013 NH6 | 1.1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2005 EL70 | 1.3 | 0 | 0 | 10 | 0 | 0 | 0 |
| 2011 AZ36 | 4.1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 2011 DV10 | 11.7 | 0 | 0 | 0 | 0 | 0 | 0 |
| 99 942 | 88.5 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2016 HF3 | 469.3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 29 075 | 1200.0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 101 955 | 3676.9 | 0 | 0 | 0 | 0 | 0 | 0 |
ЗАКЛЮЧЕНИЕ
Создана программа R0, значительно ускорившая расчет траекторий опасных астероидов. Различие результатов со старой программой v19, а также с результатами NASA, невелико, что показывает потенциальную пригодность программы R0 в задачах астероидно-кометной безопасности. Хотя, например, астероиды 29 075 и 101 955 (в конце таблицы) демонстрируют существенное различие, оно естественным образом проистекает из отсутствия возможных соударений до 2132 г. и их наличием значительно позже. В большинстве же случаев интервал исследования NASA меньше, поэтому вероятность по результатам R0 обычно больше. Следует, однако, с осторожностью полагаться на полученные вероятности. В ряде случаев положенные в основу предположения и ошибки самого метода могут исказить результат на порядок и более.
Расчеты показывают, что многие из угрожающих Земле астероидов имеют вероятность столкновения не только с Землей, но и с Луной и другими планетами Солнечной системы. Столкновение с другим телом может быть использовано для устранения угрозы.
В будущем планируются некоторые модификации программы. В частности, для повышения надежности результата имеет смысл улучшить модель движения и проверить влияние на результат различных эффектов. Кроме того, поскольку сразу большое количество астероидов интегрируется параллельно, планируется версия программы для графического процессора.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-32-90149.
Список литературы
Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычислительные технологии. 2010. Т. 15. № 4. С. 31–36.
Соколов Л.Л., Башаков А.А., Питьев Н.П. Особенности движения астероида 99942 Апофис // Астрон. вестн. 2008. Т. 42. № 1. С. 20–29. (Sokolov L.L., Bashakov A.A., Pitjev N.P. Peculiarities of the motion of asteroid 99942 Apophis // Sol.Syst. Res. 2008. V. 42. № 1. P. 18–27.)
Соколов Л.Л., Борисова Т.П., Васильев А.А., Петров Н.А. Свойства траекторий соударения астероидов с Землей // Астрон. вестн. 2013. Т. 47. № 5. С. 441. (Sokolov L.L., Borisova T.P., Vasil’ev A.A., Petrov N.A. Properties of collision trajectories of asteroids with the Earth // Sol. Syst. Res. 2013. V. 47. № 5. P. 408–413.)
Avdyushev V.A. Gauss–Everhart Integrator // Computational technologies. 2010. V. 15. № 4. P. 31–36.
Everhart E. Implicit single sequence method for integrating orbits // Celest. Mech. 1974. V. 10. P. 35–55.
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник