Астрономический вестник, 2021, T. 55, № 1, стр. 84-96

ВВЕДЕНИЕ

Все астероиды, тесно сближающиеся с Землей, непременно подлежат вероятностному обследованию на предмет их возможного столкновения с планетой (Chesley, Chodas, 2015). Даже если расчетная орбита сближающегося астероида не предрекает никакой катастрофы, это еще не является основанием, чтобы оставлять объект без пристального внимания. Расчетная орбита, определяемая из наблюдений, всегда содержит в себе некую параметрическую неопределенность, вызванную случайными ошибками наблюдений. Поэтому исключать столкновение устремленного к Земле астероида никогда нельзя, но оно допускается как вероятностное событие.

В современной практике вероятность столкновения астероида с Землей оценивается на основе стохастического моделирования орбитальной неопределенности (Muinonen, Bowell, 1993; Черницов и др., 1998; Milani, 1999; Bordovitsyna и др., 2001; Virtanen и др., 2001; Bowell и др., 2002; Muinonen и др., 2006; Avdyushev, 2011; Авдюшев, 2015). В пространстве орбитальных параметров сначала случайным образом формируется облако виртуальных объектов около номинального астероида, параметры которого определяются из наблюдений. Далее посредством орбитальной модели оно отображается в физическое пространство на период тесного сближения астероида с планетой. При этом регистрируются попадания виртуальных объектов в тело Земли. Отношение числа таких объектов к общему числу дает вероятностную оценку столкновения астероида.

Для формирования облака неопределенности обычно используется ковариационная матрица параметрических ошибок, которая всегда имеется в распоряжении после определения орбитальных параметров из наблюдений. Фактически она несет в себе информацию о вероятностном распределении параметрических ошибок линеаризированной обратной задачи и описывает, таким образом, в параметрическом пространстве эллипсоидальное облако неопределенности с нормально распределенной плотностью. Если нелинейность обратной задачи слабая, то ковариационная матрица вполне может быть пригодна для вероятностного оценивания космических угроз, иначе стохастическое моделирование будет давать неадекватные оценки.

Все обратные задачи орбитальной динамики – нелинейны. Однако проблема сильной нелинейности возникает только в тех задачах, где облако неопределенности принимает протяженные размеры, т.е. когда орбита определяется плохо вследствие скудной наблюдательной информации о движении небесного тела. Масштабное распределение виртуальных объектов (в особенности периферийных) очень сильно подвергается влиянию нелинейности, так что облако неопределенности может значительно отличаться от эллипсоидального. Разумеется, если вероятность столкновения астероида с Землей будет определяться из стохастического моделирования на основе ковариационной матрицы, то она может быть как недооценена, так и переоценена.

Для определения вероятностных оценок в сильно нелинейном случае применяются нелинейные стохастические методы (Milani, 1999; Muinonen и др., 2006; Virtanen и др., 2001; Desmars и др., 2009; Emel’yanov, 2010; Avdyushev, 2011; Avdyushev, 2017). Они дают более адекватные оценки, нежели линейные методы, хотя не всегда практически обоснованы. Главная причина сильной нелинейности – неудачный выбор орбитальных параметров (Сюсина и др., 2012). Следовательно, нелинейность можно существенно ослабить путем преобразования параметров, однако вовсе избавиться от нее нельзя. Предельно минимальная нелинейность, неустранимая посредством параметрического преобразования, обусловлена так называемой внутренней нелинейностью (Bates, Watts, 1988; Draper, Smith, 1998). Ее величина как раз и ограничивает возможности нелинейных стохастических методов и предопределяет их адекватность (Avdyushev, 2011; 2017).

Для оценивания нелинейности служат показатели нелинейности (Beale, 1960; Bates, Watts, 1980; Сюсина и др., 2012; Авдюшев, 2015; Черницов и др., 2017; Avdyushev, 2017). Все они, по сути, являются мерой смещения параметрических оценок за нелинейность относительно ожидаемых линейных аналогов. Показатели нелинейности – безразмерные величины, и совершенно очевидно, если какой-либо из них превышает, скажем, единичное значение, уверенно можно утверждать, что обратная задача – сильно нелинейна. Однако остается вопрос: какое же должно быть пороговое значение показателя, меньше которого он сигнализировал бы о слабой нелинейности? К сожалению, никто из авторов ранее так и не дал определенного ответа на этот вопрос.

В настоящей работе исследуется нелинейность в обратных задачах астероидной динамики при различных условиях наблюдений для разнообразных типов определяемых орбит. Оценивание нелинейности в такой глобальной постановке оказывается возможным в нормализованной упрощенной задаче. Приводятся формулы нормализации орбитальных параметров. Проводится также общий анализ нелинейности для всех потенциально опасных астероидов, наблюдавшихся в одном появлении (оппозиции) до июня 2020 г. Для оценивания полной, параметрической и внутренней нелинейностей вводятся оригинальные показатели с обоснованными пороговыми значениями.

ДОПУСТИМОЕ СМЕЩЕНИЕ ПАРАМЕТРИЧЕСКИХ ОЦЕНОК

Проблема сильной нелинейности в обратных задачах астероидной динамики, как уже указывалось выше, обычно возникает при большой орбитальной неопределенности, когда астероидная орбита определяется плохо вследствие малочисленного состава (угловых) наблюдений, распределенных на очень короткой орбитальной дуге. При этом облако неопределенности принимает протяженные размеры в параметрическом пространстве (как и в физическом) и вытягивается вдоль одного (аномального) направления, соответствующего медленнейшему изменению целевой функции: в физическом пространстве, как правило, от наблюдателя к объекту наблюдения. Между тем виртуальные астероиды, составляющие сигарообразное облако, распределяются вдоль аномального направления по почти нормальному закону.

Нелинейность вызывает смещение параметрических оценок. Учитывая особенность конфигурации облака неопределенности при сильной нелинейности, покажем, как смещение оценки одного параметра может повлиять на оценку вероятностной массы в одномерном случае, и каково может быть допустимое смещение при заданной точности оцениваемой вероятности.

Функция вероятностной плотности одномерного нормального распределения с нулевой средней и дисперсией ${{\sigma }^{2}}$ имеет вид

Предположим, мы определяем вероятностную массу $P$ на малом отрезке длины $\operatorname{d} {\kern 1pt} \rho $ около произвольного значения $\rho $. Приближенно ее можно представить как

Смещение значения $\rho $ на величину $\Delta \rho $ внутри отрезка влечет (с точностью до малых первого порядка) изменение вероятностной массы на величину

Тогда, согласно (2) и (3), относительное изменение вероятностной массы будет

Для нормального распределения (1) имеем

Из формулы (4) получаем допустимое относительное смещение ${{\left| {\delta \rho } \right|}_{{tol}}}$, соответствующее допустимому относительному изменению вероятностной массы ${{\left| {\delta P} \right|}_{{tol}}}$:

Допустим, на малом отрезке мы оцениваем вероятность $P$ с точностью до первого знака, следовательно, ${{\left| {\delta P} \right|}_{{tol}}} = 5 \times {{10}^{{ - 2}}}$. Тогда в окрестности граничных точек $\bar {\rho }$ доверительного интервала, соответствующего вероятности $\alpha = 0.997$, $\bar {\rho } = \pm 3\sigma $ (правило трех сигм), будем иметь допустимое смещение ${{\left| {\delta \rho } \right|}_{{tol}}} = 2.8 \times {{10}^{{ - 3}}}$. В обратных задачах астероидной динамики, где оцениваются шесть параметров, граница вытянутой доверительной области с вероятностью $\alpha = 0.997$ определяется значением $\bar {\rho } = \pm 4.5\sigma $ (Сюсина и др., 2012), отсюда ${{\left| {\delta \rho } \right|}_{{tol}}} = 1.2 \times {{10}^{{ - 3}}}$.

СМЕЩЕНИЕ МОДЕЛЬНОГО ОТКЛИКА КАК ПОКАЗАТЕЛЬ НЕЛИНЕЙНОСТИ

Возможные смещения параметрических оценок, вызванные нелинейностью модели, удобно оценивать по модельным откликам (model response)¹¹ на провоцирующие их вариации параметров. Предположим наблюдения ${{{\mathbf{p}}}^{O}} = {{(p_{1}^{O}, \ldots ,p_{N}^{O})}^{T}}$ интерпретируются моделью ${\mathbf{p}}({\mathbf{q}}) = {{({{p}_{1}}({\mathbf{q}}), \ldots ,{{p}_{N}}({\mathbf{q}}))}^{T}}$ в $N$-мерном пространстве наблюдений (observation space), где q – вектор параметров в $K$-мерном параметрическом пространстве (parameter space). Обозначим ${\mathbf{\hat {p}}} = {\mathbf{p}}({\mathbf{\hat {q}}})$ модельное представление наблюдений, соответствующее оценке ${\mathbf{\hat {q}}}$, определяемой из наблюдений ${{{\mathbf{p}}}^{O}}$.

В линейной задаче ${\mathbf{p}}({\mathbf{q}}) = {\mathbf{Aq}}$, где ${\mathbf{A}}$ – постоянная матрица размера $N \times K$, и тогда модельный отклик ${\mathbf{p}} - {\mathbf{\hat {p}}}$ около оценки ${\mathbf{\hat {p}}}$ будет связан с вариацией параметрической оценки ${\mathbf{q}} - {\mathbf{\hat {q}}}$ линейно: ${\mathbf{p}} - {\mathbf{\hat {p}}} = {\mathbf{A}}({\mathbf{q}} - {\mathbf{\hat {q}}}).$ Целесообразно исследовать смещение оценок на границе ${\mathbf{\bar {q}}}$ некоторой стандартной доверительной эллипсоидальной области (Draper, Smith, 1998), определяемой в рамках линейной задачи наименьших квадратов. Вообще достаточно рассмотреть лишь вершины эллипсоида ${{{\mathbf{\bar {q}}}}_{i}}$ $(i = 1, \ldots ,K)$, которым будут соответствовать модельные отклики

Согласно (6), относительное изменение $\delta \bar {\rho }$ параметра $\bar {\rho }$ влечет относительные смещения вершин доверительной области $\left\| {\delta {{{{\mathbf{\bar {q}}}}}_{i}}} \right\| = \left| {\delta \bar {\rho }} \right|$ $(i = 1, \ldots ,K)$ в параметрическом пространстве, а также их модельных образов $\delta {{{\mathbf{\bar {p}}}}_{i}}$ $(i = 1, \ldots ,K)$ в пространстве наблюдений. С другой стороны, образ доверительного эллипсоида в $N$-мерном пространстве наблюдений является $K$-мерным шаром, т.е. для всех граничных точек ${\mathbf{\bar {p}}}$

Следовательно, величина $\left\| {\delta {\mathbf{\bar {p}}}} \right\|$ позволяет приближенно судить о возможном относительном смещении параметрической оценки $\left\| {\delta {\mathbf{\bar {q}}}} \right\|$ около границы доверительного эллипсоида ${\mathbf{\bar {q}}}$.

В нелинейной задаче смещение модельного отклика $\delta {\mathbf{p}}$ вызывается нелинейностью и, таким образом, величину $\left\| {\delta {\mathbf{p}}} \right\|$, определяемую в соответствии с (8), можно принять в качестве показателя нелинейности. Однако в этом случае ${\mathbf{\tilde {p}}} = {\mathbf{p}}({\mathbf{\bar {q}}})$, а ${\mathbf{\bar {p}}} = {\mathbf{\hat {p}}} + {\mathbf{A}}({\mathbf{\bar {q}}} - {\mathbf{\hat {q}}})$, где ${\mathbf{A}}$ – постоянная матрица линеаризированной задачи, вычисляемая в оценке ${\mathbf{\hat {q}}}$, т.е. ${\mathbf{A}} = {{{\mathbf{p}}}_{{\mathbf{q}}}}{\kern 1pt} '({\mathbf{\hat {q}}})$. Следует заметить, что максимальное относительное смещение модельного отклика $\left\| {\delta {\mathbf{p}}} \right\|$, как показывает практика, обычно имеет место вдоль аномального направления в двух противоположных вершинах доверительного эллипсоида, которые максимально удалены от оценки ${\mathbf{\hat {q}}}$, иначе говоря, соответствуют минимальному собственному числу нормальной матрицы ${\mathbf{Q}}$, и тогда $\left\| {\delta {\mathbf{p}}} \right\| \approx \left| {\delta \rho } \right|$.

ПОКАЗАТЕЛИ ПОЛНОЙ, ПАРАМЕТРИЧЕСКОЙ И ВНУТРЕННЕЙ НЕЛИНЕЙНОСТЕЙ

Введем величины

Учитывая, что $\left\| {{\mathbf{A}}\Delta {\mathbf{q}}} \right\| \approx \left\| {\Delta {\mathbf{p}}} \right\|,$ определим показатель нелинейности как

С точки зрения геометрической интерпретации нелинейной задачи наименьших квадратов (Bates, Watts, 1988; Draper, Smith, 1998) столбцы матрицы ${\mathbf{A}}$ представляют собой в $N$-мерном пространстве наблюдений ${\mathbf{p}}$ некий векторный базис $K$-мерного тангенциального подпространства (tangent subspace), которое в точке ${\mathbf{\hat {p}}}$ касается $K$-мерного подпространства оценок ${\mathbf{p}}({\mathbf{q}})$(estimation subspace, solution locus). Ортогональное к нему – $(N - K)$-мерное подпространство невязок (residual subspace). Таким образом, вариацию $\Delta {\mathbf{p}}$ можно представить как сумму ее проекций на эти взаимно ортогональные подпространства:

Разложение вариации $\Delta {\mathbf{p}}$ (10) на ортогональные составляющие ${\mathbf{\Pi }}\Delta {\mathbf{p}}$ и $({\mathbf{E}} - {\mathbf{\Pi }})\Delta {\mathbf{p}}$, тангенциальную и нормальную, позволяет ввести еще два важных показателя – параметрической нелинейности (parameter-effect nonlinearity) и внутренней (intrinsic nonlinearity) (Bates, Watts, 1988; Draper, Smith, 1998):

При этом они должны удовлетворять соотношению ${{\unicode{230} }^{2}} = \unicode{230} _{P}^{2} + \unicode{230} _{I}^{2}.$

Параметрическая нелинейность проявляется, главным образом, в неравномерном изменении модельного отклика на равномерное изменение параметров модели, а также в тангенциальной (геодезической) кривизне параметрических линий в подпространстве оценок. Теоретически существуют такие (нелинейные) преобразования параметров, которые сводят параметрическую нелинейность к нулю. Однако представить их в аналитической форме практически невозможно.

Внутренняя нелинейность обусловлена непосредственно нормальной кривизной подпространства оценок и не зависит от преобразования параметров. Поэтому она неустранима и, следовательно, определяет предельный уровень минимальной нелинейности, которая может быть достигнута в результате преобразований параметров, т.е. при ${{\unicode{230} }_{P}} = 0$. Если ${{\unicode{230} }_{I}} = 0$, а $\unicode{230} = {{\unicode{230} }_{P}} \ne 0$, то говорят, что обратная задача или модель внутренне линейна (intrinsically linear) или внешне нелинейная (nonintrinsically nonlinear) (Bates, Watts, 1988; Draper, Smith, 1998).

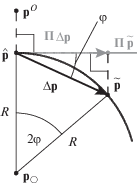
На рис. 1 показана геометрия внутренней нелинейности в плоскости направлений невязок ${{{\mathbf{p}}}^{O}}{\kern 1pt} - {\mathbf{\hat {p}}}$ и вариации $\Delta {\mathbf{p}} = {\mathbf{\tilde {p}}} - {\mathbf{\hat {p}}}$. Здесь $\varphi $ – угловое отклонение модельного отклика $\Delta {\mathbf{p}}$ от тангенциального направления ${\mathbf{\Pi }}\Delta {\mathbf{p}}$ (серый цвет) за нормальную кривизну параметрической линии; $R$ и ${{{\mathbf{p}}}_{\bigcirc }}$ – радиус и центр кривизны соответственно. Из рисунка становится понятен геометрический смысл показателя ${{\unicode{230} }_{I}}$.

Рис. 1.

Геометрия внутренней нелинейности.

Действительно,

Сильная полная нелинейность часто сопряжена с большими отклонениями модельного отклика $\Delta {\mathbf{p}}$, которые провоцируются, главным образом, параметрической нелинейностью. Тогда оценка ${{\unicode{230} }_{I}}$ (12) может неадекватно отображать влияние внутренней нелинейности, вызываемой нормальной кривизной подпространства оценок ${{\kappa }_{N}}$, которая обычно мала. В этом случае, согласно (13), целесообразно использовать альтернативную оценку

Несмотря на большие отклонения $\Delta {\mathbf{p}}$, оценка малой нормальной кривизны ${{\kappa }_{N}}$ (15) должна быть достаточно точной для адекватного оценивания внутренней нелинейности.

Фактически главная цель настоящей работы состояла как раз в исследовании внутренней нелинейности в зависимости от различных типов астероидных орбит и всевозможных обстоятельств наблюдений. Мы должны были выяснить, для каких астероидов и при каких условиях обратной задачи внутренняя нелинейность оказывается незначительной, невзирая на сильную параметрическую нелинейность. Вопрос этот весьма важный в стохастическом моделировании орбитальной неопределенности, поскольку ответ на него в действительности дает надежное практическое основание для так называемого метода возмущенных (зашумленных) наблюдений (observational Monte-Carlo) (Press и др., 2007; Avdyushev, 2011; 2017), который остается пока безальтернативным как наиболее адекватный среди других стохастических методов при доверительном оценивании в сильно нелинейных обратных задачах.

НОРМАЛИЗОВАННАЯ ОБРАТНАЯ ЗАДАЧА

Покажем теперь, что посредством масштабирования, а также преобразований вращения и переноса к геоцентру любую размерную обратную задачу орбитальной динамики можно свести к нормализованной, где гравитационный параметр – единичный, начальный вектор положения является ортом оси абсцисс, а вектор скорости лежит в плоскости абсцисс и ординат (рис. 2).

Рис. 2.

Конфигурация объектов в нормализованной задаче. Серой кривой показана орбита астероида, пунктирной – граница области положений Солнца, соответствующих благоприятным условиям для наземных наблюдений астероида на ночном небе ($90^\circ < \varphi < 270^\circ $).

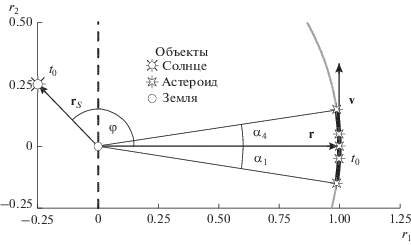
Пусть в исходной размерной задаче $\mu {\kern 1pt} $ – гравитационный параметр Солнца, а ${\mathbf{x}}$ и ${\mathbf{\dot {x}}}$ – гелиоцентрические положение и скорость астероида. Поскольку сильная нелинейность проявляется при обработке наблюдений на очень короткой орбитальной дуге, для ее исследования, игнорируя возмущающие силы, можно прибегнуть к упрощенной динамической модели

Тогда, согласно (16) и (17), геоцентрическое движение астероида ${\mathbf{\rho }} = {\mathbf{x}} - {{{\mathbf{x}}}_{E}}$ будет приближенно описываться формулой

Здесь ${{\rho }_{0}} = {{{\mathbf{x}}}_{0}} - {{{\mathbf{x}}}_{{E0}}}$, ${{\dot {\rho }}_{0}} = {{{\mathbf{\dot {x}}}}_{0}} - {{{\mathbf{\dot {x}}}}_{{E0}}}$ и ${{\rho }_{{S0}}} = - {{{\mathbf{x}}}_{{E0}}}$ – геоцентрические положение и скорость астероида, а также геоцентрическое положение Солнца соответственно на момент ${{t}_{0}}$.

Применив к (18) преобразования масштабирования и вращения:

Таким образом, любая обратная астероидная задача может быть сведена к нормализованной (20) с безразмерными орбитальными параметрам ${{{\mathbf{r}}}_{0}}$ и ${{{\mathbf{v}}}_{0}},$ т.е. ${\mathbf{q}} = {{({{{\mathbf{r}}}_{0}},{{{\mathbf{v}}}_{0}})}^{T}}$. Поскольку параметрические преобразования масштабирования и вращения (19) являются линейными, они не должны влиять на показатели нелинейности (9) и (12). Следовательно, мы можем сфокусировать свое внимание на исследование нелинейности в безразмерной (нормализованной) задаче при всевозможных обстоятельствах наблюдений объектов с различными типами орбит, что тем самым позволит нам рассмотреть проблему нелинейности в целом для всех астероидов Солнечной системы, в том числе еще не открытых.

ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Тестовые астероиды

Поскольку нормализованная модель (20) весьма приближенно представляет орбитальное движение, то ее показатели нелинейности должны отличаться от соответствующих показателей высокоточной модели. Предварительно на примере некоторых астероидов мы проверили, насколько существенными могут быть такие различия в оценках нелинейности для нормализованной приближенной обратной задачи и размерной высокоточной. Как выяснилось, при сильной нелинейности, обусловленной малыми наблюдаемыми орбитальными дугами, показатели совпадали с точностью до одной–двух значащих цифр. Между тем при очень слабой нелинейности, когда наблюдаемые дуги достаточно большие и модель (20) становится грубой для описания орбитального движения, показатели порой плохо совпадали, хотя для приближенной модели они все же были значительно меньше. Таким образом, можно уверенно полагать, что для исследования, по крайней мере, сильной нелинейности и выявления условий ее вызывающих приближенная модель (20) вполне приемлема.

Мы рассмотрели различные условия нормализованной обратной задачи при значениях удаленности Солнца ${{r}_{S}} = 0.5,0.25,0.1$, которые условно соответствуют семействам астероидов главного пояса, троянцев и кентавров (см. табл. 1). Для всех астероидов первая компонента вектора скорости ${{{\mathbf{v}}}_{0}}$ задавалась нулевой, т.е. $\theta = 0$. Моделирование астероидного движения и вычисление показателей нелинейности выполнялись в программной среде Mathematica с четверной точностью.

Таблица 1.  

Параметры приближенной модели в нормализованной задаче для семейств астероидов при наблюдениях в противостоянии ($\theta = 0,\varphi = 180^\circ ,\psi = 0$)

Астероид	$a$ (а. е.)	${{v}^{\operatorname{T} }}$	$\eta $	${{r}_{S}}$	$\Delta t$, сут	${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$	$\Delta \tau $	$\Delta s$
Главный пояс	3	0.6	1.8	0.5	275	0.15	1.67	1
Троянцы	5	1.1	1.4	0.25	420	0.10	0.91
Кентавры	11	2.2	1.2	0.1	832	0.06	0.46

В качестве наблюдаемых величин принимались угловые координаты относительно геоцентра – прямое восхождение $\alpha $ и склонение $\delta $:

$\alpha = \operatorname{arctg} \frac{{{{r}_{2}}}}{{{{r}_{1}}}},\,\,\,\,\delta = \arcsin \frac{{{{r}_{3}}}}{{\left| {\mathbf{r}} \right|}}.$

Наблюдения моделировались на четыре равномерно распределенных момента времени ($L = 4$):

${{\tau }_{i}} = - {{\Delta \tau } \mathord{\left/ {\vphantom {{\Delta \tau } 2}} \right. \kern-0em} 2} + \Delta \tau {{(i - 1)} \mathord{\left/ {\vphantom {{(i - 1)} {(L - 1)\,\,\,\,(i = 1, \ldots ,L)}}} \right. \kern-0em} {(L - 1)\,\,\,\,(i = 1, \ldots ,L)}},$

где $\Delta \tau $ – временной интервал наблюдения. Мы намеренно выбрали предельно минимальное количество наблюдений, с тем чтобы создать критические условия для обратной задачи, когда эффект нелинейности максимален. При $L = 3$ задача уже сводится к предварительному определению орбиты по трем наблюдениям $(N = 2L = K = 6)$ и тогда внутренняя нелинейность становится нулевой: ${{\unicode{230} }_{I}} = 0$. Таким образом, количество наблюдаемых величин составляло $N = 8$, а вектор наблюдений формировался как ${\mathbf{p}} = {{({{\alpha }_{1}}, \ldots ,{{\delta }_{4}})}^{T}}$.

Интересной особенностью нормализованной обратной задачи является то, что при малых наблюдаемых орбитальных дугах $\Delta s$ координата $\delta $ почти нулевая и длину дуги можно приближенно представить как

$\Delta s \approx \frac{{\left| {{{{\mathbf{\rho }}}_{0}} \times {{{{\mathbf{\dot {\rho }}}}}_{0}}} \right|}}{{{{{\left| {{{{\mathbf{\rho }}}_{0}}} \right|}}^{2}}}}\Delta t = \left| {{{{\mathbf{r}}}_{0}} \times {{{\mathbf{v}}}_{0}}} \right|\Delta \tau = {{v}^{\operatorname{T} }}\Delta \tau ,$

следовательно, $\Delta \tau \approx {{\Delta s} \mathord{\left/ {\vphantom {{\Delta s} {{{v}^{\operatorname{T} }}}}} \right. \kern-0em} {{{v}^{\operatorname{T} }}}}$. Мы моделировали наблюдения на трех дугах: $\Delta s = 0.1,0.01,0.001$. В табл. 1 для каждого семейства астероидов приведены значения $\Delta t$, ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$ и $\Delta \tau $, соответствующие длине орбитальной дуги в один радиан. Из значений $\Delta t$, в частности, можно оценить длительность наблюдений. Например, для главного пояса длина дуги $\Delta s = 0.001 \approx 3.4{\kern 1pt} '$ соответствует наблюдениям в течение одной ночи, а $\Delta s = 0.01 \approx 0.57^\circ $ – наблюдениям двух–трех ночей.

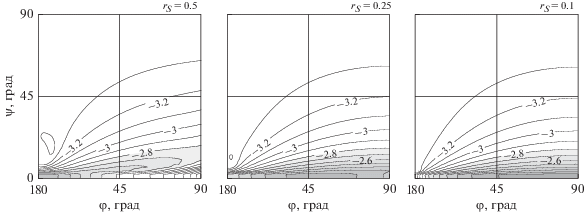
На рис. 3–5 представлены показатели нелинейности в зависимости от сферических геоцентрических координат Солнца $\varphi $ и $\psi $ при 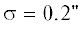(характерная дисперсия ошибок современных наземных ПЗС-наблюдений) и ${{\chi }_{{6,0.997}}} = 4.5$. Здесь заливка полутонами серого цвета применяется только к уровням показателей, превышающих околокритическое значение ${{10}^{{ - 3}}}$. Координата $\varphi $ варьировалась на отрезке $[90^\circ ,270^\circ ]$, что соответствует благоприятным конфигурациям Солнце–Земля–астероид для наземных наблюдений малого небесного тела на ночном небе. Как ожидалось, распределения показателей оказались симметричными относительно осей $\varphi = 180^\circ $ и $\psi = 0$, поэтому на рисунках для каждой задачи показана лишь четверть $(\varphi ,\psi ) \in [90^\circ ,\,\,180^\circ ] \times [0^\circ ,\,\,90^\circ ]$ от всей области изменения угловых координат Солнца.

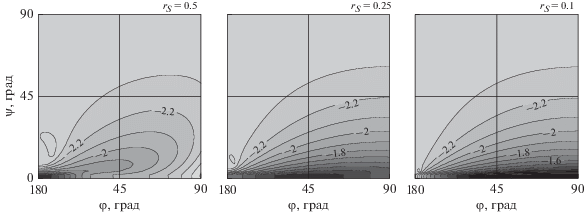
Рис. 3.

Полная нелинейность $lg\unicode{230} $ в нормализованной задаче при наблюдаемой орбитальной дуге $\Delta s = 0.1$ на множестве положений Солнца ${{{\mathbf{r}}}_{S}}$ в сферических слоях ${{r}_{S}} = 0.1,0.25,0.5$.

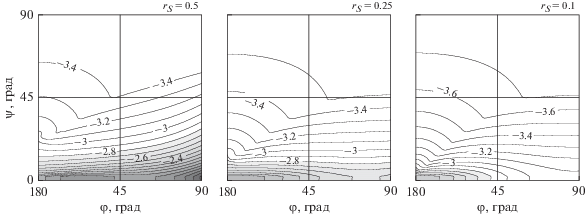
Рис. 4.

Внутренняя нелинейность $lg{{\unicode{230} }_{I}}$ в нормализованной задаче при наблюдаемой орбитальной дуге $\Delta s = 0.01$ на множестве положений Солнца ${{{\mathbf{r}}}_{S}}$ в сферических слоях ${{r}_{S}} = 0.1,0.25,0.5$.

Рис. 5.

То же, что и на рис. 4, но при наблюдаемой орбитальной дуге $\Delta s = 0.001$.

Как видно из рис. 3, полная нелинейность при наблюдаемой орбитальной дуге $\Delta s = 0.1 \approx 5.7^\circ $ в основном слабая $(\unicode{230} < {{10}^{{ - 3}}})$ либо умеренная $({{10}^{{ - 3}}} < \unicode{230} < {{10}^{{ - 2}}})$. Большие показатели нелинейности возникают при малых значениях $\psi $, т.е. когда астероид находится вблизи плоскости эклиптики. В таких условиях наблюдаемая орбитальная дуга едва ли не вырождается в отрезок, что приводит, в свою очередь, к ухудшению обусловленности обратной задачи и усилению нелинейности. Между тем показатели для кентавров в общем достаточно малы, что может объясняться длительностью периода наблюдений почти до трех месяцев. За это время Земля проходит значительный участок своей орбиты и вследствие усложненного относительного движения удаленного астероида его наблюдаемая траектория становится более изогнутой, нежели той же длины траектория близкого астероида, например, главного пояса. Формально кривизна траектории определяется, главным образом, членом второго порядка в модели (20), а именно членом ${{{{{{{\mathbf{r}}}_{{S0}}}} \mathord{\left/ {\vphantom {{{{{\mathbf{r}}}_{{S0}}}} {\left| {{{{\mathbf{r}}}_{{S0}}}} \right|}}} \right. \kern-0em} {\left| {{{{\mathbf{r}}}_{{S0}}}} \right|}}}^{3}}$. Следовательно, чем меньше $\left| {{{{\mathbf{r}}}_{{S0}}}} \right|$ или чем дальше наблюдаемый объект, тем больше кривизна его наблюдаемой траектории в картинной плоскости.

При уменьшении орбитальной дуги до $\Delta s = 0.01$ полная нелинейность значительно ухудшается для любых $\varphi $ и $\psi $ во всех задачах: ее показатель не достигает даже значения ${{10}^{{ - 2}}}$. Тем не менее, как показывает рис. 4, внутренняя нелинейность остается еще достаточно слабой. Интересно заметить, что структура распределения значений ее показателя в задачах очень похожа. Впрочем, уже при дуге $\Delta s = 0.001$ (рис. 5) ощутимо ухудшается и внутренняя нелинейность: ее показатель увеличивается ровно на порядок и для наблюдаемых объектов вблизи эклиптики достигает значений до $0.05$. Таким образом, чтобы внутренняя нелинейность обратной задачи была приемлемо слабой, обрабатываемые наблюдения должны охватывать периоды, по меньшей мере, от трех ночей для объектов главного пояса и до восьми ночей для кентавров, когда орбитальная дуга порядка $\Delta s = 0.01$ (см. табл. 1).

Разумеется, нелинейность зависит не только от длины наблюдаемой орбитальной дуги $\Delta s$, но и от таких параметров обратной задачи, как $L$ (количество моментов наблюдений); $\theta $ (отклонение вектора скорости от трансверсального направления); $\sigma $ (дисперсия ошибок); ${{\chi }_{{K,\alpha }}}$ ($\alpha $-квантиль функции распределения $\chi _{K}^{2}$). Мы исследовали, как зависит нелинейность от этих параметров на примере тестового объекта типа Цереры с круговой орбитой радиуса $a = 3$ а. е. и наклонением $I = 10^\circ $. В качестве исходных мы приняли следующие значения параметров: $\Delta s = 0.001$; $L = 4$; 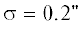; ${{\chi }_{{6,0.997}}} = 4.5$; ${{v}^{\operatorname{T} }} = 0.588$; $\theta = 0$; ${{r}_{S}} = {\text{0}}{\text{.506}}$; $\varphi = 180^\circ $; $\psi = 15^\circ $. При этом показатели параметрической и внутренней нелинейностей составили ${{\unicode{230} }_{P}} = 13.8$ и ${{\unicode{230} }_{I}} = 4.39 \times {{10}^{{ - 3}}}$ соответственно.

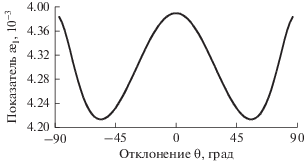
Варьируя параметр $\theta $, мы обнаружили, что нелинейность (как параметрическая, так и внутренняя) слабо чувствительна к нему. Из рис. 6 видно, что показатель внутренней нелинейности в ответ на существенные вариации $\theta $ изменяется только во второй значащей цифре около ${{\unicode{230} }_{I}} = 4.3 \times {{10}^{{ - 3}}}$. Показатель параметрической нелинейности имеет точно такой же характер изменения, но около ${{\unicode{230} }_{P}} = 13.4$. Следовательно, нелинейность предопределяется, главным образом, трансверсальной составляющей наблюдаемого астероидного движения относительно Земли. Кстати, именно она фактически отображается в наблюдениях в картинной плоскости. Этот результат тем более повышает практическую значимость результатов выше (рис. 3–5), поскольку они становятся применимы уже к любым орбитам вплоть до гиперболических.

Рис. 6.

Внутренняя нелинейность в зависимости от отклонения вектора скорости $\theta $ (относительно трансверсального направления) ($\Delta s = 0.001$, $L = 4$, 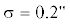, ${{\chi }_{{6,0.997}}} = 4.5$).

Очевидно, что с удалением от оценки ${\mathbf{\hat {q}}}$ в параметрическом пространстве влияние нелинейности усиливается. Показатели нелинейности (9) и (12) вводятся для максимально удаленной от ${\mathbf{\hat {q}}}$ точки на границе доверительного эллипсоида вероятности $\alpha $. Размер доверительного эллипсоида задается квантилем ${{\chi }_{{K,\alpha }}}$ и среднеквадратической ошибкой $\sigma $, точнее, их произведением $\sigma {{\chi }_{{K,\alpha }}}$. Чтобы оценить зависимость нелинейности от удаленности от оценки ${\mathbf{\hat {q}}}$, мы проварьировали лишь значения квантиля $\chi $. Как видно из рис. 7, показатель внутренней нелинейности (как и параметрической) прямо пропорционален квантилю, иначе говоря, размеру принятой доверительной области, на границе которой оценивается нелинейность. В частности, поэтому высокоточные наблюдения являются залогом слабой нелинейности. Кроме того, размер доверительного эллипсоида зависит от количества наблюдений: чем больше наблюдений $N = 2L$, тем больше собственные числа нормальной матрицы ${\mathbf{Q}}$, в том числе и ${{\lambda }_{{\min }}}$ (9), и тем меньше размер эллипсоида. Следовательно, увеличение количества наблюдений также ослабляет нелинейность (см. рис. 8).

Рис. 7.

Внутренняя нелинейность в зависимости от коэффициента $\chi $ при $\sigma $ ($\Delta s = 0.001$, $L = 8$, 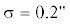, $\theta = 90^\circ $).

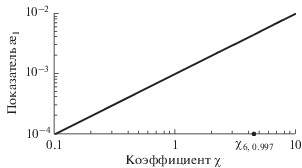
Рис. 8.

Нелинейность в зависимости от длины наблюдаемой орбитальной дуги ${{\Delta }_{S}}$ и количества моментов наблюдений $L$ ($\sigma = 0.2$'', ${{\chi }_{{6,0.997}}} = 4.5$, $\theta = 90^\circ $).

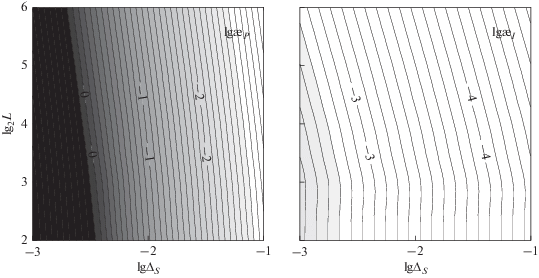
Важными параметрами информативности об астероидном движении являются длина наблюдаемой орбитальной дуги $\Delta s$ и количество моментов наблюдений $L$. Исследуя нелинейность при их различных значениях (рис. 8), мы установили, что оба показателя нелинейности почти пропорциональны ${{L}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, но ${{\unicode{230} }_{P}} \sim \Delta {{s}^{{ - 2}}}$ и ${{\unicode{230} }_{I}} \sim \Delta {{s}^{{ - 1}}}$ при $\Delta s \to 0$. В частности, это говорит о том, что проблема сильной нелинейности эффективнее разрешается скорее увеличением продолжительности наблюдений, нежели увеличением их объема. С другой стороны, поскольку внутренняя нелинейность менее чувствительна к вариациям длины наблюдаемой орбитальной дуги, нежели параметрическая, она даже при очень малой дуге еще достаточно слабая, тогда как полная нелинейность становится чрезвычайно сильной. Следовательно, это дает нам практическое основание для использования метода возмущенных (зашумленных) наблюдений при стохастическом моделировании орбитальной неопределенности, когда линейные методы уже непригодны.

Потенциально опасные астероиды

Главными объектами нашего исследования на предмет нелинейности являлись потенциально опасные астероиды. Мы проанализировали 395 объектов, наблюдавшихся в одном появлении (оппозиции) до июня 2020 г. Именно эти астероиды представляли для нас особый интерес, поскольку многие из них наблюдались на очень коротких орбитальных дугах. Поэтому их орбиты имеют достаточно большую неопределенность, что сопряжено с проблемой сильной нелинейности.

Орбитальные параметры астероидов ${{{\mathbf{x}}}_{0}}$ и ${{{\mathbf{\dot {x}}}}_{0}}$ определялись из позиционных наблюдений, размещенных на сайте Центра малых планет (www.minorplanetcenter.net). Начальная эпоха ${{t}_{0}}$ для каждого астероида выбиралась как среднеарифметическое всех моментов наблюдений ${{t}_{i}}\;(i = 1, \ldots ,L)$, поскольку отнесенные к ней орбитальные параметры обеспечивают наименьшую полную (параметрическую) нелинейность (Черницов, 1975)²². Астероидные орбиты моделировались на основе дифференциальных уравнений гравитационной задачи многих тел (Солнце, планеты, Луна, астероид), которые интегрировались численно методом Эверхарта (Everhart, 1974; Авдюшев, 2015).

Общий анализ показал, что в задачах вероятностного оценивания линейное стохастическое моделирование орбитальной неопределенности недопустимо для почти половины объектов (44% при ${{\unicode{230} }_{P}} > {{10}^{{ - 3}}}$) (рис. 9, табл. 2). Впрочем, для подавляющего большинства астероидов (92%) внутренняя нелинейность слабая (${{\unicode{230} }_{I}} < {{10}^{{ - 3}}}$) и, следовательно, для стохастического моделирования могут быть применены нелинейные методы. Тем не менее, 8% (${{\unicode{230} }_{I}} > {{10}^{{ - 3}}}$) пока не имеют достаточно информативных наблюдений, которые бы давали возможность адекватно исследовать их орбитальные неопределенности даже нелинейными методами.

Рис. 9.

Распределение показателей нелинейности для потенциально опасных астероидов, наблюдавшихся в одном появлении.

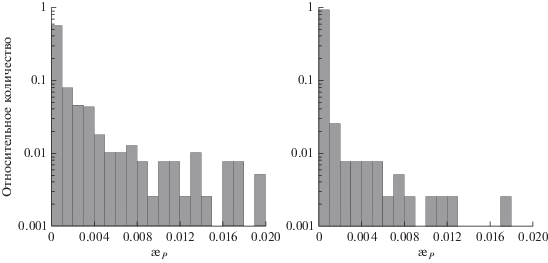
Таблица 2.  

Статистика показателей нелинейности для потенциально опасных астероидов, наблюдавшихся в одном появлении

Нелинейность	Показатели, %
	$(0,{{10}^{{ - 3}}}]$	$({{10}^{{ - 3}}},{{10}^{{ - 2}}})$	$[{{10}^{{ - 2}}},\infty )$
Параметрическая	56	23	21
Внутренняя	92	6	2

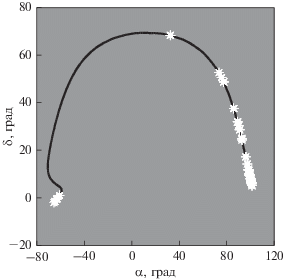
Наблюдаемые траектории многих астероидов весьма сложные, поскольку наблюдались они на подлете к Земле (рис. 10). Кроме того, в отличие от нормализованной задачи, распределения наблюдений таких объектов очень неоднородны (рис. 10). Поэтому нам было довольно сложно выявить связь между показателями нелинейностей и спецификой условий наблюдений для реальных астероидов.

Рис. 10.

Наблюдения астероида 2017 BQ6 (звездочки) и его траектория движения (черная кривая) на небесной сфере. Орбитальные элементы: $a = {\text{1}}{\text{.94}}\;{\text{a}}{\text{.}}\,\,{\text{e}}{\text{.}}$, $e = 0.{\text{53}}$, $I = 9.04^\circ $ (${{t}_{0}} = {\text{07}}{\text{.02}}{\text{.2017}}$). Минимальное расстояние: ${{\rho }_{{\min }}} = 5.5$ млн км. Наблюдения: $L = 224$, $\Delta t = 130$ сут (26.01.2017–05.06.2017), 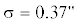. Нелинейность: ${{\unicode{230} }_{P}} = 1.6 \times {{10}^{{ - 5}}}$, ${{\unicode{230} }_{I}} = {{10}^{{ - 6}}}$.

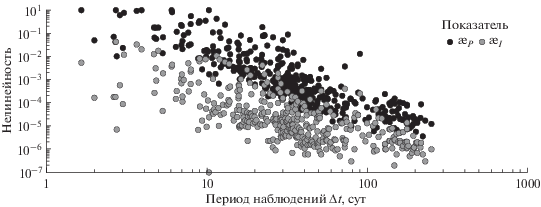
Тем не менее, проявляется некоторая корреляция между показателями и периодом наблюдений (рис. 11). Имеет место очевидная тенденция к уменьшению показателей с увеличением периода наблюдений. Так, согласно рис. 11, если астероид наблюдается менее 10 суток, параметрическая (полная) нелинейность – сильная, тогда как внутренняя может быть очень слабой. Гарантированно внутренняя нелинейность будет слабой в том случае, когда объект наблюдается более месяца. Наконец, обратная задача становится полностью слабо нелинейной только после трех месяцев наблюдений.

Рис. 11.

Нелинейность в зависимости от периода наблюдений для потенциально опасных астероидов, наблюдавшихся в одном появлении.

ЗАКЛЮЧЕНИЕ

В итоге исследования нелинейности в обратных задачах астероидной динамики мы приходим к следующему заключению. В контексте обстоятельств позиционных (угловых) наблюдений главными факторами сильной нелинейности, как и большой орбитальной неопределенности, являются короткая наблюдаемая орбитальная дуга и малый период наблюдения. При этом ситуация усугубляется, если движение астероида во время наблюдения совершается вдоль и около эклиптики по дуге с малой кривизной.

Для оценивания полной, параметрической и внутренней нелинейностей мы вводим оригинальные показатели с обоснованными пороговыми значениями, определяемыми из предельно допустимых смещений вероятностных оценок за нелинейность. Исследование нелинейности с применением предлагаемых показателей в нормализованной задаче приводит нас к общим практическим выводам.

Если на отдалении от эклиптики астероид наблюдается на дуге в несколько градусов и более, уверенно можно ожидать, что обратная задача будет слабо нелинейной и поэтому для моделирования орбитальной неопределенности в задачах вероятностного оценивания могут применяться линейные стохастические методы. При дугах меньше одного градуса задача становится сильно нелинейной. Однако, если наблюдения охватывают несколько ночей и более, внутренняя нелинейность обратной задачи оказывается еще достаточно слабой и поэтому для стохастического моделирования вполне применимы нелинейные методы.

На основании общего анализа нелинейности для всех потенциально опасных астероидов, наблюдавшихся в одном появлении до июня 2020 г., установлено, что вследствие сильной нелинейности в задачах вероятностного оценивания для почти половины объектов (44%) требуются нелинейные стохастические методы. Хотя 8% пока еще не имеют достаточно информативных наблюдений, которые бы давали возможность адекватно исследовать их орбитальные неопределенности даже нелинейными методами, поскольку внутренняя нелинейность для таких объектов довольно сильная.

Ввиду сложности наблюдаемых траекторий многих потенциально опасных астероидов и неоднородности в пространственно-временном распределении их наблюдений, трудно выявить, какие характерные обстоятельства наблюдений могут быть сопряжены с сильной нелинейностью. Таким образом, нельзя наперед определить степень нелинейности обратной задачи и поэтому для каждого астероида требуется непосредственное ее оценивание с применением предлагаемых в работе показателей.

Тем не менее, некоторая корреляция проявляется между нелинейностью и периодом наблюдений. Если наблюдения охватывают период менее 10 сут, обратная задача – сильно нелинейная. Внутренняя нелинейность – гарантированно слабая, если астероид наблюдается более одного месяца. Наконец, обратная задача становится полностью слабо нелинейной только после трех месяцев наблюдений.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № 0721-2020-0049).