Астрономический вестник, 2021, T. 55, № 1, стр. 34-37

Приблизительная обратная квадратичность спектров рельефа планет десятки лет оставалась необъяснимой загадкой в планетной астрономии. Это свойство было отмечено в начале 1960-х гг. американским геодезистом Вольфгангом Каула, когда он заметил, что сферические гармоники флуктуаций силы тяжести, а затем и рельефа (Kaula, 1966; Turcotte, 1997; Гледзер, Голицын, 2019), убывают как квадрат номера гармоники, начиная с $n \geqslant 4$. Позднее такое свойство было отмечено для Венеры, Марса, Луны, для астероида Веста и для совсем мелкого астероида порядка километра (Гледзер, Голицын, 2019; Gledzer, Golitsyn, 2019). Несколько лет назад методы анализа сферических гармоник были существенно улучшены, и число гармоник достигло 46 200 для Земли и Луны и 23 100 для Марса. Для Земли спектральный анализ охватывает масштабы порядка 600 м, а для Луны – 120 м (Rexer, Hirt, 2015). Объяснение правила Каулы как следствие вероятностных законов А.Н. Колмогорова и его школы было опубликовано в 2019 г. Е.Б. Гледзером и Г.С. Голицыным (Гледзер, Голицын, 2019) и в более полной статье (Gledzer, Golitsyn, 2019).

Законы Колмогорова (Kolmogorov, 1934) и их первичный анализ в приложении к пространственной структуре турбулентности А.М. Обуховым (Obukhov, 1959) были использованы более 60 лет назад, и их подробный анализ описан в книге А.С. Монина и А.М. Яглома “Статистическая гидромеханика” (Монин, Яглом, 1967) вместе с техническим аппаратом для анализа экспериментальных данных. Однако кроме турбулентности эти вероятностные идеи нигде не использовались, и только к 2018 г. стало ясно широкое поле их использования для описания многих статистических законов природы, как то: законы Гутенберга–Рихтера для частоты землетрясений, распределения литосферных плит по размерам, частотного спектрального состава морских ветровых волн и законов их разгона, скоростей и размера ураганов и т.д. (Golitsyn, 2018). В настоящее время автор, пользуясь карантином, готовит книгу по всем этим вопросам.

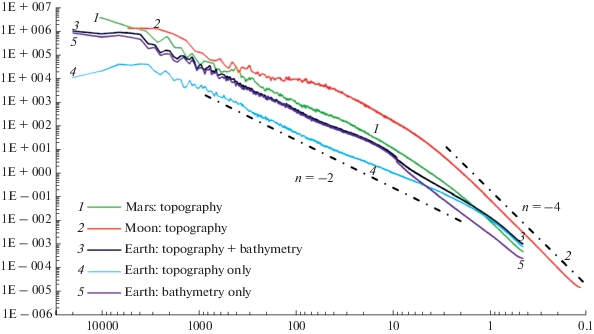
Однако вернемся к рельефам. Рис. 1 из (Rexer, Hirt, 2015; Gledzer, Golitsyn, 2019) дает экспериментальные спектры рельефа для Луны, Марса и Земли, причем для последней – полный, только для твердой поверхности и для морского дна. Все они имеют четкий наклон спектров ${{k}^{{ - 2}}}$, начиная с размеров порядка четверти радиуса, k ~ 1/y. Спектр Луны в интервале масштабов 200–10 км идет выше спектра ${{k}^{{ - 2}}}$. Очевидно, это связано с бомбардировкой ее поверхности астероидами километрового размера, образующими кратеры с диаметрами на порядок больше размера ударных тел.

Для Земли и Марса их атмосферы препятствуют проникновению к поверхности небольших тел, поэтому спектр рельефа у них не имеет такое четкой особенности. У Луны, начиная с $y \leqslant 3$ км спектр рельефа укручается, приближаясь в более мелких масштабах к ${{k}^{{ - 4}}}$. Для двух наших планет начало укручения спектров тоже намечается с масштабов $y \leqslant 1$ км. И это связано с физико-математической моделью образования рельефа, в основе которой лежат идеи (Kolmogorov, 1934; Obukhov, 1959; Монин, Яглом, 1967; Golitsyn, 2018).

Работу А.Н. Колмогорова (Kolmogorov, 1934) “Случайные движения” можно найти в издававшихся неоднократно собраниях его сочинений. Она содержит распределения вероятностей $p({{x}_{i}},{{u}_{i}},t)$ для шестимерного вектора координат ${{x}_{i}}$ и скоростей ${{u}_{i}}$ в их зависимости от времени t на основе обобщенного уравнения Фоккера–Планка–Колмогорова

В (Kolmogorov, 1934; Монин, Яглом, 1967) записано фундаментальное решение этого уравнения. А.М. Обухов показал, что в случае турбулентности коэффициент диффузии $D = \varepsilon $, скорости генерации/диссипации кинетической энергии, т.е. ε – коэффициент диффузии в пространстве скоростей. В (Монин, Яглом, 1967) показано, что частотный спектр ε постоянен, т.е. это белый шум (Яглом, 1949). В (Гледзер, Голицын, 2010) показано, что замена переменных ${{u}_{i}} = {{\tilde {u}}_{i}}{{(\varepsilon t)}^{{1/2}}}$ и ${{x}_{i}} = {{\tilde {x}}_{i}}{{(\varepsilon {{t}^{3}})}^{{1/2}}}$ сводит (1) к безразмерному виду, т.е. в масштабах ${{\tilde {u}}_{i}}$ и ${{\tilde {x}}_{i}}$ уравнение (1) становится автомодельным. Это значит, что средние значения

так зависят от времени. Численные расчеты (Гледзер, Голицын, 2010) были проведены в зависимости от числа частиц N, ускоряемых случайным образом и независимо друг от друга. Расчеты показали, что даже при N = 10 зависимости (2) выполняются вполне удовлетворительно, а при N = 100 рассчитанные значения практически не отличаются от их теоретических значений.

Наши расчеты (Гледзер, Голицын, 2010) и теория (Kolmogorov, 1934) отличаются тем, что Колмогоров принимал ускорения распределенными по Маркову, т.е. равномерно случайными. В (Гледзер, Голицын, 2010) эти распределения считались для различных распределений, и все равно зависимости (2) выполнялись также хорошо. По сути дела, в (Гледзер, Голицын, 2010) считались уравнения Ньютона для движений N частиц с единичной массой со случайными ускорениями по времени для каждой частицы, некоррелированной с соседними, и находились структурные функции для взаимных скоростей и положений, и все равно зависимости (2) выполнялись также хорошо.

В настоящее время большинство измерительных приборов дают результаты, удобные для представления в спектральном виде. Спектры связаны со структурными функциями преобразованиями типа Фурье (Obukhov, 1959; Монин, Яглом, 1967; Golitsyn, 2018; Гледзер, Голицын, 2010; Яглом,1955; Голицын, Фортус, 2020). При этом положительный показатель степени у степенной зависимости ${{t}^{n}}$ связан с отрицательным показателем спектра ${{\omega }^{{ - {\kern 1pt} m}}}$ соотношением $m - 1 = n$.

Рельеф h(y) измеряется часто альтиметрами, установленными на спутниках или других аппаратах, летающих с известной скоростью $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} $. Поэтому временной сигнал $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{u} h(t) = h(y)$ таким преобразованием переводится в пространственный случайный сигнал. При этом первый масштаб Колмогорова в (2) может быть записан как

где коэффициент диффузии $D$ должен определяться из результатов измерений. Однако следует считать, что измеренное тем или иным способом пространственное распределение рельефа устанавливается за многие миллионы лет, и к нему сразу можно применять уравнение Фоккера–Планка–Колмогорова с заменой времени на y и координаты x на высоту h, и тогда преобразование типа Фурье функции (3), как структурной, дает пространственный спектр рельефа

Такие спектры приведены в (Turcotte, 1997; Голицын, 2012). Для масштабов от 0.3 до 30 км для трех типов рельефа, равнинного, холмистого и горного. По 20 разрезам для каждого типа спектр весьма близок к (4) со средним показателем $n = 2.03 \pm 0.04$ (Голицын, 2003; 2012). Крупные сферические гармоники с номерами $n \leqslant 4$ отклоняются вниз от зависимости ${{n}^{{ - 2}}}$ для их амплитуд и, очевидно, связаны с глобальной тектоникой (Kaula, 1966; Turcotte, 1997).

Еще в (Голицын, 2003) было отмечено, что форма спектра ${{k}^{{ - 2}}}$ (4) означает, что спектр уклонов $\alpha $ рельефа, т.е. величины $\alpha = {{dh(y)} \mathord{\left/ {\vphantom {{dh(y)} {dy}}} \right. \kern-0em} {dy}}$, постоянен с частотой:

т.е. это белый шум. Это соответствует гипотезе А.Н. Колмогорова о марковости распределений вероятностей для ускорений (Kolmogorov, 1934; Гледзер, Голицын, 2010). Квадрат скорости – есть энергия, работа, производимая полем силы тяжести над частицей при ее подъеме на высоту $h(z)$. Производная рельефа по координате есть уклон, вдоль которого действует сила тяжести, и если спектр углов есть белый шум, то и ускорения в такой системе будут марковскими. По углам течет вода, сыплется порода, на такую поверхность действует ветер и т.п.

Однако и визуальная картина земного рельефа для малых масштабов показывает какую-то корреляцию между углами. Это четко видно на рис. 1 для Луны и намечается для Земли и Марса в укручении спектров от ${{k}^{{ - 2}}}$ до ${{k}^{{ - 4}}}$. Для лунной поверхности на рис. 1 этот переход происходит в районе ${{y}_{0}}$ ~ 4 км, а для марсианского и земного рельефов при полутора км и нескольких стах метров. Для описания этих изменений в спектрах примем, что между углами в этом интервале имеет место простейшая корреляция $\alpha ({{y}_{1}})\alpha ({{y}_{2}})$ = $ = {{\exp ( - ({{y}_{1}} - {{y}_{2}})} \mathord{\left/ {\vphantom {{\exp ( - ({{y}_{1}} - {{y}_{2}})} {{{y}_{0}})}}} \right. \kern-0em} {{{y}_{0}})}}$ , спектр которой

Тогда согласно (5) спектр рельефа поверхности будет

т.е. при ${{({k \mathord{\left/ {\vphantom {k {{{k}_{0}}}}} \right. \kern-0em} {{{k}_{0}}}})}^{2}}$ $ \ll $ 1 спектр рельефа будет ${{S}_{h}}(k)$ ~ ${{k}^{{ - 2}}}$, а при k $ \gg $ ${{k}_{0}}$ спектр ~${{k}^{{ - 4}}}$.

Остается понять физический смысл масштаба ${{y}_{0}} = k_{0}^{{ - 1}}$, что непросто, так как физические условия образования рельефов и их эволюции на Луне, где нет атмосферы и жидкой воды, отличны от Земли и Марса. На Луне действует только сила тяжести и ударная бомбардировка поверхности, т.е. надо знать и механические свойства поверхности. Отсутствие атмосферы, очевидно, объясняет, что из трех спектров рис. 1 лунный спектр максимален по амплитудам, т.е. выше других, а земной – минимален.

Переход от спектра ${{k}^{{ - 2}}}$ к ${{k}^{{ - 4}}}$ занимает какой-то интервал масштабов, и этот интервал строго определить по экспериментальным данным нелегко. Координату такого перехода определим по экспериментальным данным как его середину. Эти значения ${{y}_{0}}$, как размеры и ускорение силы тяжести представлены в таблице.

То, что укручение спектра начинается раньше всего у Луны, а позже – у Земли, говорит о том, что величина ${{y}_{0}}$ обратно пропорциональна гравитационному ускорению. Попытаемся найти величину ${{y}_{0}}$ из соображений подобия и размерности при ударном формировании рельефа как на Луне: происходит разрушение породы и ее разброс по сторонам. Здесь должны быть учтены плотность породы ρ и его модуль Юнга μ. Последняя величина тесно связана с внутренней энергией тела. Величина

определяет квадрат скорости упругих волн. Величина с – это скорость фононов, а ее квадрат можно связать с внутренней энергией породы на единицу массы. Для простоты пренебрежем различиями ${{c}^{2}}$ для наших объектов. Разлет породы обратно пропорционален g, поэтому примерное постоянство произведения $g{{y}_{0}}$ представляется непротиворечивым нашим представлениям об ударных свойствах рельефа безатмосферных тел в малых масштабах.

Соображения подобия дают (Баренблатт, 2009)

где численный коэффициент $a = {{10}^{{ - 3}}}$, оцениваемый по данным таблицы при ${{с}^{2}} \approx {{10}^{7}}$м²/с², иллюстрируют 4-й и 5-й ее столбцы.

Глобальный параметр подобия объединяет в себе все основные свойства твердых объектов

где ${{G}^{{ - 1}}} = 1.5 \times {{10}^{{10}}}$ кг с²/м³ – обратная величина гравитационной постоянной. Этот параметр подобия приведен в последнем столбце и сопоставляет наши три тела в их начальный период жизни, подчеркивая влияние силы тяжести на величину и характер рельефа.

Для автора данный текст представляет попытку увидеть и в статистике рельефа небесных тел проявления законов теории вероятности Колмогорова и его школы и служит кратким дополнением к работам (Гледзер, Голицын, 2019; Gledzer, Golitsyn, 2019).

Автор благодарен рецензенту, замечания которого позволили существенно улучшить представление материала статьи.