1. На главную
  2. Электронные версии
  3. Астрономический вестник
  4. T. 55, № 1, 2021

Астрономический вестник, 2021, T. 55, № 1, стр. 13-21

Анализ данных топографии и гравитационного поля землеподобной Венеры

Т. И. Менщикова a, Т. В. Гудкова a, *, В. Н. Жарков a

a Институт физики Земли им. О.Ю. Шмидта РАН
Москва, Россия

* E-mail: gudkova@ifz.ru

Поступила в редакцию 15.07.2020
После доработки 09.09.2020
Принята к публикации 11.09.2020

Полный текст (PDF)

Аннотация

Рассмотрен вопрос о выборе референсной поверхности для анализа данных топографии и гравитационного поля Венеры. Используется гипотеза, что Венера землеподобна. За референсную поверхность выбирается поверхность эффективно равновесной Венеры, которая сохранилось от более ранней эпохи. Для набора землеподобных моделей внутреннего строения Венеры рассчитаны параметры равновесной фигуры. Проведен анализ высот геоида и отклонений силы тяжести от гидростатически равновесных значений для различных районов.

Ключевые слова: Венера, землеподобная модель внутреннего строения, параметры равновесной фигуры, топография, гравитационное поле

ВВЕДЕНИЕ

В 1960–1980-х годах Венера интенсивно исследовалась советскими и американскими космическими аппаратами. Первые фотографии и панорамы поверхности Венеры были получены советскими спускаемыми космическими аппаратами (КА) Венера 9 и 10 (Florensky и др., 1977). Они измерили температуру и давление на поверхности планеты, определили плотность пород в районе станции.

Основные наблюдательные данные, которые позволяют продвигаться в изучении недр Венеры, это снимки ее поверхности со спутников, данные топографии и гравитационного поля. Разработаны геологические карты Венеры (Barsukov и др., 1986; Basilevsky, 2008; Ivanov, Нead, 2011). На поверхности планеты имеется множество различных структур (цепи горных массивов, щитовые вулканы, рифтовые равнины), а также такие необычные детали рельефа как венцы (кольцевые структуры размером от 150 до 600 км) и следы серий растяжения и сжатия на равнинах, так называемые тессеры – чередующиеся хребты и долины, напоминающие черепицу). Подробное изучение и анализ морфологии тектонических структур и их расположения проводились в работах (Basilevsky, Head, 1998; 2000; Ivanov, Нead, 2011; 2013; 2015).

В 1982 году на Венере были проведены первые сейсмические эксперименты. Приборы регистрировали колебания поверхности в течение часа: датчик КА Венера 13 не зарегистрировал колебаний, на датчике КА Венера 14 зафиксировано два микросейсма (Ksanfomaliti и др., 1982). Интерпретация этих данных неоднозначна.

В отсутствии сейсмических данных, совместный анализ гравитационного поля и топографии Венеры позволяет получать представление о распределении плотностных неоднородностей в приповерхностных областях планеты, проводить оценки толщины коры и литосферы под локальными структурами, а также исследовать вопросы о способе поддержки топографии (изостатически и/или динамически – мантийные течения, поднимающиеся или опускающиеся плюмы) (Breuer, Moore, 2007; Wieczorek, 2015; Jimenez-Diaz и др., 2015; Yang и др., 2016; Li и др., 2015).

Интерес к анализу имеющихся данных топографии и гравитационного поля связан с планируемыми миссиями по исследованию Венеры: проект Роскосмоса и NASA “Венера-Д”, проект EnVision ЕКА (Ghail и др., 2018), направленный на уточнение данных о гравитационном поле Венеры, миссия VERITAS (NASA) для улучшения точности гравитационного поля Венеры до 3 мГал и пространственным разрешением 145 км (Smrekar и др., 2016).

При работе с данными топографии и гравитационного поля встает вопрос о выборе поверхности отсчета или референсной поверхности. Для Венеры выбор поверхности отсчета отличается от выбора референсной поверхности для Земли и Марса. Земля и Марс находятся близко к состоянию гидростатического равновесия. Венера принципиально отлична от Земли и Марса, она сильно отклонена от состояния гидростатическиго равновесия.

Для равновесной планеты величины малого параметра теории фигуры m и гравитационный момент J2 одного порядка малости. Для Венеры J2 в 72 раза больше, чем m. Вращение Венеры было сильно замедлено приливным трением. В работе (Жарков, Гудкова, 2019) отношение J2/m для эффективно равновесной Венеры было принято равным 0.3 (таким же как для Земли), считая, что в более раннюю эпоху равновесная фигура планеты зафиксировалась, также как и значение J2, которое сохранилось до настоящего времени. Для планеты, отклоняющейся от состояния гидростатического равновесия, разница главных моментов инерции по отношению к осям в экваториальной плоскости, f = (B – A)/MR2 = 4√($C_{{22}}^{2} + S_{{22}}^{2}$) не равна нулю (М – масса, R – средний радиус, C22 и S22 – коэффициенты разложения гравитационного потенциала по сферическим функциям). Для Венеры величина f мала и близка к значению для Земли (f = 3.5 × 10–6 для Венеры и f = 7.2 × 10–6 для Земли). Это говорит о том, что распределение плотности близко к осесимметричному с хорошей точностью (Zharkov, 1983). Этот факт также укрепляет идею, что огромное неравновесное значение J2 для планеты представляет реликтовое значение, которое соответствовало быстро вращающейся Венере в некоторую ранюю эпоху.

Вышесказанное позволяет оптимальным образом выбрать отсчетную поверхность, предположив, что Венера как и Земля находилась в гидростатически равновесном состоянии. В данной работе за референсную поверхность принимается поверхность эффективно равновесной Венеры, которая сохранилось от более ранней эпохи. Для ряда модельных распределений плотности в недрах Венеры будут получены параметры равновесной фигуры и равновесные значения гравитационных моментов $J_{2}^{0}$ и $J_{4}^{0}$ землеподобной Венеры и проведено разделение гравитационного потенциала на гидростатически равновесную часть и неравновесную компоненту. Затем проведен анализ высот геоида и отклонений силы тяжести от гидростатически равновесных значений землеподобной Венеры для различных районов.

ВЫБОР ПАРАМЕТРОВ РАВНОВЕСНОЙ ФИГУРЫ ВЕНЕРЫ

В наблюдаемом гравитационном поле планеты можно выделить: 1) поле равновесного сфероида (гравитационное поле гидростатически равновесной планеты, которое отражает подстройку распределения масс в планете к ее собственному гравитационному и центробежному потенциалу и к потенциалам всех внешних возмущающих масс), 2) отклонение гравитационного поля от состояния гидростатического равновесия, которое называется неравновесной частью. При рассмотрении структуры гравитационного поля встает вопрос о поверхности отсчета, от которой отсчитываются высоты рельефа и геоида, а также строятся аномалии гравитационного ускорения.

Теория фигуры гравитирующих тел, находящихся в гидростатическом равновесии, применима не только к жидким, но и к твердым планетам, для которых время релаксации значительно меньше, чем характерные времена, за которые происходит заметное изменение скорости вращения (Жарков, Трубицын, 1980). Задача теории фигуры сводится к нахождению уравнения эквипотенциальных (уровенных) поверхностей тела, определенных из условия

(1)
$U\left( r \right) = V\left( r \right) + Q\left( r \right) = {\text{const}},~$
где U – потенциал силы тяжести, V – гравитационный потенциал, Q – центробежный потенциал. При этом задано распределение плотности ρ(s) внутри равновесного тела вдоль какого-либо направления θ и угловая скорость вращения ω.

Мы заменяем Венеру моделью. Выбранные модельные распределения плотности из работы (Жарков, Гудкова, 2019), удовлетворяющие значению массы и величине числа Лява k2 (Konopliv, Yoder, 1996), служат достаточно хорошим приближением распределения плотности для построения равновесной фигуры. Фигура модели планеты оказывается связанной с распределением плотности в ней (Жарков, Гудкова, 2016).

Малым параметром теории фигуры является безразмерный квадрат угловой скорости вращения планеты:

(2)
$m = \frac{{{{\omega }^{2}}{{R}^{3}}}}{{GM}} = \frac{{3\pi }}{{G{{\rho }_{0}}{{\tau }^{2}}}},$
где τ и ρ0 – период вращения и средняя плотность планеты соответственно.

Уравнение уровенной поверхности ищется в виде разложения по полиномам Лежандра

(3)
$r\left( {s,\theta } \right) = s\left\{ {1 + \sum\limits_{n = 0}^\infty {{{s}_{{2n}}}} \left( s \right){{P}_{{2n}}}\left( {{\text{cos}}\theta } \right)} \right\},$
где s – средний радиус текущей уровенной поверхности.

После подстановки r(s, θ) в (1) возникают различные произведения и степени рядов по Pn(cosθ). После приведения произведений Pn(cosθ) Pк(cosθ) к их суммам потенциал силы тяжести преобразуется к виду (Жарков, Трубицын, 1980)

(4)
$U\left( {r,~\theta } \right) = \sum\limits_{n = 0}^\infty {{{A}_{{2n}}}} \left( s \right){{P}_{{2n}}}\left( {\cos \theta } \right).$

Из условия (1) следует, что при n > 0 все A2n(s) = 0. Эти равенства представляют собой интегро-дифференциальные уравнения для функций фигуры sn(s), которые решаются методом итераций (Жарков, Трубицын, 1980). Функции фигуры sn(s), взятые на поверхности планеты, определяют гравитационные моменты – коэффициенты разложения внешнего гравитационного поля Jn.

В табл. 1 представлены параметры равновесной фигуры Венеры на поверхности и равновесные значения $J_{2}^{0}$ и $J_{4}^{0}$ для модельных распределений плотности в трех выбранных пробных моделях внутреннего строения из работы (Гудкова, Жарков, 2020). Для вычислений взято два значения малого параметра: 1) малый параметр, соответствующий современному периоду вращения Венеры (m = 6.1 × 10–8) и 2) малый параметр для эффективно равновесной Венеры (m = 1.5 × 10–5) (Жарков, Гудкова, 2019). В работе (Жарков, Гудкова, 2019) было отмечено, что в результате остывания, недра Венеры стали слишком твердыми (или очень вязкими), фигура планеты “зафиксировалась”, какой была в отдаленную эпоху, и поэтому не соответствует современному значению угловой скорости вращения планеты. Значение малого параметра для эффективно равновесной Венеры сохранилось от эпохи, когда была зафиксирована равновесная фигура планеты.

Зональные гравитационные моменты Jn связаны с коэффициентами Cno (нормированные тессеральные гравитационные моменты) соотношением Jn = = –(2n + 1)1/2Cno. Подставляя значения Сno из модели гравитационного поля (модель SHGJ180u) (Konopliv и др., 1999) получаем наблюдаемые значения гравитационных моментов в настоящее время: $J_{2}^{{{\text{obs}}}}$ = 4.40 × 10–6 и $J_{4}^{{{\text{obs}}}}$ = –2.14 × 10–6.

Современное значение малого параметра m Венеры очень мало из-за того, что за время существования Солнечной системы планета подверглась приливному торможению, в результате которого в настоящее время она вращается очень медленно. Поэтому наблюдаемые зональные гармоники $J_{2}^{{{\text{obs}}}}$ и $J_{4}^{{{\text{obs}}}}$ на несколько порядков величины выше, чем можно ожидать в случае гидростатического равновесия для современного значения малого параметра m = 6.1 × 10–8 ($J_{2}^{0}$ ≈ 1.9 × 10–8 и $J_{4}^{0}$ ≈ 9.5 × 10–16). В этом случае, даже слагаемое с n = 2 определяется, в основном, отклонением от гидростатического равновесия. Наблюдаемое современное значение для зональной гармоники с n = 2 соответствует равновесному модельному значению эффективно равновесной Венеры (m = = 1.5 × 10–5) в некоторую более раннюю эпоху, когда Венера не была замедлена приливным трением.

ДАННЫЕ ТОПОГРАФИИ И ГРАВИТАЦИОННОГО ПОЛЯ

В работе использованы данные топографии и гравитационного поля Венеры, полученные с космического аппарата “Магеллан”. Модели представляет собой ряд полностью нормализованных коэффициентов и доступны на сайте Системы Планетных данных (http://pds-geosciences.wustl.edu).

Данные топографии (модель SHTJV360u) представлены в виде коэффициентов разложения по полиномам Лежандра высот рельефа относительно центра масс до 360 степени и порядка группой (Rappaport и др., 1999):

(5)
$\begin{gathered} {{R}_{{{\text{relief}}}}}\left( {r,\varphi ,\lambda } \right) = \\ = R + \sum\limits_{n = 1}^{{\text{360}}} {\sum\limits_{m = 0}^n {\left[ {{{C}_{{tnm}}}{\text{cos}}m\lambda + {{S}_{{tnm}}}{\text{sin}}m\lambda } \right]} } {{P}_{{nm}}}\left( {{\text{sin}}\varphi } \right), \\ \end{gathered} $
где R – средний радиус Венеры, φ и $\lambda $ – геооцентрические широта и долгота, ${{C}_{{tnm}}}$ и ${{S}_{{tnm}}}$ – гармонические коэффициенты в разложении рельефа (в метрах), Pnm – нормализованные функции Лежандра степени n и азимутального числа m, удовлетворяющие соотношению

${{P}_{{nm}}}\left( t \right) = \begin{array}{*{20}{c}} {\left\{ \begin{gathered} {{\left[ {\frac{{2\left( {n - m} \right)!\left( {2n + 1} \right)}}{{\left( {n + m} \right)!}}} \right]}^{{1/2}}}P_{n}^{m},\,\,\,\,m \ne 0 \hfill \\ {{\left[ {\frac{{\left( {n - m} \right)!\left( {2n + 1} \right)}}{{\left( {n + m} \right)!}}} \right]}^{{1/2}}}P_{n}^{m},\,\,\,\,m = 0 \hfill \\ \end{gathered} \right.} \end{array}.$

Фигура Венеры близка к сфере. Поэтому за референсную поверхность часто выбирают сферу со средним радиусом R (Zharkov, 1992). В данной работе топография Венеры определяется по отношению к референсной поверхности, за которую выбирается равновесный сфероид $r\left( {s,\theta } \right)$ со средним радиусом R (см. (3)). Предполагается, что фигура равновесной планеты “зафиксировалась”, какой была в отдаленную эпоху, и не соответствует современному значению угловой скорости вращения планеты. Для дальнейших вычислений параметры равновесной фигуры берутся для значения малого параметра эффективно равновесной Венеры (Жарков, Гудкова, 2019) (см. табл. 1).

Таблица 1.

Параметры равновесной фигуры Венеры для моделей внутреннего строения из работы (Гудкова, Жарков, 2020) с разной толщиной коры: 30 км (V16), 70 км (V5) и 100 км (V17)

Модель m = 6.1 × 10–8 m = 1.5 × 10–5
-s2, 10–8 -s4, 10–15 $J_{2}^{0}$, 10–8 -$J_{4}^{0}$, 10–16 -s2, 10–6 -s4, 10–11 $J_{2}^{0}$, 10–6 -$J_{4}^{0}$, 10–11
V5
V16
V17 		3.97
3.94
3.93 		1.41
1.40
1.39 		1.94
1.91
1.90 		9.57
9.32
9.23 		9.77
9.69
9.67 		8.53
8.44
8.39 		4.77
4.69
4.67 		5.79
5.64
5.58

В результате, топография Венеры определяется соотношением:

(6)
${{h}_{{{\text{Venus}}}}}\left( {r,\varphi ,\lambda } \right) = {{R}_{{{\text{relief}}}}}\left( {r,\varphi ,\lambda } \right) - r\left( {s,\varphi } \right).$

Вулканические процессы определили облик современной поверхности Венеры: горячее вещество мантии эпизодически прорывается на поверхность, образуя вулканы и поднятия. Венера имеет молодую по сравнению с Землей поверхность с выраженными вулканическими (щитовые вулканы) и тектоническими чертами. Поверхность Венеры характеризуется небольшим перепадом высот, 80% ее поверхности составляют широкие равнины, образованные в результате извержения базальтовых лав с низкой вязкостью (Basilevsky, Нead, 2003). При этом имеются значительные поднятия, такие как земля Иштар (65° С, 0° В) с плато Лакшми, на котором расположены горы Максвелла – высочайшие вершины Венеры (высота 11 км), горы Акны (7 км) и горы Фрейи (7 км); земля Афродиты – большой растянувшийся вдоль экватора “континент” примерно между долготами 60° и 210°; а также область Бета (30° С, 80° З) – образование, скорее всего, вулканического происхождения и области Фебы и Фемиды.

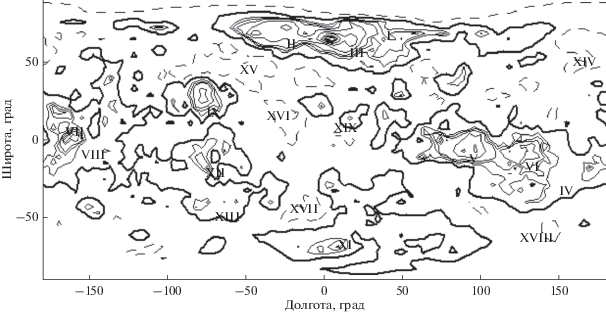
На рис. 1 представлена карта изолиний высот рельефа Венеры. Видны основные особенности топографии Венеры: Земля Иштар с плато Лакшми, находящаяся в высоких северных широтах и расположенные на ней горы Максвелла, заметная возвышенность Земля Афродиты, лежащая вдоль экватора, с расположенными на ней областями Атлы, Овды и Тефии, вулкан Маат, земля Лады, расположенная в малоизученной области южного полушария планеты. Отмечены изолированные поднятия, такие как, области Альфа и Бета.

Рис. 1.

Карта изолиний высот рельефа Венеры по данным топографии (модель SHTJV360u). Нулевой уровень (жирная сплошная линия) соответствует равновесной фигуре. Сплошные линии соответствуют положительным высотам, пунктирные – отрицательным. Условные обозначения: I – Земля Иштар, II – плато Лакшми, III – горы Максвелла, IV – Земля Афродиты, V – область Овда, VI – область Тефии, VII – область Атла, VIII– гора Маат, IX – область Бета, X – область Альфа, XI – Земля Лады, XII – область Фебе, XIII – область Тетис, XIV – равнина Атланты; XV – равнина Седны; XVI – равнина Гиневры; XVII – равнина Лавинии; XVIII – равнина Айно; XIX – область Эйстлы.

Гравитационное поле в сферической системе координат с началом в центре масс (модель SHGJ180u) (Konopliv и др., 1999) имеет стандартный вид:

(7)
$V\left( {r,\varphi ,\lambda } \right) = \frac{{GM}}{r}\left[ {1 + \sum\limits_{n = 2}^{180} {\sum\limits_{m = 0}^n {{{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{n}}} } ({{c}_{{gnm}}}\cos m\lambda + {{s}_{{gnm}}}\sin m\lambda ){{P}_{{nm}}}(\sin \varphi )} \right],$
где r – расстояние от точки наблюдения до начала координат, М – масса планеты, G – гравитационная постоянная, ${{C}_{{gnm}}}$ и ${{S}_{{gnm}}}$ – нормализованные гравитационные моменты.

Потенциал силы тяжести W на поверхности Венеры складывается из внешнего гравитационного потенциала V и центробежного Q:

$W = V + Q,\,\,\,\,Q = \frac{{{{\omega }^{2}}{{r}^{2}}}}{3}\left[ {1 - {{P}_{2}}\left( {{\text{sin}}\varphi } \right)} \right],$
где ω – угловая скорость вращения планеты. Выделим во внешнем потенциале (7) компоненту V0 соответствующую гидростатически равновесной Венере.

В разложении внешнего гравитационного поля гидростатически равновесной планеты

(8)
$\begin{gathered} V\left( {r,t} \right) = \frac{{GM}}{r} \times \\ \times \,\,\left\{ {1 - {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{2}}J_{2}^{0}{{P}_{2}}(t) - {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{4}}J_{4}^{0}{{P}_{4}}(t) - \ldots } \right\} \\ \end{gathered} $
содержатся только четные зональные моменты $J_{n}^{0}$, которые с ростом степени n убывают как mn, где $m$ – малый параметр теории фигуры (2). В формуле (8): r – расстояние от центра планеты, Re – экваториальная полуось (нормирующий радиус в V(r, t)), M – масса планеты и G – гравитационная постоянная. В случае Венеры Vo = GM/r называют нормальным внешним потенциалом (Zharkov, 1992).

В данной работе в компоненту соответствующую гидростатически равновесной Венере включим ньютоновский член GM/r, введенный Клеро член, пропорциональный $J_{2}^{*}$ и член порядка квадрата сжатия $J_{4}^{*}$. Как отмечено выше, cовременное значение J2 соответствует эффективно равновесной Венере в некоторую более ранюю эпоху, когда Венера, не была замедлена приливным трением. Примем $J_{2}^{*} = J_{2}^{{{\text{obs}}}}$, $J_{4}^{*}$ = $J_{4}^{0}$ для эффективно равновесной Венеры. Значение $J_{4}^{*}$ отличается от наблюдаемого момента J4. Тогда

(9)
$\begin{gathered} C_{{g20}}^{0} = {{ - J_{2}^{0}} \mathord{\left/ {\vphantom {{ - J_{2}^{0}} {\sqrt 5 }}} \right. \kern-0em} {\sqrt 5 }} = - 1.97 \times {{10}^{{ - 6}}}, \\ C_{{g40}}^{0} = {{J_{4}^{0}} \mathord{\left/ {\vphantom {{J_{4}^{0}} 3}} \right. \kern-0em} 3} = 1.93 \times {{10}^{{ - 11}}}. \\ \end{gathered} $

Таким образом, V0 можно представить в виде

$\begin{gathered} {{V}^{0}}\left( {r,\varphi } \right) = \frac{{GM}}{r} \times \\ \times \,\,\left( {1 + {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{2}}C_{{g20}}^{0}{{P}_{{20}}}(\sin \varphi ) + {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{4}}C_{{g40}}^{0}{{P}_{{40}}}(\sin \varphi )} \right). \\ \end{gathered} $

В дальнейшем, чтобы не усложнять обозначений и выписанных формул, будем рассматривать лишь неравновесную компоненту гравитационного поля Венеры, полагая в качестве второго и четвертого зональных коэффициентов С20 и С40 их негидростатические составляющие, получаемые вычитанием из измеренных величин, входящих в (7), значений (9).

Выделим теперь главную часть W0 потенциала силы тяжести, называемую нормальным потенциалом:

$W = {{W}_{0}} + T,\,\,\,\,{{W}_{0}} = {{V}_{0}} + Q.$

Здесь Т является возмущением, обусловленным отклонением планеты от гидростатического равновесия и определяет отклонение от нормального потенциала.

Высоты геоида N, т.е. высоты эквипотенциальной поверхности потенциала Т, отнесенные к нормальной фигуре, определяются формулой:

(10)
$\begin{gathered} N\left( {\varphi ,\lambda } \right) = \frac{T}{{{{g}_{0}}}} = \\ = R\sum\limits_{n = 2}^{{\text{180}}} {\sum\limits_{m = 0}^n {{{P}_{{nm}}}} } \left( {{\text{sin}}\varphi } \right) \times \\ \times \,\,\left( {{{C}_{{gnm}}}{\text{cos}}\left( {m\lambda } \right) + {{S}_{{gnm}}}{\text{sin}}\left( {m\lambda } \right)} \right), \\ \end{gathered} $
где g0 = GM/R2 = 8.87 м/с2.

Гравитационные аномалии δg (аномалии в свободном воздухе) имеют вид (Жарков, Трубицын, 1980)

(11)
$\begin{gathered} dg\left( {\varphi ,\lambda } \right) = - \frac{{\partial T}}{{\partial r}} = {{g}_{0}}\sum\limits_{n = 2}^{{\text{180}}} {\sum\limits_{m = 0}^n {\left( {n + 1} \right)} {{{\left( {\frac{{{{R}_{e}}}}{r}} \right)}}^{n}} \times } \\ \times \,\,{{P}_{{nm}}}(\sin \varphi )({{C}_{{gnm}}}\cos (m\lambda ) + {{S}_{{gnm}}}\sin (m\lambda )). \\ \end{gathered} $

Порядковые дисперсии топографии и гравитационного поля рассчитываются по формулам:

(12а)
$\begin{gathered} {{({{D}_{t}})}_{n}} = \sum\limits_{m = 0}^n {(C_{{tnm}}^{2} + S_{{tnm}}^{2})} , \\ {{({{D}_{g}})}_{n}} = \sum\limits_{m = 0}^n {(C_{{gnm}}^{2} + S_{g}^{2})} . \\ \end{gathered} $

Учитывая, что суммы содержат по (2n + 1) членов, удобно ввести величины

(12б)
${{({{\sigma }_{t}})}_{n}} = \sqrt {\frac{{{{{({{D}_{t}})}}_{n}}}}{{2n + 1}}} \,\,\,\,{\text{и}}\,\,\,\,{{({{\sigma }_{g}})}_{n}} = \sqrt {\frac{{{{{({{D}_{g}})}}_{n}}}}{{2n + 1}}} ,$

имеющие смысл среднего квадратичного значения для одной элементарной гармоники порядка n.

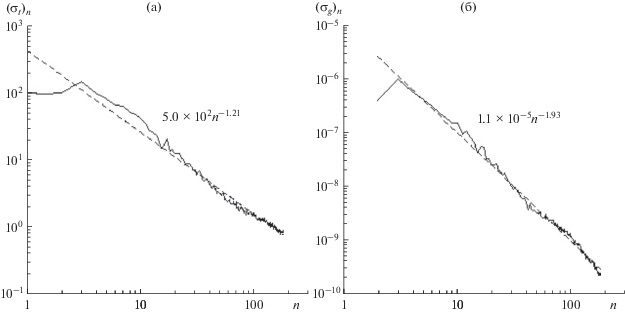
Результаты расчетов порядковых дисперсий представлены на рис. 2, где также изображены кривые для степенных законов, наилучшим образом описывающих поведение обеих дисперсий. Степенной закон для коэффициентов топографии, разложения по сферическим функциям следует закону n–2 (Ermakov и др., 2018). Из рис. 2 видно, что для Венеры спектр имеет меньший уклон (–1.21). Порядковые дисперсии неравновесной части гравитационного потенциала с ростом n убывают быстрее. Степенные спектры топографии и гравитационного поля отражают уровень изостатической компенсации. Уменьшение величины степени (уклона) может говорить об изостазии. Величина уменьшения зависит от механических свойств материала и скачка плотности между внешним слоем и подстилающей поверхностью, при этом может иметь место различная степень компенсации для низших и высоких гармоник.

Рис. 2.

Порядковые дисперсии: (a) высот рельефа относительно равновесной фигуры и (б) неравновесной части гравитационного потенциала Т.

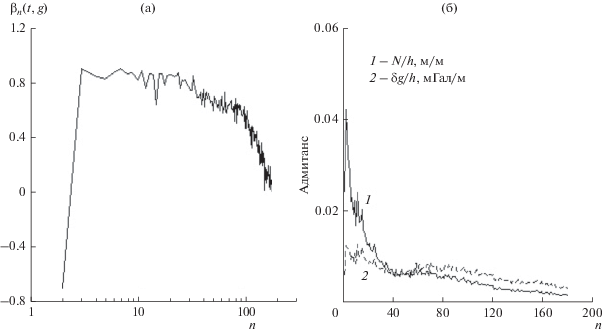
На рис. 3 приведены коэффициенты порядковой корреляции топографии и гравитационного поля Венеры β (t, g), которые вычисляются по формуле

(13)
${{\beta }_{n}}\left( {t,g} \right) = \frac{{\sum\limits_{m = 0}^n {\left( {{{C}_{{tnm}}}{{C}_{{gnm}}} + {{S}_{{tnm}}}{{S}_{{gnm}}}} \right)} }}{{\sqrt {{{{({{D}_{t}})}}_{n}}{{{({{D}_{g}})}}_{n}}} }},$
и адмитанс: отношения высот геоида Венеры N (10) и гравитационных аномалий δg (11) к топографии (6), определяемые как $R{{{{{({{\sigma }_{g}})}}_{n}}} \mathord{\left/ {\vphantom {{{{{({{\sigma }_{g}})}}_{n}}} {{{{({{\sigma }_{t}})}}_{n}}}}} \right. \kern-0em} {{{{({{\sigma }_{t}})}}_{n}}}}$ и ${{g}_{0}}{{({{\sigma }_{g}})}_{n}}{{\sqrt {(n + 1)} } \mathord{\left/ {\vphantom {{\sqrt {(n + 1)} } {{{{({{\sigma }_{t}})}}_{n}}}}} \right. \kern-0em} {{{{({{\sigma }_{t}})}}_{n}}}}$, соответственно.

Рис. 3.

Коэффициенты порядковой корреляции топографии и гравитационного поля (а); и адмитанс: отношения высот ареоида N (10) и гравитационных отклонений (11) к топографии (6) (б).

Значения коэффициента корреляции –1 ≤ β ≤ 1 говорит о том, что поле высот рельефа и поле гравитационного потенциала антикоррелирует (β = –1), не коррелирует (β = 0) или коррелирует (β = +1) для порядка n соответственно в зависимости от близости его значения к –1, 0, +1.

Из рис. 3 видно, что вторые гармоники топографии и гравитационного поля Венеры не коррелируют, и даже антикоррелируют. Для гармоник степеней n ≥ 3 высоты рельефа хорошо коррелируют с неравновесным гравитационным полем. Этот факт может говорить о частичной изостатической компенсации длинноволнового рельефа Венеры с n ≥ 3.

Для дальнейших вычислений мы будем использовать гармоники с n < 70, так как корреляция между гравитационным полем и топографией резко убывает для гармоник выше 70, что означает неточность короткопериодных компонент в модели гравитационного поля.

Ниже проанализируем кратко карты изолиний N и δg, акцентируя внимание на корреляции рассматриваемых полей с основными топографическими структурами Венеры.

Высоты геоида

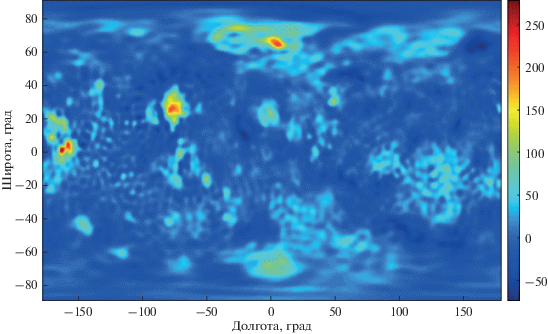
На рис. 4 показаны высоты геоида Венеры (10). Как и для геоида Земли, высоты геоида Венеры (рис. 4) имеют отклонения с амплитудами порядка нескольких десятков метров. При детальном рассмотрении можно обнаружить существенные различия. Известно, что земной геоид имеет слабую корреляцию (или отсутствие) корреляции с основными топографическими структурами, такими как континенты и горные массивы. На карте геоида Венеры можно отчетливо различить небольшое число так называемых “континентов”. Это земля Иштар, где находятся самые высокие вершины Венеры – горы Максвелла, область Бета и большой вытянутый вдоль экватора “континент” земля Афродиты. Забегая вперед, стоит отметить, что на каждой из этих возвышенностей или вблизи них обнаружено повышенное значение ускорений силы тяжести.

Рис. 4.

Карта высот геоида Венеры N (10) (м) относительно равновесной фигуры с учетом сферических гармоник от 2 до 70.

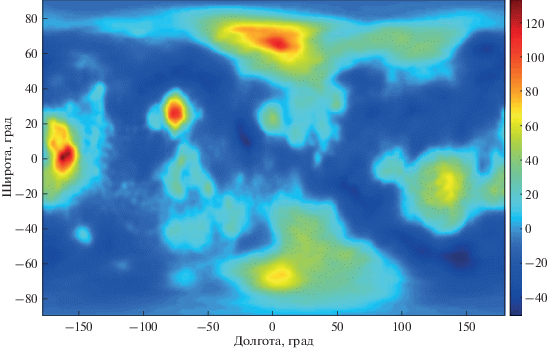
Высоты геоида, изображенные на рис. 4 показывают, что самые большие значения высот геоида Венеры соответствуют областям Бета и Овда и зонам так называемых “континентов” – земель Афродиты, Иштар и Лады.

Видно, что равнины с самыми низкими высотами имеют отрицательные значения высот геоида. В общем, геоид хорошо коррелирует с топографией. Динамический диапазон высот геоида относительно равновесной фигуры Венеры, как и на Земле, составляет около 200 м.

Аномалии ускорения силы тяжести

На рис. 5 приведена карта изолиний гравитационных аномалий δg (11) на поверхности Венеры. Низменности на Венере характеризуются отрицательными гравитационными аномалиями. Возвышенные плато имеют небольшие гравитационные аномалии (возможная изостатическая компенсация), вулканические поднятия характеризуются большими гравитационными аномалиями. Значительными гравитационными аномалиями обладают возвышенности областей Бета и Атла, горы Максвелла, а также более мелкие вулканические возвышенности. В целом, гравитационные возмущения на поверхности Венеры небольшие, как результат гладкой топографии, исключение составляют некоторые районы. Максимальные гравитационные возмущения достигают 250 мГал. Из приведенных рисунков видно, что большинство гравитационных аномалий и высот геоида сильно коррелируют с рельефом поверхности.

Рис. 5.

Карта отклонений ускорения силы тяжести от гидростатически равновесных значений δg (11) (мГал) на поверхности Венеры для гармоник степеней со 2-й по 70-ю.

ЗАКЛЮЧЕНИЕ

Венера является самой неравновесной планетой в Солнечной Системе. В результате приливного торможения планета вращается очень медленно. Значение малого параметра m Венеры, соответствующее современному значению периода вращения, очень мало. Соответственно, модельные зональные гармоники, рассчитанные в случае гидростатического равновесия для современного значения малого параметра m = 6.1 × 10–8 ($J_{2}^{0}$ = 1.9 × × 10–8 и $J_{4}^{0}$ = 9.5 × 10–16), на несколько порядков величины ниже, чем наблюдаемые величины J2 и J4 для Венеры.

В статье существенно используется гипотеза, что Венера землеподобна. В работе (Жарков, Гудкова, 2019) для Венеры было принято отношение J2/m такое же как для Земли, и было отмечено, что равновесноая фигура планеты “зафиксировалась”, какой была в отдаленную эпоху, и не соответствует современному значению угловой скорости вращения планеты.

В данной работе, предполагая землеподобность гравитационного поля Венеры, для вычислений параметров равновесной фигуры принято значение малого параметра эффективно равновесной Венеры (см. табл. 1). Для трех пробных моделей внутреннего строения Венеры из работы (Гудкова, Жарков, 2020) рассчитаны параметры равновесной фигуры планеты и равновесные значения коэффициентов гравитационных моментов $J_{2}^{0}$ и $J_{4}^{0}$.

Проведен анализ высот геоида и отклонений силы тяжести от гидростатически равновесных значений для различных районов Венеры. Карта гравитационных возмущений и геоид позволяют оценить, имеется ли корреляция между гравитационным полем и топографией, как было бы в случае слабой изостатической компенсации. Высоты геоида имеют тенденцию к увеличению значения в областях увеличения гравитационных возмущений (т.е. там, где имеется дополнительная нескомпенсированная масса). Считается, что степень изостатической компенсации в Земле значительно выше, чем это имеет место на Венере. На карте геоида Земли – континенты и основные горные массивы не видны, на карте геоида Венеры мы видим “континенты” (зоны поднятий).

Дальнейший совместный анализ гравитационного поля и топографии и геоморфологии может дать дополнительную информацию о недрах Венеры и наложить дополнительные ограничения на модель внутреннего строения планеты в отсутствии сейсмических данных.

Данная работа выполнена в рамках госзадания ИФЗ РАН.

Список литературы

  1. Гудкова Т.В., Жарков В.Н. Модели внутреннего строения землеподобной Венеры // Астрон. вестн. 2020. Т. 54. № 1 С. 24–32.

  2. Жарков В.Н., Трубицин В.П., Самсоненко Л.В. Физика Земли и планет. М.: Наука, 1971. 384 с.

  3. Жарков В.Н., Трубицин В.П. Физика планетных недр. М.: Наука, 1980. 448 с.

  4. Жарков В.Н., Гудкова Т.В. О модельной структуре гравитационного поля Марса // Астрон. вестн. 2016. Т. 50. № 4. С. 252–267. (Zharkov V.N., Gudkova T.V. On the model structure of the gravity field of Mars // Sol. Syst. Res. 2016. V. 50. № 4. P. 235–250).

  5. Жарков В.Н., Гудкова Т.В. О параметрах землеподобной модели Венеры // Астрон. вестн. 2019. Т. 53. № 1 С. 3–6. (Zharkov V.N., Gudkova T.V. On Parameters of the Earth-like model of Venus // Sol. Syst. Res. 2019. V. 53. № P. 1–4).

  6. Barsukov V.L., Basilevsky A.T., Burba G.A. et al. The geology and geomorphology of the Venus surface as revealed by the radar images obtained by Venera 15 and 16 // J. Geophys. Res. 1986. V. 91. P. D399–D411.

  7. Basilevsky A.T. Geologic Map of the Beta Regio Quadrangle (V–17), Venus // USGS Scientific Investigations. 2008. Map 3023.

  8. Basilevsky A.T., Head J.W. The geologic history of Venus: a stratigraphic view // J. Geophys. Res. 1998. V. 103. P. 8531–8544.

  9. Basilevsky A.T., Head J.W. Geologic units on Venus: evidence for their global Correlation // Planet. and Space Sci. 2000. V. 48. P. 75–111.

  10. Basilevsky A.T., Head J.W. The surface of Venus // Reports on progress in Physics. 2003. V. 66(10). P. 1699–1734.

  11. Basilevsky A.T., Head J.W. Beta region, Venus: Evidence for uplift, rifting, and volcanism dur to a mantle plume // Icarus. 2007. V. 192. P. 167–186.

  12. Breuer D., Moore W.B. Dynamics and thermal history of the terrestrial planets, the Moon and Io / Ed. Spohn T. Treatise on geophysics // Planets and Moons. 2007. V. 10. P. 299–348.

  13. Ermakov A.I., Park R.S., Bills B.G. Power laws of topography and gravity spectra of the Solar System bodies // J. Geophys. Res. Planets. 2018. V. 123. P. 2038–2064.

  14. Florensky, C.P., Ronca L.B., Basilevsky A.T., Burba G.A., Nikolaeva О.V., Pronin A.A., Trakhtman A.M., Volkov V.P., Zazetsky V.V. The surface of Venus as revealed by Soviet Venera 9 and 10 // Geological Society of American Bulletin. 1977. V. 88. P. 1537–1545.

  15. Ghail R.C., Hall D., Mason P.J., Herrick R.R., Carter L.M., Williams Ed. VenSAR onEnVision: Takingearth observation radar to venus // Intern. J. Appl. Earth Observation and Geoinformation. 2018. V. 64. P. 365–376.

  16. Ivanov M.A., Head J.W. Global geological map of Venus // Planet. and Space Sci. 2011. V. 59. P. 1559–1600.

  17. Ivanov M.A., Head J.W. The history of volcanism on Venus // Planet. and Space Sci. 2013. V. 84. P. 66–92.

  18. Ivanov M.A., Head J.W. The history of tectonism on Venus: A stratigraphic analysis // Planet. and Space Sci. 2015. V. 113–114. P. 10–32.

  19. Jimenez-Dìaz, A., Ruiz, J., Kirby J.F., Romeo I., Tejero R., Capote R. Lithopsheric structure ofVenus from gravity and topography // Icarus. 2005. V. 260. P. 215–231.

  20. Ksanfomality L.V., Zubkova V.M., Morozov N., Petrova E. Microseisms at the Venera 13 and Venera 14 landing sites // Sov. Astron. Lett. 1982. V. 8 (4). P. 241–242.

  21. Konopliv A.S., Yoder C.F. Venusian k2 tidal Love number from Magellan and PVO tracking data // Geophys. Res. Lett. 1996. V. 23. P. 1857–1860.

  22. Konopliv A.S., Banerdt W.B., Sjogren W.L. Venus gravity:180th degree and order model // Icarus. 1999. V. 139. P. 3–18. https://doi.org/10.1006/icar.1999.6086

  23. Li F., Yan J., Xu L., Jin S., Rodriguez A.P., Dohm J.H. A 10 km-resolution synthetic Venus gravityfield model based on topography // Icarus. 2015. V. 247. P. 103–111.

  24. Rappaport N.J., Konopliv A.S., Kucinskas A.B. Animproved 360 degree and order model of Venus topography // Icarus. 1999. V. 139. P. 19–31. https://doi.org/10.1006/icar.1999.6081

  25. Smrekar S.E., Hensley S., Dyar M.D., Helbert J. VERITAS (Venus Emissivity, radio Science, InSAR, topography and Spectroscopy): A proposed discovery mission // Lunar and Planet. Sci. Conf. 2016. V. 47. P. 2439.

  26. Yang, A., Huang. J., Wei, D. Separation of dynamic and isostatic components of The Venusian gravity and topography and determination of the crustal thickness of Venus // Planet. and Space. Sci. 2016. V. 129. P. 24–31.

  27. Wieczorek M.A. Gravity and topography of the terrestrial planets / Ed. Spohn T. Treatise on geophysics. Planets and Moons. Amsterdam: Elsevier, 2015. V. 10. P. 153–193.

  28. Zharkov V.N. Models of the internal structure of Venus // Moon and the Planets. 1983. V. 29. P. 139–175.

  29. Zharkov V.N. Gravity field, loading coefficients, anomalous density waves and the case of long waves // Venus geology, geochemistry and geophysics research results from the USSR / Eds Barsukov V.L., Basilevsky A.T., Volkov V.P., Zharkov V.N. Univ. Arizona Press, 1992. P. 219–228.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал