Астрономический вестник, 2021, T. 55, № 2, стр. 182-192

Численно-аналитическое исследование сцепленных орбит в ограниченной эллиптической двукратно осредненной задаче трех тел

М. А. Вашковьяк^*

Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 06.10.2020
После доработки 25.10.2020
Принята к публикации 06.11.2020

DOI: 10.31857/S0320930X21020067

Аннотация

Рассмотрена ограниченная эллиптическая двукратно осредненная задача трех тел. В разложении возмущающей функции задачи сохранены слагаемые до второй степени включительно относительно эксцентриситета орбиты возмущающего тела. Элементы эллиптической орбиты возмущаемого тела считаются произвольными. С помощью численного интегрирования осредненных уравнений в кеплеровских элементах проведено исследование специальных, так называемых сцепленных орбит тела пренебрежимо малой массы. Для таких орбит точки их пересечения с плоскостью орбиты возмущающего тела находятся по разные стороны от нее. В простейшей модели Солнце–Юпитер–комета описаны особенности эволюции гипотетических и некоторых реальных кометных орбит, выявлены их отличия от соответствующих орбит круговой задачи.

Ключевые слова: ограниченная эллиптическая задача трех тел, двукратное осреднение, сцепленные орбиты, численное интегрирование

ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

Исследования долговременной эволюции орбит в ограниченной эллиптической задаче трех тел, как правило, проводятся в двукратно осредненной постановке. При этом широкое использование получил интегрируемый случай круговой орбиты возмущающего тела. Исследования этого случая, начатые известными учеными Х. фон Цейпелем (Zeipel, 1910) и Н.Д. Моисеевым (Моисеев, 1945), были существенно развиты М.Л. Лидовым (Лидов, 1961; Lidov, 1962) и И. Козаи (Kozai, 1962). Эти исследования детально описаны в монографиях (Shevchenko, 2017) и (Ito, Ohtsuka, 2019). Отметим, что обширная статья Х. фон Цейпеля стала заслуженно известной и нашла свое отражение в вышеуказанном научно-историческом исследовании (Ito, Ohtsuka, 2019) лишь вследствие ссылки на нее в работе (Baily, Emel’yanenko, 1996) в связи изучением эволюции одного из типов кометных орбит. Работы Моисеева, Лидова и Козаи, выполненные позднее, явились как результатами качественного изучения осредненной задачи трех тел, так и необходимостью исследования орбитальной динамики искусственных спутников планет и динамики астероидов.

В обширной статье (Zeipel, 1910) выделены и качественно изучены три основных случая расположения орбиты возмущаемого тела в двукратно осредненной круговой задаче: внутренний, внешний и случай пересекающихся, в частности, так называемых сцепленных орбит. Пространственное расположение сцепленных орбит характеризуется тем, что одна из точек пересечения орбиты тела пренебрежимо малой массы с плоскостью орбиты возмущающего тела находится внутри нее, а другая – вне. Подобная классификация в ограниченной круговой двукратно осредненной задаче трех тел для равномерно близких орбит вместе с анализом условий их пересечения была предложена в работе (Lidov, Ziglin, 1974). Топология двух сцепленных и несцепленных кеплеровских орбит всех тех типов детально описана К.В. Холшевниковым и В.Б. Титовым (Холшевников, Титов, 2007).

Заметим, что русский термин “сцепленные орбиты” ассоциируется с английским “linked orbits”, хотя более воспринимаемым и геометрически понятным является словосочетание “like the rings of a chain”, предложенное в монографии (Ito, Ohtsuka, 2019) как английский аналог французского термина “comme les anneaux d’une shaîne”, используемого работе (Zeipel, 1910). Сцепленные орбиты в ограниченной эллиптической двукратно осредненной задаче трех тел и являются предметом исследования данной работы.

Рассмотрим движение материальной точки Р пренебрежимо малой массы под действием притяжения центральной точки S массы m и возмущающей точки J массы m₁$ \ll $ m, движущейся относительно S по эллиптической орбите с большой полуосью а₁ и эксцентриситетом е₁. Введем прямоугольную систему координат Oxyz c началом в точке S, основная плоскость xOy которой совпадает с плоскостью орбиты точки J. Ось Ox пусть направлена в перицентр орбиты точки J, ось Oy – в сторону ее движения от перицентра в основной плоскости, а ось Oz дополняет систему координат до правой. Возмущенная орбита точки P(x, y, z) характеризуется оскулирующими кеплеровскими элементами: большой полуосью а, эксцентриситетом е, наклонением i, аргументом перицентра ω и долготой восходящего узла Ω. В выбранной системе возмущающая точка J имеет координаты x₁, y₁, а аппликата z₁= 0.

Для исследования эволюции орбиты точки Р используется вековая часть W полной возмущающей функции

(1)

$W\left( {a,e,i,{\omega },\Omega ,{{a}_{1}},{{e}_{1}}} \right) = \frac{{f{{m}_{1}}}}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\frac{1}{{\Delta \left( {\lambda ,{{\lambda }_{1}}} \right)}}} } d{{\lambda }_{1}}d\lambda .$

Здесь $\Delta = \left| {{\mathbf{r}} - {{{\mathbf{r}}}_{1}}} \right| = \sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{y}_{1}}} \right)}}^{2}} + {{z}^{2}}} $ – расстояние между возмущаемой и возмущающей точками, λ и λ₁ – средние долготы этих точек, f – гравитационная постоянная. Предполагается отсутствие соизмеримостей низких порядков между средними движениями точек J и P. В функции W a₁ и e₁ играют роль параметров эволюционной задачи.

Первые интегралы уравнений возмущенного движения в элементах имеют вид

(2)

$a = {\text{const}},\,\,\,\,~W(a,e,i,\omega ,\Omega ,{{a}_{1}},{{e}_{1}}) = {\text{const}},$

а в случае е₁ = 0 существует еще один первый интеграл (Моисеев, 1945)

(3)

$\left( {1 - {{e}^{2}}} \right){{\cos }^{2}}i = {{c}_{1}} = {\text{const}}.$

ОСРЕДНЕННАЯ ВОЗМУЩАЮЩАЯ ФУНКЦИЯ И ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ

В аналитических исследованиях нередко используется и другое, равносильное (1), выражение функции W с помощью известных формул

(4)

$\begin{gathered} W = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} V\left( E \right)dE, \\ V\left( E \right) = \frac{{f{{m}_{1}}}}{{2\pi }}\int\limits_0^{2\pi } {\frac{{d{{\lambda }_{1}}}}{{\Delta \left( {{{\lambda }_{1}},E} \right)}}} , \\ \end{gathered} $

где V представляет собой силовую функцию притяжения эллиптического гауссова кольца, моделирующего осредненное влияние возмущающей точки, Е – эксцентрическая аномалия точки Р.

Поскольку для рассматриваемых орбит в процессе эволюции расстояние r может быть как меньше, так и больше r₁, то обычно применяемые разложения обратного расстояния 1/Δ в ряды по полиномам Лежандра неприменимы. Поэтому в данной работе будет использовано аналитическое выражение функции V, хотя и с ограниченной точностью до $e_{1}^{2}$, включительно, приведенное в статье (Вашковьяк, 1986) для почти компланарной системы N слабоэллиптических гауссовых колец, но справедливое при любом соотношении r и r₁. Учитывая ориентацию введенной системы координат и полагая в формулах (6)–(8) этой статьи N = 1, i₁ = ω₁ = Ω₁ = k₁ = u₁ = v₁ = 0, h₁ = e₁, получим

(5)

$V\left( E \right) = \frac{{f{{m}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\Phi \left( {x,y,z} \right),$

а для связности изложения мы позволим себе воспроизвести и основные упрощенные вычислительные формулы этой работы, дополнив их новыми аналитическими соотношениями.

Функция Ф, зависящая от прямоугольных координат x, y, z, выражается через гипергеометрические функции Гаусса F

(6)

$\begin{gathered} \Phi = \left( {1 - \varepsilon + \mu } \right)F\left( {\frac{1}{4},\frac{3}{4};1;\zeta } \right) + \\ + \,\,\left( {\nu - \frac{1}{2}\varepsilon } \right)F\left( {\frac{5}{4},\frac{3}{4};2;\zeta } \right), \\ \end{gathered} $

причем для их вычисления используются функциональные ряды различной структуры в зависимости от численного значения аргумента ζ ($\left| \zeta \right| < 1$), так что

(7)

$\Phi = \left\{ \begin{gathered} \mathop \sum \limits_{n = 0}^\infty \left[ {1 + \mu - \frac{{3\left( {2n + 1} \right)}}{{2\left( {n + 1} \right)}}\varepsilon + \frac{{4n + 1}}{{n + 1}}\nu } \right]{{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}; \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {\left[ {{{H}_{n}} - \ln \left( {1 - \zeta } \right)} \right]\left[ {1 + \mu + 4\left( {4n + 1} \right)\nu - \left( {8n + 3} \right)\varepsilon } \right] + 8\left( {\varepsilon - 2\nu } \right)} \right\}} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}. \hfill \\ \end{gathered} \right.$

Здесь

(8)

$\begin{gathered} \varepsilon = \frac{{{{a}_{1}}{{e}_{1}}x}}{{a_{1}^{2} + {{r}^{2}}}},\,\,\,\,\mu = {{\varepsilon }^{2}}\left( {2 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{2{{\rho }^{2}}}}} \right) - \frac{{a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{\left( {a_{1}^{2} + {{r}^{2}}} \right){{\rho }^{2}}}}, \\ \nu = \frac{3}{2}{{\varepsilon }^{2}} - \frac{{a_{1}^{2}e_{1}^{2}}}{{2\left( {a_{1}^{2} + {{r}^{2}}} \right)}},\,\,\,\,{{r}^{2}} = {{\rho }^{2}} + {{z}^{2}}, \\ {{\rho }^{2}} = {{x}^{2}} + {{y}^{2}},\,\,\,\,\zeta = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}} \times \\ \times \,\,\left[ {{{\rho }^{2}} + 2\varepsilon \left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right) + \theta } \right], \\ \theta = e_{1}^{2}\left\{ {a_{1}^{2} - {{x}^{2}}\left[ {\frac{{6a_{1}^{2}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}} + \frac{{a_{1}^{2} + {{r}^{2}}}}{{{{\rho }^{2}}}}} \right]} \right. + \\ \left. {\frac{{^{{^{{^{{^{{}}}}}}}}}}{{_{{_{{_{{}}}}}}}} + \,\,{{y}^{2}}\left( {\frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}} - \frac{{4a_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right\}. \\ \end{gathered} $

Постоянные коэффициенты B_n и H_n определяются рекуррентными соотношениями

(9)

$\begin{gathered} {{B}_{n}} = \frac{{\left( {4n - 3} \right)\left( {4n - 1} \right)}}{{{\text{16}}{{n}^{2}}}}{{B}_{{n - 1}}},\,\,\,\,{{B}_{0}} = 1, \\ {{H}_{n}} = {{H}_{{n - 1}}} + \frac{{2\left( {3 - 8n} \right)}}{{n\left( {4n - 3} \right)\left( {4n - 1} \right)}},\,\,\,{{H}_{0}} = 6{\kern 1pt} {\text{ln}}{\kern 1pt} 2, \\ \end{gathered} $

а эмпирическое значение величины ζ* принято равным 0.5.

Замечание: Функция V зависит лишь от квадратов координат y и z, а координата x входит в эту функцию как квадратично, так и линейно (в числитель ε и посредством него – в ζ). Из подобной двойной симметрии функции V относительно y и z следует существование двух плоских частных решений y = 0 и z = 0 в однократно осредненной (только по λ₁) эволюционной задаче.

Прямоугольные координаты x, y, z выражаются через Е известными формулами невозмущенного кеплеровского движения

(10)

$\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\| = a\left\{ {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\| + \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\|} \right\},$

(11)

$\begin{gathered} {{p}_{1}} = {\text{cos}}\omega {\text{cos}}\Omega - {\text{sin}}\omega {\text{sin}}\Omega {\text{cos}}i, \\ {{p}_{2}} = {\text{cos}}\omega {\text{sin}}\Omega + {\text{sin}}\omega {\text{cos}}\Omega {\text{cos}}i,\,\,\,\,{{p}_{3}} = {\text{sin}}\omega {\text{sin}}i, \\ {{q}_{1}} = - {\text{sin}}\omega {\text{cos}}\Omega - {\text{cos}}\omega {\text{sin}}\Omega {\text{cos}}i, \\ {{q}_{2}} = - {\text{sin}}\omega {\text{sin}}\Omega + {\text{cos}}\omega {\text{cos}}\Omega {\text{cos}}i,\,\,\,{{q}_{3}} = {\text{cos}}\omega {\text{sin}}i{\text{.}} \\ \end{gathered} $

Далее будет удобно ввести новую независимую переменную – “безразмерное время” τ, согласно формуле

(12)

$\tau = \frac{{{{m}_{1}}a}}{{m{{a}_{1}}}}n\left( {t - {{t}_{0}}} \right),$

где $n = \frac{{\sqrt {fm} }}{{{{a}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}$ – среднее движение точки Р, и нормированную возмущающую функцию

(13)

$w = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}W = {\text{const}}.$

Для описания эволюции орбит будут использованы уравнения Лагранжа в элементах с функцией w, являющейся их первым и единственным интегралом

(14)

$\begin{gathered} \frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\,\frac{{di}}{{d\tau }} = \frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \omega }} - \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \Omega }}, \\ \frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}} - \frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}, \\ \frac{{d\Omega }}{{d\tau }} = \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}. \\ \end{gathered} $

При выполнении условий $\frac{{de}}{{d\tau }} = \frac{{di}}{{d\tau }} = \frac{{d\omega }}{{d\tau }} = \frac{{d\Omega }}{{d\tau }} = 0$ возможно существование стационарных решений этих уравнений.

ЧАСТНЫЕ ПРОИЗВОДНЫЕ НОРМИРОВАННОЙ ФУНКЦИИ w ПО ЭЛЕМЕНТАМ

В общем случае для произвольных орбит точки Р решение уравнений (14) может быть найдено, по-видимому, лишь численным методом, а процесс вычислений может контролироваться постоянством функции w вдоль этого решения. В работе (Вашковьяк, 1986) частные производные функции w по элементам вычислялись разностным способом. Здесь используется комбинированный метод, в котором нижеприведенные квадратуры

(15)

$\begin{gathered} \frac{{\partial w}}{{\partial e}} = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left[ {\left( {1 - e\cos E} \right)\frac{{\partial{ \tilde {V}}}}{{\partial e}} - \tilde {V}\cos E} \right]} dE, \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial w}}{{\partial i}}} \\ {\frac{{\partial w}}{{\partial \omega }}} \\ {\frac{{\partial w}}{{\partial \Omega }}} \end{array}} \right\| = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {V}}}}{{\partial i}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \omega }}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \Omega }}} \end{array}} \right\|dE \\ \end{gathered} $

находятся численно по способу Гаусса, а производные нормированной функции

(16)

$\tilde {V} = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}V = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\Phi \left( {x,y,z} \right)$

находятся аналитически. Для полноты совокупности формул мы приводим необходимые выражения для вычисления производных функции $\tilde {V}$ по элементам орбиты

(17)

$\left\| {\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {V}}}}{{\partial e}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial i}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \omega }}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial{ \tilde {V}}}}{{\partial x}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial e}}} \\ {\frac{{\partial x}}{{\partial i}}} \\ {\frac{{\partial x}}{{\partial \omega }}} \\ {\frac{{\partial x}}{{\partial \Omega }}} \end{array}} \right\| + \frac{{\partial{ \tilde {V}}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial e}}} \\ {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial \omega }}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \end{array}} \right\| + \frac{{\partial{ \tilde {V}}}}{{\partial z}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial z}}{{\partial e}}} \\ {\frac{{\partial z}}{{\partial i}}} \\ {\frac{{\partial z}}{{\partial \omega }}} \\ {\frac{{\partial z}}{{\partial \Omega }}} \end{array}} \right\|,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {V}}}}{{\partial x}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial y}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial z}}} \end{array}} \right\| = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\left( {\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \Phi }}{{\partial x}}} \\ {\frac{{\partial \Phi }}{{\partial y}}} \\ {\frac{{\partial \Phi }}{{\partial z}}} \end{array}} \right\| - \frac{\Phi }{{a_{1}^{2} + {{r}^{2}}}}\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\|} \right).$

(18)

$\begin{gathered} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial e}}} \\ {\frac{{\partial y}}{{\partial e}}} \\ {\frac{{\partial z}}{{\partial e}}} \end{array}} \right\| = - a\left( {\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\| + \frac{{e{\text{sin}}E}}{{\sqrt {1 - {{e}^{2}}} }}\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\|} \right),\,\,\,\,\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial z}}{{\partial i}}} \end{array}} \right\| = a\left[ {\left( {{\text{cos}}E - e} \right){\text{sin}}\omega + \sqrt {1 - {{e}^{2}}} {\text{cos}}\omega {\text{sin}}E} \right]\left\| {\begin{array}{*{20}{c}} {{{r}_{1}}} \\ {{{r}_{2}}} \\ {{{r}_{3}}} \end{array}} \right\|, \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \omega }}} \\ {\frac{{\partial y}}{{\partial \omega }}} \\ {\frac{{\partial z}}{{\partial \omega }}} \end{array}} \right\| = a\left( {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\| - \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\|} \right),\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \Omega }}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \\ {\frac{{\partial z}}{{\partial \Omega }}} \end{array}} \right\| = a\left( {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} { - {{p}_{2}}} \\ {{{p}_{1}}} \\ 0 \end{array}} \right\| + \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} { - {{q}_{2}}} \\ {{{q}_{1}}} \\ 0 \end{array}} \right\|} \right), \\ {{r}_{1}} = {\text{sin}}i{\text{sin}}\Omega ,\,\,\,\,{{r}_{2}} = - {\text{sin}}i{\text{cos}}\Omega ,\,\,\,\,{{r}_{3}} = {\text{cos}}i. \\ \end{gathered} $

(19)

$\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \Phi }}{{\partial x}}} \\ {\frac{{\partial \Phi }}{{\partial y}}} \\ {\frac{{\partial \Phi }}{{\partial z}}} \end{array}} \right\| = \frac{{\partial \Phi }}{{\partial \varepsilon }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial x}}} \\ {\frac{{\partial \varepsilon }}{{\partial y}}} \\ {\frac{{\partial \varepsilon }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \zeta }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \zeta }}{{\partial x}}} \\ {\frac{{\partial \zeta }}{{\partial y}}} \\ {\frac{{\partial \zeta }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \mu }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \mu }}{{\partial x}}} \\ {\frac{{\partial \mu }}{{\partial y}}} \\ {\frac{{\partial \mu }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \nu }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \nu }}{{\partial x}}} \\ {\frac{{\partial \nu }}{{\partial y}}} \\ {\frac{{\partial \nu }}{{\partial z}}} \end{array}} \right\|,$

(20)

$\begin{gathered} \frac{{\partial \varepsilon }}{{\partial x}} = \frac{{{{a}_{1}}{{e}_{1}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{x}^{2}} + {{y}^{2}} + {{z}^{2}}} \right),\,\,\,\,\,\,\frac{{\partial \varepsilon }}{{\partial y}} = - \frac{{2{{a}_{1}}{{e}_{1}}xy}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}},\,\,\,\,\frac{{\partial \varepsilon }}{{\partial z}} = \frac{{2{{a}_{1}}{{e}_{1}}xz}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}, \\ \frac{{\partial \mu }}{{\partial x}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial x}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{x}{{{{\rho }^{4}}}} \times \,\,\left[ {\frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} + 2{{x}^{2}} + 2{{y}^{2}} + {{z}^{2}}} \right) - {{\varepsilon }^{2}}\left( {a_{1}^{2} + {{z}^{2}}} \right)} \right], \\ \frac{{\partial \mu }}{{\partial y}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial y}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{y}{{{{\rho }^{4}}}} \times \,\,\left[ {\frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} + 2{{x}^{2}} + 2{{y}^{2}} + {{z}^{2}}} \right) - {{\varepsilon }^{2}}\left( {a_{1}^{2} + {{z}^{2}}} \right)} \right] \times \,\,\frac{{2a_{1}^{2}e_{1}^{2}y}}{{\left( {a_{1}^{2} + {{r}^{2}}} \right){{\rho }^{2}}}}, \\ \frac{{\partial \mu }}{{\partial z}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial z}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{z}{{{{\rho }^{2}}}}\left[ {{{\varepsilon }^{2}} + \frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}} \right], \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \nu }}{{\partial x}}} \\ {\frac{{\partial \nu }}{{\partial y}}} \\ {\frac{{\partial \nu }}{{\partial z}}} \end{array}} \right\| = 3\varepsilon \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial x}}} \\ {\frac{{\partial \varepsilon }}{{\partial y}}} \\ {\frac{{\partial \varepsilon }}{{\partial z}}} \end{array}} \right\| + \frac{{a_{1}^{2}e_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\|. \\ \end{gathered} $

(21)

$\begin{gathered} \frac{{\partial \zeta }}{{\partial x}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial x}} - \frac{{4\varepsilon x}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right. + \left. {\,\,2x\left( {1 - 2\varepsilon } \right) - \frac{{4x}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial x}}} \right], \\ \frac{{\partial \zeta }}{{\partial y}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial y}} - \frac{{4\varepsilon y}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right.\left. { + \,\,2y\left( {1 - 2\varepsilon } \right) - \frac{{4y}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial y}}} \right], \\ \frac{{\partial \zeta }}{{\partial z}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial z}} - \frac{{4\varepsilon z}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right.\left. { + \,\,4\varepsilon z - \frac{{4z}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial z}}} \right], \\ \frac{{\partial \theta }}{{\partial x}} = 2e_{1}^{2}x\left[ \begin{gathered} - \frac{{6a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {1 - \frac{{2{{x}^{2}}}}{{a_{1}^{2} + {{r}^{2}}}}} \right) + \frac{{2a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {3{{x}^{2}} + 2{{y}^{2}}} \right) - \hfill \\ - \frac{{{{y}^{2}}}}{{{{\rho }^{4}}}}\left( {2a_{1}^{2} - {{\rho }^{2}} + 2{{z}^{2}}} \right) - \frac{{{{x}^{2}}}}{{{{\rho }^{2}}}} \hfill \\ \end{gathered} \right], \\ \frac{{\partial \theta }}{{\partial y}} = 4e_{1}^{2}y\left\{ {\frac{{{{x}^{2}}}}{{{{\rho }^{4}}}}\left( {a_{1}^{2} + {{z}^{2}}} \right) + \frac{{a_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}\left[ {\frac{{6x_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right) + \frac{{3{{x}^{2}} + 2{{y}^{2}}}}{{a_{1}^{2} + {{r}^{2}}}} - 2} \right]} \right\}, \\ \frac{{\partial \theta }}{{\partial z}} = 2e_{1}^{2}z\left\{ {\frac{{{{y}^{2}} - {{x}^{2}}}}{{{{\rho }^{2}}}} + \frac{{2a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2{{y}^{2}} - 3{{x}^{2}} + \frac{{6x_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)} \right]} \right\}. \\ \end{gathered} $

(22)

$\begin{gathered} \frac{{\partial \Phi }}{{\partial \varepsilon }} = \left\{ \begin{gathered} - \frac{3}{2}\sum\limits_{n = 0}^\infty {\frac{{2n + 1}}{{n + 1}}} {{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {8 - \left( {8n + 3} \right)\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right]} \right\}} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}. \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \zeta }} = \left\{ \begin{gathered} \mathop \sum \limits_{n = 1}^\infty \left[ {1 + \mu - \frac{{3\left( {2n + 1} \right)}}{{2\left( {n + 1} \right)}}\varepsilon + \frac{{4n + 1}}{{n + 1}}\nu } \right]n{{B}_{n}}{{\zeta }^{{n - 1}}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {\left[ {1 - \left( {8n + 3} \right)\varepsilon + \mu + 4\left( {4n + 1} \right)\nu } \right]\left[ {1 - n\left( {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right) - 8n\left( {\varepsilon - 2\nu } \right)} \right]} \right\}{{B}_{n}}{{{\left( {1 - \zeta } \right)}}^{{n - 1}}}} ,\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}} \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \mu }} = \left\{ \begin{gathered} \sum\limits_{n = 0}^\infty {{{B}_{n}}{{\zeta }^{n}}} ,\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right]} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}, \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \nu }} = \left\{ \begin{gathered} \mathop \sum \limits_{n = 0}^\infty \frac{{4n + 1}}{{n + 1}}{{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{4}{{\pi \sqrt 2 }}\mathop \sum \limits_{n = 0}^\infty \left\{ {\left( {4n + 1} \right)\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right] - 4} \right\}{{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}{\text{.}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $

Соотношения (7)–(11) и (15)–(22) представляют собой полный набор формул для вычисления правых частей эволюционных уравнений (14).

Отметим, что, в силу свойств функции V (см. замечание в предыдущем разделе) система (14) имеет два частных решения или интегрируемых случая.

Случай 1. Если sini = 0, то плоскость орбиты точки Р совпадает с орбитальной плоскостью возмущающей точки J. При этом в силу симметрии оказывается, что di/dτ = 0. Однако в этом плоском решении при любых значениях а, а₁ и e₁, наряду с регулярными орбитами, существуют нерегулярные, пересекающиеся (но не “сцепленные”) с орбитой точки J (Вашковьяк, 1982).

Случай 2. Если cos i = 0 и sinΩ = 0, то в рассматриваемой эллиптической задаче плоскость орбиты точки Р располагается ортогонально орбитальной плоскости возмущающей точки J и проходит через ее линию апсид. При этом в силу симметрии оказывается, что di/dτ = 0 и dΩ/dτ = 0. Вышеприведенные формулы квадратичного приближения относительно е₁ позволяют убедиться в этом и непосредственно. Действительно, для cosi = 0 и sinΩ = 0 имеем

(23)

$\begin{gathered} \delta = {\text{sign}}\left( {\cos \Omega } \right) = \pm 1, \\ {{p}_{1}} = \delta \cos \omega ,\,\,\,\,{{p}_{2}} = 0,\,\,\,\,{{p}_{3}} = \sin \omega , \\ {{q}_{1}} = - \delta \sin \omega ,\,\,\,\,{{q}_{2}} = 0,\,\,\,\,{{q}_{3}} = \cos \omega , \\ {{r}_{1}} = 0,\,\,\,\,{{r}_{2}} = - \delta ,\,\,\,\,{{r}_{3}} = 0, \\ x = a\delta \left[ {\left( {\cos E - e} \right)\cos \omega - \sin \omega \sqrt {1 - {{e}^{2}}} \sin E} \right], \\ y = 0, \\ z = a\left[ {\left( {\cos E - e} \right)\sin \omega + \cos \omega \sqrt {1 - {{e}^{2}}} \sin E} \right], \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial w}}{{\partial i}}} \\ {\frac{{\partial w}}{{\partial \Omega }}} \end{array}} \right\| = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {V}}}}{{\partial i}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \Omega }}} \end{array}} \right\|dE. \\ \end{gathered} $

При этом

(24)

$\begin{gathered} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial{ \tilde {V}}}}{{\partial i}}} \\ {\frac{{\partial{ \tilde {V}}}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial{ \tilde {V}}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial{ \tilde {V}}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\| = \\ = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\frac{{\partial \Phi }}{{\partial y}}\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\| = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }} \times \\ \times \,\,\left( {\frac{{\partial \Phi }}{{\partial \varepsilon }}\frac{{\partial \varepsilon }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \zeta }}\frac{{\partial \zeta }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \mu }}\frac{{\partial \mu }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \nu }}\frac{{\partial \nu }}{{\partial y}}} \right)\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\|{\text{.}} \\ \end{gathered} $

Нетрудно убедиться, что при y = 0 производные по y функций ε, ζ, μ, ν обращаются в нуль, так что $\frac{{\partial w}}{{\partial i}} = \frac{{\partial w}}{{\partial \Omega }} = 0$ и $\frac{{di}}{{d\tau }} = \frac{{d\Omega }}{{d\tau }} = 0.$

Уравнения (14), упрощенные для данного случая ортогонально – апсидальных орбит, принимают вид

(25)

$\frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$

Общее качественное исследование этого случая с учетом возможных пересечений орбит точек Р и J было проведено с помощью численно-аналитического метода в работе (Вашковьяк, 1984) для произвольных значений a, а₁ и е₁. В данной работе большее внимание уделено сцепленным орбитам, и в частности, стационарным решениям уравнений (25), существующим при ω₀ = 0, π. Можно показать, что при этом $\frac{{\partial w}}{{\partial \omega }} = 0$, а сами стационарные значения эксцентриситета определяются как корни трансцендентного уравнения

(26)

$\frac{{\partial w\left( {a,{{a}_{1}},{{e}_{1}},{{e}_{0}},{{\omega }_{0}} = 0,\pi ;{{\Omega }_{0}} = 0,\pi } \right)}}{{\partial e}} = 0.$

ОБ ЭВОЛЮЦИИ НЕКОТОРЫХ ГИПОТЕТИЧЕСКИХ И РЕАЛЬНЫХ ОРБИТ КОМЕТНОГО ТИПА В МОДЕЛИ СОЛНЕЧНОЙ СИСТЕМЫ

Вначале мы обратимся к сцепленным орбитам точки Р, сильно наклоненным к основной плоскости. В интегрируемом случае ортогонально-апсидальных орбит численное решение уравнения (26) дает возможность найти стационарные значения эксцентриситета е₀ при заданных ω₀ = 0°, 180°, Ω₀ = 0°, 180° и фиксированных параметрах а, а₁, е₁. Вдобавок, можно показать, что значения е₀ зависят от ω₀ и Ω₀ только посредством комбинации δ₁ = sign(cosω₀cosΩ₀) = ±1. Однако отличие в е₀ при различных знаках δ₁ достаточно мало и имеет порядок $e_{1}^{2}$.

При значениях наклонения и долготы восходящего узла, отличных от принятых в случае 2, все элементы орбиты будут изменяться со временем. Выполненное численное интегрирование эволюционной системы (14) методом Рунге–Кутта при а₁ = 5.2 а. е., е₁ = 0.048 и отношении масс m/m₁ в системе Солнце–Юпитер дает возможность получить оценку подобных изменений для фиктивных (или гипотетических) орбит кометного типа. Таблицы 1 и 2 дают такую оценку на интервале времени t* = 500 тыс. лет для орбит с большой полуосью а = 10а₁ = 52 а. е., e₀(δ₁ = 1) = = 0.9890, е₀(δ₁ = –1) = 0.9905. В этих таблицах представлены значения

$\begin{gathered} {{\Delta }_{1}} = {\text{max}}\left| {e\left( {t{\text{*}}} \right)--{{e}_{0}}} \right|,\,\,\,\,{{\Delta }_{2}} = {\text{max}}\left| {i(t*)--{{i}_{0}}} \right|, \\ {{\Delta }_{3}} = {\text{max}}\left| {\omega (t*)--{{\omega }_{0}}} \right|,{{\Delta }_{4}} = {\text{max}}\left| {\Omega (t*)--{{\Omega }_{0}}} \right|. \\ \end{gathered} $

Таблица 1.

Максимальные изменения элементов e, i, ω, Ω на интервале 500 тыс. лет для i₀= 90°, 90° ± 5°

i₀, град	Ω₀, град	Δ₁	Δ₂, град	Δ₃, град	Δ₄, град
90	60	0.001	24.3	1.0	21.9
90	120	0.002	20.8	1.1	20.3
85	0	0.0003	2.2	0.3	10.3
85	60	0.0004	24.0	0.8	12.3
85	120	0.0017	22.5	1.2	12.4
85	180	0.0001	2.0	0.2	7.5
95	60	0.0022	23.8	0.6	31.6
95	120	0.0028	18.7	1.4	28.2

Таблица 2.

То же самое, что и в табл. 1, но для i₀ = 90° ± 30°

i₀, град	Ω₀, град	Δ₁	Δ₂, град	Δ₃, град	Δ₄, град
60	0	0.010	1.4	9.8	60.0
60	60	0.003	19.8	7.3	35.1
60	120	0.004	29.0	8.3	26.5
60	180	0.005	15.1	7.9	42.6
120	60	0.013	9.1	9.6	74.3
120	120	0.010	2.9	10.2	63.0

Таблица 1 составлена для трех значений i₀ = = 90°, 85°, 95°. В точном решении уравнений (14) i₀ = 90°, Ω₀ = 0°, 180° отклонения нулевые, поэтому соответствующие строки опущены. При Ω₀ = 0° и 180° также опущены результаты для i₀ = 95°, тождественные соответствующим данным для i₀ = 85°.

Начальные отклонения по i₀ и Ω₀ от их равновесных значений при t = t* приводят к незначительным изменениям формы орбиты (Δ₁, Δ₃), но к заметному изменению ее ориентации (Δ₂ достигает значения 24°, Δ₄ – около 32°).

Таблица 2 составлена для более значительных начальных отклонений орбиты от ортогональной i₀ = 90° ± 30°. В ней при Ω₀ = 0° и 180° также результаты для i₀ = 120°, тождественные соответствующим данным для i₀ = 60°. В этом случае наклонение также остается близким к начальному, но отклонения остальных элементов составляют десятки градусов, доходя примерно до 75°.

Далее будут рассматриваться орбиты точки Р, сцепленные с орбитой точки J, но с произвольной пространственной ориентацией. Эволюция подобных орбит даже в интегрируемой двукратно осредненной круговой задаче (е₁ = 0) из-за отсутствия строгого аналитического выражения осредненной возмущающей функции обычно изучается с использованием численных методов. В работе (Ito, Ohtsuka, 2019, раздел 5.8, рис. 24 ) приводятся построенные как изолинии функции W семейства фазовых траекторий в плоскости (еcosω, esinω). Эти семейства соответствуют гипотетическим сцепленным орбитам точки Р, для трех пар значений отношения a/a₁ и постоянной интеграла с₁. Во всех трех рассмотренных вариантах

$\begin{gathered} {\mathbf{I}}\,({a \mathord{\left/ {\vphantom {a {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}} = {\text{ }}0.9,\,\,{{c}_{1}} = {\text{ }}0.4);~\,\,\,\,~{\mathbf{II}}\,({{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} a}} \right. \kern-0em} a} = {\text{ }}0.7,\,\,{{c}_{1}} = {\text{ }}0.6); \\ ~{\mathbf{III}}\,({{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} a}} \right. \kern-0em} a} = {\text{ }}0.8,\,\,{{c}_{1}} = {\text{ }}0.313) \\ \end{gathered} $

в фазовой плоскости существуют стационарные особые точки типа “центр” и охватывающие их замкнутые периодические траектории.

Эллиптичность орбиты возмущающей точки J, естественно, приводит к качественным изменениям семейств траекторий круговой задачи. Поскольку из-за отсутствия интеграла с₁ в эллиптической задаче уравнения для е и ω не отщепляются от остальных, как это имеет место при е₁ = 0, эволюцию этих элементов возможно проследить лишь в проекции фазовой траектории на плоскость (еcosω, esinω) или (ω, е). В данной работе выполнено численное интегрирование системы (14) для а₁ = 5.2 а. е., е₁ = 0.048 и отношения масс m/m₁ в системе Солнце–Юпитер. Отличие этого отношения от принятого в расчетах (Ito, Ohtsuka, 2019) для системы Солнце–(Земля + Луна) не сказывается на структуре фазовых траекторий, а приводит лишь к изменению временнóго масштаба.

Для сопоставления с результатами круговой задачи в вариантах I, II, III из всех семейств интегральных кривых круговой задачи были выбраны траектории с ω₀ = 180° и начальными значениями е₀ = 0.55, 0.4, 0.65, соответственно. Начальные наклонения вычислялись по е₀ и с₁ как ${{i}_{0}} = {\text{arccos}}\sqrt {\frac{{{{c}_{1}}}}{{1 - e_{0}^{2}}}} $, а начальная долгота восходящего узла Ω₀ принята равной нулю.

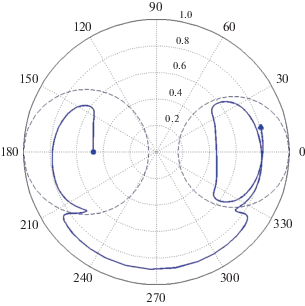
На рис. 1–3 показаны траектории для вариантов I, II, III, соответственно, и фрагменты полярных диаграмм с нанесенными численными значениями углов – ω и радиусов – е. Кружками отмечены начальные точки, треугольниками – конечные. Интервалы времени составляют 100 тыс. лет для вариантов I, II и 500 тыс. лет для варианта III. Штриховые линии – это так называемые “сепаратрисы”, не являющиеся интегральными кривыми и соответствующие пересечениям орбит точек P и J. Они определяются уравнениями

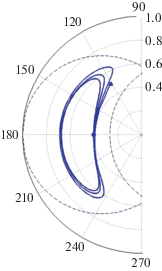
$\frac{{a\left( {1 - {{e}^{2}}} \right)}}{{{{a}_{1}}\left( {1 \pm {{e}_{1}}} \right)}} \pm e{\text{cos}}\omega - 1 = 0.$

Рис. 1.

Полярная диаграмма или проекция фазовой траектории на плоскость координат (еcosω, esinω) для варианта I (е₀ = 0.55, i₀ = 40°.78).

Рис. 2.

То же самое, что и на рис. 1, но для варианта II (е₀ = 0.4, i₀ = 32°.31).

Рис. 3.

То же самое, что и на рис. 1, но для варианта III (е₀ = 0.65, i₀ = 42°.59).

Во всех трех вариантах замкнутые периодические траектории круговой задачи видоизменяются и становятся непериодическими, тем не менее сохраняя колебательный характер и оставаясь в областях сцепленных орбит. Амплитуда этих колебаний может со временем как уменьшаться (рис. 1, 3 ), так и увеличиваться (рис. 2).

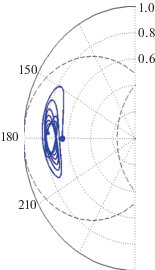
Однако эксцентричность орбиты Юпитера может приводить и к качественным изменениям поведения траектории. На рис. 4 показана хаотическая траектория, начинающаяся в области либрации ω при ω₀ = 180°, переходящая затем в область циркуляции и возвращающаяся в либрационную область, но относительно ω = 0. В процессе эволюции изначально сцепленная орбита точки Р пересекает орбиту возмущающей точки J, выходя из одной области сцепления, затем проходит область несцепленных орбит и входит в другую область сцепления.

Рис. 4.

Пример хаотической траектории со сменой режимов изменения аргумента перигелия и с пересечениями орбиты возмущающей точки на интервале 55 тыс. лет для варианта I, но при е₀ = 0.475, i₀ = 44°.052.

Интересно, что в рамках рассматриваемой модели (Солнце‒Юпитер‒комета) обнаруживаются и реальные кометные орбиты, почти ортогональные к эклиптике, причем имеющие указанные типы эволюции. Если на множестве кометных орбит, представленных в базе данных JPL (https://ssd.jpl.nasa.gov/sbdb_query.cgi#x), произвести селекцию по расстоянию перигелия q < 2 а. е. и наклонению 85° < i < 95°, то в данной выборке остается лишь 10 орбит. Эволюция семи из них сводится к последовательным пересечениям орбиты Юпитера с прохождениями областей сцепления. Рисунки 5–7 дают представление об эволюции остальных трех орбит. В отличие от предыдущих рисунков, показаны фрагменты плоскости (ω, е) не в полярной, а в прямоугольной системе, более удобной для сильноэллиптических орбит. Современные (начальные) значения элементов для численного интегрирования взяты из вышеуказанной базы данных JPL. Начальные значения в плоскости (ω – е) отмечены кружками, конечные – треугольниками.

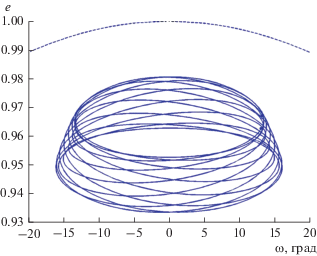
Рис. 5.

Изменение аргумента перигелия и эксцентриситета орбиты кометы C/1955 L1 (Mrkos) на интервале времени 1 млн лет в упрощенной модели (Солнце–Юпитер–комета).

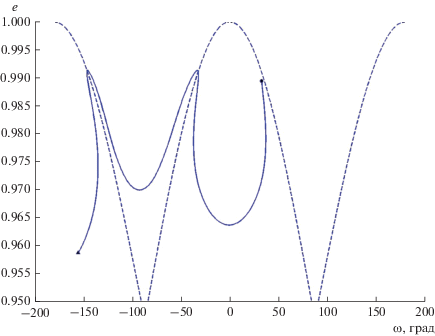
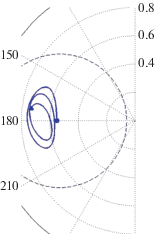
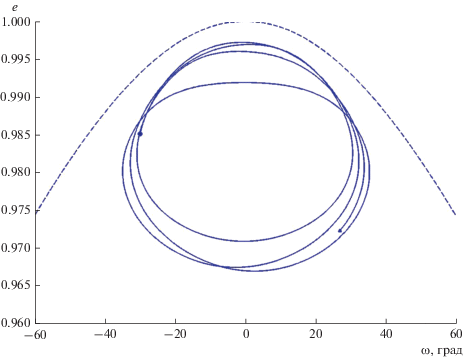
Рис. 6.

То же самое, что и на рис. 5, но для кометы C/1861 J1 (Great comet) и интервала времени 3 млн лет.

Рис. 7.

То же самое, что и на рис. 6, но для кометы 122P/de Vico.

На рис. 5 представлено изменение элементов орбиты кометы C/1955 L1 (Mrkos) на интервале времени 1 млн лет. Движение фазовой точки начинается в области орбитального сцепления и либрации ω, а соответствующее стационарное значение эксцентриситета, вычисленное решением уравнения (26), равно е₀ = 0.9818. Фазовая точка не успевает совершить ни одного оборота относительно центра либрации, а траектория проходит через “сепаратрису”, соответствующую пересечению орбиты кометы с орбитой Юпитера. После относительно небольшого промежутка времени примерно 200 тыс. лет происходит второе пересечение этих орбит и вход в другую область сцепления с центром либрации ω, отстоящим на 180° от исходного. При этом изначально прямое движение кометы уже через 100 тыс. лет становится обратным, а наклонение, увеличиваясь монотонно, достигает значения около 115°.

На рис. 6 представлено изменение элементов орбиты кометы C/1861 J1 (Great comet) на интервале времени 3 млн лет. Движение фазовой точки начинается и остается в области орбитального сцепления и либрации ω, а соответствующее стационарное значение эксцентриситета равно е₀ = = 0.9820. При этом изначально прямое движение кометы через 2 млн лет становится обратным, а наклонение достигает значения около 132° при минимуме 31°.

На рис. 7 представлено изменение элементов орбиты кометы 122P/de Vico на интервале времени 3 млн лет. Движение фазовой точки также начинается и остается в области орбитального сцепления и либрации ω, а соответствующее стационарное значение эксцентриситета равно е₀ = 0.9630. С течением времени движение меняется с прямого на обратное и наоборот. Экстремальные значения наклонения составляют 43° и 138°.

В заключение следует напомнить, что все вышеприведенные примеры орбитальной эволюции и, в частности, примеры либрационного изменения аргумента перигелия построены в рамках принятой модели (Солнце‒Юпитер‒комета). Однако реальные движения комет в Солнечной системе могут отличаться от их модельных движений, причем даже качественно. Эти отличия обусловлены как пренебрежением влияния остальных планет, кроме Юпитера, так и осредненной моделью задачи. Так, в строгом решении полной системы неосредненных дифференциальных уравнений либрационный характер изменения аргумента перигелия может измениться на циркуляционный. Таким примером хаотической орбитальной эволюции в реальной кометной среде является орбита кометы 122P/de Vico, однако это свойство обнаруживается лишь в неосредненной модели Солнечной системы, включающей в себя как несколько возмущающих тел (Baily и др., 1992), так и одно (Ito, Ohtsuka, 2019, раздел 5.8, рис. 25 ).

Касаясь методических особенностей работы, описанной в данной статье, укажем, что, благодаря исследованиям, выполненным относительно недавно и отраженным в монографиях и статье (Кондратьев, 2007; 2012; Антонов и др., 2008), представление силовой функции эллиптического гауссова кольца получено в замкнутом виде без разложений по каким-либо параметрам. Однако его практическое использование сопряжено с известными трудностями и может в будущем составить предмет специального исследования.

Список литературы

Антонов В.А., Никифоров И.И., Холшевников К.В. Элементы теории гравитационного потенциала и некоторые случаи его явного выражения. СПб.: Изд-во С.-Петерб. ун-та, 2008. 208 с.
Вашковьяк М.А. Эволюция орбит в плоской ограниченной эллиптической двукратно осредненной задаче трех тел // Космич. исслед. 1982. Т. 20. Вып. 3. С. 332–41. (Vashkov’yak M.A. Evolution of orbits in the two-dimensional restricted elliptical twice-averaged three-body problem // Cosmic Research. 1982. V. 20. № 3. P. 236–244).
Вашковьяк М.А. Об интегрируемых случаях ограниченной двукратно осредненной задачи трех тел // Космич. исслед. 1984. Т. 22. Вып. 3. С. 327–334. (Vashkov’yak M.A. Integrable cases of the restricted twice-averaged three-body problem // Cosmic Research. 1984. V. 22. № 3. P. 260–267).
Вашковьяк М.А. Исследование эволюции некоторых астероидных орбит // Космич. исслед. 1986. Т. 24. Вып. 3. С. 323–336. (Vashkov’yak M.A. An investigation of the evolution of some asteroid orbits // Cosmic Research. 1986. V. 24. №. 3. P. 255–266).
Кондратьев Б.П. Теория потенциала. Новые методы и задачи с решениями. М.: Мир, 2007. 512 с.
Кондратьев Б.П. Потенциал кольца Гаусса. Новый подход // Астрон. вестн. 2012. Т. 46. № 5. С. 380–391. (Kondratyev B.P. Potential of a Gaussian Ring. A New Approach // Sol. Syst. Res. 2012. V. 46. № 5. P. 352–362).
Лидов М.Л. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел // Искусственные спутники Земли. 1961. Вып. 8. С. 5–45.
Моисеев Н.Д. О некоторых основных упрощенных схемах небесной механики, получаемых при помощи осреднения ограниченной круговой проблемы трех точек. 2. Об осредненных вариантах пространственной ограниченной круговой проблемы трех точек // Тр. ГАИШ. 1945. Т. 15. Вып. 1. С. 100–117.
Холшевников К.В., Титов В.Б. Задача двух тел. Спб.: 2007.180 с.
Bailey M.E., Chambers J.E., Hahn G. Origin of sungrazers: a frequent cometary end-state // Astron. and Astrophys. 1992. V. 257. P. 315–322.
Bailey M.E., Emel’yanenko V.V. Dynamical evolution of Halley-type comets // Mon. Notic. Roy. Astron. Soc. 1996. V. 278. P. 1087–1110.
Ito T., Ohtsuka K. The Lidov-Kozai Oscillation and Hugo von Zeipel // Environ. Earth Planets. 2019. V. 7. №. 1. P. 1–113. https://doi.org/10.5047/meep.2019.00701.0001
Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P 591–598.
Lidov M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies // Planet. Space Sci. 1962. № 9. P. 719–759.
Lidov M.L., Ziglin S.L. The analysis of restricted circular twice-averaged three body problem in the case of close orbits // Celest. Mech. 1974. V. 10. № 2. P. 151.
Shevchenko I. The Lidov-Kozai Effect – Applications in Exoplanet Research and Dynamical Astronomy of Astrophysics and Space Science Library. International Publishing Switzeland. Dordrecht: Springer, 2017. V. 441. 194 p.
von Zeipel H. Sur l’application des séries de M. Lindstedt `a l’étude du mouvement des comètes périodiques // Astron. Nachrichten. 1910. V. 183. P. 345–418.
https://doi.org/10.1002/asna.19091832202]. A full-text open access PDF file is available from ADS, https://ui.adsabs.harvard.edu/abs/1910AN….183..345V.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал