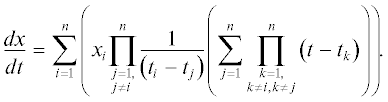1. На главную
  2. Электронные версии
  3. Астрономический вестник
  4. T. 55, № 3, 2021

Астрономический вестник, 2021, T. 55, № 3, стр. 272-287

Вековые резонансы в динамике объектов, движущихся в областях LEO–MEO околоземного орбитального пространства

А. Г. Александрова a, *, Е. В. Блинкова a, **, Т. В. Бордовицына a, ***, Н. А. Попандопуло a, ****, И. В. Томилова a, *****

a Томский государственный университет
Томск, Россия

* E-mail: aleksann@sibmail.com
** E-mail: zbizk322@mail.ru
*** E-mail: tvbord@sibmail.com
**** E-mail: nikas.popandopulos@gmail.com
***** E-mail: irisha_tom@mail.ru

Поступила в редакцию 09.04.2020
После доработки 17.02.2021
Принята к публикации 24.02.2021

Полный текст (PDF)

Аннотация

В работе представлены результаты выявления вековых резонансов, действующих на объекты, движущиеся в областях LEO–MEO. Результаты получены на основании обработки данных обширного численного эксперимента по исследованию орбитальной эволюции объектов, движущихся в диапазоне больших полуосей от 8000 км до зоны функционирования навигационной систем ГЛОНАСС (25 500 км), с наклонениями от 0° до 180° вне зон орбитальных резонансов. Даны карты распределения выявленных вековых резонансов. Приведен анализ орбитальной эволюции объектов.

Ключевые слова: динамика околоземных объектов, области LEO–MEO, вековые резонансы, особенности орбитальной эволюции

ВВЕДЕНИЕ

Настоящая работа является одной из серии работ, спланированных авторами по исследованию динамической структуры всего околоземного орбитального пространства. Ранее нами столь подробно динамическая структура рассматривалась только для областей функционирования навигационных систем GPS и ГЛОНАСС (Томилова и др., 2018), и областей с орбитальным резонансом, например, вся область орбитального резонанса 1 : 2 с вращением Земли (Томилова и др., 2020) и 1 : 3 (Томилова и др., 2019).

Областям с орбитальными резонансами посвящено довольно много работ (например, Кузнецов и др., 2012; 2014; Allan, 1967a; 1967b; Gedeon, 1969; Sochilina, 1982; Вашковьяк, 1991; Томилова и др., 2018; 2019; 2020). В данной работе приведены результаты исследования структуры вековых резонансов в областях LEO–MEO (Low Earth Orbit – Medium Earth Orbit) с наклонениями от 0° до 180°, начиная от 8000 км по большой полуоси (где уже не так сильно действие атмосферы и имеет смысл рассматривать влияние вековых резонансов) и до зоны функционирования навигационной системы ГЛОНАСС (25 500 км), которая была исследована ранее (Томилова и др., 2018). Рассматриваемая область является очень сложной в динамическом отношении, поскольку в ней действуют и орбитальные, и вековые резонансы. Данная работа посвящена выявлению и анализу действия только вековых резонансов и не затрагивает орбитальные резонансы.

Как мы уже отмечали ранее, исследование динамической структуры околоземного орбитального пространства является актуальной задачей, поскольку знание динамических особенностей различных областей этого пространства необходимо и при разработке новых спутниковых систем, и при определении областей паркинга отработавших объектов.

В данной работе мы не рассматривали влияние светового давления на объекты. Сила светового давления способна кардинально менять орбитальную эволюцию объектов с большой парусностью (отношением площади миделева сечения к массе) (Кузнецов, 2011; Кузнецов и др., 2011; Александрова и др., 2018a; 2019) и является вторым по величине воздействия возмущающим фактором после гравитационного поля Земли для таких объектов (Кузнецов и др., 2012; 2014). В случае малой парусности динамическая структура с учетом светового давления и без него совпадает (Александрова и др., 2018a; 2018b). Исследованию резонансной структуры околоземного пространства с учетом влияния светового давления для различных значений парусности будет посвящена отдельная работа.

Мы не рассматриваем также влияние на динамическую эволюцию параметров вывода объекта в точку стояния. Эти вопросы исследованы (см., например, Прохоренко, 2006).

МЕТОДИКА ИССЛЕДОВАНИЯ

Поставленная цель была реализована как с использованием отработанного в указанных выше работах алгоритма, так и с применением нового подхода к анализу вековых резонансов, предложенному в (Александрова и др., 2020) и позволяющему все исследования проводить в рамках численного моделирования. Аналитический подход используется только для того, чтобы обозначить типы рассматриваемых вековых резонансов

Исследование динамической структуры орбитального пространства осуществлялось с использованием быстрой ляпуновской характеристики MEGNO (Mean Exponential Growth of Nearby Orbits) (Cincotta, Simo, 2000; Cincotta и др., 2003; Valk и др., 2009).

Численное моделирование движения объектов производилось на кластере “СКИФ Cyberia” Томского государственного университета с использованием программного комплекса “Численная модель движения систем ИСЗ” (Александрова и др., 2017), и его модифицированной версии (Александрова и др., 2020), построенных с использованием высокоточного интегратора Гаусса–Эверхарта (Авдюшев, 2010). В процессе моделирования учитывались возмущения от гармоник геопотенциала до 10 порядка и степени, а также возмущения от Луны и Солнца. Совместно с уравнениями движения интегрировались уравнения для вычисления параметров MEGNO (Бордовицына и др., 2010).

Исследование структуры вековых резонансов осуществлялось при помощи численно-аналитической методики, которая была изложена в наших более ранних работах, например, (Бордовицына, Томилова, 2016; Александрова и др., 2018b; 2019), а также дополнена новым подходом, представленным в (Александрова и др., 2020).

Для того, чтобы обозначить вековые резонансы, проявление которых возможно в динамике рассматриваемых объектов используется аналитическая методика: из аргументов возмущающей функции для однократно (1) и двукратно (2) осредненной ограниченной задачи трех тел

(1)
$\begin{gathered} \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } = (l - 2p{\kern 1pt} '\,\, + q{\kern 1pt} ')M{\kern 1pt} '\,\, + (l - 2p)\omega - \\ - \,\,(l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, + \bar {m}(\Omega - \Omega {\kern 1pt} '), \\ \end{gathered} $
(2)
$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = (l - 2p)\omega - (l - 2p{\kern 1pt} ')\omega {\kern 1pt} '\,\, + \bar {m}(\Omega - \Omega {\kern 1pt} ')$
выбираются соотношения, которые при определенном наборе целочисленных индексов ${\text{ }}l,p,p{\kern 1pt} ',\bar {m},q{\kern 1pt} '$ удовлетворяют правилу
(3)
$\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } \approx 0,\,\,\,\,\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } } \approx 0,$
т.е. являются резонансными соотношениями. Далее одно или два подчеркивания $\psi $ и $\dot {\psi }$ указывают на полувековой или вековой характер резонанса соответственно.

Здесь обозначения элементов орбит общепринятые

(4)
$\begin{gathered} M{\kern 1pt} ' = M_{0}^{'} + \bar {n}{\kern 1pt} '\left( {t - {{t}_{0}}} \right),\,\,\,\,\omega {\kern 1pt} ' = \omega _{0}^{'} + \dot {\omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \Omega {\kern 1pt} ' = \Omega _{0}^{'} + \dot {\Omega }{\kern 1pt} '\left( {t - {{t}_{0}}} \right), \\ \omega = {{\omega }_{0}} + \dot {\omega }\left( {t - {{t}_{0}}} \right),\,\,\,\,\Omega = {{\Omega }_{0}} + \dot {\Omega }\left( {t - {{t}_{0}}} \right), \\ \end{gathered} $
причем штрихом помечены орбитальные элементы возмущающего тела.

В процессе исследования вековые частоты в движении спутника $\dot {\Omega },{\text{ }}\dot {\omega }$ определяются путем численного моделирования (Александрова и др., 2020) с использованием уравнений Ньютона Эйлера

(5)
$\begin{gathered} \frac{{d\Omega }}{{dt}} = \frac{r}{p}\frac{{\sin u}}{{\sin i}}W; \\ \frac{{d\omega }}{{dt}} = - \frac{{\cos \upsilon }}{e}S + \frac{{\sin \upsilon }}{e}\left( {1 + \frac{r}{p}} \right)T - \frac{r}{p}\frac{{\sin u}}{{\operatorname{tg} i}}W, \\ \end{gathered} $
где S, T, W – возмущающие ускорения, записанные в орбитальной системе координат и связанные с правыми частями уравнений движения известными соотношениями (Бордовицыны, Авдюшев, 2016). Вековые частоты возмущающих тел также получаются численно с использованием фонда координат больших планет DE438 и производной от интерполяционного полинома Лагранжа 12-го порядка:

(6)

В формулах (5), (6) обозначения орбитальных элементов также общепринятые.

Исследование эволюции резонансных аргументов (1) и (2) обязательно (Мюррей, Дермотт, 2010) для выявления наличия резонанса и его характера. Если резонансный аргумент испытывает либрационное изменение во времени, то резонанс считается устойчивым, а при наличии переходов от либрационного изменения к циркуляционному и обратно резонанс неустойчив. При чисто циркуляционном изменении резонансного аргумента считается, что резонанс отсутствует.

Для определения границ устойчивости резонанса в данной методике используются динамические портреты вековых резонансов, которые строятся в фазовой плоскости (Мюррей, Дермотт, 2010; Морбиделли, 2014)

(7)
$x = e\cos \psi ,\,\,\,\,y = e\sin \psi ,$
где е – эксцентриситет орбиты спутника, ψ – критический аргумент.

В табл. 1 и 2 приведены наборы рассматриваемых вековых резонансов: апсидально-нодальных до четвертого порядка включительно (табл. 1) и резонансов, связанных со средним движением возмущающего тела, второго–пятого порядков (табл. 2). Причем, индексы L и S относятся к возмущениям от Луны и Солнца соответственно.

Таблица 1.

Типы апсидально-нодальных вековых резонансов $\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } }$ низких порядков

№ Тип резонансного
соотношения 		№ Тип резонансного
соотношения 		№ Тип резонансного
соотношения
1 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ 8 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega } - 2\dot {\omega }_{{S,L}}^{'}$ 15 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }_{{S,L}}^{'}$
2 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ 9 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }$ 16 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }_{{S,L}}^{'}$
3 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega } + \dot {\omega }_{{S,L}}^{'}$ 10 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }$ 17 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right)$
4 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega } - \dot {\omega }_{{S,L}}^{'}$ 11 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega }$ 18 $\dot {\omega } - \dot {\omega }_{{S,L}}^{'}$
5 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega } - 2\dot {\omega }_{{S,L}}^{'}$ 12 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega }$ 19 $\dot {\omega } + \dot {\omega }_{{S,L}}^{'}$
6 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - 2\dot {\omega } + 2\dot {\omega }_{{S,L}}^{'}$ 13 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + \dot {\omega }_{{S,L}}^{'}$ 20 $\dot {\omega }$
7 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) + 2\dot {\omega } + 2\dot {\omega }_{{S,L}}^{'}$ 14 $\left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) - \dot {\omega }_{{S,L}}^{'}$    
Таблица 2.  

Типы полувековых резонансов $\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } }$ со скоростью движения возмущающего тела второго–пятого порядков

№ Тип резонансного
соотношения 		№ Тип
резонансного
соотношения 		№ Тип
резонансного
соотношения 		№ Тип
резонансного
соотношения
1 $\bar {n}_{{S,L}}^{'} - \dot {\omega }$ 5 $\bar {n}_{{S,L}}^{'} - (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 9 $\bar {n}_{{S,L}}^{'} - \dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 13 $\bar {n}_{{S,L}}^{'} - 2\dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$
2 $\bar {n}_{{S,L}}^{'} + \dot {\omega }$ 6 $\bar {n}_{{S,L}}^{'} + (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 10 $\bar {n}_{{S,L}}^{'} + \dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 14 $\bar {n}_{{S,L}}^{'} + 2\dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$
3 $\bar {n}_{{S,L}}^{'} - 2\dot {\omega }$ 7 $\bar {n}_{{S,L}}^{'} + \dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 11 $\bar {n}_{{S,L}}^{'} - 2(\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 15 $\bar {n}_{{S,L}}^{'} - 2\dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$
4 $\bar {n}_{{S,L}}^{'} + 2\dot {\omega }$ 8 $\bar {n}_{{S,L}}^{'} - \dot {\omega } + (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 12 $\bar {n}_{{S,L}}^{'} + 2(\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$ 16 $\bar {n}_{{S,L}}^{'} + 2\dot {\omega } - (\dot {\Omega } - \dot {\Omega }{\kern 1pt} ')$

Поскольку величины $\dot {\omega }_{S}^{'}$ и $\dot {\Omega }_{S}^{'}$, связанные с прецессией орбиты Земли, пренебрежимо малы, формулы, приведенные в табл. 1 для апсидально-нодальных резонансов, связанных с Солнцем, существенно упрощаются, и эти резонансы практически становятся геометрическими.

Геометрический резонанс $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \dot {\omega } \approx 0,$ трактуемый как $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \dot {\pi } \pm \dot {\Omega } = \dot {\omega } \approx 0$ (Shevchenko, 2017) является резонансом первого порядка. Для двукратно осредненной ограниченной задачи трех тел этот резонанс был открыт Лидовым (1961) в задачах о движении ИСЗ и Козаи (1962) – в динамике астероидов. В наших исследованиях мы используем численное моделирование без какого-либо осреднения. Поэтому все выявленные нами резонансы будут резонансами полной возмущенной задачи, содержащей влияние несферичности потенциала Земли, а также влияние притяжения Луны и Солнца. Влияние каждого из возмущающих факторов на движения спутника может давать $\dot {\omega } \approx 0,$ поэтому мы будем отделять суммарное влияние всех трех возмущающих факторов от влияния каждого из них.

При этом там, где это возможно, мы будем использовать для сравнения результаты, полученные М.Л. Лидовым (1961) и другими авторами в рамках осредненной задачи. По нашему мнению, это сравнение интересно и с теоретической, и с практической точки зрения.

Классификация основной части вековых резонансов, действующих на движение ИСЗ, была впервые дана Дж. Куком (Cook, 1962), а аналитическая теория вековых спутниковых резонансов представлена в работах (Breiter, 2001a; 2001b; Daquin и др., 2016), термин “резонанс Лидова–Козаи” впервые появился в работе (Breiter, 2001b). С. Хьюз (1980; 1981) был первым, кто предложил использовать численное моделирование в исследовании влияния вековых резонансов. В работах (Chao, Gick, 2004; Rossi, 2008) были впервые применены совместно аналитический и численный подходы к исследованию проблемы.

АНАЛИЗ СТРУКТУРЫ ВЕКОВЫХ РЕЗОНАНСОВ В РАССМАТРИВАЕМОЙ ОБЛАСТИ ОРБИТАЛЬНОГО ПРОСТРАНСТВА

Общая оценка динамической структуры вековых резонансов осуществлялась на основе результатов численного эксперимента, который проводился по методике, изложенной в предыдущем разделе. Принимались во внимание только гравитационные возмущения, определяемые влиянием несферичности гравитационного поля Земли, а также притяжением Луны и Солнца.

Все исследования проводились на модельных объектах, которые были распределены равномерно в интервале больших полуосей от 8000 до 25500 км с шагом в 200 км, с наклонениями от 0° до 180° с шагом 5° и начальным эксцентриситетом, равным 0.001. Расчет орбитальной эволюции проводился на интервале времени 100 лет и в случае необходимости продлевался до 300 лет.

На рис. 1 и 2 приведены данные о распределении вековых апсидально-нодальных резонансов, являющихся следствием соизмеримости параметров прецессии орбиты спутника, возникающей под действием возмущений, и параметров прецессии возмущающих тел: Солнца (рис. 1) и Луны (рис. 2). (На рис. 1–4 для краткости критический аргумент обозначен без подчеркивания, как ψ с нижним индексом, который отражает номер резонанса для рис. 1–2 из табл. 1, а для рис. 3–4 из табл. 2.) Как было отмечено выше, параметры прецессии орбиты Солнца, являющиеся отражением прецессии орбиты Земли, пренебрежимо малы, поэтому многие резонансные соотношения для Солнца, приведенные в табл. 1 совпадают, что и показано на рис. 1. Кроме того, все эти резонансы являются геометрическими, то есть связывают только параметры прецессии орбиты самого спутника, возникающие под действием возмущений, и зависят от наклонения.

Рис. 1.

Распределение апсидально-нодальных вековых резонансов, связанных с прецессией орбиты Солнца. Классификация выполнена по типу колебаний критического аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике обозначен без подчеркивания, чтобы не загромождать рисунок).

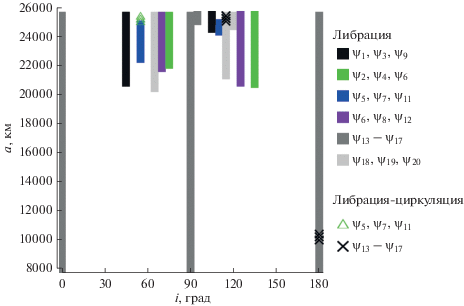
Рис. 2.

Распределение апсидально-нодальных вековых резонансов, связанных с прецессией орбиты Луны. Классификация выполнена по типу колебаний критического аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике обозначен без подчеркивания, чтобы не загромождать рисунок).

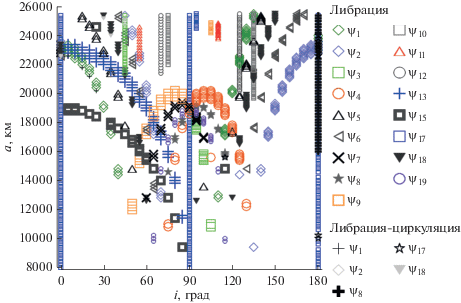
Рис. 3.

Распределение вековых резонансов, связанных со средним движением Солнца. Классификация выполнена по типу колебаний критического аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } $ (на графике обозначен без подчеркивания, чтобы не загромождать рисунок).

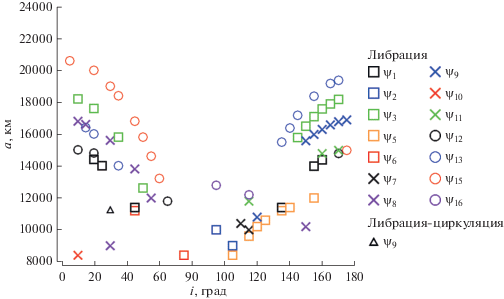
Рис. 4.

Распределение вековых резонансов, связанных со средним движением Луны. Классификация выполнена по типу колебаний критического аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } $ (на графике обозначен без подчеркивания, чтобы не загромождать рисунок).

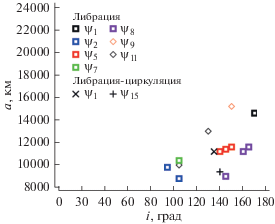
Таким образом, на рис. 1 апсидально-нодальные резонансы с номерами 18, 19 и 20 являются резонансом $\dot {\omega } \approx 0$. Как было показано в нашей работе (Александрова и др., 2016), влияние этого резонанса впервые становится заметным в этой области орбитального пространства. Далее мы рассмотрим этот вопрос более подробно.

Апсидально-нодальные резонансы, связанные с прецессией орбиты Луны (рис. 2), более плотно покрывают рассматриваемую область орбитального пространства. Обращает на себя внимание тот факт, что резонанс $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0$ с номером 17 присутствует и для Солнца, и для Луны на всем диапазоне больших полуосей при трех значениях наклонения 0°, 90° и 180°. В следующем разделе мы также рассмотрим этот вопрос на конкретных примерах орбитальной эволюции объектов.

На рис. 3 и 4 показано распределение вековых резонансов, возникающих вследствие соизмеримости параметров прецессии орбиты спутника со средними движениями возмущающих тел: Солнца (рис. 3) и Луны (рис. 4). Вековые резонансы со средним движением Солнца распределены в диапазоне больших полуосей от 8000 до 21 000 км по обе стороны от наклонения 90°, а вековые резонансы со средним движением Луны проявляются только на орбитах, большие полуоси которых менее 16 000 км и только в динамике объектов с обратным движением.

Полученные сведения о распределении резонансов были сопоставлены с орбитальной эволюцией объектов.

ОСОБЕННОСТИ ОРБИТАЛЬНОЙ ЭВОЛЮЦИИ ОБЪЕКТОВ

Орбитальная эволюция объектов рассматриваемой области не отличается существенным разнообразием, несмотря на большое количество действующих резонансов. Наибольший интерес представляет влияние вековых резонансов первого порядка. К таковым относятся апсидально-нодальный резонанс $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \dot {\pi } \pm \dot {\Omega } = \dot {\omega } \approx 0$ и нодальные резонансы $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0.$

Остановимся на действии этих резонансов более подробно.

Сложность проявления резонанса $\dot {\omega } \approx 0$ в динамике околоземных объектов состоит в том, что помимо влияния внешних тел, которое приводит к появлению резонанса типа Лидова–Козаи, на эти объекты действует несферичность Земли, влияние которой в окрестности критического наклонения тоже может давать $\dot {\omega } \approx 0.$ Наложение этих влияний может приводить к различным эффектам, которые до настоящего времени мало изучены.

Применяемая нами методика позволяет выявить наличие резонанса $\dot {\omega } \approx 0$ в динамике объекта на 100-летнем интервале времени при больших полуосях от 10 000 км, хотя в орбитальной эволюции этот резонанс проявляется очень незначительным ростом эксцентриситета, только начиная с больших полуосей равных 23 000 км (рис. 5). Результаты, приведенные на рис. 5, получены при значениях долгот, равных $\omega = 90^\circ ,\,\,\Omega = 0^\circ .$

Рис. 5.

Особенности динамики объекта под действием резонанса $\dot {\omega } \approx 0,$ с учетом возмущений от несферичности Земли и притяжения Луны и Солнца: (а) орбитальная эволюция на 100-летнем интервале времени; (б) орбитальная эволюция на 300-летнем интервале времени; (в, г) изменение во времени параметров резонанса: резонансного соотношения $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } $ и резонансного аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике обозначения даны без подчеркивания, чтобы не загромождать рисунок).

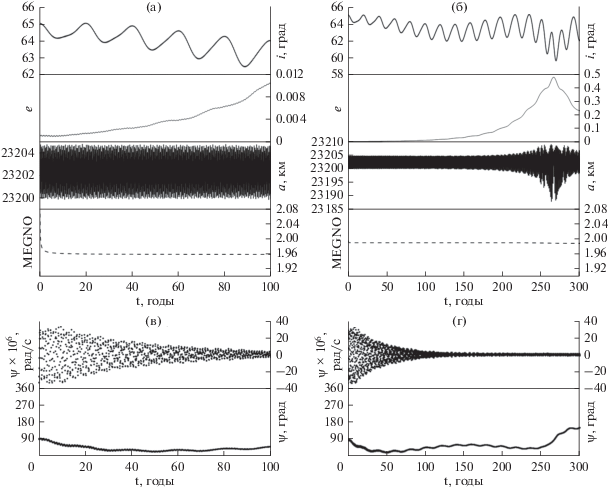
Здесь и далее в данных об орбитальной эволюции приводится осредненный параметр MEGNO, показанный пунктирной линией. Для осредненного параметра MEGNO характерны следующие свойства: для устойчивых орбит типа гармонического осциллятора он стремится к 0, для квазипериодических (регулярных) орбит – к 2, для неустойчивых орбит принимает значения существенно большее 2 (Cincotta и др., 2003).

Результаты показывают, что только на 300-летнем интервале времени удается увидеть появление эффекта взаимосвязанных колебаний значений аргумента перицентра и эксцентриситета (своеобразной перекачки энергии между эксцентриситетом и наклонением), который похож на эффект Лидова–Козаи. Интересно было понять, как взаимодействуют все три возмущающих фактора. Для этого была рассмотрена идеализированная задача: движение объекта моделировалось в предположении, что не только Луна и Солнце, но и центральное притяжение являются притяжением точечных масс, а сжатие Земли рассматривается как самостоятельная сила. При этих предположениях на 300-летнем интервале времени в эклиптической системе координат была исследована эволюция данного объекта под влиянием различных сочетаний, действующих факторов (рис. 6). Наклонение объекта при переходе к эклиптике составило примерно 40°.

Рис. 6.

Орбитальная эволюция объекта при наклонении орбиты к эклиптике примерно 40° на 300-летнем интервале времени под действием: (а) возмущений от сжатия Земли, (б) возмущения от Луны, (в) возмущения от Солнца, (г) возмущения от Луны и Солнца.

Данные, приведенные на рис. 6, показывают, что действие Луны, Солнца и даже совместное действие Луны и Солнца не приводят к хоть сколько-то значительному росту эксцентриситета (${{e}_{{\max }}} = 0.01$) и только действие трех факторов дает заметный эффект (${{e}_{{\max }}} = 0.5$) (рис. 5б).

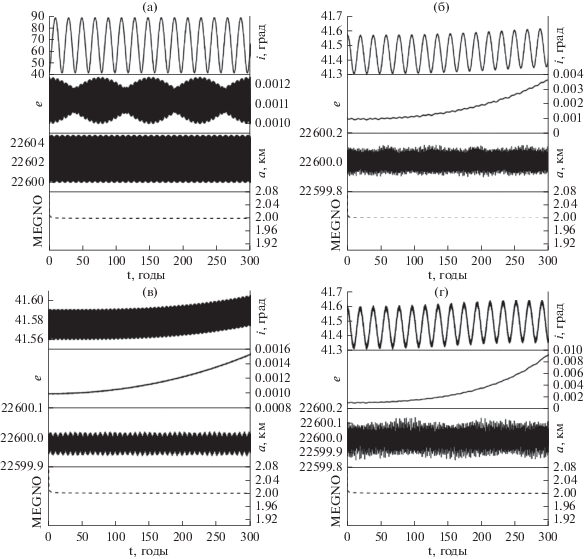
Однако сжатие не всегда усиливает указанный выше эффект. Может быть и обратное действие (Томилова и др., 2020). Все зависит от того, каким будет наклонение орбиты объекта в эклиптической системе координат. Для того, чтобы в этом убедиться, рассмотрим в рамках той же идеализированной задачи движение объекта с близкими значениями позиционных переменных, но при значениях долгот, равных $\omega = 90^\circ ,\,\,\Omega = 180^\circ $ (рис. 7). Наклонение при переходе к плоскости эклиптики составляет примерно 88°.

Рис. 7.

Особенности динамики объекта при наклонении орбиты к эклиптике примерно 88° на 300-летнем интервале: (а) орбитальная эволюция объекта в экваториальной системе координат с учетом возмущения от сжатия и внешних тел, далее орбитальная эволюция в эклиптической системе координат с учетом: (б) возмущения от сжатия Земли, (в) возмущения от Луны, (г) возмущения от Солнца, (д) возмущений от Луны и Солнца, (е) орбитальная эволюция под действием всех трех возмущающих факторов. На рис. (в, д) на графиках эволюции эксцентриситета пунктирная линия отсекает значения эксцентриситета, по достижении которых в реальной задаче спутник попадает в плотные слои атмосферы и сгорает.

Приведенные на рис. 7 результаты показывают, что главным источником возникновения эффекта перекачки энергии между эксцентриситетом и наклонением (т.е. эффекта взаимосвязанных колебаний значений аргумента перицентра и эксцентриситета), в данном случае являются возмущения от Луны, влияние Солнца способствует более раннему проявлению эффекта, а возмущения от сжатия Земли эффект полностью нивелируют. Это особенно заметно в эклиптической системе координат.

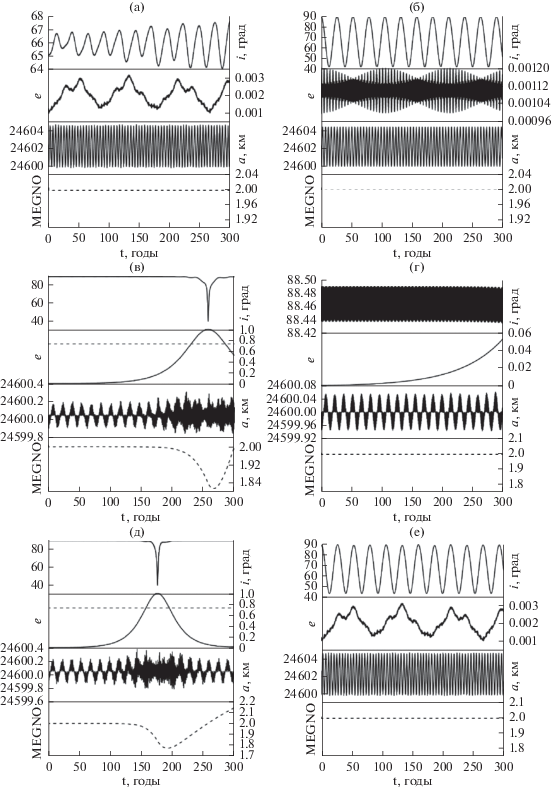
Обратимся к резонансным характеристикам идеализированной задачи (рис. 8) и сравним их с известными из литературных источников (Лидов, 1961; Вашковьяк, Тесленко, 2016) характеристиками проявления резонанса и эффекта Лидова–Козаи в двукратно осредненной задаче. Характерными особенностями орбитальной эволюции объектов, подверженных действию резонанса Лидова–Козаи, является рост эксцентриситета орбиты, который на длительных интервалах времени может сопровождаться перекачкой энергии между эксцентриситетом и наклонением (эффект Лидова–Козаи) при сохранении интеграла ${{c}_{1}} = \sqrt {1 - {{е}^{2}}} \cos i,$ причем ${{c}_{1}}$ должно лежать в пределах $0 \leqslant {{c}_{1}} \leqslant {3 \mathord{\left/ {\vphantom {3 5}} \right. \kern-0em} 5}$. Острый резонанс Лидова–Козаи и быстрый рост эксцентриситета имеет место при долготе перицентра от узла ${{\omega }} = 90^\circ ,$ при близости к нулю значения интеграла Лидова–Козаи и при отрицательном значении интеграла Лидова

${{c}_{2}} = {{e}^{2}}\left( {{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-0em} 5} - {{{\sin }}^{2}}\omega {{{\sin }}^{2}}i} \right).$
Рис. 8.

Резонансные характеристики динамики объекта, приведенного на рис. 7: (а, в) с учетом возмущений от Луны и Солнца; (б, г) с учетом возмущений от сжатия Земли и притяжения Луны и Солнца; (а, б) изменение во времени резонансного соотношения $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } $ и резонансного аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике обозначения даны без подчеркивания, чтобы не загромождать рисунок); (в, г) эволюция во времени интегралов Лидова и Лидова–Козаи.

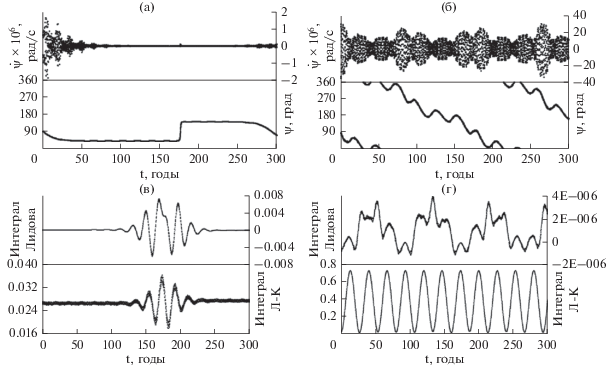
На рис. 8 приведены резонансные характеристики для двух случаев орбитальной эволюции. Рис. 8а и 8в показывают поведение резонансных характеристик и численных аналогов интегралов движения ${{c}_{1}},{{c}_{2}}$ в динамике объекта при учете возмущений от Луны и Солнца, а рис. 8б, 8г – при учете трех возмущающих факторов: сжатия Земли, а также притяжения Луны и Солнца. Кроме интеграла Лидова–Козаи, приведен интеграл Лидова.

Представленные на рис. 7 и 8 данные показывают, что явления, подобные эффекту и резонансу Лидова–Козаи, присутствуют в динамике рассматриваемого объекта, причем острый резонанс проявляется около момента времени, соответствующего 175 гг. В окрестности этого момента имеет место быстрый рост эксцентриситета, долгота перицентра от узла ${{\omega }} = 90^\circ ,$ при близости к нулю значения интеграла Лидова–Козаи и при отрицательном значении интеграла Лидова, что находится в соответствии с теоретическими результатами, полученными в осредненной задаче (Лидов, 1961; Вашковьяк, Тесленко, 2016). Влияние сжатия полностью искажает картину. Эксцентриситет уже не растет, а колеблется в пределах 0.001–0.003, интеграл Лидова–Козаи колеблется в достаточно больших пределах, а интеграл Лидова переходит в зону положительных значений, резонансное соотношение по-прежнему неоднократно проходит через нулевое значение, но резонансный аргумент демонстрирует переходы от либрации к циркуляции, т.е. резонанс есть, но он неустойчив.

Приведенный пример показывает, что существует прямая связь между явлениями, наблюдаемыми в численном моделировании и эффектами, полученными в двукратно осредненной задаче.

Можно предположить, что на более низких орбитах действие резонанса, подобного резонансу Лидова–Козаи, нивелируется влиянием сжатия Земли.

Пример такой орбитальной эволюции приведен на рис. 9. Рассмотрена орбитальная эволюция объекта и его резонансных характеристик при совместном действии трех факторов: сжатия Земли, Луны и Солнца (рис. 9а, 9б), а также при раздельном влиянии сжатия Земли (рис. 9в, 9г), и Луны, и Солнца (рис. 9д, 9ж). При отсутствии сжатия влияние Луны и Солнца проявляется ростом эксцентриситета, и резонансные характеристики указывают на наличие устойчивого резонанса типа Лидова–Козаи. При совместном учете всех трех факторов влияние сжатия превалирует.

Рис. 9.

Особенности динамической эволюции объектов на более низких орбитах: слева – орбитальная эволюция объектов и справа – для резонанса $\dot {\omega } \approx 0$ изменение во времени резонансного соотношения $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } $ и резонансного аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике, как и ранее подчеркивания опущены, чтобы не загромождать рисунок): (а, б) в экваториальной системе координат с учетом возмущения от сжатия Земли и притяжения внешних тел; (в, г) в эклиптической системе координат с учетом возмущения от сжатия Земли; (д, е) в эклиптической системе координат с учетом возмущений от Луны и Солнца.

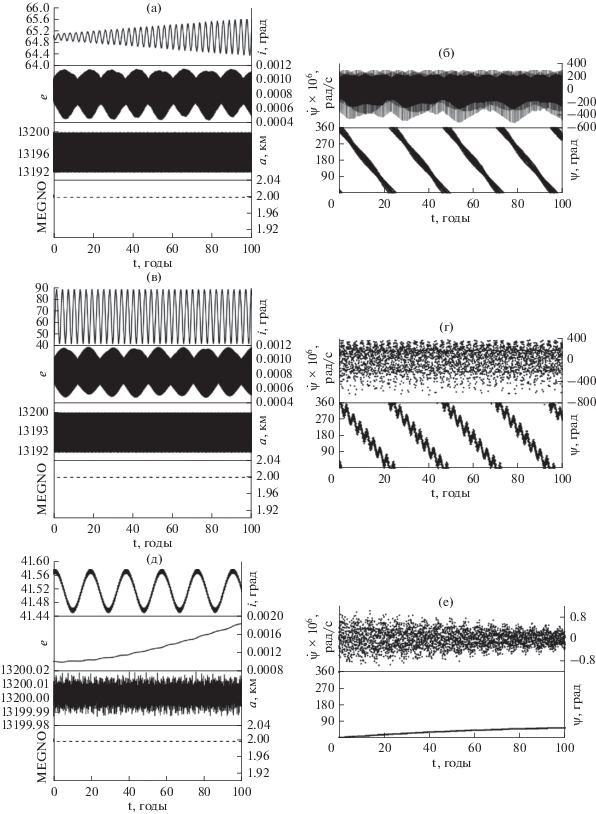
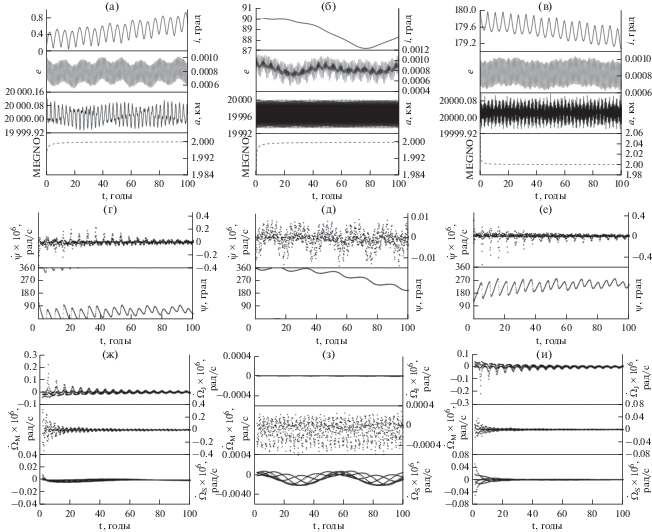
Рис. 10.

Особенности динамики объектов в условиях действия векового резонанса $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right) \approx 0:$ орбитальная эволюция объекта с наклонением орбиты (а) 0°; (б) 90°; (в) 180°; пункты г), д), е) соответствующие пунктам (а), (б), (в) резонансные характеристики: изменение во времени резонансного соотношения $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } $ и резонансного аргумента $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } $ (на графике, как и ранее, подчеркивания опущены, чтобы не загромождать рисунок); пункты (ж), (з), (и) соответствующие пунктам (г),( д), (е) покомпонентные расшифровки структуры $\dot {\Omega }$.

Интересно отметить, что проблема совместного влияния сжатия и векового апсидально нодального резонанса $\dot {\omega } \approx 0$ на движение ИСЗ была впервые сформулирована М.Л. Лидовым в работе (Лидов, Ярская, 1974), а для спутников Урана было показано, что значительное влияние сжатия удерживает на орбитах спутники, наклоненные к плоскости ураноцентрической орбиты Солнца на 98° (Вашковьк, Тесленко, 2016).

Рассмотрим далее влияние на динамику околоземных объектов нодального резонанса $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0.$ Как было показано выше, он присутствует в динамике объектов на всем исследуемом диапазоне больших полуосей при трех значениях наклонения 0°, 90° и 180°.

На рис. 10 для сравнения показана орбитальная эволюция трех объектов, имеющих одинаковые значения большой полуоси 20 000 км, одинаковые начальные эксцентриситеты, равные 0.001, и разные наклонения орбит: 0°, 90° и 180°. Кроме того приведены данные об изменении резонансных характеристик объектов и об эволюции компонент составляющей резонанса величины $\dot {\Omega }$, формула (5). Движение во всех трех случаях регулярно. Для объектов с наклонениями 0° и 180° орбитальная эволюция подобна (рис. 10а, 10б), присутствует вековой уход по наклонению в пределах одного градуса. Орбитальная эволюция объекта с наклонением 90° несколько иная. Здесь имеют место долгопериодические колебания.

Остановимся на резонансных характеристиках, приведенных на рис. 10г, 10д, 10е. Численные оценки поведения резонансных соотношений указывают на множественное прохождение этих соотношений через нулевые значения. Окрестность, в которой колеблется около нуля резонансное соотношение для объекта с наклонением 90° существенно меньше, чем у объектов с наклонениями 0° и 180°. Приведенные изменения во времени компонент величины $\dot {\Omega }$ показывают, что амплитуды колебаний компонент около нуля для объекта с наклонением 90° на три порядка меньше, чем для двух других объектов. Учитывая, что величина $\dot {\Omega }{{_{L}^{'}}_{{}}}$ имеет порядок примерно $1 \times {{10}^{{ - 8}}}$, обращение в ноль величины $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }{{{_{L}^{'}}}_{{}}}} \right)$ зависит от значений входящей в него величины $\dot {\Omega }$. То же самое можно сказать и о резонансе $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{S}^{'}} \right).$

Совместное действие нескольких устойчивых вековых резонансов не приводит к возникновению хаотичности в движении объекта (Бордовицына, Томилова, 2016). Пример такого движения приведен на рис. 11, 12.

Рис. 11.

Орбитальная эволюция объекта, подверженного действию четырех устойчивых вековых апсидально-нодальных резонансов.

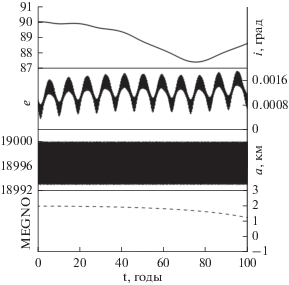
Рис. 12.

Резонансные характеристики четырех вековых резонансов, действующих на объект, приведенный на рис. 11: для резонансов (а, б) $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right) - \dot {\omega } - \dot {\omega }_{L}^{'}$, (в, г) $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right) + 2\dot {\omega } + 2\dot {\omega }_{L}^{'}$, (д, е) $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = \left( {\dot {\Omega } - \dot {\Omega }_{L}^{'}} \right)$, (ж, з) $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = \left( {\dot {\Omega } - \dot {\Omega }{{{_{S}^{'}}}_{{}}}} \right)$ (а, в, д, ж) эволюция резонансных соотношений и соответствующих резонансных аргументов (на графике, как и ранее, подчеркивания опущены); (б, г, е, з) фазовые портреты.

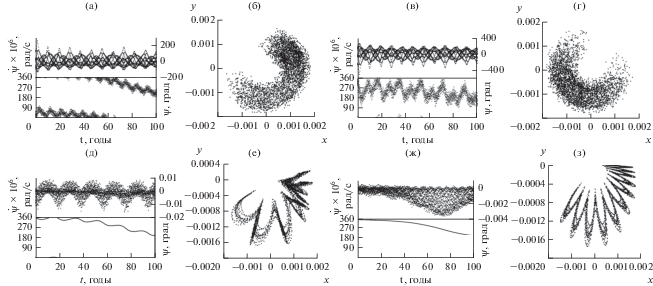
На рис. 11 дана орбитальная эволюция объекта, подверженного действию четырех устойчивых вековых апсидально-нодальных резонансов, а на рис. 12 даны резонансные характеристики движения. На рис. 12а, 12в, 12д, 12ж приведены (сверху вниз) изменения резонансных соотношений и резонансных аргументов. На рис. 12б, 12г, 12е, 12з показаны фазовые портреты. Приведенные на рис. 12 данные позволяют с уверенностью говорить о том, что резонансы устойчивы на всем рассматриваемом временном интервале. Других резонансов в движении объекта нет. Таким образом, наложение нескольких устойчивых вековых резонансов не приводит к возникновению хаотичности (рис. 11 MEGNO меньше 2). В эволюции наклонения орбиты заметно влияние резонансов $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0$.

И наоборот, совместное действие устойчивых и неустойчивых вековых резонансов вызывает появление хаотичности в движении объекта (рис. 13).

Рис. 13.

Орбитальная эволюция объекта, подверженного действию двух устойчивых и четырех неустойчивых вековых резонансов: (а) орбитальная эволюция объекта, (б–з) изменение во времени резонансных характеристик и фазовые портреты резонансов; (б) для резонанса со средним движением Луны и Солнца $\dot {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\psi } } = \bar {n}_{{L,S}}^{'} + \dot {\omega } \approx 0$; для резонанса $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \Omega _{{S,L}}^{'}} \right) + \dot {\omega } \approx 0$, (в) с Луной, (г) с Солнцем; для $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }{{{_{{S,L}}^{'}}}_{{S,L}}}} \right) - \dot {\omega } \approx 0$, (д) с Луной, (е) с Солнцем; для $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }{{{_{{S,L}}^{'}}}_{{S,L}}}} \right) \approx 0$, (ж) с Луной, (з) с Солнцем. На графиках, как и ранее, подчеркивания опущены.

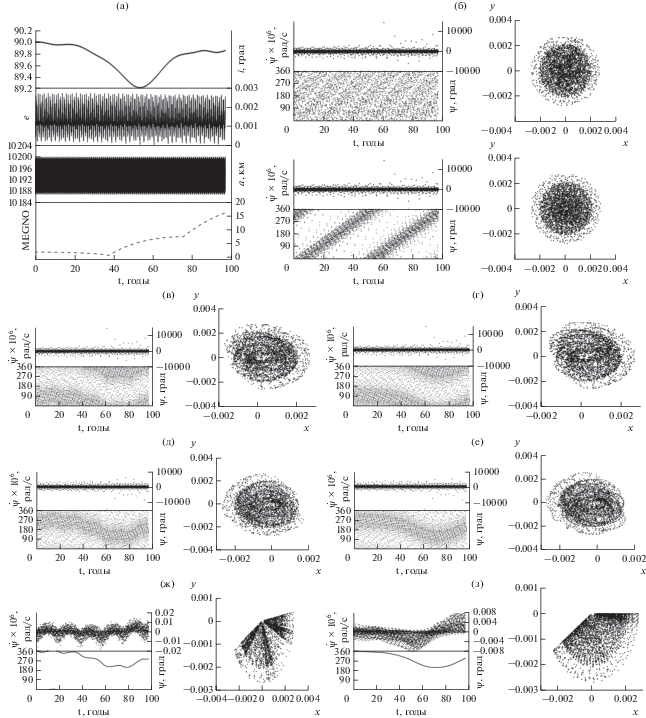
На объект, эволюция которого показана на рис. 13, действуют на всем интервале прогнозирования два устойчивых вековых резонанса первого порядка и четыре неустойчивых резонанса более высоких порядков, в том числе два со средними движениями Луны и Солнца. Движение объекта имеет высокую степень хаотичности (MEGNO значительно больше 2), а в орбитальной эволюции просматривается влияние устойчивых резонансов $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0.$

ЗАКЛЮЧЕНИЕ

Представленные в данной работе результаты по выявлению вековых резонансов, действующих на объекты, движущиеся в областях LEO–MEO, и анализу их влияния на орбитальную эволюцию позволяют сделать ряд выводов.

Апсидально-нодальные резонансы, связанные с прецессией орбиты Луны более плотно покрывают рассматриваемую область орбитального пространства, чем аналогичные резонансы, связанные с прецессией орбиты Солнца, которая является отражением прецессии орбиты Земли.

Используемая методика выявляет резонанс $\dot {\omega } \approx 0$, начиная с больших полуосей, равных 20 000 км, при наклонении близком 65° к экватору Земли. Для объектов, движущихся в рассматриваемом диапазоне больших полуосей, на 100-летнем интервале времени эффект взаимосвязанных колебаний значений аргумента перицентра и эксцентриситета (перекачки энергии между эксцентриситетом и наклонением), подобный эффекту Лидова–Козаи не успевает проявиться. Однако орбитальная эволюция на 300-летнем интервале показывает наличие такого эффекта, который может либо подавляться, либо усиливаться действием несферичности Земли в зависимости от наклонения орбиты к плоскости эклиптики. Анализ орбитальной эволюции объектов, имеющих наклонение орбиты к экватору 65° показывает, что подобный эффект присутствует и на более низких орбитах, но его проявление подавляется влиянием несферичности Земли.

Обращает на себя внимание тот факт, что резонанс $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\dot {\psi }} } = \left( {\dot {\Omega } - \dot {\Omega }_{{S,L}}^{'}} \right) \approx 0$ присутствует и для Солнца, и для Луны на всем диапазоне больших полуосей при трех значениях наклонения 0°, 90° и 180°. В орбитальной эволюции действие этого резонанса проявляется наличием долгопериодических колебаний в наклонении орбиты. Причем наибольшая амплитуда при одних и тех же значениях больших полуосей у объектов с наклонением орбиты 90°. Величина амплитуды растет с увеличением большой полуоси.

В нижней части рассматриваемой области появляются резонансы, связанные со средним движением возмущающих тел Луны и Солнца. Несмотря на обилие резонансов, совместное действие нескольких резонансов встречается нечасто. Наложение нескольких устойчивых вековых резонансов разных типов не приводит к возникновению хаотичности в движении объектов, а при совместном действии устойчивых и неустойчивых вековых резонансов наблюдается рост хаотичности движения.

Исследование выполнено за счет гранта Российского научного фонда (проект № 19-72-10022).

Список литературы

  1. Авдюшев В.А. Интегратор Гаусса–Эверхарта // Вычисл. технологии. 2010. Т. 15. № 4. С. 31–47.

  2. Александрова А.Г., Бордовицына Т.В., Чувашов И.Н. Численное моделирование в задачах динамики околоземных объектов // Изв. вузов. Физика. 2017. Т. 60. № 1. С. 69–76.

  3. Александрова А.Г., Бордовицына Т.В., Томилова И.В. Особенности совместного влияния вековых резонансов низких порядков и светового давления на движение околоземных космических объектов // Изв. вузов. Физика. 2019. 2018a. Т. 61. № 4(724). С. 75–80.

  4. Александрова А.Г., Бордовицына Т.В., Томилова И.В. Исследование влияния светового давления на динамику околоземных объектов на резонансных орбитах // Астрон. вестн. 2018b. Т. 52. № 5. С. 447–462. (Aleksandrova A.G., Bordovitsyna T.V., Tomilova I.V. Investigation of light pressure influence on dynamics of near-earth objects in resonant orbits // Sol. Syst. Res. 2018. Т. 52. № 5. P. 435–449.)

  5. Александрова А.Г., Бордовицына Т.В., Александров В.Б. Исследование влияния светового давления на динамику околоземных объектов с обратным движением // Изв. вузов. Физика. 2019. Т. 62. № 3(735). С. 86–91.

  6. Александрова А.Г., Бордовицына Т.В., Попандопуло Н.А., Томилова И.В. Новый подход к вычислению вековых частот в динамике околоземных объектов на орбитах с большими эксцентриситетами // Изв. вузов. Физика. 2020. Т. 63. № 1(745). С. 57–62.

  7. Бордовицына Т.В., Авдюшев В.А.Теория движения ИСЗ. Аналитические и численные методы. Томск: Изд-во ТГУ. 2016. 262 с.

  8. Бордовицына Т.В., Александрова А.Г., Чувашов И.Н. Комплекс алгоритмов и программ для исследования хаотичности в динамике искусственных спутников Земли // Изв. вузов. Физика. 2010. Т. 53. № 8–2. С. 14–21.

  9. Бордовицына Т.В, Томилова И.В. Особенности структуры вековых резонансов в динамике околоземных космических объектов // Изв. вузов. Физика. 2016. Т.59. № 3. С. 41–48.

  10. Вашковьяк М.А., Тесленко Н.М. Михаил Львович Лидов – яркое имя в космической науке Сб. докл. “Михаил Львович Лидов – яркое имя в космической науке” / Ред. Вашковяк М.А. М.: ИПМ им. М.В. Келдыша, 2016. С. 9–38.

  11. Кузнецов Э.Д. О влиянии светового давления на орбитальную эволюцию геосинхронных спутников // Астрон. вестн. 2011. Т. 45. № 5. С. 444–457. (Kuznetsov E.D. The effect of the radiation pressure on the orbital evolution of geosynchronous objects // Sol. Syst. Res. 2011. V. 45. № 5. P. 433–446.)

  12. Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Шагабутдинов А.И., Кудрявцев С.О. Особенности орбитальной эволюции спутников Земли, обладающих большой парусностью, в окрестности резонансов низких порядков // Вестн. сибир. гос. аэрокосмич. университета им. акад. М.Ф. Решетнева. 2011. Вып. 6(39). С. 148–151.

  13. Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Шагабутдинов А.И., Кудрявцев С.О. О влиянии светового давления на орбитальную эволюцию объектов, движущихся в окрестности резонансов низких порядков // Астрон. вестн. 2012. Т. 46. № 6. С. 480–488. (Kuznetsov E.D., Zakharova P.E., Glamazda D.V., Shagabutdinov A.I., Kudryavtsev S.O. Light pressure effect on the orbital evolution of objects moving in the neighborhood of low-order resonances // Sol. Syst. Res. 2012. V. 46. № 6. P. 442–449.) https://doi.org/10.1134/S0038094612050073

  14. Кузнецов Э.Д., Захарова П.Е., Гламазда Д.В., Кудрявцев С.О. Влияние резонансов высоких порядков на орбитальную эволюцию объектов в окрестности геостационарной орбиты // Астрон. вестн. 2014. Т. 48. № 6. С. 482–494. (Kuznetsov E.D., Zakharova P.E., Glamazda D.V., Kudryavtsev S.O. Effect of the high-order resonances on the orbital evolution of objects near geostationary orbit // Sol. Syst. Res. 2014. V. 48. № 6. P. 446–459.) https://doi.org/10.7868/S0320930X14060048

  15. Лидов М.Л. Эволюция искусственных спутников планет под действием гравитационных возмущений от внешнего тела // Искусственные спутники Земли. 1961. Т. 8. С. 5–45.

  16. Морбиделли А. Современная небесная механика. Аспекты динамики Солнечной системы. М.–Ижевск: Ин-т компьютерных исследований, 2014. 432 с.

  17. Мюррей К., Дермотт С. Динамика Солнечной системы. М.: Физматлит, 2010. 588 с.

  18. Прохоренко В.И. Долговременная эволюция орбит ИСЗ под влиянием гравитационных возмущений, обусловленных сжатием Земли, с учетом возмущений от третьих тел// Изв. вузов. Физика. 2006. № 2. С. 63–73.

  19. Томилова И.В., Бордовицына Т.В., Красавин Д.С. Динамическая структура орбитального пространства ГЛОНАСС и GPS. Проблема утилизации отработавших объектов // Астрон. вестн. 2018. Т. 52. № 5. С. 463–478. (Tomilova I.V., Bordovitsyna T.V., Krasavin D.S. Dynamic Structure of the GLONASS and GPS Orbital Space: Problem of Disposal of Retired Objects // Sol. Syst. Res. 2018. V. 52. № 5. Р. 450–465.)

  20. Томилова И.В., Блинкова Е.В., Бордовицына Т.В. Особенности динамики объектов, движущихся в окрестности резонанса 1 : 3 с вращением Земли // Астрон. вестн. 2019. Т. 53. № 5. С. 323–338 (Tomilova I.V., Blinkova E.V., Bordovitsyna T.V. Features of the Dynamics of Objects Moving in the Neighborhood of the 1:3 Resonance with the Earth’s Rotation // Sol. Syst. Res. 2019. V. 53. № 5. Р. 1–15.)

  21. Томилова И.В., Красавин Д.С., Бордовицына Т.В. Динамическая структура околоземного орбитального пространства в области резонанса 1 : 2 со скоростью вращения Земли // Астрон. вестн. 2021 (в печати).

  22. Allan R.R. Resonance effects due to the longitude dependence of the gravitational field of a rotating primary // Planet. and Space Sci. 1967a. V. 15. P. 53–76.

  23. Allan R.R. Satellites resonance with the longitude dependent gravity. II. Effects involving the eccentricity // Planet. and Space Sci. 1967b. V. 15. P. 1829–1845.

  24. Breiter S. On the coupling of lunisolar resonances for Earth satellite orbits // Celest. Mech. Dyn. Astron. 2001a. V. 80. P. 1–20.

  25. Breiter S. Lunisolar resonances revisited // Celest. Mech. Dyn. Astron. 2001b. V. 81. P. 81–91.

  26. Chao C., Gick R. Long-term evolution of navigation satellite orbits // Adv. Space Res. 2004. V. 34. P. 1221–1226.

  27. Cincotta P.M., Simó C. Simple tools to study global dynamics in non-axisymmetric galactic potentials – I // Astron. and Astrophys. Suppl. 2000. V. 147. P. 205–228.

  28. Cincotta P.M., Girdano C.M., Simo C. Phase space structure of multi-dimensional systems by means of the mean exponential growth factor of nearby orbits // Physica D. 2003.V. 182. P. 151–178.

  29. Cook G.E. Luni-Solar Perturbations of the Orbit of an Earth Satellite // Geophys. J. 1962. V. 6. № 3. P. 271–291.

  30. Daquin J., Rosengren A.J., Alessi E.M., Deleflie F., Valsecchi G.B., Rossi A. The dynamical structure of the MEO region: long-term stability, chaos, and transport // Celest. Mech. Dyn. Astron. 2016. V. 124(4). P. 335–366.

  31. Gedeon G.S. Tesseral Resonance Effects on Satellite Orbits // Celest. Mech. 1969. V. 1. P. 167–189.

  32. Hughes S. Earth satellite orbits with resonant lunisolar perturbations, I. Resonances dependent only on inclination // Proc. Roy. Soc. Lond. 1980. A 372. P. 243–264.

  33. Hughes S. Earth satellite orbits with resonant lunisolar perturbations, II. Some resonances dependent on the semi-major axis, eccentricity and inclination // Proc. Roy. Soc. Lond. 1981. A 375. P. 379–396.

  34. Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.

  35. Lidov M.L., Yarskaya M.V. Integrable Cases in the Problem of the Evolution of a Satellite Orbit under the Joint Effect of an Outside Bode and Noncentrality of the Planetary Field // Cosmic. Res. 1974. V. 12. № 2. P. 139–152.

  36. Rossi A. Resonant dynamics of Medium Earth Orbits: space debris // Celest. Mech. Dyn. Astr. 2008. V. 100 P. 267–286.

  37. Shevchenko I. The Lidov-Kozai effect – Applications in exoplanet research and dynamical astronomy. 2017. Doi https://doi.org/10.1007/978-3-319-43522-0

  38. Sochilina A.S. On the motion of a satellite in resonance with its rotating planet // Celest. Mech. 1982. V. 26. P. 337–352.

  39. Valk S., Delsate N., Lemaitre A., Carletti T. Global dynamics of high area-to-mass ratios GEO space debris by means of the MEGNO indicator// Adv. Space Res. 2009. V. 43. № 7. P. 1509–1526.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал