Астрономический вестник, 2021, T. 55, № 4, стр. 359-367

ВВЕДЕНИЕ

В работе (Кузнецов, 2016) для определения предварительной параболической орбиты по трем наблюдениям, в моменты времени t₁, t₂ и t₃, был предложен метод алгебраических уравнений, восходящий к Лагранжу (Lagrange, 1778) и Субботину (Субботин, 1933), который позволил отказаться от линейных ограничений метода Ольберса и строго описать задачу. Для орбит, находящихся вне плоскости эклиптики, была получена система из двух алгебраических уравнений для двух неизвестных и поставлена задача поиска эффективного алгоритма для ее решения. Была произведена оценка максимального числа возможных решений и согласно теореме Бернштейна (Бернштейн, 1975) показано, что оно не может превосходить 1152. Данная статья является продолжением этой работы.

Кратко напомним суть предложенного метода. Параболические орбиты представляют собой предельный (граничный) случай для эллиптического и гиперболического движения. Поэтому определение предварительной параболической орбиты, с приемлемой точностью возможно для долгопериодических комет, движущихся по близпараболическим орбитам с эксцентриситетом e > 0.99. Обозначим через r₁, r₂ и r₃ – радиус-векторы орбиты наблюдаемого тела в соответствующие моменты времени. Тогда уравнения для гелиоцентрических радиус-векторов будут иметь следующий вид:

где e₁, e₂ и e₃ – единичные векторы наблюденного направления на объект (известны из угловых наблюдений в соответствующие моменты времени), R₁, R₂ и R₃ – векторы положения Солнца относительно топоцентра (также считаются известными). Таким образом, неизвестными остаются только три топоцентрических расстояния между наблюдателем и кометой: ρ₁, ρ₂ и ρ₃. Определение орбиты в некомпланарном случае сводится к решению системы двух уравнений относительно трех топоцентрических расстояний до кометы. Она была получена в предыдущей работе (Кузнецов, 2016) в виде системы уравнений (11). С учетом орбитальных дуг >π и после несложных преобразований она приводится к виду: где τ₂₁ = k(t₂ – t₁), τ₃₂ = k(t₃ – t₂), k = 0.01720209895 – постоянная Гаусса, L = 0.00576832 [сут/(а. е.)] – аберрационная постоянная. В “$ \mp $” верхний знак соответствует углу между векторами <π, а нижний >π. Стоит отметить, что в (2) только один из двух углов между векторами может быть >π и, следовательно, система уравнений (2) имеет три возможных варианта представления. Система уравнений строго соответствует движению по параболе и, как уже отмечалось выше, может быть применима к близпараболическим орбитам (e > 0.99). В силу того, что искомая орбита плоская, радиус-векторы (1) связаны между собой уравнением компланарности:

Уравнение (3) позволяет выразить одно из топоцентрических расстояний через два других. Выразим ρ₂ ≥ 0 через ρ₁ и ρ₃:

Система уравнений (2) зависит от трех переменных: ρ₁, ρ₂ и ρ₃. Если мы подставим (4) в (2), то получим систему из двух алгебраических уравнений относительно двух неизвестных ρ₁ и ρ₃. При этом в виду нелинейности системы (2), возможно появление нескольких решений.

Целью настоящей работы является построение алгоритма численного решения системы уравнений, с нахождением всех возможных орбит.

ПЕРЕХОД К НОВЫМ ПЕРЕМЕННЫМ

Топоцентрические расстояния ρ₁ и ρ₃ могут принимать только положительные значения. Таким образом, область искомых решений представляет собой открытый квадрант, который нужно ограничить максимальными значениями. Для этого в работе (Кузнецов, 2019) предлагалось перейти к нормированным безразмерным переменным. Рассмотрим единичный вектор N = (N_x, N_y, N_z), представляющий собой вектор нормали к плоскости искомой орбиты. Для удобства связи N с элементами орбиты выберем эклиптическую систему координат. Выразим ρ_i (i = 1, 2, 3) через N. Если уравнения (1) скалярно умножить на N, то получим выражения для ρ_i (Sarnecki, 1997):

Условие единичности N можно определить так:

Теперь мы можем подставить (5) во все уравнения для некомпланарных орбит. Получаем аналог (2) с ограничением (6) и безразмерными неизвестными {N_x, N_y, N_z}:

Область решения ограничивается поверхностью единичной сферы. Точки пересечения f₁ и f₂ являются возможными направлениями N. Так как кривые (7) симметричны относительно плоскости эклиптики, то можно выбрать одну из полусфер с прямым или обратным орбитальным движением. Тогда условие (6) можно записать как:

и отобразить область решения единичной сферы на единичную область круга эклиптики. Таким образом, мы вернулись к двумерному случаю с неизвестными N_x и N_y. Дополнительным достоинством новых переменных является то, что они напрямую не связаны с конкретными наблюдениями и их числом, а это упрощает работу по созданию целевой функции. Из единичного круга следует исключить области с отрицательными топоцентрическими расстояниями и параметром орбиты p. Введение таких ограничений позволяет сузить поиск решения со всего единичного круга до его отдельных областей.

Мы свели задачу к поиску решения в единичном круге. Однако круг не очень удобен для разбиения и плотного покрытия простыми геометрическими фигурами, например, треугольниками. Для триангуляции больше подходит квадрат, описывающий данный круг, т.е. имеющий единичную длину полу стороны. Отображение круга единичного радиуса на соответствующий квадрат осуществляется по следующим формулам (Fong, 2014):

где N_xs и N_ys – координаты, соответствующие квадрату.

ПОРЯДОК ПОЛОЖЕНИЙ ОБЪЕКТА НА ОРБИТЕ

При решении, как правило, не учитывается порядок точек пересечения лучей зрения (наблюдений) с орбитой. Отсюда, возможно появление решений, для которых порядок соответствующих точек орбиты не соответствует хронологическому. Для их контроля можно воспользоваться следующими условиями:

где Δθ_ij величины углов (в радианах) между r_i и r_j.

ОСОБЫЕ ТОЧКИ В ОБЛАСТИ ПОИСКА

Как и в случае топоцентрических расстояний {ρ₁, ρ₃}, так и для безразмерных переменных {N_xs, N_ys} существуют особые точки, в которых либо ρ₂ из (4), либо все ρ_i из (5) становятся неопределенными. В зависимости от того, обращается числитель или знаменатель в ноль, значение соответствующего топоцентрического расстояния может стать либо бесконечно малым, либо бесконечно большим. Если же и числитель и знаменатель равны нулю, то топоцентрическое расстояние не определено. К тому же, положительность расстояний требует одного знака для числителя и знаменателя. Три уравнения (5) задают сетку из шести кривых, попарное пересечение которых задает границы областей, в которых может быть определено искомое решение. Знание координат точек пересечения кривых, определяемых числителями и знаменателями (5) позволяет определить наименьший масштаб триангуляции. Уравнения в “квадратных” координатах будут иметь следующий вид (i, j = 1, 2, 3):

где R_i = (X_i, Y_i, Z_i) – эклиптические векторы положения Солнца относительно топоцентра, e_j = (e_jx, e_jy, e_jz) – единичные эклиптические векторы наблюденного направления на объект.

Система (11) нелинейная и для поиска ее решения удобно применить метод продолжения решения по параметру с наилучшей параметризацией (Шалашилин, 1999). Идея метода заключается в следующем: пусть $H\left( {x\left( \mu \right)} \right) = 0$ – уравнение, которое мы хотим решить, а μ – некий параметр. Пусть для некоторого значения μ = μ₀ известно решение x₍₀₎, т.е. $H\left( {{{x}_{{(0)}}}\left( {{{\mu }_{0}}} \right)} \right) = 0$ и в этой точке выполняется теорема о неявной функции. Тогда рассмотрим глобальную гомотопию:

где μ ∊ [0,1] и x₀ – начальное приближение (x₀ = 0).

• Если μ = 0, тогда $G\left( {x,0} \right) = H\left( x \right) = 0$ – исходное уравнение.

• Если μ = 1, тогда $G\left( {x,1} \right) = H\left( x \right) - H\left( {{{x}_{0}}} \right) = 0$ и x = x₀, т.е. получаем известное решение.

Введем новый параметр s ∊ [0, L], L = const:

где s – длина дуги кривой множества решений (12). Параметр s – наилучший для поиска решения. Тогда уравнение (12) можно записать как:

Рассмотрим задачу Коши в начальной точке x₀:

Ее можно привести к нормальной системе из двух обыкновенных дифференциальных уравнений (ОДУ):

Следует интегрировать систему (13) в направлении роста параметра s, пока не будет достигнуто μ = 0. Это будет первое решение. Интегрируя дальше, до заданного L, мы найдем остальные решения (если они существуют).

Применим эту методику для уравнений (11) и примем x = {N_xs, N_ys}. Тогда мы получим систему ОДУ (16) в виде (i, j = 1, 2, 3):

где в третьем уравнении в квадратных скобках представлено смешанное произведение векторов в эклиптической системе координат, а в первых двух уравнениях нижние индексы у векторного произведения обозначают соответствующие компоненты. Решение системы (17) даст нам до девяти точек, минимальные и максимальные координаты которых позволят нам ограничить на нашем квадрате прямоугольную область с возможно наиболее плотным расположением искомых решений системы (7).

ТРИАНГУЛЯЦИЯ ОБЛАСТИ ПОИСКА РЕШЕНИЯ

Решение системы (7) предлагается искать в виде минимума целевой функции

Причем поиск основывается на использовании триангуляции, т.е. на разбиении области возможных решений на непересекающиеся треугольники (Самотохин, 2014). Эти треугольники необходимы как начальное приближение для переменных симплексов – подвижных треугольников, по которым производится поиск минимума целевой функции методом Нелдера–Мида (Химмельблау, 1975).

Вся максимально-возможная область решений представляет собой квадрат с полустороной единичной длины. В качестве базовой триангуляции разобьем этот квадрат на 64 “малых квадрата”, каждый с длиной стороны равной 0.25. Затем каждый из этих “малых квадратов” разобьем на четыре равных треугольника с общей вершиной в центре (рис. 1).

Этими равнобедренными треугольниками, с длиной основания 0.25, мы заполняем всю область, для которой хотя бы одна из вершин треугольника удовлетворяет условию положительности трех уравнений (5). Исключением является “область особых точек” (описанная в предыдущем разделе). Она увеличивается во все стороны, до совпадения с границами ближайшего “малого квадрата” и получает вид прямоугольника с длиной сторон кратной 0.25. Далее мы разбиваем эту область на квадраты в четыре раза меньшего размера, т.е. с длиной стороны 0.0625. Затем мы разбиваем полученные “малые квадраты” на треугольники с общей вершиной в центре. Для них также выполняется проверка того, что хотя бы для одной из вершин все ρ_i > 0 (i = 1, 2, 3) и условие (10).

Таким образом, мы заполняем всю область возможных решений треугольниками двух видов. Они упорядочены в последовательность по мере построчного заполнения с левого нижнего угла “большого квадрата” до правого верхнего угла. Порядок внутри “малого квадрата” показан на рис. 1. За “большими треугольниками” в последовательности по тому же правилу идут “малые”.

ОПРЕДЕЛЕНИЕ РАНГОВ ТРЕУГОЛЬНИКОВ

Полученное множество из нескольких сотен треугольников, с точки зрения перспективы поиска решений, можно разделить на несколько классов. В работе Самотохина и Хуторовского (Самотохин, 2014) вводится понятие ранга треугольника. Авторы предлагают произвести линейную интерполяцию возможного решения по значениям функций f₁ и f₂ в вершинах треугольника, обозначим их как f_1(i) и f_2(i) (i = 1, 2, 3). Тогда координаты точки линейной интерполяции (N_xs(0), N_ys(0)) можно выразить так:

где (N_xs(i), N_ys(i)) (i = 1, 2, 3) – координаты соответствующих вершин,

Точка (N_xs(0), N_ys(0)) будет внутри треугольника при выполнении следующих условий:

Указанная интерполяция является обобщением метода хорд для решения нелинейного уравнения от одной переменной. При этом необходимо учесть, что подобная линеаризация при выполнении (21) не гарантирует существование реального решения внутри треугольника. Здесь условия (7) соответствуют двум прямым линиям – линиям нулевого уровня, пересекающимся в точке (N_xs(0), N_ys(0)).

Опишем возможные ранги треугольников:

• 0 – ни одна из линий нулевого уровня не пересекает ни одной из сторон треугольника (значения f₁ и f₂ для всех вершин имеют один знак);

• 1 – только одна из линий нулевого уровня имеет пересечения со сторонами треугольника (значения либо f₁, либо f₂ имеют разные знаки для разных вершин);

• 2 – обе линии нулевого уровня пересекают стороны треугольника, но точка (N_xs(0), N_ys(0)) находится вне треугольника (значения f₁ и f₂ имеют разные знаки для разных вершин, но условия (21) не выполняются);

• 3 – точка (N_xs(0), N_ys(0)) лежит внутри треугольника, но одна из сторон треугольника не пересекается ни одной из линий нулевого уровня (условия (21) выполняются, но суммы знаков произведений значений f₁ и f₂ для вершин каждой из сторон нигде не равны нулю);

• 4 – точка (N_xs(0), N_ys(0)) лежит внутри треугольника и все три стороны треугольника пересекаются с линиями нулевого уровня (условия (21) выполняются и есть стороны, для которых суммы знаков произведений значений f₁ и f₂ для их вершин равны нулю).

Подобное ранжирование удобно для уменьшения объема вычислений. При наличии треугольников с рангом 4 и 3, поиск решения следует начать с них. Затем, при отсутствии результата или для проверки его полноты, следует перейти к треугольникам с рангом 2. Обычно этого достаточно для нахождения всех приемлемых решений. К треугольникам с рангом 1, следует обращаться только в случае отсутствия решений, для того, чтобы в этом окончательно убедиться.

МЕТОД НЕЛДЕРА–МИДА

После того, как произведено ранжирование треугольников, можно переходить к поиску решений. Для этого хорошо подходит метод Нелдера–Мида. Этот итерационный метод относится к безградиентным, т.е. не использующим производные. В нем только производится оценка значений целевой функции в вершинах деформируемого на каждой итерации треугольника. Описание алгоритма и текст программы на языке фортран представлены в (Потемкин, 2005; Арушанян, 2006).

В качестве нулевого приближения рассматривается равнобедренный треугольник из раздела “Особые точки…”. После оценки целевой функции во всех вершинах симплекса находим точку (1) с максимальным значением f_goal(N₍₁₎) и точку (3) с минимальным f_goal(N₍₃₎). Далее, по двум оставшимся вершинам (2) и (3) строим “центр тяжести” – точку (0):

Поиск новой вершины производится вдоль прямой (1)–(0). Сначала производится операция “отражение”: находим отражение точки (1) относительно точки (0):

где α > 0 – коэффициент отражения.

Если f (N₍₄₎) ≤ f (N₍₃₎), то вектор N₍₄₎–N₍₀₎ растягивается в соответствии с соотношением:

где γ > 1 – коэффициент растяжения. Если f (N₍₅₎) < < f (N₍₃₎), то N₍₁₎ заменяем на N₍₅₎, в противном случае, N₍₁₎ заменяем на N₍₄₎. Затем, начинаем следующую итерацию с операции “отражение”.

Если f (N₍₄₎) > f (N_(i)), для всех i ≠ 1, то вектор N₍₁₎–N₍₀₎ растягивается в соответствии с соотношением:

где 0 < β <1 – коэффициент сжатия. Заменяем N₍₁₎ на N₍₆₎ затем, начинаем следующую итерацию с операции “отражение”.

Если f (N₍₄₎) > f (N₍₁₎), то для всех i ≠ 3 векторы N_(i)–N₍₃₎ уменьшаются в два раза в соответствии с формулой:

Затем начинаем следующую итерацию с операции “отражение”.

Критерий окончания итерационного процесса состоит в проверке условия:

где ε – произвольное малое число.

ПОИСК РЕШЕНИЙ И ПРЕДСТАВЛЕНИЕ НАБЛЮДЕНИЙ

Как было описано в разделе “Определение рангов…”, поиск решений осуществляется по всем треугольникам с рангами 4 и 3, если таковые имеются и 2, если в этом есть необходимость. Полученные решения необходимо попарно сравнить и отбросить кратные. Условием кратности будет расстояние между точками меньше заданного малого числа. Затем мы переводим координаты N в квадрате на координаты на круге (9) и от эклиптических координат переходим к экваториальным ${{{\mathbf{N}}}^{{eqv}}} = \left\{ {N_{x}^{{eqv}},N_{y}^{{eqv}},N_{z}^{{eqv}}} \right\}:$

где ψ – угол наклона экватора к эклиптике. Подставляя N^eqv в (5), получим значения трех топоцентрических расстояний ρ_i (i = 1, 2, 3). После их подстановки в (1) определим векторы гелиоцентрического положения для трех моментов времени. С этими данными, по r₁ и r₃ можно вычислить параболические орбиты для всех найденных решений (Дубошин, 1976). Представление наблюдений наилучшим образом (значения “О–С”) позволит выбрать искомое решение.

ПРИМЕР

В качестве численного примера рассмотрим определение орбиты кометы 153P/Ikeya‒Zhang на короткой дуге. Для этого были выбраны наблюдения уже использованные в предыдущей работе (Кузнецов, 2016). Здесь мы повторим определение орбиты относительно других переменных.

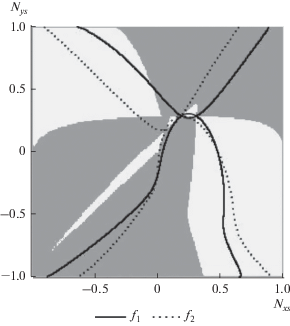
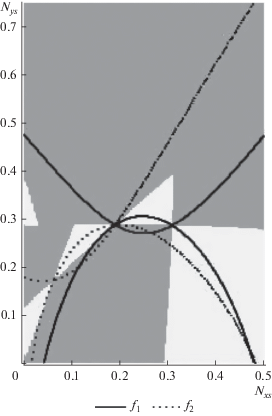
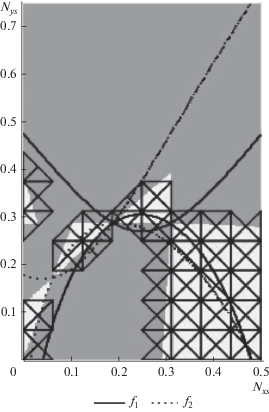
Построим графики (7) в “квадратных” координатах по осям N_xs и N_ys. Закрасим серым цветом области с отрицательными топоцентрическими расстояниями и параметром орбиты p, а также там, где условие (10) не выполняется, соответственно, области возможных решений будут окрашены белым (рис. 2, 3).

На рис. 3 в центре хорошо заметны две небольшие области белого цвета, образованные пересечением кривых (11) и условий (10). Точки касания этих областей между собой, а также с большими областями белого цвета справа и слева от них соответствуют одновременному равенству нулю, как числителя, так и знаменателя (5). Уравнения (5) в этих точках не определены, а соответственно и система (7), однако в их малых окрестностях функции f₁ и f₂ близки друг к другу. Найдем координаты девяти точек пересечения (11) из решения системы (17) (табл. 2).

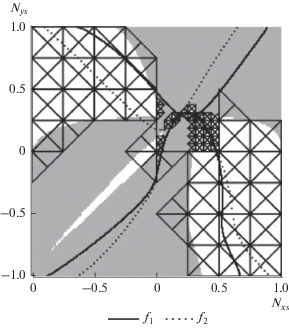
Все девять точек расположены в прямоугольнике [0.062, 0.313] × [0.080, 0.737]. Увеличим границы до величин кратных 0.25: [0.0, 0.5] × [0.0, 0.75] – получим прямоугольник с соотношением сторон 2 : 3. Его удобно разбить на 8 × 12 “малых” квадратов и 384 “малых” треугольников, соответственно. Число “больших” квадратов составит 58, а треугольников 232. После проверки на покрытие областей возможных решений останется 231 треугольник: 122 “больших” и 109 “малых” (рис. 4, 5).

Ранжирование треугольников дает: 4 – четвертого ранга, 3 – третьего, 27 – второго, 60 – первого и 137 – нулевого.

Поиск минимумов целевой функции (17) производился методом Нелдера–Мида при следующих параметрах определенных в разделе “Поиск решений…”: α = 1, β = 0.5, γ = 2, ε = 10^–16.

Четыре треугольника 4-го ранга дали два решения. Все три треугольника 3-го ранга дали по одному решению. Из 27 треугольников 2-го ранга решения были найдены для 22.

Реальных решений, конечно же, меньше 27 и необходимо отбросить все дубликаты, оставив в каждом случае лишь одно, с наименьшим значением целевой функции. В качестве минимального расстояния между различными решениями была принята величина 10^–5. После проверки расстояний между решениями, были получены 3 независимых набора.

Решения, в которых целевая функция принимает минимальные значения, по каждому из наборов, представлены в табл. 3.

После перехода к эклиптическим координатам на круге (9) и от них к экваториальным координатам (28), из (5) можно получить значения топоцентрических расстояний, которые представлены в табл. 4.

Для первого решения не выполняются условия (10), второе решение содержит отрицательные значения топоцентрических расстояний и поэтому они могут быть сразу отброшены. Для оставшегося третьего решения элементы орбиты представлены в табл. 5. Момент прохождения перигелия T₀ определяется как среднеарифметическое по трем моментам времени.

ЗАКЛЮЧЕНИЕ

Представленный в статье метод демонстрирует эффективный подход к численному решению системы алгебраических уравнений, для определения параболической орбиты в некомпланарном случае. Переход от топоцентрических расстояний в качестве неизвестных к безразмерным величинам, определяющим ориентацию орбиты, позволяет ограничить область решения и упростить алгоритм его поиска. Использование метода Нелдера–Мида не требует вычисления производных целевой функции и обеспечивает нахождение всех возможных решений.