Астрономический вестник, 2021, T. 55, № 5, стр. 485-490
Нелинейность в обратных задачах динамики внешних спутников Юпитера
М. А. Баньщикова a, *, В. А. Авдюшев b, Е. Е. Шмидт b
a Томский государственный университет
Томск, Россия
b НИИ прикладной математики и механики Томского госуниверситета
Томск, Россия
* E-mail: mba-tomsk@mail.ru
Поступила в редакцию 31.03.2021
После доработки 14.06.2021
Принята к публикации 21.06.2021
Аннотация
В работе представлены результаты исследования полной и внутренней нелинейностей в обратных задачах динамики далеких спутников Юпитера, наблюдавшихся на очень коротких орбитальных дугах. Выявлена взаимосвязь между нелинейностью и условиями спутниковых наблюдений. В частности, показано, что очень сильная полная нелинейность имеет место, когда период наблюдений меньше 0.1 от орбитального периода. Кроме того, показано, что внутренняя нелинейность достаточно слабая для всех спутников. Это указывает на возможность применения нелинейных методов для адекватного моделирования их орбитальной неопределенности.
ВВЕДЕНИЕ
Большинство внешних спутников Юпитера было открыто в самом начале XXI столетия (Sheppard и др., 2002). Несмотря на то, что со времени открытия спутников прошло уже почти два десятка лет, орбиты многих из этих спутников до сих пор плохо определены вследствие скудного состава их наблюдений. Для некоторых объектов орбиты определены настолько ненадежно, что даже не совсем ясно, являются ли они вообще спутниками или это – астероиды, временно захваченные Юпитером (Авдюшев, Баньщикова, 2010). Ответить на этот вопрос можно только исходя из вероятностных оценок, полученных на основе стохастического моделирования орбитальной неопределенности (Авдюшев, Баньщикова, 2007; Desmars и др., 2009; Emel’yanov, 2010; Avdyushev, 2011).
Обычно, для исследования орбитальной неопределенности применяют стохастические методы с использованием ковариационных матриц. Фактически, любая ковариационная матрица несет в себе информацию о вероятностном распределении ошибок в орбитальных параметрах для линеаризированной обратной задачи, в которой связь между модельными представлениями наблюдений и параметрами линейная. Поэтому ковариационная матрица описывает в параметрическом пространстве эллипсоидальное облако неопределенности с нормально распределенной плотностью около оценки, получаемой из наблюдений.
Однако вследствие малоинформативных наблюдений и нелинейности обратной задачи конфигурация большого облака неопределенности может сильно отличаться от эллипсоидального, и тогда для его моделирования нужно прибегать к нелинейным стохастическим методам (Milani, 1999; Virtanen и др., 2001; Muinonen и др., 2006; Desmars и др., 2009; Emel’yanov, 2010; Avdyushev, 2011). Под нелинейностью обратной задачи мы фактически понимаем нелинейность интерпретирующей наблюдения модели по ее параметрам. Если любой линейный стохастический метод предполагает линеаризацию обратной задачи, то нелинейный моделирует параметрическую (орбитальную) неопределенность в рамках исходной (нелинейной) задачи.
Таким образом, на практике исследователь встает перед выбором метода стохастического моделирования: линейного или нелинейного. Линейные методы – очень простые, но недостаточно точные для моделирования большой неопределенности. Нелинейные методы очень сложные и трудоемкие. Выбор в пользу линейного метода всегда очевиден, если нелинейность слабая. С другой стороны, когда исследователь вынужден прибегать к нелинейным методам при сильной нелинейности, всегда нужно иметь в виду, что их адекватность определяется так называемой внутренней нелинейностью (Bates, Watts, 1988; Draper, Smith, 1998; Avdyushev, 2011; 2017; Авдюшев и др., 2021), т.е. предельно минимальной нелинейностью, которая может быть достижима путем параметрических преобразований.
В настоящей работе мы поставили перед собой цель оценить нелинейность в обратных задачах орбитальной динамики для всех новых внешних спутников Юпитера, используя показатели нелинейности, предложенные в работе (Авдюшев и др., 2021). Один из основных вопросов, который нас интересовал прежде всего, – насколько мала внутренняя нелинейность в этих задачах, с тем чтобы нелинейные методы имели практическое основание для использования.
ОБЩИЙ АНАЛИЗ НЕЛИНЕЙНОСТИ
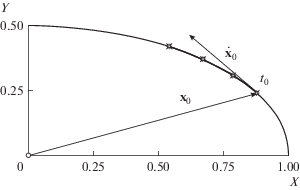
Взаимосвязь между обстоятельствами наблюдений и нелинейностью можно наглядно представить на примере нормализованной задачи двух тел. Рассмотрим движение спутника на круговой орбите единичного радиуса с периодом $2\pi $. В качестве определяемых параметров примем компоненты вектора начального динамического состояния ${\mathbf{q}} = {{({{{\mathbf{x}}}_{0}},{{{\mathbf{\dot {x}}}}_{0}})}^{T}}$ $(\dim {\mathbf{q}} = 6)$, где ${{{\mathbf{x}}}_{0}}$ и ${{{\mathbf{\dot {x}}}}_{0}}$ – положение и скорость спутника на нулевой момент времени $({{t}_{0}} = 0)$. Моделируя $L$ положений объекта ${{{\mathbf{x}}}_{i}}$ $(i = 1, \ldots ,L)$ и отображая их на картинную плоскость$(X,Y)$ получим, таким образом, вектор наблюдаемых величин
Координаты спутника в картинной плоскости (рис. 1) рассчитывались как
Наблюдения моделировались на трех орбитальных дугах: ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {2\pi }}} \right. \kern-0em} {2\pi }} = 0.1,0.01,0.001$, на четыре равномерно распределенных момента времени $(L = 4)$ (рис. 1):
Мы намеренно выбрали предельно минимальное количество наблюдений, с тем чтобы создать критические условия для обратной задачи, когда эффект нелинейности максимален. При $L = 3$ задача уже сводится к предварительному определению орбиты по трем наблюдениям, и тогда внутренняя нелинейность становится нулевой.
Внутренняя и так называемая параметрическая нелинейность составляют (полную) нелинейность обратной задачи (Bates, Watts, 1988; Draper, Smith, 1998; Avdyushev, 2011; 2017; Авдюшев и др., 2021). Параметрическая нелинейность обусловлена неудачным выбором состава оцениваемых параметров. Теоретически существуют такие (нелинейные) преобразования параметров, которые сводят параметрическую нелинейность к нулю, хотя представить их в аналитической форме практически невозможно. Внутренняя нелинейность заложена в геометрии обратной задачи, и она не зависит от преобразования параметров. Поэтому внутренняя нелинейность неустранима и, следовательно, определяет предельный уровень минимальной нелинейности, которая может быть достигнута в результате преобразований параметров.
В работе мы исследовали только полную и внутреннюю нелинейности. Параметрическую нелинейность не рассматривали, поскольку обычно она вносит основной вклад в полную нелинейность и поэтому показатели обоих практически совпадают. Показатели полной æ и внутренней æI нелинейностей вычисляются по формулам (Авдюшев и др., 2021)
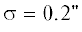 – среднеквадратическая ошибка наблюдений (выбранное значение типичное для ошибок
наземных ПЗС-наблюдений), $\Delta {\mathbf{p}} = {\mathbf{p}}({\mathbf{q}} + \Delta {\mathbf{q}}) - {\mathbf{p}}({\mathbf{q}})$ – вариация в векторе наблюдений, вызванная вариацией параметрического вектора $\Delta {\mathbf{q}}$ около оценки ${\mathbf{\hat {q}}}$, полученной из наблюдений.
– среднеквадратическая ошибка наблюдений (выбранное значение типичное для ошибок
наземных ПЗС-наблюдений), $\Delta {\mathbf{p}} = {\mathbf{p}}({\mathbf{q}} + \Delta {\mathbf{q}}) - {\mathbf{p}}({\mathbf{q}})$ – вариация в векторе наблюдений, вызванная вариацией параметрического вектора $\Delta {\mathbf{q}}$ около оценки ${\mathbf{\hat {q}}}$, полученной из наблюдений.
Если показатель меньше порогового значения ${{\unicode{230} }_{{tol}}} = {{10}^{{ - 3}}}$ (Авдюшев и др., 2021), нелинейность – слабая. Если показатель больше ${{10}^{{ - 2}}}$, нелинейность – определенно сильная. При показателях между этими пороговыми значениями мы рассматриваем нелинейность как умеренную (Авдюшев и др., 2021). Слабая и сильная нелинейности предопределяют очевидный выбор стохастического метода для моделирования орбитальной неопределенности. В случае же умеренной нелинейности в задачах вероятностной орбитальной эволюции внешних спутников Юпитера для надежности получаемых вероятностных оценок мы все же склоняемся к использованию нелинейных методов.
На рис. 2 показаны значения показателей нелинейности в зависимости от начального положения объекта, определяемого истинной аномалией $\varphi $, и от угла между картиной и орбитальной плоскостями $\psi $ на двух орбитальных дугах: ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {2\pi }}} \right. \kern-0em} {2\pi }} = 0.1,0.01$. Заливка полутонами серого цвета на рисунке применяется только к уровням показателей, превышающих пороговое значение ${{10}^{{ - 3}}}$(Авдюшев и др., 2021).
Рис. 2.
Внутренняя $lg{{\unicode{230} }_{I}}$ и полная $lg\unicode{230} $ нелинейности в модельной задаче.
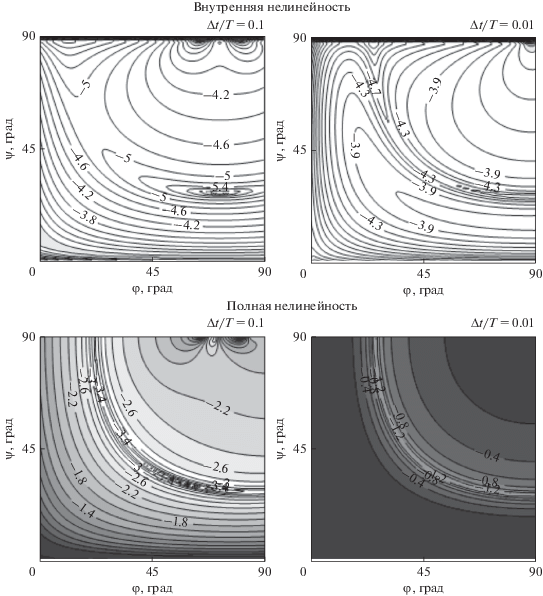
Как видно из рисунка, внутренняя нелинейность при всех обстоятельствах наблюдений довольно слабая, что является практическим основанием для применения нелинейных методов стохастического моделирования при исследовании орбитальной неопределенности. Полная нелинейность значительно сильнее и ее показатели в большинстве случаев превышают критическое значение. Слабая полная нелинейность имеет место лишь при определенных обстоятельствах, когда ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {2\pi }}} \right. \kern-0em} {2\pi }} = 0.1$. На рисунке им соответствуют угловые величины около оврага, проходящего через значения $\varphi = 30^\circ \;{\text{и}}\;\psi = 75^\circ $, $\varphi = 45^\circ \;{\text{и}}\;\psi = 45^\circ $, $\varphi = 75^\circ \;{\text{и}}\;\psi = 30^\circ $.
Разумеется, нелинейность зависит не только от периода наблюдений $\Delta t$ и угловых параметров $\varphi \;{\text{и}}\;\psi $, но и от таких параметров обратной задачи, как L (количество моментов наблюдений); $\sigma $ (дисперсия ошибок); ${{\chi }_{{6,\alpha }}} = \sqrt {\chi _{{6,\alpha }}^{2}} $ ($\alpha $ – квантиль функции распределения $\chi _{6}^{2}$); ${{t}_{0}}$ (начальная эпоха). Мы исследовали, как зависит нелинейность от этих параметров на
примере тестового объекта, где в качестве исходных мы приняли следующие значения параметров:
$\varphi = 45^\circ \;{\text{и}}\;\psi = 45^\circ $; $N = 2L = 8$; 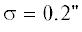 ; ${{\chi }_{{6,0.997}}} = 4.5$; ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {T = 0.25}}} \right. \kern-0em} {T = 0.25}}$; ${{t}_{0}} = 0$.
; ${{\chi }_{{6,0.997}}} = 4.5$; ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} {T = 0.25}}} \right. \kern-0em} {T = 0.25}}$; ${{t}_{0}} = 0$.
Показатели æ и æI дают оценки нелинейности в максимально удаленных от центра ${\mathbf{\hat {q}}}$ вершинах доверительного эллипсоида. При уменьшении размеров эллипсоида (скажем, вследствие уменьшения среднеквадратической ошибки $\sigma $ или вероятности $\alpha $) нелинейность ослабевает. На рис. 3 показана зависимость показателей нелинейности от квантиля $\chi $, который задает размеры доверительной области. Фактически, рисунок показывает, что в параметрическом пространстве нелинейность прямо пропорциональна отдалению от оценки ${\mathbf{\hat {q}}}$.
Рис. 3.
Показатели внутренней ${{\unicode{230} }_{I}}$ (сплошная линия) и полной $\unicode{230} $ (пунктирная линия) нелинейности в зависимости от изменения длины наблюдаемой орбитальной дуги ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$, коэффициента $\chi $ и количества измерений $N$.
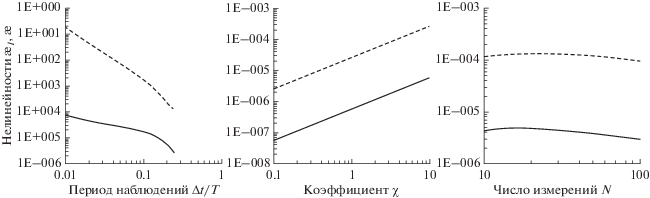
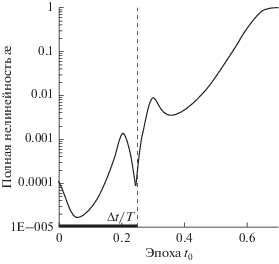
Полная нелинейность весьма чувствительная к выбору начальной эпохи ${{t}_{0}}$. Как видно на рис. 4, показатель полной нелинейности стремительно возрастает сразу же за пределами периода наблюдений и уже на отдалении от него в два периода достигает единичного значения. С точки зрения математической статистики изменение начальной эпохи, по сути, является преобразованием параметров, поскольку отнесенные на разные эпохи начальные положения ${{{\mathbf{x}}}_{0}}$ и скорости ${{{\mathbf{\dot {x}}}}_{0}}$ суть разные параметры, хотя преобразуются друг в друга посредством орбитальной модели. Поэтому внутренняя нелинейность, не зависящая вообще от параметрических преобразований, нечувствительна к вариации начальной эпохи, хотя ее показатель как приближенная оценка все же изменяется в пределах первого знака около $2 \times {{10}^{{ - 4}}}$. Таким образом, для адекватного моделирования параметрической неопределенности линейными методами при информативном составе наблюдений начальную эпоху следует выбирать в пределах периода наблюдений, где полная нелинейность слабая, иначе необходимо прибегать к нелинейным методам стохастического моделирования.
НЕЛИНЕЙНОСТЬ ДЛЯ ВНЕШНИХ СПУТНИКОВ ЮПИТЕРА
В данном разделе мы приводим результаты исследования нелинейности для 13 представителей групп внешних спутников Юпитера11. Использованные нами наблюдательные данные спутников были взяты из базы данных NSDB (http://www.sai.msu.ru/neb/nss/html/obspos/bjupoour.htm) на дату 28.01.2021 г. Интервалы наблюдения исследованных спутников $\Delta t$ меньше одного орбитального периода $T$. Это малые небесные объекты. Их средние расстояния от центра Юпитера – 18–28 млн км; наклонения – 140°–165°; периоды обращения – до трех лет. Ввиду удаленности от Юпитера внешние спутники испытывают достаточно сильное гравитационное влияние от Солнца.
Движение спутников моделировалось на основе дифференциальных уравнений в прямоугольных координатах, в которых учитывались гравитация Юпитера как протяженного тела (с точностью до шестой зональной гармоники в разложении гравитационного поля Юпитера), силы притяжения Солнца, планет-гигантов, галилеевых спутников как материальных точек, а также релятивистские эффекты от Юпитера в рамках задачи Шварцшильда. Уравнения интегрировалась численно методом Эверхарта 15-го порядка с переменным шагом в компьютерной арифметике с двойной точностью. Орбиты определялись из позиционных наблюдений спутников (http://www.sai.msu.ru/neb/nss/html/obspos/bjupoour.htm) в рамках задачи наименьших квадратов. Изохронные производные, необходимые для определения орбит и оценивания нелинейности, вычислялись путем численного интегрирования их дифференциальных уравнений совместно с уравнениями движения.
Показатели нелинейности для далеких спутников Юпитера
| Спутник | $\unicode{230} $ | ${{\unicode{230} }_{I}}$ | L | ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$ | Спутник | $\unicode{230} $ | ${{\unicode{230} }_{I}}$ | L | ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$ |
|---|---|---|---|---|---|---|---|---|---|
| 2016J01 | 0.0017 | 0.0002 | 15 | 0.6662 | 2017J08 | 0.0487 | 0.0001 | 13 | 0.6036 |
| 2010J02 | 0.0032 | 0.0003 | 116 | 0.6683 | 2003J09 | 0.1600 | 0.0035 | 17 | 0.0658 |
| 2017J09 | 0.0041 | 0.0002 | 15 | 0.6669 | 2003J12 | 0.8100 | 0.0018 | 11 | 0.0562 |
| 2017J05 | 0.0212 | 0.0000 | 14 | 0.5891 | 2003J02 | 0.9000 | 0.0114 | 8 | 0.0294 |
| 2017J07 | 0.0251 | 0.0002 | 18 | 0.6986 | 2003J10 | 0.9100 | 0.0047 | 11 | 0.0423 |
| 2017J06 | 0.0300 | 0.0009 | 16 | 0.6024 | 2003J04 | 1.0000 | 0.0008 | 11 | 0.0529 |
| 2003J23 | 0.0317 | 0.0011 | 16 | 0.0396 |
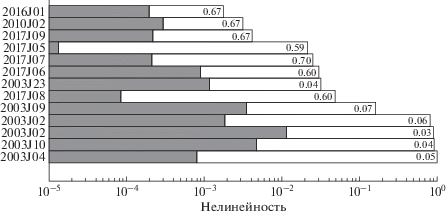
В таблице приведены значения показателей нелинейности æ, æI, количество наблюдений L и интервалы наблюдения ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$. Светло-серым цветом отмечены спутники с умеренной нелинейностью, а темно-серым – с сильной нелинейностью. Результаты в таблице без заливки – нелинейность слабая. Показатели нелинейности для всех спутников также представлены графически на рис. 5: белая гистограмма – полная нелинейность; серая – внутренняя. Числа на белой гистограмме – ${{\Delta t} \mathord{\left/ {\vphantom {{\Delta t} T}} \right. \kern-0em} T}$.
Как видно на рис. 5, показатель полной нелинейности увеличивается с уменьшением дуги орбиты. Впрочем, строгой корреляции нет между нелинейностью и периодом наблюдений. Дело в том, что нелинейность зависит не только от длины дуги, но и от количества наблюдений и их распределения в картинной плоскости и во времени.
Рис. 5 также показывает, что для подавляющего большинства спутников внутренняя нелинейность слабая $(\unicode{230} < {{10}^{{ - 3}}})$ (серая гистограмма). Следовательно, для стохастического моделирования неопределенностей в спутниковых орбитах уверенно можно применять нелинейные методы.
ЗАКЛЮЧЕНИЕ
Таким образом, в работе представлены результаты исследования полной и внутренней нелинейностей применительно к далеким спутникам Юпитера, наблюдавшимся на короткой дуге. Выявлена взаимосвязь между нелинейностью и условиями спутниковых наблюдений. Показано, что полная нелинейность очень сильная, когда период наблюдений меньше 0.1 от орбитального периода, в то время как внутренняя нелинейность достаточно слабая для всех спутников, что указывает на возможность применения нелинейных методов для адекватного моделирования их орбитальной неопределенности.
Настоящая работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № 0721-2020-0049).
Список литературы
Авдюшев В.А., Баньщикова М.А. Области возможных движений новых спутников Юпитера // Астрон. вестн. 2007. Т. 41. № 5. С. 446–452. (Avdyushev V.A., Banschikova M.A. Regions of possible motions for new Jovian satellites // Sol. Syst. Res. 2007. V. 41. № 5. С. 413–419.)
Авдюшев В.А., Баньщикова М.А. Альтернативные орбиты новых спутников Юпитера // Изв. вузов Физика. 2010. Т. 53. Вып. 10. С. 27–30.
Авдюшев В.А., Сюсина О.М. Тамаров В.А. Нелинейность в обратных задачах астероидной динамики // Астрон. вестн. 2021. Т. 55. № 1. С. 1–13. (Avdyushev V.A., Syusina O.M., Tamarov V.A. Nonlinearity in inverse problems of asteroid dynamics // Sol. Syst. Res. 2021. V. 55. № 1. P. 71–82.)
Avdyushev V.A. Nonlinear methods of statistic simulation of virtual parameter values for investigating uncertainties in orbits determined from observations // Celest. Mech. 2011. V. 110(4). P. 369–388.
Avdyushev V.A. Intrinsic nonlinearity and method of disturbed observations in inverse problems of celestial mechanics // Celest. Mech. 2017. V. 129(4). P. 537–552.
Bates D.M., Watts D.G. Nonlinear Regression Analysis and Its Applications. John Wiley & Sons Inc., 1988. 365 p.
Desmars J., Arlot S., Arlot J.-E., Lainey V., Vienne A. Estimating the accuracy of satellite ephemerides using the bootstrap method // Astron. and Astrophys. 2009. V. 62. P. 321–330.
Draper N.R., Smith H. Applied Regression Analysis. John Wiley & Sons Inc., 1998. 706 p.
Emel’yanov N. Precision of the ephemerides of outer planetary satellites // PSS. 2010. V. 58. Iss. 3. P. 411–420.
Jacobson R.A. The orbits of the outer Jovian satellites // Astron. J. 2000. V. 120. Iss. 5. P. 2679–2686.
Milani A. The identification problem I: Recovery of lost asteroids // Icarus. 1999. V. 137. P. 269–292.
Muinonen K., Virtanen J., Granvik M., Laakso T. Asteroid orbits using phase-space volumes of variation // Mon. Notic. Roy. Astron. Soc. 2006. V. 368. P. 809–818.
Sheppard S.S., Jewitt D.C., Kleyna J., Marsden B.G., Jacobson R.A. Satellites of Jupiter // IAU Circ. 2002. № 7900.
Virtanen J., Muinonen K., Bowell E. Statistical ranging of asteroid orbits // Icarus. 2001. V. 154. P. 412–431.
http://www.sai.msu.ru/neb/nss/html/obspos/bjupoour.htm
Дополнительные материалы отсутствуют.
Инструменты
Астрономический вестник