Астрономический вестник, 2021, T. 55, № 5, стр. 476-484

О силе притяжения эллиптического гауссова кольца

М. А. Вашковьяк^*

Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия

Поступила в редакцию 05.04.2021
После доработки 28.05.2021
Принята к публикации 16.06.2021

DOI: 10.31857/S0320930X21050066

Аннотация

Описан численно-аналитический метод анализа орбитальной эволюции спутника планеты под влиянием возмущающего тела, движущегося по эллиптической орбите. В используемой осредненной схеме Гаусса это влияние заменено притяжением материального эллиптического кольца соответствующей массы. На основе полученного Б.П. Кондратьевым замкнутого аналитического выражения силовой функции такого кольца представлены формулы для компонент силы притяжения, действующего на спутник планеты. Для анализа орбитальной эволюции использован метод численного интегрирования осредненных уравнений в кеплеровских элементах. Рассмотрены два методических иллюстративных примера: главное тело Меркурий – возмущающее тело Солнце – искусственный спутник Меркурия типа “Messenger”; главное тело Земля – возмущающие тела Луна и Солнце – гипотетический ИСЗ с апогеем вне сферы радиуса лунной орбиты. Описанный метод может быть использован в эволюционных задачах небесной механики при изучении возмущенного движения малых тел Солнечной системы.

Ключевые слова: эволюция спутниковых орбит, эллиптическое кольцо Гаусса, силовая функция, компоненты силы, осредненные уравнения, численное интегрирование

ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

Аналитические исследования эволюции спутниковых орбит, как правило, используют предположение о слабой эллиптичности орбит возмущающих тел. Тем не менее в Солнечной системе существуют эллиптические орбиты планет и их естественных спутников с заметным эксцентриситетом. Для анализа орбитальной эволюции спутников таких планет важен максимально строгий учет гравитационных возмущений без использования разложения возмущающей функции в ряд по степеням эксцентриситета гелиоцентрической орбиты планеты (или планетоцентрической орбиты возмущающего тела). В спутниковых задачах предполагается, что движение тела пренебрежимо малой массы происходит под действием притяжения главного (центрального) тела массы m и внешнего возмущающего тела массы m₁, а при исследовании орбитальной эволюции нередко используется возмущающая функция, осредненная по наиболее быстрым переменным. В одном из возможных вариантов, в рамках ограниченной эллиптической задачи трех тел предусмотрено осреднение по средней долготе возмущающего тела. Динамической интерпретацией такого осреднения служит замена реального притяжения тела бесконечно малой массы со стороны возмущающего тела массы m₁, движущегося по планетоцентрической эллиптической кеплеровской орбите с большой полуосью а₁ и эксцентриситетом е₁ < 1, притяжением материального гауссова кольца той же массы, специальным образом распределенной по его периметру.

Задача о нахождении потенциала (или силовой функции) притяжения эллиптического гауссова кольца U в замкнутом виде долгое время считалась неразрешимой. Так, в одном из классических сочинений Г.Н. Дубошина в параграфе, посвященном притяжению материального гауссова кольца (Дубошин, 1961), на c. 109 находим: “Функция U не может быть выражена ни в элементарных, ни в известных трансцендентных функциях. Однако составляющие силы притяжения … можно выразить через эллиптические функции, но … эти формулы чрезвычайно громоздки и неудобны для пользования”. В нижнем колонтитуле этой страницы содержится указание: “Вывод этих формул можно найти в известном трактате Тиссерана”.

В связи с этим отметим, что, благодаря исследованиям, выполненным относительно недавно известными российскими учеными и отраженным в монографии и статье (Антонов и др., 2008; Кондратьев, 2012), силовая функция эллиптического гауссова кольца получена в замкнутом виде без разложений по каким-либо параметрам. Что же касается составляющих силы его притяжения, то в указанном трактате (Tisserand, 1889, Т. I, С. 440) можно найти лишь промежуточные формулы для ее проекций на некоторые специальные оси. Они связаны с конусом, опирающимся на эллиптическое кольцо, и с вершиной в пробной точке. Для дальнейших преобразований с введением эллиптических функций предлагается обратиться к трактату (Halphen, 1888), где окончательный результат представлен (Т. I, С. 326) в виде линейной комбинации некоторого гипергеометрического ряда и его первой производной. В силу сложности восприятия приведенных там формул и неудобства их использования, в данной работе в качестве необходимой методической компоненты описан алгоритм вычисления составляющих силы притяжения эллиптического гауссова кольца в виде последовательности математических операций на основе одного из замкнутых выражений его силовой функции. Полученные аналитические выражения используются для дополнительного численного осреднения возмущающей функции по средней долготе спутника и для нахождения правых частей эволюционных уравнений, решение которых также проводится численным способом.

Рассмотрим планетоцентрическую эклиптическую систему координат Oxyz, в которой описываются эллиптические орбиты спутника Р и возмущающего тела. Эллиптическая орбита спутника характеризуется ее оскулирующими кеплеровскими элементами: большой полуосью – а, эксцентриситетом – е, наклонением – i, аргументом перигея – ω и долготой восходящего узла – Ω. Орбита возмущающего тела описывается такими же элементами, но с нижним индексом “1”.

Двукратно осредненная возмущающая функция задачи W определяется формулой

(1)

$W = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} U\left[ {{\mathbf{r}}\left( E \right)} \right]dE,$

где Е – эксцентрическая аномалия спутника, а U[r(E)] в подынтегральном выражении – силовая функция эллиптического гауссова кольца, аппроксимирующего орбиту возмущающего тела. Положение спутника в исходной системе координат характеризуется вектором r = (x, y, z)^т (здесь и далее верхний значок “т” означает транспонирование), а координаты x, y, z как функции Е определяются известными формулами невозмущенного кеплеровского движения.

Для связности изложения мы вначале с минимальными очевидными изменениями в обозначениях воспроизведем необходимые формулы работы (Кондратьев, 2012), в которой замкнутое выражение для силовой функции эллиптического гауссова кольца получено в двух эквивалентных компактных формах: в эллипсоидальных координатах λ, μ, ν и в прямоугольных координатах x₁, x₂, x₃.

Начало О декартовой системы Оx₁x₂x₃ находится в одном из фокусов эллиптического кольца, а именно – в так называемом активном фокусе (в центре масс планеты). Ось Оx₁ направлена в перицентр эллипса (планетоцентрической орбиты возмущающего тела), ось Оx₃ – по нормали к его основной (или главной) плоскости, ось Оx₂ дополняет систему до правой. Связь координат x, y, z с координатами x₁, x₂, x₃ определяется матрицей G и соотношениями

(2)

$\begin{gathered} \left\| {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right\| = G\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\|,\,\,\,\,\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\| = {{G}^{{\text{т}}}}\left\| {\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ {{{x}_{3}}} \end{array}} \right\|,\,\,\,\,G = \left\| {\begin{array}{*{20}{c}} {{{P}_{x}}}&{{{P}_{y}}}&{{{P}_{z}}} \\ {{{Q}_{x}}}&{{{Q}_{y}}}&{{{Q}_{z}}} \\ {{{R}_{x}}}&{{{R}_{y}}}&{{{R}_{z}}} \end{array}} \right\|, \\ {{P}_{x}} = \cos {{\omega }_{1}}\cos {{\Omega }_{1}} - \sin {{\omega }_{1}}\sin {{\Omega }_{1}}\cos {{i}_{1}},\,\,\,\,{{Q}_{x}} = - \sin {{\omega }_{1}}\cos {{\Omega }_{1}} - \cos {{\omega }_{1}}\sin {{\Omega }_{1}}\cos {{i}_{1}},\,\,\,\,{{R}_{x}} = \sin {{i}_{1}}\sin {{\Omega }_{1}}, \\ {{P}_{y}} = \cos {{\omega }_{1}}\sin {{\Omega }_{1}} + \sin {{\omega }_{1}}\cos {{\Omega }_{1}}\cos {{i}_{1}},\,\,\,\,{{Q}_{y}} = - \sin {{\omega }_{1}}\sin {{\Omega }_{1}} + \cos {{\omega }_{1}}\cos {{\Omega }_{1}}\cos {{i}_{1}},\,\,\,\,{{R}_{y}} = - \sin {{i}_{1}}\cos {{\Omega }_{1}}, \\ {{P}_{z}} = \sin {{\omega }_{1}}\sin {{i}_{1}},\mathop {}\limits^{} {{Q}_{z}} = \cos {{\omega }_{1}}\sin {{i}_{1}},\,\,\,\,{{R}_{z}} = \cos {{i}_{1}},\,\,\,\,{{\omega }_{1}} = {{\pi }_{1}} - {{\Omega }_{1}},\,\,\,\,{{\pi }_{1}} = {{\pi }_{{10}}} + {{{\dot {\pi }}}_{1}}\left( {t - {{t}_{0}}} \right),\,\,\,\,{{\Omega }_{1}} = {{\Omega }_{{10}}} + {{{\dot {\Omega }}}_{1}}\left( {t - {{t}_{0}}} \right). \\ \end{gathered} $

Здесь i₁ – наклонение орбиты возмущающего тела относительно основной координатной плоскости, π₁, Ω₁ – долготы перицентра и восходящего узла, соответственно, π₁₀ и Ω₁₀ – их значения в начальный момент времени t₀. Матрица G становится единичной, если орбита возмущающего тела лежит в основной плоскости (sin i₁ = 0) и не эволюционирует, сохраняя свою форму (е₁ = const) и специальную пространственную ориентацию $(\sin {{\pi }_{1}} = 0,{{\dot {\pi }}_{1}} = {{\dot {\Omega }}_{1}} = 0).$

СИЛОВАЯ ФУНКЦИЯ ЭЛЛИПТИЧЕСКОГО ГАУССОВА КОЛЬЦА

В прямоугольных координатах x₁, x₂, x₃ функция U определяется формулой (67) работы (Кондратьев, 2012).

(3)

$\begin{gathered} U\left( {\mathbf{r}} \right) = \frac{{2f{{m}_{1}}}}{{\pi \sqrt {{{y}_{1}} - {{y}_{3}}} }} \times \\ \times \,\,\left\{ {{\mathbf{{\rm K}}}\left( k \right) + \frac{{{{a}_{1}}{{e}_{1}}\left( {{{x}_{1}} + {{a}_{1}}{{e}_{1}}} \right)}}{{a_{1}^{2} + {{y}_{3}} - {a \mathord{\left/ {\vphantom {a 3}} \right. \kern-0em} 3}}}\left[ {{\mathbf{\Pi }}\left( {n,k} \right) - {\mathbf{{\rm K}}}\left( k \right)} \right]} \right\}, \\ n = \frac{{a_{1}^{2} + {{y}_{3}} - {a \mathord{\left/ {\vphantom {a 3}} \right. \kern-0em} 3}}}{{{{y}_{3}} - {{y}_{1}}}},\,\,\,\,k = \sqrt {\frac{{\sin \left( {{a \mathord{\left/ {\vphantom {a 3}} \right. \kern-0em} 3}} \right)}}{{\cos \left( {{a \mathord{\left/ {\vphantom {a 3}} \right. \kern-0em} 3} - {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}} \right)}}} . \\ \end{gathered} $

Величины K(k) и П(n,k) – суть полные эллиптические интегралы Лежандра первого и третьего рода, соответственно, с модулем k и параметром n, причем из неравенств, приведенных в (1), следует, что k < 1, n < 0. Заметим, что для П(n, k) принято определение со знаком минус перед параметром, использованное, в частности, в справочном руководстве (Byrd, Friedman, 1953)

(4)

${\mathbf{\Pi }}\left( {n,k} \right) = \int\limits_0^{\pi /2} {\frac{{d\varphi }}{{\left( {1 - n{{{\sin }}^{2}}\varphi } \right)\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}\varphi } }}} .$.

Кроме того, в формулах (1) и (2) f – гравитационная постоянная, а обозначения a, y₁, y₂, y₃, α как функции переменных x₁, x₂, x₃ объяснены в вышеуказанной работе (Кондратьев, 2012). Из этих обозначений и формулы (3) следует несимметричность функции U относительно координаты x₁, т.е. U (–x₁, x₂, x₃) ≠ U(x₁, x₂, x₃).

В дальнейшем все переменные, имеющие размерность длины, удобно нормировать на величину большой полуоси эллипса а₁, так что выражение для функции U с введением безразмерных переменных

(5)

$\begin{gathered} \xi = {{{{x}_{1}}} \mathord{\left/ {\vphantom {{{{x}_{1}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}} + {{e}_{1}},\,\,\,\,\eta = {{{{x}_{2}}} \mathord{\left/ {\vphantom {{{{x}_{2}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}},\,\,\,\,\zeta = {{{{x}_{3}}} \mathord{\left/ {\vphantom {{{{x}_{3}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}, \\ {\mathbf{\rho }} = {{\left( {\xi ,\eta ,\zeta } \right)}^{{\text{т}}}},\,\,\,\,\rho = \sqrt {{{\xi }^{2}} + {{\eta }^{2}} + {{\zeta }^{2}}} \\ \end{gathered} $

примет вид

(6)

$\begin{gathered} U\left( {\mathbf{\rho }} \right) = \frac{{f{{m}_{1}}}}{{{{a}_{1}}}}V\left( {\mathbf{\rho }} \right),\,\,\,\,V\left( {\mathbf{\rho }} \right) = \frac{2}{{\pi \sqrt {{{Y}_{1}} - {{Y}_{3}}} }} \times \\ \times \,\,\left\{ {{\mathbf{{\rm K}}}\left( k \right) + \beta \left[ {{\mathbf{\Pi }}\left( {n,k} \right) - {\mathbf{{\rm K}}}\left( k \right)} \right]} \right\}. \\ \end{gathered} $

Здесь V(ρ) – силовая функция эллиптического гауссова кольца, нормированная на величину fm₁/a₁. Эта функция безразмерна так же, как Y₁, Y₃.

Далее приводятся формулы в порядке, удобном для последовательного вычисления V как функции безразмерных координат, а также основные соотношения, следующие из работы (Кондратьев, 2012), в том числе и связывающие новые (нормированные) величины с исходными (ненормированными) а, b, c, p, q, y₁, y ₂, y₃

(7)

$\begin{gathered} A = {a \mathord{\left/ {\vphantom {a {a_{1}^{2}}}} \right. \kern-0em} {a_{1}^{2}}} = 2 - e_{1}^{2} - {{\rho }^{2}},\,\,\,\,B = {b \mathord{\left/ {\vphantom {b {a_{1}^{4}}}} \right. \kern-0em} {a_{1}^{4}}} = \\ = \left( {1 - e_{1}^{2}} \right)\left( {1 - {{\xi }^{2}}} \right) - {{\eta }^{2}} + \left( {e_{1}^{2} - 2} \right){{\zeta }^{2}}, \\ C = {c \mathord{\left/ {\vphantom {c {a_{1}^{6}}}} \right. \kern-0em} {a_{1}^{6}}} = \left( {e_{1}^{2} - 1} \right){{\zeta }^{2}},\,\,\,\,P = {p \mathord{\left/ {\vphantom {p {a_{1}^{4}}}} \right. \kern-0em} {a_{1}^{4}}} = {{ - {{A}^{2}}} \mathord{\left/ {\vphantom {{ - {{A}^{2}}} 3}} \right. \kern-0em} 3} + B,\mathop {}\limits^{} \\ Q = {q \mathord{\left/ {\vphantom {q {a_{1}^{6}}}} \right. \kern-0em} {a_{1}^{6}}} = 2{{\left( {\frac{A}{3}} \right)}^{3}} - \frac{1}{3}AB + C,\,\,\,\,R = - \frac{P}{3}, \\ {{Y}_{1}} = {{{{y}_{1}}} \mathord{\left/ {\vphantom {{{{y}_{1}}} {a_{1}^{2}}}} \right. \kern-0em} {a_{1}^{2}}} = 2\sqrt R \cos \left( {\frac{\alpha }{3}} \right),\,\,\,{{Y}_{{2,3}}} = {{{{y}_{{2,3}}}} \mathord{\left/ {\vphantom {{{{y}_{{2,3}}}} {a_{1}^{2}}}} \right. \kern-0em} {a_{1}^{2}}} = \\ = - 2\sqrt R \cos \left( {\frac{{\alpha \pm \pi }}{3}} \right),\,\,\,\alpha = \arccos \left[ { - \frac{1}{2}Q{{R}^{{ - 3/2}}}} \right], \\ n = \frac{\gamma }{{{{Y}_{3}} - {{Y}_{1}}}},\,\,\,\,k = \sqrt {\frac{{{{Y}_{2}} - {{Y}_{3}}}}{{{{Y}_{1}} - {{Y}_{3}}}} = } \sqrt {\frac{{\sin \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 3}} \right. \kern-0em} 3}} \right)}}{{\cos \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 3}} \right. \kern-0em} 3} - {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}} \right)}}} , \\ \beta = \frac{{{{e}_{1}}\xi }}{\gamma },\,\,\,\gamma = 1 + {{Y}_{3}} - {A \mathord{\left/ {\vphantom {A 3}} \right. \kern-0em} 3}. \\ \end{gathered} $

КОМПОНЕНТЫ СИЛЫ ПРИТЯЖЕНИЯ ЭЛЛИПТИЧЕСКОГО ГАУССОВА КОЛЬЦА

Компоненты силы притяжения f = (f_x, f_y, f_z) как ее проекции на выбранные оси находятся дифференцированием функции U в (3), а ее частные производные по x, y, z с учетом преобразований (2) и (5) определяются формулой

(8)

${\mathbf{f}} = \frac{{f{{m}_{1}}}}{{a_{1}^{2}}}{{G}^{{\text{т}}}}\frac{{\partial V}}{{\partial {\mathbf{\rho }}}}.$

В последующих формулах для сокращения записи опущены модуль k и параметр n в полных эллиптических интегралах К, П и в их производных.

(9)

$\begin{gathered} \frac{{\partial V}}{{\partial {\mathbf{\rho }}}} = \frac{2}{{\pi \sqrt {{{Y}_{1}} - {{Y}_{3}}} }}\left\{ {{\mathbf{\delta }}{{D}_{0}} + \left( {\frac{{\partial {{Y}_{3}}}}{{\partial {\mathbf{\rho }}}} - \frac{{\partial {{Y}_{1}}}}{{\partial {\mathbf{\rho }}}}} \right){{D}_{1}}} \right. + \\ \left. { + \,\,\frac{{\partial k}}{{\partial {\mathbf{\rho }}}}{{D}_{2}} + \frac{{\partial n}}{{\partial {\mathbf{\rho }}}}{{D}_{3}} + \left( {\frac{{\partial {{Y}_{3}}}}{{\partial {\mathbf{\rho }}}} - \frac{1}{3}\frac{{\partial A}}{{\partial {\mathbf{\rho }}}}} \right){{D}_{4}}} \right\}, \\ {{D}_{0}} = {\mathbf{\Pi }} - {\mathbf{{\rm K}}},\,\,\,\,{{D}_{1}} = \frac{{{\mathbf{{\rm K}}} + \beta {{D}_{0}}}}{{2\left( {{{Y}_{1}} - {{Y}_{3}}} \right)}}, \\ {{D}_{2}} = \left( {1 - \beta } \right)\frac{{d{\mathbf{{\rm K}}}}}{{dk}} + \beta \frac{{\partial {\mathbf{\Pi }}}}{{\partial k}},\,\,\,{{D}_{3}} = \beta \frac{{\partial {\mathbf{\Pi }}}}{{\partial n}},\,\,\,\,{{D}_{4}} = - \frac{\beta }{\gamma }{{D}_{0}}, \\ \end{gathered} $

где введенный формально вектор δ = (e₁/γ, 0, 0)^т отражает асимметричность функции (6) относительно ξ.

Ниже приводятся формулы в порядке, удобном для вычисления нормированной силовой функции эллиптического гауссова кольца вместе с компонентами силы его притяжения. Производные от функций А, В, С находятся по очевидным формулам

(10)

$\begin{gathered} \frac{{\partial A}}{{\partial {\mathbf{\rho }}}} = - 2{\mathbf{\rho }},\,\,\,\,\frac{{\partial B}}{{\partial {\mathbf{\rho }}}} = 2{{\left[ {\left( {e_{1}^{2} - 1} \right)\xi , - \eta ,\left( {e_{1}^{2} - 2} \right)\zeta } \right]}^{{\text{т}}}}, \\ \frac{{\partial C}}{{\partial {\mathbf{\rho }}}} = 2{{\left[ {0,0,\left( {e_{1}^{2} - 1} \right)\zeta } \right]}^{{\text{т}}}}. \\ \end{gathered} $

Комментарий: Нетрудно заметить, что в частных случаях, когда η = 0 либо ζ = 0, соответствующие 2-й и 3-й компонентам векторов (10) (так же, как и вектора (8)) равны нулю. Из этого следует известный факт существования двух частных плоских решений ограниченной эллиптической осредненной задачи трех тел: x₂ = 0 – ортогонально-апсидальные орбиты (Вашковьяк, 1984) и x₃ = 0 – орбиты, лежащие в плоскости кольца (Аксенов, 1979).

Далее находятся частные производные от R, Q по следующим формулам

(11)

$\begin{gathered} \frac{{\partial R}}{{\partial {\mathbf{\rho }}}} = \frac{1}{9}\left( {2A\frac{{\partial A}}{{\partial {\mathbf{\rho }}}} - 3\frac{{\partial B}}{{\partial {\mathbf{\rho }}}}} \right), \\ \frac{{\partial Q}}{{\partial {\mathbf{\rho }}}} = \frac{1}{9}\left( {2{{A}^{2}} - 3B} \right)\frac{{\partial A}}{{\partial {\mathbf{\rho }}}} - \frac{1}{3}A\frac{{\partial B}}{{\partial {\mathbf{\rho }}}} + \frac{{\partial C}}{{\partial {\mathbf{\rho }}}}. \\ \end{gathered} $

После этого вычисляются производные функций Y_1,2,3 и аргументов k, n полных эллиптических интегралов, согласно формулам

(12)

$\begin{gathered} \frac{{\partial {{Y}_{1}}}}{{\partial {\mathbf{\rho }}}} = \frac{1}{{\sqrt R }}\left[ {\frac{{\partial R}}{{\partial {\mathbf{\rho }}}}\cos \frac{\alpha }{3} - \frac{1}{3}{\mathbf{S}}\sin \frac{\alpha }{3}} \right], \\ \frac{{\partial {{Y}_{{2,3}}}}}{{\partial {\mathbf{\rho }}}} = - \frac{1}{{\sqrt R }}\left[ {\frac{{\partial R}}{{\partial {\mathbf{\rho }}}}\cos \frac{{\alpha \pm \pi }}{3} - \frac{1}{3}{\mathbf{S}}\sin \frac{{\alpha \pm \pi }}{3}} \right], \\ \frac{{\partial k}}{{\partial {\mathbf{\rho }}}} = \frac{{\sqrt 3 {{k}^{3}}}}{{24R{{{\sin }}^{2}}\left( {{\alpha \mathord{\left/ {\vphantom {\alpha 3}} \right. \kern-0em} 3}} \right)}}{\mathbf{S}},\,\,\,\,\frac{{\partial n}}{{\partial {\mathbf{\rho }}}} = \frac{1}{{{{{\left( {{{Y}_{3}} - {{Y}_{1}}} \right)}}^{2}}}} \times \\ \times \,\,\left[ {\gamma \frac{{\partial {{Y}_{1}}}}{{\partial {\mathbf{\rho }}}} - \left( {1 + {{Y}_{1}} - \frac{A}{3}} \right)\frac{{\partial {{Y}_{3}}}}{{\partial {\mathbf{\rho }}}} + \frac{{{{Y}_{1}} - {{Y}_{3}}}}{3}\frac{{\partial A}}{{\partial {\mathbf{\rho }}}}} \right], \\ {\mathbf{S}} = {{\left( {4{{R}^{3}} - {{Q}^{2}}} \right)}^{{ - 1/2}}}\left( {2R\frac{{\partial Q}}{{\partial {\mathbf{\rho }}}} - 3Q\frac{{\partial R}}{{\partial {\mathbf{\rho }}}}} \right). \\ \end{gathered} $

Формулы для необходимых производных от полных эллиптических интегралов приводятся в различных справочных руководствах, в частности, в (Byrd, Friedman, 1953). Для полноты вычислительного алгоритма они воспроизводятся ниже вместе с формулами вычисления П в интересующем нас случае n < 0:

(13)

$\begin{gathered} \frac{{d{\mathbf{K}}}}{{dk}} = \frac{1}{k}\left[ {\frac{1}{{k{\kern 1pt} {{'}^{2}}}}{\mathbf{E}} - {\mathbf{K}}} \right],\,\,\,\,\frac{{\partial {\mathbf{\Pi }}}}{{\partial k}} = \frac{k}{{{{k}^{2}} - n}}\left[ {\frac{1}{{k{\kern 1pt} {{'}^{2}}}}{\mathbf{E}} - {\mathbf{\Pi }}} \right], \\ \frac{{\partial {\mathbf{\Pi }}}}{{\partial n}} = \frac{1}{{2n\left( {n - 1} \right)\left( {{{k}^{2}} - n} \right)}} \times \\ \times \,\,\left[ {\left( {{{k}^{2}} - n} \right){\mathbf{K}} + n{\mathbf{E}} + ({{n}^{2}} - {{k}^{2}}){\mathbf{\Pi }}} \right], \\ {\mathbf{\Pi }}\left( {n < 0,{{k}^{2}}} \right) = \frac{{{{k}^{2}}}}{{{{k}^{2}} - n}}{\mathbf{K}} - \frac{n}{{\sqrt {n\left( {1 - n} \right)(n - {{k}^{2}})} }} \times \\ \times \,\,\left\{ {{\mathbf{E}}F\left( {\psi ,k{\kern 1pt} '} \right) + {\mathbf{K}}\left[ {E\left( {\psi ,k{\kern 1pt} '} \right) - F\left( {\psi ,k{\kern 1pt} '} \right)} \right]} \right\}, \\ \psi = \arcsin \sqrt {{n \mathord{\left/ {\vphantom {n {(n - {{k}^{2}})}}} \right. \kern-0em} {(n - {{k}^{2}})}}} \,\,k{\kern 1pt} ' = \sqrt {1 - {{k}^{2}}} . \\ \end{gathered} $

Здесь E = Е(k) – полный эллиптический интеграл второго рода, $F\left( {\psi ,k{\kern 1pt} '} \right),E\left( {\psi ,k{\kern 1pt} '} \right)$ – неполные эллиптические интегралы 1-го и 2-го рода, соответственно, с аргументом ψ и дополнительным модулем $k{\kern 1pt} '$.

Имея в виду вычислительный аспект, отметим также статью (Анахаев, 2017), в которой для полных эллиптических интегралов предлагаются приближенные аналитические формулы с оценкой их относительной погрешности порядка 2%.

Интересно отметить, что выражения для силовой функции кругового гауссова кольца

(14)

$\begin{gathered} {{U}_{0}}\left( {\mathbf{r}} \right) = \frac{{2f{{m}_{1}}{\mathbf{{\rm K}}}\left( {{{k}_{0}}} \right)}}{{\pi \sqrt {{{{\left( {{{a}_{1}} + \sigma } \right)}}^{2}} + x_{3}^{2}} }}, \\ \sigma = \sqrt {x_{1}^{2} + x_{2}^{2}} ,\,\,\,\,{{k}_{0}} = \sqrt {\frac{{4{{a}_{1}}\sigma }}{{{{{\left( {{{a}_{1}} + \sigma } \right)}}^{2}} + x_{3}^{2}}}} \\ \end{gathered} $

и для компонент силы его притяжения

(15)

$\begin{gathered} \frac{{\partial {{U}_{0}}}}{{\partial {\mathbf{r}}}} = \left\| {\begin{array}{*{20}{c}} {\frac{{{{x}_{1}}}}{\sigma }\frac{{\partial {{U}_{0}}}}{{\partial \sigma }}} \\ {\frac{{{{x}_{2}}}}{\sigma }\frac{{\partial {{U}_{0}}}}{{\partial \sigma }}} \\ { - \frac{{2f{{m}_{1}}{{x}_{3}}{{{\left[ {{{{\left( {{{a}_{1}} - \sigma } \right)}}^{2}} + x_{3}^{2}} \right]}}^{{ - 1}}}}}{{\pi \sqrt {{{{\left( {{{a}_{1}} + \sigma } \right)}}^{2}} + x_{3}^{2}} }}E\left( {{{k}_{0}}} \right)} \end{array}} \right\|, \\ \frac{{\partial {{U}_{0}}}}{{\partial \sigma }} = \frac{{f{{m}_{1}}}}{{\pi \sigma \sqrt {{{{\left( {{{a}_{1}} + \sigma } \right)}}^{2}} + x_{3}^{2}} }} \times \\ \times \,\,\left[ {\frac{{a_{1}^{2} - {{\sigma }^{2}} + x_{3}^{2}}}{{{{{\left( {{{a}_{1}} - \sigma } \right)}}^{2}} + x_{3}^{2}}}E\left( {{{k}_{0}}} \right) - K\left( {{{k}_{0}}} \right)} \right] \\ \end{gathered} $

не удается получить непосредственным предельным переходом, полагая в формулах (2), (3), (8) е₁ = 0. Это возможно лишь с использованием преобразования Ландена и связано со спецификой эллипсоидальных координат (Кондратьев, 2020).

Отметим, кроме того, что формула для третьей компоненты вектора $\frac{{\partial {{U}_{0}}}}{{\partial {\mathbf{r}}}}$ в (15) отличается от соответствующей формулы (3.7) в работе (Дубошин, 1961, стр. 111), приведенной с опечатками, несомненно, типографского происхождения.

ЭВОЛЮЦИОННЫЕ УРАВНЕНИЯ. МЕТОДИЧЕСКИЕ ПРИМЕРЫ

Для анализа эволюции спутниковой орбиты, так же как и в работе (Вашковьяк, 2021), используются уравнения Лагранжа в кеплеровских оскулирующих элементах с нормированной безразмерной независимой переменной

(16)

$\tau = \frac{{{{m}_{1}}a}}{{m{{a}_{1}}}}N\left( {t - {{t}_{0}}} \right),$

где $N = \frac{{\sqrt {fm} }}{{{{a}^{{3/2}}}}}$ – среднее движение спутника,и нормированной возмущающей функцией

(17)

$w = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}W = \frac{1}{{2\pi a}}\int\limits_0^{2\pi } {r\left( E \right)} V\left[ {{\mathbf{r}}\left( E \right)} \right]dE.$

Большая полуось спутниковой орбиты a при нормирующем преобразовании, так же, как и при осреднении, считается постоянной. В этом допущении мы пренебрегаем ее колебаниями достаточно малых амплитуд порядка ${{\dot {\pi }}_{1}}{{e}_{1}}$ и ${{\dot {\Omega }}_{1}}\sin {{i}_{1}}$, связанными с медленными изменениями углов π₁, Ω₁.

Вычисление частных производных функции w методически выполняется так же, как в работе (Вашковьяк, 2021) с использованием квадратурного способа Гаусса и формул, связывающих производные этой функции по элементам и прямоугольным координатам. При этом используются формулы (9) и (17).

В рассматриваемом общем случае эволюционирующей планетоцентрической орбиты возмущающего тела решение уравнений

(18)

$\begin{gathered} \frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{di}}{{d\tau }} = \frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \omega }} - \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \Omega }}, \\ \frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}} - \frac{{{\text{ctg}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}},\,\,\,\,\frac{{d\Omega }}{{d\tau }} = \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}. \\ \end{gathered} $

может быть найдено, по-видимому, лишь численным методом. Тем не менее отметим, что в упрощающем предположении постоянства пространственной ориентации орбиты возмущающего тела (${{\dot {\Omega }}_{1}} = 0$ и ${{\dot {\pi }}_{1}} = 0$) уравнения (18) допускают первый интеграл w = с₀ = const. Если, вдобавок, предположить, что е₁ = sini₁ = 0, то существует еще один первый интеграл (1 – e²) cos²i = с₁ = const.

В качестве методических примеров интересно рассмотреть, прежде всего, системы с достаточно заметными эксцентриситетами орбит возмущающих тел, а также спутниковые орбиты, для которых планетоцентрическое расстояние до спутника может быть как меньше, так и больше расстояния до возмущающего тела. В нижеприведенных примерах для численного интегрирования эволюционных уравнений в системе “MATLAB” использован метод Рунге–Кутта 4-го порядка с минимально возможным значением параметра, характеризующего точность вычислений. На рассматриваемых интервалах времени относительная погрешность по ориентировочным оценкам не превышает величины порядка сотых долей процента.

ОРБИТА ИСКУССТВЕННОГО СПУТНИКА МЕРКУРИЯ ТИПА “MESSENGER”

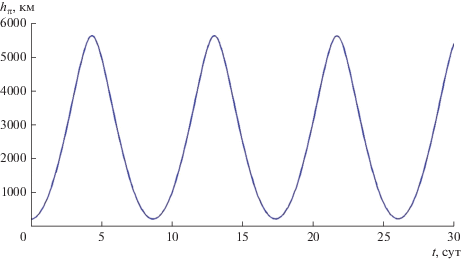
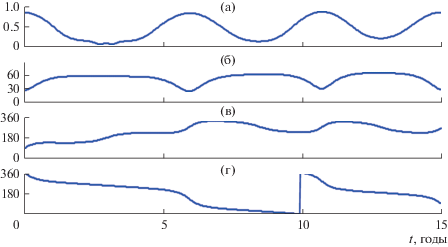
В качестве первого примера рассмотрим эллиптическую орбиту искусственного спутника Меркурия как планеты, имеющей орбитальный эксцентриситет е₁ = 0.2056, заметно превосходящий эксцентриситеты орбит остальных планет Солнечной системы. В силу этой причины эллиптичность планетоцентрической орбиты Солнца как главного возмущающего тела может вносить качественные изменения в орбитальную эволюцию спутника Меркурия по сравнению с моделью интегрируемой осредненной круговой задачи (и задачи Хилла). Подобные изменения непосредственно прослеживаются в эволюции сильно эллиптической спутниковой орбиты с высотой перицентра h_π примерно 200 км и высотой апоцентра h_α примерно 15 000 км. Такими параметрами обладала исходная орбита искусственного спутника Меркурия “Messenger”, начавшего свою работу 18 марта 2011 г. (https://messenger.jhuapl.edu/About/Mission-Timeline.html). В дальнейшем проводились множественные коррекции этой орбиты для поддержания высоты ее перицентра и достижения целей проекта. Для начальной орбиты отношение расстояния ее перицентра к среднему расстоянию Меркурия от Солнца составляет величину α порядка 0.0003. Характерный параметр солнечных возмущений имеет порядок α², в то время как эллиптичность орбиты Меркурия вносит возмущения порядка αе₁$ \gg $ α². Поэтому в качестве первого методического приближения необходимо использование модели ограниченной эллиптической задачи трех тел. Кроме размерных параметров h_π и h_α, угловые элементы орбиты спутника i, ω, Ω также определяют характер орбитальной эволюции и, в частности, функционально важное время его жизни – время, в течение которого высота перицентра над поверхностью планеты остается существенно положительной. Для принятых в дальнейшем начальных значений эклиптических элементов i₀ = 82° и ω₀ = 90°, отвечающих (хотя и весьма приближенно) исходной орбите “Messenger”, это время существенно зависит от начального значения Ω₀ и может изменяться в широких пределах. Зависимости элементов орбиты от времени, полученные описанным численно-аналитическим методом, показаны на рис. 1 для Ω₀ = π₁₀ – 90° (угловые элементы приведены в градусах). При е₁ = = 0.2056 изменение элементов со временем, естественно, отличается от известных закономерностей в случае двукратно осредненной задачи Хилла (Лидов, 1961; Lidov, 1962; Kozai, 1962). Так, изменение долготы узла носит либрационный характер, в процессе эволюции наклонение может колебаться в достаточно широких пределах относительно 90°, а из-за отсутствия интеграла с₁ колебания эксцентриситета и наклонения не находятся в противофазе.

Рис. 1.

Зависимости элементов орбиты типа “Messenger” от времени: а – эксцентриситет, б – наклонение, в – аргумент широты перицентра, г – долгота восходящего узла.

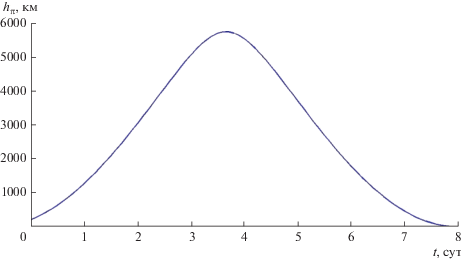
Для данного значения Ω₀ время жизни заведомо превышает 30 суток, в то время как для Ω₀ = π₁₀ – 105° оно составляет всего около восьми. На соответствующих рис. 2 и 3 показаны зависимости h_π от времени.

Рис. 2.

Зависимость h_π от времени для Ω₀ = π₁₀ – 90°.

Рис. 3.

То же самое, что и на рис. 2, но для Ω₀ = π₁₀ – 105°.

Для сравнения отметим, что в тестовых расчетах, выполненных с теми же начальными условиями, но при е₁ = 0, фиктивное время жизни составляло более полутора лет.

ОРБИТА ИСКУССТВЕННОГО СПУТНИКА ЗЕМЛИ С “ЗАЛУННЫМ” АПОГЕЕМ

В качестве второго примера рассмотрим эллиптическую орбиту гипотетического далекого искусственного спутника Земли с перигеем на “геостационарном” расстоянии 42 200 км и с апогеем 500 000 км вне сферы радиуса лунной орбиты. И хотя подобные орбиты пока не вызвали своего практического интереса, в будущем, с освоением далекого околоземного (и “залунного”) космического пространства, он вполне может возникнуть. Данный пример отличается от предыдущего наличием двух возмущающих тел. В методическом плане эллиптическим гауссовым кольцом моделируется осредненное влияние первого тела (Луны, α₁ > 1, е₁ = 0.0549). Если в первом методическом примере силовая функция “солнечного” гауссова кольца и компоненты силы его притяжения вычисляются в сравнительно небольшой окрестности основного притягивающего центра, то во втором они вычисляются как внутри, так и вне сферы с радиусом, равным апогейному расстоянию лунной орбиты r_1α = a₁(1 + e₁). На таких геоцентрических расстояниях необходим учет как лунных, так и солнечных возмущений. Поэтому возмущающая функция W₁ = W в (1) дополняется известным “солнечным” слагаемым (α₂ ~ 0.003, е₂= 0) в приближении Хилла (Лидов, 1961; Lidov, 1962; Kozai, 1962)

(19)

$\begin{gathered} {{W}_{2}} = \frac{{3f{{m}_{2}}}}{{16a}}{{\left( {\frac{a}{{a{}_{2}}}} \right)}^{3}} \times \\ \times \,\,\left[ {2\left( {{{e}^{2}} - {{{\sin }}^{2}}i} \right) + {{e}^{2}}{{{\sin }}^{2}}i\left( {5\cos 2\omega - 3} \right)} \right], \\ \end{gathered} $

где m₂ и а₂ – масса Солнца и радиус земной орбиты, соответственно. Функция w₁ = w в (17) дополняется соответствующим слагаемым ${{w}_{2}} = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}{{W}_{2}}$, а производные W₂ по элементам для дополнения правых частей эволюционных уравнений (18) находятся непосредственно дифференцированием (19).

Конечно, используемая осредненная схема Гаусса применима для орбит ИСЗ, достаточно удаленных от пересечения с лунной орбитой. Это условие выполнено для принятых в данном методическом примере начальных угловых элементов спутниковой орбиты: i₀ = 27°, ω₀ = 90°, Ω₀ = 360°.

На рис. 4 показано изменение элементов со временем на интервале 15 лет для суммарной возмущающей функции w = w₁+ w₂. Тестовые расчеты показали, что без учета солнечных возмущений (при m₂ = 0) качественный характер эволюции не изменяется, однако заметно увеличиваются периоды колебаний е, i, ω и циркуляции Ω. Напротив, при m₁ = 0 либрационное изменение ω становится циркуляционным.

Рис. 4.

Зависимости элементов орбиты далекого ИСЗ с “залунным” апогеем от времени: а – эксцентриситет, б – наклонение, в – аргумент широты перицентра, г – долгота восходящего узла.

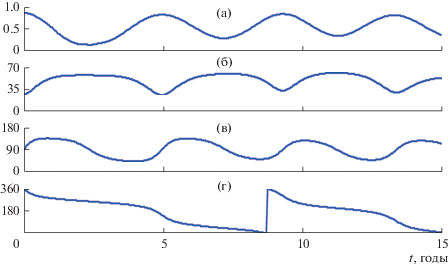
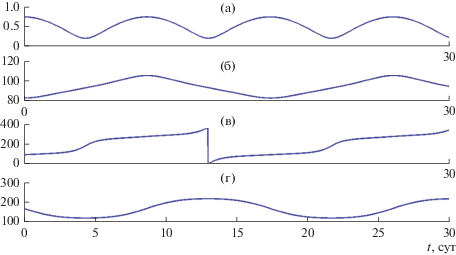
Вклад эксцентриситета лунной орбиты е₁ также достаточно заметен. На рис. 5 показаны аналогичные зависимости, полученные в тестовом расчете при е₁ = 0 (но m₁ ≠ 0). Кроме количественных изменений в основных периодах, в данном примере происходит и качественное изменение. “Намечавшаяся” изначально либрация ω около значения 90° перешла в циркуляцию, которая затем вернулась в либрацию, но уже относительно 270°.

Рис. 5.

То же самое, что на рис. 4, но при е₁ = 0.

ЗАКЛЮЧЕНИЕ

В данной статье на основе полученного Б.П. Кондратьевым неизвестного ранее строгого аналитического выражения силовой функции эллиптического гауссова кольца через полные эллиптические интегралы 1-го и 3-го рода описан алгоритм вычисления компонентов силы его притяжения. Целью явилась адаптация этого алгоритма к численно-аналитическому методу исследования орбитальной эволюции спутников, движение которых возмущается телом, движущимся по эллиптической орбите с заметным эксцентриситетом. Свидетельством работоспособности алгоритма служат два методических иллюстративных примера расчета эволюции искусственного спутника Меркурия типа “Messenger” и гипотетического далекого ИСЗ с “залунным” апогеем.

Автор выражает благодарность двум уважаемым рецензентам за полезные замечания по статье и выявленные погрешности ее текста.

Список литературы

Аксенов Е.П. Двукратно осредненная эллиптическая ограниченная задача трех тел // Астрон. журн. 1979. Т. 56. № 2. С. 419–426.
Анахаев К.Н. О полных эллиптических интегралах 3-го рода в задачах механики // Докл. РАН. 2017. Т. 473. № 2. С. 151–153.
Антонов В.А., Никифоров И.И., Холшевников К.В. Элементы теории гравитационного потенциала и некоторые случаи его явного выражения. СПб: Изд-во С.-Петерб. ун-та, 2008. 208 с.
Вашковьяк М.А. Об интегрируемых случаях ограниченной двукратно осредненной задачи трех тел // Космич. исслед. 1984. Т. 22. Вып. 3. С. 327–334. (Vashkov’yak M.A. Integrable cases of the restricted twice-averaged three-body problem // Cosmic Research. 1984. V. 22. № 3. P. 260–267).
Вашковьяк М.А. Численно-аналитическое исследование сцепленных орбит в ограниченной эллиптической двукратно осредненной задаче трех тел // Астрон. вестн. 2021. Т. 55. № 2. С. 182–192 (Vashkov’yak M.A. Numerical-analytical study of linked orbits in the restricted elliptic double averaged three-body problem // Sol. Syst. Res. 2021. V. 55. № 2. P. 159–168.)
Дубошин Г.Н. Теория притяжения. М.: ФМ, 1961. 288 с.
Кондратьев Б.П. Потенциал гауссова кольца. Новый подход // Астрон. вестн. 2012. Т. 46. № 5. С. 380–391. (Kondratyev B.P. Potential of Gaussian ring. a new approach // Sol. Syst. Res. 2012. V. 46. № 5. P. 352–362.)
Кондратьев Б.П. 2020 (приватное сообщение).
Лидов М.Л. Эволюция орбит искусственных спутников планет под действием гравитационных возмущений внешних тел // Искусственные спутники Земли. 1961. Вып. 8. С. 5–45.
Byrd P.F., Friedman M.D. Handbook of elliptic integrals for engineers and physicists. Berlin Heidelberg: Springer-Verlag, 1953. 358 p.
Halphen G.-H. Traite de function elliptique et de leur application. Paris: Gauthier-Villards et fils, 1888. 659 p.
Kozai Y. Secular perturbations of asteroids with high inclination and eccentricity // Astron. J. 1962. V. 67. P. 591–598.
Lidov M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies // Planet. and Space Sci. 1962. № 9. P. 719–759.
Tisserand. F. Traite de mecanique celeste. Paris: Gauthier-Villards et fils, 1889. T. I. 474 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал