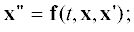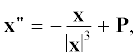Астрономический вестник, 2022, T. 56, № 1, стр. 36-46

ВВЕДЕНИЕ

В работе (Авдюшев, 2020) мы представили новый коллокационный интегратор Lobbie на разбиении Гаусса–Лобатто для численного решения смешанных систем дифференциальных уравнений динамики первого и второго порядков вида

где ${\mathbf{x}}$ – вектор положения динамической системы; ${\mathbf{z}}$ – вектор вспомогательных динамических величин; ${\mathbf{f}}$ и ${\mathbf{g}}$ – известные вектор-функции времени $t$, положения ${\mathbf{x}}$, скорости ${\mathbf{x}}{\kern 1pt} '$ и вектора ${\mathbf{z}};$ штрих означает полную производную по времени. Смешанные системы типа (1) применяются для исследования динамического хаоса (Cincotta и др., 2003), а также для линеаризации, регуляризации и стабилизации уравнений динамики (Kustaanheimo, Stiefel, 1965; Burdet, 1968; Baumgarte, 1972; Шефер, 1991; Avdyushev, 2003).

Применительно к системе (1) сводка основных формул интегратора на шаге величины $h$ с разбиением Гаусса–Лобатто ${{c}_{1}}, \ldots ,{{c}_{s}}$ (${{c}_{1}} = 0$, ${{c}_{s}} = 1$) представима как

Здесь ${{{\mathbf{x}}}_{0}}$, ${\mathbf{x}}_{0}^{'}$ и ${{{\mathbf{z}}}_{0}}$ – начальные значения интегрируемых переменных; ${{{\mathbf{x}}}_{1}}$, ${\mathbf{x}}_{1}^{'}$ и ${{{\mathbf{z}}}_{1}}$ – их значения на конце шага; ${{{\mathbf{u}}}_{i}}$, ${{{\mathbf{v}}}_{i}}$ и ${{{\mathbf{w}}}_{i}}$$(i = 1, \ldots ,s)$ – промежуточные решения в точках коллокаций ${{c}_{1}}, \ldots ,{{c}_{s}}$; ${{{\mathbf{\alpha }}}_{i}}$ и ${{{\mathbf{\beta }}}_{i}}$$(i = 1, \ldots ,s)$ – разделенные разности, получаемые из коллокационных значений функций ${\mathbf{f}}$ и ${\mathbf{g}}$ соответственно; ${{a}_{{ij}}}$ и ${{b}_{{ij}}}$$(i,j = 1, \ldots ,s)$ – константы интегратора, определяемые рекуррентно из узловых значений ${{c}_{1}}, \ldots ,{{c}_{s}}$(Авдюшев, 2020). Схема интегрирования (2) на разбиении Гаусса–Лобатто имеет порядок $p = 2s - 2$.

Интегратор Lobbie – неявный, поскольку все промежуточные решения в (2) (кроме ${{{\mathbf{u}}}_{1}}$, ${{{\mathbf{v}}}_{1}}$ и ${{{\mathbf{w}}}_{1}}$) задаются неявным образом и на каждом шаге определяются методом простых итераций в модификации Зейделя. При $ni$ итерациях требуется $ni(s - 1)$ вычислений функций дифференциальных уравнений. Начальные приближения промежуточных решений получаются из разделенных разностей, вычисляемых по экстраполированным значениям функций дифференциальных уравнений на основе их интерполянтов на предыдущем шаге. При запуске интегратора итерационный процесс стартует от нулевых разделенных разностей.

Интегратор позволяет выполнять пошаговое интегрирование дифференциальных уравнений с переменной величиной шага $h$, к чему целесообразно прибегать при численном моделировании нерегулярной динамики. Величина шага выбирается таким образом, чтобы сохранялась задаваемая пользователем величина ${{\left\| {\mathbf{e}} \right\|}_{{tol}}}$ приближенной оценки члена ряда Тейлора $s$-го порядка для вектора скорости (Авдюшев, 2020):

В соответствии с формулой (3) величина следующего шага $\hbar $ выбирается как

где $h$ – величина текущего шага. Величина стартового шага подбирается итерационно с использованием формулы (4), пока не выполнится условие ${{\sigma }^{{ - {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}} < {\hbar \mathord{\left/ {\vphantom {\hbar h}} \right. \kern-0em} h} < {{\sigma }^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}$, где $\sigma = \sqrt {10} $ (Авдюшев, 2020). Начальное приближение $\hbar $ соответствует заданной величине ${{\left\| {\mathbf{e}} \right\|}_{{tol}}}$ для схемы интегрирования второго порядка $(s = 2)$.

Интегратор Lobbie реализован на процедурном языке Фортран до 32-го порядка для компьютерной арифметики с двойной и четверной точностью (double & quadruple precision). Код интегратора размещен на репозитории Zenodo (DOI: 10.5281/zenodo.5067498). Вызов программной процедуры Lobbie выполняется командой

Здесь x, y, z – массивы интегрируемых переменных ${\mathbf{x}},{\mathbf{x}}{\kern 1pt} ',{\mathbf{z}}$ соответственно: на входе значения на начальный момент времени (ts), на выходе значения на конечный момент времени (tf); step – стартовая величина шага интегрирования: при автоматическом выборе на выходе величина предпоследнего шага, при нулевом значении step величина шага задается интегратором; etol – ${{\left\| {\mathbf{e}} \right\|}_{{tol}}}$: при нулевом значении – режим постоянного шага, величина которого задается пользователем; nxy и nz – размерности массивов x,y ($\dim {\mathbf{x}} = \dim {\mathbf{x}}{\kern 1pt} '$) и z ($\dim {\mathbf{z}}$), соответственно; ns – количество узловых значений $s$; ni – максимальное количество итераций на шаге для решения нелинейных уравнений относительно ${{{\mathbf{u}}}_{1}}, \ldots ,{{{\mathbf{u}}}_{s}}$,${{{\mathbf{v}}}_{1}}, \ldots ,{{{\mathbf{v}}}_{s}}$ и ${{{\mathbf{w}}}_{1}}, \ldots ,{{{\mathbf{w}}}_{s}}$; nst и ncf – количество выполненных шагов и обращений к процедуре fun для вычисления функций ${\mathbf{f}}$ и ${\mathbf{g}}$ на всем интервале интегрирования. Процедура fun задается как

где t – текущий момент времени $t$; x, y, z – массивы интегрируемых переменных со значениями на момент $t$; f – выходной массив значений функций ${\mathbf{f}}$ и ${\mathbf{g}}$ размерности $\dim {\mathbf{f}} + \dim {\mathbf{g}}$.

Помимо гибридного интегратора (5) для решения смешанной системы уравнений (1) мы также разработали два интегратора для решения уравнений только второго порядка:

и только первого порядка:

Первый (DOI: 10.5281/zenodo.5067701) вызывается командой

второй (DOI: 10.5281/zenodo.5067154) –

где nx – размерность массива x. Процедура fun задается соответственно как

В настоящей работе мы приводим результаты тестирования интеграторов Lobbie (5), (8) и (9) в задачах орбитальной динамики. Показываем его эффективность в сравнении с другими широко используемыми на практике интеграторами, а именно с коллокационным Рунге–Кутты; экстраполяционным Грэгга–Булирша–Штера, многошаговым Адамса–Мультона–Башфорта (Hairer и др., 2008), а также с хорошо известным в небесной механике интегратором Эверхарта (Everhart, 1974, 1985).

ЗАДАЧА ДВУХ ТЕЛ

Динамическая астрономия предоставляет обширный полигон задач для тестирования численных интеграторов. По крайней мере, на задаче двух тел, как мы считаем, обязан пройти испытание каждый универсальный интегратор.

Дифференциальное уравнение нормализованной задачи, описывающее движение одной гравитирующей точки относительно другой, имеет вид

где ${\mathbf{x}}$ – вектор положения движущей точки. Уравнение второго порядка (10) можно представить как систему уравнений первого порядка для векторов положения ${\mathbf{x}}$ и скорости ${\mathbf{\dot {x}}}$:

Мы сравнивали эффективность пяти интеграторов: двух новых коллокационных Lobbie – L(II) (8) и L(I) (9) – применительно к уравнениям (10) и (11), соответственно, а также коллокационного Рунге–Кутты на разбиении Гаусса–Лобатто (RK), экстраполяционного Грэгга–Булирша–Штера (GBS) и многошагового Адамса–Мультона–Башфорта (AMB), решающие уравнения первого порядка. Все интеграторы, кроме GBS, – неявные. Для получения промежуточных решений в неявных схемах интегрирования на каждом шаге выполнялись две итерации. Предиктор в RK реализуется посредством экстраполирования функций дифференциальных уравнений на основе полиномиальных интерполянтов Лагранжа, применяемых к функциям на предыдущем шаге (Авдюшев, 2020). В качестве предиктора в AMB используется вложенная явная многошаговая схема Адамса–Башфорта. Переменный шаг в интеграторах RK, GBS и AMB выбирается по тому же алгоритму, что и в интеграторах Lobbie (Авдюшев, 2015, 2020).

На рис. 1 показаны характеристики эффективности (точность–быстродействие) для интеграторов 8-го и 12-го порядков в круговой и эллиптической задачах. Большие полуоси орбит в обоих случаях единичные, следовательно, орбитальные периоды – $2\pi $. Интегрирование выполнялось в арифметике с двойной точностью на интервале 1000 оборотов. Ошибка интегрирования ($\left| {\Delta {\mathbf{x}}} \right|$) оценивалась в векторе положения как максимальная величина разности между расчетным положением и точным на всем интервале интегрирования. В качестве показателя быстродействия рассматривалось количество вычислений функций дифференциальных уравнений (NCF). Показатель NCF обычно используют для сравнительного анализа эффективности интеграторов (Hairer и др., 2008) в предположении, что основной объем компьютерного времени приходится именно на вычисления сложных функций дифференциальных уравнений. В динамической астрономии такие уравнения, например, описывают орбитальное движение с насыщенной структурой возмущений. Несмотря на то, что в численном эксперименте интеграторы тестируются на простых орбитальных моделях, полученные для них показатели NCF вполне позволяют предвосхитить сравнительное быстродействие интеграторов применительно к сложным моделям. Кроме того, показатель NCF удобен тем, что, в отличие от процессорного времени, инвариантен на любой компьютерной платформе и не зависит от уровня оптимизации программного кода орбитальной модели.

Характеристики эффективности получены по результатам многократных расчетов при различной задаваемой точности ${{\left\| {\mathbf{e}} \right\|}_{{tol}}}$. Каждая характеристика (в логарифмических шкалах) имеет форму клюшки. Ее черенок представляет зависимость методической точности от объема вычислений, который обратно пропорционален средней величине шага. Крутизна черенка обусловлена порядком интегратора: чем выше порядок, тем круче черенок. Крюк характеристики вызван влиянием ошибок округления, которые фактически задают предел наивысшей достижимой точности вычислений. Таким образом, эффективность интегратора тем выше, чем левее и ниже на графике ее характеристика.

Итак, как показывают характеристики, наиболее эффективным является новый интегратор L(II). Если сравнивать быстродействие интеграторов L(I) и L(II) при одинаковой точности, то мы можем увидеть, что интегрирование уравнения второго порядка (10) выполняется быстрее, нежели первого порядка (11), в 2–3 раза. Объясняется это тем, что схема интегрирования в L(II) для координат точнее на порядок (Авдюшев, 2020) и, кроме того, итерационный процесс для вычисления промежуточных решений на шаге сходится лучше.

Несмотря на то что интеграторы L(I) и RK оба являются коллокационными и применяются к одним и тем же уравнениям (11), первый работает быстрее: в эллиптическом случае почти в 1.5 раза. Связано это также со сходимостью итерационного процесса для получения промежуточных решений. В интеграторе Рунге–Кутты решения формируются непосредственно через функции дифференциальных уравнений, тогда как в новом интеграторе – через их разделенные разности и, видимо, эта особенность благоприятно влияет на сходимость итераций. Кроме того, уровень предельно достижимой вычислительной точности для интегратора Рунге–Кутты в случае 12-го порядка заметно ниже.

В круговой задаче неплохую эффективность демонстрирует многошаговый интегратор AMB 8-го порядка. При высокой точности он уступает новому интегратору L(II) лишь в 1.5 раза. Хотя многошаговая схема весьма чувствительна к ошибкам округления и поэтому ее уровень предельно достижимой вычислительной точности ниже на два порядка (не только в круговом случае, но и в эллиптическом). При интегрировании эллиптической орбиты эффективность AMB значительно ухудшается и становится сравнимой с эффективностью RK. Результаты для AMB 12-го порядка мы не приводим, поскольку многошаговая схема становится неустойчивой (Авдюшев, 2015).

Экстраполяционный интегратор GBS значительно уступает в эффективности всем интеграторам. Он работает в 1.5 раза медленнее, чем даже коллокационный интегратор Рунге–Кутты. Вообще говоря, использование интеграторов GBS высоких порядков сопряжено с большими вычислительными затратами. Дело в том, что величина NCF пропорциональна ${{p}^{2}}$, поскольку на каждом шаге требуется ${{(p} \mathord{\left/ {\vphantom {{(p} 2}} \right. \kern-0em} 2}{{)}^{2}} + p$ вычислений функций дифференциальных уравнений¹¹: таким образом, для 8-го порядка – 24, а для 12-го – уже 48. Между тем новый интегратор L(I) на двух итерациях требует лишь $p( = 2s - 2)$ вычислений на каждом шаге (Авдюшев, 2020) и, следовательно, для тех же рассматриваемых порядков – 8 и 12 соответственно.

На рис. 1 не приводятся результаты для коллокационных интеграторов Эверхарта, поскольку на разбиениях Гаусса–Радау все они имеют только нечетные порядки (Everhart, 1974; 1985), тогда как новые интеграторы – только четные, а для корректного сравнения эффективности интеграторов следовало бы рассматривать характеристики для одних и тех же порядков. Тем не менее мы провели анализ эффективности для соседних порядков, причем для новых интеграторов выбирали порядки меньшие. Напомним, что интеграторы Эверхарта, как и Lobbie, позволяют решать дифференциальные уравнения второго порядка.

Из рис. 2 видно, что эффективность интеграторов Эверхарта (E) в сравнении с интеграторами Lobbie чуть ниже, несмотря на то, что их порядки выше. В эллиптическом случае, например, интегратор Эверхарта уступает по точности примерно на один порядок. Такой неожиданный результат имеет место по трем причинам. Во-первых, у всех симметричных интеграторов, к которым относится и Lobbie, при (четном) порядке $p$ глобальная ошибка пропорциональна не ${{h}^{p}}$, как у обычных интеграторов, а ${{h}^{{p + 1}}}$ (Hairer и др., 2002; 2008). Следовательно, у сравниваемых интеграторов порядок глобальной ошибки один и тот же. Во-вторых, интегратор Эверхарта на каждом шаге с двумя итерациями требует $p( = 2s - 1)$ вычислений функций дифференциальных уравнений, т.е. на одно больше, чем в интеграторе Lobbie, хотя количество узловых точек $s$для сравниваемых интеграторов одинаковое. В-третьих, предиктор в новых интеграторах точнее, поскольку экстраполяция функций дифференциальных уравнений на следующий шаг выполняется на основе их интерполянтов на всем текущем шаге: первая узловая точка интерполянтов $({{c}_{1}} = 0)$ совпадает с началом шага, тогда как последняя $({{c}_{s}} = 1)$ – с его концом. В то же время узловые точки любого (левого) разбиения Гаусса–Радау в интеграторах Эверхарта охватывают не весь шаг интегрирования, так как ${{c}_{s}} < 1$.

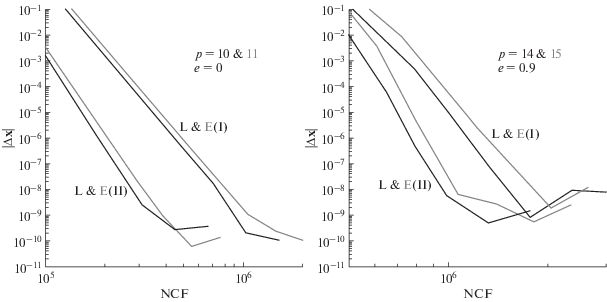
В круговом случае можно считать, что численные результаты интеграторов Эверхарта и Lobbie сопоставимы, т.е. интеграторы одинаково эффективны. Это объясняется тем, что в обоих интеграторах итерационный процесс для вычисления промежуточных решений реализуется похожим образом через разделенные разности функций дифференциальных уравнений. Хотя в интеграторе Эверхарта они выступают в качестве посредников для формирования решения на шаге (Everhart, 1974; 1985), тогда как в Lobbie разделенные разности входят в схему интегрирования явно.

Коллокационные интеграторы на разбиениях Гаусса–Лобатто обладают геометрическими свойствами (Hairer и др., 2002). Они симметричные и орбитально устойчивые (Авдюшев, 2015). Эти свойства позволяют удерживать расчетное положение около орбиты, сохранять интегралы и улучшать поведение глобальной ошибки. Впрочем, все это будет иметь место только в том случае, если промежуточные решения будут точно удовлетворять их неявным уравнениям, т.е. итерационный процесс для их определения должен выполняться до полной сходимости.

На рис. 3 показано отклонение вычисляемого положения ($\Delta \left| {\mathbf{x}} \right|$) от эталонной орбиты в круговой задаче при использовании коллокационных интеграторов на разбиениях Гаусса–Лобатто (Lobbie) и Гаусса–Радау (RK). Все результаты получены с постоянным шагом $h = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {16}}} \right. \kern-0em} {16}}$, т.е. при 16 шагах за оборот. В описанных выше экспериментах для определения промежуточных решений во всех неявных интеграторах мы выполняли только две итерации на шаге. Однако, как видно из рисунка, по меньшей мере, три итерации требуются, для того чтобы интегратор Lobbie был орбитально устойчив, что обеспечивает длительное пребывание расчетного положения вблизи орбиты. При двух итерациях интегратор теряет свои геометрические свойства, и тогда положение постепенно удаляется от орбиты по спирали. То же самое, но несколько медленнее, происходит для интегратора RK, хотя итерационный процесс в нем выполнялся до полной сходимости.

Интеграторы Lobbie также сохраняют некоторые интегралы задачи двух тел. Свойство симметричности интеграторов, в частности, позволяет ограничить поведение глобальной ошибки в энергии (Hairer и др., 2002). Из рис. 4 видно, что геометрические свойства возможны лишь при выполнении не менее трех итераций на шаге для реализации неявной схемы интегрирования. При этом ошибка в энергии не превышает ${{10}^{{ - 9}}}$. Отсюда следует, что сохраняются и все другие энергетические переменные, такие как орбитальный период или большая полуось орбиты.

При использовании обычных негеометрических интеграторов линейный рост ошибки в энергетических переменных, в частности, в среднем движении приводит к квадратичному росту ошибки в средней аномалии и, как следствие, в векторе положения (рис. 5). Между тем, геометрические интеграторы ограничивают ошибку в энергии, и это кардинально меняет характер поведения ошибки в векторе положения: она возрастает уже линейно со временем (рис. 5), т.е. медленнее. Таким образом, эффективность геометрических интеграторов должна проявляться в значительной степени при длительном численном моделировании орбитального движения.

Вместе с тем интеграторы Lobbie также ограничивают ошибку в векторе момента количества движения (рис. 6). Вообще говоря, это означает, что при численном интегрировании сохраняется ориентация орбитальной плоскости и, следовательно, сохраняются угловые величины, отвечающие за ориентацию, а именно долгота восходящего узла и наклонение орбиты.

Впрочем, ошибка в векторе Лапласа неограниченно возрастает со временем (рис. 6). Из анализа точности орбитальных элементов мы выяснили, что она обусловлена, главным образом, возрастающей ошибкой в аргументе перицентра, который определяет направление вектора Лапласа в орбитальной плоскости. При этом его величина, а потому и эксцентриситет орбиты, сохраняются. Интересно заметить, что такая же ситуация в целом с поведением ошибок в орбитальных элементах имеет место при использовании симплектических интеграторов (Kinoshita и др., 1990), которые также являются геометрическими (Hairer и др., 2002).

ВОЗМУЩЕННАЯ ЗАДАЧА ДВУХ ТЕЛ

Как мы видели, сохранение энергии существенно улучшает поведение глобальной ошибки пошагового интегрирования. В возмущенной задаче двух тел интегралов, вообще говоря, нет, и энергия – переменная величина. Однако, если учитывать, что ограничение ошибки в энергии благоприятно влияет на численный процесс, то для повышения эффективности интегрирования целесообразно все же каким-либо способом удерживать расчетное динамическое состояние около энергетической гиперповерхности. С этой целью можно прибегнуть к стабилизации дифференциальных уравнений методом Баумгарте (Baumgarte, 1972).

Дифференциальное уравнение орбитального движения в нормализованной возмущенной задаче имеет вид

где ${\mathbf{P}}$ – возмущающая сила. Стабилизация Баумгарте предполагает введение в уравнение (12) искусственного возмущающего члена, призванного возвращать численное решение на энергетическую гиперповерхность. Возмущающий член, в свою очередь, требует подключения нового дифференциального уравнения для энергии $h$, которая выступает как самостоятельная переменная. Таким образом, необходимо решать смешанную систему уравнений второго и первого порядков (Baumgarte, 1972)

Здесь $\gamma $ – свободный параметр, который подбирается по достижении наилучшей эффективности численного интегрирования. Обычно его оптимальное значение близко среднему движению (Avdyushev, 2003).

К улучшению эффективности численного интегрирования приводят также регуляризирующие преобразования (Kustaanheimo, Stiefel, 1965; Burdet, 1968; Шефер, 1991), в особенности при моделировании сильноэллиптических орбит. Преобразования Шперлинга–Бюрде, например, дают смешанную систему уравнений (Авдюшев, 2015)

где ${\mathbf{G}}$ – вектор Лапласа; $\tau $ – временной элемент; штрих означает производную по фиктивному времени $s$, которое связано с физическим временем $t$ посредством дифференциального соотношения $\operatorname{d} t = \left| {\mathbf{x}} \right|\operatorname{d} s$. Следует заметить, что уравнения (14), как и (13), обладают стабилизирующим эффектом, поскольку энергия $h$ здесь также рассматривается как самостоятельная переменная, независящая от интегрируемых переменных ${\mathbf{x}}$ и ${\mathbf{x}}{\kern 1pt} '$.

Мы исследовали эффективность интегратора Lobbie 8-го порядка в связке с дифференциальными уравнениями возмущенной задачи (12)–(14) на примере астероида Гефест (рис. 7; Hephaistos). Орбита астероида сильно вытянутая (с эксцентриситетом почти 0.84) и близка к эклиптике (наклонение составляет чуть более 11 градусов). Большая полуось – около 2.16 а.е., орбитальный период – 3.2 года. Гефест – околоземный объект, который относится к группе аполлонов. Минимальное расстояние между орбитами Гефеста и Земли составляет почти 0.12 а.е. В афелии при сближении с Юпитером астероид сильно возмущается планетой.

Моделирование астероидного движения выполнялось на интервале времени 1000 оборотов. Системы (13) и (14) решались гибридным интегратором Lobbie – L(III) (5). Начальные условия для уравнений были получены из орбитальных элементов, взятых на сайте Центра малых планет (minorplanetcenter.net) (кроме большой полуоси, которая в нормализованной задаче принималась за единицу). В качестве возмущающего фактора учитывалось только притяжение Юпитера, которое моделировалось по формуле

где ${{\mu }_{P}} = 0.001$ и ${{{\mathbf{x}}}_{P}}$ – гравитационный параметр и положение планеты, соответственно. Движение Юпитера моделировалось на круговой орбите радиуса $\left| {{{{\mathbf{x}}}_{P}}} \right| = 2.4$ в плоскости $({{x}_{1}},{{x}_{2}})$.

Рис. 8 показывает, насколько существенно может быть повышена эффективность численного интегрирования путем преобразования дифференциальных уравнений. Так, если сравнивать характеристики эффективности для интеграторов L(III) и L(II), мы увидим, что стабилизация (st) позволяет повысить точность вычислений на 3 порядка. С другой стороны, это можно интерпретировать как повышение быстродействия (при заданном уровне точности) почти в 2 раза. В то же время колоссальное повышение эффективности дают регуляризирующие преобразования Шперлинга–Бюрде (sb). Регулярные уравнения (14) обладают стабилизирующим эффектом и, кроме того, их функции (правые части) ведут себя менее эксцентрично, нежели функции уравнений (12) и (13). Все это позволяет повысить быстродействие в 10 раз.

На рисунке также показаны характеристики эффективности для интегратора L(I) применительно к системам, где уравнения движения второго порядка в (13) и (14) приводятся к уравнениям первого порядка путем введения скорости в состав интегрируемых величин. Здесь эффективность L(I) в сравнении с L(III) при интегрировании уравнений Шперлинга–Бюрде (14) фактически такая же, как и в невозмущенной эллиптической задаче (рис. 1). Например, L(I) уступает L(III) по быстродействию в два раза. Хотя при интегрировании стабилизированных уравнений (13) L(I) работает медленнее только в 1.5 раза.

Заметим, что интегратор Эверхарта так же хорош, как и Lobbie в решении дифференциальных уравнений второго порядка, но он не позволяет решать смешанные системы уравнений типа (1), и тогда, чтобы воспользоваться им, необходимо приводить уравнения второго порядка к первому порядку. Таким образом, учитывая сопоставимую эффективность интеграторов Эверхарта и Lobbie в версии L(I) применительно к системам уравнений первого порядка (см. рис. 2), мы можем говорить о том, что эффективность Lobbie в общем выше, поскольку для интегратора Эверхарта, как и для L(I) результаты L(III), в принципе недостижимы.

ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ

Для полноценной апробации интегратора необходимо было провести его испытание на нерегулярном орбитальном движении, усложненном гравитационными маневрами. С этой целью мы обратились к одной задаче астродинамики, которая некогда, на заре космической эры, находилась под пристальным вниманием теоретиков.

В 1963 г. Arenstorf (1963) спроектировал периодическую орбиту (рис. 9) для миссий Apollo с целью доставки припасов и астронавтов с Земли (Earth) на Луну (Moon). Эта орбита является частным случаем ограниченной плоской задачи трех тел. Ее нормализованные дифференциальные уравнения во вращающейся системе координат можно представить в виде

где ${{\mu }_{E}} = 1 - {{\mu }_{M}}$ и ${{\mu }_{M}}$ – массы Земли и Луны, а ${{{\mathbf{x}}}_{E}} = {{( - {{\mu }_{M}},0)}^{T}}$ и ${{{\mathbf{x}}}_{M}} = {{({{\mu }_{E}},0)}^{T}}$ – их положения, соответственно²². Первые две составляющие в (15) – инерциальные силы: центробежная и кориолисова, следующие две – притяжение Земли и Луны. Космический аппарат (SC) стартует на минимальном расстоянии от Луны (рис. 9) и возвращается в то же положение приблизительно через 2.7 периодов вращения системы Земля–Луна.

Как видно из рис. 10, эффективность новых интеграторов по-прежнему остается выше, нежели у других, хотя здесь она уже не столь впечатляющая, как, например, в задаче двух тел (рис. 1). Заметим также, что на умеренных точностях весьма нестабильно работает явный экстраполяционный интегратор GBS. Конечно же, с первого взгляда может вызвать недоумение сопоставимая эффективность интеграторов L(I) и L(II), хотя, казалось бы, последний должен давать лучшие результаты. Дело в том, что в функцию дифференциального уравнения (15) входит скорость ${\mathbf{x}}{\kern 1pt} '$, а порядок схемы интегрирования для нее в L(II) ниже, чем у схемы для положения ${\mathbf{x}}$. По этой причине точность вычисления положения становится заметно хуже ожидаемой.

Однако эффективность интегратора L(II) можно повысить, если перейти к уравнению движения в невращающейся системе координат

где отсутствуют инерциальные силы, а потому и скорость. Уравнение (16) отличается от уравнения (15) еще и тем, что в первом гравитирующие точки ${{{\mathbf{x}}}_{E}}$ и ${{{\mathbf{x}}}_{M}}$ уже не стационарны, а двигаются по круговым орбитам с радиусами ${{\mu }_{M}}$ и ${{\mu }_{E}}$, соответственно.

Действительно, переход к уравнению (16) позволяет вернуть реноме интегратору L(II) и его эффективность (рис. 10; характеристика серого цвета) в сравнении с другими интеграторами становится почти такой же, как и в эллиптической задаче двух тел (рис. 1). Например, L(II) работает быстрее многошагового интегратора AMB в 2–3 раза. В то же время формализация орбиты Аренсторфа в виде (16) не приводит к повышению эффективности для других интеграторов, поэтому их характеристики мы не приводим.

Заметим, что наличие скорости в уравнениях (13) и (14) не критично, поскольку она умножается на малые величины, а именно на возмущающую силу ${\mathbf{P}}$ в разных вариантах, а в стабилизирующим члене (13) на разность $H - h$, которая фактически является ошибкой в энергии H, вычисляемой по интегрируемым переменным.

ЗАКЛЮЧЕНИЕ

Таким образом, в задачах орбитальной динамики коллокационный интегратор Lobbie проявил себя весьма достойно, особенно в версии для решения дифференциальных уравнений второго порядка. При моделировании сложного орбитального движения (сильноэллиптического или с гравитационными маневрами) Lobbie превосходит по быстродействию другие рассматриваемые в работе интеграторы (кроме Эверхарта) в несколько раз, а по точности – на несколько порядков.

Корректное сравнение эффективности интегратора Эверхарта и Lobbie не представляется возможным, поскольку они не имеют общих порядков: у первого на разбиениях Радау только нечетные порядки, тогда как у последнего на разбиениях Лобатто только четные. Тем не менее, если сравнивать эффективность интеграторов смежных порядков, то в сильноэллиптическом случае интегратор Эверхарта (с более высоким порядком) уступает Lobbie по точности на один порядок.

Достоинством нового интегратора является также то, что он позволяет решать смешанные системы дифференциальных уравнений второго и первого порядков, которые, например, применяются в небесной механике для исследования динамического хаоса, а также для линеаризации, регуляризации и стабилизации уравнений движения. Чтобы воспользоваться интегратором Эверхарта для решения таких систем необходимо все уравнения второго порядка приводить к первому. Однако применительно к системам уравнений первого порядка эффективность интегратора Эверхарта становится значительно хуже.

Стабилизирующие и регуляризирующие преобразования уравнений движения позволяют существенно улучшить эффективность Lobbie, в особенности при моделировании сильноэллиптических орбит. Например, в случае астероида Гефест быстродействие повышается на порядок, тогда как точность – на десять порядков. В задаче двух тел новый интегратор раскрывает свои геометрические свойства, а именно орбитальную устойчивость и способность сохранять интегралы, что благоприятно влияет на точность численного интегрирования. На примере задачи трех тел показано, что явное присутствие скорости в динамических уравнениях, вообще говоря, нежелательно в виду сравнительно низкой эффективности их интегрирования и поэтому по возможности следует прибегать к альтернативной формализации движения.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № 0721-2020-0049).