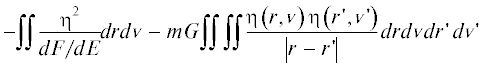1. На главную
  2. Электронные версии
  3. Астрономический вестник
  4. T. 57, № 1, 2023

Астрономический вестник, 2023, T. 57, № 1, стр. 81-99

Избранные проблемы классической и современной небесной механики и звездной динамики. I. Классические результаты

И. И. Шевченко a, b, *, А. В. Мельников c, В. Б. Титов a, Р. В. Балуев a, А. В. Веселова a, А. В. Кривов a, Д. В. Микрюков a, Д. В. Миланов a, А. А. Мюлляри a, И. И. Никифоров a, Н. П. Питьев a, Е. Н. Поляхова a, Л. Л. Соколов a, В. Ш. Шайдулин a

a Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

b Институт прикладной астрономии РАН
Санкт-Петербург, Россия

c Главная (Пулковская) астрономическая обсерватория РАН
Санкт-Петербург, Россия

* E-mail: i.shevchenko@spbu.ru

Поступила в редакцию 30.05.2022
После доработки 22.06.2022
Принята к публикации 26.08.2022

Полный текст (PDF)

Аннотация

В обзоре освещены, в современном контексте приложений, важнейшие научные результаты ученых и выпускников СПбГУ в области небесной механики и звездной динамики. Обзор включает следующие темы: законы звездной динамики Антонова, точки либрации Абалакина–Батракова, метрики Холшевникова, гомологическая область Агекяна–Аносовой, метастабильные тройные системы Орлова, модели Огородникова–Милна, модели Осипкова–Меррита, оценки и вычисление параметра MOID, фотогравитационная небесная механика и солнечный парус, проблемы астероидно-кометной опасности, пылевые комплексы в Солнечной системе, вращательная динамика спутников планет, циркумбинарная динамика, методы открытий и определения орбит экзопланет. В первую часть обзора вошли классические результаты.

Ключевые слова: небесная механика, звездная динамика, Солнечная система, звездные системы

ВВЕДЕНИЕ

В обзоре освещены, в современном контексте приложений, важнейшие научные результаты ученых и выпускников СПбГУ в области небесной механики и звездной динамики. Обзор состоит из двух частей – “Классические результаты” (часть I) и “Современные исследования” (часть II), – разделенных на тематические главы.

В 2024 г. будет отмечаться 300-летний юбилей Санкт-Петербургского университета. Авторы посвящают этот обзор знаменательной дате – 300‑летию Санкт-Петербургского университета.

ЗАКОНЫ ЗВЕЗДНОЙ ДИНАМИКИ АНТОНОВА

В исследованиях сферических звездных систем В.А. Антонов развил гидродинамическую аналогию между задачей об устойчивости звездной системы и задачей об устойчивости газовой баротропной системы. Используя оригинальный математический аппарат, он получил важные результаты и критерии по устойчивости звездных систем. Пионерские результаты В.А. Антонова опираются на разработанный им в 1960-х годах вариационный метод исследования устойчивости сферических звездных систем с изотропным распределением скоростей (Антонов, 1960). Позже он рассмотрел также некоторые случаи с анизотропным распределением скоростей.

Формулировка критерия и доказательство устойчивости звездной системы как единого целого объекта приведены в статье 1960 г. Используя методы и условия устойчивости Ляпунова по первому приближению, Антонов получил критерий устойчивости сферических звездных систем с изотропным распределением скоростей. Позже этот критерий был назван вариационным принципом Антонова (Binney, Tremaine, 1987; 2008).

Рассмотрим случай стационарной звездной системы с фазовой плотностью F = F(E), где E – полная энергия, причем F – убывающая функция от E. Для устойчивости звездной системы необходимо и достаточно, чтобы выражение

было положительным при любом выборе непрерывной, не тождественно равной нулю функции η(r, v), G – гравитационная постоянная, m – средняя масса звезды, r, r' – радиусы-векторы, v, v' – векторы скорости.

На основе найденного им критерия Антонов вывел и доказал ряд утверждений (Антонов, 1962б) для сферических звездных систем, у которых фазовая плотность – убывающая функция интеграла энергии. Среди них (Антонов, 1962б):

– для устойчивости звездной системы могут быть опасны только возмущения, сохраняющие сферическую симметрию;

– для устойчивости звездной системы достаточно выполнения условия d3ρ/dU3 ≥ 0 при всех значениях r, где ρ – звездная плотность, U – потенциал.

Основные результаты Антонова, приведенные в этой статье, сформулированы в фундаментальной монографии “Galactic Dynamics” (Binney, Tremaine, 1987; 2008) в виде четырех “законов Антонова.”

Первый закон Антонова. Сферическая звездная система с фазовой плотностью F = F(E) и dF/dE < 0 устойчива, если баротропная газовая система с аналогичной фазовой плотностью устойчива.

Второй закон Антонова. Сферическая звездная система с фазовой плотностью F = F(E) и dF/dE < 0 устойчива ко всем нерадиальным возмущениям.

Первый закон Антонова дает достаточные условия устойчивости в отношении радиальных возмущений для звездных систем, но не дает необходимых условий. Поэтому его можно использовать только для проверки устойчивости в том случае, если баротропный аналог устойчив.

Наибольший интерес имеют звездные политропы с индексом n ≥ 5 (γ ≤ 6/5), γ = (n + 1)/n. Но баротропные аналоги этих систем неустойчивы. В отличие от газовых политроп, при сжимании звездной политропы вся высвобождаемая гравитационная энергия идет на поступательные движения звезд/тел, и возрастающие движения сопротивляются увеличивающимся силам притяжения. Поэтому ожидается, что звездные системы будут более устойчивыми, чем газовые.

Это подтверждается результатом, опубликованным Антоновым в той же статье и также опирающимся на выведенный им вариационный принцип:

Третий закон Антонова. Сферическая звездная система с фазовой плотностью F = F(E) и dF/dE < 0 устойчива к радиальным возмущениям, если ее плотность ρ = ρ(r) и потенциал U = U(r) удовлетворяют всюду неравенству d3ρ/dU3 ≤ 0.

Из этих результатов следует, что почти все реалистичные модели сферических систем с F = F(E) устойчивы. В частности, все политропные модели с n > 3/2 являются устойчивыми. К этому случаю относится и известная модель Пламмера–Шустера c n = 5, в которой плотность ρ ~ 1/(r2 + + a2)5/2, где a – эффективный радиус сферической системы. Такое распределение плотности близко для многих наблюдаемых сферических систем среди рассеянных и шаровых скоплений звезд.

Четвертый закон Антонова. В этой же статье (Антонов, 1962б), хотя в заголовке статьи говорится только о системах Эмдена, Антонов рассмотрел и случай, когда в сферической системе распределение по скоростям не является изотропным. В исследованном им случае функция распределения F = F(E, L) зависит от интегралов энергии E и вращательного момента L, тензор дисперсии скоростей анизотропен, и Антонов доказал, что сферическая звездная система с F = F(E, L) и dF/dE < 0 устойчива к радиальным возмущениям, если функция плотности

$\rho \left( {U,L} \right) = \int {F\left( {\frac{{{{v}^{2}}}}{2} - U,L} \right)d{v},} $
где L рассматривается как константа, удовлетворяющая неравенству ∂ρ3(U, L)/∂U3 ≤ 0 для всех L. Антонов получил достаточные условия, и этот критерий позволяет установить устойчивость для многих моделей анизотропных сферических систем к радиальным возмущениям. В частности, все часто используемые модели Michie (1963) устойчивы.

Важным исследованием стала работа Антонова о системах с чисто радиальными орбитами. В реальных сферических звездных скоплениях и галактиках, вероятно, имеется много сильно вытянутых орбит звезд. Предельным случаем являются модели с чисто радиальными траекториями.

Для случая предельно анизотропной сферической системы с чисто радиальными орбитами Антонов привел доказательство неустойчивости (Антонов, 1973). Им было показано, что сферические звездные системы с чисто радиальными движениями крайне неустойчивы.

В 1987 г. появился английский перевод этой работы, после чего она стала одной из наиболее цитируемых работ Антонова. Многие авторы исследовали при разных предположениях доказанную в статье “неустойчивость радиальных орбит”, играющую, по современным представлениям, важную роль в ранней эволюции галактик.

Большое число откликов вызвала статья Антонова “Наивероятнейшее фазовое распределение в сферических звездных системах и условия его существования” (Антонов, 1962а), продолжающая работы К.Ф. Огородникова по статистической механике звездных систем. В ней Антонов доказал, опираясь на закон возрастания энтропии, что для гравитирующих систем не существует абсолютного максимума энтропии. Им же была показана возможность при определенных условиях контраста плотностей неограниченного сжатия системы и роста центральной дисперсии скоростей. Линден-Белл подробно разъяснил смысл открытого Антоновым явления, которое предложил называть “гравитермальной катастрофой”. Такой процесс определяет финальную эволюцию звездных скоплений. По существу, результаты Антонова показали, что в условиях законов гравитации “тепловая смерть” невозможна. Поэтому ведшиеся в литературе в 1950-е годы дискуссии о тепловой смерти Вселенной и способах ее избежать представляются сейчас беспредметными.

ТОЧКИ ЛИБРАЦИИ АБАЛАКИНА–БАТРАКОВА

Ю.В. Батраков и В.К. Абалакин в пионерских работах 1957 г. по динамике точечной массы в поле тяготения вращающегося трехосного однородного эллипсоида выявили точки либрации гравитирующего эллипсоида и охарактеризовали их устойчивость (Батраков, 1957; Абалакин, 1957).

Во вращающейся с угловой скоростью n' вращения эллипсоида системе координат (x, y, z) уравнения движения точечной массы имеют вид

(1)
$\begin{gathered} \ddot {x} - 2n{\kern 1pt} '{\kern 1pt} \dot {y} - n{\kern 1pt} {{'}^{2}}x = \frac{{\partial V}}{{\partial x}}, \\ \ddot {x} + 2n{\kern 1pt} '\dot {x} - n{{'}^{2}}y = \frac{{\partial V}}{{\partial y}}, \\ \ddot {z} = \frac{{\partial V}}{{\partial z}}. \\ \end{gathered} $

Если предположить, что однородный эллипсоид с массой M и с осями a, b и c мало отличается от сферы радиуса R, и в разложении для потенциала V оставить два доминирующих слагаемых, то потенциал можно записать в виде

$V = \frac{{{{\varkappa }^{2}}M}}{r} + \frac{3}{{10}}{{\varkappa }^{2}}M\frac{{\alpha {{x}^{2}} + \beta {{y}^{2}} + \gamma {{z}^{2}}}}{{{{r}^{5}}}},$
где α = a2 – R2, β = b2 – R2, γ = c2 – R2, ϰ – постоянная Гаусса. Имеем α + β + γ = 0, и можно ввести малый безразмерный параметр θ такой, что 3/10ϰ2Mα = θλ, 3/10ϰ2Mβ = θμ, 3/10ϰ2Mγ = θν. Тогда

(2)
$V = {{V}_{0}} + \theta {{V}_{1}} + \ldots \approx {{V}_{0}} + \theta \frac{{\lambda {{x}^{2}} + \mu {{y}^{2}} + \nu {{z}^{2}}}}{{{{r}^{5}}}}.$

Также в данном приближении имеем λ + μ + ν = 0.

При θ = 0 движение точечной массы происходит по невозмущенному кеплерову эллипсу. Слагаемое θV1 рассматривается как пертурбационная функция. Величина V1 выражается через элементы кеплерова эллипса следующим образом:

(3)
$\begin{gathered} {{V}_{1}} = \frac{{\lambda + \mu }}{{2{{r}^{3}}}}\left\{ {1 - 6{{\sigma }^{2}} + 6{{\sigma }^{4}} + \kappa {{{\left( {1 - {{\sigma }^{2}}} \right)}}^{2}}\cos \left( {2u + 2\Omega } \right)} \right. + \\ + \,\,\kappa {{\sigma }^{4}}\cos \left( {2u - 2\Omega } \right) + 2\kappa {{\sigma }^{2}}\left( {1 - {{\sigma }^{2}}} \right)\cos 2\Omega + \\ \left. { + \,\,6{{\sigma }^{2}}\left( {1 - {{\sigma }^{2}}} \right)\cos 2u} \right\}, \\ \end{gathered} $
где σ = sin (i/2), κ = (λ – μ)/(λ + μ), u – аргумент широты, Ω – долгота восходящего узла, i – наклон орбиты.

Чтобы получить окончательное разложение пертурбационной функции, остается только использовать известные разложения для r–3, r–3cos 2v и r–3sin2v (v – истинная аномалия). В работе (Батраков, 1957) эти разложения ограничиваются четвертой степенью эксцентриситета.

Уравнения (1) допускают интеграл Якоби и, следовательно, определена поверхность нулевой скорости (Батраков, 1957):

(4)
$n{\kern 1pt} {{'}^{2}}\left( {{{x}^{2}} + {{y}^{2}}} \right) + \frac{{2{{\varkappa }^{2}}}}{r} + 2\theta \frac{{\lambda {{x}^{2}} + \mu {{y}^{2}} + \nu {{z}^{2}}}}{{{{r}^{5}}}} = C.$

Эта поверхность похожа на поверхность нулевой скорости задачи Хилла, и при некоторых значениях C она имеет особые точки. Четыре точки либрации расположены на осях эллипсоида в экваториальной плоскости. Частица, помещенная в любую из них, будет находиться в состоянии покоя относительно вращающейся системы координат. Сечения поверхности нулевой скорости в плоскости xz и плоскости yz представлены на рис. 1.

Рис. 1.

Пример сечений поверхности нулевой скорости плоскостью xz (слева) и плоскостью yz (справа); h = 3.005; где h = С при n' = 1, κ = 1, θ = 1, λ = 0.003, μ = 0.002, ν = –0.005.

Ю.В. Батраков рассмотрел периодические решения третьего (наклоны не равны нулю), второго (наклоны равны нулю, эксцентриситеты конечны) и первого (наклоны равны нулю, эксцентриситеты малы) сортов (Батраков, 1957). Им было доказано существование периодических решений третьего сорта для ряда соизмеримостей n/n' = 1/1, 1/2, 2/5, 1/3, 2/7, … Любопытно, что при e = 0 порождающее решение с соизмеримостью 2/5 имеет наклон, равный критическому наклону в задаче о движении ИСЗ в поле тяготения сфероидальной планеты. Найдены условия существования периодических орбит второго сорта. Орбиты же первого сорта существуют для всех соизмеримостей, кроме n0/n' = (1 + m)/m (m = ±1, ±2, …).

В.К. Абалакин исследовал устойчивость движения в выявленных Ю.В. Батраковым точках либрации и получил периодические решения в окрестности этих точек (Абалакин, 1957). Четыре точки либрации имеют координаты

$\begin{gathered} {{L}_{{1,3}}}:{{x}_{0}} = \pm \left( {{{a}_{0}} + \frac{\lambda }{{{{a}_{0}}}}} \right),\,\,\,\,{{y}_{0}} = 0,\,\,\,\,{{z}_{0}} = 0, \hfill \\ {{L}_{{2,4}}}:{{x}_{0}} = 0,\,\,\,\,{{y}_{0}} = \pm \left( {{{a}_{0}} + \frac{\mu }{{{{a}_{0}}}}} \right),\,\,\,\,{{z}_{0}} = 0. \hfill \\ \end{gathered} $

Параметр a0 = ϰ2Mn'–2. В силу симметрии достаточно провести анализ лишь для одной точки, например, L1(x0, 0, 0). Из (1) получаем уравнения в вариациях:

(5)
$\begin{gathered} \ddot {\xi } - 2n{\kern 1pt} '\dot {\eta } = [n{\kern 1pt} {{'}^{2}}\, + 2(A + B\lambda )]\xi , \\ \ddot {\eta } + 2n{\kern 1pt} '\dot {\xi } = [n{\kern 1pt} {{'}^{2}}\, - (A - 2B\mu )]\eta , \\ \ddot {\zeta } = - \left( {A - 2B\nu } \right)\zeta , \\ \end{gathered} $
где ξ = x – x0, η = y, ζ = z, A = ϰ2M(${1 \mathord{\left/ {\vphantom {1 {x_{0}^{3}}}} \right. \kern-0em} {x_{0}^{3}}}$ + ${{5\lambda } \mathord{\left/ {\vphantom {{5\lambda } {x_{0}^{5}}}} \right. \kern-0em} {x_{0}^{5}}}$ + …), B = ϰ2M(${1 \mathord{\left/ {\vphantom {1 {x_{0}^{5}}}} \right. \kern-0em} {x_{0}^{5}}}$ + …).

Третье уравнение этой системы не зависит от двух других, его решение

(6)
$\zeta = {{C}_{1}}\sin \sqrt {A - 2B\nu } t + {{C}_{2}}\cos \sqrt {A - 2B\nu } t,\,\,\,\nu < \frac{A}{{2B}}.$

Характеристическое уравнение первых двух уравнений системы (5) приводится к виду

(7)
${{\beta }^{4}} + \left( {1 - \frac{{4\lambda + 2\mu }}{{a_{0}^{2}}}} \right){{\beta }^{2}} + \frac{{6\left( {\mu - \lambda } \right)}}{{a_{0}^{2}}} = 0,$

где β = α/n'.

При λ < μ характеристическое уравнение имеет четыре чисто мнимых корня, то есть точка либрации L1 (на малой оси сечения в плоскости орбиты) является устойчивой в первом приближении. Таким образом, при λ < μ имеются два семейства периодических решений: решение долгого периода по эллипсу с эксцентриситетом e = 1 – ${{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\left( {\mu --\lambda } \right)} \mathord{\left/ {\vphantom {{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}\left( {\mu --\lambda } \right)} {a_{0}^{2}}}} \right. \kern-0em} {a_{0}^{2}}}$ и периодом 2πa0/(n' (6(μ – λ))1/2) и по эллипсу с эксцентриситетом e = 31/2/2 и периодом 2π/n'. При λ > μ существует только одна пара чисто мнимых корней и, значит, одно семейство периодических решений с периодом 2π/n'.

Журавлев (1968) рассмотрел критические случаи, когда устойчивые в первом приближении точки либрации оказываются неустойчивыми, если частоты λ1 и λ2 линейной системы находятся в резонансном соотношении и λ1 = 2λ2. В работах (Zhuravlev, 1972; 1973) рассматриваются также случаи других резонансов, их устойчивость либо неустойчивость. Косенко (1981) исследовал геометрию областей устойчивости точек либрации трехосного эллипсоида с потенциалом, заданным в замкнутой интегральной форме. В работах Гасанова и Лукьянова (2002) и Гасанова (2007) рассматривается движение звезды в поле вращающейся эллиптической галактики; в этой задаче потенциал имеет такой же вид, как и в исходной задаче Батракова–Абалакина.

МЕТРИКИ ХОЛШЕВНИКОВА

Метрика дает способ вычисления расстояния между двумя любыми элементами некоторого множества. Выбор того или иного способа зависит от стоящей перед нами задачи и предполагаемых средств ее решения. Геодезист вычислит расстояние между двумя точками земной поверхности как длину соединяющей их кратчайшей, а путешественнику важнее время, за которое из одного пункта можно добраться в другой, пользуясь доступным транспортом. И в том и в другом случае каждой паре точек на карте сопоставляется число, и на основании этих чисел проводятся расчеты и делаются выводы.

Мысль ввести функцию расстояния на множестве орбит небесных тел возникла с накоплением наблюдательных данных о метеорных потоках. Первый численный критерий близости орбит был предложен в 1963 г. (Southworth, Hawkins, 1963). С его помощью авторы классифицировали массив фотографических наблюдений метеоров, относя метеор к одному из известных потоков, если расстояние между орбитой метеороида и средней орбитой потока не превышало порогового значения.

Развитие вычислительной техники и автоматизации наблюдений открыло широкие возможности статистической обработки массивов орбитальных данных. Критерии близости орбит стали ключевым инструментом поиска метеорных потоков и отождествления их родительских тел. Открылась новая область применения критериев: каталогизация семейств астероидов (Lindblad, Southworth, 1971). Формула (Southworth, Hawkins, 1963) была подвергнута критическому анализу, ее модификации предложили Drummond (1981) и Jopek (1993).

Фундаментальные результаты о взаимном расположении и расстоянии между парой кеплеровских орбит получены К.В. Холшевниковым. Отправной точкой исследований можно считать задачу о вычислении MOID – минимального расстояния между точками двух орбит (по данной теме см. также раздел “Оценки и вычисление параметра MOID” во второй части обзора). В работе (Kholshevnikov, Vassiliev, 1999b) эта задача для эллиптических орбит сведена к тригонометрическому уравнению восьмой степени и показано, что такая степень уравнения – минимально возможная при определенных ограничениях на коэффициенты. В работе (Baluyev, Kholshevnikov, 2005) получено обобщение результата на произвольные кеплеровские орбиты. Задача о зацеплении пары орбит, также связанная с вопросом о минимальном расстоянии, рассмотрена в (Kholshevnikov, Vassiliev, 1999a). Коэффициент зацепления, введенный в этой статье, характеризует взаимное расположение орбит и оценивает расстояние сверху.

MOID – важная численная характеристика в задачах предсказания сближений тел, но мало подходящая для решения вопросов об их общем происхождении: ничто не мешает двум совершенно разным орбитам иметь сколь угодно малое значение минимального расстояния между ними. Метрика, описывающая именно “похожесть” орбит, была предложена в статье (Kholshevnikov, Vassiliev, 2004) и представляла собой гельдеровское расстояние между орбитами, параметризованными эксцентрической аномалией. Метрика эта, однако, была определена лишь для эллиптических орбит и неограниченно росла при приближении к параболическому пределу.

Новый тип расстояния появляется в статьях (Kholshevnikov, 2008) и (Kholshevnikov и др., 2016) и определяется как функция интегралов движения материальной точки в центральном поле тяготения: векторов момента импульса и Лапласа–Рунге–Ленца

(8)
${\mathbf{K}} = {\mathbf{r}} \times {\mathbf{\dot {r}}},\,\,\,{\mathbf{e}} = \frac{{{\mathbf{\dot {r}}} \times {\mathbf{K}}}}{{{{\varkappa }^{2}}}} - \frac{{\mathbf{r}}}{r}.$
Здесь r и $\dot {r}$ обозначают радиус-вектор точки и ее скорость в системе координат, связанной с притягивающим центром, r = |r| и ϰ2 – гравитационный параметр. Расстояние между непрямолинейными орбитами x и y определяется так:
(9)
${{\rho }_{2}}\left( {x,y} \right) = \sqrt {{{{\left| {{{{\mathbf{u}}}_{x}} - {{{\mathbf{u}}}_{y}}} \right|}}^{2}} + {{{\left| {{{{\mathbf{v}}}_{x}} - {{{\mathbf{v}}}_{y}}} \right|}}^{2}}} ,$
где ux, vx и uy, vy – отвечающие орбитам x и y пары векторов, сонаправленных с K и e, заданные формулами

u = K/ϰ, v = e |u|.

Наглядное представление о связи векторов u и v с орбитами небесных тел дает рис. 2. Слева на нем изображены орбиты нескольких метеороидов из потока июльских гамма-Драконид, в проекции на плоскость эклиптики, а справа – соответствующие этим орбитам пары векторов. Показаны также средняя орбита потока и орбита Земли.

Рис. 2.

Июльские гамма-Дракониды (GDR); слева – проекции орбит на плоскость эклиптики, справа – соответствующие орбитам векторы u (синий) и v (красный). Зеленым цветом выделена средняя орбита потока, голубым – орбита Земли. Данные взяты из Jenniskens и др. (2016).

Формула (9), выраженная через кеплеровские элементы, выглядит следующим образом:

(10)
$\begin{gathered} {{\rho }_{2}}\left( {x,y} \right) = \\ = \sqrt {\left( {1\, + \,e_{x}^{2}} \right){{p}_{x}}\, + \,\left( {1\, + \,e_{y}^{2}} \right){{p}_{y}} - 2\sqrt {{{p}_{x}}{{p}_{y}}} \left( {\cos I + {{e}_{x}}{{e}_{y}}{\kern 1pt} \cos {\kern 1pt} P} \right)} , \\ \end{gathered} $
где p, e – фокальный параметр и эксцентриситет орбиты, обозначенной нижним индексом. Взаимный наклон орбит I и угол между векторами эксцентриситета P можно выразить через угловые параметры орбит: наклонение i, аргумент перицентра ω и долготу восходящего узла Ω (Kholshevnikov и др., 2016).

Такой подход к определению расстояния заметно отличается от предшествовавших ему критериев близости орбит. В самом деле, критерий Southworth, Hawkins (1963) и его варианты определяются с помощью конкретной системы орбитальных элементов и потому имеют локальный характер в той же мере, в какой локальна параметризация многообразия орбит данной системой элементов. В работе (Kholshevnikov и др., 2016) отмечено, что эта локальность проявляется в “неудобном” поведении критериев в окрестности круговых орбит и на парах орбит с противоположным направлением движения, лежащих в одной плоскости. Напротив, метрика ρ2 определяется через интегралы задачи двух тел, не зависящие от конкретной системы элементов, что делает ее естественной мерой расстояния между любой парой непрямолинейных кеплеровых орбит. Добавление в (9) члена, пропорционального квадрату разности потенциальных энергий тел, позволяет расширить область определения метрики и на прямолинейные орбиты (Kholshevnikov, 2008). Однако такая модификация усложняет работу с метрикой, не принося ощутимой практической пользы.

Расстояние ρ2, определенное формулой (9), удовлетворяет аксиоматическому определению метрики, принятому в математике (Александров, 1977). Это важное свойство выгодно отличает его от других критериев близости. Множество, снабженное метрикой – классический объект анализа и топологии, отправная точка построений метрической геометрии. Абстракция метрического пространства позволяет ввести на множестве орбит полезные понятия среднего (Jopek и др., 2006; Миланов, Щепалова, 2021), меры и размерности (Milanov, 2019).

Под действием возмущений со стороны планет орбиты тел Солнечной системы со временем изменяются, причем характер эволюции различных элементов орбит неодинаков. В отсутствие резонансов и тесных сближений аргумент перицентра ω и долгота восходящего узла Ω орбиты изменяются значительно быстрее по сравнению с другими параметрами орбиты. Для сопоставления орбит, претерпевших длительную эволюцию, в работах (Kholshevnikov, 2008) и (Kholshevnikov и др., 2016) были введены функции расстояния, игнорирующие различия быстро меняющихся элементов ω и Ω:

(11)
${{\rho }_{3}} = \mathop {\min }\limits_{{{\Omega }_{1}},{{\Omega }_{2}}} {{\rho }_{2}},\,\,\,{{\rho }_{4}} = \mathop {\min }\limits_{{{\omega }_{1}},{{\omega }_{2}}} {{\rho }_{2}},\,\,\,\,{{\rho }_{5}} = \mathop {\min }\limits_{{{\Omega }_{1}},{{\Omega }_{2}},{{\omega }_{1}},{{\omega }_{2}}} {{\rho }_{2}}.$
Значения этих функций на паре орбит x и y равны минимальным расстояниям ρ2 между орбитами, все кеплеровские элементы которых, кроме указанных под знаком минимума, совпадают с соответствующими элементами x и y. Все три минимума выражаются в элементарных функциях кеплеровых элементов.

Если считать одинаковыми любые две орбиты, различающиеся лишь долготой восходящего узла, то множество всех орбит превратится в фактор-множество – совокупность классов эквивалентности орбит. Нетрудно убедиться в том, что функция ρ3 корректно определена на этой совокупности. То же верно для ρ4 и ρ5, но с другими отношениями эквивалентности: в первом случае отождествляются орбиты, различающиеся лишь аргументом перицентра, а во втором класс эквивалентности состоит из объектов со всевозможными Ω и ω. В работе (Milanov, 2018) показано, что каждая из функций ρ3, ρ4, ρ5 удовлетворяет аксиомам метрического пространства на своем фактор-множестве. Более того, фактор-пространства с метриками ρ4 и ρ5 изометричны подмножествам довольно простого вида в R4 и R3. Этот факт позволяет определить среднее семейства орбит как образ среднего арифметического соответствующих им точек евклидова пространства (Milanov и др., 2019).

В работе (Kholshevnikov и др., 2020) введено еще одно фактор-пространство, моделирующее метеорные потоки с постоянной долготой перицентра $\varpi $ = Ω + ω. Элементами этого пространства служат классы орбит, у которых параметры p, e, i и $\varpi $ одинаковы. Функция расстояния ρ6 определена на нем аналогично (11):

${{\rho }_{6}} = \mathop {\min }\limits_{{{\Omega }_{1}},{{\Omega }_{2}},{{\omega }_{1}},{{\omega }_{2}}} {{\rho }_{2}},$
где минимум вычисляется при условии постоянства сумм Ω1 + ω1 = ${{\varpi }_{1}}$ и Ω2 + ω2 = ${{\varpi }_{2}}$. Оказалось, что ρ6 не является метрикой на всем пространстве орбит: существует тройка гиперболических орбит, для которой неравенство треугольника не выполнено (Kholshevnikov и др., 2021). Вопрос о том, справедливо ли неравенство на множестве негиперболических орбит, пока открыт.

Метрики Холшевникова дают полезный и многообещающий инструмент для изучения соотношений между орбитами небесных тел. Появившись сравнительно недавно, они были взяты на вооружение исследователями малых тел Солнечной системы и с успехом применяются для поиска пар астероидов (Kholshevnikov, Shchepalova, 2018; Kuznetsov, Safronova, 2018) и транснептуновых объектов (Кузнецов и др., 2021; Kuznetsov и др., 2021) с близкими орбитами, предположительно имеющих общее происхождение, для выявления кластеров среди астероидов, сближающихся с Землей (Jopek, 2020), отождествления родительских тел метеорных потоков (Kokhirova и др., 2018; Сергиенко и др., 2020; Sergienko и др., 2021), подтверждения родства астероидов, ассоциированных с метеорными роями (Kokhirova и др., 2018), определения характеристик генераторов случайных орбит (Jopek, 2021). Пространство кеплеровых орбит с метриками ρ2 – ρ6 – красивый математический объект: уже тот факт, что функции, определенные простыми формулами (11), удовлетворяют неравенству треугольника, говорит о наличии неочевидных внутренних симметрий. Теоретические свойства метрик еще не до конца изучены: не решен вопрос о том, метрика ли ρ6 на множестве эллиптических орбит, не для всех фактор-пространств получены формулы вычисления средних орбит, не выяснена зависимость расстояния от величины возмущения, переводящего одну орбиту в другую. Исследование метрик продолжается, а их применение к задачам, связанным с близостью орбит, даст еще немало прекрасных результатов.

ГОМОЛОГИЧЕСКАЯ ОБЛАСТЬ АГЕКЯНА–АНОСОВОЙ

Для численного интегрирования задачи трех тел необходимо задать массы тел и начальные условия: для каждого тела массу, три пространственные координаты и три скорости; для системы из трех тел всего 21 параметр. Мы можем несколько уменьшить это число, используя интегралы движения, но все равно пространство начальных условий будет иметь высокую размерность, что затрудняет выбор начальных условий и ограничивает возможность представить результаты исследований в наглядной и удобной для анализа форме. Вопрос, как объять необъятное и как выбирать начальные условия для численного исследования задачи трех тел, оставался актуальным вплоть до 1960-х годов. В статье 1967 года, посвященной исследованию динамики тройных систем методом статистических испытаний, Т.А. Агекян и Ж.П. Аносова вводят понятие D‑области. Так появилась знаменитая “область D” (Агекян, Аносова, 1967), в англоязычных работах часто называемая “областью D Агекяна–Аносовой” или “отображением Агекяна–Аносовой” (Agekian–Anosova region D, Agekian–Anosova map). Позже было предложено название “гомологическая область D” (Chernin и др., 1994).

Область D появилась как результат разработки методики задания начальных условий, подходящего для статистического анализа тройных систем. Вначале для упрощения все три тела полагались имеющими одинаковые массы (равные единице). Следующее упрощение – пусть все три тела неподвижны в начальный момент. Это вносит существенное облегчение – задача из пространственной становится плоской. В этом случае необходимо задать только начальные координаты тел, всего три пары, то есть шесть чисел, но размерность все еще высока и не допускает простой визуализации.

Область D представляет собой множество всевозможных конфигураций тройной системы с равными массами и определяется следующим образом. Три тела – A1, A2, A3 – расположены в точках с координатами (–1/2, 0), (+1/2, 0) и (ξ, η). Начало координат (ξ, η) расположено посередине между точками A1, A2, расстояние между которыми принимается равным единице. Проводится дуга окружности единичного радиуса с центром в точке A1, вместе с координатными осями ограничивающая область различных конфигураций (заштрихованная область на рис. 3) с точностью до подобия, поворотов и отражений. В случае расположения точки A3 вблизи пересечения дуги окружности с осью η конфигурация напоминает равносторонний треугольник, при расположении A3 в точке (0, 0) все три тела выстраиваются вдоль одной прямой.

Рис. 3.

Схематичное изображение гомологической области Агекяна–Аносовой – D-области. Рис. из работы (Агекян, Аносова, 1967).

Таким образом, идея области D проста: если мы поместим два тела в точки с координатами (–1/2, 0) и (+1/2, 0), то все возможные различные геометрические конфигурации мы получим, поместив третье тело в область, ограниченную (положительными) осями координат и дугой единичной окружности с центром в точке (–0.5, 0) (см. рис. 3 ).

Таким образом, если мы рассматриваем систему с телами равных масс и нулевыми начальными скоростями, все возможные начальные условия получаются заданием всего двух чисел – координат (x, y) третьего тела. Системы с телами равных масс, отличных от единицы, и/или с другими размерами (но с конгруэнтными начальными условиями) сводятся к “стандартной” изменением шкал расстояния и времени – нормированием расстояний по максимальному расстоянию между телами в начальный момент и нормированием времени по среднему времени пересечения системы

$\tau = \frac{{G\sqrt {\sum\limits_{i = 1}^3 {{{m}_{i}}} } \sum\limits_{i \ne j} {{{m}_{i}}{{m}_{j}}} }}{{{{{\left( {2\left| E \right|} \right)}}^{{3/2}}}}},$
где G – гравитационная постоянная, mi – массы тел (i = 1, 2, 3), E – полная энергия системы.

Использование области D не только упрощает выбор начальных условий, но, что очень важно, позволяет осуществить простую визуализацию результатов (см. рис. 4, иллюстрирующий времена жизни тройных систем).

Рис. 4.

Времена жизни тройных систем (заданы равные массы и нулевые начальные скорости). Темные области соответствуют короткоживущим системам. Рис. из работы (Мартынова и др., 2010).

В работе (Агекян, Аносова, 1967) телам приданы небольшие начальные скорости для того, чтобы избежать тесных сближений, так как интегрирование проводилось без регуляризации. В следующей статье (Агекян, Аносова, 1968) регуляризация уже использовалась, так что не было необходимости вносить эти добавки. В работе (Агекян, Аносова, 1967) изучалось время жизни тройных систем и был получен прообраз рис. 4. В работе Агекяна и Аносовой (1968) изучалась структура области D и были выделены подобласти с разным качественным поведением траекторий (распад после разного количества тройных сближений и др.). Начальные условия генерировались случайным образом, равномерно в области D. Позднее, с развитием компьютеров, стало возможным сканирование области D с мелким шагом.

Область D также можно рассматривать как отображение: в любой момент времени для анализа геометрической конфигурации системы (в том числе и в трехмерном случае) мы можем упорядочить тела по взаимным расстояниям в текущий момент, нормировать расстояния (координаты тел) по максимальному из трех и поместить тела с максимальным разделением на горизонтальной оси в точки (–0.5, 0) и (0.5, 0), располагая наиболее близкие тела справа; третье тело окажется в области D (см., например, Valtonen, Karttunen, 2009). Тогда можно анализировать эволюцию геометрии системы, отслеживая движение точки в области D. Типичный конец эволюции тройной системы с нулевым угловым моментом – распад: после тройного сближения одно из тел получает гиперболическую скорость и уходит прочь от образовавшейся тесной двойной. В этом случае траектория в области D будет приближаться к точке (0.5, 0), выступающей в роли аттрактора. Возможно обобщение на случай разных масс – нужно просто рассмотреть все 6 возможных перестановок трех тел.

Начиная с конца 1960-х годов, понятие D-области широко используется в работах по изучению динамики тройных систем. Так, Агекян и др. (1983) проводят численные эксперименты для 1000 начальных конфигураций в D-области и определяют среднее время, необходимое выбрасываемому из системы компоненту для удаления на заданное расстояние; при этом среднее время для безусловного выброса из системы стремится к бесконечности. Anosova и др. (1994) продолжают ряд работ по численному исследованию задачи о свободном падении в системе трех тел. При равномерном распределении начальных значений по D-области и по круговой области выполняется численное моделирование движения в тройной системе до ухода или далекого отклонения одного из компонентов системы.

Chernin и др. (1994) в рамках изучения конфигураций тройных галактик используют результаты Агекяна и Аносовой (1967), выделяя при этом в D-области несколько регионов с определенными свойствами конфигураций. Так, верхний угол карты назван областью лагранжевых треугольников, нижний правый угол соответствует иерархическим конфигурациям, область внизу карты связана с коллинеарными конфигурациями.

Tanikawa и др. (1995) исследуют свободное падение в задаче трех тел и описывают возможные конфигурации при помощи D-области, ссылаясь на работы петербургской научной школы (Т.А. Агекян, Ж.П. Аносова, В.В. Орлов и др.). Авторы определяют множество начальных условий в D-области, приводящих к двойным и тройным соударениям. Результаты численного моделирования приводят к ряду выводов: так, в области D начальные условия, приводящие к двойным соударениям, расположены вдоль структур–арок; начальные условия для тройного соударения соответствуют пересечениям трех арок двойного соударения; вдоль границы – дуги окружности D-области – расположено бесконечно большое количество начальных условий для тройного соударения.

Tanikawa и др. (2019) используют методы символьных последовательностей и ранее разработанные алгоритмы регуляризации для поиска тройных соударений, симметричных во времени, при этом D-область обобщается на случаи систем с неравными массами. Было получено дополнительное условие на пересечение кривых двойных соударений, соответствующее тройному соударению. Авторы обнаружили 11 точек в D-области, приводящих к тройным соударениям; таких точек должно быть бесконечно много. Также выделено два типа орбит тройного соударения, классифицируемых в зависимости от перемены упорядоченности точек треугольника.

Boekholt и др. (2020) исследуют проблему хаотичности движения в задаче трех тел со свободным падением в начальный момент времени. В качестве начальных данных выбираются конфигурации из D-области.

Manwadkar и др. (2020) подробно исследуют D‑область, вводя две новые метрики и используя их для разделения различных видов взаимодействий и динамического поведения, таких как эргодические взаимодействия и полеты Леви двух типов, определенных в работе Shevchenko (2010). Авторы предложили новую модель оценки времени жизни тройной системы, а также новый механизм процесса релаксации в системе трех тел.

Идея области D нашла применение не только в небесной механике и звездной астрономии. Так, Sano (2007) в работе, посвященной задаче о динамике трех заряженных тел, – так называемой классической кулоновской задаче трех тел, – выделяет более сложное множество начальных конфигураций, концептуально сходное с D-областью. Область D появляется в работах по физике и физической химии (см., например, книгу Toda и др., 2005).

МЕТАСТАБИЛЬНЫЕ ТРОЙНЫЕ СИСТЕМЫ ОРЛОВА

В начале 2000-х годов в исследованиях устойчивости периодических орбит было замечено, что в ряде случаев системы, близкие к периодическим, проводят долгое время в окрестности периодической орбиты. Эффект “прилипания”, заключающийся в том, что траектория проводит долгое время в некоторой ограниченной области фазового пространства вблизи границы хаоса, прежде чем уйти от границы, был известен ранее; см., например, статьи (Contopoulos, 1971) и (Chirikov, 1979; 1991). В задаче трех тел он был обнаружен в приложении к динамике астероидов (Shevchenko, Scholl, 1997), задаче Ситникова (Dvorak и др., 1998). В задаче трех тел с равными массами и нулевыми начальными скоростями В.В. Орловым с коллегами и студентами были обнаружены системы, проводящие долгое время в окрестности устойчивых периодических орбит, приведенных на рис. 5: орбиты Брука, орбиты Шубарта и орбиты “восьмерки”.

Рис. 5.

Устойчивые периодические орбиты: (а) орбита Шубарта; (б) орбита Брука; (в) орбита “восьмерка”. Рис. из работы (Orlov и др., 2004).

Примеры показаны на рис. 6. Системы с таким поведением были названы метастабильными (Martynova и др., 2003). Метастабильная система в ходе эволюции проводит долгое время в окрестности периодической орбиты, “прилипая” к ней, затем уходит в хаотическую область, с возможными далекими выбросами и интенсивными тройными взаимодействиями, затем возможен распад системы или попадание опять в область регулярности – в окрестность той же или другой периодической орбиты. В статье (Martynova и др., 2003) авторы искали метастабильные системы на границе гомологической области D, описанной выше в разделе “Гомологическая область Агекяна–Аносовой,” выделяя системы трех типов: прилипающих к решению Шубарта (тип 1), восьмерке (тип 2) или орбите Брука (тип 3) (см. рис. 7).

Рис. 6.

Траектории в окрестности устойчивых периодических орбит. Рис. из статьи (Мартынова, Орлов, 2013).

Рис. 7.

Начальные условия метастабильных систем в окрестности границы области D. Точки – тип 1, плюсы – тип 2, кружки – тип 3. Рис. из статьи (Martynova и др., 2003).

В работе (Orlov и др., 2004) авторы в поиске метастабильных систем сканировали область D с шагом 0.001 по обеим осям. Из около 300 тысяч рассмотренных систем примерно 9000 проводили в метастабильном режиме более 100 средних времен пересечения. Соответствующие начальные условия показаны на рис. 8. Вполне естественно, метастабильные системы следует искать среди долгоживущих систем: см. рис. 8, а также рис. 3 в статье (Orlov и др., 2004). Авторы перечисляют возможные подходы для поиска и исследования метастабильных систем: визуальный анализ траекторий, статистический анализ последовательностей состояний систем, использование методов символической динамики, различных энтропийных характеристик, вейвлет-анализа.

Рис. 8.

Начальные условия метастабильных систем. Рис. из статьи (Orlov и др., 2004).

Возможен поиск метастабильных систем и в случае ненулевых начальных скоростей, а также в окрестности других периодических решений; см., например, (Мартынова, Орлов, 2013). Отметим вслед за авторами (Orlov и др., 2004), что явление метастабильности имеет временный характер: некоторое (иногда довольно продолжительное) время система проводит в окрестности устойчивой периодической орбиты, “прилипая” к ней, но в итоге (возможно, после нескольких этапов метастабильного поведения, чередующихся с выбросами и активными тройными взаимодействиями) эволюция системы заканчивается распадом.

Эффекты “прилипания” траекторий к границам областей хаоса в фазовом пространстве обусловливают специфический степенной характер распределения длин возвратов Пуанкаре в подобных системах (см. Shevchenko, Scholl, 1997; Orlov и др., 2010; Shevchenko, 2010).

МОДЕЛИ ОГОРОДНИКОВА–МИЛНА

В 1930-х годах К.Ф. Огородников развил концепцию звездной системы как непрерывной среды на основе понятия центроида, который представляет собой математическую точку, неподвижную по отношению к элементарному макроскопическому объему системы, центром которого она является (Ogorodnikoff, 1932; см. также Огородников, 1958, обзор в работе Ossipkov, 2001). При таком рассмотрении каждая точка звездной системы характеризуется своей скоростью – средней скоростью звезд в окрестности этой точки, то есть скоростью центроида (вектор “streaming” в терминах работы (Ogorodnikoff, 1932)).

Модель Огородникова в общем виде представляет собой приложение теоремы Гельмгольца к векторному полю скоростей центроидов, устанавливающее аналогию между движением звездных систем и движением непрерывной среды. Если предположить, что скорость центроида есть непрерывная (и дифференцируемая) функция – V = V(R), где R – радиус-вектор точки в некоторой неподвижной (точнее, инерциальной) системе координат, и что проекции этой скорости на координатные оси имеют непрерывные частные производные первых двух порядков, то для малых гелиоцентрических расстояний r вектор-функцию V(R) можно разложить в ряд по степеням гелиоцентрических прямоугольных координат x, y, z, сохраняя лишь члены первого порядка. В такой модели векторное поле скоростей центроидов представляется линейным выражением

(12)
${\mathbf{V}}({\mathbf{R}}) = {{{\mathbf{V}}}_{0}} + M{\mathbf{r}},$
где V0 = (u0, v0, w0) – скорость центроида наблюдателя (центроида Солнца), M – матрица смещения, r – гелиоцентрический радиус-вектор центроида звезд (Ogorodnikoff, 1932; Огородников, 1958). Матрица M в современных обозначениях (см., например, Витязев, Цветков, 2012) представляется в виде
(13)
$M = {{M}^{ + }} + {{M}^{ - }},$
где M + – симметричная матрица локальной деформации поля скоростей, а M – – антисимметричная матрица локального вращения:

(14)
${{M}^{ + }} = \left( {\begin{array}{*{20}{c}} {M_{{11}}^{ + }}&{M_{{12}}^{ + }}&{M_{{13}}^{ + }} \\ {M_{{12}}^{ + }}&{M_{{22}}^{ + }}&{M_{{23}}^{ + }} \\ {M_{{13}}^{ + }}&{M_{{23}}^{ + }}&{M_{{33}}^{ + }} \end{array}} \right),\,\,{{M}^{ - }} = \left( {\begin{array}{*{20}{c}} 0&{ - {{\Omega }_{3}}}&{{{\Omega }_{2}}} \\ {{{\Omega }_{3}}}&0&{ - {{\Omega }_{1}}} \\ { - {{\Omega }_{2}}}&{{{\Omega }_{1}}}&0 \end{array}} \right).$

Таким образом, в модели Огородникова (12)–(14) внутри малой окрестности произвольной точки звездной системы поле скоростей центроидов разлагается на три компоненты, содержащие 12 параметров: 1) скорость поступательного движения малой окрестности как твердого тела с параметрами u0, v0, w0; 2) скорость твердотельного вращения этой окрестности с компонентами вектора мгновенной угловой скорости Ω1, Ω2, Ω3 в качестве параметров; 3) скорости деформации окрестности с параметрами $M_{{11}}^{ + },$ $M_{{21}}^{ + },$ $M_{{33}}^{ + },$ описывающими сжатие–растяжение поля скоростей вдоль осей системы координат (x, y, z), и с параметрами $M_{{12}}^{ + },$ $M_{{13}}^{ + },$ $M_{{23}}^{ + },$ описывающими деформацию поля скоростей в основной плоскости (x, y) и двух перпендикулярных к ней плоскостях. Заметим, что (остаточное) движение Солнца относительно своего центроида должно быть учтено при вычислении скоростей V(R). Однако, если поле V(R) рассматривается относительно системы координат, связанной с центроидом Солнца, то u0, v0, w0 становятся параметрами остаточной скорости Солнца и могут быть определены из наблюдений вместе с остальными параметрами модели Огородникова.

В предположении, что движение центроидов происходит параллельно галактической плоскости, модель (12)–(14) приводит к следующим выражениям для компонент скорости центроида звезд относительно центроида Солнца:

(15)
${{V}_{{{\text{r\;}}}}} = \left( {M_{{12}}^{ + } + \sin 2l + C\cos ~2l + K} \right)~r~{{\cos }^{{2~}}}b,$
(16)
${{V}_{{{\text{l}}~}}} = \left( {M_{{12}}^{ + } + \cos ~2l - C\sin ~2l + {{\Omega }_{3}}} \right)r\cos ~b,$
(17)
${{V}_{{\text{b}}}} = - {{V}_{{\text{r}}}}\,{\text{tg}}\,b,$
где Vr – лучевая скорость, Vl и Vb – компоненты по галактическим долготе и широте, C = 1/2($M_{{11}}^{ + }$ – $M_{{22}}^{ + }$), K = 1/2 ($M_{{11}}^{ + }$ + $M_{{22}}^{ + }$). Если при этом центроиды вращаются вокруг оси Галактики (C = 0), то (15)–(16) приводят к обобщенным формулам Оорта, выведенным Огородниковым:
(18)
${{V}_{{\text{r}}}} = A\left( {\sin 2l + K} \right)r{{\cos }^{2}}b,$
(19)
${{V}_{{\text{l}}}} = A\left( {\cos 2l + B} \right)r\cos b,$
где A и B (= Ω3) – постоянные Оорта (Ogorodnikoff, 1932; Огородников, 1958; см. также Зонн, Рудницкий, 1959). Коэффициент K в формуле (18) выражает гидродинамическое расхождение (расширение или сжатие) поля скоростей центроидов. При K = 0 формулы (18) и (19) совпадают с оортовскими. Значение K ≠ 0 означает локальное отклонение от модели Оорта–Линдблада (ОЛ) чистого цилиндрического вращения центроидов в Галактике.

Формулы (15)–(17) показывают, что лучевые и тангенциальные скорости звезд должны давать двойную волну (с периодом 180○) вдоль оси l не только в модели ОЛ, но и в случае произвольного движения центроидов параллельно галактической плоскости, причем независимо от закона изменения скоростей центроидов от галактоцентрического расстояния.

Теорию Огородникова обобщил Milne (1935): даже при произвольном движении центроидов, если их скорость есть непрерывная (и дифференцируемая) функция положения, то есть без всяких динамических теорий для стационарной или нестационарной системы, синусоиды с периодом 180○ получаются во всех трех компонентах скоростей в произвольной системе сферических координат (см. также Паренаго, 1954; Зонн, Рудницкий, 1959). Модель Огородникова–Милна (ОМ) сыграла большую роль в теоретическом осмыслении различных эффектов и моделей галактической кинематики, известных в тот период (см. Ossipkov, 2001). В дальнейшем подход Огородникова–Милна продолжал развиваться (см. обзор в работе Осипкова, 1975), в частности, в направлении разработки теории второго порядка (Эдмондсон, 1962; Осипков, 1975). Однако последняя предсказывает существование большого числа гармоник, не наблюдающихся в реальных данных (Витязев, Цветков, 2009), поэтому на практике она применялась лишь в отдельных работах (Hernández-Pajares, Núñez, 1990). Заметим также, что увеличение порядка теории не устраняет принципиального ее ограничения – применимости только в окрестности (обычно околосолнечной) той или иной малости; в общем случае следует основываться на формулах Боттлингера–Пиловского (см., например, Зонн, Рудницкий, 1959). Вместе с тем, модели ОМ оказались весьма полезными для исследования локального объема (в большинстве работ), малых нелокальных объемов, крупномасштабного поля остаточных скоростей.

Анализ наблюдательных данных показывает, что модели ОМ, действительно, лучше в сравнении с моделью ОЛ описывают кинематику звезд в широкой окрестности Солнца – до расстояний ~2 кпк (например, Rybka, 2004a) и даже до 3 кпк (за исключением определения параметра v0; см. Цветков, Амосов, 2019). Из параметров, демонстрирующих отличие от модели ОЛ, значимыми чаще всего получаются параметры C и K (см., например, Rybka, 2004a; 2004b; Бобылев и др., 2009). Для некоторых звездных подсистем и каталогов данных модель ОМ (15)–(17) с движениями центроидов вдоль плоскости Галактики (4 параметра) оказалась достаточной для представления локального поля скоростей (Rybka, 2004a; 2004b; Бобылев и др., 2009), иногда именно такую модель принимают изначально (Olling, Dehnen, 2003).

Модели ОМ применялись для анализа трехмерных скоростей, а также собственных движений и лучевых скоростей, взятых по отдельности. В последнем случае сравнение двух результатов может содержать дополнительную информацию (см., например, Витязев, Цветков, 2009; Velichko и др., 2020).

Альтернативным разложениям в моделях ОМ и ОЛ является подход к построению моделей поля скоростей в локальном макроскопическом объеме, основанный на представлении данных при помощи полных ортогональных систем функций. Полученные так полные модели использовались для оценки параметров модели ОМ, защищенных от смещений со стороны явлений, не включенных в модель (см., например, Витязев, Цветков, 1989; Hernández-Pajares, Núñez, 1990; Витязев и др., 2017; 2018; Velichko и др., 2020). С другой стороны, модели ОМ служат репером, по отношению к которому методом разложения по скалярным или векторным сферическим функциям выявляются дополнительные систематические компоненты, не описываемые данной моделью (например, Витязев, Цветков, 2009; Цветков и др., 2020; Velichko и др., 2020). Так, применение этого метода к собственным движениям звезд в северном и южном полушариях Галактики позволило обнаружить, что статистически надежные значения параметров $M_{{23}}^{ + }$ и Ω1 модели ОМ имеют разные знаки в разных полушариях, что является следствием замедления скорости вращения Галактики по мере возрастания расстояния от ее основной плоскости (Витязев, Цветков, 2012; Vityazev, Tsvetkov, 2013; 2014; Velichko и др., 2020).

Модель Огородникова–Милна широко востребована как эффективный инструмент в многоплановых исследованиях кинематики галактических объектов не только в местном макроскопическом объеме, но и в областях другой локализации.

Линейная модель ОМ многократно применялась: для изучения Местной звездной системы по собственным движениям звезд (Bobylev, 2001); для проверки инерциальности системы каталогов собственных движений (найдено формальное вращение звезд вокруг галактической оси y, направленной в сторону вращения Галактики; Бобылев, Ховричев, 2006; Akhmetov и др., 2015); для описания систематических различий между собственными движениями звезд в разных каталогах (Витязев и др., 2017). При помощи моделей ОМ было найдено вращение вокруг оси x, направленной на центр Галактики, которое было интерпретировано как кинематическое проявление искривления звездно-газового галактического диска (Бобылев, 2013). Модель ОМ также применялась для анализа поля остаточных скоростей, причем обнаруженное вращение вокруг оси y также было увязано с искривлением тонкого диска Галактики (Бобылев, Байкова, 2021). Fedorov и др. (2021) предложили способ построения кривой вращения Галактики без использования величины расстояния от Солнца до центра Галактики (R0): рассматривать центроиды с радиусами 0.5–1.0 кпк вдоль направления центр–антицентр Галактики на R = 0–16 кпк, применяя к каждому из центроидов модель ОМ.

МОДЕЛИ ОСИПКОВА–МЕРРИТА

Исследование сферических и эллипсоидальных звездных систем, таких как эллиптические галактики, ведется на протяжении более чем столетия. Однозначная связь между фазовой и пространственной плотностями в случае изотропного распределения скоростей была установлена еще Эддингтоном (Eddington, 1916). Для создания полного набора анизотропных функций распределения, соответствующих произвольному сферическому распределению массы, были предложены различные методы, как аналитические, так и численные. При этом зачастую алгоритмы оказывались слишком громоздкими или медленно сходящимися.

В работе 1979 г. Осипков разработал метод построения самогравитирующих сферических моделей с эллипсоидальным распределением скоростей. В стационарной сферической системе с эллипсоидальным распределением скоростей фазовая плотность зависит только от линейной комбинации xλ = x0 – λξ интеграла энергии x0 и квадрата кинетического момента ξ = ${{r}^{2}}v_{t}^{2}$ (на единицу массы). Величина λ имеет смысл параметра анизотропии распределения скоростей. При известном пространственном распределении вещества и фиксированном параметре анизотропии решение интегрального уравнения относительно функции фазовой плотности становится возможным путем сведения к уравнению Абеля и получения при этом итогового решения в конечном виде. Частным случаем решения такого уравнения при нулевом значении λ является решение Эддингтона. Предложенный метод был применен к построению таких сравнительно простых моделей, как однородный шар единичного радиуса, сферическая модель с потенциалом Паренаго и сферическая модель Шустера–Пламмера. Для однородного шара получен вывод о невозможности существования не только модели со сферическим распределением скоростей, но и с эллипсоидальным кроме случая λ = –1.

Меррит (Merritt, 1985) представил метод для создания семейств анизотропных функций распределения, согласующихся со сферически-симметричными профилями плотности. Каждое из получаемых решений характеризуется единственным параметром ra – радиусом анизотропии: в качестве переменной используется величина Q = E ± ${{{{J}^{2}}} \mathord{\left/ {\vphantom {{{{J}^{2}}} {2r_{{\text{a}}}^{2}}}} \right. \kern-0em} {2r_{{\text{a}}}^{2}}},$ где E – энергия, J – угловой момент (на единицу массы). При этом вблизи центра системы распределение скоростей изотропно, а на периферии – радиально или тангенциально анизотропно. В работе автор обсуждает два основных способа получения анизотропных решений – получение радиально анизотропных решений (f = f(E + + ${{{{J}^{2}}} \mathord{\left/ {\vphantom {{{{J}^{2}}} {2r_{{\text{a}}}^{2}}}} \right. \kern-0em} {2r_{{\text{a}}}^{2}}}$)) и двух типов тангенциально анизотропных решений (f =  f(E – ${{{{J}^{2}}} \mathord{\left/ {\vphantom {{{{J}^{2}}} {2r_{{\text{a}}}^{2}}}} \right. \kern-0em} {2r_{{\text{a}}}^{2}}}$)), а также определяет расположение соответствующих решениям орбит на диаграмме Линдблада (E, J). Сочетание нескольких решений с различными радиусами анизотропии позволяет получить модели с практически произвольными характеристиками дисперсии скоростей. Меррит предложил применять представленный метод для моделирования профилей дисперсии скоростей сферических систем, таких как эллиптические галактики. Обычно наблюдаемый профиль дисперсии скоростей представляют сглаженной кривой. В методе Меррита в применении к модельной галактике с профилем де Вокулера подходящими оказались решения первого типа, что позволило прийти к выводу об удобстве использования полученных решений, в том числе и вследствие заметного сокращения времени вычислений. Тем не менее автор указывает на наличие разрыва при r = ra.

Во многих исследованиях авторы ссылаются на методы Осипкова и Меррита как на единый алгоритм, метод Осипкова–Меррита. Так, в работе (Ostriker и др., 1989) об исследовании влияния трехосности эллиптических галактик на орбиты шаровых скоплений авторы предлагают использовать метод Осипкова–Меррита для получения функций распределения fk(E, J), позволяющих находить как ящикообразные, так и трубкообразные траектории скоплений в галактике с учетом согласования с заданной функцией распределения плотности излучающего вещества. Cuddeford (1991) обобщает метод Осипкова–Меррита, как метод инверсии фундаментального интегрального уравнения, что позволяет получать двухпараметрические функции распределения, согласующиеся с произвольным заданным профилем плотности. С точки зрения математики, функции распределения представляют собой степенные выражения от углового момента, домноженные на функции модели Осипкова–Меррита. С точки зрения физики, представленное обобщение позволяет учесть произвольную тангенциальную анизотропию, что позволяет исследовать устойчивость самосогласованных сферически-симметричных звездных систем. Полученные в качестве примера семейства аналитических моделей Пламмера и Яффе показали существенную зависимость центральной плотности и дисперсии скоростей от анизотропии скоростей. Alimi и др. (1999) исследовали устойчивость вращающихся столкновительных самогравитирующих сферических систем, при этом к модели Осипкова–Меррита анизотропной сферической системы было добавлено вращение в двух возможных вариантах – как при сохранении анизотропии функции распределения, так и при деформации системы в пространстве скоростей; показано, что на устойчивость существенно влияют анизотропия скоростей и отношение полной кинетической энергии к энергии вращения.

В настоящее время модели Осипкова–Меррита широко используются и обсуждаются. Сотникова и Родионов (2008) применили итеративный метод при создании моделей анизотропных сферически-симметричных темных гало с фиксированным профилем дисперсии скоростей и обсудили применимость метода Осипкова–Меррита; отмечены существенные расхождения профилей анизотропии, получаемых в модели Осипкова–Меррита, и наблюдаемых по данным космологического моделирования. Метод Осипкова–Меррита применим для внутренних областей сферически-симметричных моделей галактик: в работе Ciotti и др. (2019) такая модель анизотропной звездной компоненты рассмотрена в совокупности с изотропным темным гало и черной дырой в центре галактики; для звездной компоненты аналитически решаются уравнения Джинса, получен предел параметров анизотропии, при котором еще не развивается неустойчивость радиальных орбит.

Baes, Dejonghe (2021) в рамках изучения дифференциального распределения энергии в стационарных динамических системах вносили анизотропию с профилем из модели Осипкова–Меррита в дифференциальное распределение энергии в модели Хернквиста; получившиеся модели были изотропны в центральных областях и практически полностью радиально анизотропны во внешней области. Численные эксперименты показали, что средняя энергия связи на единицу массы не зависит от принятого профиля анизотропии.

Модели Осипкова–Меррита используются в программных комплексах для динамического моделирования звездных систем. Baes и др. (2021) разработали программный код SpheCow, позволяющий исследовать структуру и динамику моделей сферических систем в предположении как изотропной, так и анизотропной по Осипкову и Мерриту структуры орбит.

ФОТОГРАВИТАЦИОННАЯ НЕБЕСНАЯ МЕХАНИКА И СОЛНЕЧНЫЙ ПАРУС

При обсуждении основных проблем фотогравитационной небесной механики (ФНМ) следует иметь в виду, что к ним принято относить задачи о движении малых небесных тел естественного или искусственного происхождения, испытывающих в силу своих физических свойств существенное влияние светового давления солнечных лучей. Это относится как к гелиоцентрическим, так и к геоцентрическим движениям.

Сила лучевого отталкивания, то есть прямое световое давление (эффект Лебедева), не является функцией только лишь массы и положения облучаемого тела, а зависит еще от его размеров и формы, от его ориентации к лучам света, от температуры и светоотражательных свойств его поверхности. В полной модели давления светового излучения кроме прямого давления (в качестве главного слагаемого) присутствуют еще и релятивистские поправки, зависящие кроме перечисленных факторов еще и от отношения орбитальной скорости тела к скорости света. В ряде случаев, причем в первую очередь для тел с высоким значением парусности (отношения “поперечное сечение–масса”) приходится переходить от традиционной модели гравитационного поля в космическом пространстве к модели фотогравитационного поля, в котором наряду с гравитационным притяжением существует и радиативное отталкивание. Основы такого подхода были заложены еще П.Н. Лебедевым.

Фотогравитационное силовое поле, являющееся наложением гравитационного и радиативного полей, неконсервативно. Соответствующее изменение орбитальной энергии небесного тела приводит к эволюции его орбиты, темп и интенсивность которой определяются уровнем воздействия сил светового давления (космической радиативной среды) на это тело. Многоплановые исследования такой эволюции привели к созданию целого раздела небесной механики – фотогравитационной небесной механики. Фундаментальные исследования в этой области касаются, прежде всего, постановок фотогравитационных задач двух и трех тел (Поляхова, 1980).

Классификация соответствующих задач включает в себя наряду с задачами классической небесной механики, обобщенными на случай возмущений от сил светового давления, еще и задачи космического полета под действием этих сил, то есть задачи теории управления. Здесь неразрывно связаны между собой задачи гелиоцентрические и геоцентрические, стационарные и нестационарные, задачи о возмущениях движения искусственных спутников Земли (ИСЗ) и космических аппаратов (КА) под действием сил светового давления и задачи об управляемом полете с солнечным парусом (СП). Кроме орбитальных задач важной областью являются и задачи о вращательном движении под действием давления излучения.

Попытки провести классификацию задач ФНМ неизменно приводят к некоторым условным схемам типа “Главные задачи ФНМ” и “Объекты ФНМ”. В рамках первой схемы уместно упомянуть две базовые задачи: ФНМ с одним излучающим центром (Солнечная система, 7 точек либрации) и ФНМ с двумя гравитирующими центрами излучения (двойная звездная система, 9 точек либрации). Обобщение этих задач приводит к неограниченным постановкам задач трех или многих тел в рамках ФНМ.

В задаче с излучением Солнца уместно выделить три очевидные пересекающиеся позиции (Поляхова, 2010):

1. гелиоцентрические движения: гелиоцентрическая задача двух тел о движении микрометеороидов; ограниченная задача трех тел типа Солнце–Юпитер–частица или Солнце–комета–частица хвоста; исследование устойчивости семи точек либрации, нестационарные постановки задач двух или трех тел в рамках ФНМ;

2. геоцентрические (планетоцентрические) задачи возмущенного спутникового движения под действием возмущений от эффектов светового давления;

3. теория управляемого полета с СП, гелиоцентрические полеты: к Солнцу, большим планетам, спутникам планет, астероидам, кометам; полеты геоцентрические: типа разгона к Луне или работы СП в роли орбитального осветителя или пассивного ретранслятора; СП в роли защитного экрана, помещенного в гелиоцентрическую точку либрации между Солнцем и Землей и предохраняющего Землю от перегрева вследствие глобального парникового эффекта.

С предлагаемой классификацией альтернативным образом пересекается классификация “по объектам”. Имея в виду, что речь в ФНМ вообще может идти лишь об объектах с высокой парусностью, объекты можно разделить только на два класса:

– естественные малые тела Солнечной системы;

– искусственные небесные тела (ИСЗ, КА).

В рамках п. 1 уместно рассматривать орбитальные и вращательные движения пылевых частиц, микрометеороидов, малоразмерных астероидов, околопланетных пылевых структур и др., используя достаточно сложные модели сил светового давления с учетом различных слабых эффектов, таких, например, как аберрационные и ротационные эффекты (Поляхова, 1986; 2004; 2010). Что же касается объектов из п. 2, т.е. ИСЗ с высокой парусностью типа баллонов, КА с СП, то для описания их орбитального или вращательного движения обычно используют самую простую модель силы светового давления, обращая, однако, особое внимание на динамические особенности движения, будь то межпланетный орбитальный перелет с СП, стабилизация ИСЗ или КА по трем осям в световом потоке.

Все это очевидное разнообразие пересекающихся задач ФНМ не позволяет уложить ее в жесткие рамки каких-либо формальных и четких классификаций, тем более что развитие космической науки постоянно предлагает ученым новые и зачастую неожиданные проблемы.

Авторы благодарны рецензенту за полезные замечания.

Список литературы

  1. Абалакин В.К. К вопросу об устойчивости точек либрации в окрестности вращающегося трехосного эллипсоида // Бюлл. Инст. Теор. Астрон. 1957. Т. 6. С. 543–549.

  2. Агекян Т.А., Аносова Ж.П. Исследование динамики тройных систем методом статистических испытаний // Астрон. журн. 1967. Т. 44. С. 1261.

  3. Агекян Т.А., Аносова Ж.П. Исследование динамики тройных систем методом статистических испытаний. II. // Астрофизика. 1968. Т. 4. С. 31.

  4. Агекян Т.А., Аносова Ж.П., Орлов В.В. Время распада тройных систем // Астрофизика. 1983. Т. 19. № 1. С. 111–117.

  5. Александров П.С. Введение в теорию множеств и общую топологию. М.: Наука, 1977. 368 с.

  6. Антонов В.А. Замечания к проблеме устойчивости в звездной динамике // Астрон. журн. 1960. Т. 37. № 5. С. 918–926.

  7. Антонов В.А. Наивероятнейшее фазовое распределение в сферических звездных системах и условия его существования // Вестн. Ленинградского ун-та. 1962а. Т. 7. С. 135–146.

  8. Антонов В.А. Решение задачи об устойчивости звездной системы с законом плотности Эмдена и сферическим распределением скоростей // Вестн. Ленинградского ун-та. 1962б. Т. 19. С. 96–111.

  9. Антонов В.А. О неустойчивости стационарных сферических моделей с чисто радиальными движениями // Динамика галактик и звездных скоплений / Ред. Омаров Г.Б. Алма-Ата: Изд-во Наука, 1973. С. 139–143.

  10. Батраков Ю.В. Периодические движения частицы в поле тяготения вращающегося трехосного эллипсоида // Бюл. Инст. Теор. Астрон. 1957. Т. 6. С. 524–542.

  11. Бобылев В.В. Кинематика цефеид и изгиб диска Галактики // Письма в Астрон. журн. 2013. Т. 39. С. 909–915.

  12. Бобылев В.В., Байкова А.Т. Особенности трехмерной кинематики классических цефеид // Письма в Астрон. журн. 2021. Т. 47. С. 634–645.

  13. Бобылев В.В., Ховричев М.Ю. Кинематический контроль инерциальности системы собственных движений звезд каталогов TYCHO-2 и UCAC2 // Письма в Астрон. журн. 2006. Т. 32. С. 676–690.

  14. Бобылев В.В., Степанищев А.С., Байкова А.Т., Гончаров Г.А. Кинематика звезд TYCHO-2, принадлежащих сгущению красных гигантов // Письма в Астрон. журн. 2009. Т. 35. С. 920–933.

  15. Витязев В.В., Попов А.В., Цветков А.С., Петров С.Д., Трофимов Д.А., Кияев В.И. Новые детали эффекта Паренаго по данным первого релиза проекта GAIA DR1 // Письма в Астрон. журн. 2018. Т. 44. С. 688–704.

  16. Витязев В.В., Цветков А.С. Представление кинематических компонент в собственных движениях звезд с помощью сферических функций // Вестн. Ленинградского ун-та. Сер. 1. 1989. Вып. 2. С. 73–79.

  17. Витязев В.В., Цветков А.С. Анализ трехмерного поля скоростей звезд с помощью векторных сферических функций // Письма в Астрон. журн. 2009. Т. 35. С. 114–128.

  18. Витязев В.В., Цветков А.С. Кинематические исследования собственных движений звезд зонных каталогов // Вестн. Санкт-Петербургского ун-та. Сер. 1. 2012. Вып. 1. С. 128–136.

  19. Витязев В.В., Цветков А.С., Петров С.Д., Трофимов Д.А., Кияев В.И. Свойства каталога TYCHO-2 по данным первого релиза проекта GAIA // Письма в Астрон. журн. 2017. Т. 43. С. 807–827.

  20. Гасанов С.А. Задача о движении звезды внутри слоисто-неоднородной эллиптической галактики с переменной массой // Письма в Астрон. журн. 2007. Т. 33. С. 925–941.

  21. Гасанов С.А., Лукьянов Л.Г. О точках либрации в задаче о движении звезды внутри эллиптической галактики // Астрон. журн. 2002. Т. 79. № 10. С. 944–951.

  22. Журавлев С.Г. О неустойчивости точек либрации в окрестности вращающегося гравитирующего эллипсоида // Сб. научн. раб. асп. Универс. Друж. Нар. 1968. Вып. 1. С. 169–183.

  23. Зонн В., Рудницкий К. Звездная астрономия. М.: Изд-во Иностранной литературы. 1959. 448 с.

  24. Косенко И.И. Точки либрации в задаче о трехосном гравитирующем эллипсоиде. Геометрия области устойчивости // Космич. исслед. 1981. Т. 19. № 2. С. 200–209.

  25. Кузнецов Э.Д., Аль-Шиблави О.М., Гусев В.Д., Устинов Д.С. Пары транснептуновых объектов на близких орбитах // Астрономия и исследование космического пространства. Екатеринбург: Изд-во Уральского ун-та, 2021. 222 с.

  26. Мартынова А.И., Орлов В.В. Периодические орбиты в общей задаче трех тел // Астрон. вестн. 2013. Т. 47. № 5. С. 395–407. (Martynova, A.I., Orlov, V.V. Periodic orbits in the general three-body problem // Solar System Research. 2013. V. 47. № 5. P. 363–375.) https://doi.org/10.7868/S0320930X13040038

  27. Мартынова А.И., Орлов В.В., Рубинов А.В., Соколов Л.Л., Никифоров И.И. Динамика тройных систем: учебное пособие. СПб.: Изд-во С.-Петерб. ун-та, 2010. 216 с.

  28. Миланов Д.В., Щепалова А.С. Определение средней орбиты семейства кеплеровых орбит // Изв. Нац. акад. наук Таджикистана. Отделение физико-математических, химических, геологических и технических наук. 2021. Т. 183. № 2. С. 37–43.

  29. Огородников К.Ф. Динамика звездных систем. М.: Гос. Изд-во физ.-мат. литературы. 1958. 628 с.

  30. Осипков Л.П. Некоторые теоретические аспекты кинематики Огородникова–Милна // Динамика и эволюция звездных систем / Ред.: Огородников К.Ф. и др. М.-Л.: АН СССР, ВАГО, ГАО. 1975. С. 66–75.

  31. Осипков Л.П. Сферические системы гравитирующих тел с эллипсоидальным распределением скоростей // Письма в Астрон. журн. 1979. Т. 5. № 6. С. 77–80.

  32. Паренаго П.П. Курс звездной астрономии. М.: Гос. изд-во технико-теоретической литературы. 1954. 476 с.

  33. Поляхова Е.Н. Возмущающее влияние светового давления Солнца на движение ИСЗ // Итоги науки и техники. Сер. Исслед. космич. пространства. Т. 15. Движение искусственных спутников Земли / Ред.: Демин В.Г. М.: ВИНИТИ, 1980. С. 82–114.

  34. Поляхова Е.Н. Космический полет с солнечным парусом. (Монография). М.: Изд-во Наука, 1986. 304 с. (Второе издание, расш. М.: Изд-во Либроком (URSS), 2009, 320 с. Третье издание, стер. Там же. 2018. 320 с.)

  35. Поляхова Е.Н. К столетию фотогравитационной небесной механики // Вестн. Санкт-Петербургского ун-та. Сер. 1. Математика. Механика. Астрономия. 2004. Вып. 4. С. 89–118.

  36. Поляхова Е.Н. Введение в теорию солнечного паруса (2-е изд., испр. и доп.). М.: Изд-во URSS. 2010. 96 с.

  37. Сергиенко М.В., Соколова М.Г., Холшевников К.В. Многофакторная методика поиска малых тел на близких орбитах // Астрон. журн. 2020. Т. 97. № 5. С. 432–440.

  38. Сотникова Н.Я., Родионов С.А. Анизотропные модели темных гало // Письма в Астрон. журн. 2008. Т. 34. № 10. С. 734–745.

  39. Цветков А.С., Амосов Ф.А. Кинематические параметры поля скоростей звезд области вокруг Солнца радиусом до 3 кпк по данным каталога Gaia Data Release 2 with radial velocities // Письма в Астрон. журн. 2019. Т. 45. С. 517–528.

  40. Цветков А.С., Амосов Ф.А., Трофимов Д.А., Петров C.Д. Исследование кинематики звезд каталога Gaia Data Release 2 with radial velocities с помощью скалярных и векторных сферических функций // Письма в Астрон. журн. 2020. Т. 46. С. 61–75.

  41. Эдмондсон Ф. Кинематические основы динамики Галактики // Строение звездных систем / Ред.: Холопов П.Н. М.: Изд-во иностранной литературы, 1962. С. 17–38.

  42. Akhmetov V.S., Fedorov P.N., Velichko A.B., Shulga V.M. The kinematics parameters of the Galaxy using data of modern astrometric catalogues // Odessa Astron. Publ. 2015. V. 28. P. 154.

  43. Alimi J.-M., Perez J., Serna A. Stability of rotating spherical stellar systems // Mon. Notic. Roy. Astron. Soc. 1999. V. 305. P. 859–865.

  44. Anosova J.P., Orlov V.V., Aarseth S.J. Initial conditions and dynamics of triple systems // Celest. Mech. and Dyn. Astron. 1994. V. 60. P. 365–372.

  45. Baes M., Camps P., Vandenbroucke B. SpheCow: Flexible dynamical models for galaxies and dark matter haloes // Astron. and Astrophys. 2021. V. 652. id. A36.

  46. Baes M., Dejonghe H. The differential energy distribution and the total integrated binding energy of dynamical models // Astron. and Astrophys. 2021. V. 653. id. A140.

  47. Baluyev R.V., Kholshevnikov K.V. Distance between two arbitrary unperturbed orbits // Celest. Mech. and Dyn. Astron. 2005. V. 91. № 3–4. P. 287–300.

  48. Binney J., Tremaine S. Galactic Dynamics. Princeton, New Jersey: Princeton Univ. Press, 1987. 733 p.

  49. Binney J., Tremaine S. Galactic Dynamics. Second Edition. Princeton, Oxford: Princeton Univ. Press, 2008. 920 p.

  50. Bobylev V.V. Application of Ogorodnikov–Milne Model to Investigation of the Local Stellar System Kinematics // Stellar Dynamics: from Classic to Modern / Eds: Ossipkov L.P., Nikiforov I.I. St. Petersburg: St. Petersburg Univ. Press, 2001. P. 32–35.

  51. Boekholt T.C.N., Portegies Z.S.F., Valtonen M. Gargantuan chaotic gravitational three-body systems and their irreversibility to the Planck length // Mon. Notic. Roy. Astron. Soc. 2020. V. 493. P. 3932–3937.

  52. Chernin A.D., Ivanov A.V., Trofimof A.V., Mikkola S. Configurations and morphology of triple galaxies: Evidence for dark matter? // Astron. and Astrophys. 1994. V. 281. P. 685–690.

  53. Chirikov B.V. A universal instability of many-dimensional oscillator systems // Phys. Rep. 1979. V. 52. P. 263–379.

  54. Chirikov B.V. Patterns in chaos // Chaos, Solitons and Fractals. 1991. V. 1. P. 79–103.

  55. Ciotti L., Mancino A., Pellegrini S. A new class of galaxy models with a central BH. I. The spherical case // Mon. Notic. Roy. Astron. Soc. 2019. V. 490. P. 2656–2667.

  56. Contopoulos G. Orbits in highly perturbed systems. III. Nonperiodic orbits // Astron. J. 1971. V. 76. P. 147–156.

  57. Cuddeford P. An analytic inversion for anisotropic spherical galaxies // Mon. Notic. Roy. Astron. Soc. 1991. V. 253. P. 414–426.

  58. Drummond J.D. A test of comet and meteor shower associations // Icarus. 1981. V. 45. № 3. P. 545–553.

  59. Dvorak R., Contopoulos G., Efthymiopoulos Ch., Voglis N. “Stickiness” in mappings and dynamical systems // Planet. and Space Sci. 1998. V. 46. P. 1567–1578.

  60. Eddington A.S. The distribution of stars in globular clusters // Mon. Notic. Roy. Astron. Soc. 1916. V. 76. P. 572–585.

  61. Fedorov P.N., Akhmetov V.S., Velichko A.B., Dmytrenko A.M., Denischenko S.I. Kinematics of the Milky Way from the Gaia EDR3 red giants and subgiants // Mon. Notic. Roy. Astron. Soc. 2021. V. 508. P. 3055–3067.

  62. Hernández-Pajares M., Núñez J. Combined study of the solar neighbourhood kinematics: Spherical harmonics and Taylor expansions // Astrophys. and Space Sci. 1990. V. 170. P. 187–195.

  63. Jenniskens P., Nénon Q., Albers J., Gural P.S., Haberman B., Holman D., Morales R., Grigsby B.J., Samuels D., Johannink C. The established meteor showers as observed by CAMS // Icarus. 2016. V. 266. P. 331–354.

  64. Jopek T.J. Remarks on the meteor orbital similarity D-criterion // Icarus. 1993. V. 106. № 2. P. 603–607.

  65. Jopek T.J. The orbital clusters among the near-Earth asteroids // Mon. Notic. Roy. Astron. Soc. 2020. V. 494. № 1. P. 680–693.

  66. Jopek T.J. Remarks on generating realistic synthetic meteoroid orbits // Astron. and Astrophys. 2021. V. 645. id. A82.

  67. Jopek T.J., Rudawska R., Pretka-Ziomek H. Calculation of the mean orbit of a meteoroid stream // Mon. Notic. Roy. Astron. Soc. 2006. V. 371. № 3. P. 1367–1372.

  68. Kholshevnikov K.V. Metric spaces of Keplerian orbits // Celest. Mech. and Dyn. Astron. 2008. V. 100. № 2. P. 169–179.

  69. Kholshevnikov K.V., Kokhirova G.I., Babadzhanov P.B., Khamroev U.H. Metrics in the space of orbits and their application to searching for celestial objects of common origin // Mon. Notic. Roy. Astron. Soc. 2016. V. 462. № 2. P. 2275–2283.

  70. Kholshevnikov K.V., Milanov D.V., Shchepalova A.S. The space of Keplerian orbits and a family of its quotient spaces // Vestnik St. Petersburg Univ. Mathematics. 2021. V. 54. № 2. P. 213–220.

  71. Kholshevnikov K.V., Shchepalova A.S. On distances between orbits of planets and asteroids // Vestnik St. Petersburg Univ. Mathematics. 2018. V. 51. № 3. P. 305–316.

  72. Kholshevnikov K.V., Shchepalova A.S., Jazmati M.S. On a quotient space of Keplerian orbits // Vestnik St. Petersburg Univ. Mathematics. 2020. V. 53. № 1. P. 108–114.

  73. Kholshevnikov K.V., Vassiliev N.N. On linking coefficient of two Keplerian orbits // Celest. Mech. and Dyn. Astron. 1999a. V. 75. № 1. P. 67–74.

  74. Kholshevnikov K.V., Vassiliev N.N. On the distance function between two Keplerian elliptic orbits // Celest. Mech. and Dyn. Astron. 1999b. V. 75. № 2. P. 75–83.

  75. Kholshevnikov K.V., Vassiliev N.N. Natural metrics in the spaces of elliptic orbits // Celest. Mech. and Dyn. Astron. 2004. V. 89. № 2. P. 119–125.

  76. Kokhirova G.I., Kholshevnikov K.V., Babadzhanov P.B., Khamroev U.H., Milanov D.V. Metric approaches to identify a common origin of objects in σ-Capricornids complex // Planet. and Space Sci. 2018. V. 157. P. 28–33.

  77. Kuznetsov E.D., Al-Shiblawi O.M., Gusev V.D. Dynamic evolution of pairs of trans-Neptunian objects: The case of binary and single objects in pair // Contrib. Astron. Observatory Skalnaté Pleso. 2021. V. 51. № 3. P. 226–240.

  78. Kuznetsov E.D., Safronova V.S. Application of metrics in the space of orbits to search for asteroids on close orbits // Planet. and Space Sci. 2018. V. 157. P. 22–27.

  79. Lindblad B.A., Southworth R.B. A study of asteroid families and streams by computer techniques // Int. Astron. Union Colloq. 1971. V. 12. P. 337–352.

  80. Manwadkar V., Trani A.A., Leigh N.W.C. Chaos and Levy flights in the three-body problem // Mon. Notic. Roy. Astron. Soc. 2020. V. 497. P. 3694–3712.

  81. Martynova A.I., Orlov V.V., Rubinov A.V. Metastability in the evolution of triple systems // Mon. Notic. Roy. Astron. Soc. 2003. V. 344. P. 1091–1096.

  82. Merritt D. Spherical stellar systems with spheroidal velocity distributions // Astron. J. 1985. V. 90. P. 1027–1037.

  83. Michie R.W. On the distribution of high energy stars in spherical stellar systems // Mon. Notic. Roy. Astron. Soc. 1963. V. 125. P. 127–139.

  84. Milanov D.V. Metrics in Keplerian orbits quotient spaces // Celest. Mech. and Dyn. Astron. 2018. V. 130. id. 27.

  85. Milanov D.V. On local normability of spaces of Keplerian orbits // Vestnik St. Petersburg Univ. Mathematics. 2019. V. 52. № 3. P. 317–226.

  86. Milanov D.V., Milanova Y.V., Kholshevnikov K.V. Relaxed triangle inequality for the orbital similarity criterion by Southworth and Hawkins and its variants // Celest. Mech. and Dyn. Astron. 2019. V. 131. id. 5.

  87. Milne E.A. Stellar kinematics and the K-effect // Mon. Notic. Roy. Astron. Soc. 1935. V. 95. P. 560–573.

  88. Ogorodnikoff K. A theory of streaming in the system of B stars // Zeitschrift für Astrophysik. 1932. Bd. 4. H. 2. S. 190.

  89. Olling R.P., Dehnen W. The Oort constants measured from proper motions // Astrophys. J. 2003. V. 599. P. 275–296.

  90. Orlov V., Petrova A., Rubinov A. Metastable trajectories in free-fall three-body problem // Order and Chaos in Stellar and Planetary Systems. ASP Conference Series. V. 316 / Eds: Byrd G., Kholshevnikov K., Myllari A., Nikiforov I., Orlov V. San Francisco: Astron. Soc. Pacific, 2004. P. 70.

  91. Orlov V.V., Rubinov A.V., Shevchenko I.I. The disruption of three-body gravitational systems: lifetime statistics // Mon. Notic. Roy. Astron. Soc. 2010. V. 408. P. 1623–1627.

  92. Ossipkov L.P. Kyrill Fedorovich Ogorodnikov (1900–1985) // Stellar Dynamics: from Classic to Modern / Eds: Ossipkov L.P., Nikiforov I.I. St. Petersburg: St. Petersburg Univ. Press, 2001. P. xx–xxviii.

  93. Ostriker J.P., Binney J., Saha P. The effect of galaxy triaxiality on globular clusters // Mon. Notic. Roy. Astron. Soc. 1989. V. 241. P. 849–871.

  94. Rybka S.P. Local kinematics of dwarfs from the Tycho-2 data // Kinematika i Fizika Nebesnykh Tel. 2004a. V. 20. P. 133–141.

  95. Rybka S.P. Kinematic analysis of red giant stars in the vicinity of the Sun // Kinematika i Fizika Nebesnykh Tel. 2004b. V. 20. P. 437–443.

  96. Sano M.M. Dynamics starting from zero velocities in the classical Coulomb three-body problem // Phys. Rev. E. 2007. V. 75. id 026203.

  97. Sergienko M.V., Sokolova M.G., Andreev A.O., Nefedyev Y.A. Search for possible connections of the h-Virginids meteor shower with near-Earth asteroids // J. Physics: Conf. Ser. 2021. V. 2103. id. 012037.

  98. Shevchenko I.I. Hamiltonian intermittency and Lévy flights in the three-body problem // Phys. Rev. E. 2010. V. 81. id. 066216.

  99. Shevchenko I.I., Scholl H. Intermittent trajectories in the 3/1 Jovian resonance // Celest. Mech. and Dyn. Astron. 1997. V. 68. P. 163–175.

  100. Southworth R.B., Hawkins G.S. Statistics of meteor streams // Smithsonian Contrib. Astrophys. 1963. V. 7. P. 261–285.

  101. Tanikawa K., Umehara H., Abe H. A search for collision orbits in the free-fall three-body problem. I. Numerical procedure // Celest. Mech. and Dyn. Astron. 1995. V. 62. P. 335–362.

  102. Tanikawa K., Saito M.M., Mikkola S. A search for triple collision orbits inside the domain of the free-fall three-body problem // Celest. Mech. and Dyn. Astron. 2019. V. 131. id. 24.

  103. Toda M., Komatsuzaki T., Konishi T., Berry R.S., Rice S.A. (Editors). Geometric Structures of Phase Space in Multidimensional Chaos. A Special Volume of Advances in Chemical Physics. V. 130. Pt. A. John Wiley & Sons, Inc., 2005. 1224 p.

  104. Valtonen M., Karttunen H. The Three-Body Problem. Cambridge Univ. Press, 2009. 345 p.

  105. Velichko A.B., Fedorov P.N., Akhmetov V.S. Kinematics of main-sequence stars from the Gaia DR2 and PMA proper motions // Mon. Notic. Roy. Astron. Soc. 2020. V. 494. P. 1430–1447.

  106. Vityazev V.V., Tsvetkov A.S. UCAC4: Stellar kinematics with vector spherical functions // Astron. Nachrichten. 2013. V. 334. P. 760–768.

  107. Vityazev V.V., Tsvetkov A.S. Intercomparison of kinematics derived from catalogues UCAC4, PPMXL and XPM with vector spherical harmonics // Mon. Notic. Roy. Astron. Soc. 2014. V. 442. P. 1249–1264.

  108. Zhuravlev S.G. Stability of the libration points of a rotating triaxial points of ellipsoid // Celest. Mech. 1972. V. 6. P. 255–267.

  109. Zhuravlev S.G. About the stability of the libration points of a rotating triaxial ellipsoid in a degenerate case // Celest. Mech. 1973. V. 8. P. 75–84.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Астрономический вестник

Архивы выпусков Информация о журнале Отправить рукопись в журнал