1. На главную
  2. Электронные версии
  3. Биологические мембраны: Журнал мембранной и клеточной биологии
  4. T. 37, № 2, 2020

Биологические мембраны: Журнал мембранной и клеточной биологии, 2020, T. 37, № 2, стр. 83-93

Латеральное взаимодействие влияет на кинетику метастабильных сквозных пор в липидных мембранах

Т. Р. Галимзянов a, b, Р. Ю. Молотковский a, М. А. Калуцкий a, b, К. В. Пинигин a, c, П. И. Кузьмин a, О. В. Батищев a, c, С. А. Акимов a, b, *

a Институт физической химии и электрохимии им. А. Н. Фрумкина РАН
119071 Москва, Россия

b Национальный исследовательский технологический университет “МИСиС”
119049 Москва, Россия

c Московский физико-технический институт (государственный университет)
141700 Московская обл., г. Долгопрудный, Россия

* E-mail: akimov@misis.ru

Поступила в редакцию 04.04.2019
После доработки 26.04.2019
Принята к публикации 26.04.2019

Полный текст (PDF)

Аннотация

Формирование сквозных пор в липидных бислойных мембранах происходит в ряде клеточных процессов; кроме того, порация мембран используется в различных биотехнологических и биомедицинских приложениях. В классической теории порообразования рассматривается диффузия мембранных дефектов в пространстве радиусов. Когда первая пора достигает критического радиуса, происходит необратимый разрыв мембраны. Обычно считается, что диффузия дефектов происходит независимо, их возможное латеральное взаимодействие не учитывается. В настоящей работе рассматривается возможное влияние латерального взаимодействия метастабильных сквозных пор на их кинетику. Предполагается, что взаимодействие происходит за счет перекрытия упругих деформационных полей, возникающих на кромках двух пор. Энергия взаимодействия двух круглых пор рассчитывалась в приближении Дерягина. В рамках теории упругости жидких кристаллов, адаптированной к липидным мембранам, вычислен одномерный потенциал взаимодействия двух линейных параллельных кромок пор, сформированных в мембранах различного липидного состава. Показано, что взаимодействие должно приводить к эффективному уменьшению измеряемого линейного натяжения кромки поры. Кроме того, за счет взаимодействия время жизни двух оптимально расположенных метастабильных пор может увеличиваться приблизительно в 10 раз. Экстраполяция полученных результатов на случай большего числа взаимодействующих пор позволяет предсказать увеличение времени жизни еще на один-два порядка величины.

Ключевые слова: липидная мембрана, пора, взаимодействие пор, приближение Дерягина, теория упругости

ВВЕДЕНИЕ

Липиды являются важными структурными элементами клеточных мембран. Липидные молекулы амфифильны, т.е. в их составе комбинируются полярные и гидрофобные группы. В воде такие молекулы самоорганизуются в разнообразные структуры, стремясь уменьшить площадь контакта своих гидрофобных частей и воды. Тип образующейся структуры зависит от соотношения количества липида и воды в системе, т.е. смесь вода–липид является лиофильной [1]. Некоторые липиды способны формировать протяженные ламеллярные фазы – липидные бислои, которые и составляют основу клеточных мембран. Амфифильная природа липидных молекул является причиной чрезвычайно низкой проницаемости мембран по отношению к различным веществам [2, 3]. Полярные молекулы не могут преодолеть гидрофобную зону бислоя, в то время как гидрофобные молекулы, напротив, задерживаются в ней и не могут покинуть мембрану. Этим обусловлена основная функция клеточных мембран – барьерная. Клетки являются открытыми неравновесными системами, для жизнедеятельности которых необходимо создание и поддержание неоднородных распределений различных веществ и градиентов электрохимических потенциалов. Барьерные свойства мембран позволяют поддерживать внутри клеточных органелл химический состав, отличающийся от состава цитоплазмы, а в цитоплазме – отличный от состава внешней среды.

Повышение проницаемости мембран за счет образования в них сквозных пор происходит в ряде клеточных процессов, как нормальных, так и патологических. В результате некоторых видов апоптоза в плазматической мембране и в мембранах митохондрий формируются сквозные поры [5, 6]. Амфипатические пептиды, вырабатываемые иммунной системой некоторых организмов, способны индуцировать образование пор в бактериальных мембранах [7–9]. Порация клеточных мембран и модельных липосом используется в различных биотехнологических и биомедицинских приложениях, в частности для электротрансфекции [10, 11], для заполнения водного объема липосом требуемым веществом [12], для отбора проб крови из подкожных капилляров [13] и т.д. Липидные мембраны, как правило, очень стабильны, поэтому для образования поры необходимо сильное внешнее воздействие. Обычно для порации к мембране прикладывается либо латеральное натяжение [14–17], либо трансмембранная разность электрических потенциалов [18–20]. В мембранах, сформированных из “обычных” липидов (например, диолеоилфосфатидилхолина (ДОФХ) или пальмитоилолеоилфосфатидилхолина (ПОФХ)), поры формируются при латеральном натяжении ∼7 мН/м или при трансмембранном потенциале ∼200 мВ за характерное время порядка десяти секунд [14, 16, 18, 19]. Мембрана, окруженная электролитом, при приложении трансмембранного потенциала аналогична электрическому конденсатору. Статическая диэлектрическая проницаемость липида приблизительно равна 2, воды – 81. В такой системе энергетически выгодно увеличение емкости конденсатора, что может достигаться за счет частичного замещения среды с низкой диэлектрической проницаемостью (мембраны) средой с высокой диэлектрической проницаемостью (водой), т.е. за счет формирования сквозной поры. Электрическое поле индуцирует эффективное латеральное давление в мембране, в результате чего образуются многочисленные сквозные “дефекты”, заполняемые водой. Если мембрана рассматривается как бесконечно тонкая бесструктурная пленка, то латеральное давление оказывается аналогично латеральному натяжению. В этом приближении энергия мембраны, к которой приложено латеральное натяжение (или давление) σ и в которой образовалась сквозная пора радиуса R, может быть записана в виде [21]:

(1)
$E = 2\pi R\gamma --\pi {{R}^{2}}\sigma ,$
где γ – линейное натяжение, т.е. энергия кромки поры, отнесенная к ее периметру. Зависимость (1) схематически изображена на рис. 1а (сплошная черная кривая). При малом радиусе поры основной вклад в энергию дает линейное по радиусу слагаемое, и пора стремится закрыться, поскольку ее энергия уменьшается при уменьшении R. При больших радиусах энергия определяется квадратичным по радиусу слагаемым, и энергия поры уменьшается с ростом R, что соответствует необратимому разрыву мембраны. При критическом радиусе поры R * = γ/σ энергия системы максимальна и равна E * = πγ2/σ; при R = R* имеется неустойчивое положение равновесия. Зависимость энергии вида (1) характерна для метастабильных систем [21]. Для “обычного” липида линейное натяжение кромки поры составляет γ ≈ ≈  8–20 пН [22], и, соответственно, критический радиус R * ≈ (8–20 пН)/(7 мН/м) ≈ 1–3 нм.

Рис. 1.

а – Зависимости энергии поры от ее радиуса в различных моделях. Сплошная черная кривая – приближение бесконечно тонкой бесструктурной пленки с приложенным латеральным натяжением σ, зависимость описывается уравнением (1). При критическом радиусе поры R * энергия максимальна (E *). Поры, радиус которых меньше критического, спонтанно закрываются. Если радиус поры больше критического, пора неограниченно растет. Черная штриховая кривая – энергия деформаций мембраны на кромке поры, рассчитываемая в рамках теории упругости сплошной среды, при нулевом латеральном натяжении. Зависимость имеет локальный минимум (M) при радиусе поры Rm; для закрытия поры (R → 0) необходимо преодолеть энергетический барьер (X). Серая толстая кривая – энергия деформаций мембраны на кромке поры, рассчитываемая в рамках теории упругости сплошной среды, при ненулевом латеральном натяжении. б – Схематическое изображение сечения мембраны с круглой порой радиуса R плоскостью, проходящей через ось цилиндрической симметрии. Мембрана показана серым цветом. Липид на кромке поры испытывает деформацию поперечного изгиба; в среднем, молекулы формируют веерообразную структуру. в – Типичная зависимость энергии деформаций мембраны, индуцированных двумя мембранными включениями, от расстояния между включениями L. При больших L включения не взаимодействуют, и энергия равна сумме энергий деформаций, индуцированных изолированными включениями (2W0). Зависимость имеет глобальный минимум (I).

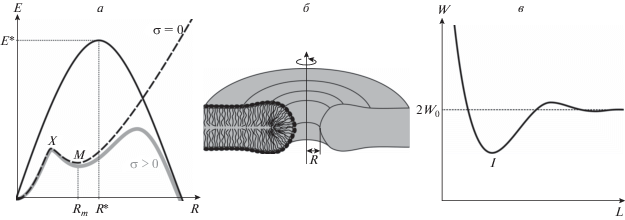
Применимость выражения (1) для расчета энергии поры ограничена. Толщина “типичной” липидной мембраны составляет около 4 нм [23]. Приближение бесконечно тонкой бесструктурной пленки корректно применять к мембране, только если радиус поры в ней значительно превышает толщину мембраны. Действительно, при малых радиусах свойства поры, в частности ее электрическая проводимость, существенно зависят от конкретной формы поверхности кромки. Однако, как следует из приведенной выше оценки, критический радиус поры, как правило, меньше толщины мембраны и может быть даже меньше толщины липидного монослоя. Считается, что величина линейного натяжения определяется, прежде всего, энергией упругих деформаций липида на кромке поры. Основной вклад в эту энергию дает деформация поперечного изгиба, при которой между осями, характеризующими среднюю ориентацию липидов, возникает угол; липиды формируют веерообразную структуру (рис. 1б). Энергия этой деформации пропорциональна квадрату геометрической кривизны поверхности монослоя и немонотонно зависит от радиуса поры [24–26]. Кроме того, упругая энергия возрастает при приложении латерального натяжения, однако не изменяется, если к кромке поры приложено латеральное давление [26]. Это приводит к тому, что линейное натяжение оказывается не постоянным, а зависит как от радиуса поры R, так и от латерального натяжения σ, т.е., вообще говоря, выражение (1) должно быть переписано в виде:

(2)
$E = 2\pi R\gamma (R,\sigma )--\pi {{R}^{2}}\sigma .$
Типичные зависимости энергии поры от радиуса показаны на рис. 1а [25, 26]. Практически для всех липидов эти зависимости имеют локальный минимум (обозначен буквой M на рис. 1а) при радиусах Rm ∼ 1–2 нм, т.е. пора может быть метастабильной и обладать конечным временем жизни. Для закрытия (т.е. R → 0) поре необходимо преодолеть энергетический барьер, обозначенный буквой X на рис. 1а. Положение и высота этого барьера определяются физико-химическими свойствами липида (в том числе спонтанной кривизной и толщиной монослоя, гидрофобностью углеводородных цепей) и слабо зависят от внешних факторов, в частности от латерального натяжения (рис. 1а) [25, 26]. Экспериментально было показано, что при трансмембранном потенциале 250 мВ среднее время жизни проводящих дефектов в мембране, сформированной из азолектина, составляет 3 мс, однако некоторые поры остаются открытыми в течение 1 с; при этом необратимый электрический пробой мембраны не наступает [18]. В мембране с высоким содержанием лизолипидов и холестерина время жизни проводящих пор может составлять до 7 с [12]. Возможность образования метастабильных пор предполагалась уже в самых ранних работах по электропорации мембран [19]. В работе [27] было показано, что при приложении к мембране серии электрических импульсов плотность метастабильных пор может достигать 105 см–2.

В кинетической теории электропорации обычно предполагается, что в мембране имеется большое количество так называемых пор нулевого радиуса или предпор – структур, в которых липиды ориентированы, как и в обычной проводящей поре (рис. 1б), но радиус просвета которых настолько мал, что ионы не могут пройти через предпору [28, 29]. Далее рассматривается диффузия таких дефектов в пространстве радиусов от нулевого радиуса до критического, по аналогии с кинетической теорией фазового разделения [30]. Считается, что происходит необратимый электрический пробой мембраны, когда первая пора достигает критического радиуса. При этом рассматривается идеальная диффузия, т.е. считается, что все предпоры развиваются независимо, и какое-либо взаимодействие предпор между собой не учитывается. Однако липид на кромке поры сильно деформирован [31, 32]. Упругие деформации мембраны распространяются в латеральном направлении на несколько нанометров [33–35]. Когда поры находятся достаточно далеко друг от друга, индуцируемые ими деформации действительно независимы, и энергия пор аддитивна. Однако при сближении пор деформации начинают перекрываться, что должно приводить к эффективному латеральному взаимодействию [36–39]. Ранее мы показали, что энергия взаимодействия различных мембранных включений, индуцирующих деформации мембраны, немонотонно зависит от расстояния между ними: как правило, при некотором расстоянии энергия имеет локальный (или глобальный) минимум. В качестве включений рассматривались амфипатические и гидрофобные пептиды, трансмембранные белки и т.д. [37–39]. Типичная зависимость энергии деформаций мембраны, индуцированных двумя мембранными включениями, от расстояния между включениями схематически изображена на рис. 1в (ср. с рис. 3а, 3б). Таким образом, если в мембране имеются две метастабильные поры, расположенные на расстоянии, соответствующем минимуму энергии их взаимодействия (обозначен буквой I на рис. 1в), то их время жизни должно быть выше, чем время жизни таких же изолированных (бесконечно удаленных друг от друга) пор. Действительно, время жизни поры определяется высотой энергетического барьера на закрытие поры (обозначен буквой X на рис. 1а) относительно локального минимума энергии (обозначен буквой M на рис. 1а). При оптимальном расстоянии между порами энергия деформаций мембраны оказывается ниже, чем суммарная энергия деформаций, индуцированных двумя изолированными порами. Это означает, что энергия каждой поры эффективно уменьшается, когда на оптимальном расстоянии от нее находится такая же пора. Высота энергетического барьера X на закрытие поры (R → 0) определяется физико-химическими свойствами липида и практически не зависит от внешних факторов [25, 26]. Таким образом, взаимодействие метастабильных пор должно приводить к понижению энергии в точках их локальных минимумов M, при неизменной высоте барьера на закрытие поры X. Это означает, что высота барьера на закрытие поры относительно локального минимума энергии M возрастает, что должно приводить к увеличению времени жизни метастабильной проводящей поры.

В настоящей работе мы рассмотрели взаимодействие двух пор, опосредованное упругими деформациями мембраны, возникающими на их кромках. Деформации, возникающие вблизи изолированной круглой поры, обладают цилиндрической симметрией. Это позволяет получить аналитические выражения для пространственного распределения деформаций и их энергии [25, 26]. Однако при взаимодействии двух круглых пор цилиндрическая симметрия системы в целом теряется, и решить задачу о нахождении распределения деформаций и энергии аналитически не удается. Ранее мы показали, что для расчета энергии взаимодействия произвольно расположенных мембранных включений можно пользоваться аналогом приближения Дерягина для взаимодействия трехмерных объектов [39, 40]. В рамках этого приближения аналитически рассчитывается одномерный потенциал взаимодействия двух линейных параллельных кромок пор (энергия, отнесенная к единице длины кромки). Для получения энергии взаимодействия двух круглых пор радиуса R, одномерный потенциал нужно умножить на эффективную длину Leff, которая приближенно может быть записана в виде Leff ≈ 2R + + 2lW, где lW ∼ 1 нм – характерная длина затухания плотности упругой энергии [39]. Согласно нашим расчетам, время жизни двух метастабильных пор, расположенных на оптимальном расстоянии друг от друга, может увеличиваться приблизительно в 10 раз по сравнению со временем жизни изолированных пор.

ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ

Будем рассматривать мембрану в качестве анизотропной жидкокристаллической сплошной среды. Среднюю ориентацию липидных молекул в составе липидного монослоя будем характеризовать векторным полем единичных векторов n, называемых директорами. Деформации, модули упругости и поле директоров будем относить к некоторой поверхности, называемой разделяющей, проходящей внутри монослоя параллельно его внешней (полярной) границе. Разделяющая поверхность определяется векторным полем ее единичных нормалей N. Будем рассматривать три основные деформации мембраны [41]: 1) поперечный изгиб, поверхностная плотность энергии которого пропорциональна (div(n))2 (дивергенция берется вдоль разделяющей поверхности); 2) наклон, поверхностная плотность энергии которого пропорциональна квадрату вектор наклона, t2 = (n – N)2; 3) латеральное растяжение–сжатие, поверхностная плотность энергии которого пропорциональна квадрату относительного изменения площади разделяющей поверхности, α2 = [(a – a0)/a0]2 (a – текущая площадь элемента разделяющей поверхности; a0 – его площадь в исходном недеформированном состоянии). Деформации считаются малыми, и поверхностная плотность энергии вычисляется во втором порядке по ним. Поверхностная плотность энергии деформированного монослоя может быть записана в следующем виде [41]:

(3)
$w = \frac{B}{2}{{\left( {{\text{div}}{\kern 1pt} \left( {\mathbf{n}} \right) + {{J}_{0}}} \right)}^{2}} - \frac{B}{2}J_{0}^{2} + \frac{{{{K}_{t}}}}{2}{{{\mathbf{t}}}^{2}} + \frac{{{{K}_{A}}}}{2}{{\alpha }^{2}},$
где B, Kt, KA – модули поперечного изгиба, наклона и латерального растяжения/сжатия, соответственно; J0 – спонтанная кривизна монослоя, которая равна геометрической кривизне разделяющей поверхности свободного монослоя (в отсутствие внешних сил и моментов). Энергия отсчитывается от энергии плоского монослоя, имеющего нулевую геометрическую кривизну. Формально, свободная энергия деформаций во втором порядке малости должна содержать перекрестное слагаемое по деформациям поперечного изгиба и латерального растяжения–сжатия вида ∼α div(n); при этом энергия не может содержать слагаемых, перекрестных по деформации наклона, поскольку t – векторная величина, которая не может линейно входить в энергию, являющуюся скаляром. Деформации и модули упругости относятся к разделяющей поверхности и, очевидно, зависят от положения этой поверхности внутри монослоя. Экспериментально было показано, что коэффициент (модуль), стоящий перед перекрестным слагаемым ∼α div(n), можно сделать нулевым за счет специфического выбора положения разделяющей поверхности. Такая разделяющая поверхность называется нейтральной; она проходит на расстоянии ∼0.7 нм от внешней полярной границы монослоя [42]. В дальнейшем мы будет относить деформации и модули упругости к нейтральной поверхности. Для получения полной упругой энергии участка деформированного монослоя поверхностную плотность энергии (3) необходимо проинтегрировать по нейтральной поверхности монослоя.

Модуль объемного сжатия мембраны очень велик [43], что позволяет считать ее объемно несжимаемой средой. Условие объемной несжимаемости налагает связь на возможные деформации. С требуемой точностью его можно записать в следующем виде [41]:

(4)
${{h}_{с}} = h - \frac{{{{h}^{2}}}}{2}\operatorname{div} \left( {\mathbf{n}} \right) - h\alpha ,$
где hc – текущая толщина гидрофобной части монослоя; h – толщина гидрофобной части монослоя в исходном недеформированном состоянии. Для простоты в дальнейшем будем называть hc и h просто толщиной монослоя в текущем и исходном состояниях соответственно.

Деформации мембраны на кромке поры велики, и предположения, в которых были получены выражения (3), (4), вообще говоря, не выполняются. Однако мембрану вблизи кромки поры можно разбить на несколько участков таким образом, чтобы внутри каждого участка деформации были относительно невелики. Формально это соответствует введению нескольких систем координат, расположенных таким образом, чтобы в каждой из них для некоторого участка липидного монослоя выполнялись условия |div(n)| $ \ll $ 1/h; |t| $ \ll $ 1; α $ \ll $ 1. Деформации, параметризованные в разных системах координат, сопрягаются на границах участков, исходя из непрерывности директора и нейтральной поверхности. Затем полная энергия системы, записываемая как сумма упругих энергий соответствующих участков монослоя, минимизируется по координатам границ участков, определяемых в лабораторной системе координат. Ранее нами было показано, что можно разбить кромку поры на два участка таким образом, что добавление новых участков (с новыми системами координат) не приводит к изменению расчетной величины упругой энергии [25, 26, 33].

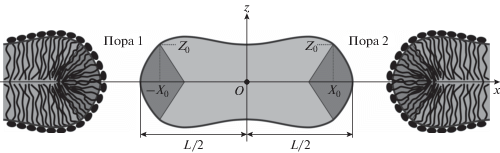
Чтобы задать участки, на которые разбивается кромка поры, рассмотрим горизонтальную мембрану с двумя сквозными порами (рис. 2). Будем считать, что система обладает зеркальной симметрией относительно плоскости межмонослойной поверхности. Для расчета одномерного потенциала взаимодействия пор также будем считать, что в системе имеется трансляционная симметрия вдоль кромки поры. Расстояние между точками пересечения межмонослойной плоскости и нейтральных поверхностей обозначим через L (рис. 2). Введем декартову систему координат Oxyz, начало координат O которой расположено на межмонослойной поверхности посередине между двумя кромками пор; ось Oz направлена перпендикулярно плоскости невозмущенной мембраны; ось Oy параллельна направлению трансляционной симметрии (вдоль кромки поры; на рис. 2 эта ось направлена от читателя), ось Ox перпендикулярна осям Oy и Oz. Каждая кромка разбивается на два участка: 1) “горизонтальный бислойный” участок, в котором директора и нормали к нейтральной поверхности слабо отклоняются от направления оси Oz; 2) “вертикальный монослойный” участок, в котором директора и нормали слабо отклоняются от направления оси Ox. Участки двух кромок сопрягаются вдоль линий {±X0, ±Z0} (рис. 2).

Рис. 2.

Схематическое изображение сечения мембраны плоскостью, перпендикулярной линейным параллельным кромкам двух пор. Горизонтальный бислойный участок мембраны между двух кромок, в котором директора и нормали направлены приблизительно вдоль оси Oz, показан светло-серым цветом. Вертикальные монослойные участки мембраны, в которых директора и нормали слабо отклоняются от направления оси Ox, показаны темно-серым цветом. Вертикальные и горизонтальные участки сопрягаются вдоль линий {±X0, ±Z0}. Расстояние между кромками двух пор L. Ось Oy направлена от читателя.

Горизонтальный бислойный участок. Вследствие трансляционной симметрии системы вдоль оси Oy все величины, относящиеся к горизонтальному бислойному участку, зависят только от координаты x. В этом случае векторные величины можно заменить их проекциями на ось Ox: n → nx = n, N → Nx = N, а дивергенция директора с необходимой точностью равна div(n) ≈ n′(x), где штрих обозначает производную по координате x. Зеркальная симметрия системы относительно межмонослойной поверхности позволяет рассматривать только один монослой бислойного участка, для определенности, верхний. Форму нейтральной поверхности верхнего монослоя будем характеризовать функцией H(x), равной расстоянию от межмонослойной поверхности до нейтральной поверхности монослоя, измеренному вдоль перпендикуляра к межмонослойной поверхности. С требуемой точностью N ≈ grad(H) и, соответственно, Nx = N = H ′. Для горизонтального бислойного участка условие локальной объемной несжимаемости (4) может быть переписано в виде:

(5)
$H = h - \frac{{{{h}^{2}}}}{2}n{\kern 1pt} '\, - h\alpha ,$
где для простоты опущен аргумент x. Проекция вектора наклона на ось Ox равна t = n – N ≈ n – H ′. Выражая относительное растяжение-сжатие α из уравнения (5) и подставляя α, дивергенцию директора div(n) ≈ n′ и проекцию вектора наклона t ≈ n – H ′ в выражение для поверхностной плотности энергии (3), интегрируя по нейтральной поверхности верхнего монослоя, получим функционал энергии горизонтального бислойного участка:
(6)
$\begin{gathered} {{W}_{b}} = 2\int\limits_{ - {{X}_{0}}}^{{{X}_{0}}} {\frac{{{{K}_{t}}}}{2}} \left\{ {{{l}^{2}}{{{\left( {n{\kern 1pt} '\, + {{J}_{0}}} \right)}}^{2}} - {{l}^{2}}J_{0}^{2}} \right. + \\ \left. { + \,\,{{{\left( {n - H{\kern 1pt} '} \right)}}^{2}} + \frac{A}{{{{h}^{2}}}}{{{\left( {h - \frac{{{{h}^{2}}}}{2}n{\kern 1pt} '\, - H} \right)}}^{2}}} \right\}dx, \\ \end{gathered} $
где l 2 = B/Kt, A = KA/Kt. Множитель 2 перед интегралом учитывает два монослоя в составе горизонтального бислойного участка. Вариация этого функционала по функциям n(x) и H(x) приводит к линейной системе дифференциальных уравнений Эйлера–Лагранжа:
(7)
$\left\{ \begin{gathered} \left( {l_{{}}^{2} + \frac{{h_{{}}^{2}A}}{4}} \right)n{\kern 1pt} ''\, - n + \left( {1 + \frac{A}{2}} \right)H{\kern 1pt} '\, = 0 \hfill \\ \left( {1 + \frac{A}{2}} \right)n{\kern 1pt} '\, - H{\kern 1pt} ''\, + \frac{A}{{h_{{}}^{2}}}\left( {H - h} \right) = 0. \hfill \\ \end{gathered} \right.$
Общее решение этих уравнений может быть записано в виде:
(8)
$\begin{gathered} H\left( x \right) = h + {{c}_{1}}{{e}^{{\lambda x}}} + {{c}_{2}}{{e}^{{ - \lambda x}}} + c_{1}^{*}{{e}^{{\lambda {\text{*}}x}}} + c_{2}^{*}{{e}^{{ - \lambda {\text{*}}x}}}, \\ n\left( x \right) = 2{{c}_{1}}\frac{{{{h}^{2}}{{\lambda }^{2}} - A}}{{\lambda {{h}^{2}}\left( {A + 1} \right)}}{{e}^{{\lambda x}}} - 2{{c}_{1}}\frac{{{{h}^{2}}{{\lambda }^{2}} - A}}{{\lambda {{h}^{2}}\left( {A + 1} \right)}}{{e}^{{ - \lambda x}}} + \\ + \,\,2c_{1}^{*}\frac{{{{h}^{2}}{{{\left( {\lambda {\text{*}}} \right)}}^{2}} - A}}{{\lambda {\text{*}}{{h}^{2}}\left( {A + 1} \right)}}{{e}^{{\lambda {\text{*}}x}}} - 2c_{1}^{*}\frac{{{{h}^{2}}{{{\left( {\lambda {\text{*}}} \right)}}^{2}} - A}}{{\lambda {\text{*}}{{h}^{2}}\left( {A + 1} \right)}}{{e}^{{ - \lambda {\text{*}}x}}}, \\ \lambda = \frac{1}{h}\sqrt {\frac{{2A{{l}^{2}} - 2{{h}^{2}}A - 2il\sqrt {4{{h}^{2}}A + {{A}^{2}}\left( {2{{h}^{2}} - {{l}^{2}}} \right)} }}{{{{h}^{2}}A + 4{{l}^{2}}}}} , \\ \end{gathered} $
где звездочка в верхнем индексе обозначает комплексное сопряжение, i – мнимая единица; c1, c2 – комплексные коэффициенты, которые следует определить из граничных условий. Найденное общее решение (8) затем подставляется в функционал энергии (6). Интегрируя по нейтральной поверхности верхнего монослоя, получим аналитическое выражение для энергии деформированного горизонтального бислойного участка. Это выражение очень громоздкое, поэтому здесь не приводится.

Вертикальный монослойный участок. Деформации в системе симметричны по отношению к отражению относительно плоскости x = 0, поэтому мы опишем ниже построение функционала упругой энергии только для одной из кромок, для определенности, правой. Форму нейтральной поверхности вертикального монослойного участка будем характеризовать функцией Hv(z), равной расстоянию от плоскости x = L/2 до нейтральной поверхности вертикального монослоя, измеренному вдоль направления оси Ox. Эта функция также определяет проекцию нормали к нейтральной поверхности, Nv(z), на ось Oz. Проекцию директора на ось Oz обозначим v(z), относительное латеральное растяжение–сжатие нейтральной поверхности – через β(z). Форму поверхности, огибающую концы липидных цепей (поверхность, аналогичную межмонослойной поверхности в случае бислоя), будем описывать функцией M(z), равной расстоянию от плоскости x = L/2 до этой поверхности, измеренному вдоль направления оси Ox. При слабом отклонении директора от направления оси Ox div(n) ≈ v ′, где штрих обозначает производную по координате z. В таких обозначениях функционал упругой энергии может быть записан в следующем виде:

(9)
$\begin{gathered} {{W}_{m}} = 4\int\limits_0^{{{Z}_{0}}} {\sqrt {1 + {{{(H_{{v}}^{{\text{'}}})}}^{2}}} \times } \\ \times \,\,\left\{ {\frac{B}{2}{{{\left( {{v}{\kern 1pt} '\, + {{J}_{0}}} \right)}}^{2}} - \frac{B}{2}J_{0}^{2} + \frac{{{{K}_{t}}}}{2}{{{\left( {{v} - {{N}_{{v}}}} \right)}}^{2}}} \right.\left. { + \frac{{{{K}_{A}}}}{2}{{\beta }^{2}}} \right\}dz. \\ \end{gathered} $
Множитель 4 учитывает, что в системе имеются две симметричные кромки поры, обладающие также зеркальной симметрией относительно межмонослойной поверхности. В этом выражении для простоты опущен аргумент z; штрих обозначает производную по координате z. Заметим, что с необходимой точностью проекция единичной нормали на ось Oz равна Nv = $ - H_{{v}}^{{\text{'}}}$(z). Для вертикального монослойного участка условие локальной объемной несжимаемости (4) может быть записано в виде:
(10)
$M - {{H}_{{v}}} = h - \frac{{{{h}^{2}}}}{2}{v}{\kern 1pt} '\, - h\beta {\kern 1pt} .$
Это условие задействует дополнительную функцию M(z), не входящую явно в функционал энергии (9), и одновременно налагает дополнительную связь на деформации. Таким образом, число независимых функций остается неизменным. Функционал энергии (9) можно минимизировать по функциям β(z), v(z), Hv(z) и их производным (предварительно разложив по малым величинам в ряд Тейлора до второго порядка), не используя условие локальной объемной несжимаемости; это условие может потребоваться для нахождения функции M(z). Минимизируя функционал, получим систему трех линейных дифференциальных уравнений Эйлера–Лагранжа. Общее решение этих уравнений может быть записано в виде:
(11)
$\begin{gathered} \beta \left( z \right) = 0, \\ {v}\left( z \right) = - {{d}_{1}}{{l}^{2}} - {{d}_{1}}\frac{{{{z}^{2}}}}{2} - {{d}_{2}}z - {{d}_{3}}, \\ {{H}_{{v}}}\left( z \right) = {{d}_{1}}\frac{{{{z}^{3}}}}{6} + {{d}_{2}}\frac{{{{z}^{2}}}}{2} + {{d}_{3}}z + {{d}_{4}}, \\ \end{gathered} $
где d1, d2, d3, d4 – вещественные коэффициенты, которые следует определить из граничных условий.

Граничные условия. Решения, полученные для горизонтального бислойного и вертикального монослойного участков, необходимо согласовать на их границах – прямых линиях {±X0, Z0}, – исходя из непрерывности нейтральных поверхностей и директора. В первом порядке по деформациям граничные условия на правой верхней линии сопряжения могут быть записаны в виде:

(12)
$\begin{gathered} H\left( {{{X}_{0}}} \right) = {{Z}_{0}},\,\,\,\,{{H}_{{v}}}\left( {{{Z}_{0}}} \right) = {{X}_{0}}, \\ n\left( {{{X}_{0}}} \right)--{v}\left( {{{Z}_{0}}} \right) = 1. \\ \end{gathered} $
Здесь n – проекция директора на ось Ox, v – проекция директора на ось Oz. Аналогичные условия ставятся на остальных линиях сопряжения участков. Кроме того, необходимо, чтобы все функции были вещественны при любых вещественных значениях z и x. Это налагает условия на мнимые и вещественные части комплексных коэффициентов c1, c2 и d1, d2, d3, d4. Из приведенных условий можно определить часть неопределенных коэффициентов c1, c2 и d1, d2, d3, d4. Остальные коэффициенты находятся из условия минимума полной энергии, которая равна

(13)
$W = {{W}_{b}} + {{W}_{m}}.$

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Полученные результаты проиллюстрируем графически для метастабильных пор, сформированных в мембранах, состоящих из ДОФХ, ПОФХ и димиристоилфосфатидилхолина (ДМФХ). Для ДОФХ экспериментально были определены следующие значения упругих параметров: модуль изгиба B = 10 kBT (kBT ≈ 4 × 10–21 Дж) [23]; модуль латерального растяжения–сжатия KA = 134 мН/м [23]; толщина гидрофобной части монослоя h = = 1.45 нм [23]. Для ПОФХ были измерены следующие величины упругих параметров: модуль изгиба B = 11 kBT [23, 44]; модуль латерального растяжения–сжатия KA = 117 мН/м [23]; толщина гидрофобной части монослоя h = 1.46 нм [23]. Для ДМФХ были экспериментально определены следующие значения упругих параметров: модуль изгиба B = 6.8 kBT [23, 44]; модуль латерального растяжения-сжатия KA = 117 мН/м [23]; толщина гидрофобной части монослоя h = 1.37 нм [23]. Приведенные величины модулей упругости относятся к одному монослою. Модуль наклона считается для всех липидов одинаковым и равным Kt = 40 мН/м (на монослой) [41, 45]. Спонтанная кривизна монослоя не дает вклада в энергию взаимодействия пор, поскольку она не входит в уравнения Эйлера–Лагранжа (см. уравнения (7) и (11)), и при фиксированных граничных директорах соответствующий вклад сводится к постоянному слагаемому, не зависящему от расстояния между порами. Это видно, если раскрыть скобки в выражении (3). Слагаемые, относящиеся к деформации поперечного изгиба, сводятся к $\frac{B}{2}{{\left( {{\text{div}}{\kern 1pt} \left( {\mathbf{n}} \right) + {{J}_{0}}} \right)}^{2}} - \frac{B}{2}J_{0}^{2}$ = $\frac{B}{2}{{\left( {\operatorname{div} \left( {\mathbf{n}} \right)} \right)}^{2}} + B{{J}_{0}}\operatorname{div} \left( {\mathbf{n}} \right)$. Второе слагаемое, содержащее спонтанную кривизну, при последующем интегрировании по нейтральной поверхности сведется к постоянному члену, пропорциональному произведению спонтанной кривизны и граничного директора.

Зависимость энергии двух линейных параллельных кромок пор (в расчете на 1 нм длины вдоль кромки) от расстояния между кромками приведена на рис. 3а для мембран, сформированных из ДОФХ, ПОФХ, ДМФХ. Из рисунка видно, что глобальный минимум упругой энергии достигается при расстоянии между порами L = 4–5 нм. При сближении, L < 4 нм, поры отталкиваются. При увеличении расстояния между кромками 4 нм < L < 8 нм поры притягиваются друг к другу. При расстоянии между кромками L ≈ 12 нм имеется локальный минимум упругой энергии, однако его глубина крайне мала (<0.1 kBT). В целом, можно считать, что поры практически не взаимодействуют друг с другом при расстоянии между их кромками L > L0 ≈ 10 нм. Ранее в ряде работ проводилось численное моделирование пор в мембранах методом молекулярной динамики [31, 32, 46, 47]. В таких расчетах, как правило, используются периодические граничные условия. Из зависимостей энергии от расстояния между кромками пор, представленных на рис. 3а, следует, что для исключения взаимодействия моделируемых методом молекулярной динамики кромок пор с границей расчетной ячейки латеральный размер ячейки должен быть больше, чем (2R + L0) ≈ 16 нм при максимальном радиусе моделируемой поры R ≈ 3 нм.

Рис. 3.

а – Зависимость энергии двух линейных параллельных кромок пор (в расчете на 1 нм длины вдоль кромки) от расстояния между кромками. б – Энергия взаимодействия двух метастабильных пор. Результаты представлены для мембран, сформированных из ДОФХ (сплошные кривые), ПОФХ (штриховые кривые), ДМФХ (пунктирные кривые).

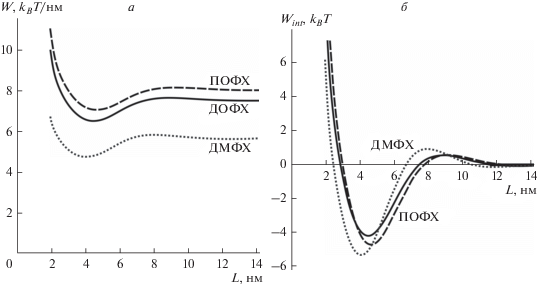
Из графиков рис. 3а видно, что за счет взаимодействия двух оптимально расположенных пор может понижаться погонная энергия частей их кромок. Это эквивалентно понижению линейного натяжения на части периметра поры и, как следствие, среднего линейного натяжения всей кромки поры. Для двух кромок понижение погонной энергии составляет ∼1 kBT/нм (рис. 3а); в силу симметрии понижение линейного натяжения одной кромки поры составляет 0.5 kBT/нм ≈ ≈ 2 пН. Если предположить, что во взаимодейсвтии участвует примерно половина периметра каждой кромки поры, то за счет взаимодействия среднее линейное натяжение кромки поры будет уменьшаться приблизительно на 1 пН. Экстраполируя полученные результаты на случай взаимодействия оптимальным образом расположенных трех пор и предполагая независимость попарных взаимодействий, можно предсказать уменьшение среднего линейного натяжени кромки поры на ∼1.3 пН, считая, что во взаимодействии участвует 2/3 периметра каждой поры.

Для того чтобы определить полную (а не погонную) энергию взаимодействия двух круглых пор, погонную плотность энергии необходимо умножить на эффективную длину взаимодействия Leff ≈ 2R + 2lW, где lW = 1/Re(2λ) ≈ 1 нм – характерная длина затухания плотности упругой энергии (см. выражение (8)) [39]. Из выражения (8) видно, что деформации мембраны на горизонтальном бислойном участке, определяющие взаимодействие двух пор, затухают экспоненциально, что обеспечивает применимость приближения Дерягина. Энергию взаимодействия Wint нормируем (сдвинем на константу) таким образом, чтобы она была равна нулю для двух бесконечно удаленных пор. В качестве радиуса поры R используем радиус Rm, соответствующий локальному минимуму энергии поры, т.е. ее метастабильному состоянию (см. рис. 1а). Ранее в работах [25, 26] было показано, что в случае мембраны, сформированной из ДОФХ, Rm ≈ 1.1 нм, для ПОФХ – Rm ≈ 1.4 нм, для ДМФХ – Rm = 1.9 нм, т.е. эффективные длины взаимодействия пор для этих мембран составляют Leff ≈ 4.2, 4.8, 5.8 нм соответственно. Зависимости энергии взаимодействия пор, рассчитанные для этих трех липидов, представлены на рис. 3б. Из рисунка видно, что за счет оптимального расположения двух пор их энергия может понижаться на 4–5 kBT по сравнению с суммарной энергией двух изолированных пор. В силу симметрии системы можно считать, что энергия каждой поры уменьшается на половину этой величины, т.е. на 2–2.5 kBT. В предположении, что высота энергетического барьера на закрытие поры не изменяется при взаимодействии, такое понижение энергии метастабильных пор должно приводить к увеличению их времени жизни в ∼e2–2.5 ≈ 7.5–12 раз. Экстраполируя полученные результаты на случай взаимодействия оптимальным образом расположенных трех пор и предполагая независимость попарных взаимодействий, можно предсказать увеличение времени жизни метастабильных пор до ∼e5 ≈ 150 раз (выигрыш в энергии за счет взаимодействия по ∼5 kBT на каждую пару пор, которых всего 3 пары, т.е. в среднем по 5 kBT на каждую пору, что дает увеличение времени жизни в ∼e5 раз). Аналогично, для семи пор, расположенных в вершинах и центре правильного шестиугольника с оптимальной длиной стороны, увеличение времени жизни может составлять ∼e8.57 ≈ 5250 раз (выигрыш в энергии за счет взаимодействия по ∼5 kBT на каждую пару пор, которых всего 12 пар, что дает в сумме 5 kBT × 12 пар = 60 kBT, т.е. в среднем по 60/7 ≈ 8.57 kBT на каждую пору, что дает увеличение времени жизни в ∼e8.57 раз) в предположении о независимости попарных взаимодействий пор.

Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации, а также при частичной финансовой поддержке Российского фонда фундаментальных исследований (гранты № 17-04-02070 и № 18-54-74 001).

Список литературы

  1. Davis H.T. 1996. Statistical mechanics of phases, interfaces, and thin films. New York: Wiley-VCH.

  2. Cass A., Finkelstein A. 1967. Water permeability of thin lipid membranes. J. Gen. Physiol. 50, 1765–1784.

  3. Peterlin P., Arrigler V., Diamant H., Haleva E. 2012. Permeability of phospholipid membrane for small polar molecules determined from osmotic swelling of giant phospholipid vesicles. Advances in planar lipid bilayers and liposomes. 16, 301–335.

  4. Nicholls D. 2013. Bioenergetics. 4th edn. Amsterdam: Acad. Press. 434 p.

  5. Renault T.T., Floros K.V., Elkholi R., Corrigan K.A., Kushnareva Y., Wieder S.Y., Lindtner C., Serasinghe M.N., Asciolla J.J., Buettner C., Newmeyer D.D., Chipuk J.E. 2015. Mitochondrial shape governs BAX-induced membrane permeabilization and apoptosis. Mol. Cell. 57, 69–82.

  6. Basañez G., Sharpe J.C., Galanis J., Brandt T.B., Hardwick J.M., Zimmerberg J. 2002. BAX-type apoptotic proteins porate pure lipid bilayers through a mechanism sensitive to intrinsic monolayer curvature. J. Biol. Chem. 277, 49360–49365.

  7. Li C., Salditt T. 2006. Structure of magainin and alamethicin in model membranes studied by X-ray reflectivity. Biophys. J. 91, 3285–3300.

  8. Sychev S.V., Balandin S.V., Panteleev P.V., Barsukov L.I., Ovchinnikova T.V. 2015. Lipid-dependent pore formation by antimicrobial peptides arenicin-2 and melittin demonstrated by their proton transfer activity. J. Pept. Sci. 21, 71–76.

  9. Karal M.A.S., Alam J.M., Takahashi T., Levadny V., Yamazaki M. 2015. Stretch-activated pore of the antimicrobial peptide, magainin 2. Langmuir 31, 3391–3401.

  10. Cervia L.D., Chang C.C., Wang L., Mao M., Yuan F. 2018. Enhancing electrotransfection efficiency through improvement in nuclear entry of plasmid DNA. Mol. Ther. Nucleic Acids 11, 263–271.

  11. Pavlin M., Kandušer M. 2015. New insights into the mechanisms of gene electrotransfer–experimental and theoretical analysis. Sci. Rep. 5, 9132.

  12. Карпунин Д.В., Акимов С.А., Фролов В.А. 2005. Формирование пор в плоских липидных мембранах, содержащих лизолипиды и холестерин. Биол. мембраны. 22, 429–432.

  13. Bruen D., Delaney C., Florea L., Diamond D. 2017. Glucose sensing for diabetes monitoring: Recent developments. Sensors. 17, 1866.

  14. Evans E., Smith B.A. 2011. Kinetics of hole nucleation in biomembrane rupture. New J. Phys. 13, 095010.

  15. Karal M.A.S., Yamazaki M. 2015. Communication: Activation energy of tension-induced pore formation in lipid membranes. J. Chem. Phys. 143, 081103.

  16. Karal M.A.S., Levadnyy V., Yamazaki M. 2016. Analysis of constant tension-induced rupture of lipid membranes using activation energy. Phys. Chem. Chem. Phys. 18, 13487–13495.

  17. Evans E., Heinrich V., Ludwig F., Rawicz W. 2003. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 85, 2342–2350.

  18. Melikov K.C., Frolov V.A., Shcherbakov A., Samsonov A.V., Chizmadzhev Y.A., Chernomordik L.V. 2001. Voltage-induced nonconductive pre-pores and metastable single pores in unmodified planar lipid bilayer. Biophys. J. 80, 1829–1836.

  19. Abidor I.G., Arakelyan V.B., Chernomordik L.V., Chizmadzhev Y.A., Pastushenko V.F., Tarasevich M.R. 1979. Electric breakdown of bilayer lipid membranes I. The main experimental facts and their qualitative discussion. J. Electroanal. Chem. 104, 37–52.

  20. Панов П.В., Акимов С.А., Батищев О.В. 2014. Изопреноидные цепи липидов повышают устойчивость мембран к формированию сквозных пор. Биол. мембраны. 31, 331–335.

  21. Derjaguin B.V. 1989. Theory of stability of colloids and thin films. Springer US. 258 p. ISBN 978-0-306-11022-1.

  22. Portet T., Dimova R. 2010. A new method for measuring edge tensions and stability of lipid bilayers: Effect of membrane composition. Biophys. J. 99, 3264–3273.

  23. Rawicz W., Olbrich K.C., McIntosh T., Needham D., Evans E. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339.

  24. Helfrich W. 1973. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforsch. C 28, 693–703.

  25. Akimov S.A., Volynsky P.E., Galimzyanov T.R., Kuzmin P.I., Pavlov K.V., Batishchev O.V. 2017. Pore formation in lipid membrane I: Continuous reversible trajectory from intact bilayer through hydrophobic defect to transversal pore. Sci. Rep. 7, 12152.

  26. Akimov S.A., Volynsky P.E., Galimzyanov T.R., Kuzmin P.I., Pavlov K.V., Batishchev O.V. 2017. Pore formation in lipid membrane II: Energy landscape under external stress. Sci. Rep. 7, 12509.

  27. Маркин В.С., Козлов М.М. 1985. Статистика пор в бислойных липидных мембранах. Биол. мембраны. 2, 205–223.

  28. Pastushenko V.F., Chizmadzhev Y.A., Arakelyan V.B. 1979. Electric breakdown of bilayer lipid membranes II. Calculation of the membrane lifetime in the steady-state diffusion approximation. J. Electroanal. Chem. 104, 37–52.

  29. Weaver J.C., Chizmadzhev Y.A. 1996. Theory of electroporation: A review. Bioelectrochem. Bioenerg. 41, 135–160.

  30. Лифшиц Е.М., Ландау Л.Д., Питаевский Л.П. 2002. Курс теоретической физики. Т. 10. Физическая кинетика. Под ред. Питаевского Л.П. М.: Физматлит.

  31. Awasthi N., Hub J.S. 2016. Simulations of pore formation in lipid membranes: reaction coordinates, convergence, hysteresis, and finite-size effects. J. Chem. Theory Comput. 12, 3261–3269.

  32. Kirsch S.A., Böckmann R.A. 2016. Membrane pore formation in atomistic and coarse-grained simulations. Biochim. Biophys. Acta. 1858, 2266–2277.

  33. Молотковский Р.Ю., Акимов С.А. 2009. Расчет линейного натяжения в различных моделях кромки поры в липидном бислое. Биол. мембраны. 26, 149–158.

  34. Галимзянов Т.Р., Молотковский Р.Ю., Кузьмин П.И., Акимов С.А. 2011. Стабилизация бислойной структуры рафтов за счет упругих деформаций мембраны. Биол. мембраны. 28, 307–314.

  35. Akimov S.A., Frolov V.A., Kuzmin P.I., Zimmerberg J., Chizmadzhev Y.A., Cohen F.S. 2008. Domain formation in membranes caused by lipid wetting of protein. Phys. Rev. E. 77, 051901.

  36. Galimzyanov T.R., Molotkovsky R.J., Kheyfets B.B., Akimov S.A. 2013. Energy of the interaction between membrane lipid domains calculated from splay and tilt deformations. JETP Lett. 96, 681–686.

  37. Акимов С.А., Александрова В.В., Галимзянов Т.Р., Батищев О.В. 2017. Взаимодействие амфипатических пептидов, опосредованное упругими деформациями мембраны. Биол. мембраны. 34, 162–173.

  38. Kondrashov O.V., Galimzyanov T.R., Pavlov K.V., Kotova E.A., Antonenko Y.N., Akimov S.A. 2018. Membrane elastic deformations modulate gramicidin A transbilayer dimerization and lateral clustering. Biophys. J. 115, 478–493.

  39. Kondrashov O.V., Galimzyanov T.R., Jiménez-Munguía I., Batishchev O.V., Akimov S.A. 2019. Membrane-mediated interaction of amphipathic peptides can be described by a one-dimensional approach. Phys. Rev. E. 99, 022401.

  40. Israelachvili J. 2011. Intermolecular and surface forces. New York: Academic Press.

  41. Hamm M., Kozlov M.M. 2000. Elastic energy of tilt and bending of fluid membranes. Eur. Phys. J. E. 3, 323–335.

  42. Leikin S., Kozlov M.M., Fuller N.L., Rand R.P. 1996. Measured effects of diacylglycerol on structural and elastic properties of phospholipid membranes. Biophys. J. 71, 2623–2632.

  43. Nagle J.F., Wilkinson D.A. 1978. Lecithin bilayers. Density measurement and molecular interactions. Biophys. J. 23, 159–175.

  44. Dimova R. 2014. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 208, 225–234.

  45. Hamm M., Kozlov M.M. 1998. Tilt model of inverted amphiphilic mesophase. Eur. Phys. J. B. 6, 519–528.

  46. Bennett W.D., Sapay N., Tieleman D.P. 2014. Atomistic simulations of pore formation and closure in lipid bilayers. Biophys. J. 106, 210–219.

  47. Wohlert J., den Otter W.K., Edholm O., Briels W.J. 2006. Free energy of a trans-membrane pore calculated from atomistic molecular dynamics simulations. J. Chem. Phys. 124, 154905.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Биологические мембраны: Журнал мембранной и клеточной биологии

Архивы выпусков Информация о журнале Отправить рукопись в журнал