Доклады Российской академии наук. Физика, технические науки, 2020, T. 491, № 1, стр. 52-57

ПОСТАНОВКА ЗАДАЧИ

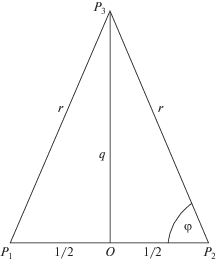
Рассмотрим движение трех материальных точек ${{P}_{i}}$ ($i = 1,2,3$), притягивающихся по закону Ньютона. Массы точек ${{P}_{1}}$ и ${{P}_{2}}$ предполагаем равными (${{M}_{1}} = {{M}_{2}} = M$), а массу третьей точки ${{P}_{3}}$ считаем настолько малой по сравнению с M, что ее влиянием на движение точек ${{P}_{1}}$ и ${{P}_{2}}$ можно пренебречь. Будем предполагать, что точки ${{P}_{1}}$ и ${{P}_{2}}$ движутся по круговым орбитам вокруг их общего центра масс O. Угловая скорость $\Omega $ при таком движении равна $\frac{{\sqrt {2\gamma M} }}{{{{\ell }^{{3/2}}}}}$, где $\gamma $ – универсальная гравитационная постоянная, а $\ell $ – диаметр окружности, по которой движутся точки ${{P}_{1}}$ и ${{P}_{2}}$. Задача о движении точки ${{P}_{3}}$ под действием притяжения точек ${{P}_{1}}$ и ${{P}_{2}}$ допускает частное решение, для которого точка ${{P}_{3}}$ движется по прямой, перпендикулярной плоскости, в которой движутся точки ${{P}_{1}}$ и ${{P}_{2}}$, и проходящей через центр масс $O$ этих точек [1, 2].

За координату, задающую положение точки ${{P}_{3}}$ на ее прямолинейной траектории, примем (см. рис. 1) величину $q$ ($ - \infty < q < \infty $, $\ell \left| q \right|{\text{ }}$ – расстояние от точки ${{P}_{3}}$ до точки O).

В качестве независимой переменной, вместо времени t, возьмем безразмерную величину $\nu = \Omega t$. Движение точки ${{P}_{3}}$ описывается системой двух канонических дифференциальных уравнений

с функцией Гамильтона

Уравнения (1) допускают интеграл энергии

Движение системы с функцией Гамильтона (2) подробно изучено [1–5]. В частности показано, что при h = –2 точка ${{P}_{3}}$ находится в устойчивом положении равновесия q = 0, совпадающем с центром масс O точек ${{P}_{1}}$ и ${{P}_{2}}$, а при $ - 2 < h < 0$ точка ${{P}_{3}}$ совершает периодические колебания в окрестности равновесия. При этом $ - {{q}_{{\max }}} < q$ < < q_max, где ${{q}_{{\max }}}$ – максимальное отклонение точки ${{P}_{3}}$ от положения равновесия:

Здесь φ_max – максимальное значение угла φ, который составляет отрезок ${{P}_{3}}{{P}_{2}}$ с отрезком ${{P}_{1}}{{P}_{2}}$ (рис. 1). Очевидно, что $0 < {{\varphi }_{{\max }}} < \pi {\text{/}}2$, поэтому

Постоянная h интеграла энергии (3) выражается через k по формуле

Значения $h \geqslant 0$ отвечают неограниченным движением точки ${{P}_{3}}$.

Работа посвящена случаю колебаний, когда выполняется условие (5). Основная цель состоит в нахождении переменных действие–угол I, w. Для случая нелинейных колебаний с амплитудой, малой по сравнению с расстоянием между точками ${{P}_{1}}$ и ${{P}_{2}}$, замена переменных $q,p \to w,I$получена в виде сходящихся рядов по параметру k ($0 < k \ll 1$). Найдено также выражение для функции Гамильтона через переменную I в случае больших амплитуд колебаний, когда $0 < \mu \ll 1$, где

Ограниченной задаче трех точек в случае равных масс точек ${{P}_{1}}$ и ${{P}_{2}}$ в последние десятилетия уделялось очень большое внимание. Особенно много работ появилось после публикации статьи [6], в которой рассматривался случай эллиптической ограниченной задачи и показано существование движений, для которых величина $\left| {q(t)} \right|$ принимает сколь угодно большие значения как при q > 0, так и при q < 0, но не имеет предела при $t \to \infty $ (осциллирующие движения точки ${{P}_{3}}$). К настоящему времени весьма подробно исследована задача о существовании, устойчивости и бифуркациях периодических движений (не только прямолинейных, но и произвольных пространственных) в круговой и эллиптической задачах, дан анализ возможности возникновения хаотических движений, рассмотрены обобщения классической задачи на случай, учитывающий световое давление, а также на случай, когда количество точек конечных масс больше двух. Обширная библиография упомянутых исследований содержится в публикациях [5–12].

ПРЕОБРАЗОВАНИЕ ФУНКЦИИ ГАМИЛЬТОНА. ВЫЧИСЛЕНИЕ ПЕРЕМЕННОЙ ДЕЙСТВИЕ

При помощи канонических преобразований приведем функцию Гамильтона (2) к форме, более удобной для целей нашего исследования. Первое преобразование $q,p \to \varphi ,{{p}_{\varphi }}$ задается равенствами (смысл угла $\varphi $ виден из рис. 1)

Второе преобразование $\varphi ,{{p}_{\varphi }} \to x,{{p}_{x}}$ задается формулами

в которых величина k определена равенствами (4). В переменных x, p_x функция (2) записывается в виде

Из интеграла (3) следует, что

В плоскости x, p_x фазовые траектории являются замкнутыми кривыми, окружающими точку x = 0, ${{p}_{x}} = 0$ и симметричными относительно осей $x$ и p_x. Величина $x$ меняется в интервале (–1, 1), величина же |p_x| может быть сколь угодно большой, если значение параметра $k$ близко к $\frac{{\sqrt 2 }}{2}$.

Переменная действие I равняется поделенной на $2\pi $ площади, заключенной внутри фазовой траектории. Ввиду упомянутой симметрии и при учете выражения (11) имеем

Интеграл в (12) можно выразить через полные эллиптические интегралы 1-го, 2-го и 3-го родов. Получим

Здесь и далее используются общепринятые [13–15] обозначения для эллиптических интегралов и функций.

Функция (13) имеет обратную, так как $\frac{{\partial I}}{{\partial k}} \ne 0$. Действительно, воспользовавшись известными правилами дифференцирования полных эллиптических интегралов [14], из (13) получаем

При выполнении неравенства (5) $\Pi (2{{k}^{2}},k) > 0$, а $2E(k) > K(k)$. Поэтому $\frac{{\partial I}}{{\partial k}} > 0$.

Функция Гамильтона зависит только от одной переменной I:

где $k = k(I)$ – функция, обратная функции $I(k)$ из (13). Частота колебаний $\omega $ вычисляется согласно равенствам

В переменных действие–угол I, w исходные уравнения движения (1) записываются в виде

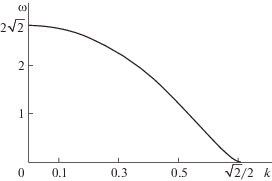
Частота (16) является монотонно убывающей функцией параметра k. При $0 < k < \frac{{\sqrt 2 }}{2}$ она удовлетворяет неравенству $0 < \omega < 2\sqrt 2 $. Наибольшее значение $\omega $ отвечает малым линейным колебаниям (0 < $k \ll 1$), при возрастании k частота убывает и при $k \to \frac{{\sqrt 2 }}{2}$ стремится к нулю. График функции $\omega (k)$ приведен на рис. 2.

ЗАМЕНА ПЕРЕМЕННЫХ $q,p \to w,I$

Сделаем еще одно каноническое преобразование $x,{{p}_{x}} \to u,{{p}_{u}}$ по формулам

Функция Гамильтона (10) принимает вид

Из интеграла энергии (3) следует, что

Отсюда и из уравнения $\frac{{du}}{{d\nu }} = \frac{{\partial H}}{{\partial {{p}_{u}}}}$ получаем

Без ограничения общности будем считать, что при $\nu = 0$ выполнены условия q = 0, $p = 2\sqrt 2 k$. Тогда при ν = 0 имеем φ = 0, ${{p}_{\varphi }} = \sqrt 2 k$; x = 0, p_x = = $2\sqrt 2 {{k}^{2}}$; u = 0, ${{p}_{u}} = 2\sqrt 2 {{k}^{2}}$. Из замен переменных (8), (9), (18) следуют равенства

Полагая, что при $\nu = 0$ переменная $w$ равна нулю, и опираясь на уравнения (17) и (21), получаем следующую зависимость между переменными $u$ и $w$:

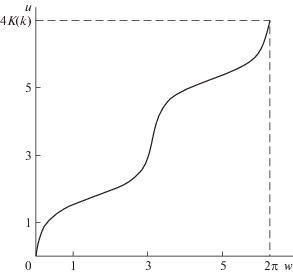
Несложно убедиться, что (помимо очевидного равенства $w(0,k) = 0$) справедливо равенство $w(4K(k),k)$ = 2π. На рис. 3 показана зависимость получаемой из (23) функции $u = u(w,k)$ от $w$ для случая k = 0.6.

Справедлива следующая

Теорема. При помощи $2\pi $-периодического по $w$ унивалентного канонического преобразования, задаваемого равенствами (22), в которых величина $u$ выражается через $w$ посредством равенства (23), функция Гамильтона (2) приводится к виду (15), отвечающему переменным действие–угол $I,w$; величина $\omega $ определяется по формуле (16), а k выражается через I согласно равенству (13).

Доказательство теоремы сразу следует из проведенных выше вычислений. Надо только показать, что замена переменных $q,p \to w,I$, определяемая равенствами (22), (23), является унивалентным каноническим преобразованием. Для этого достаточно убедиться, что якобиан функций $q$, $p$ по переменным $w$, I равняется единице:

Но левую часть равенства (24) можно представить в виде произведения двух якобианов

Воспользовавшись теперь известными правилами дифференцирования эллиптических функций Якоби по аргументу $u$ и модулю $k$ и приняв во внимание, что $\frac{{\partial k}}{{\partial w}} = 0$, придем к соотношению

из которого следует справедливость равенства (24).

Замечание 1. Нетрудно проверить, что функции (23) являются решениями следующей (негамильтоновой) системы уравнений:

c начальными условиями $q(0) = 0$, $p(0) = 2\sqrt 2 k$.

Замечание 2. Если при помощи первого из уравнений (17) перейти к независимой переменной $w$, то исходные уравнения (1) запишутся в виде

Решение $q = q(w,k)$, $p = p(w,k)$ этих уравнений с начальными условиями $q(0,k) = 0$, $p(0,k) = 2\sqrt[{}]{2}k$ задает описанное выше 2π-периодическое по $w$ каноническое преобразование $q,p \to w,I$, вводящее переменные действие–угол.

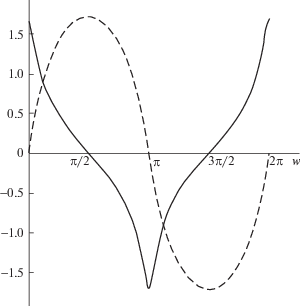
На рис. 4 показаны графики функций q = = $q(w,k)$ и $p = p(w,k)$для случая k = 0.6.

О ЗАМЕНЕ $q,p \to w,I$ В СЛУЧАЕ МАЛЫХ КОЛЕБАНИЙ $(0 < k \ll 1)$

При малых $k$ частота колебаний (16) представима сходящимся рядом вида

Из (23) и (27) можно найти функцию $u = u(w,k)$, обратную $w$, в виде ряда по степеням k. Подставив эту функцию в (22), найдем, что разложение для переменной q имеет следующую структуру:

где ${{c}_{{2(n + m) - 1}}}$ – не зависящие от k и $w$ числовые коэффициенты. Если разложение (28) найдено, то разложение для p легко получается из (27) и первого из уравнений (26).

С погрешностью порядка ${{k}^{{11}}}$ разложение (28) имеет вид

Из (13) следует, что величина k представима в виде ряда по полуцелым степеням переменной действие:

Функция Гамильтона (15), выраженная через переменную I, имеет вид

О СЛУЧАЕ КОЛЕБАНИЙ БОЛЬШОЙ АМПЛИТУДЫ

Пусть величина $k$ близка к $\frac{{\sqrt 2 }}{2}$. Тогда параметр $\mu $, задаваемый равенством (7), мал ($0 < \mu \ll 1$). Величина интеграла $\Pi (2{{k}^{2}},k)$ при значениях $k$, близких $\frac{{\sqrt 2 }}{2}$, имеет порядок ${{\mu }^{{ - 1}}}$ [14]. Проведя несколько громоздкие вычисления, для него можно найти такое асимптотическое представление:

где введено обозначение $a = K\left( {\frac{{\sqrt 2 }}{2}} \right)$.

Для частоты колебаний (16) и переменной действие (13) при малых $\mu $ справедливы разложения

а функция Гамильтона (15) представима в виде ряда по отрицательным степеням $I$: