Доклады Российской академии наук. Физика, технические науки, 2020, T. 491, № 1, стр. 18-23
ИСПОЛЬЗОВАНИЕ ГРАФЕНОВЫХ КОМПОЗИТОВ ДЛЯ ДОПОЛНИТЕЛЬНОГО ДЕМПФИРОВАНИЯ КОЛЕБАНИЙ SMART-СТРУКТУР НА ОСНОВЕ ПЬЕЗОЭЛЕМЕНТОВ
Академик РАН В. П. Матвеенко 1, Д. А. Ошмарин 1, Н. А. Юрлова 1, *
1 Институт механики сплошных сред
Уральского отделения Российской академии наук
Пермь, Россия
* E-mail: yurlova@icmm.ru
Поступила в редакцию 20.01.2020
После доработки 27.02.2020
Принята к публикации 28.02.2020
Аннотация
Рассматривается вариант smart-структуры, представляющей собой кусочно-однородное тело, состоящее из упругих, вязкоупругих материалов, а также пьезоэлементов, к электродированным поверхностям которых могут быть присоединены шунтирующие цепи. В качестве одной из основных задач для таких структур рассматривается демпфирование колебаний. Содержание работы связано с вариантом использования в шунтирующей цепи вместо классического резистора графенового композита, который в smart-структуре является не только механическим деформируемым телом, но и выполняет роль резистора. Приводится математическая постановка задачи о вынужденных установившихся колебаниях и собственных колебаниях конструкций, состоящих из упругих и вязкоупругих элементов, пьезоэлементов и графеновых композитов, выполняющих роль деформируемого тела и резистора. Результаты численных экспериментов демонстрируют использование графеновых композитов для реализации дополнительного механизма демпфирования колебаний smart-структур на основе пьезоэлементов.
ВВЕДЕНИЕ
В общем случае smart-материалы обладают способностью фиксировать и изменять свои характеристики в зависимости от состояния окружающей среды [1]. Реализация этих задач достигается при наличии в smart-материалах, или, что точнее, в smart-структурах, элементов, выполняющих функции сенсоров, актуаторов и процессоров, устанавливающих заданные связи между сенсорами и актуаторами. В многообразии smart-структур возможны варианты с различными комбинациями этих элементов и, соответственно, с частично выполняющими перечисленные задачи [2].
Следует отметить в последние два-три десятилетия почти экспоненциальный рост числа публикаций, посвященных различным аспектам smart-структур и их практическим приложениям. Для smart-структур, у которых основные параметры связаны с их механическим поведением, наибольшее распространение в качестве сенсоров получили пьезоэлектрические и оптоволоконные датчики, а в качестве актуаторов используются элементы, обладающие памятью формы, пьезоэлектрическими, магнитореологическими, электрореологическими, термоупругими свойствами.
В работе рассматриваются smart-структуры на основе пьезоэлементов. Следует отметить, что компонентная база для таких smart-структур быстро развивается. В настоящее время число материалов, обладающих пьезоэффектом, более полутора тысяч [3]. Для smart-структур на основе пьезоэлементов появляется дополнительная возможность управления их динамическим поведением, связанная с подключением к электродированным поверхностям пьезоэлементов шунтирующих электрических цепей, состоящих из резистивных, емкостных и индуктивных элементов. В таких системах электрический потенциал с пьезоэлементов рассеивается в шунтирующих цепях в виде тепла или электромагнитного излучения, а элементы шунтирующей цепи являются механическими аналогами дополнительной массы, упругости, вязкости. Возможность использования в smart-структурах шунтирующих электрических цепей стимулирует развитие соответствующей элементной базы для выполнения резистивных, емкостных и индуктивных свойств.
Анализ информации о графеновых композитах [4, 5] позволяет сделать заключение, что механическое поведение этих композитов может быть описано моделью упругого или вязкоупругого тела. При этом элементы из этих материалов могут выполнять роль резистора.
Основное содержание настоящего сообщения связано с предложением использования графеновых композитов одновременно в качестве конструкционного материала и резистора.
МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧ О КОЛЕБАНИЯХ ДЕФОРМИРУЕМЫХ ТЕЛ С ЭЛЕМЕНТАМИ ИЗ ПЬЕЗОМАТЕРИАЛОВ И РЕЗИСТОРАМИ
Для математической постановки задач о колебаниях деформируемых тел с пьезоэлементами используется вариационное уравнение движения деформируемого тела, элементы которого проявляют пьезоэффект [6, 7]
(1)
$\begin{gathered} \sum\limits_{k = 1}^N {\left( {\int\limits_{V_{1}^{k}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} + {{\rho }_{k}}{{{\ddot {u}}}_{{_{i}}}}\delta {{u}_{i}}} \right)\,} dV} \right)} + \\ + \;\int\limits_{{{V}_{2}}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} - {{D}_{i}}\delta {{E}_{i}} + \rho {{{\ddot {u}}}_{i}}\delta {{u}_{i}}} \right)} \,dV = \\ = \int\limits_{{{S}_{\sigma }}} {{{p}_{i}}\delta {{u}_{i}}dS + \int\limits_{{{S}_{p}}} {{{q}_{e}}\delta \varphi dS} } . \\ \end{gathered} $Здесь ${{V}_{1}} = \sum\limits_k^N {V_{1}^{k}} $ – часть объема кусочно-однородного тела $V = {{V}_{1}} + {{V}_{2}}$, состоящая из однородных упругих или вязкоупругих элементов, V2 – объем элемента, обладающего пьезоэлектрическими свойствами; ${{D}_{i}}$, ${{E}_{i}}$ – компоненты вектора электрической индукции и напряженности электрического поля; σij – компоненты симметричного тензора напряжений Коши, ${{\varepsilon }_{{ij}}}$ – компоненты тензора линейных деформаций, ${{u}_{i}}$ – компоненты вектора перемещений, ${{\rho }_{k}}$ – удельная плотность материала k-й составляющей кусочно-однородного тела $V_{1}^{k}$, $\rho $ – удельная плотность пьезоэлектрического материала, ${{S}_{\sigma }}$ – часть поверхности тела объемом V2, на которой заданы поверхностные усилия ${{p}_{i}}$, ${{S}_{p}}$ – поверхность пьезоэлектрического тела объемом V2, ${{q}_{e}}$ – поверхностная плотность свободных зарядов, $\varphi $ – электрический потенциал.
Для электрического поля выполняется условие потенциальности
Для рассматриваемого тела принимаются следующие физические соотношения:
для упругих элементов объема ${{V}_{1}}$
(3)
${{\sigma }_{{ij}}} - \sigma {{\delta }_{{ij}}} = 2{{G}_{k}}\left( {{{\varepsilon }_{{ij}}} - \frac{1}{3}\vartheta {{\delta }_{{ij}}}} \right),\quad \sigma = {{B}_{k}}\vartheta ,$(4)
$\begin{gathered} {{s}_{{ij}}} = 2G_{k}^{0}\left( {{{e}_{{ij}}} - \int\limits_0^t {{{R}_{k}}(t - \tau ){{e}_{{ij}}}(\tau )d\tau } } \right), \hfill \\ \sigma = B_{k}^{0}\left( {\vartheta - \int\limits_0^t {{{U}_{k}}\left( {t - \tau } \right)\vartheta \left( \tau \right)d\tau } } \right), \hfill \\ \end{gathered} $(5)
$\begin{gathered} {{\sigma }_{{ij}}} = {{C}_{{ijkl}}}{{\varepsilon }_{{kl}}} - {{\beta }_{{ijk}}}{{E}_{k}}, \\ {{D}_{k}} = {{\beta }_{{ijk}}}{{\varepsilon }_{{ij}}} + {{э}_{{ki}}}{{E}_{i}}. \\ \end{gathered} $Здесь ${{G}_{k}}$, ${{B}_{k}}$ – упругие сдвиговые и объемные модули, $G_{k}^{0}$, $B_{k}^{0}$ – мгновенные сдвиговые и объемные модули, ${{R}_{k}}$, ${{U}_{k}}$ – ядра релаксации, $\sigma $ – среднее напряжение, $\vartheta $ – объемная деформация, ${{s}_{{ij}}}$, ${{e}_{{ij}}}$ – компоненты девиаторов тензоров напряжений и деформаций, ${{C}_{{ijkl}}}$ – компоненты тензора упругих констант пьезоэлемента, ${{\beta }_{{ijk}}}$ и ${{э}_{{ki}}}$ – компоненты тензоров пьезоэлектрических и диэлектрических коэффициентов.
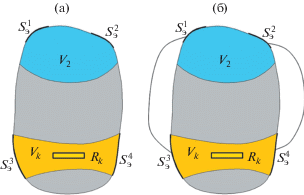
В рассматриваемой задаче отдельные элементы объема V1 могут быть выполнены из графеновых композитов, которые наряду с механическими свойствами, которые описываются соотношениями (3) или (4), обладают электрической проводимостью и, следовательно, могут выполнять дополнительно роль резистора. В этом случае при наличии электродированных поверхностей $(S_{ \mathrel\backepsilon }^{i})$ у элемента из графенового композита $\left( {{{V}_{k}}} \right)$ (рис. 1а), последний дополнительно к деформационным свойствам будет выполнять роль резистора ${{R}_{k}}$, а при соединении проводником (рис. 1б) электродированных поверхностей пьезоэлемента ($S_{ \mathrel\backepsilon }^{1}$, $S_{ \mathrel\backepsilon }^{2}$) с электродированными поверхностями элемента из графенового композита ($S_{ \mathrel\backepsilon }^{3}$, $S_{ \mathrel\backepsilon }^{4}$) систему следует рассматривать как электродеформируемое тело из упругих и вязкоупругих элементов с резистором.
Рис. 1.
Кусочно-однородное тело с элементами, обладающими пьезоэлектрическими свойствами (V2), элементами из графенового композита (Vk) и электродированными поверхностями ($S_{ \mathrel\backepsilon }^{1}$, $S_{ \mathrel\backepsilon }^{2}$, $S_{ \mathrel\backepsilon }^{3}$, $S_{ \mathrel\backepsilon }^{4}$).
При наличии такого резистора в уравнении (1) должно быть добавлено слагаемое $\delta {{A}_{R}}$, учитывающее работу электрического поля с разностью потенциалов Δφ по перемещению заряда q на сопротивлении R:
(6)
$\Delta {{\varphi }_{R}} = \varphi _{1}^{R} - \varphi _{2}^{R},\quad \delta {{A}_{R}} = \frac{1}{R}\int {(\varphi _{1}^{R} - \varphi _{2}^{R})} \delta \varphi dt.$Здесь $\varphi _{1}^{R}$, $\varphi _{2}^{R}$ – электрические потенциалы на электродированных поверхностях пьезоэлемента.
С учетом выражения (6) вариационное уравнение движения электровязкопругого тела с резистором записывается в следующем виде [9]:
(7)
$\begin{gathered} \sum\limits_{k = 1}^N {\left( {\int\limits_{V_{1}^{k}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} + {{\rho }_{k}}{{{\ddot {u}}}_{i}}\delta {{u}_{i}}} \right)} dV} \right)} + \\ + \;\int\limits_{{{V}_{2}}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} - {{D}_{i}}\delta {{E}_{i}} + \rho {{{\ddot {u}}}_{i}}\delta {{u}_{i}}} \right)} dV - \\ - \;\int\limits_{{{S}_{\sigma }}} {{{p}_{i}}\delta {{u}_{i}}dS} - \int\limits_{{{S}_{p}}} {{{q}_{e}}\delta \varphi dS} + \\ + \;\sum\limits_{q = 1}^{{{n}_{R}}} {\frac{1}{{{{R}_{q}}}}\int {(\varphi _{1}^{{{{R}_{q}}}} - \varphi _{2}^{{{{R}_{q}}}})} \delta \varphi dt} = 0. \\ \end{gathered} $Здесь nR – количество реализованных в системе резисторов.
Оценка диссипативных свойств в рассматриваемых системах проводится на основе величин амплитудных значений перемещений для резонансных режимов при вынужденных установившихся колебаниях или по скорости затухания соответствующей моды при собственных колебаниях.
Решение задачи о вынужденных установившихся колебаниях отыскивается в форме [9]
(8)
${{u}_{i}}\left( {x,t} \right) = {{\bar {U}}_{i}}\left( x \right){{e}^{{ipt}}},\quad {{\varphi }_{i}}\left( {x,t} \right) = {{\bar {\varphi }}_{i}}\left( x \right){{e}^{{ipt}}},$Характеристикой скорости затухания колебаний является мнимая составляющая комплексной собственной частоты колебаний [8, 10]. В задаче о собственных колебаниях при однородных граничных условиях решение принимается как
(9)
${{u}_{i}}\left( {x,t} \right) = {{\bar {u}}_{i}}\left( x \right){{e}^{{i\omega t}}},\quad \varphi \left( {x,t} \right) = \bar {\varphi }\left( x \right){{e}^{{i\omega t}}}.$Здесь $\omega = {{\omega }_{R}} + i{{\omega }_{I}}$ – комплексная собственная частота колебаний, где ${{\omega }_{R}}$ соответствует собственной частоте, а ${{\omega }_{I}}$ характеризует скорость затухания колебаний, ${{\bar {u}}_{i}}\left( x \right)$, ${{\bar {\varphi }}_{i}}\left( x \right)$ – собственные формы колебаний. В задачах о собственных колебаниях физические уравнения (4) заменяются их комплексными аналогами (10) [10]:
(10)
$\begin{gathered} {{s}_{{ij}}} = 2(G_{k}^{R} + iG_{k}^{I}){{e}_{{ij}}}, \\ \sigma = (B_{k}^{R} + iB_{k}^{I})\vartheta , \\ \end{gathered} $C учетом вида решения (9) вариационное уравнение для задачи о собственных колебаниях электровязкоупругого тела с внешними электрическими цепями может быть представлено в виде
(11)
$\begin{gathered} \sum\limits_{k = 1}^N {\left( {\int\limits_{V_{1}^{k}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} + {{\rho }_{k}}{{\omega }^{2}}{{u}_{i}}\delta {{u}_{i}}} \right)} \,dV} \right)} + \\ + \;\int\limits_{{{V}_{2}}} {\left( {{{\sigma }_{{ij}}}\delta {{\varepsilon }_{{ij}}} - {{D}_{i}}\delta {{E}_{i}} + \rho {{\omega }^{2}}{{u}_{i}}\delta {{u}_{i}}} \right)} \,dV + \\ + \;\sum\limits_{q = 1}^{{{n}_{R}}} {\frac{1}{{i\omega {{R}_{q}}}}\int {(\varphi _{1}^{{{{R}_{q}}}} - \varphi _{2}^{{{{R}_{q}}}})} \,\delta \varphi dt} = 0. \\ \end{gathered} $ЧИСЛЕННАЯ ДЕМОНСТРАЦИЯ ДИССИПАТИВНЫХ СВОЙСТВ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА ИЗ УПРУГИХ И ВЯЗКОУПРУГИХ ЭЛЕМЕНТОВ ПРИ НАЛИЧИИ РЕЗИСТИВНОГО ЭЛЕМЕНТА
Для численной реализации задачи о вынужденных установившихся колебаниях и о собственных колебаниях электровязкоупругого тела с электрическими цепями, состоящими из резисторов, емкостей и индуктивностей, используется процедура метода конечных элементов [9, 11].
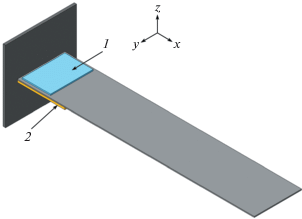
Численная демонстрация рассматриваемой задачи приводится на примере пластинки (500 × × 100 × 1 мм), представленной на рис. 2. Основная пластина выполнена из алюминия: E = 6.85 × × 1010 Па; ν = 0.3; ρ = 2750 кг/м3. Пьезоэлемент (60 × 90 × 1.3 мм) выполнен из материала ПКР7: ${{C}_{{11}}} = {{C}_{{22}}} = 12.5$ × 1010 Па, ${{C}_{{12}}} = 8.40$ × 1010 Па, ${{C}_{{13}}} = {{C}_{{23}}} = 8.10$ × 1010 Па, ${{C}_{{33}}} = 12.1$ × 1010 Па, ${{C}_{{44}}} = 2.05$ × 1010 Па, ${{C}_{{55}}} = {{C}_{{66}}} = 2.36$ × 1010 Па, ${{\beta }_{{31}}} = {{\beta }_{{32}}} = - 9.0$ Кл/м2, ${{\beta }_{{33}}} = 28.3$ Кл/м2, ${{\beta }_{{52}}} = {{\beta }_{{61}}} = 17.9$ Кл/м2, ${{э}_{{11}}} = {{э}_{{22}}} = 1.27$ × 10–8 Ф/м, ${{э}_{{33}}} = 1.20$ × 10–8 Ф/м, $\rho = 7500$ кг/м3.
В выполненных расчетах рассмотрен вариант графенового композита, в котором в качестве матрицы используется полиметилметакрилат (ПММА), а графен выполняет роль наполнителя [4]. При моделировании этого элемента в рамках упругой модели были заданы следующие свойства материала: модуль сдвига G = 2.29 × 108 Па; объемный модуль B = 5.96 × 108 Па; удельная плотность ρ = 1190 кг/м3. При моделировании элемента в рамках вязкоупругой модели комплексный модуль сдвига $G = {{G}^{R}} + i{{G}^{I}}$ и упругий объемный модуль задавались следующим образом: ${{G}^{R}} = 2.29$ × 108 Па, ${{G}^{I}} = 5.73$ × 107 Па, $B$ = 5.96 × 108 Па.
В задаче о вынужденных установившихся колебаниях принимается, что закрепленный торец пластины совершает колебания
На рис. 3 приведены амплитудно-частотные характеристики компоненты вектора перемещений uz свободного торца в окрестности первого и второго резонансов для трех вариантов:
Рис. 3.
Амплитудно-частотные характеристики для uz в окрестности первого резонанса (а) и в окрестности второго резонанса (б).
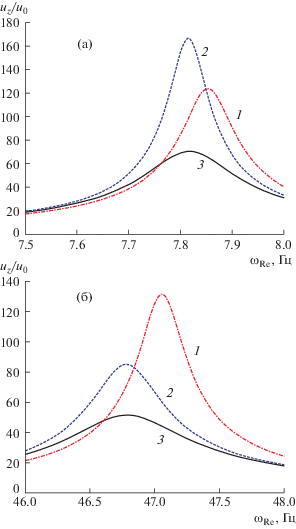
1) учитываются только вязкоупругие свойства элемента из графенового композита (штрих-пунктирная линия 1);
2) графеновый композит – упругий и реализует функцию резистора (пунктирная линия 2);
3) графеновый композит – вязкоупругий и реализует функцию резистора (сплошная линия 3).
Для этих же вариантов получены значения комплексных собственных частот колебаний. В табл. 1 для этих же вариантов приведены комплексные собственные частоты для первых двух мод собственных колебаний. Мнимые части этих собственных частот характеризуют скорость затухания собственных форм колебаний.
Таблица 1
| Вариант | $\omega = {{\omega }_{R}} + i{{\omega }_{I}}$ |
|---|---|
| Первая мода колебаний | |
| 1 | 7.81597 – i ⋅ 0.04401 |
| 2 | 7.78116 – i ⋅ 0.03360 |
| 3 | 7.78344 – i ⋅ 0.07784 |
| Вторая мода колебаний | |
| 1 | 46.33836 – i ⋅ 0.16603 |
| 2 | 46.10908 – i ⋅ 0.22177 |
| 3 | 46.11665 – i ⋅ 0.38729 |
Для приведенных результатов значения сопротивления для первой моды колебаний 210 кОм, для второй моды – 35 кОм, были найдены при численном моделировании из условия обеспечения максимального демпфирования колебаний. Омическое сопротивление элемента из графенового материала может быть рассчитано по следующей формуле:
где ρ – удельное сопротивление материала проводника; σ – удельная проводимость проводника (величина обратная удельному сопротивлению); l – длина проводника; S – площадь поперечного сечения проводника.Для рассматриваемого элемента из графенового композита могут быть реализованы два варианта электродированных поверхностей: две противоположные боковые поверхности; две большие поверхности элемента. В первом случае l = = 100 мм, $S = 100 \times 2$ мм2, а во втором случае $l = 2$ мм, $S = 100 \times 100$ мм2.
Исходя из этого, для найденных оптимальных значений сопротивлений должны быть следующие значения удельной проводимости графенового композита соответственно для первого и второго вариантов электродирования поверхностей:
для первой моды колебаний
σ1 = $\frac{1}{\rho }$ ≈ 2.38 × 10–3 См/м, ${{\sigma }_{2}} = \frac{1}{\rho } \approx 9.52$ × 10–7 См/м;
для второй моды колебаний
σ1 = $\frac{1}{\rho }$ ≈ 1.42 × 10–2 См/м, ${{\sigma }_{2}} = \frac{1}{\rho } \approx 5.71$ × 10–6 См/м.
Следует заметить, что величина σ1 находится в области значений удельной проводимости графеновых композитов, приведенных в работах [5, 12].
Анализ результатов, приведенных на рис. 3, и полученных значений комплексных собственных частот колебаний показывает, что использование свойств электрической проводимости графеновых композитов в smart-материалах, основанных на применении пьезоэлементов, дает дополнительный механизм демпфирования колебаний.
ВЫВОДЫ
Предлагается вариант smart-структур на основе пьезоэлементов с шунтирующей цепью, в которой роль резистора выполняет деформируемый элемент из графенового композита. Приведена математическая постановка задачи о вынужденных установившихся колебаниях и собственных колебаниях smart-структур, представляющих собой кусочно-однородное тело, состоящее из упругих и вязкоупругих элементов, пьезоэлементов и элементов из графеновых композитов, которые являются не только механически деформируемым телом, но и выполняют роль резистора. Численными экспериментами продемонстрированы в рассмотренных smart-структурах дополнительный механизм демпфирования при использовании электрической проводимости графенового композита.
Список литературы
Concise encyclopedia of composite materials / Ed. Anthony Kelly. England, 1994. 350 p.
Reza Moheimani S.O., Fleming A.J. Piezoelectric transducers for vibration control and damping. Springer, 2006. 272 p.
Janos B.Z., Hagood N.W. Owerview of Active Fiber Composite Technologies // MST News. Actuator Applications. Home Automation. 1998. № 3. P. 25–29.
Kumar A., Sharma K., Dixit A.R. A Review of the Mechanical and Thermal Properties of Grapheme and Its Hybrid Polymer Nanocomposites for Structural Applications // J. Mater. Sci. 2019. V. 54. P. 5992–6026.
Marsden A.J., Papageorgiou D.G., Vallés C., Liscio A., Palermo V., Bissett M.A., Young R.J., Kinloch I.A. Electrical percolation in graphene–polymer Composites // 2D Mater. 2018. V. 5. art. № 032003.
Washizu. K. Variational Methods in Elasticity and Plasticity. London: Pergamon Press. 1982.
Карнаухов В.Г., Киричок И.Ф. Электротермовязкоупругость. Киев: Наук. думка, 1988. 319 с.
Адамов А.А., Матвеенко В.П., Труфанов Н.А. и др. Методы прикладной вязкоупругости. Екатеринбург: УрО РАН, 2003. 411 с.
Матвеенко В.П., Ошмарин Д.А., Севодина Н.В. и др. Задача о собственных колебаниях электровязкоупругих тел с внешними электрическими цепями и конечно-элементные соотношения для ее численной реализации // Вычислительная механика сплошных сред. 2016. Т. 9. № 4. С. 476–485.
Kligman E.P., Matveenko V.P. Natural Vibration Problem of Viscoelastic Solids as Applied to Optimization of Dissipative Properties of Constructions // Intern. J. Vibration and Control. 1997. V. 3. № 1. P. 87–102.
Iurlova N.A., Sevodina N.V., Oshmarin D.A., et al. Algorithm for Solving Problems Related to the Natural Vibrations of Electro-Viscoelastic Structures with Shunt Circuits Using ANSYS Data // Intern. J. Smart and Nano Materials. 2019. V. 10. № 2. P. 156–176.
Alemour B., Yaacob M.H., Lim H.N., et al. Review of Electrical Properties of Graphene Conductive Composites // Intern. J. Nanoelectronics and Materials. 2018. V. 11. № 4. P. 371–398.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Физика, технические науки