1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Физика, технические науки
  4. T. 492, № 1, 2020

Доклады Российской академии наук. Физика, технические науки, 2020, T. 492, № 1, стр. 88-91

ОПРЕДЕЛЕНИЕ МАССОВОГО РАСХОДА КРОВИ В КРОВЕНОСНОМ СОСУДЕ ПО СОБСТВЕННЫМ ЧАСТОТАМ ИЗГИБНЫХ КОЛЕБАНИЙ

Член-корреспондент РАН В. М. Тимербулатов 1, *, Ш. В. Тимербулатов 1, **, А. Г. Хакимов 2, ***

1 Башкирский государственный медицинский университет
Уфа, Россия

2 Институт механики им. Р.Р. Мавлютова Уфимского федерального исследовательского центра Российской академии наук
Уфа, Россия

* E-mail: timervil@yandex.ru
** E-mail: timersh@yandex.ru
*** E-mail: hakimov@anrb.ru

Поступила в редакцию 04.07.2019
После доработки 20.03.2020
Принята к публикации 20.03.2020

Полный текст (PDF)

Аннотация

Исследованы собственные изгибные колебания кровеносного сосуда с движущейся кровью, находящегося под действием растягивающей силы и давления в сосуде. Учитываются силы инерции кровеносного сосуда, кориолисовые и центробежные силы, обусловленные движением крови. Определяются волновые числа, а используя граничные условия, находится частотное уравнение. По двум частотам изгибных колебаний можно определить скоростной параметр, относительную массу крови на единицу длины кровеносного сосуда и, как следствие, массовый расход крови по кровеносному сосуду. Полученные результаты могут быть использованы для акустического метода определения скорости крови, относительной массы крови на единицу длины кровеносного сосуда и массового расхода крови по кровеносному сосуду.

Ключевые слова: кровеносный сосуд, изгибные колебания, собственные частоты, скорость, прямая и обратная задачи

В проведенном исследовании [1] при выполнении лапароскопии 10 пациентам, подписавшим добровольное информированное согласие, при помощи ультразвукового исследования измеряли диаметр бедренной вены и скорость кровотока в ней при разных уровнях давления в животе, создаваемого инсуфлятором, после статистической обработки полученных данных авторы показали наличие зависимости диаметра общей бедренной вены и скорости кровотока в ней от уровня интраабдоминального давления. Ввиду наличия пропорциональной почти линейной функциональной зависимости диаметра бедренной вены от уровня внутрибрюшного давления авторы предложили использовать данный показатель с целью мониторинга динамики интраабдоминального давления. С возрастом происходит постепенное увеличение диаметра просвета центральных артерий вместе с утолще\нием и уплотнением сосудистой стенки, отмечено в работе [2].

Рассматриваются собственные частоты изгибных колебаний кровеносного сосуда с кровью под давлением. Исследуется случай жесткого защемления концов кровеносного сосуда. В обширной литературе, посвященной колебаниям трубопроводов, также широко используются условия “шарнирного опирания” и “свободных концов”, однако, как отмечено в [3], они не являются очевидными, нуждаются в обосновании и, возможно, требуют замены на другие. Решена обратная задача определения скоростного параметра, относительной массы крови на единицу длины кровеносного сосуда.

ПОСТАНОВКА ЗАДАЧИ

Исследуются собственные частоты изгибных колебаний кровеносного сосуда длины L, содержащего кровь, движущуюся с постоянной скоростью V. Кровеносный сосуд находится в упругой среде под давлением и действием растягивающей силы T. Требуется определить скоростной параметр, относительную массу крови на единицу длины кровеносного сосуда по собственным частотам изгибных колебаний.

Уравнение изгибных колебаний кровеносного сосуда по модели Кирхгофа имеет вид [4–7]

(1)
$\begin{gathered} EJ\frac{{{{\partial }^{4}}{{w}_{*}}}}{{\partial {{x}^{4}}}} + ({{\rho }_{i}}{{F}_{i}}{{V}^{2}} + {{P}_{i}}{{F}_{i}} - T)\frac{{{{\partial }^{2}}{{w}_{*}}}}{{\partial {{x}^{2}}}} + \\ \, + 2{{\rho }_{i}}{{F}_{i}}V\frac{{{{\partial }^{2}}{{w}_{*}}}}{{\partial x\partial t}} + \left[ {\rho F + {{\rho }_{i}}{{F}_{i}}} \right]\frac{{{{\partial }^{2}}{{w}_{*}}}}{{\partial {{t}^{2}}}} + {{q}_{s}}{{w}_{*}} = 0, \\ \end{gathered} $
где E, ρ, J, F – модуль упругости, плотность, осевой момент инерции и площадь поперечного сечения кровеносного сосуда, ρi, Pi, Fi – плотность, давление внутри кровеносного сосуда, площадь сечения в свету кровеносного сосуда, w* – прогиб кровеносного сосуда, qs – коэффициент жесткости окружающей среды, x – координата, направленная по оси кровеносного сосуда, t – время. Перейдя к безразмерным величинам
$\begin{gathered} {\xi } = \frac{x}{L},\quad w = \frac{{{{w}_{*}}}}{L},\quad \tau = \nu t,\quad {{\nu }^{2}} = \frac{{EJ}}{{\rho F{{L}^{4}}}}, \\ R = \frac{{(T - {{P}_{i}}{{F}_{i}}){{L}^{2}}}}{{EJ}},\quad \alpha = \frac{V}{{\nu L}},\quad \beta = \frac{{{{\rho }_{i}}{{F}_{i}}}}{{\rho F}},\quad \gamma = \frac{{{{q}_{s}}{{L}^{4}}}}{{EJ}}, \\ p = {{\alpha }^{2}}\beta - R,\quad q = 2\alpha \beta \Omega ,\quad r = - \left( {1 + \beta } \right){{\Omega }^{2}} + \gamma , \\ \end{gathered} $
$\begin{gathered} {{\Omega }^{2}} = \frac{{\rho F{{L}^{4}}{{{\omega }}^{2}}}}{{EJ}},\quad {{F}_{i}} = {\pi }R_{i}^{2}, \\ F = {\pi [}{{({{R}_{i}} + h)}^{2}} - R_{i}^{2}{\text{]}},\quad J = \frac{{{\pi }[{{{({{R}_{i}} + h)}}^{4}} - R_{i}^{4}]}}{4}, \\ \end{gathered} $
сделаем подстановку $w = W\left( \xi \right)\exp \left( {i\Omega \tau } \right)$ и получим уравнение, определяющее форму изгибных колебаний кровеносного сосуда
(2)
$\frac{{{{\partial }^{4}}W}}{{\partial {{\xi }^{4}}}} + p\frac{{{{\partial }^{2}}W}}{{\partial {{\xi }^{2}}}} + iq\frac{{\partial W}}{{\partial \xi }} + rW = 0,$
где ω – круговая частота, Ri – внутренний радиус кровеносного сосуда, α – скоростной параметр, β – параметр массы крови в кровеносном сосуде.

Граничные условия для защемленного по краям кровеносного сосуда

(3)
$w = 0,\quad \frac{{\partial w}}{{\partial \xi }} = 0\quad {\kern 1pt} \left( {\xi = 0,\;1} \right).$

Общее решение уравнения (2) будем определять в виде $W\left( \xi \right) = \exp \left( {k\xi } \right)$, тогда получим характеристическое уравнение для нахождения неизвестных значений комплексного волнового параметра kj = kj (α, β, R, Ω), j = 1, 2, 3, 4:

(4)
${{k}^{4}} + p{{k}^{2}} + iqk + r = 0.$

По формулам Феррари определяются волновые числа kj = kj(α, β, R, Ω), а общее решение уравнения (2) записывается в виде

(5)
$W\left( \xi \right) = \sum\limits_{j = 1}^4 {{{C}_{j}}} \exp \left( {{{k}_{j}}\xi } \right).$

Подставляя (5) в граничные условия (3), получим однородную систему линейных уравнений относительно неизвестных постоянных Cj. Для того чтобы постоянные Cj не были равны нулю одновременно, необходимо, чтобы определитель основной матрицы был равен нулю. Это условие дает частотное уравнение [8]

(6)
$D = \left| {\begin{array}{*{20}{c}} 1&1&1&1 \\ {{{k}_{1}}}&{{{k}_{2}}}&{{{k}_{3}}}&{{{k}_{4}}} \\ {{{e}^{{{{k}_{1}}}}}}&{{{e}^{{{{k}_{2}}}}}}&{{{e}^{{{{k}_{3}}}}}}&{{{e}^{{{{k}_{4}}}}}} \\ {{{k}_{1}}{{e}^{{{{k}_{1}}}}}}&{{{k}_{2}}{{e}^{{{{k}_{2}}}}}}&{{{k}_{3}}{{e}^{{{{k}_{3}}}}}}&{{{k}_{4}}{{e}^{{{{k}_{4}}}}}} \end{array}} \right| = 0.$

В [3] доказана теорема, что для любых α и β (R = 0) собственные частоты Ω краевой задачи (1), (3) действительны.

Таким образом, в приведенной простейшей модели кровеносного сосуда с движущейся кровью под давлением фигурируют параметры R, α, β, которые зависят от усилия натяжения в кровеносном сосуде T, давления внутри кровеносного сосуда Pi, площади сечения в свету кровеносного сосуда Fi, скорости течения крови внутри кровеносного сосуда V. Подробнее остановимся на влиянии этих факторов на собственные частоты изгибных колебаний. Зависимости первой и второй собственной частот изгибных колебаний стержня от скоростного параметра α для различных значений параметра R и анализ полученных результатов приводятся в [8]. В отличие от работы [8] здесь дается постановка и решение обратной задачи определения скоростного параметра, относительной погонной массы движущейся крови в кровеносном сосуде по двум собственным частотам изгибных колебаний. Безразмерный массовый расход m по кровеносному сосуду определяется по формуле

$m = \alpha \beta = \frac{{{{\rho }_{i}}{{F}_{i}}V}}{{\rho F\nu L}} = \frac{{{{\rho }_{i}}{{F}_{i}}VL}}{{\sqrt {\rho FEJ} }}.$

При α = 0 и R = 0 собственные функции W(ξ) действительны и совпадают с собственными функциями стержня с жестко защемленными концами [8].

Если R = 0, β = 1, γ = 0, то характеристическое уравнение (4) допускает факторизацию и его корни kj находятся в явном виде как функции частоты Ω. Для вещественных собственных частот Ωn(α) получается довольно простое вековое уравнение, которое решается одним из численных методов [9, 10].

В других случаях корни характеристического уравнения находятся с помощью формул Феррари. Последние, по мнению авторов [8], почти не применялись в задачах математической физики и механики (редким исключением являются работы [8, 10]).

ПРЯМАЯ ЗАДАЧА

Расчеты проведены для следующих параметров кровеносного сосуда: модуль упругости вены [11 ] E = 0.853 × 106 Н/м2, плотность ρ = 1058.2 кг/м3, толщина стенки кровеносного сосуда h = 0.5 мм, внутренний радиус кровеносного сосуда Ri = 6 мм, осевое усилие T = 0, давление внутри кровеносного сосуда Pi = 10 мм рт. ст. = 1333.22 Па, плотность крови в кровеносном сосуде ρi = 1052 кг/м3, скорость крови внутри кровеносного сосуда V = = 0.1 м/с, длина кровеносного сосуда между “опорами” L = 0.1 м, а параметры R = –4.602, α = = 0.0796, β = 5.72. Решение прямой задачи для сосуда с вышеприведенными параметрами дает, что низшие две собственные частоты кровеносного сосуда f1 = 16.21 Гц, f2 = 46.17 Гц (Ω1 = 8.114, Ω2 = = 23.10).

На рис. 1 дается зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от давления внутри кровеносного сосуда. С ростом давления внутри кровеносного сосуда и с уменьшением модуля упругости частоты изгибных колебаний уменьшаются.

Рис. 1.

Зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от давления внутри кровеносного сосуда Pi (мм рт. ст.) для параметра β = 5.72 и различных значений модуля упругости E = 0.853; 0.6; 0.4 МПа (кривые 1–3 соответственно).

На рис. 2 представлена зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от параметра R. С ростом параметра R частоты изгибных колебаний увеличиваются. На рис. 3 приводится зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от параметра β. Видно, что с ростом параметра β частоты изгибных колебаний уменьшаются.

Рис. 2.

Зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от параметра R для скоростного параметра α = 0.0796 и различных значений параметра β = 1; 3; 5 (кривые 1–3 соответственно).

Рис. 3.

Зависимость первой собственной частоты изгибных колебаний кровеносного сосуда от параметра β для скоростного параметра α = 0.0796 и различных значений параметра R = –4; 0; 4 (кривые 1–3 соответственно).

ОБРАТНАЯ ЗАДАЧА

В точке М0(α0, β0) ${{D}_{{\text{1}}}}({{\alpha }_{0}},{{\beta }_{0}},{{\Omega }_{{\text{1}}}}) = {{u}_{1}},$ ${{D}_{2}}({{\alpha }_{0}},{{\beta }_{0}}$, Ω1) = u2, поэтому можем записать

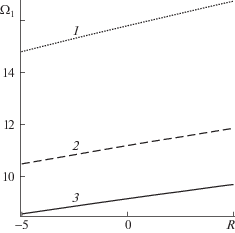
$\begin{gathered} \frac{{\partial {{D}_{{\text{1}}}}}}{{\partial \alpha }}d\alpha + \frac{{\partial {{D}_{{\text{1}}}}}}{{\partial \beta }}d\beta = - {{u}_{1}}, \\ \frac{{\partial {{D}_{2}}}}{{\partial \alpha }}d\alpha + \frac{{\partial {{D}_{2}}}}{{\partial \beta }}d\beta = - {{u}_{2}}. \\ \end{gathered} $

По этим формулам определяются dα, dβ, далее, α0 = α0 + dα, β0 = β0 + dβ. Процесс последовательных приближений продолжается до тех пор, пока не выполнится условие точности. Решение этой системы уравнений определяется методом последовательных приближений в области однозначной зависимости параметров α, β от частоты изгибных колебаний кровеносного сосуда. Решение обратной задачи для кровеносного сосуда с вышеприведенными данными при γ = 0, R = 0, Ω1 = 9.1, Ω2 = 25.1 (f1 = 18.18 Гц, f2 = 50.16 Гц) дает, что α = = 0.0978, β = 5.034 (V = 1.543 м/с, ρi = = 924.8 кг/м3). На рис. 4 приводится зависимость от первой частоты изгибных колебаний Ω1 массового расхода m по кровеносному сосуду. По двум частотам изгибных колебаний можно определить скоростной параметр α, параметр β или массу жидкости на единицу длины и безразмерный массовый расход m жидкости по кровеносному сосуду.

Рис. 4.

Зависимость от первой частоты изгибных колебаний Ω1 массового расхода m по кровеносному сосуду для различных частот изгибных колебаний Ω2: кривая 1 – 25.1; 2 – 25.0; 3 – 24.9.

Получено, что с увеличением силового параметра частоты изгибных колебаний увеличиваются. Показано, что с увеличением массы кровеносного сосуда с жидкостью на единицу длины происходит уменьшение собственных частот изгибных колебаний сосуда. По двум частотам изгибных колебаний можно определить скоростной параметр, массу крови на единицу длины и безразмерный массовый расход крови по кровеносному сосуду.

Список литературы

  1. Тимербулатов. В.М., Гареев Р.Н., Тимербулатов Ш.В., Сагитов Р.Б. и др. Динамика скоростных показателей кровотока в бедренных венах и их диаметра в зависимости от уровня давления в брюшной полости: практическое применение // Инфекции в хирургии. 2015. № 2. С. 22–25.

  2. Терегулов Ю.Э., Маянская С.Д., Терегулова Е.Т. Изменения эластических свойств артерий и гемодинамические процессы // Практическая медицина. 2017. № 2 (103). С. 14–20.

  3. Акуленко Л.Д., Иванов М.И., Коровина Л.И., Нестеров С.В. Основные свойства собственных колебаний протяженного участка трубопровода // Известия РАН. МТТ. 2013. № 4. С. 119–134.

  4. Светлицкий В.А. Механика стержней. Т. 2. М.: Высшая школа, 1987. 304 с.

  5. Mote C.D. A study of band saw vibrations // J. Franklin Inst. June. 1965. V. 279. № 6. P. 430–444.

  6. Ильгамов М.А. Статические задачи гидроупругости. Казань, 1994. 208 с.

  7. Dowell E.H., Ilgamov M.A. Studies in Nonlinear Aeroelasticity. N.Y.; L.; Tokyo: Springer-Verlag, 1988. 456 p.

  8. Акуленко Л.Д., Коровина Л.И., Нестеров С.В. Собственные колебания участка трубопровода // Известия РАН. МТТ. 2011. № 1. С. 172–187.

  9. Kong L., Parker R.G. Approximate eigensolutions of axially moving beams with small flexural stiffness // J. Sound and Vibr. 2004. V. 276. P. 459–469.

  10. Акуленко Л.Д., Нестеров С.В. Изгибные колебания движущегося стержня // ПММ. 2008. Т. 72. Вып. 5. С. 766–781.

  11. Березовский В.А., Колотилов Н.Н. Биофизические характеристики тканей человека. Справочник. Киев: Наук. думка, 1990. С. 224.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал