Доклады Российской академии наук. Физика, технические науки, 2021, T. 499, № 1, стр. 12-16

Связанные состояния трех попарно невзаимодействующих частиц, известные как состояния Ефимова [1], экспериментально реализуются и исследуются в системе ультрахолодных атомов [2]. Топологическим образом подобных состояний являются кольца Борромео, удаление одного из которых из связанной тройки разрывает связь двух других. По этой аналогии трехбозонные связанные состояния также называют и состояниями Борромео [3]. В нелинейных бозонных системах твердого тела (магнонах, фононах, поляритонах, гибридизированных возбуждениях) образование и исследование трехбозонных связанных состояний возможно в нормальных лабораторных условиях. Идея формирования трехбозонных связанных возбуждений в системе гибридизированных фононов и магнонов, предложенная профессором В.И. Ожогиным в 2007 г., была экспериментально реализована в работе [4] на объемной моде акустических колебаний в кристаллическом антиферромагнитном резонаторе α-Fe₂O₃. Выбор объекта исследования был обусловлен гигантской акустической нелинейностью антиферромагнетиков, управляемой внешним магнитным полем [5]. Теоретический анализ [4, 6] показал возможность возникновения взрывной неустойчивости трехфононных связанных возбуждений, которая в последующем наблюдалась экспериментально на кристаллических резонаторах α-Fe₂O₃ и FeBO₃ [7, 8]. Тем не менее, продемонстрировать принадлежность исследуемых возбуждений к типу состояний Борромео в указанных экспериментах не представлялось возможным.

В настоящей работе сообщается о прямом наблюдении состояний Борромео при взаимодействии акустической моды дискретного спектра с парой встречных фононов непрерывного спектра. Выбранная схема эксперимента позволяет разделить взаимодействующие возбуждения по частоте и направлению распространения, что дает возможность селективно исключать из взаимодействия отдельные компоненты. Эффекты взаимодействия возбуждений непрерывного и дискретного спектров, известные как резонансы Фано–Фешбаха [9, 10], являются эффективным инструментом исследования в разнообразных областях физики от сверххолодных атомов до фотоники и акустики микроструктур [11–14]. В работе [15] теоретически исследована возможность использования параметрического резонанса Фешбаха для возбуждения фононных триад в магнетике в поле электромагнитной накачки. В соответствии с теоретической моделью, трехфононные связанные возбуждения возникают при выполнении условия синхронизма

где ω_p – частота переменного поля накачки, Ω – частота дискретной моды упругих колебаний, ω_k и ω_–k – частоты встречных фазосопряженных бегущих акустических волн. Условие синхронизма иллюстрируется диаграммой, представленной на рис. 1 [15].

В работе для экспериментальной реализации состояния Борромео в условиях резонанса Фешбаха использовалась пластина антиферромагнетика α-Fe₂O₃ с размерами 34 × 9.3 × 1.4 мм, вырезанная в базисной плоскости, перпендикулярной тригональной кристаллографической оси C₃||z. На рис. 2 приведена схема эксперимента. Переменное магнитное поле с частотой ω_p/2π = 44 MГц прикладывалось параллельно бинарной оси U₂||x нормально к намагничивающему полю ${{H}_{0}}{\text{||}}y$ (геометрия поперечной накачки).

Дискретная мода колебаний сдвига по толщине возбуждалась поперечным импульсным переменным полем с частотой Ω/2π = 1.230 MГц с помощью катушки индуктивности. Длительность импульса выбиралась достаточной для достижения установившихся колебаний. Амплитуда колебаний моды контролировалась по сигналу U_m, наводимому в катушке колебаниями намагниченности, вызванными переменной деформацией кристалла. Пьезоэлектрический преобразователь возбуждал в кристалле импульсную сдвиговую бегущую волну с поляризацией $e\left\| y \right.$ в плоскости пластины, распространяющуюся вдоль бинарной оси. Для выполнения резонансного условия (рис. 1) частота волны выбиралась равной полуразности частот накачки и дискретной моды: ω_k/2π = 21.385 MГц. Длительность излучаемого акустического импульса составляла 5 мкс. Тем же преобразователем регистрировалась генерируемая в процессе параметрического взаимодействия обратная волна, спектр которой обрабатывался численно. К моменту включения импульса электрического напряжения на преобразователе, импульс возбуждения дискретной моды выключался и колебания переходили в режим свободной релаксации. Время релаксации значительно превосходило время регистрации трехфононного взаимодействия. Через 5 мкс после начала возбуждения акустического импульса включался импульс электромагнитной накачки длительностью 6 мкс, амплитуда которого устанавливалась по напряжению U_p на контрольном выходе высокочастотного усилителя.

На рис. 3 приведены данные регистрации спектров обратной волны, принятой преобразователем при возбуждении и в отсутствие колебаний дискретной моды.

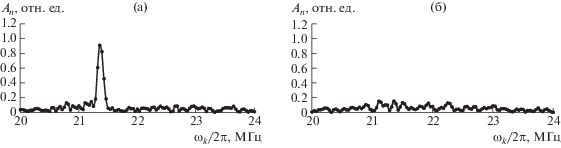
В отсутствие возбуждения дискретной моды или прямой акустической волны сигнал обратной волны отсутствовал.

На рис. 4 приведены характерные спектры обратной волны для двух значений амплитуды импульса накачки. Зависимости сигнала обратной волны от амплитуд накачки и дискретной моды колебаний приведены на рис. 5a, 5б.

На зависимости рис. 5б видна тенденция к насыщению сигнала обратной волны с ростом амплитуды дискретной моды, что обусловлено ограниченностью угла поворота переменной намагниченности в поле резонансных деформаций, превышающих деформации спонтанной стрикции. В то же время с ростом амплитуды накачки сигнал обратной волны монотонно и нелинейно нарастает.

Обсуждение полученных результатов проведем в сопоставлении с теоретической моделью работы [15]. В основе механизма наблюдаемого взаимодействия лежит модуляция нелинейного модуля упругости ${{C}_{{566}}}(H)$ переменным магнитным полем накачки h_p(t). Энергия рассматриваемых акустических возбуждений в схеме рис. 2 имеет вид

где v – скорость упругого смещения, u_ij – тензор переменных деформаций, ρ – плотность кристалла, С_ij – линейные модули упругости, Ψ_p – амплитуда нелинейного параметрического взаимодействия:

Зависимость амплитуды взаимодействия от напряженности намагничивающего поля приведена в [15].

Следуя подходу, развитому в работе [15], представим упругое смещение и скорость деформации в канонических переменных для непрерывных α_k и дискретной β мод с частотами ω_k и Ω соответственно:

где l – толщина пластины,

В указанных переменных энергия системы (1) преобразуется к виду

где

Гамильтониан взаимодействия (5) описывает процесс одновременного рождения трех связанных фононов, один из которых относится к дискретному, а два других к непрерывному спектру. Переменные α_k и β подчинены каноническим уравнениям движения:

Соответствующая система уравнений для амплитуд возбуждений ${{a}_{k}} = {{\alpha }_{k}}{{e}^{{ - i{{\omega }_{k}}t}}}$, ${{a}_{{ - k}}} = {{\alpha }_{{ - k}}}{{e}^{{ - i{{\omega }_{k}}t}}}$, b = = $(\eta {\text{/}}l)\beta {{e}^{{ - i\Omega t}}}$ приводится к виду:

где Φ_k = 2ω_kΨ_p/C₆₆ – параметр трехфононного взаимодействия, Δω_p = ω_p – 2ω_k – Ω – расстройка частоты накачки относительно частоты резонанса Фешбаха. Связь возбуждений наиболее эффективна в условиях резонанса Δω_p = 0.

Система уравнений (7) описывает динамические возбуждения типа состояний Борромео. Отсутствие одного из трех возбуждений приводит к разрыву связи двух других. Прямое экспериментальное подтверждение этого свойства у наблюдаемых параметрически связанных фононных триад иллюстрируется спектрограммами сигнала обратной волны, приведенными на рис. 3a, б.

Другой особенностью рассматриваемых возбуждений является их взрывная неустойчивость при достаточно высоких уровнях накачки [14]. Для относительно малых амплитуд волны на входе кристалла неустойчивость начинает развиваться при условии $\left| {{{\Phi }_{k}}{{h}_{0}}{{\beta }_{0}}} \right|kL{\text{/}}{{\omega }_{k}} > \pi {\text{/}}2$, где L – длина активной зоны действия накачки. Формально аналогичным неравенством определяется порог неустойчивости при двухфононном процессе параметрического обращения волнового фронта. Существенное отличие состоит в том, что в данном случае пороговое условие зависит не только от амплитуды поля накачки, но и от начальной амплитуды β₀ дискретной моды. Отметим, что нелинейный рост амплитуды сигнала обратной волны с ростом амплитуды накачки на экспериментальной кривой рис. 4б указывает на близость экспериментальных условий возбуждения к порогу трехфононной неустойчивости. Динамика системы при более высоких уровнях накачки на временах достаточно больших для развития неустойчивости требует специального экспериментального исследования.