Доклады Российской академии наук. Физика, технические науки, 2021, T. 501, № 1, стр. 8-13

1. При изучении эксплуатационных характеристик углеродной нанотрубки, в том числе ее статического и динамического поведения под действием приложенных нагрузок, применяются методы молекулярной динамики, молекулярной механики, континуальной механики [1–5]. В последнем случае вводятся в рассмотрение эффективные размеры трубки, эффективные упругие и массовые параметры. В данной работе используются соотношения теории тонких оболочек и параметр, определенный из сравнения собственных частот в рамках молекулярной динамики и классической механики.

Рассматривается воздействие всестороннего динамического давления на внешнюю поверхность однослойной углеродной нанотрубки. Вопросы воздействия давлений на нанотрубки рассматриваются в обзорах [6, 7]. Имеются экспериментальные исследования динамических, структурных, электрических свойств однослойных и многослойных нанотрубок в зависимости от всестороннего статического и динамического давления [8–13]. В указанных работах приведено также теоретическое моделирование в рамках молекулярной динамики и континуальной механики. Дается анализ деформации изолированной нанотрубки под статическим давлением, который является необходимым шагом при изучении сложного поведения пучка нанотрубок под динамическим давлением. Показано [10, 11], что при увеличении статического давления до ${{p}_{1}} \approx 3D{{R}^{{ - 3}}}$ поперечное сечение трубки приобретает форму эллипса (D – изгибная жесткость, R – радиус). При этом радиальная жесткость трубки уменьшается на два порядка [11]. Увеличение давления до p₂ ≈ p₁(1 – $\ln ({{F}_{2}}F_{1}^{{ - 1}}))$ приводит к форме сечения с двумя противоположными точками с нулевой кривизной. При дальнейшем увеличении давления до ${{p}_{3}} \approx {{p}_{1}}(1 - \ln ({{F}_{3}}F_{1}^{{ - 1}}))$ происходит рост деформации и изменение электрических свойств трубки (появление полупроводникового состояния). Здесь ${{F}_{1}}$, ${{F}_{2}}$, ${{F}_{3}}$ – площади поперечного сечения, соответствующие давлениям ${{p}_{1}}$, ${{p}_{2}}$, ${{p}_{3}}$. Для однослойной нанотрубки (10, 10) ${{p}_{1}} = 1.55$ ГПа, ${{p}_{2}} = 1.75$ ГПа, ${{p}_{3}} = 2.2$ ГПа [10].

Рассматриваются вопросы структурных переходов в пучках нанотрубок при лазерном обжатии, возникающие при этом колебания [8, 9, 12]. В этих и других работах при экспериментальных исследованиях широко применяется Раман-спектроскопия. Изучено поведение нанотрубок в зависимости от расстояния между ними в пучке (эксперименты при расстояниях 1.5–1.7 нм). В [13] исследовано изменение свойств одиночной многослойной нанотрубки при ударном обжатии бойком через окружающий упругий материал.

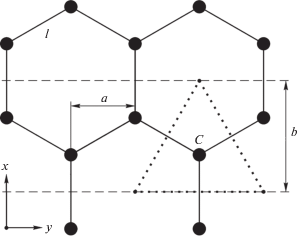
Ввиду одинакового давления по всей поверхности трубки объектом исследования может быть принято кольцо с эффективными значениями радиуса R, толщины h, ширины b, плотности по площади ρh, модуля упругости Е и коэффициента Пуассона ν. Кольцо образуется зигзагообразным рядом атомов углерода, расстояние между которыми $l = 0.142$ нм (рис. 1). Если ось x направлена вдоль трубки, ось $y = R\theta $ по окружности (θ – центральный угол), то расстояние по y равно $a = l{\text{cos}}30^\circ $ = 0.123 нм. На рис. 1 в виде равностороннего треугольника показана площадь S, приходящаяся на один атом. При $4S = 3\sqrt 3 {{l}^{2}}$ эффективная ширина кольца равна $b = S{{a}^{{ - 1}}}$ = 0.213 нм. Так как масса атома углерода равна $m = 1.99 \times {{10}^{{ - 26}}}$ кг, то эффективная плотность по площади

Во многих работах (в том числе в обзорных статьях [1, 2]) приводятся значения модуля упругости Е = (1÷5) × 10⁶ МПа, толщины однослойного графена h = 0.07÷0.34 нм. Эти данные получены экспериментально, а также с привлечением теоретического моделирования. Разброс значений Е и h объясняется разными образцами для испытаний, аппаратурой, методами определения и т.д. Эффективный радиус R определяется через число атомов N, образующих кольцо,

В [14–16] вводится параметр

В [14] его численное значение определено по известным эффективным значениям Е, ν, ρ и равняется $\xi = 600$ нм²/нс. В [15, 16] этот параметр определяется путем сравнения собственных частот радиальных колебаний кругового кольца по цепной модели в молекулярной динамике при условии $N > 78$, n = 2 и по теории тонких оболочек и равняется $\xi = 581$ нм²/нс.

Как показано в [16], при $N < 78$ значение ξ меньше, чем приведенное выше. В этом проявляется размерный фактор. В данном исследовании предполагается $N \geqslant 100$ и принимается второе значение.

Внешнее равномерное избыточное давление на поверхность трубки принимается в виде ступеньки по времени (p = 0 при t < 0, p = const при t ≥ 0). Начальное давление р₀ действует на внешнюю и внутреннюю поверхности. Не учитывается влияние присоединенной массы окружающей газовой среды на колебания нанотрубки, что допустимо в случае легких газов. В статической задаче деформации под действием гидростатического давления это ограничение снимается.

2. Предполагаем, что имеется малое начальное отклонение w₀(θ) от идеальной круговой формы в момент времени t = 0. Оно может быть описано разными способами [17], например, распределением Гаусса по гармоникам n, зависимостью вида n^−α и т.д. Примем

где W₀ – амплитуда отклонения по форме n = 2. Равномерному распределению начального прогиба по гармоникам соответствует значение α = 0. Отклонение (4) можно считать за сумму амплитуд свободных радиальных колебаний кольца в начале отсчета времени где точка над буквой означает производную по времени.

Уравнение радиальной динамики тонкого кольца относительно функции прогиба w(θ, t) в рамках гипотез Кирхгоффа имеет вид [17]

Так как эффективная ширина b кольца линейно входит в значение массы, жесткости и давления, то она сокращается в уравнении (6). Решение его разыскиваем в виде

Из (6) и (7) получаем

где Ω_n – собственные частоты при нулевом давлении р, ${{p}_{*}}$ – значение статического давления, при котором происходит потеря устойчивости круговой формы кольца в виде эллипса (n = 2). Оно может быть выражено также через ξ по (3).

По приведенным выше значениям ρh и ξ из (1), (3) следует $D = {{\xi }^{2}}\rho h = 25.65$ × 10^–20 кг · м²/с². Пусть число атомов N = 200, радиус трубки R = = 3.915 нм. Тогда критическое значение давления по (8) равно ${{p}_{*}}$ = 12.82 МПа, а частота низшей гармоники (n = 2, р = 0) ${{f}_{2}} = {{\Omega }_{2}}{{(2\pi )}^{{ - 1}}} = 16$ ГГц. При таком определении ${{p}_{*}}$ и Ω_n их значения являются единственными. Если исходить из значений Е, h с учетом указанного выше их разброса, то будет соответствующий разброс значений ${{p}_{*}}$ и f_n. Внешнее давление р приводит к понижению частоты  f₂, внутренний перепад (–р) – к ее повышению.

Удовлетворяя решение уравнения (8)

W_n = ${{A}_{n}}{\text{exp}}({{\omega }_{n}}t) + {{B}_{n}}{\text{exp}}( - {{\omega }_{n}}t)$

условиям (4), (5), получаем

Из (8), (9) следует, что в зависимости от ${{p}_{*}}$, р, n имеет место как колебательный режим (ω_n < 0), так и экспоненциальное возрастание начальных прогибов (ω_n> 0)

При относительно малом давлении р и высоких значениях n, задаваемых начальным прогибом, реализуется первое решение (10), в противном случае – второе решение (10). Число n_R, разделяющее эти режимы, определяется из условия ω_n = 0 или

Значение n_R необходимо округлять до ближайшего меньшего целого числа. Решение (7), (10) можно записать в виде

Из (12) и выражения для ω_n в (8) следует, что рост возмущений происходит тем быстрее, чем больше давление и меньше плотность материала. Число волн n = n_L, при котором происходит наибольшее возрастание возмущений, определяется из условия dω_n/dn = 0. Если принять α = 0, n⁴$ \gg $ 1, то это условие дает

Согласно (13) значение n_L несколько меньше значения n_R. Это означает, что наиболее быстро возрастает амплитуда гармоники, соответствующей переходу от экспоненциального роста к колебаниям. Например, при n_R = 4.9 рост возмущений описывается суммой от n = 2 до n = 4, а начиная с n = 5 происходят колебания с возрастающей частотой и уменьшающейся амплитудой около основного движения. В этом случае решение (12) имеет вид

причем аргументы функций chω_nt и cosω_nt равны соответственно

В последнем выражении учтено, что для высоких мод n²$ \gg $ 1. Несмотря на то, что число n_R нужно округлять до целого, при вычислении выражений (15) необходимо использовать истинное значение n_R = 4.9.

На рис. 2 показаны зависимости первых трех членов в (14), (15). При равномерном распределении начального прогиба по гармоникам (α = 0) преобладающей является гармоника n = 4, что объясняется приведенным выше значением n_L. Однако в пределах рис. 2 амплитуда гармоники n = 3 остается величиной одного порядка с амплитудой гармоники n = 4. При α = 1 в начале процесса преобладает гармоника n = 2, так как это имеет место в начальном распределении гармоник (4). Около τ = 0.2 начинают преобладать гармоники n = 3 и n = 4. При τ $ \gg $ 1 наибольшей является гармоника n = 4 (пересечение кривых n = 4 и n = 3 при τ ≈ 1.7). Амплитуды колебаний, определяемые в (14), (15) членами с n ≥ 4, сравнимы с ${{W}_{n}}W_{0}^{{ - 1}}$ (n ≤ 3) только в самый начальный момент времени.

Таким образом, при динамическом выпучивании кольца с убывающим распределением по гармоникам малого начального прогиба происходит их перестройка с течением времени. В начале процесса преобладает гармоника с наибольшей амплитудой (n = 2) в начальном прогибе, в дальнейшем преобладают другие гармоники. При больших значениях времени преобладающей становится гармоника n_L, определенная в (13). Эта формула может быть выражена также через отношение действующего давления к его критическому значению $\eta = pp_{*}^{{ - 1}}$:

Если имеются какие-либо ограничители перемещения по радиусу, например, контактирующие среды, то гармоника n_L может и не стать преобладающей. Это может иметь место также при учете нелинейностей.

Значения ${{p}_{*}}$, ω_n в (8) могут быть выражены через количество атомов, образующих кольцо, исключением в них R по (2). Так как значения а, ρh, ξ заданы, то ${{p}_{*}}$, ω_n при этом зависят только от числа атомов N и действующего давления р. С возрастанием числа N значение ${{p}_{*}}$ падает как ${{N}^{{ - 3}}}$, а собственные частоты Ω_n как ${{N}^{{ - 2}}}$. При этом частоты ω_n падают еще быстрее, чем Ω_n. При одном и том же давлении р кольца, образованные из разного количества атомов N, ведут себя по разному. При приведенных выше N = 200, р = 2.84 МПа, ${{p}_{*}}$ = = 12.82 МПа возникают только колебания, так как р < ${{p}_{*}}$. Если N = 400 и, соответственно, ${{p}_{*}}$ = = 1.60 МПа, то после приложения давления происходят экспоненциальное возрастание прогиба по гармонике n = 2 и колебания по высшим гармоникам.

3. Динамические свойства углеродной нанотрубки могут быть определены с удовлетворительной точностью с использованием ее эффективных жесткостных и массовых характеристик и уравнений теории тонкостенных оболочек. В данной работе таким образом рассмотрено поведение однослойной нанотрубки под действием динамического давления на ее внешнюю поверхность. Давление принимается равномерным по всей поверхности в виде ступеньки по времени. Далее оно остается постоянным.

В условиях плоской деформации трубки может быть рассмотрено кольцо прямоугольного поперечного сечения. Малое начальное отклонение от круговой формы задается в виде суммы гармоник с убывающими амплитудами. Важными параметрами в анализе являются статическое критическое значение давления и собственные частоты радиальных колебаний. Они зависят от количества атомов, образующих кольцо, и его эффективных характеристик. Если действующее давление меньше статического критического давления, то возбуждаются колебания кольца. В противном случае прогибы в линейном анализе неограниченно возрастают. Они сопровождаются высокочастотными колебаниями с уменьшающимися амплитудами по росту гармоник. Определяется преобладающая гармоника в различные моменты динамического выпучивания в зависимости от количества атомов, образующих кольцо. В начале процесса преобладает низшая гармоника с наибольшей амплитудой в начальном прогибе, в дальнейшем быстрее возрастают другие гармоники и происходит их перестройка в зависимости от входных параметров.

Эти результаты относятся к линейной стадии развития прогибов нанотрубки. В нелинейной стадии возможна очередная перестройка гармоник, так как потенциальная энергия деформации при более высоких гармониках растет быстрее, чем для низших гармоник. Поэтому при любом их начальном распределении и преобладающих гармониках в зависимости от отношения давления к его критическому значению основной формой деформации может являться низшая гармоника.