1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Физика, технические науки
  4. T. 508, № 1, 2023

Доклады Российской академии наук. Физика, технические науки, 2023, T. 508, № 1, стр. 53-58

ОЦЕНКА ТЕМПЕРАТУРНЫХ НАПРЯЖЕНИЙ В ЛИТОСФЕРЕ РАННЕЙ ЛУНЫ

С. А. Воропаев 1, *, А. П. Кривенко 1, **

1 Институт геохимии и аналитической химии им. В.И. Вернадского Российской академии наук
Москва, Россия

* E-mail: voropaev@geokhi.ru
** E-mail: krivenko@geokhi.ru

Поступила в редакцию 18.04.2022
После доработки 18.04.2022
Принята к публикации 10.08.2022

Полный текст (PDF)

Аннотация

На ранних этапах развития Луны ее растущая литосфера испытала сложные изменяющиеся во времени температурные и гравитационные напряжения. Несмотря на последующее интенсивное ударное преобразование поверхности, в ходе гравиметрической съемки космической миссии GRAIL было обнаружено наличие реликтовых глубинных разломов. Анализ линейных гравитационных аномалий показывает расширение внешнего жесткого слоя планеты на определенном раннем этапе эволюции Луны из-за превышения температурных напряжений над гравитационным сжатием. Получение зависимости временного интервала расширения литосферы от ряда безразмерных параметров теплопроводности позволит уточнить существующие модели тепловой и геохимической эволюции ранней Луны.

Ключевые слова: температурные напряжения, деформации, тепловое расширение, гравитация, радиоактивный разогрев, Луна

Формирование коры и мантии ранней Луны сопровождалось возникновением температурных и гравитационных напряжений в растущей литосфере, с чем связаны особенности ее гравитационного поля, отражающие наличие реликтовых разломов и гравитационных аномалий (масконов). Космическая миссия GRAIL по изучению внешнего гравитационного поля Луны с помощью взаимного зондирования движения двух спутников на низкой орбите позволила обнаружить скрытые подповерхностные геологические структуры [1]. Предыдущие исследования ограничивались крупномасштабной съемкой низкого разрешения, при которой вклад только значительных объектов был заметен в сигнале. Тем не менее это позволило сделать ряд важных выводов о внутренней структуре Луны (малое ядро, реликтовый приливной выступ) и обнаружить гравитационные аномалии (масконы) под основными лунными морями [2]. GRAIL позволил довести разложение гравитационного поля по сферическим гармоникам до 420 порядка (модель GLA 0420A), что соответствует пространственному разрешению ~13 км на поверхности планеты. Это сделало возможным исследование ранней эволюции Луны, поскольку ударными кратерами стерло большую часть геологической летописи первых ~700 млн лет ее истории.

Полученная карта распределения горизонтального градиента потенциала Буге отображает богатый набор коротковолновых структур в лунной коре. Особенно заметен ряд удлиненных линейных гравитационных аномалий (ЛГА), характеризующихся отрицательными градиентами, которые четко выделяются над фоновой изменчивостью. Четыре крупных ЛГА имеют протяженность более 500 км, оценка 22 наиболее отчетливых ЛГА дает общую протяженность 5300 км и еще 44 возможные аномалии имеют общую протяженность 8160 км [3]. Из земной геологии известно, что плоские магматические интрузии формируются перпендикулярно направлению растягивающего главного напряжения с образованием вертикальных даек в горизонтальном поле напряжений растяжения и складок в горизонтальном поле напряжений сжатия. Хотя локальные напряжения при изгибе литосферы могут изменять ориентацию интрузии, в общем ЛГА равномерно распределены по всей Луне и не показывают четкой предпочтительной ориентации или связи с морями. Эта закономерность указывает на изотропное глобальное горизонтальное расширение литосферы в прошлом.

U–Pb-изотопные исследования большинства отобранных образцов морских базальтов показали возраст экструзии магмы в интервале примерно 3.9–3.1 млрд лет назад [4]. Геологические оценки времени формирования грабенов возле масконов указывают на глобальное прекращение этого процесса примерно 3.6 млрд лет назад [5]. Это накладывает временные ограничения как на тепловые модели, так и на смену режимов растяжение–сжатие литосферы ранней Луны. Анализ геофизических данных о текущем тепловом состоянии Луны на основе тепловых потоков, сейсмических данных и электромагнитного зондирования [6] показал, что внешние слои Луны являются субсолидусными. При этом, ниже примерно 1000 км, температуры, возможно, находятся на уровне точки плавления. Это подтверждает тот факт, что хрупкое разрушение в виде лунных землетрясений происходит примерно на глубине 1000 км. Таким образом, в силу малого размера Луны, ее магматический океан (МО) был ограничен по размеру и довольно быстро, по геологическим масштабам времени, закристаллизовался [7]. Магматические извержения моложе 3 млрд лет объясняются уже локальными причинами: значительными ударными событиями и сопровождавшими их подъемами мантийного вещества с последующим декомпрессионным плавлением.

Поскольку большую часть своей истории породы Луны были в субсолидусном состоянии, мы можем для оценки напряжений периода после застывания МО использовать простую сферически-симметричную модель твердого шара с однородным распределением радиоактивных изотопов в качестве внутреннего источника тепла. При расчете упругих деформаций литосферы Луны под действием внешних нагрузок может быть применена хорошо разработанная методика с использованием гравитационного (приливного, центробежного и др.) потенциала [8]. Результирующая сила F в объеме тела может быть определена с помощью градиента полного потенциала

(1)
$\begin{gathered} {\mathbf{F}} = {{\rho }_{0}}\,{\text{grad}}[V({\mathbf{r}})],~ \\ V({\mathbf{r}}) = {{V}_{g}}({\mathbf{r}}) + {{V}_{\omega }}({\mathbf{r}}) + {{V}_{t}}({\mathbf{r}}), \\ \end{gathered} $
где ρ0 – средняя плотность, Vg – гравитационный, Vω – центробежный и Vt – приливной потенциалы. Для твердого шара радиуса R, в случае сферической симметрии всех нагрузок, вектор деформации u имеет только радиальную компоненту u(r), а тензоры деформации εij и напряжений σij – радиальную и тангенциальную компоненты. Условия равновесия вещества в объеме изотропного тела под действием результирующей силы имеют вид
(2)
$\mu {\mathbf{\Delta u}}{\text{ }} + (\lambda + \mu ){\text{grad}}({\text{div}}{\mathbf{u}}) = --{\mathbf{F}},$
$\mu {\text{ }} = {\text{ }}\frac{E}{{2\left( {1 + \nu } \right)}};\quad \lambda = \nu \frac{E}{{(1 + \nu )(1--2\nu )}},$
где μ, λ – упругие постоянные Ламе, ν – коэффициент Пуассона, а Е – модуль Юнга для вещества тела. Данные ограничения на поле деформаций должны быть дополнены граничными условиями нагрузки на поверхность. Если внешняя поверхность свободна от внешней нагрузки, как это обычно бывает для безатмосферных планет и малых тел, то σrr(R) = 0 при r = R.

Предположим, что изменение начальной температуры, T0, на ∆T = T – T0 не повлияло существенно на механические свойства лунных пород. Тогда единственным следствием нагрева будет возникновение дополнительных деформаций, обусловленных всесторонним тепловым расширением с коэффициентом α. Эти деформации накладываются на упругие и должны быть учтены как вызывающие температурные напряжения. В таком случае, связь тензоров деформации εij и напряжений σij может быть выражена следующим образом:

${{\sigma }_{{ij}}} = 2\mu {{\varepsilon }_{{ij}}} + \lambda \varepsilon --\left( {2\mu + 3\lambda } \right)\alpha \Delta T,$
а выражение (1) обобщено как

(3)
${\mathbf{F}} = {{\rho }_{0}}{\text{grad}}\left( {V({\mathbf{r}})} \right)--\left( {2\mu + 3\lambda } \right)\alpha {\text{grad}}\left( {\Delta T} \right).$

В силу линейности уравнения равновесия (2), удобно разделить решение для радиального смещения u(r) с помощью (3) на две части: гравитационную uG – с силой тяжести, g(r) = dVg/dr, и температурную uT – с α∆T(r):

(4a)
$\frac{{E(1--\nu )}}{{(1 + \nu )(1--2\nu )}}\frac{{d\left( {\frac{1}{{{{r}^{2}}}}\frac{{d({{r}^{2}}{{u}_{G}})}}{{dr}}} \right)}}{{dr}} = {{\rho }_{0}}g(r)\frac{r}{R},$
(4б)
$\frac{{{{d}^{2}}{{u}_{T}}}}{{d{{r}^{2}}}} + \frac{2}{r}\frac{{d{{u}_{T}}}}{{dr}}--\frac{{2{{u}_{T}}}}{{{{r}^{2}}}}\,~\, = \frac{{1 + \nu }}{{1--\nu }}\alpha \frac{{d\Delta T}}{{dr}}.$

Решение (4a), удовлетворяющее граничному условию σrr(R) = 0, при r = R имеет вид

(5)
$u = {{\rho }_{0}}{{g}_{0}}\frac{{R(1 + \nu )(1--2\nu )}}{{10E(1--\nu )}}r\,\left[ {{{{\left( {\frac{r}{R}} \right)}}^{2}}--\frac{{3--\nu }}{{1 + \nu }}} \right],$
где ${{g}_{0}} = G\frac{4}{3}\pi {{\rho }_{0}}R$ – ускорение свободного падения на поверхности, G – гравитационная постоянная. Компоненты тензора напряжений σr и σt можно представить в виде

(6a)
${{\sigma }_{r}} = {{\rho }_{0}}{{g}_{0}}R\frac{{3{\text{ }}--\nu }}{{10}}(1--\nu ){\text{ }}\left[ {{{{\left( {\frac{r}{R}} \right)}}^{2}}--1} \right],$
(6б)
${{\sigma }_{r}} = {{\rho }_{0}}{{g}_{0}}R\frac{{1 + 3\nu }}{{10}}(1--\nu )\left[ {{{{\left( {\frac{r}{R}} \right)}}^{2}}--\frac{{3--\nu }}{{1 + 3\nu }}} \right].$

Легко заметить, что при любом значении коэффициента Пуассона в разумном интервале, ν = = 0–0.5, компоненты σr и σt отрицательны, что указывает на общее сжатие пород под действием гравитации.

Решение (4б) имеет общий вид:

(7)
$u(r) = \frac{{1 + \nu }}{{1--\nu }}\frac{\alpha }{{{{r}^{2}}}}\int\limits_a^r {T(x){{x}^{2}}dx} + {{C}_{1}}r + \frac{{{{C}_{2}}}}{{{{r}^{2}}}},$
где С1 и С2 – постоянные интегрирования, определяемые граничными условиями; a – удобный нижний предел интегрирования, например, нижняя граница литосферы Луны; T(r) – отклонение температуры ∆T от начальной, при которой напряжения полагаются нулевыми. В этом случае, согласно (7), компоненты тензора напряжений σr, и σt, можно представить как

$\begin{gathered} {{\sigma }_{r}} = --\frac{{2\alpha E}}{{(1--\nu )}}\frac{1}{{{{r}^{3}}}}\int\limits_a^r {T(x){{x}^{2}}dx} + \\ + \,\frac{{E{{C}_{1}}}}{{(1--2\nu )}}--2\frac{{E{{C}_{2}}}}{{(1 + \nu )}}\frac{1}{{{{r}^{3}}}}, \\ \end{gathered} $
$\begin{gathered} {{\sigma }_{t}} = \frac{{2\alpha E}}{{(1--\nu )}}\frac{1}{{{{r}^{3}}}}\int\limits_a^r {T(x){{x}^{2}}dx} + \frac{{E{{C}_{1}}}}{{(1--2\nu )}} + {\text{ }} \\ + \,\frac{{E{{C}_{2}}}}{{\left( {1 + \nu } \right)}}\frac{1}{{{{r}^{3}}}}--\frac{{\alpha ET(r)}}{{\left( {1--\nu } \right)}}. \\ \end{gathered} $

Для сплошного шара a = 0 и при смещении в центре u(0) = 0, C2 = 0. Тогда при свободной от нагрузок внешней поверхности

$\frac{{E{{C}_{1}}}}{{(1 - 2\nu )}} = \frac{{2\alpha E}}{{(1 - \nu )}}\frac{1}{{{{R}^{3}}}}\int\limits_0^R {T(x){{x}^{2}}dx} ,$
а компоненты тензора напряжений (7) принимают вид

(8a)
$\begin{gathered} {{\sigma }_{r}} = 2\alpha \frac{E}{{(1--\nu )}}\left[ {\frac{1}{{{{R}^{3}}}}\int\limits_0^R {T(x){{x}^{2}}dx - } } \right. \\ \left. { - \frac{1}{{{{r}^{3}}}}\int\limits_0^r {T(x){{x}^{2}}dx} } \right], \\ \end{gathered} $
(8б)
$\begin{gathered} {{\sigma }_{t}} = \alpha \frac{E}{{(1--\nu )}}\left[ {\frac{1}{{{{r}^{3}}}}\int\limits_0^r {T(x){{x}^{2}}dx} } \right. + \\ \left. { + \frac{2}{{{{R}^{3}}}}\int\limits_0^R {T(x){{x}^{2}}dx - T(r)} } \right]. \\ \end{gathered} $

Средняя температура сферы Ť(r) внутри радиуса r составит

(9)
$\check{T}(r) = \frac{{4\pi \int\limits_0^r {T(x){{x}^{2}}dx} }}{{\frac{4}{3}\pi {{r}^{3}}}} = \frac{3}{{{{r}^{3}}}}\int\limits_0^r {T(x){{x}^{2}}dx.} $

Следовательно, радиальное напряжение σr при любом радиусе r пропорционально разности между средней температурой всей сферы Ť(R) и средней температурой сферы радиуса r Ť(r):

(10a)
${{\sigma }_{r}} = \frac{2}{3}\alpha \frac{E}{{1--\nu }}[\check{T}\left( R \right)--\check{T}\left( r \right)].$

Аналогично, для тангенциального напряжения σt

(10б)
${{\sigma }_{t}} = \alpha \frac{E}{{1--\nu }}\left[ {\check{T}(r)--T(r) + \frac{2}{3}(\check{T}(R)--\check{T}(r))} \right].$

Из данных выражений легко увидеть, что горячая внутренняя часть вызывает радиальное сжатие более холодной внешней поверхности σr < 0, с одновременным ее тангенциальным растяжением σt > 0.

Для определения величины и временного поведения температуры в недрах Луны необходимо оценить мощность внутренних источников тепла. Нестабильные изотопы 26Al, 60Fe и другие короткоживущие изотопы могли обеспечивать теплогенерацию лишь первые несколько миллионов лет существования Солнечной системы. Радиоактивный разогрев мантии и коры как Земли, так и Луны происходил в основном за счет распада долгоживущих изотопов урана 235U и 238U, тория 232Тh и 40К. Удельная теплогенерация Q, связанная с этими элементами, и их периоды полураспада приведены в табл. 1 [9].

Таблица 1.

Значения теплогенерации основных радиоактивных элементов в земных недрах

Изотоп Q, Вт/кг t1/2, лет Концентрация С, кг/кг
238U 9.37 × 10–5 4.47 × 109 25.5 × 10–9
235U 5.69 × 10–4 7.04 × 108 0.185 × 10–9
U 9.71 × 10–5 – 25.7 × 10–9
232Th 2.69 × 10–5 1.40 × 1010 103 × 10–9
40K 2.79 × 10–5 1.25 × 109 32.9 × 10–9
K 3.56 × 10–9 – 25.7 × 10–5

Тепловыделение подсчитано на основе современных средних значений концентрации радиоактивных элементов в мантии Земли. Полагая общий источник вещества при формировании Земли и Луны, оценочно можно принять схожие значения концентраций и для мантии Луны.

Описанная выше длительность магматической активности Луны – примерно 1 млрд лет, указывает на вероятный источник тепла – радиоактивный распад нестабильного изотопа калия 40К с периодом полураспада 1.25 млрд лет. Соответственно, удельное тепло w(t), выделявшееся в недрах ранней Луны, будет определяться первоначальной концентрацией 40K и зависеть от времени по закону

(11)
$w\left( t \right) = {{w}_{0}}{\text{exp}}\left( {--\lambda t} \right),\quad {\text{где}}\quad {{w}_{0}} = {{Q}_{0}}{{\rho }_{0}},$
где константа λ связана с периодом полураспада простым соотношением:

$\lambda = \frac{{{\text{ln}}2}}{{{{t}_{{1/2}}}}} = \frac{{0.693}}{{1.25 \times {{{10}}^{9}}\,{\text{лет}}}} = 5.54 \times {{10}^{{--10}}}\,{\text{го}}{{{\text{д}}}^{{--1}}}.$

Будем считать, что в некоторый (начальный для расчетов) момент времени Луна оказывается в среде с постоянной температурой Тс < Т, а теплообмен между поверхностью планеты и окружающей средой происходит по закону Ньютона. Это отображает в первом приближении сложный лучистый и конвективный теплообмен, в котором доля лучистого потока тепла является преобладающей. Решение упрощенного уравнения теплопроводности для сферически симметричной Луны радиуса R, с однородным распределением плотности ρ(r) = ρ0 и теплоемкости слагающих пород Cp(r, t) = С, позволяет аналитически оценить поведение температуры со временем

(12)
$\begin{gathered} \frac{{\partial (rT(r,t))}}{{\partial t}} = a\frac{{{{\partial }^{2}}\left[ {rT\left( {r,t} \right)} \right]}}{{\partial {{r}^{2}}}} + \frac{{{{w}_{0}}}}{C}{{\rho }_{0}}re\left( { - \lambda t} \right),{\text{ }} \\ 0 \leqslant r \leqslant R, \\ \end{gathered} $
с известными граничными и начальными условиями:
$--\frac{{\partial (T(R,t))}}{{\partial r}} + H({{T}_{c}}--T(R,t)) = 0\quad {\text{при}}\quad r = R,$
(13)
$\frac{{\partial T(0,t)}}{{\partial r}} = 0\quad {\text{при}}\quad r \to 0;$
$T(r,0) = f(r) = {{T}_{0}}\quad {\text{при}}\quad t = 0,$
где r – текущее радиальное расстояние от центра планеты, a – коэффициент температуропроводности пород Луны, H – коэффициент теплообмена.

Вид уравнения (11) позволяет найти общее решение методом разделения переменных:

$\begin{gathered} \theta (r,t) = T(r,t)--{{T}_{c}}_{~} = --\frac{{{{w}_{0}}}}{C}{{\rho }_{0}}{{k}_{0}}{\text{exp}}\left( {--\lambda t} \right){\text{ + }} \\ + \,A\frac{{{\text{sin}}({{k}_{0}}r)}}{r}e\left( {--\lambda t} \right) + {{C}_{n}}\frac{{{\text{sin}}({{k}_{n}}r)}}{r}{\text{exp(}}{\kern 1pt} --{\kern 1pt} k_{n}^{2}at), \\ \end{gathered} $
где $k_{0}^{2}a = \lambda $ и $\frac{{\partial (\theta (R,t))}}{{\partial r}} = --H\theta (R,t)$ при r = R. Начальное условие T0 = сonst при t = 0 определяет возможные значения kn следующим выражением для μn = knR:

(14)
${\text{tg}}({{\mu }_{n}}) = --\frac{{{{\mu }_{n}}}}{{HR--{\text{ }}1}},\quad n = 1,2,3,{\text{ }} \ldots $

Некоторые частные решения уравнения (14) приведены в табл. 2.

Таблица 2.

Значения μn = knR для различных Bi = HR

Bi = HR μ1 μ2 μ3 μ4 μ5 μ6
0.05 0.3854 4.5045 7.7317 10.9087 14.0697 17.2237
2 2.0288 4.9132 7.9787 11.0856 14.2075 17.3364
8 2.7654 5.6078 8.5406 11.5408 14.5817 17.6567
16 2.9476 5.9080 8.8898 11.8959 14.9251 17.9742

В безразмерной форме, с помощью разложения Фурье, поведение температуры представляется в виде

$\begin{gathered} {\text{ - - O}} = \frac{{T(r,t)--{{T}_{0}}}}{{{{T}_{0}}--{{T}_{c}}}} = 1 + {\text{Po}} \cdot {\text{exp}}\left( {--\lambda t} \right) \times \\ \times \,\left[ {1\,--\,{\text{Bi}} \cdot \frac{{\sin ({{k}_{0}}r)}}{{(r{\text{/}}R)}}{\text{/}}({{k}_{0}}R\cos ({{k}_{0}}R)\, + \,\sin ({{k}_{0}}R)({\text{Bi}}\,--\,1))} \right]{\text{ + }} \\ + \,\sum\limits_n^{} {{{C}_{n}}} ({\text{Bi}},{{\mu }_{n}}){\text{exp}}\left( {--\mu _{n}^{2}at{\text{/}}{{R}^{2}}} \right){\text{sin}}\left( {{{\mu }_{n}}r{\text{/}}R} \right){\text{/}}(r{\text{/}}R) \times \\ \times \,\,\left[ {1 + \frac{{{\text{Po}}}}{{\left( {1--\frac{{\mu _{n}^{2}}}{{{{{({{k}_{0}}R)}}^{2}}}}} \right)}}} \right], \\ \end{gathered} $
где

(15)
$\begin{gathered} {{C}_{n}}({\text{Bi}},{{\mu }_{n}}) = \\ = 2{\text{cos}}({{\mu }_{n}})\frac{{{\text{Bi}}}}{{{\text{Bi}}--1}}({{\mu }_{n}}--{\text{sin}}({{\mu }_{n}}){\text{cos}}({{\mu }_{n}})). \\ \end{gathered} $

Безразмерные величины Bi (параметр Био), Pd (критерий Предводителева) и Po (критерий Померанцева) хорошо известны из теории теплопроводности [10] как Bi = HR, Po = $\frac{{{{w}_{0}}}}{C}{{\rho }_{0}}\lambda {\text{ }}({{T}_{0}}--{{T}_{c}})$ и ${\text{Pd}} = {\text{ }}{{({{k}_{0}}R)}^{2}} = {\text{ }}\lambda \frac{{{{R}^{2}}}}{a} = {\text{ln}}\left( 2 \right)\frac{{t{\kern 1pt} *}}{{{{t}_{{1/2}}}}}$, где $t{\kern 1pt} * = \frac{{{{R}^{2}}}}{a}$. Их физический смысл определяется как безразмерные отношения скоростей теплообмена с внешней средой, внутренней теплогенерации и охлаждения за счет теплопроводности. На рис. 1 приведены два примера временного поведения безразмерной температуры ${\text{ - - O }} = \frac{{{\text{ }}T(r,t){\text{ }}--{{T}_{0}}}}{{{{T}_{0}}--{{T}_{c}}}}$ с глубиной  при различных значениях величин Bi, Po и Pd.

Рис. 1.

Временное поведение ${\text{ - - O }} = \frac{{T(r,t){\text{ }}--{{T}_{0}}}}{{{{T}_{0}}--{{T}_{c}}}}$ на разных глубинах: (a) Bi = 2, Po = 450, Pd = 0.2; (б) Bi = 8, Po = 300, Pd = 0.5.

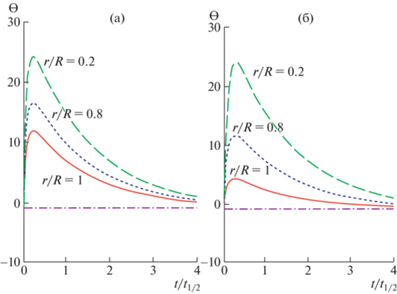
Заметно, что большая интенсивность теплообмена с окружающей средой (см. рис. 1б, Bi = 8) способствует более холодной литосфере, при сравнимом поведении температуры в мантии.

Общее тангенциальное напряжение в недрах планеты определяется суммой выражений (6б) и (10б) в безразмерной форме:

(16)
$\begin{gathered} {{\sigma }_{r}} = \frac{{{{\sigma }_{0}}}}{{1 - \nu }}\left\{ {\left[ {{\text{ - - O}}(r) - \Theta (r) + \left. {\frac{2}{3}(\Theta (R) - \Theta (r))} \right]} \right.} \right. + \\ \left. { + \,p\left( {1 + 3\nu } \right)\left[ {{{{\left( {\frac{r}{R}} \right)}}^{2}}--\frac{{3 - \nu }}{{1 + 3\nu }}} \right]} \right\},~~ \\ \end{gathered} $
$\begin{gathered} {{\sigma }_{0}} = \alpha E({{T}_{0}} - {{T}_{c}}), \\ p = {{\rho }_{0}}{{g}_{0}}\frac{R}{{10}}\alpha E({{T}_{0}} - {{T}_{c}}), \\ \end{gathered} $
где Θ(r) – средняя безразмерная температура сферы радиуса r согласно (9); p – новый безразмерный параметр, определяемый отношением гравитационных и температурных напряжений. Для оценки возможного интервала значений параметра p мы используем как физические величины, хорошо известные для Луны: ρ0 ≈ 3300 кг/м3, g0 ≈ 1.63 м/с2 и R ≈ 1730 км, так и приблизительные, характерные для схожих горных пород (базальты): α ≈ 1–10 × 10–6 1/град, E ≈ 10–100 ГПa, T0 – Tc ≈ ≈ 100–1000°С: p ≈ 1–10. На рис. 2 приведены два примера временного поведения тангенциального напряжения с глубиной в литосфере при различных значениях величин Bi, Po и Pd, использованных нами ранее при оценке поведения температуры.
Рис. 2.

Временное поведение στ/σ0 на разных глубинах литосферы, ν = 0.2: (a) Bi = 2, Po = 450, Pd = 0.2, p = 2; (б) Bi = 8, Po = 300, Pd = 0.5, p = 5.

Заметно, что большая интенсивность теплообмена с окружающей средой (см. рис. 2б, Bi = 8) способствует более быстрому переходу от расширения к сжатию в более холодной литосфере.

Приведенные расчеты температурных напряжений в литосфере ранней Луны показали принципиальную применимость использованной простой тепловой модели. На основе точных решений, возможных в сферически-симметричной постановке задачи теплопроводности, получено качественно правильное временное поведение температуры и напряжений, согласующееся с геологическими данными. Для типичных параметров горной породы: α ≈ 10–5 1/градус, E ≈ 60 ГПa, ν ≈ ≈ 0.2 и T0 – Tc ≈ 100°С, максимальное общее растягивающее напряжение в литосфере Луны могло достигать 120 МПа. Это большая величина, вполне достаточная для образования трещин и разломов [11]. Более точная модель должна учитывать неоднородное распределение радиоактивных элементов в мантии Луны и зависимость физических параметров (плотность, температуропроводность) от глубины в соответствии с уравнением состояния [12]. Такое уточненное рассмотрение требует уже численного моделирования и является предметом последующей работы.

Список литературы

  1. Zuber M.T. et al. Gravity field of the Moon from the Gravity Recovery and Interior Laboratory (GRAIL) mission // Science. 2013. V. 339. P. 668–671. https://doi.org/10.1126/science.1231507

  2. Zuber M.T., Smith D.E., Lemoine F.G., Neumann G.A. The shape and internal structure of the Moon from the Clementine mission // Science. 1994. V. 266. P. 1839–1843. https://doi.org/10.1126/science.266.5192.1839

  3. Andrews-Hanna J.C. et al. Ancient Igneous Intrusions and Early Expansion of the Moon Revealed by GRAIL Gravity Gradiometry // Science. 2012. V. 339. P. 675–678. https://doi.org/10.1126/science.1231753

  4. Shearer C.K. et al. Thermal and Magmatic Evolution of the Moon // Reviews in Mineralogy & Geochemistry. 2006. V. 60. P. 365–518. https://doi.org/10.2138/rmg.2006.60.4

  5. Solomon S., Head J. W. Lunar mascon basins: Lava filling, tectonics, and evolution of the lithosphere // Rev Geophys Space Phys. 1980. V. 18. P. 107–141.

  6. Hood L.L., Zuber M.T. Recent refinements in geophysical constraints on lunar origin and evolution / In: Origin of the Earth and Moon. Canup R.M., Righter K. (eds). Univ Arizona Press, 2000. P. 397–412.

  7. Elkins-Tanton L.T. Magma Oceans in the Inner Solar System // Annual Review Earth Planetary Science. 2012. V. 40. P. 113–139.

  8. Воропаев С.А., Джианго Я., Барриот Ж.-П. Разрыв вытянутого малого тела приливными силами при подлете: возможные сценарии // Астрономический вестник. 2020. Т. 54. № 2. С. 171–182.

  9. Теркот Д., Шуберт Дж. Геодинамика. Геологические приложения физики сплошных сред. М.: Мир, 1985. Т. 1. 381 с.

  10. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1987. 602 с.

  11. Воропаев С.А., Нугманов И.И., Душенко Н.В., Джинго Я. Зависимость упругих свойств Н5-хондритов (NWA 12370) от давления // ДАН. Физика, Технические науки. 2020. Т. 495. С. 14–17.

  12. Жарков В.Н., Трубицын В.П., Самсоненко Л.В. Физика Земли и планет. Фигуры и внутреннее строение. М.: Наука, 1971. 383 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Физика, технические науки

Архивы выпусков Информация о журнале Отправить рукопись в журнал