Доклады Российской академии наук. Химия, науки о материалах , 2022, T. 504, № 1, стр. 72-102
НЕЙРОСЕТЕВОЕ ПРОГНОЗИРОВАНИЕ МЕЖАТОМНОГО ВЗАИМОДЕЙСТВИЯ В МУЛЬТИЭЛЕМЕНТНЫХ ВЕЩЕСТВАХ И ВЫСОКОЭНТРОПИЙНЫХ СПЛАВАХ. ОБЗОР
А. А. Мирзоев 1, Б. Р. Гельчинский 2, академик РАН А. А. Ремпель 2, *
1 Южно-Уральский государственный университет
454080 Челябинск, Россия
2 Институт металлургии
Уральского отделения Российской академии наук
620016 Екатеринбург, Россия
* E-mail: rempel.imet@mail.ru
Поступила в редакцию 23.03.2022
После доработки 23.05.2022
Принята к публикации 01.06.2022
- EDN: RVFPSE
- DOI: 10.31857/S2686953522700066
Аннотация
Одним из самых захватывающих инструментов, вошедших в последние годы в арсенал современной науки и техники, является машинное обучение, способное эффективно решать задачи аппроксимации многомерных функций. Наблюдается бурный рост работ по разработке и применению машинного обучения в физике и химии. Настоящий обзор посвящен возможностям прогнозирования межатомных взаимодействий в мультиэлементных веществах и высокоэнтропийных сплавах с помощью искусственного интеллекта на основе нейронных сетей и их активного машинного обучения, в котором предоставлены исчерпывающий обзор и анализ последних исследований по этой теме. Актуальность этого направления связана с тем, что предсказания структуры и свойств материалов с помощью квантово-механического атомистического моделирования с использованием теории функционала плотности (DFT) во многих случаях затруднены из-за быстрого роста вычислительных затрат при увеличении размеров в соответствии с размером объекта. Методы машинного обучения позволяют воссоздавать реальные потенциалы межчастичного взаимодействия исследуемой системы на основе имеющихся в литературе DFT-расчетов, а затем на их основе моделировать требуемые свойства методом молекулярной динамики в многократно увеличенном пространственно-временном масштабе. В качестве отправной точки мы знакомим с принципами машинного обучения, алгоритмами, дескрипторами и базами данных в материаловедении. Описано конструирование поверхности потенциальной энергии и потенциалов межатомного взаимодействия в твердых растворах, высокоэнтропийных сплавах, высокоэнтропийных соединениях металлов с углеродом, азотом и кислородом, а также в объемоаморфных материалах.
I. ВВЕДЕНИЕ 73
II. МАШИННОЕ ОБУЧЕНИЕ НЕЙРОННЫХ СЕТЕЙ 75
III. МЕТОДЫ МАШИННОГО ОБУЧЕНИЯ ДЛЯ КОНСТРУИРОВАНИЯ ПОВЕРХНОСТИ МЕЖАТОМНОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ (ППЭ) 84
IV. ПРОГНОЗИРОВАНИЕ МЕЖАТОМНЫХ ПОТЕНЦИАЛОВ МАШИННОГО ОБУЧЕНИЯ (MLIP) ДЛЯ МОДЕЛИРОВАНИЯ МУЛЬТИЭЛЕМЕНТНЫХ ВЕЩЕСТВ 87
V. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ВЫСОКОЭНТРОПИЙНЫХ СПЛАВОВ (HEAS) С ПОМОЩЬЮ МЕЖАТОМНЫХ ПОТЕНЦИАЛОВ МАШИННОГО ОБУЧЕНИЯ (MLIP) 93
VI. ЗАКЛЮЧЕНИЕ 97
СПИСОК ЛИТЕРАТУРЫ 97
СПИСОК СОКРАЩЕНИЙ
ANN – искусственные нейронные сети (artificial neural networks)
CE – метод кластерного разложения (cluster-expansion approach)
DFT – теория функционала плотности (density functional theory)
DNN – глубокие нейронные сети (deep neural nets)
EAD – дескриптор погруженной атомной плотности (embedded atomic density)
EAM – потенциал погруженного атома (embedded atom model)
GAP – потенциалы гауссовой аппроксимации (Gaussian approximation potentials)
HEA – высокоэнтропийный сплав (high entropy alloy)
MLIP – межатомные потенциалы машинного обучения (machine learning interatomic potential)
MTP – потенциалы на тензора моментов атомных окружений (moment tensor potentials)
SNAP – потенциал на основе спектрального анализа окружения (spectral neighbor analysis potential)
SQS – специальные квазислучайные структуры (special quasi-random structures)
SRO – ближний порядок (short range order)
QM – квантово-механический (quantum mechanics)
МД – молекулярная динамика (molecular dynamics)
МК – Монте-Карло (Monte Carlo )
ППЭ – поверхность потенциальной энергии (potential energy surface, PES)
ЭДУ – энергия дефекта упаковки (packing defect energy)
ВЭС – высокоэнтропийные системы (high entropy systems)
I. ВВЕДЕНИЕ
Компьютерное моделирование играет важную роль в ускорении разработки состава сплава и прогнозировании явлений, определяющих эволюцию его микроструктуры в процессе его термообработки и эксплуатации. При этом моделирование охватывает широкий диапазон пространственных объемов и временных масштабов, поэтому, как правило, требуется многомасштабный подход. Ab initio расчеты, основанные на теории функционала плотности (DFT) [1–3], используются для описания электронной структуры, колебательных мод и энергетических параметров ячеек кристалла с идеальной структурой, что соответствует случаю бездефектного материала при нулевой температуре. Ab initio молекулярная динамика (AIMD) [4, 5] имеет точность, обеспечиваемую теорией функционала плотности, но ее огромные вычислительные затраты ограничивают типичные приложения сотнями атомов и временными масштабами порядка 100 пс. Атомистическое моделирование методами Монте-Карло (МК) и молекулярной динамики (МД) [6–9] открывает путь к большим масштабам, с объемными размерами и временами (порядка 1 мкм3 и 1 мкс соответственно). Такое мезомасштабное моделирование уже позволяет оценить влияние температуры и деформаций на эволюцию дефектной микроструктуры, определяющей реальный уровень прочности вещества [10, 11]. Однако для МД и МК-моделирования требуется модель межатомного взаимодействия, которая предсказывала бы силы, действующие на атомы, в зависимости от расположения окружающих их соседей. Для этого необходимо знание поверхности потенциальной энергии (ППЭ) изучаемой системы в каждый из моментов времени, на котором изучается ее эволюция. Для построения ППЭ возможно использование нескольких подходов. Наиболее точным является подход, основанный на расчете потенциальной энергии в рамках квантовой теории DFT [1], который может обеспечить ППЭ для произвольной системы, но, как мы уже отмечали, очень требователен в вычислительном отношении и не подходит для мезомасштабного моделирования. Второй подход – это эмпирические и полуэмпирические модели ППЭ. В отличие от квантово-механических моделей (QM), такие модели позволяют проводить быстрые вычисления больших атомистических систем (до миллионов атомов) в течение длительного времени (до микросекунд), но их точность часто недостаточна для количественного анализа.
Потенциальную энергию, описывающую взаимодействие системы из N атомов, в общем случае можно разделить на одно-, двух-, трехчастичные и т.д., вплоть до N-атомных вкладов, следующим образом [12]
(1)
$\begin{gathered} {{E}_{{{\text{total}}}}}\left( {{{r}_{1}},{{r}_{2}} \ldots {{r}_{N}}} \right) = \\ = \mathop \sum \limits_{i = 1}^N {{\phi }_{1}}\left( {{{r}_{i}}} \right) + \mathop \sum \limits_{\begin{array}{*{20}{c}} {i,j = 1} \\ {i < j} \end{array}}^N {{\phi }_{2}}\left( {{{r}_{i}},{{r}_{j}}} \right) + \mathop \sum \limits_{\begin{array}{*{20}{c}} {i,j,k = 1} \\ {i < j < k} \end{array}}^N {{\phi }_{3}}\left( {{{r}_{i}},{{r}_{j}},{{r}_{k}}} \right) + \ldots , \\ \end{gathered} $Чтобы это представление было полезным для описания ППЭ при компьютерном моделировании материалов, слагаемые этого ряда n-частичных вкладов быстро сходились к нулю при увеличении n. Заметим, что одночастичный потенциал ϕ1(ri) описывает внешние силы, действующие на частицы вещества. Если они отсутствуют, то разложение (1), в принципе, начинается с членов парного взаимодействия ${{\phi }_{2}}({{r}_{i}},{{r}_{j}})$.
Исходя из разложения (1), межатомные потенциалы можно условно разделить на два типа: парные потенциалы, в которых присутствуют только двухатомные члены, и многочастичные потенциалы, в которых включены трехатомные и более высокие члены. К простейшим классическим парным потенциалам относятся потенциал твердых сфер, потенциал Леннард-Джонса (2), потенциал Морзе и потенциал Борна–Майера, особенности которых можно найти в обзорах [13, 14]. Атомы рассматриваются как материальные точки, которые имеют центральное взаимодействие со своими ближайшими соседями. Взаимодействие любой пары атомов зависит только от их взаимного расстояния. Это означает, что такие потенциалы радиально симметричны и не зависят от углового положения других атомов поблизости. Подбор констант, определяющих вид потенциалов, производится путем подбора для воспроизведения требуемых свойств вещества, доступных в экспериментах.
(2)
$U(r) = 4\varepsilon \left[ {{{{\left( {\frac{\sigma }{r}} \right)}}^{{12}}} - {{{\left( {\frac{\sigma }{r}} \right)}}^{6}}} \right],$В первых работах по молекулярной динамике в 1950–1970 гг. для описания взаимодействий атомов ограничивались использованием парных потенциалов [15, 16]. По физическому смыслу используемых эмпирических функций (отталкивание Паули, диполь-дипольное притяжение) парные потенциалы представляют собой хорошую характеристику одноатомных газов с закрытой оболочкой, таких как аргон или гелий.
Хотя парные потенциалы позволяют быстро осуществлять атомистическое моделирование, они имеют некоторые существенные недостатки [17, 18]. Поэтому в 70–80-х годах продолжались попытки улучшить описание межатомных потенциалов путем учета многоатомных (коллективных) эффектов.
Один из подходов состоит в явном включении трехатомных членов в разложение потенциальной энергии, и этот подход часто используется при построении эмпирических потенциалов для полупроводников, например, Si, Ga, As, Ge и C. Первым успехом такого подхода стал потенциал Стиллинджера–Вебера [19] для полупроводникового кремния, в котором потенциальная энергия представлена в виде
(3)
$\begin{gathered} {{E}_{{{\text{total}}}}}\left( {{{r}_{1}},{{r}_{2}} \ldots {{r}_{N}}} \right) = \\ = U + \frac{1}{2}\mathop \sum \limits_{i,j = 1}^N {{\phi }_{2}}\left( {{{r}_{{ij}}}} \right) + \mathop \sum \limits_{\begin{array}{*{20}{c}} {i,j,k = 1} \\ {i < j < k} \end{array}}^N g({{r}_{{ij}}})g\left( {{{r}_{{ik}}}} \right){{\left( {{\text{cos}}{{\theta }_{{ijk}}} + \frac{1}{3}} \right)}^{2}}, \\ \end{gathered} $Другой аналитический потенциал, учитывающий влияние ближнего порядка, был основан на концепции химической связи, возникающей в результате перекрывания валентных орбиталей ближайших атомов. Величина химической связи и, соответственно, потенциала определяется порядком связи для групп (кластеров) s-валентных атомов, который позволяет напрямую определять влияние локального атомного окружения на прочность связи. По этой причине данные потенциалы получили названия потенциалов порядка связи (bond-order potentials) [21].
Потенциальная энергия группы (кластера) s-валентных атомов может быть записана в виде
(4)
${{E}_{{{\text{total}}}}}\left( {{{r}_{1}},{{r}_{2}} \ldots {{r}_{N}}} \right) = \frac{1}{2}\mathop \sum \limits_{i,j = 1}^N {{\Phi }}\left( {{{r}_{{ij}}}} \right) + \frac{1}{2}\mathop \sum \limits_{i,j = 1}^N h\left( {{{r}_{{ij}}}} \right){{{{\Theta }}}_{{ij}}},$Для металлических систем достаточно реалистичным подходом к включению многоатомных эффектов является так называемый парно-функциональный потенциал, в котором коллективные эффекты неявно включены через зависимость взаимодействия пары атомов от окружающей среды. Влияние окружающей среды происходит посредством учета локальной электронной плотности в том месте, где находится атом, поскольку вклад в электронную плотность в этом узле обусловлен соседними атомами. В основе подхода лежит предположение, что энергия когезии атома в металле в значительной степени определяется локальной электронной плотностью в том месте, в которое этот атом помещен [23]. Несмотря на то что названия потенциалов, связанные с этим подходом, различны: метод погруженного атома (EAM), теория эффективной среды, потенциал Финниса–Синклера (подробности и сравнение в обзорах [24, 25]), все они дают очень похожие выражения для полной энергии металла, содержащего N атомов:
(5)
$\begin{gathered} {{E}_{{{\text{total}}}}}\left( {{{r}_{1}},{{r}_{2}} \ldots {{r}_{N}}} \right) = \frac{1}{2}\mathop \sum \limits_{i,j = 1}^N {{\varphi }}\left( {{{r}_{{ij}}}} \right) + \mathop \sum \limits_{i = 1}^N {{F}_{i}}\left( {{{\rho }_{i}}} \right) \\ {{\rho }_{i}} = \mathop \sum \limits_{j \ne i} {{\psi }_{{ij}}}, \\ \end{gathered} $Таким образом, для атомистического моделирования указанных проблем ни квантовые, ни эмпирические потенциалы не подходят. Именно это стимулировало появление нового класса моделей межатомного взаимодействия – межатомных потенциалов машинного обучения (MLIP) [28]. Если рассмотренные выше парные или парно-функциональные потенциалы используют для представления энергетической поверхности функции определенного вида, заточенные на описание определенного типа химической связи, то при разработке MLIP-потенциалов, напротив, используют очень общие функциональные формы (например, сплайны или гауссианы), по которым происходит разложение ППЭ. Количество подгоночных параметров при этом резко возрастает, поэтому для построения надежных потенциалов требуется тщательный процесс подгонки, а также необходимы подробные проверки полученного ППЭ, чтобы убедиться, что он имеет правильную форму. Однако, если поверхность потенциальной энергии воспроизведена достаточно точно, то сконструированные потенциалы могут быть численно очень точными, и у них есть то преимущество, что они “не смещены”, т.е. они одинаково хорошо описывают любой тип взаимодействия, например, металлическую, ковалентную или ионную связь.
II. МАШИННОЕ ОБУЧЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
Машинным обучением называется разработка программных методов, которые позволяют компьютерам обучаться без изменения машинного кода. Преимущество эффективного алгоритма машинного обучения очевидно. Вместо трудоемкого создания множества программ для решения разнообразных проблем, единый алгоритм машинного обучения позволит обрабатывать каждую новую проблему с помощью процессов, называемых обучением. Поскольку мозг – лучшая из известных в настоящее время «машин» для обучения и решения проблем, то вполне естественно стремление разработчиков использовать, точнее имитировать, принципы функционирования мозга в той мере, насколько мы понимаем его устройство. Нейронные сети – одно из основных направлений исследований в проблеме машинного обучения.
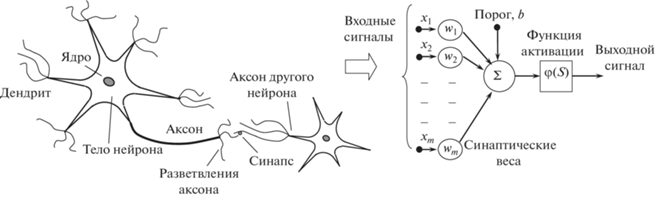
В настоящее время считается, что нервная система мозга состоит из узкоспециализированных клеток – нейронов (рис. 1). Нейрон имеет разветвленную структуру ввода информации (дендриты), ядро и разветвляющийся выход (аксон). Аксоны клетки соединяются с дендритами других клеток с помощью синапсов. При активации нейрон посылает электрохимический сигнал по своему аксону. Через синапсы этот сигнал достигает других нейронов, которые могут в свою очередь активироваться. Нейрон активируется тогда, когда суммарный уровень сигналов, пришедших в его ядро из дендритов, превысит определенный уровень (порог активации). Возможность активации нейрона сильно зависит от активности синапсов. Канадский физиолог и нейропсихолог Д. Хебб сформулировал постулат о том, что обучение заключается в первую очередь в изменениях “силы” синаптических связей под действием коррелирующих во времени событий [29]. Например, в классическом опыте Павлова, когда непосредственно перед кормлением собаки звонил колокольчик, синаптические связи между участками коры головного мозга собаки, ответственными за слух, и слюнными железами усиливались, и при возбуждении коры звуком колокольчика у собаки начиналось слюноотделение. Таким образом, будучи построен из очень большого числа простых элементов, мозг способен решать чрезвычайно сложные задачи.
Искусственный нейрон. Если сконцентрировать внимание только на переработке сигналов рецепторов, т.е. отбросить детали строения и жизнеобеспечения нейрона, то модель, которая описывает прием сигнала, переработку и передачу его другим нейронам, называют искусственным нейроном. В этой модели можно выделить три основных элемента (рис. 1, справа):
1. Набор синапсов или связей, через которые нейрон получает входные сигналы Xj. Каждая связь характеризуется своим весом (wj) или силой, на который умножается входной сигнал Xj. В отличие от синапсов мозга, синаптический вес искусственного нейрона может иметь как положительные, так и отрицательные значения.
2. С каждым нейроном связано определенное значение порога возбуждения (bias), который обозначен символом b. Сумматор Σ складывает взвешенную сумму входных сигналов ${{w}_{i}}{{X}_{i}}$ и вычитает из нее пороговое значение. Полученный результат определяет постсинаптический потенциал или величину активации k нейрона S. Эту операцию можно описать как линейную комбинацию
3. Функция активации, или передающая функция, ограничивает амплитуду выходного сигнала нейрона. Эта функция также называется функцией сжатия. Обычно нормализованный диапазон амплитуд выхода нейрона лежит в интервалах [0, 1] или [1, 1 ]. Чаще всего используется сигмоидальная функция вида
(7)
${{\sigma }}\left( x \right) = \frac{1}{{1 + {\text{exp}}\left( { - \frac{x}{{{\rho }}}} \right)}},$Изменяемые значения весов связей, наличие порога возбуждения b и масштабирующей функции активации делают каждый искусственный нейрон существенно нелинейным элементом.
Архитектура нейронных сетей. Теперь, естественно, возникает вопрос о способах соединения нейронов между собой, т.е. об архитектуре нейронных сетей (НС). Существует множество типов искусственных нейронных сетей для решения различных типов проблем, таких как моделирование памяти, распознавание образов и управление динамическими системами при неполной информации. Обзор архитектуры НС дан в работе [31].
Можно выделить три основных сетевых типа архитектуры: сети прямого распространения, рекуррентные сети и сети трансформеры [32]. Наиболее простым является первый тип архитектуры. Более сложные типы имеют свои преимущества, например, позволяют распараллеливать программы, однако делают задачу определения весов связей при машинном обучении намного более сложной и неоднозначной. В связи с этим для задачи аппроксимации поверхности потенциальной энергии в настоящее время применяется только архитектура сетей прямого распространения, в которой сигнал передается от одного слоя нейронов к другому. Метод машинного обучения, использующий сети прямого распространения, детально описан в книгах [32, 33].
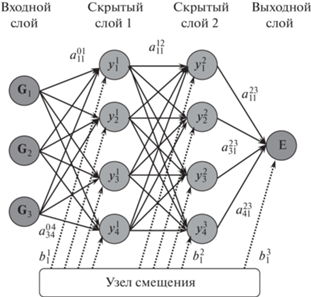
Схематическое изображение вычислительной нейронной сети прямого распространения показано на рис. 2. Нейроны во входном слое получают некоторые значения и передают их нейронам средних слоев сети, которые часто называют “скрытыми слоями”, поскольку они не “видны” из внешнего мира. Взвешенные суммы из одного или нескольких скрытых слоев в конечном итоге передаются на выходной уровень, который представляет окончательные результаты для пользователя. Каждая связь между элементами i слоя n и j слоя m = (n + 1) умножает входной сигнал на свой весовой параметр $a_{{ij}}^{{nm}}$, прежде чем передать его новому узлу. Каждый узел i слоя n суммирует свои входные данные и, после смещения их на величину порогового значения $b_{i}^{n}$, применяет к полученному значению функцию активации. Выходной слой собирает информацию из скрытого слоя и снова ее преобразует. Название – сеть прямого распространения – связано со структурой сети, в которой каждый узел подключен к каждому узлу последующего слоя, тогда как узлы одного слоя не связаны, и информация передается только в одном направлении. Весовые параметры $a_{{ij}}^{{nm}}$ и пороговые смещения $~b_{i}^{n}$ являются параметрами сети, которые настраиваются в процессе обучения для каждой решаемой задачи. Нейронные сети, имеющие более одного скрытого слоя, принято называть “глубокими” (deep neural nets, DNN), чтобы отличать от сетей с одним скрытым слоем, за которыми исторически закрепился термин “перцептрон”, введенный в классической работе Ф. Розенблатта [29], где впервые была предложена схема устройства, моделирующего процесс человеческого восприятия (перцепции). В настоящее время типичное количество сетевых уровней, используемых в глубоком обучении, колеблется от пяти до нескольких тысяч. Чем больше количество скрытых слоев входит в состав НС, тем более сложные корреляции в поведении анализируемого вещества способна она изучать.
Использование нейронных сетей для моделирования ППЭ основано на доказанной в 1989 г. теореме Г. Цыбенко [34]. В терминах теории нейросетей эта теорема формулируется так: любую непрерывную на компакте функцию нескольких переменных можно с произвольной точностью реализовать с помощью обычной трехслойной нейронной сети прямого распространения с достаточным количеством нейронов в скрытом слое.
Метод обучения нейронных сетей. В процессе обучения ошибки сети при прогнозировании ожидаемых значений обучающих данных используются для изменения весов. Наиболее часто используется метод обратного распространения ошибок [35]. Рассмотрим принцип его работы на примере сети с одним скрытым слоем – перцептрона, – слой которого содержит n нейронов. Каждый скрытый и выходной нейроны получают несколько входов. Активация нейрона k, обозначенная Sk, затем определяется как сумма произведений входных данных Xj от нейрона j на соответствующий вес связи wkj между входом j и нейроном k за вычетом порога активации нейрона k:
Пусть X = (x1, x2, …, xm) – вектор входных сигналов скрытого слоя k для одного из обучающих примеров, а E = (e1, e2, … en) – вектор сигналов, которые должны быть получены от перцептрона в этом случае. Входные сигналы, поступив на входы k-слоя, были взвешены и просуммированы, в результате чего получен вектор Y = (y1, y2, … yn) выходных значений:
(9)
${{y}_{k}} = \sigma \left( {{{s}_{k}}} \right) = \sigma \left( {\mathop \sum \limits_i {{w}_{{kj}}}{{X}_{j}} - {{b}_{k}}} \right).$Здесь сигмоидальная функция σ действует как нелинейная передаточная функция, определяя, как выход нейрона зависит от его активации.
Тогда можно определить вектор ошибок (дельта) D = (d1, d2, … dn) , размерность которого совпадает с размерностью вектора выходных сигналов:
где компоненты векторы ошибок определяются как разность между ожидаемыми (в соответствии с обучающим примером) и фактическими значениями на выходных нейронах.В таких обозначениях формулу для корректировки веса связи входа j с нейроном k можно записать следующим образом (“правило дельты”):
где коэффициент η, на который умножается величина ошибки, называют скоростью (шагом) обучения, а величина t – номер текущего шага обучения. Таким образом, вес входного сигнала нейрона изменяется в сторону уменьшения ошибки пропорционально величине суммарной ошибки нейрона.Для случая более сложных сетей, содержащих несколько скрытых слоев, вводится функция ошибки E(d1, d2, …, dn), которая, например, в методе наименьших квадратов, имеет вид:
(12)
$E\left( {{{d}_{1}},{{d}_{2}},{\text{\;}}...,\,\,{{d}_{n}}} \right) = \frac{1}{n}\mathop \sum \limits_{i~ = ~1}^n d_{i}^{2}.$Заметим, что решаемая при обучении сети задача относится к классу задач регрессии. Действительно, по сути дела мы пытаемся восстановить непрерывную поверхность потенциальной энергии (ППЭ) по ряду известных точек обучающего набора. Хорошо известно, что такая задача относится к классу некорректно поставленных задач и для своего решения требует использования методов регуляризации [36]. Удачный выбор функции ошибки – один из важнейших приемов такой регуляризации.
Функция Е рассматривается как сложная функция весов всех связей сети ${{w}_{{ij~}}}$, и коррекция весов производится методом случайного градиентного спуска в этом многомерном пространстве [37]. В этом случае изменение весов принимают пропорционально градиенту
Несмотря на многочисленные успешные применения метода обратного распространения, он имеет ряд недостатков. Больше всего неприятностей приносит довольно долгий процесс обучения, занимающий дни или даже недели. Это может быть связано с несколькими причинами:
1. В процессе обучения значения весов большинства связей могут в результате коррекции стать очень большими величинами. Это приведет к тому, что указанные нейроны будут функционировать в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть (т.н. “паралич сети”).
2. Неверный выбор параметра шага обучения. Если размер шага фиксирован и очень мал, то сходимость слишком медленная, если же он фиксирован и слишком велик, то может возникнуть паралич или постоянная неустойчивость. Эффективно увеличивать шаг до тех пор, пока не прекратится улучшение оценки и уменьшать, если такого улучшения не происходит.
3. Если число параметров (веса связей и величины порогов) модели окажется меньше, чем число обучающих примеров, то сеть не только “запомнит” все комбинации вход–выход в примерах обучающего множества, но начнет “подстраиваться” под особенности отдельных примеров. В итоге сеть начнет проверять новые предъявляемые ей наблюдения не на соответствие зависимости, а на соответствие отдельным примерам обучающего множества. В результате эффективность распознавания резко падает. Такую сеть называют “переобученной”.
Чтобы избежать данной ошибки, обычно разделяют имеющийся набор обучающих данных на обучающую и тестовую выборки. Обучающую выборку используют для определения параметров модели, а тестовую – для оценки ее качества. При этом мы, во-первых, снижаем опасность переобучения сети, а во-вторых, оцениваем способность модели работать на новых для нее данных.
Мы остановились на использовании искусственных нейронных сетей для решения проблемы машинного обучения, поскольку в идейном отношении данный подход наиболее понятен. Однако существует большое количество и других методов машинного обучения. При моделировании поверхности потенциальной энергии для различных типов материалов приходится делать выбор в пользу одного из них. Необходимость такого выбора заставляет посмотреть на проблему машинного обучения с более общей точки зрения, позволяющей сравнить указанные методики, выявить их достоинства и недостатки. Этому вопросу посвящена следующая глава.
III. МЕТОДЫ МАШИННОГО ОБУЧЕНИЯ ДЛЯ КОНСТРУИРОВАНИЯ ПОВЕРХНОСТИ МЕЖАТОМНОЙ ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ (ППЭ)
III.1. Межатомные потенциалы машинного обучения
Межатомные потенциалы машинного обучения (machine learning interatomic potentials, MLIP) за последнее десятилетие достигли определенной зрелости и стали достойной альтернативой обычным межатомным потенциалам. Этому успеху во многом способствовала американская Инициатива по геному материалов [38], а также поддержка Европейским советом по моделированию материалов [39], в рамках которых основаны, например, открытая и бесплатная интернет-платформа NanoHUB, база квантовых данных о свойствах материалов (OQMD) [40], автоматическая система поиска материалов (AFLOW) [41, 42] и многие другие.
По сравнению с традиционным подходом, процесс проектирования межатомных потенциалов методами машинного обучения имеет несколько особенностей. Во-первых, конструирование MLIP требует использования обширной обучающей базы данных, поскольку ее содержание и полнота оказывают сильное влияние на точность и переносимость потенциала. Во-вторых, перед выполнением подгонки все конфигурации базы данных с различным числом атомов отображаются в уникальное пространство, называемое пространством дескрипторов (термин, заимствованный из хемоинформатики [43]). Дескрипторы – это выраженный в числовой форме набор результатов логической или математической обработки информации, полностью описывающий моделируемую систему. В пространстве дескрипторов выполняется алгоритм подгонки, а процедура машинного обучения определяет характеристики и ограничения потенциала (или иного интересующего свойства системы). Двумя основными частями конструирования являются числовое представление входных данных (дескрипторов) и алгоритм обучения (рис. 3). Ниже представлено описание каждого из этих пунктов, которые определяют эффективность потенциала машинного обучения.
Рис. 3.
Структура типичного процесса машинного обучения для предсказания свойств сложных веществ. Химический состав и структура преобразуются в числовые характеристики, называемые дескрипторами. Дескрипторы используются в качестве входных данных для модели машинного обучения, которая в результате тренировки на обучающем наборе данных позволяет прогнозировать требуемое свойство для вещества произвольного состава и структуры.

Отметим, что к настоящему моменту развито уже впечатляющее количество методов машинного обучения потенциалов для атомистического моделирования и этот процесс продолжается. Причины такого состоят в том, что существует определенное противоречие в двух основных пунктах схемы на рис. 3. Если во главу угла ставить быстродействие и качество обучающей модели, то это обычно требует максимального расширения пространства дескрипторов. Такой подход можно условно назвать “математическим”. Противоположный подход, “физический”, стремится выбрать пространство дескрипторов максимально приближенным к физике процессов межчастичного взаимодействия. При этом пространство дескрипторов сужается, что накладывает ограничения на методику обучения. Найти оптимальное соотношение “математического” и “физического” подходов для различных типов материалов довольно сложно. По этой причине нам представляется важным ознакомить читателя не с описанием более чем десятка существующих методик построения MLIP, а объяснить основные принципы их работы.
Как уже отмечалось, аппроксимация вида (прогнозирование) ППЭ на основе данных первопринципных расчетов, относится к методам машинного обучения с учителем ( так называемое контролируемое обучение). Все такие методы удобно рассматривать на основе формального статистического подхода [44, 45]. Пусть у нас есть обучающий набор D из n результатов первопринципного моделирования, D = {xi, yi} i = 1, …, n}, где х – входной вектор параметров исследуемого материала размерности D, а у – скалярный результат расчета потенциальной энергии. Обозначим через Х матрицу размером D × n, в которой собраны все входные данные обучающей выборки, а через y – вектор выходных данных тестовой выборки. Общий результат прогнозирования можно математически сформулировать как построение некоторой функции f, которая отображает набор обучающих данных x (серые точки на рис. 4) на прогнозируемый результат y. Наша цель – использовать такие обучающие данные, а также любые другие предшествующие знания, чтобы идентифицировать функцию, которая способна точно предсказать выходное значение для любых значений х из набора входных данных, не совпадающих с обучающим. Если допустимые выходные значения y образуют непрерывный диапазон, тогда процесс поиска функции f называется регрессией. Назовем пространством гипотез все возможные функции, которые нам может выдать процесс обучения. Пространство гипотез содержит все гипотезы (т.е. функции), которые могут быть возвращены алгоритмом обучения. Однако в этом пространстве будет много функций, которые точно воспроизводят данные обучения (рис. 4), и необходимо каким-то образом ограничить (отфильтровать) это пространство гипотез, приписывая функциям некоторые веса так, чтобы одни функции были более предпочтительными, чем другие. Например, очень часто пространство гипотез ограничивают так, чтобы оставались лишь функции, выражающие линейную зависимость (линейная регрессия) между входными и выходными значениями (сплошная линия на рис. 4). Заметим, что в пространстве гипотез может не оказаться функции, которая производит наблюдаемые выходные значения для всех возможных наборов входных значений. Это может произойти по нескольким причинам:
Рис. 4.
Три различные функции, подогнанные под один и тот же тестовый набор (серые точки): точечная и пунктирная линии полностью воспроизводят данные набора, сплошная линия – нет.

1) пространство гипотез было ограничено способом, исключающим функцию, которая идеально отображает входные значения в выходные значения. Например, пространство гипотез может быть ограничено включением только линейных функций, тогда как нелинейная функция входных переменных может воспроизводить наблюдаемые выходные значения (пунктирная и точечная линии на рис. 4);
2) наблюдаемые выходные значения являются результатом процесса, который по своей природе случаен (например, в качестве обучающего набора использованы данные эксперимента);
3) некоторые входные данные, имеющие особую важность для вычисления правильных выходных значений, отсутствуют (например, точка вблизи х = 0, значение которой (y(0)) могло бы полностью отвергнуть гипотезу о линейности регрессии).
В этих ситуациях любая функция в пространстве гипотез приведет к некоторой ошибке в предсказанных значениях. Чтобы учесть эту ошибку, выходные значения могут быть записаны в виде:
где f – функция, содержащаяся в пространстве гипотез, ε – случайная ошибка. Пусть g представляет собой распределение вероятностей величины ε. Другими словами, g(ε) – это плотность вероятности того, что y – f(x) = ε. Распределение g может зависеть от входных данных, но для простоты мы обычно предполагаем, что это не так. Как правило, функция f и распределение вероятностей g неизвестны.III.2.1. Формальная вероятностная основа контролируемого обучения
Для заданного распределения вероятностей g мы можем оценить плотность вероятности того, что функция f удовлетворяет уравнению (15). Эта плотность вероятности выражается как P( f |D, g), где D – вектор наблюдаемых данных обучения, и может быть вычислена с помощью формулы Байеса (18).
Правило Байеса – это фундаментальная статистическая теорема, которая может быть выведена из того факта, что вероятность двух событий A и B возникает как вероятность того, что B произойдет, умноженная на условную вероятность того, что A произойдет, при условии, что B уже реализовалось.
Математически это записывается как:
Аналогично,
Комбинируя уравнения (16) и (17) приходим к формуле Байеса:
(17)
$P\left( {{\text{A|B}}} \right) = \frac{{P\left( {{\text{B|A}}} \right)}}{{P\left( {\text{B}} \right)}}P\left( {\text{A}} \right).$В контексте обучения с учителем правило Байеса дает
(18)
$P\left( {f{\text{|}}D,g} \right) = \frac{{P\left( {D\,{\text{|}}\,f,g} \right)}}{{P\left( {D\,{\text{|}}\,g} \right)}}P\left( {f{\text{|}}\,g} \right).$Распределение вероятностей P( f |g) дает плотность вероятности того, что функция f удовлетворяет уравнению (14) до получения информации, содержащейся в обучающем наборе данных. По этой причине оно известно как априорное распределение вероятностей. Распределение вероятностей P( f |D, g) представляет собой вероятность того же события после учета обучающих данных. Это известно как апостериорное распределение вероятностей. Распределение P(D| f, g), широко известное как функция правдоподобия, представляет собой вероятность наблюдения обучающих данных D при заданных f и g. Остаю- щийся член P(D|g) в формуле (18) не зависит от f и может эффективно рассматриваться как нормировочная константа.
Правило Байеса обеспечивает естественную и интуитивно понятную основу для описания обучения. Первоначально пространство гипотез ограничено (или взвешено с определенными весами) посредством априорного распределения вероятностей. Всем функциям, которые исключены из пространства гипотез, назначается вероятность, равная нулю, а функциям, которые не исключены, назначаются ненулевые априорные вероятности. Эти вероятности представляют собой предварительное суждение о том, какие функции удовлетворяют уравнению (14). По мере наблюдения за данными обучения эти вероятности обновляются с учетом новых знаний, что приводит к апостериорному распределению вероятностей, – это этап обучения.
Алгоритмы обучения возвращают единственную функцию fmax, которая максимизирует апостериорную плотность вероятности:
Подставляя (19) в (20), приходим к формуле:
(20)
${{f}_{{{\text{max}}}}} = {\text{max}}\left[ {P\left( {D\,{\text{|}}\,f,g} \right) \cdot P\left( {f{\text{|}}\,g} \right)} \right].$Учитывая, что логарифмическая функция является монотонно возрастающей, это соотношение можно представить в виде:
(21)
${{f}_{{{\text{max}}}}} = {\text{min}}\left[ { - {\text{ln}}P\left( {D{\text{|}}\,f,g} \right) - {\text{ln}}P\left( {f{\text{|}}\,g} \right)} \right].$Член в квадратных скобках в правой части уравнения (21) называется целевой функцией, которую нужно минимизировать. Функция, которая с максимальной апостериорной вероятностью удовлетворяет уравнению (15), приводит целевую функцию к минимуму. Идея поиска функции P(D| f, g), которая минимизирует целевую функцию, является общей для методов машинного обучения.
Первый член –lnP(D| f, g) в уравнении (21) представляет эмпирический риск – меру того, насколько хорошо данная функция воспроизводит обучающие данные. Предполагая, что все наблюдения в обучающих данных независимы, из уравнения (14) и определения g можно написать:
(22)
$P\left( {D{\text{|}}\,f,g} \right) = \mathop \prod \limits_i g\left[ {{{y}_{i}} - f\left( {{{x}_{i}}} \right)} \right]{\text{\;}},$(23)
$ - {\text{ln}}P\left( {D{\text{|}}\,f,g} \right) = - \mathop \sum \limits_i {\text{ln}}g\left[ {{{y}_{i}} - f({{{\mathbf{x}}}_{i}})} \right]$В более общем виде эмпирический риск записывают как:
где L – так называемая штрафная функция (или функция потерь), которая вычисляет штраф за большие различия между yi и f (xi).III.2.2. Алгоритмы контролируемого обучения
Рассмотрим лишь несколько наиболее распространенных методов.
а) Метод линейной регрессии с гауссовым шумом (метод наименьших квадратов) является одним из наиболее широко используемых методов подгонки линейных функций по обучающей выборке. В этом методе делается предположение, что распределение g(ε) является гауссовским:
(25)
$g\left[ {{{y}_{i}} - f\left( {{{x}_{i}}} \right)} \right] = \frac{1}{{\sigma \sqrt {2\pi } }}{{e}^{{\frac{{{{{\left[ {{{y}_{i}} - f\left( {{{x}_{i}}} \right)} \right]}}^{2}}}}{{2{{\sigma }^{2}}}}}}}.$Тогда эмпирический риск принимает вид:
(26)
$ - {\text{ln}}P(D{\text{|}}\,f,g) = \frac{1}{{2{{\sigma }^{2}}}}\mathop \sum \limits_i \left\{ {{{{[{{y}_{i}} - f({{x}_{i}})]}}^{2}} - {\text{ln}}\left( {\frac{1}{{\sigma \sqrt {2\pi } }}} \right)} \right\}.$Этот подход приводит к аппроксимации методом наименьших квадратов, где сумма берется по всем элементам обучающей выборки. Видим, что функция потерь зависит от квадрата разницы между наблюдаемыми и прогнозируемыми выходными значениями, а минимизация эмпирического риска дает
(27)
${{f}_{{{\text{max}}}}} = {\text{min}}\mathop \sum \limits_i {{\left[ {{{y}_{i}} - f\left( {{{x}_{i}}} \right)} \right]}^{2}}.$Уравнение (27) описывает аппроксимацию методом наименьших квадратов, в котором выбранная функция минимизирует сумму квадратов ошибок по всем элементам обучающего набора. Штрафная функция в уравнении (27), известная как квадратичный штраф ошибки, обычно и используется в алгоритмах машинного обучения.
В случае линейной регрессии пространство гипотез ограничено только линейными функциями входных значений:
где w – вектор параметров линейной модели.Выходным значением метода в этом случае является оптимальный набор w, определяемых в силу соотношения (27), как:
Уникальное решение уравнения (29) существует, только если матрица XXT невырожденная. Часто можно улучшить аппроксимацию методом наименьших квадратов, используя набор коэффициентов, определяемых выражениемУравнение (30) представляет собой тип аппроксимации методом наименьших квадратов, известный как регуляризация Тихонова [36]. Когда нормальная аппроксимация методом наименьших квадратов некорректна (например, когда величина XXT сингулярна), регуляризация Тихонова может сделать задачу корректной.
б) Метод воспроизводящих ядер (kernel trick). Линейные методы наименьших квадратов очень популярны из-за высокой скорости и простоты, которые связаны с основным предположением, что выходные значения должно быть линейной функцией входных переменных. Во многих случаях это предположение нереально. Однако можно преобразовать исходное одномерное входное значение (xi) в пространство признаков, обладающее большей размерностью (например, $({{x}_{i}},~x_{i}^{2},~x_{i}^{3}, \ldots ~x_{i}^{n})$), в котором уже возможна линейная регрессия [45, 46]. Их можно использовать в алгоритмах машинного обучения, просто подставив преобразованные входные переменные φ(x) вместо исходных входных переменных x. Однако многие алгоритмы, включая линейный метод наименьших квадратов, могут быть выражены способом, который зависит от входных переменных только через внутренние (скалярные) произведения, такие как (x1 · x2). В таких случаях достаточно найти функцию k(xi, xj), называемую ядром, которая позволяет определить скалярное произведение между φ(xi) и φ(xj):
Чтобы использовать алгоритм обучения в заданном пространстве функций, все, что нужно сделать, это использовать ядро интегрального преобразования k(xi, xj) вместо скалярного произведения (xi · xj) на протяжении всего алгоритма обучения. Такой способ в англоязычной литературе получил название как трюк с ядром (kernel trick) [46].
в) Гребневая регрессия c помощью ядер. Для воспроизводящего ядра k(x1, x2) рассмотрим пространство функций f, которые задаются формулой
(32)
$f\left( {\mathbf{x}} \right) = \mathop \sum \limits_j {{{{\alpha }}}_{j}}k({{{\mathbf{x}}}_{j}},{\mathbf{x}}),$(33)
${{\langle k\left( {{{x}_{i}},x} \right),k({{x}_{j}},x)\rangle }_{{\text{H}}}} = k({{x}_{i}},{{x}_{j}}).$Это функциональное пространство известно как гильбертово пространство воспроизводящего ядра [46].
В гильбертовом пространстве определяется норма || f ||H:
(34)
${\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{\text{H}}}} \equiv \sqrt {{{{\langle f,f\rangle }}_{{\text{H}}}}} ,$Воспроизводящие ядерные гильбертовы пространства обладают особыми свойствами, которые делают их особенно полезными для машинного обучения с учителем. Рассмотрим ситуацию, в которой пространство гипотез является гильбертовым пространством некоторого ядра. Если, например, используется гауссовское ядро, пространство гипотез будет состоять из линейных комбинаций гауссовых функций. Пусть член регуляризации задается как r(|| f ||H), где r – монотонно возрастающая функция. Пусть эмпирический риск принимает общий вид $\mathop \sum \limits_i L\left( {{{y}_{i}},f({{x}_{i}})} \right)$, где сумма берется по всем точкам данных в обучающей выборке. Следовательно, целевая функция имеет вид:
(35)
$\mathop \sum \limits_i L\left( {{{y}_{i}},f({{x}_{i}}} \right)) + r\left( {{\text{||}}\Delta \,f\,{\text{|}}{{{\text{|}}}_{{\text{H}}}}} \right).$Тогда теорема о представителе [47] утверждает, что функция, которая минимизирует эту целевую функцию, должна иметь вид:
где сумма ведется по всем элементам обучающей выборки. Таким образом, проблема нахождения fmax сводится к задаче нахождения коэффициентов ci, которые минимизируют целевую функцию.Если используется квадратичная функция потерь и $r\left( {{\text{||}}\Delta \,f\,{\text{|}}{{{\text{|}}}_{{\text{H}}}}} \right) = {{\lambda ||}}\Delta \,f\,{\text{|}}{{{\text{|}}}_{{\text{H}}}}$ для некоторой положительной величины λ, то несложно показать, что целевая функция может быть записана как
(37)
$\mathop \sum \limits_i L\left( {{{y}_{i}},f({{x}_{i}})} \right) + r\left( {{\text{||}}\Delta \,f\,{\text{|}}{{{\text{|}}}_{{\text{H}}}}} \right) = \frac{1}{2}{\text{||}}\,y - Kc\,{\text{|}}{{{\text{|}}}^{2}} + \lambda {{c}^{T}}Kc,$Этот подход известен как нелинейная гребневая регрессия с помощью ядер [48]. Он похож на регуляризованный линейный метод наименьших квадратов (уравнения (27)–(29)) с двумя основными отличиями. Во-первых, больше нет необходимости работать в пространстве гипотез линейных функций. Во-вторых, количество строк и столбцов в матрице, которые нужно инвертировать, теперь равно количеству элементов в обучающем наборе, а не количеству входных переменных. Таким образом, хотя вычисления могут занимать больше времени в ситуациях, в которых имеется много обучающих данных, этот подход можно использовать для гораздо более широкого разнообразия пространств гипотез. Гибкость и простота гребневой регрессии сделали ее популярным инструментом в компьютерном материаловедении.
г) Регрессия на основе гауссовского процесса (РГП) основана на несколько другом подходе в рамках байесовского описания [49]. Если в методах линейной и гребневой регрессии пытаются выразить выходную функцию f(x) через модельные функции путем подбора параметров разложения, то гауссовский процесс представляет f(x) косвенным, более тонким образом.
Гауссовским процессом называется случайный процесс $\xi (x,t)$, все конечномерные распределения которого для любого момента времени t нормальные, с ковариационной функцией C(x, x'). В случае машинного обучения гауссовский процесс – это набор случайных величин, любое конечное число которых имеет совместное гауссово распределение с заданным средним значением m и ковариационной функцией.
(39)
$P\left[ {\xi \left( {{{x}_{1}}} \right),\xi \left( {{{x}_{2}}} \right) \ldots \xi \left( {{{x}_{n}}} \right)} \right] = N\left( {m,{\text{C}}} \right).$Рассмотрим задачу восстановления регрессии по обучающей выборке yi = f(xi), где величины yi есть значения реализации случайного процесса (поля) при входных значениях xi для i-го обучающего примера. Возникает задача прогноза значения поля у в новой точке x при условии, что в точках обучающей выборки поле наблюдались значения yi:
(40)
$P\left( {\xi \left( x \right){\text{|}}\xi \left( {{{x}_{1}}} \right) = {{y}_{1}},\quad \xi \left( {{{x}_{2}}} \right) = {{y}_{2}} \ldots \xi \left( {{{x}_{n}}} \right) = {{y}_{n}}} \right).$Заметим, что по определению (40) для гауссовского случайного процесса c нулевым средним (m = 0)
(41)
$\tilde {С} = \left( {\begin{array}{*{20}{c}} C&k \\ {{{k}^{T}}}&{{\text{C}}\left( {x,x} \right)} \end{array}} \right),$Учитывая, что по определению условной вероятности
(42)
$m = {{k}^{T}}{{C}^{{ - 1}}}y,\quad ~{{{{\sigma }}}^{2}} = C\left( {x,x} \right) - {{k}^{T}}{{C}^{{ - 1}}}k~{\text{.}}$Метод РГП широко применяется в машинном обучении благодаря своему основному достоинству – отсутствию необходимости предугадывать вид функций, входящих в пространство гипотез. Вместо того чтобы утверждать, что f(x) относится к некоторым конкретным моделям (например, f(x) = mx + c), гауссовский процесс описывает эту функцию косвенным образом (непараметрическим), позволяя при этом обучающим данным четко “говорить” самим за себя. Однако, поскольку мы отказываемся определять выходную функцию f(x) относительно небольшим набором параметров, входящих в разложение по модельным функциям, то на каждом шагу регрессии приходится проводить вычисления по соотношению (42), куда входит весь набор обучающих данных. Это приводит к резкому росту вычислительных затрат при большом наборе тестовых примеров (кубический рост).
д) Искусственные нейронные сети прямого распространения. Использование нейронных сетей прямого распространения – это один из наиболее эффективных методов машинного обучения, активно развивающийся в последние годы [50]. Идея метода состоит в имитации работы биологического мозга посредством искусственных нейронных сетей (ИНС), о которых подробно сообщалось в предыдущем разделе. Пространство гипотез в нейронной сети определяется топологией соединений между узлами и параметризованными функциями активации, используемыми узлами. Оптимизация весов многослойной нейронной сети эффективно выполняется с помощью алгоритма обратного распространения, который эффективно минимизирует квадрат потерь с помощью градиентного спуска. Преимущества заключаются в высокой точности, высокой способности к обучению и высокой отказоустойчивости для зашумленных данных. Так же как и РГП, ИНС является непараметрическим методом, в котором заранее не делается предположений о виде функций f(x), в силу чего требуется относительно длительный процесс обучения. Это обстоятельство затрудняет использование метода “on the fly”, т.е. встраивание его в программы Монте-Карло или МД-моделирования.
III.3. Дескрипторы
Ключевым фактором, определяющим быстродействие методов потенциалов машинного обучения, является представление данных о химических, структурных и основных термодинамических характеристиках моделируемых систем. Наборы числовых значений, поставленные в соответствие указанным данным представления соединений, называются “признаками” или “дескрипторами”. Для выбора хороших дескрипторов используются предварительные знания или оценка экспертов о корреляции между ПЭС и свойствами системы. Однако набор дескрипторов во многих случаях исследуется методом проб и ошибок, потому что эффективность прогнозирования (т.е. ошибка прогнозирования и эффективность модели) сильно зависит от их качества и числа. В идеале число дескрипторов должно быть минимальным, но в то же время они должны содержать всю информацию, необходимую для различения всевозможных атомных или кристаллических сред. Концепция дескрипторов очень напоминает идею введения обобщенных координат в лагранжевой механике. Действительно, переход к обобщенным координатам резко снижает их количество, хотя описание механической системы по-прежнему остается однозначным.
В ряде работ, вдохновленных примером вычислительной фармхимии, где полуэмпирическое конструирование на основе количественной связи структуры и активности молекул (QSAR) успешно использовалось для открытия новых лекарств, использовались комбинации различных дескрипторов с подходами машинного обучения. В качестве дескрипторов могут использоваться энтальпии смешения легирующих элементов, разности атомных радиусов, разность электроотрицательностей и концентраций валентных электронов [51, 52]. Однако такой подход довольно ограничен, поскольку отсутствие точного учета изменения электронной структуры, ближнего порядка и магнитных взаимодействий делает его применимым только в сплавы определенного и довольно узкого класса.
Более широкую область применения и точность имеет метод кластерного разложения (cluster expansion, CE), который широко используется в различных приложениях для поиска материалов с требуемыми свойствами [53, 54]. Этот метод используется для расчета энергии конфигурации (но не сил, действующих на атомы) в структурах с кристаллической решеткой определенного типа. Поэтому часто потенциалы взаимодействия, построенные в модели СЕ, называют “потенциалами на решетке”. Кластерные разложения быстры и вполне успешны, когда стабильные структуры являются производными от определенной структуры (ГЦК, ОЦК и т.д.), но значительно менее полезны в более сложных случаях, когда атомные радиусы компонентов сильно отличаются и важными становятся эффекты релаксации структуры [55]. Мы не будем останавливаться на работах, использующих указанные подходы, поскольку они полно представлены в недавнем обзоре [56].
Далее сконцентрируемся на методах машинного обучения для регрессии потенциальной энергии как функции координат всех атомов системы, необходимых для проведения атомистического моделирования сложных соединений. В работах по моделированию конденсированных сред термин “дескриптор” употребляют реже, заменяя полный набор дескрипторов термином “структурное представление”. В данной работе мы не будем проводить различия между этими терминами, считая их эквивалентными. Мы знаем, что заряды ядер и положения атомов являются достаточными характеристиками для описания электронной плотности и полной энергии любой конденсированной системы [2], поскольку гамильтониан системы обычно полностью определяется этими величинами. В первых работах по конструированию MLIP для молекулярных систем [57] на вход нейронной сети подавались все декартовы координаты атомов системы. Вскоре были выявлены два основных недостатка такого подхода. Во-первых, большинство моделей машинного обучения требуют на входе фиксированного количества функций, поэтому переход от системы с одним количеством атомов в суперъ-ячейке к другой приводит к серьезным проблемам. Во-вторых, декартовы координаты плохо подходят в качестве дескрипторов, поскольку они не инвариантны относительно преобразований симметрии (вращения, трансляции, перестановки одинаковых атомов) суперъячейки сложного соединения, поэтому их число чрезвычайно избыточно. Действительно, суперъячейку одноэлементного кристалла можно задать всего тремя векторами трансляций.
В 2007 г. Бехлер и Парринелло [58] представили новый подход к решению вышеуказанных проблем (рис. 5). В их методе полная энергия E представлена в виде суммы вкладов от отдельных атомов Ei:
Рис. 5.
Структура нейросети, использованная в работе [58]. Декартовы координаты атома i обозначены радиус-вектором Ri. Координаты затем преобразуются в набор значений функций симметрии Gi, описывающих локальную геометрию окружения атома i, зависящую от расположения всех атомов в системе (дескриптор атомарного окружения). Значения дескриптора Gi подаются на вход нейронных подсетей Si, на выходе которых формируется парциальный вклад Ei в полную энергию, связанный с i-м атомом.

Таким образом, энергия каждого атома получается в рамках процесса обучения нейронной сети, на вход которой подается информация об окружении соответствующего атома с индексом i, тем самым облегчая решение первой проблемы. При изменении числа атомов в системе необходимо просто добавить несколько новых входов на рис. 5, которые будут описываться теми же самыми весовыми коэффициентами, что и все другие строки. Вторая проблема была решена путем преобразования декартовых координат в дескриптор локального атомарного окружения каждого атома, называемого функцией симметрии, который и подается на вход нейронной сети.
Термин “симметрия” относится не к точечной группе или пространственной группе системы, а к основному требованию, что любой обмен атомами одного и того же элемента не должен влиять на вектор значений функции симметрии. Важным компонентом функции симметрии является функция отсечки fc, определяющая радиус Rc атомного окружения каждого атома (обычно несколько конфигурационных сфер):
(44)
${{f}_{c}}\left( {{{R}_{{ij}}}} \right) = \left\{ \begin{gathered} 0.5 \cdot \left[ {{\text{cos}}\left( {\frac{{\pi {{R}_{{ij}}}}}{{{{R}_{c}}}}} \right) + 1} \right]~\quad {\text{для}}\quad {{R}_{{ij}}} \leqslant {{R}_{c}} \hfill \\ 0~\quad {\text{для}}\quad {{R}_{{ij}}} > {{R}_{c}} \hfill \\ \end{gathered} \right..$При расстояниях, больших Rc, значение функции отсечки и ее производной обращается в ноль. Введение функции fc фактически означает разбиение атомной структуры на области пространства с центром в i-м атоме, каждой из которых приписывается энергия Ei. Функция симметрии состоит из двух слагаемых, первое из которых имеет вид радиально-усредненной структуры окружения:
(45)
$G_{i}^{1} = \mathop \sum \limits_{j \ne i} {{e}^{{ - \eta {{{({{R}_{{ij}}} - {{R}_{c}})}}^{2}}}}}{{f}_{c}}\left( {{{R}_{{ij}}}} \right),$(46)
$\begin{gathered} G_{i}^{2} = {{2}^{{1~ - ~\zeta }}}\mathop \sum \limits_{j,~k~ \ne ~i} {{\left( {1 + \lambda {\text{cos}}{{\theta }_{{ijk}}}} \right)}^{\zeta }} \times \\ \times \,{{e}^{{ - \eta (R_{{ij~}}^{2} + ~R_{{ik~}}^{2} + ~R_{{jk}}^{2})}}}{{f}_{c}}\left( {{{R}_{{ij}}}} \right){{f}_{c}}\left( {{{R}_{{ik}}}} \right){{f}_{c}}\left( {{{R}_{{jk}}}} \right). \\ \end{gathered} $Параметры ζ, η, λ и Rc являются подгоночными и определяются в процессе обучения нейронной сети.
Две указанные идеи, введенные впервые Бехлером и Паринелло [58], оказались настолько глубокими, что стали важным компонентом всех современных методов конструирования MLIP [59–65].
Действительно, представление энергии в виде суммы вкладов от отдельных узлов (43) очень близко по духу к идее потенциалов погруженного атома (EAM) о погружении нейтрального атома в “море” электронной плотности, создаваемой его ближайшим окружением [25]. При достаточно удачном выборе дескрипторов локального окружения можно добиться, что узельные энергии Ei, будут достаточно просто связаны с ними (по линейному, или близкому к нему закону). Тогда полная энергия E будет почти линейно зависеть от входных значений Gi , и мы приходим к простому случаю линейной регрессии.
Таким образом, любой метод конструирования MLIP по сути дела состоит из двух основных частей: 1) выбора дескриптора для описания локального окружения выбранного атома, 2) выбора эффективного алгоритма машинного обучения (регрессор), – реализующих регрессионную задачу в пространстве выбранных дескрипторов.
Нейронные сети были первой и самой популярной формой регрессора при использовании дескрипторов типа (45) и (46) для задачи конструирования MLIP [58–62]. В работах [63, 64] дескрипторы Бехлера и Паринелло уже использовались совместно с алгоритмом гребневой регрессией ядра.
Другой формой регрессора, предложенной в 2010 г., были гауссовские процессы, используемые в потенциалах гауссовой аппроксимации (GAP) [65]. При использовании с ядром гладкого перекрытия атомных позиций (SOAP) [66] они могут доказуемо аппроксимировать произвольное локальное многочастичное взаимодействие атомов, в отличие от потенциалов нейронной сети, используемых поверх двух- и трехчастичных дескрипторов [67]. Вероятно, третий по величине класс межатомных потенциалов основан на линейной регрессии с различными наборами дескрипторов локального окружения. Он включает в себя дескрипторы на основе разложения атомного кластера (Atomic cluster expansion) [68], и на основе спектрального анализа соседей (SNAP) [69, 70], включая недавнее расширение для многокомпонентных систем [71]. Одним из интенсивно развивающихся подходов к машинно-обучаемым межатомным потенциалам, появившимся в последние годы, является использование “потенциалов тензора моментов” (MTP), разработанных Шапеевым [72]. Расширение MTP на многокомпонентные системы [73] выходит за рамки линейной регрессии, однако существует альтернативная формулировка многокомпонентной MTP, которая остается линейной [74].
Существование столь большого числа дескрипторов локального окружения вызвало появление исследований [68, 75, 76], в которых проводится их сопоставление. В работе [77] было показано, что дескрипторы, которые изначально выглядят совершенно иначе, являются частными случаями общего подхода, в котором конечный набор базисных функций с возрастающими угловыми волновыми числами используется для разложения функции плотности в окрестности выбранного атома. В [68] было показано, что все перечисленные выше дескрипторы могут быть получены в рамках метода разложения атомного кластера, а в [75] была дана общая формулировка проблемы представления атомных структур в терминах (гладкой) плотности атомов.
Из вышеизложенного следует, что в настоящее время существуют 4 различных схемы машинного обучения межатомных потенциалов (MLIP), которые можно считать многообещающими. Это дескрипторы Бехлера и Паринелло (BP) в методе нейронных сетей, дескрипторы с ядром гладкого перекрытия атомных позиций (SOAP) вместе с регрессором, использующим гауссовские процессы с потенциалами гауссовой аппроксимации (GAP), метод на основе спектрального анализа соседей (SNAP) и метод “потенциалов тензора моментов” (MTP). Все 4 схемы показали очень хорошую точность, и в настоящее время не ясно, что лучше. Хотя схема BP кажется наиболее гибкой, GAP и MTP имеют лучшую производительность. В статье [72] было представлено сравнение между GAP и MTP и показано, что MTP быстрее и более точен для вольфрама. В недавней работе [78] было проведено всестороннее сравнение производительности GAP, MTP, BP и SNAP. С этой целью были использованы стандартизированные наборы DFT-данных для шести элементов (Li, Mo, Cu, Ni, Si и Ge), охватывающих различные кристаллические структуры (ГЦК, ОЦК и структура алмаза), химический состав и тип связи (металлические и ковалентные). Четыре MLIP оценивались с точки зрения их точности в воспроизведении энергий и сил DFT, а также свойств материала, таких как уравнения состояния, параметр решетки и упругие постоянные. Была предпринята попытка оценить требования к обучающему набору и относительные вычислительные затраты. В результате сравнения обнаружилось, что у всех использованных схем ключевые показатели (точность, объем обучающих данных и вычислительная стоимость) взаимосвязаны. Увеличение сложности схемы (т.е. количество степеней свободы), связанное с увеличением вычислительных затрат и увеличением обучающего набора, обычно приводит к более высокой точности. Для всех четырех схем построения MLIP существует “оптимальная” конфигурация, при которой дальнейшее увеличение количества степеней свободы дает лишь небольшое улучшение точности с увеличением вычислительных затрат. Было показано, что все схемы способны достигать точности, близкой к DFT, при прогнозировании энергии, сил и свойств материала, существенно превосходя традиционные IAP. Модели GAP и MTP демонстрируют наименьшие среднеквадратичные значения энергии и сил даже при весьма умеренном объеме обучающих данных. Однако модель GAP является одной из самых затратных с точки зрения объема вычислений для данной точности и продемонстрировала плохую экстраполяцию для полиморфных фаз в системах со структурой алмаза. Нейронносетевой подход BP показал худшую сходимость по энергии при небольших размерах обучающих данных, которая заметно улучшается при увеличении объема данных. Необходимо отметить несколько ограничений этой важной работы, которые являются возможными направлениями будущих исследований. Во-первых, сравнение проводилось для чистых элементов, не было предпринято никаких попыток включить в это исследование бинарные и, тем более, тройные системы. Во-вторых, остался открытым вопрос о том, что сильнее влияет на ключевые показатели – дескриптор или регрессор, поскольку не делалось попыток комбинировать различные дескрипторы локальной среды с различными структурами машинного обучения.
Обратим внимание читателей на новый дескриптор погруженной атомной плотности (EAD) в подходе нейросетевого машинного обучения [78], идея которого позаимствована из метода погруженного атома (EAM) [25]. В EAD электронная плотность заменяется квадратом линейной комбинации атомных орбитальных компонентов:
(47)
${{\rho }_{i}} = \mathop \sum \limits_{{{l}_{x}},{{l}_{y}},{{l}_{z}}}^{{{l}_{x}} + {{l}_{y}} + {{l}_{z}} = {{L}_{{{\text{max}}}}}} \frac{{{{L}_{{{\text{max}}}}}!}}{{{{l}_{x}}!{{l}_{y}}!{{l}_{z}}!}}{{\left[ {\mathop \sum \limits_{j \ne i}^N {{Z}_{j}}{{\Phi }}\left( {{{R}_{{ij}}}} \right)} \right]}^{2}},$(48)
$\Phi \left( {{{R}_{{ij}}}} \right) = \frac{{x_{{ij}}^{{{{l}_{x}}}} \cdot y_{{ij}}^{{{{l}_{y}}}} \cdot z_{{ij}}^{{{{l}_{z}}}}}}{{R_{c}^{{{{l}_{x}} + {{l}_{y}} + {{l}_{z}}}}}} \cdot {{e}^{{ - \eta {{{({{R}_{{ij}}} - {{R}_{c}})}}^{2}}}}} \cdot {{f}_{c}}\left( {{{R}_{{ij}}}} \right),$В заключение укажем на еще один недавно появившийся способ решения проблемы различной размерности входных данных при помощи графовых нейронных сетей [79].
IV. ПРОГНОЗИРОВАНИЕ МЕЖАТОМНЫХ ПОТЕНЦИАЛОВ МАШИННОГО ОБУЧЕНИЯ (MLIP) ДЛЯ МОДЕЛИРОВАНИЯ МУЛЬТИЭЛЕМЕНТНЫХ ВЕЩЕСТВ
IV.1. Высокоэнтропийные и мультиэлементные вещества
Исторически сложился следующий подход к разработке различных материалов: выбирается основной компонент, максимально отвечающий поставленной цели, который затем видоизменяется за счет введения небольшого количества добавок (легирование) для придания недостающих вторичных свойств. Такая стратегия привела к значительному объему знаний о материалах на основе одного компонента, а с другой – к отсутствию информации о материалах, расположенных в центре гипермерной многокомпонентной фазовой диаграммы.
Ситуация резко изменилась после выхода в 2004 г. двух важных статей научных групп из Великобритании и Гонконга [80, 81], в которых предложили для разработки перспективных материалов изучать способы получения и свойства сплавов, состоящих из нескольких основных компонентов в равных или почти равных пропорциях. Мотивация статьи [80] состояла в необходимости изучить “неисследованную центральную область фазового пространства многокомпонентных концентрированных сплавов” (multiple principal elements alloys, MPEA). В работе [81] выдвигалась идея о том, что использование концентрированных смесей многих элементов в качестве основы нового сплава, приводящее к резкому увеличению конфигурационной энтропии, будет способствовать росту области однофазности системы при высоких температурах, блокируя выделения интерметаллидных фаз. В данном подходе сплавы с 5 или более основными элементами, концентрация которых составляет от 5 до 35 ат. %, получили название высокоэнтропийных сплавов, или материалов (high entropy alloys, HEA). Обе статьи сначала были встречены без особого внимания. Тем не менее к настоящему времени исследования в этой области увеличились до тысяч статей, поскольку во всем мире увидели огромный потенциал для поиска и разработки новых материалов с интересными и ценными новыми свойствами. Соответствующие ведомства США, Европейского Союза и Китая причислили HEA к ключевым направлениям развития на ближайшее будущее. HEA превосходят традиционные сплавы по механическим свойствам, коррозионной стойкости, стойкости к окислению и т.д., а часто и по стоимости, позволяя избегать использования дорогостоящих легирующих элементов. Продолжающийся поиск новых высокоэнтропийных систем (ВЭС) недавно расширился за пределы металлов и включил керамику со стабилизированной энтропией, такую как высокоэнтропийные оксиды [82], карбиды [83] и бориды [84].
В первые годы изучения HEA-материалов акцент в первую очередь делался на достижение высокой энтропии и, соответственно, на достижение максимального числа основных компонентов, что легче всего достичь в области металлических сплавов. Однако после подведения первых итогов масштабных исследований стало ясно, что исходная идея высокоэнтропийного сплава требует определенной корректировки [85]. В первых работах энтропия сплава оценивалась в приближении идеальных растворов, так что каждая из i компонент с концентрацией хi создает вклад
Вопреки этому предположению термодинамический анализ большого числа НЕА показал, что идеальные растворы встречаются редко, поэтому простое увеличение числа основных компонентов не всегда приводит к существенному росту энтропии [86, 87]. Во-вторых, выяснилось, что рост числа основных элементов также существенно изменяет энтальпию. Причем из-за резкого увеличения количества различных пар соседствующих элементов возрастает вероятность того, что по крайней мере один тип таких пар приведет к изменению энтальпии, превосходящему рост энтропии.
Был сделан вывод, что формальное требование причислять к HEA лишь металлические системы, состоящие из 5 и более основных компонент, является слишком широким. Чтобы устранить этот барьер, был введен новый термин – комплексные концентрированные сплавы (ССА). Этот более всеобъемлющий термин сохраняет акцент на сложных по составу концентрированных сплавах, но включает в себя как HEA-сплавы, так и концентрированные тройные и четвертичные сплавы, допуская не только однофазные, но и многофазные растворы [88], включая высокоэнтропийные карбиды, нитриды и оксиды, а также объемно-аморфные материалы [89]. С учетом указанных различий в настоящем обзоре мы будем использовать термины «высокоэнтропийный материал» и «комплексный концентрированный материал» как синонимы.
IV.2. Прогнозирование стабильности высокоэнтропийных сплавов
Как уже отмечалось, основная идея НЕА состоит в том, чтобы за счет увеличения числа компонентов N максимизировать конфигурационную энтропию, чтобы добиться стабильности неупорядоченной фазы твердого раствора, подавляя таким образом образование интерметаллических фаз. Стабильность HEA-материала определяется термодинамическими правилами, вытекающими из основных принципов статистической физики Гиббса. Эти правила лежат в основе методологии CALPHAD [90], которая на протяжении многих десятилетий применяется для расчета фазовых диаграмм. Центральной величиной является экстенсивная энергия Гиббса всей системы $G\left( {P,T,\left\{ {{{n}_{i}}} \right\}} \right)$, являющаяся функцией давления P, температуры T и числа молей ni для каждого элемента i = 1, …, N (N – количество элементов, для комплексных концентрированных систем N > 4). В силу экстенсивности свободная энергия может быть разложена на сумму существующих в системе фаз:
(50)
$G\left( {P,T,\left\{ {{{n}_{i}}} \right\}} \right) = \mathop \sum \limits_\alpha {{G}_{\alpha }}(P,T,\{ n_{i}^{\alpha }\} ),$При проведении атомистического моделирования более удобно использовать молярные величины $\bar {G} = G{\text{/}}n$ и ${{\bar {G}}_{\alpha }} = {{G}_{\alpha }}{\text{/}}{{n}_{\alpha }}$, где n = $\mathop \sum \limits_i {{n}_{i}},$ nα = $\mathop \sum \limits_i n_{i}^{\alpha }$, и мольные доли ${{x}_{i}} = {{n}_{i}}{\text{/}}n$ и $x_{i}^{\alpha } = n_{i}^{\alpha }{\text{/}}{{n}^{\alpha }}$. Тогда
(51)
$G\left( {P,T,\left\{ {{{n}_{i}}} \right\}} \right) = \mathop \sum \limits_\alpha {{f}_{\alpha }}{{G}_{\alpha }}(P,T,\{ x_{i}^{\alpha }\} ),$Основная проблема феноменологических теорий – получить выражение для зависимости ${{G}_{\alpha }}(P,T,\{ x_{i}^{\alpha }\} )$. CALPHAD использует для этой цели базы данных термодинамической информации, основанные на экспериментальных измерениях (если таковые имеются), дополненные схемами численной интерполяции для заполнения тех областей фазовой диаграммы, где экспериментальная информация отсутствует.
Использование CALPHAD для изучения высокоэнтропийных систем сталкивается с двумя основными проблемами. Первая проблема чисто комбинаторная. Пусть проводится исследование системы из N = 6 компонент. Тогда только число 4-компонентных фазовых подобластей полного фазового пространства составит $\frac{{N!}}{{\left( {N~ - {\text{\;}}n} \right)!n!}} = 15$, что наглядно показывает объем требуемых экспериментальных данных. Вторая и основная проблема связана с доступностью и надежностью термодинамических баз данных [91]. Дело в том, что базы данных CALPHAD были разработаны для традиционных сплавов, поэтому полная термодинамическая оценка энергий Гиббса обычно дается только для составов, обогащенных одним основным элементом. Напротив, HEA и CCA лежат в центральных областях композиционного пространства, вдали от изученных границ, ограниченных бинарными и тройными подсистемами. Следовательно, вычисления в этих обширных пространствах композиций опираются на значительные экстраполяции, точность которых критически зависит от качества диаграмм систем более низкого порядка. Таким образом, надежность и точность прогнозов могут стать сомнительными, если они получены из неполных термодинамических описаний. Сенков и соавт. [92] определили критерии достоверности для расчетов CALPHAD, основанные на доле полностью термодинамически оцененных бинарных систем (FAB) и доле полностью оцененных тройных систем (FAT), включенных в базу данных. Они показали, что приемлемая точность прогноза достигается лишь в случае полной информации о всех бинарных системах и значительной доле тройных. Хотя база данных на основе Ni успешно предсказала равновесные фазы и фазовые доли в сплавах Al–Co–Cr–Cu–Fe–Ni [93], такие достижения остаются единичными. Действительно, даже специализированные базы данных для HEA, такие как TCHEA3 от ThermoCalc, содержат почти все описания бинарных систем для 26 элементов, но только 5% описаний тройных систем полностью оценены.
Отсюда следует, что предсказательные возможности метода CALPHAD существенно ограничены недостатком экспериментальных данных. Указанные проблемы вызвали появление полуэмпирических методов для предсказания того, какие многокомпонентные сплавы образуют твердый раствор. В них в качестве инструментов прогнозирования используются дескрипторы [94, 95], параметры которых соответствуют доступным, но ограниченным экспериментальным данным.
Таким образом, надежное термодинамическое предсказание способности многокомпонентных сплавов к образованию твердого раствора остается серьезной проблемой, препятствующей открытию новых HEA.
Совершенно ясно, что огромное композиционное пространство, охватываемое HEA и CCA, не может быть исследовано только экспериментальными усилиями. Необходимо подключить все возможности компьютерного моделирования. Особенно важным вычислительным инструментом являются вычисления, основанные на первых принципах (аb initio). Такие расчеты проводятся в рамках теории функционала плотности (DFT), основаны только на квантово-механических законах и физических константах и, таким образом, позволяют предсказывать и исследовать свойства материалов без эмпирических данных. Далее мы позволим себе использовать термины ab initio и DFT как взаимозаменяемые.
Одним из магистральных путей такого моделирования является объединение методов CALPHAD с ab initio расчетами полной энергии вещества, чтобы использовать относительные преимущества каждого из них. Первопринципные расчеты превосходно подходят для предсказания низкотемпературных значений энтальпий, которые часто просто недоступны экспериментально, а также параметров структуры и магнитных моментов. CALPHAD отлично подходит для моделирования температур переходов и топологии фазовой диаграммы. Теория функционала плотности [1, 2], на которой основано ab initio моделирование, в своей первоначальной формулировке является теорией основного состояния, т.е. строго позволяет рассчитать только энергию данной конфигурации атомов в суперъячейке при 0 К. Однако энтропийный эффект, присущий высокоэнтропийным материалам, проявляется только при высоких температурах, где важную роль играют энергии возбуждений над основным состоянием – фононов, магнонов и т.д. Поэтому необходимо комбинировать DFT-вычисления с термодинамическими концепциями и статистическим усреднением.
Такая комбинация позволяет рассчитать свободную энергию Гельмгольца ${{F}_{\alpha }}\left( {V,T,\left\{ {{{n}_{i}}} \right\}} \right)$ при конечных температурах без использования данных эксперимента [96]. После этого величину Gα получают с помощью стандартного соотношения:
(52)
${{G}_{\alpha }}(P,T,\{ x_{i}^{\alpha }\} ) = {{F}_{\alpha }}\left( {V,T,\left\{ {{{n}_{i}}} \right\}} \right) + PV,$(53)
$\begin{gathered} {{F}_{{\alpha ,\mu }}}(V,T,\{ x_{i}^{{\alpha ,\mu }}\} ) = \\ = - {{k}_{B}}T \cdot {\text{ln}}\left[ {\mathop \sum \limits_{с \in \alpha ,\mu } {\text{exp}}\left( {\frac{{E_{с}^{{{\text{el,magn,vib}}}}(V,T,\{ x_{i}^{{\alpha ,\mu }}\} )}}{{{{k}_{B}}T}}} \right)} \right], \\ \end{gathered} $Выражение (53) показывает, что свободная энергия зависит не только от типа решетки фазы α, но и от типа ближнего порядка в ней. Учет ближнего порядка при проведении DFT-расчетов достаточно сложен, поэтому мы не будем его рассматривать, отправляя читателей к обзорам [96, 98].
В большинстве работ при моделировании используют упорядоченные или абсолютно неупорядоченные фазы, для которых конфигурационная энтропия может быть выражена аналитически, и которые могут достаточно хорошо быть представлены одной или небольшим количеством (в случае неупорядоченной фазы) конфигураций. В этом случае обычно применяется дополнительное предположение о независимости электронных, магнитных и колебательных степеней свободы, связанное с использованием адиабатического приближения, оправданного различными временными масштабами указанных возбуждений. В результате свободная энергия может быть записана в виде
Здесь ${{E}_{\alpha }}(V,\{ x_{i}^{\alpha }\} )$ – полная электронная энергия атомной структуры α-фазы, параметр решетки которой и положение всех атомов отрелаксированы с помощью DFT для достижения минимума при T = 0 K; $S_{\alpha }^{{{\text{conf}}}}(\{ x_{i}^{\alpha }\} )$ – конфигурационная энтропия, $F_{\alpha }^{{{\text{el}}}}(V,T,\{ x_{i}^{\alpha }\} )$ – свободная энергия, обусловленная электронными возбуждениями, $F_{\alpha }^{{{\text{mag}}}}(V,T,\{ x_{i}^{\alpha }\} )$ – свободная магнитная энергия, а $F_{\alpha }^{{{\text{vib}}}}(V,T,\{ x_{i}^{\alpha }\} )$ – свободная энергия, обусловленная колебаниями атомов.
Все указанные вклады вполне поддаются DFT-расчету [96]. Неупорядоченная химическая конфигурация моделируется на основе большой, но конечной суперъячейки с использованием периодических граничных условий. Большая суперъ-ячейка приводит к значительным вычислительным затратам, поэтому на практике расчеты для HEA-материалов выполняются с использованием базиса плоских волн и метода проекции присоединенной волны (PAW), реализованного в пакете моделирования VASP [99, 100]. В принципе, любая атомная конфигурация, полученная путем однородного случайного распределения, может быть использована для моделирования химического беспорядка внутри суперъячейки. Однако, чтобы достаточно хорошо представить идеальную химическую хаотичность, соответствующие суперъячейки потребуют нескольких сотен атомов. Поэтому более удобным является подход SQS [101], в котором частицы в суперъячейке умеренного размера (несколько десятков узлов) распределяются таким образом, чтобы минимизировать функции корреляции пар атомов. Набор полученных таким образом результатов вполне достаточен, чтобы дальнейшее уточнение ближнего порядка в системе проводить методами решеточного Монте-Карло [102].
Заметим, что моделирование HEA-материалов из первых принципов сильно осложняется большим количеством компонент, что влечет за собой комбинаторно высокие вычислительные затраты. Дополнительное усложнение в ряде случаев привносит необходимость учета беспорядка в сложной химической и магнитной структуре [94, 96]. Поэтому характерная особенность ab initio моделирования HEA-материалов состоит в обязательном использовании при вычислении обменно-корреляционного функционала электронной плотности приближения обобщенного градиента(GGA). Это связано с тем, что большинство интересных HEA-систем являются магнитными и, следовательно, требуют использования спин-поляризованной версии DFT [103]. Как известно, основным успехом GGA было правильное предсказание ферромагнитного ОЦК-состояния как основного для железа [104]. По этой причине для точного определения фазовой стабильности систем, содержащих магнитоактивные компоненты Fe, Cr, Ni, использование приближения GGA является необходимым. К настоящему времени проведены DFT-расчеты более 2000 HEA-материалов, информация о которых приведена в недавних обзорах [96, 105, 106].
IV.3. Методика атомистического моделирования HEA с применением MLIP
Первоначальное изучение фазовых равновесий в комплексных концентрированных соединениях проводилось методами вычислительной термодинамики (CALPHAD), которые позволяют экстраполировать фазовые диаграммы высокого порядка из термодинамических описаний систем низшего порядка (т.е. от унарных к двойным, от двойных к тройным и т.д., вплоть до n-го порядка). Рассмотренные в предыдущей главе ограничения существенно снижают потенциальную точность прогнозов CALPHAD применительно к высокоэнтропийным системам. С другой стороны, методы ab initio моделирования, о которых говорилось выше, имеют принципиальные ограничения по пространственно-временному масштабу моделирования [96]. Поэтому возможность получать с помощью методов машинного обучения потенциалов межатомных взаимодействий с точностью, близкой к точности DFT-расчетов, в случае высокоэнтропийных систем является прорывной идеей. Действительно, использование таких потенциалов в методах Монте-Карло и молекулярной динамики практически снимает все ограничения на моделирование механических, диффузионных и электронных характеристик.
Раннее атомистическое моделирование HEA проводилось либо с полуэмпирическими EAM-потенциалами, либо базировалось на совместном использовании DFT-расчетов в приближении когерентного потенциала (CPA) [107]. Данный подход в сочетании с моделированием Монте-Карло (MC) широко применялся в последние несколько лет для решения проблемы фазовой стабильности и ближнего порядка многокомпонентных сплавов [108–110] из-за высокой вычислительной эффективности. Однако использование метода среднего поля, характерное для когерентного потенциала, не в состоянии учитывать локальные релаксационные эффекты, которые могут быть важны для рассмотрения фазовой стабильности [110]. Более точным является моделирование методом Монте-Карло на основе DFT с использованием суперъячейки [111]. Эти вычисления, однако, чрезвычайно требовательны в вычислительном отношении и могут применяться лишь для сплавов с числом компонент не более четырех. Поэтому чаще всего данные о полной энергии ограниченного набора структур, полученных с помощью DFT, отображают на эффективных моделях, таких как метод кластерного разложения [112]. Однако последние данные показывают (см., например, обзор [113]), что использование кластерного разложения, равно как AIMD, является вычислительно неэффективным для многокомпонентных сплавов. Подробные обзоры атомистического моделирования HEA такого рода представлены в обзорах [96, 114].
Альтернативой этим подходам являются недавно разработанные потенциалы машинного обучения, которые позволяют чрезвычайно эффективно параметризовать поверхность потенциальной энергии, в том числе и для многокомпонентных сплавов [108, 113]. Поэтому в данном обзоре мы сосредоточимся на том прогрессе, который был достигнут в атомистическом моделировании HEA за счет использования потенциалов машинного обучения.
Нейронные сети были первым методом машинного обучения при построении поверхностей потенциальной энергии. Одним из наиболее успешных приложений машинного обучения для создания надежного представления поверхности потенциальной энергии является подход Белера и Парринело [58], в котором впервые было предложено представлять полную энергию системы как сумму атомных энергий:
где di является вектором признаков (также называемым дескриптором) атома i, учитывающим химическое окружение атома i, которое зависит от положений и химической идентичности его соседних атомов вплоть до заданного радиуса отсечения Ri, Ei представляет энергию атома i как функциию дескрипторов. Приближение локальности атомных взаимодействий в уравнении (54) ограничивают точность результирующего MLP, поскольку дальнодействующие взаимодействия, такие как электростатические взаимодействия, за пределами радиуса отсечки не рассматриваются. Тем не менее он имеет важное преимущество – независимый расчет атомных энергий, что позволяет использовать потенциал для систем с различным числом атомов.С момента публикации в 2007 г. в подход Белера и Парринело (NNP) было внесено несколько улучшений. В статье [115] был предложен метод учета дальнодействующих кулоновских взаимодействий для ионных систем путем уравновешивания зарядов через нейронные сети, что позволило воспроизвести несколько объемных свойств CaF2. Затем в статье [116] разработана стратегия обучения иерархических многокомпонентных систем, последовательно переходя от элементов к бинарным, а затем к тройным и т.д. системам. Тем не менее метод NNP оказался не слишком удобен для многокомпонентных систем с числом компонент N > 3. Это связано с использованием в качестве дескриптора атомно-центрированных функций симметрии. Для многокомпонентных систем функции симметрии должны быть определены отдельно для разных пар (радиальная часть) и троек атомов (угловая зависимость). В результате сложность метода экспоненциально возрастает с ростом N [117, 118]. Хотя существуют примеры использования NNP для четырехэлементных [119] и пятиэлементных [78] систем, их точность, как указано в [117], значительно ниже, чем у NNP, построенных для систем с одним-тремя элементами.
Более перспективными для многокомпонентных систем оказались методы гауссовских процессов с потенциалами гауссовской аппроксимации (GAP) [65] при использовании с ядром гладкого перекрытия атомных позиций (SOAP) [66]. Во-первых, они позволяют аппроксимировать произвольное локальное многочастичное взаимодействие атомов, в отличие от потенциалов нейронной сети, использующих лишь двух- и трехчастичные дескрипторы. Во-вторых, в методе GAP для многокомпонентных систем можно использовать весовые коэффициенты для каждого типа атомов при построении плотности соседей, поэтому вычислительные затраты растут значительно медленнее, чем у NNP [120]. Метод SNAP [69, 70] также был обобщен на многокомпонентные системы [71] и c успехом использовался для моделирования системы Be–W [121].
Вполне пригодным оказался и разработанный Шапеевым подход потенциалов тензора моментов (МТР). Метод легко различает вклад различных пар частиц в радиальные функции [73], поэтому количество параметров модели растет с увеличением числа компонент менее чем квадратично. В недавней работе [122] было проведено объективное сравнение подходов GAP-SOAP и МТР при моделировании с помощью MLIP-энергий конфигураций сплава Ag–Pd в широком диапазоне составов. Оба типа потенциалов обеспечивают превосходную точность описания фононных спектров, близкую к точности DFT, а также точек плавления и фазовых переходов. При этом метод МТР показал очень хороший баланс между точностью и вычислительной эффективностью.
В работе [89] Драутц недавно развил идею кластерного разложения применительно к построению дескрипторов и получил новый класс MLP, названный “разложением по атомным кластерам”. Основываясь на этой идее, Шапеев разработал малоранговый потенциал межатомного взаимодействия на решетке (LRP) [123]. Как и другие потенциалы межатомного взаимодействия, LRP использует соотношение (10), т.е. полная энергия системы представляется в виде суммы вкладов отдельных атомных окружений Ei. Далее предполагается, что атомы исследуемой системы не сильно смещены относительно узлов идеальной решетки, так что координационное число Nc ближайших соседей в пределах радиуса обрезания Rс не изменяется. Тогда вклад i-го атома в энергию системы однозначно определяется типом атома i и набором типов атомов (Fe, Ti, Mn и т.д.), входящих в его ближайшее окружение. Следовательно, Ei = V(σ1, . . . σn), где V(σ1, . . . σn) – потенциал межатомного взаимодействия, σ1, . . . σn – набор, характеризующий тип атома i и типы его ближайших соседей (n = Nc + 1). Потенциал V(σ1, . . . σn) с достаточной точностью представим в виде произведения малоранговых тензоров:
IV.4. Активное обучение
Известно, что MLIP дают плохое описание (большие ошибки подгонки) для областей PES, где обучающих точек недостаточно, как показано на рис. 6. Из-за огромного числа локальных минимумов на PES невозможно построить обучающий набор, охватывающий все локальные области, поэтому никогда нет гарантии, что MLIP предоставляет разумные описания для всех низкоэнергетических потенциальных ям. В наиболее серьезных случаях, когда MLIP дает плохое описание областей PES, связанных с глобальным минимумом, поиск структуры завершится ошибкой. Одним из решений для преодоления этой проблемы являются схемы активного обучения, использующие идею обучения на лету (on the fly) [126, 127]. Суть идеи – доверить уточнение обучающей выборки при проведении итераций компьютеру. Компьютерная программа определяет, находится ли возникшая при итерации структура за пределами эталонного набора данных. Если это так, то для нее проводится разовый DFT-расчет и полученные данные добавляются к обучающему набору. Таким образом, MLIP обновляется итеративно во время поиска структуры путем постоянного включения экстраполяционных конфигураций в обучающий набор.
Рис. 6.
Схематическая иллюстрация поверхности потенциальной энергии соединения в многомерном пространстве конфигураций, а также связь между референсными данными DFT-расчетов и MLIP. Сплошная линия обозначает реальный ход PES, а пунктирная линия обозначает подогнанный PES с помощью MLP. Серым фоном выделена область с недостаточным числом точек тренировочного набора. Как правило, MLP отлично подходят для регионов, плотно охваченных контрольными тренировочными точками (черные точки), и наоборот.

Таким образом, в настоящее время для моделирования комплексных концентрированных соединений на основе MLIP-потенциалов используется итерационный многомасштабный подход (рис. 7), который включает несколько основных этапов. На первом этапе выбирается решетка моделируемого вещества, узлы которой случайным образом заполняются компонентами (от 10 до 90 ат. % для каждого компонента) и таким образом генерируются начальные приближения для нескольких сотен репрезентативных структур. На втором этапе производится DFT-моделирование указанных репрезентативных структур, в результате которого определяются равновесные значения параметра решетки и полной энергии системы. Полученные результаты объединяются в базу данных. На следующем шаге на основе базы квантово-механических расчетов производится параметризация MLIP-потенциала на основе одного из методов, рассмотренных нами выше в разделе II. Далее полученный потенциал используется для моделирования эволюции атомной структуры методами Монте-Карло или молекулярной динамики (МД). По результатам моделирования отбираются наиболее репрезентативные конфигурации ВЭС. Затем для них определяется ошибка представления полной энергии по отношению к результатам DFT-расчетов. Если ошибка превосходит 5 мэВ/атом, то цикл самосогласования, изображенный на рис. 7, переходит на следующий виток. А именно, база данных дополняется новым набором репрезентативных конфигураций, на обновленной базе происходит обучение потенциала и т.д.
Рис. 7.
Схема активного обучения при использовании MLIP-потенциалов для моделирования сложных веществ.

Такая схема обеспечивает сокращение числа трудоемких DFT-вычислений и ускорение поиска, а также существенно повышает точность прогнозирования.
Алгоритм активного обучения на лету был адаптирован для оптимизации системы потенциалов нейронной сети (NNP) Артитом и Белером [128] и включен в пакет ÆNET [129], реализующий метод Белера–Паринелло. В последние годы схема итеративного построения MLIP была предложена Дерингером для метода гауссовской аппроксимации GAP [130] и Шапеевым и соавт. для потенциалов тензора моментов МТР [131]. Все эти приложения показали, что обучение и производственный цикл можно ускорить на несколько порядков.
V. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ВЫСОКОЭНТРОПИЙНЫХ СПЛАВОВ (HEAS) С ПОМОЩЬЮ МЕЖАТОМНЫХ ПОТЕНЦИАЛОВ МАШИННОГО ОБУЧЕНИЯ (MLIP)
V.1 Фазовые диаграммы
Область, в которой использование потенциалов машинного обучения принесло значительный прогресс, – это расчет термодинамических свойств, таких как фазовая стабильность и фазовые диаграммы, а также другие величины, зависящие от температуры. Основная причина успеха MLIP для термодинамических предсказаний HEA – это локализация взаимодействий в системе при в высоких температурах: дальнодействующие при 0 K межатомные взаимодействия, имеющие электронную природу, существенно ослабляются, когда возникают атомные колебания и нарушается симметрия кристалла [132]. В этом случае вычисление свободной энергии при высокой температуре представляет задачу, которая идеально подходит для потенциалов, характеризующихся ограниченным радиусом действия. Превосходная точность методов машинного обучения потенциалов для HEA была продемонстрирована в недавней работе [133], где МТР-метод Шапеева был использован для вычисления свободной энергии теплостойких ОЦК-сплавов системы NbMoTaVW при 3000 K с точностью, близкой к DFT-результатам. Численно точные колебательные свободные энергии были получены двухэтапным термодинамическим интегрированием с использованием метода динамики Ланжевена [134].
Ряд других примеров также подтверждает успешные возможности машинного обучения для анализа высокотемпературных свойств HEA: метод потенциалов низкого ранга (low range potentials, LRP) [122] совместно с Монте-Карло-моделированием был применен для исследования фазовых диаграмм ОЦК MoNbTaW и ГЦК CrFeCoNi [124, 135], причем в обоих случаях были обнаружены ранее неизвестные структуры. В работе [136] потенциал нейронной сети был использован для исследования структуры тугоплавкого высокоэнтропийного расплава.
Возможности MLIP-потенциалов позволяют рассчитывать полную свободную энергию системы при различных температурах и объемах, включая точные ангармонические составляющие. Исходя из этого могут быть точно рассчитаны такие свойства материала, как объемный модуль, теплоемкость и тепловое расширение. Хорошим примером может служить работа [137], в которой рассмотрена среднеэнтропийная тройная ГЦК-система FeCoNi и были рассчитаны локальные искажения решетки и упругие постоянные для ряда температур.
V.2. Моделирование влияния ближнего порядка на свойства HEA
В первых работах по атомистическому моделированию HEA обычно предполагалось, что эти сплавы образуют случайные твердые растворы и использовались идеально неупорядоченные конфигурации. Это приближение реалистично при высокой температуре, когда конфигурационная энтропия доминирует над всеми другими вкладами в свободную энергию. Однако при более низкой температуре распределение атомов отклоняется от случайного, и элементы располагаются в энергетически более предпочтительных упорядоченных конфигурациях. Тип конфигураций определяется пространственными корреляциями между различными элементами, вызванными их взаимным притяжением или отталкиванием. Если эти пространственные корреляции дальнодействующие, то они могут привести к кластеризации и разделению фаз, если же они короткодействующие, то являются причиной возникновения ближнего порядка (БП) в сплаве.
Ближний порядок обычно количественно описывается параметрами Уоррена–Каули [138], которые определяются парными корреляциями корреляций между элементами i и j:
где $p_{{ij}}^{m}$ – вероятность обнаружить атом j в m-й координационной сфере атома i, а ci и cj – концентрации компонентов типа i и j.БП является локальной структурной характеристикой, которую трудно зафиксировать экспериментально. Чтобы компенсировать этот недостаток, для ее расчета в HEA были успешно применены различные атомистические методы. Наиболее популярные подходы включают моделирование методом Монте-Карло с использованием потенциалов машинного обучения [124]. В качестве примера на рис. 8 показана температурная зависимость параметров Уоррена–Каули для первой оболочки четырех различных пар в четырехэлементном HEA сплаве MoNbTaW [125].
Рис. 8.
Зависимость параметров ближнего порядка Уоррена–Каули от температуры в MoNbTaW для четырех различных пар атомов по данным Костюченко [125].
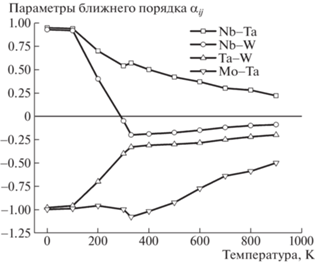
Видно, что для этого сплава две фазы B2 (Mo, Ta) и B32 (Nb, W) разделяются при низкой температуре, в то время как фаза B2 (Mo, W; Nb, Ta) с дальним порядком стабильна примерно до 600 К. Следует отметить также, что параметры Уоррена–Каули не равны нулю даже при относительно высокой температуре, что свидетельствует о наличии БП даже для неупорядоченного твердого раствора.
Ближний порядок определяется не только особенностями химического взаимодействия компонентов. Для сплавов, содержащих 3d-элементы, БП во многом определяется их магнитным взаимодействием. Так, зависимость между БП и магнетизмом имеет решающее значение для сплавов семейства CrMnFeCoNi. Это семейство представляет очень своеобразную магнитную ситуацию, в которой ферромагнитные металлы (Fe, Co и Ni) и антиферромагнитные металлы (Cr и Mn) перемешаны случайным образом. Благодаря этому конкурирующие магнитные обменные взаимодействия между атомными спинами с разной ориентацией могут приводить к эффектам магнитной фрустрации, когда, например, атомы хрома вынуждены отталкиваться друг от друга, поскольку они имеют параллельные спины из-за ферромагнитного окружения. Приведенное соображение стало основой для нескольких исследований БП в тройных и четверных сплавах CrCoNi и CrCoFeNi соответственно [139, 140]. И экспериментальное, и теоретическое исследования показали, что параметры Уоррена–Коули существенно отличаются от случайного твердого раствора: среднее количество пар ближайших соседей Cr–Cr было уменьшено примерно на 40%, тогда как количество пар Ni–Cr было увеличено. Необходимая энергетическая движущая сила для БП в этом сплаве обеспечивается магнитными обменными взаимодействиями.
Следовательно, в сплавах CrCoFeNi магнитные моменты Fe, Co и Ni в основном ориентируются параллельно, в то время как атомы Cr предпочитают антиферромагнитное упорядочение по отношению к ним.
Таким образом, можно ожидать, что при наличии нескольких магнитных элементов в НЕА перекрестные эффекты химического и магнитного взаимодействий могут приводить к возникновению сложных сценариев, для предсказания которых как нельзя лучше подходит моделирование на основе MLIP-потенциалов.
V.3. Ближний порядок и механические свойства ВЭС
Несмотря на свой локальный характер, ближний порядок может существенно влиять на макроскопические свойства ВЭС. В последние годы эксперименты позволили установить, что БП глубоко влияет также на механические свойства ВЭС. Так, в работе [141] было проведено ab initio моделирование высокоэнтропийных сплавов систем TiZrHfTa и TiZrNbHf. Данные ОЦК-сплавы демонстрируют превосходные свойства, такие как высокая прочность и высокая температура плавления, и, таким образом, являются потенциальной альтернативой суперсплавам на основе никеля. Уникальной механической прочности данных ВЭС, связанной с локальными искажениями структуры, однако, сопутствует низкая пластичность, что характерно для сплавов с ОЦК-решеткой. Как показал эксперимент, можно подобрать состав системы, чтобы достичь высокой пластичности, индуцированной трансформацией (TRIP), при фазовом переходе между ОЦК- и ω-фазами. Исследование показало, что ближний порядок и связанные с ним локальные искажения решетки в значительной степени влияют на фазовую стабильность изученных ВЭС. При правильном учете релаксационных эффектов предсказанные составы вблизи энергетического равновесия ОЦК–ГПУ оказались близкими к экспериментальным составам, для которых наблюдаются хорошая прочность и пластичность за счет TRIP-эффекта.
Ближний порядок может кардинально изменить механические свойства ГЦК-HEA. Было обнаружено, что различные локальные химические структуры влияют на энергию дефекта упаковки (ЭДУ) в тройных, четверных и пятикомпонентных сплавах семейства CrMnFeCoNi [142, 143] до такой степени, что ЭДУ даже качественно изменяется от отрицательного к положительному значению. Более высокие степени БП обычно увеличивают ЭДУ, потому что для создания дефекта упаковки необходимо локально нарушить порядок в системе, хотя бывают и исключения. Увеличение ЭДУ в ГЦК-ВЭС может изменить доминирующее деформационное поведение от мартенситного превращения к образованию двойников или простому скольжению дислокаций.
V.4 Новые типы дефектов в ВЭС: дефекты внедрения и поверхности
Раннее атомистическое моделирование дефектов в ВЭС использовалось для анализа либо вакансии и примеси замещения, либо дефекта упаковки и двойниковой границы. Однако совсем недавно были рассмотрены два новых типа дефектов: примесь внедрения и граница раздела.
Влияние легирования углеродом в ВЭС семейства материалов с элементами Cr, Mn, Fe, Co и Ni изучалось в экспериментальной работе [144], где было показано, что добавление этого элемента увеличивало текучесть и предел прочности, а также влияло на пластичность сплава. В дальнейшем эта же система исследовалась с помощью ab initio моделирования [145]. Анализировалось влияние межузельных атомов углерода на CrMnFeCoNi в ГЦК- и ГПУ-фазах. Было обнаружено, что добавление углерода энергетически стабилизирует ГЦК-фазу по отношению к ГПУ-фазе и, таким образом, увеличивает ЭДУ в ГЦК-фазе системы CrMnFeCoNi, что согласуется с экспериментальным наблюдением [146]. Еще одно применение межузельного легирования в ВЭС относится к хранению водорода. Hu и соавт. [147] исследовали TiZrNbMoHf с помощью расчетов из первых принципов и обнаружили фазовый переход ОЦК–ГЦК при высоком содержании атомов водорода, что согласуется с экспериментальными данными [148]. Они также обсудили связь между растворимостью водорода и искажениями решетки и сообщили, что искажения решетки в ВЭС может повысить растворимость водорода. На данном этапе атомистическое моделирование ВЭС как потенциальных кандидатов для хранения водорода находится на начальном этапе, однако можно надеяться на интересные результаты.
V.5. Поверхность вещества
Поверхность – это еще один тип дефектов в ВЭС, который совсем недавно привлек внимание научного сообщества. Она определяет реакционную способность и реакцию металлов на химические вещества, а в контексте ВЭС их свойства представляют интерес для коррозии и гетерогенного катализа.
Понимание коррозии в ВЭС имеет решающее значение для двух технологических аспектов. Во-первых, желательно, чтобы ВЭС с высокими механическими характеристиками, выдерживающими суровые условия окружающей среды, расширила потенциальные области применения. Во-вторых, состав ВЭС может быть адаптирован для получения покрытий с высокой энтропией, которые максимизируют адгезию и коррозионную стойкость для защиты стандартных металлов или других ВЭС.
Состав и структура поверхности ВЭС очень важны также для гетерогенного катализа. Сильно неупорядоченные конфигурации на поверхности предлагают широкий спектр участков поглощения с различной энергией связи для реагентов и промежуточных продуктов реакции, а более высокая химическая сложность, мультиэлементность увеличивают вероятность появления высокоактивных центров. Все это делает ВЭС превосходящими любые катализаторы на основе простых металлов.
Комбинация расчетов из первых принципов и машинного обучения для пятикомпонентных HEA IrPdPtRhRu, CoCuGaNiZn и AgAuCuPdPt [149, 150] была использована для поиска новых катализаторов для реакций восстановления O2, CO2 и CO: для этих сплавов база данных энергий поглощения для различных перестановок элементов, окружающих поглощенную молекулу, была приспособлена с использованием в качестве дескрипторов химических признаков атомов в первых трех соседних оболочках вокруг абсорбента. Полученная модель затем использовалась для определения наилучшего состава путем максимального увеличения количества участков с заранее определенной оптимальной энергией поглощения, что привело к значительному увеличению расчетной каталитической активности. По мнению авторов ВЭС-катализаторы выглядят весьма перспективным направлением исследований.
V.6. Высокоэнтропийная керамика
После открытия в 2015 г. высокоэнтропийных оксидов, в которых однозначно был продемонстрирован энтропийный переход к однофазной системе [81], круг высокоэнтропийных материалов стал быстро расширяться. К ним стали причислять бориды [83], карбиды, нитриды, сульфиды и силициды высокоэнтропийных сплавов, которые обладают повышенными свойствами, ведущими к их практическому применению в теплоизоляции и защите от коррозии, термоэлектричестве, расщеплении воды, катализе и накоплении энергии [105]. Сложные механизмы, лежащие в основе этих свойств, которые часто трудно установить, становятся перспективными возможностями для вычислительного моделирования. Важным шагом в этом отношении явилась работа [151], в которой стандартный DFT-подход был существенно видоизменен для расчета энергии образования многокомпонентных систем с различными типами химической связи, что существенно облегчило количественный анализ. Так, в работе [152] с помощью теории функционала плотности в сочетании со специальными квазислучайными структурами (SQS) были изучены структурные, механические и электронные свойства высокоэнтропийного карбида (TaNbHfTiZr)C в диапазоне давлений 0–50 ГПа. Было показано, что пластичность (TaNbHfTiZr)C значительно улучшается с увеличением давления, а переход от хрупкого характера разрушения к пластичному происходит примерно при 20 ГПа.
VI. ЗАКЛЮЧЕНИЕ
В настоящей статье дан обзор применения потенциалов машинного обучения для моделирования высокоэнтропийных систем (ВЭС). ВЭС быстро превратились в одну из важнейших областей исследований в области материаловедения, поскольку данные системы обещают практически неограниченное количество новых семейств сплавов и керамик с самыми неожиданными свойствами. В настоящее время уже получены весьма перспективные семейства ВЭС: коррозионно-стойкие сплавы (FeCrMoNi), тугоплавкие сплавы (MoNbTaW), легкие и прочные сплавы для аэрокосмической отрасли (AlMoNbTaTiZr), стабилизированные энтропией оксиды, нитриды, бориды перспективны для создания высокотемпературных конструкций и режущих инструментов [153–155]. Найден ряд составов с уникальными сверхпроводящими, термоэлектрическими и магнитоэлектрическими свойствами. Атомистические модели этих сплавов, которые сначала исследовались в основном экспериментально, теперь тоже вступили в золотой век. Развитие методов компьютерного моделирования дает широкие возможности для исследования многоатомных высокоэнтропийных систем. Введение потенциалов машинного обучения (MLIP) значительно расширило возможности моделирования как во временном, так и в пространственном масштабе, обеспечив при этом достаточную точность при вычислении термодинамических свойств. В данной работе подробно рассмотрены основные методы получения MLIP как с помощью искусственных нейронных сетей, так и методами регрессионного анализа. Проанализированы также результаты использования MLIP для моделирования структуры и свойств ВЭС, полученные в последнее время. Хотя применение MLIP еще только начинается, тем не менее уже получен ряд важных результатов: анализ ближнего порядка в HEA и его связь с механическими свойствами, изучение примесей внедрения (углерод и водород) и гетерогенного катализа. В перспективе ожидается применение MLIP для изучения высокоэнтропийной керамики.
Все это позволяет уверенно прогнозировать расцвет этой области в ближайшем будущем. Нет сомнений, что данное направление исследований будет одним из самых перспективных в области компьютерного материаловедения.
Список литературы
Kohn W., Sham L.J. // Phys. Rev. 1965. V. 140. № 4A. P. 1133–1138. https://doi.org/10.1103/physrev.140.a1133
Martin R.M. Electronic Structure: basic theory and practical methods. Cambridge University Press, Cambridge, England, 2004. 650 p. https://doi.org/10.1017/CBO9780511805769
Hafner J., Wolverton C., Ceder G. // MRS Bulletin. 2006. V. 31. № 9. P. 659–668. https://doi.org/10.1557/mrs2006.174
Car R., Parrinello M. // Phys. Rev. Lett. 1985. V. 55. № 22. P. 2471–2474. https://doi.org/10.1103/PhysRevLett.55.2471
Marx D., Hutter J. Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods. In: Grotendorst J. (Ed.) Modern Methods and Algorithms of Quantum Chemistry. Cambridge University Press, Cambridge, England, 2009. V. 1. P. 301–449. https://doi.org/10.1017/CBO9780511609633
Allen M.P., Tildesley D.J. Computer Simulation of Liquids. Clarendon Press, Oxford, 1989. 385 p. https://doi.org/10.1093 /oso/9780198803195.001.0001
Vitek V., Srolovitz D.J. Atomistic Simulation of Materials: Beyond Pair Potentials. Plenum Press, New York, 1989. 480 p. https://doi.org/10.1007/978-1-4684-5703-2
Raabe D. Computational Materials Science // Wiley-VCH Verlag, 1998. P. 1–400. https://doi.org/10.1002/3527601945
Frenkel D., Smit B. Understanding molecular simulation: from algorithms to applications. Elsevier, 2002. 638 p. https://doi.org/10.1016/B978-0-12-267351-1.X5000-7
Valiev R. // Nat. Mater. 2004. V. 3. № 8. P. 511–516. https://doi.org/10.1038/nmat1180
McDowell D.L. // Int. J. Plast. 2010. V. 26. № 9. P. 1280–1309. https://doi.org/10.1016/j.ijplas.2010.02.008
Heine V., Robertson L.J., Payne M.C., Murrell J.N., Phillips J.C., Weaire D. // Philos. Trans. R. Soc. Lond. A. 1991. V. 334. № 1635. P. 393–405. https://doi.org/10.1098/rsta.1991.0021
Voter A.F. // MRS Bull. 1996. V. 21. № 2. P. 17–19. https://doi.org/10.1557/S0883769400046248
Vitek V. // MRS Bull. 1996. V. 21. № 2. P. 20–23. https://doi.org/10.1557/S088376940004625X
Lennard-Jones J.E. // Proc. R. Soc. London, Ser. A. 1925. V. 109. № 752. P. 584–597. https://doi.org/10.1098/rspa.1925.0147
Rahman A. // Phys. Rev. 1964. V. 136. № 2A. P. A405–A411. https://doi.org/10.1103/physrev.136.a405
Finnis M.W., Sinclair J.E. // Philos. Mag. A. 1984. V. 50. № 1. P. 45–55. https://doi.org/10.1080/01418618408244210
Johnson R.A. // Phys. Rev. B. 1972. V. 6. № 6. P. 2094–2100. https://doi.org/10.1103/physrevb.6.2094
Stillinger F.H., Weber T.A. // Phys. Rev. B. 1985. V. 31. № 8. P. 5262–5271. https://doi.org/10.1103/physrevb.31.5262
Harrison J.A., Schall J.D., Maskey S., Mikulski P.T., Knippenberg M.T., Morrow B.H. // Appl. Phys. Rev. 2018. V. 5. Art. 031104. https://doi.org/10.1063/1.5020808
Pettifor D.G. // Phys. Rev. Lett. 1989. V. 63. № 22. P. 2480–2483. https://doi.org/10.1103/physrevlett.63.2480
Brenner D.W. // MRS Bull. 1996. V. 21. № 2. P. 36–41. https://doi.org/10.1557/S0883769400046285
Friedel J. // London, Edinburgh, and Dublin Philos. Mag. & J. Sci. 1952. V. 43. № 337. P. 153–189. https://doi.org/10.1080/14786440208561086
Foiles S.M. // MRS Bull. 1996. V. 31. № 2. P. 24–28. https://doi.org/10.1557/S0883769400046261
Jacobse K.W., Stoltze P., Nørskov J.K. // Surf. Sci. 1996. V. 366. № 2. P. 394–402. https://doi.org/10.1016/0039-6028(96)00816-3
Foiles S.M. // Phys. Rev. B. 1985. V. 32. № 6. P. 3409–3415. https://doi.org/10.1103/PhysRevB.32.3409
Asta M., Foiles S.M. // Phys. Rev. B. 1996. V. 53. № 5. P. 2389–2404. https://doi.org/10.1103/physrevb.53.2389
Rupp M. // Int. J. Quantum Chem. 2015. V. 115. № 16. P. 1058–1073. https://doi.org/10.1002/qua.24954
Rosenblatt F. // Psychol. Rev. 1958. V. 65. № 6. P. 386–408. https://doi.org/10.1037/h0042519
Bishop C.M. Neural Networks for Pattern Recognition. Clarendon Press, Oxford, 1995. 482 p. ISBN 0198538642
Gurney K. An introduction to neural networks. Taylor & Francis Group, London, 2004. 317 p. ISBN 0-203-45151-1
Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A.N., Kaiser L., Polosukhin I. Attention is all you need //Adv. Neural Information Proc. Systems. 2017. V. 30. P. 5998–6008. https://doi.org/10.48550/arXiv.1706.03762
Haykin S. Neural networks and learning machines. 3rd Int. ed.; Prentice Hall: New York, 2009. 936 p. ISBN-10: 0131471392
Cybenko G. // Math. Control. Signals, Syst. 1989. V. 2. P. 303–314. https://doi.org/10.1007/BF02551274
Rumelhart D.E., Hinton G.E., Williams R.J. Learning internal representations by error propagation. In: Rumelhart D.E., McClelland J.L. (Eds.) Parallel distributed processing. V. 1. MIT press, Cambridge, MA. 1986. P. 318–362. https://doi.org/10.1016/B978-1-4832-1446-7.50035-2
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. Москва: Наука, 1986. С. 1–286.
Qian N. // Neural Networks. 1999. V. 12. № 1. P. 145–151. https://doi.org/10.1016/S0893-6080(98)00116-6
Jain A., Ong S.P., Hautier G., Chen W., Richards W.D., Dacek S., Cholia S., Gunter D., Skinner D., Ceder G., Persson K.A. // APL Mater. 2013. V. 1. № 011002. P. 1–11. https://doi.org/10.1063/1.4812323
Saal J.E., Kirklin S., Aykol M., Meredig B., Wolverton C. // JOM. 2013. V. 65. № 11. P. 1501–1509. https://doi.org/10.1007/s11837-013-0755-4
Kirklin S., Saal J.E., Meredig B., Thompson A., Doak J.W., Aykol M., Rühl S., Wolverton C.l. // NPJ Comput. Mater. 2015. V. 1. № 1. Art. 15010. https://doi.org/10.1038/npjcompumats.2015.10
Puchala B., Tarcea G., Marquis E.A., Hedstrom M., Jagadish H.V., Allison J.E. // JOM. 2016. V. 68. № 8. P. 2035–2044. https://doi.org/10.1007/s11837-016-1998-7
Draxl C., Scheffler M. // MRS Bull. 2018. V. 43. № 9. P. 676–682. https://doi.org/10.1557/mrs.2018.208
Todeschini R., Consonni V. Molecular Descriptors for Chemoinformatics. Wiley-VCH, Weinheim, 2009. 1257 p. https://doi.org/10.1002/9783527628766
Rupp M. // Int. J. Quantum Chem. 2015. V. 115. № 16. P. 1058–1073. https://doi.org/10.1002/qua.24954
Mueller T., Kusne A.G., Ramprasad R. // Comp. Chem. Rev. 2016. V. 29. P. 186–273. https://doi.org/10.1002/9781119148739.ch4
Hofmann T., Schölkopf B., Smola A.J. // Ann. Stat. 2008. V. 36. № 3. P. 1171–1220. https://doi.org/10.1214/009053607000000677
Schölkopf B., Herbrich R., Smola A.J. A Generalized Representer Theorem / In: Helmbold D., Williamson B. (Eds.) Computational Learning Theory. COLT 2001. Lecture Notes in Computer Science. V. 2111. Springer, Berlin, Heidelberg, 2001. P. 416–426. https://doi.org/10.1007/3-540-44581-1_27
Вьюгин В.В. Математические основы машинного обучения и прогнозирования. М.: МЦНМО, 2014. 304 с.
Rasmussen C.E. Gaussian Processes in Machine Learning. In: Bousquet O., von Luxburg U., Rätsch G. (eds.) Advanced Lectures on Machine Learning. Lecture Notes in Computer Science. Springer, Berlin, Heidelberg, 2003. V. 3176. P. 63–71. https://doi.org/10.1007/978-3-540-28650-9_4
Specht D.F. // IEEE Trans. Neural Netw. 1991. V. 2. № 6. P. 568–576. https://doi.org/10.1109/72.97934
Zhou Z., Zhou Y., He Q., Ding Z., Li F., Yang Y. // Comput. Mater. 2019. V. 5. № 128. P. 1–9. https://doi.org/10.1038/s41524-019-0265-1
Isayev O., Oses C., Toher C., Gossett E., Curtarolo S., Tropsha A. // Nat. Commun. 2017. V. 8. Art. 15679. https://doi.org/10.1038/ncomms15679
Troparevsky M.C., Morris J.R., Daene M., Wang Y., Lupini A.R., Stocks G.M. // JOM. 2015. V. 67. № 10. P. 2350–2363. https://doi.org/10.1007/s11837-015-1594-2
Turchi P.E.A., Gonis A., Drchal V., Kudrnovský J. // Phys. Rev. B. 2001. V. 64. Art. 085112. https://doi.org/10.1103/physrevb.64.085112
Nguyen A.H., Rosenbrock C.W., Reese C.S., Hart G.L.W. // Phys. Rev. B. 2017. V. 96. Art. 014107. https://doi.org/10.1103/physrevb.96.014107
Widom M. // J. Mater. Res. 2018. V. 33 . P. 2881–2898. https://doi.org/10.1557/jmr.2018.222
Lorenz S., Groß A., Scheffler M. // Chem. Phys. Lett. 2004. V. 395. № 4–6. P. 210–215. https://doi.org/10.1016/j.cplett.2004.07.076
Behler J., Parrinello M. // Phys. Rev. Lett. 2007. V. 98. Art. 146401. https://doi.org/10.1103/PhysRevLett.98.146401
Artrith N., Behler J. // Phys. Rev. B. 2012. V. 85. Art. 045439. https://doi.org/10.1103/physrevb.85.045439
Behler J. // Phys. Chem. Chem. Phys. V. 13. № 40. P. 17930–17955. https://doi.org/10.1039/C1CP21668F
Behler J. // J. Chem. Phys. 2016. V. 145. Art. 170901. https://doi.org/10.1063/1.4966192
Behler J. // Angew. Chem. Int. Ed. 2017. V. 56. № 42. P. 12828–12840. https://doi.org/10.1002/anie.201703114
Botu V., Ramprasad R. // Int. J. Quantum. Chem. 2014. V. 115. № 16. P. 1074–1083. https://doi.org/10.1002/qua.24836
Botu V., Ramprasad R. // Phys. Rev. B. 2015. V. 92. № 9. Art. 094306. https://doi.org/10.1103/physrevb.92.094306
Bartók A.P., Payne M.C., Kondor R. // Phys. Rev. Lett. 2010. V. 104. Art. 136403. https://doi.org/10.1103/physrevlett.104.13640
Deringer V.L., Csányi G. // Phys. Rev. B. 2017. V. 95. № 9. Art. 094203. https://doi.org/10.1103/physrevb.95.094203
Dolgirev P.E., Kruglov I.A., Oganov A.R. // AIP Advances. 2016. V. 6. № 8. Art. 085318. https://doi.org/10.1063/1.4961886
Drautz R. // Phys. Rev. B. 2019. V. 99. № 1. Art. 014104. https://doi.org/10.1103/physrevb.99.014104
Thompson A.P., Swiler L.P., Trott C.R., Foiles S.M., Tucker G.J. // J. Comput. Phys. 2015. V. 285. P. 316–330. https://doi.org/10.1016/j.jcp.2014.12.018
Wood M.A., Thompson A.P. // J. Chem. Phys. 2018. V. 148. № 24. Art. 241721. https://doi.org/10.1063/1.5017641
Wood M.A., Cusentino M.A., Wirth B.D., Thompson A.P. // Phys. Rev. B. 2019. V. 99. Art. 184305. https://doi.org/10.1103/PhysRevB.99.184305
Shapeev A.V. // Multiscale Model. Simul. 2016. V. 14. P. 1153–1173. https://doi.org/10.1137/15m1054183
Gubaev K., Podryabinkin E.V., Hart G.L.W., Shape-ev A.V. // Comput. Mater. Sci. 2019. V. 156. P. 148–156. https://doi.org/10.1016/j.commatsci.2018.09.031
Gubaev K., Podryabinkin E.V., Shapeev A.V. // J. Chem. Phys. 2018. V. 148. № 24. Art. 241727. https://doi.org/10.1063/1.5005095
Csányi G., Willatt M.J., Ceriotti M. Machine-Learning of Atomic-Scale Properties Based on Physical Principles. In: Schütt K., Chmiela S., von Lilienfeld O., Tkatchenko A., Tsuda K., Müller K.R. (eds.) Machine Learning Meets Quantum Physics. Lecture Notes in Physics. Springer, Cham., 2020. V. 968. P. 99–127. https://doi.org/10.1007/978-3-030-40245-7_6
Zuo Y., Chen C., Li X.-G., Deng Z., Chen Y., Behler J., Csanyi G., Shapeev A.V., Thompson A.P., Wood M.A., Ong S.P.A. // J. Phys. Chem. A. 2020. V. 124. № 4. P. 731–745. https://doi.org/10.1021/acs.jpca.9b08723
Bartók A.P., Kondor R., Csányi G. // Phys. Rev. B. 2013. V. 87. № 18. Art. 184115. https://doi.org/10.1103/physrevb.87.184115
Zhang Y., Hu C., Jiang B. // J. Phys. Chem. Lett. 2019. V. 10. P. 4962–4967. https://doi.org/10.1021/acs.jpclett.9b02037
Chen C., Ye W., Zuo Y., Zheng C., Ong S.P. // Chem. Mater. 2019. V. 31. P. 3564−3572. https://doi.org/10.1021/acs.chemmater.9b01294
Cantor B., Chang I.T.H., Knight P., Vincent A.J.B. // Mater. Sci. Eng.: A. 2004. V. 375–377. P. 213–218. https://doi.org/10.1016/j.msea.2003.10.257
Yeh J.-W., Chen S.-K., Lin S.-J., Gan J.-Y., Chin T.-S., Shun T.-T., Tsau C.-H., Chang, S.-Y. // Adv. Eng. Mater. 2004. V. 6. P. 299–303. https://doi.org/10.1002/adem.200300567
Rost C., Sachet E., Borman T., Moballegh A., Dickey E.C., Hou D., Jones J.L., Curtarolo S., Maria J.-P. // Nat. Commun. 2015. V. 6. Art. 8485. https://doi.org/10.1038/ncomms9485
Castle E., Csanádi T., Grasso S., Dusza J., Reece M. // Sci. Rep. 2018. V. 8. Art. 8609. https://doi.org/10.1038/s41598-018-26827-1
Gild J., Zhang Y., Harrington T., Jiang S., Hu T., Quinn M.C., Mellor W.M., Zhou N., Vecchio R., Luo L.S. // Sci. Rep. 2016. V. 6. Art. 37946. https://doi.org/10.1038/srep37946
Gorsse S., Couzinié J.P., Miracle D.B. // C. R. Physique. 2018. V. 19. P. 721–736.https://doi.org/10.1016/j.crhy.2018.09.004
Miracle D.B., Senkov O.N. // Acta Mater. 2017. V. 122. № 1. P. 448–511. https://doi.org/10.1016/j.actamat.2016.08.081
Mukherjee S. // Metals. 2020. V. 10. № 9. Art. 1253. https://doi.org/10.3390/met10091253
von Barth U., Hedin L. // J. Phys. C. 1972. V. 5. P. 1629–1642. https://doi.org/10.1088/0022-3719/5/13/012
Wang C.S., Klein B.M., Krakauer H. // Phys. Rev. Lett. 1985. V. 54. № 16. P. 1852–1855. https://doi.org/10.1103/physrevlett.54.1852
Saunders N., Miodownik A.P. Calphad (Calculation of Phase Diagrams): A Comprehensive Guide. Pergamon, Oxford, New York. 1998. 478 p. eBook ISBN:9780080528434
Zhang F., Zhang C., Chen S.L., Zhu J., Cao W.S., Kattner U.R. // Calphad. 2014. V. 45. № 6. P. 1–10. https://doi.org/10.1016/j.calphad.2013.10.006
Senkov O., Miller J., Miracle D.B., Woodward C. // Nat. Commun. 2015. V. 6. Art. 6529. https://doi.org/10.1038/ncomms7529
Ng C., Guo S., Luan J., Shi S., Liu C.T. // Intermetallics. 2012. V. 31. P. 165– 172. https://doi.org/10.1016/j.intermet.2012.07.001
Guo S., Ng C., Wang Z., Liu S.T. // J. Alloys Compd. 2014. V. 583. P. 410–413. https://doi.org/10.1016/j.jallcom.2013.08.213
Troparevsky M.C., Morris J.R., Kent P.R.C., Lupini A.R., Stocks G.M. // Phys. Rev. X. 2015. V. 5. № 1. Art. 011041. https://doi.org/10.1103/physrevx.5.011041
Ikeda Y., Grabowski B., Körmann F. // Mater. Charact. 2018. V. 147. № 1. P. 464–511. https://doi.org/10.1016/j.matchar.2018.06.019
Van de Walle A., Ceder G. // Rev. Mod. Phys. 2002. V. 74. № 1. P. 11–45. https://doi.org/10.1103/revmodphys.74.11
Ruban A.V., Abrikosov I.A. // Rep. Prog. Phys. 2008. V. 71. № 4. Art. 046501. https://doi.org/10.1088/0034-4885/71/4/046501
Blöchl P.E. // Phys. Rev. B. 1994. V. 50. P. 17953–17979. https://doi.org/10.1103/PhysRevB.50.17953
Kresse G., Furthmüller J. // Comp. Mater. Sci. 1996. V. 6. P. 15–50. https://doi.org/10.1016/0927-0256(96)00008-0
Zunger A., Wei S.-H., Ferreira L.G., Bernard J.E. // Phys. Rev. Lett. 1990. V. 65. P. 353–356. https://doi.org/10.1103/PhysRevLett.65.353
Tamm A., Aabloo A., Klintenberg M., Stocks M., Caro A. // Acta Mater. 2015. V. 99. P. 307–312. https://doi.org/10.1016/j.actamat.2015.08.015
von Barth U., Hedin L. // J. Phys. C. 1972. V. 5. P. 1629–1642.https://doi.org/10.1088/0022-3719/5/13/012
Wang C.S., Klein B.M., Krakauer H. // Phys. Rev. Lett. 1985. V. 54. № 16. P. 1852–1855. https://doi.org/10.1103/physrevlett.54.1852
Lederer Y., Toher C., Vecchio K.S., Curtarolo S. // Acta Mater. 2018. V. 159. P. 364–383. https://doi.org/10.1016/j.actamat.2018.07.042
Oses C., Toher C., Curtarolo S. // Nat. Rev. Mater. 2020. V. 5. P. 295–309. https://doi.org/10.1038/s41578-019-0170-8
Soven P. // Phys. Rev. 1967. V. 156. № 3. P. 809–811. https://doi.org/10.1103/physrev.156.809
Singh P., Smirnov A.V., Johnson D.D. // Phys. Rev. Mater. 2018. V. 2. № 5. Art. 055004. https://doi.org/10.1103/physrevmaterials.2.05
Körmann F., Ruban A.V., Sluiter M.H.F. // Mater. Res. Lett. 2016. V. 5. № 1. P. 35–40. https://doi.org/10.1080/21663831.2016.1198837
Tian F., Varga L.K., Chen N., Delczeg L., Vitos L. // Phys. Rev. B. 2013. V. 87. № 7. Art. 075144. https://doi.org/10.1103/physrevb.87.075144
Zhao S., Stocks G.M., Zhang Y. // Acta Mater. 2017. V. 134. P. 334–345. https://doi.org/10.1016/j.actamat.2017.05.001
Sanchez J.M. // Phys. Rev. B. 2010. V. 81. Art. 224202. https://doi.org/10.1103/physrevb.81.224202
Shapeev A. // Comput. Mater. Sci. 2017. V. 139. P. 26–30. https://doi.org/10.1016/j.commatsci.2017.07.0
Aitken Z.H., Sorkin V., Zhang Y.-W. // J. Mater. Res. 2019. V. 34. P. 1509–1532. https://doi.org/10.1557/jmr.2019.50
Ghasemi S.A., Hofstetter A., Saha S., Goedecker S. // Phys. Rev. B 2015. V. 92. Art. 045131. https://doi.org/10.1103/physrevb.92.045131
Hajinazar S., Shao J., Kolmogorov A.N. // Phys. Rev. B. 2017. V. 95. № 1. Art. 014114. https://doi.org/10.1103/physrevb.95.014114
Watanabe S., Li W., Jeong W., Lee D., Shimizu K., Mimanitani E., Ando Y. Han S. // J. Phys. Energy. 2021. V. 3. Art. 012003. https://doi.org/10.1088/2515-7655/abc7f3
Von Lilienfeld O.A., Müller K.-R., Tkatchenko A. // Nat. Rev. Chem. 2020. V. 4. P. 347–358. https://doi.org/10.1038/s41570-020-0189-9
Eckhoff M., Behler J. // J. Chem. Theory Comput. 2019. V. 15. № 6. P. 3793–3809. https://doi.org/10.1021/acs.jctc.8b01288
Bartók A.P., Csányi G. // Int. J. Quantum Chem. 2015. V. 115. P. 1051–1057. https://doi.org/10.1002/qua.24927
Wood M.A., Cusentino M.A., Wirth B.D., Thompson A.P. // Phys. Rev. B. 2019. V. 99. № 18. Art. 184305. https://doi.org/10.1103/physrevb.99.184305
Rosenbrock C.W., Gubaev K., Shapeev A.V., Pártay L.B., Bernstein N., Csányi G., Hart G.L.W. // npj Comput. Mater. 2021. V. 7. Art. 24. https://doi.org/10.1038/s41524-020-00477-2
Shapeev A. // Comput. Mater. Sci. 2017. V. 139. P. 26–30. https://doi.org/10.1016/j.commatsci.2017.07.010
Meshkov E.A., Novoselov I.I., Yanilkin A.V., Rogozhkin S.V., Nikitin A.A., Khomich A.A., Shutov A.S., Tarasov B.A., Danilov S.E., Arbuzov V.L. // Phys. Solid State. 2020. V. 62. P. 389–400. https://doi.org/10.1134/S1063783420030130
Костюченко Т.С. Исследование многокомпонентных сплавов при помощи машиннообучаемых потенциалов. Дисс. на соискание степени кандидата физ.-мат. наук. Москва, МФТИ, 2021.
DeVita A., Car R. // MRS Online Proceedings Library. 1997. P. 473–480. https://doi.org/10.1557 /PROC-491-73
Csányi G., Albaret T., Payne M.C., De Vita A. // Phys. Rev. Lett. 2004. V. 93. № 17. Art. 175503. https://doi.org/10.1103/physrevlett.93.175503
Artrith N., Behler J. // Phys. Rev. B. 2012. V. 85. № 4. Art. 045439. https://doi.org/10.1103/physrevb.85.045439
Artrith N., Urban A. // Comput. Mater. Sci. 2016. V. 114. P. 135–150. https://doi.org/10.1016/j.commatsci.2015.11.047
Deringer V.L., Proserpio D.M., Csányi G., Pickard C.J. // Faraday Discuss. 2018. V. 211. P. 45–59. https://doi.org/10.1039/c8fd00034d
Podryabinkin E.V., Shapeev A.V. // Comput. Mater. Sci. 2017. V. 140. P. 171–180. https://doi.org/10.1016/j.commatsci.2017.08.031
Zhang X., Grabowsk B., Körmann F., Ruban A.V., Gong Y., Reed R.C., Hickel T., Neugebauer J. // Phys. Rev. B. 2018. V. 98. № 22. Art. 224106. https://doi.org/10.1103/physrevb.98.224106
Grabowski B., Ikeda Y., Srinivasan P., Körmann F., Freysoldt C., Duff A.I., Shapeev A., Neugebauer J. // Comput. Mater. 2019. V. 5. Art. 80. https://doi.org/10.1038/s41524-019-0218-8
Duff A.I., Davey T., Korbmacher D., Glensk A., Grabowski B., Neugebauer J., Finnis M.W. // Phys. Rev. B. 2015. V. 91. № 21. Art. 214311. https://doi.org/10. 1103/ physrevb.91.214311
Meshkov E., Novoselov I., Shapeev A.V., Yanilkin A.V. // Intermetallics. 2019. V. 112. Art. 106542. https://doi.org/10.1016/j.intermet.2019.106542
Balyakin A., Yuryev A., Gelchinski B., Rempel A. // J. Phys. Condens. Matter. 2020. V. 32. Art. 214006. https://doi.org/10.1088/1361-648X/ab6f87
Jafary-Zadeh M., Khoo K.H., Laskowski R., Branicio P.S., Shapeev A. // J. Alloys Compd. 2019. V. 803. P. 1054–1062. https://doi.org/10.1016/j.jallcom.2019.06.318
Cowley J.M. // Phys. Rev. 1950. V. 77. № 5. P. 669–675. https://doi.org/10.1103/physrev.77.669
Niu C., LaRosa C.R., Mills M.J., Ghazisaeidi M. // Nat. Commun. 2018. V. 9. Art. 1363. https://doi.org/10.1038/s41467-018-03846-0
Zhang R., Zhao S., Ding J., Chong Y., Jia T., Ophus C., Asta M., Ritchie R.O., Minor A. // Nature. 2020. V. 581. P. 283–287. https://doi.org/10.1038/s41586-020-2275-z
Ikeda Y., Gubaev K., Neugebauer J., Grabowski B., Körmann F. // Comput. Mater. 2021. V. 7. Art. 34. https://doi.org/10.1038/s41524-021-00502-y
Zhang Y.H., Zhuang Y., Hu A., Kai J.J., Liu C.T. // Scripta Mater. 2017. V. 130. № 3. P. 96–99. https://doi.org/10.1016/ j.scriptamat
Ikeda Y., Körmann F., Tanaka I., Neugebauer J. // Entropy. 2018. V. 20. № 9. Art. 655. https://doi.org/10.3390/e20090655
Wu Z., Parish C., Bei H. // J. Alloys Compd. 2015. V. 647. P. 815–822 . https://doi.org/10.1016/j.jallcom.2015.05.224
Ikeda Y., Tanaka I., Neugebauer J., Körmann F. // Phys. Rev. Mater. 2019. V. 3. № 11. Art. 113603. https://doi.org/10.1103/physrevmaterials.3.11.113603
Li Z. // Acta Mater. 2019. V. 164. P. 400–412. https://doi.org/10.1016/j.actamat.2018.10.050
Hu J., Shen H., Jiang M., Gong H., Xiao H., Liu Z., Sun G., Zu X. // Nanomaterials. 2019. V. 9. № 3. Art. 461. https://doi.org/10.3390/nano9030461
Hu J., Zhang J., Xiao H., Hu J., Zhang J., Xiao H., Xie L., Shen H., Li P., Zu X. // Inorg. Chem. 2020. V. 59. № 14. P. 9774–9782. https://doi.org/10.1021/acs.inorgchem.0c00989
Batchelor T.A., Pedersen J.K., Winther S.H., Castelli I.E., Jacobsen K.W., Rossmeisl J. // Joul. 2019. V. 3. № 3. P. 834–845. https://doi.org/10.1016/j.joule.2018.12.015
Pedersen J.K., Batchelor T.A., Bagger A., Rossmeisl J. // ACS Catal. 2020. V. 10. P. 2169–2176. https://doi.org/10.1021/acscatal.9b04343
Stevanović V., Lany S., Zhang X., Zunger A. // Phys. Rev. B. 2012. V. 5. № 11. Art. 115104. https://doi.org/10.1103/physrevb.85.115104
Yang Y., Wang W., Gan G.-Y., Shi X.-F., Tang B.-Y. // Physica B: Condens. Matter. 2018. V. 550. P. 163–170. https://doi.org/10.1016/j.physb.2018.09.014
Miracle D.B., Senkov O.N. //Acta Mater. 2017. V. 122. P. 448–511. https://doi.org/10.1016/j.actamat.2016.08.081
Lewin E. // J. Appl. Phys. 2020. V. 127. № 16. Art. 160901. https://doi.org/10.1063/1.5144154
Gelchinski B.R., Balyakin I.A., Yuriev A.A., Rempel A.A. // Russ. Chem. Rev. 2022. V. 91. Art. RCR5023. https://doi.org/10.1070/RCR5023
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Химия, науки о материалах