Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 29-34

Пусть k – поле характеристики нуль с алгебраическим замыканием $K$. $G$ – связная редуктивная k-группа, действующая на алгебраическом k-многообразии X. Обозначим через $P \subseteq G$ минимальную параболическую k-подгруппу, для которой зафиксируем разложение $P = {{L}_{{{\text{an}}}}}A{{P}_{u}}$, где ${{P}_{u}}$ – унипотентный радикал, ${{L}_{{{\text{an}}}}}$ – максимальная анизотропная подгруппа группы $P$, а $A$ – максимальный расщепимый тор, который централизует ${{L}_{{{\text{an}}}}}$. Положим $L = {{L}_{{{\text{an}}}}}A$, $P{\text{'}} = {{L}_{{{\text{an}}}}}{{P}_{u}}$, а также зафиксируем $T \subseteq L$ – максимальный $k$-тор в $G$, содержащий $A$ (см. [1, 16.1.1]). Размерности многообразий мы всегда будем рассматривать над полем $K$. Для алгебраического многообразия $X$ или алгебраической группы $H$, определенных над $k$, множество их k-точек обозначим через ${{X}_{k}}$, ${{H}_{k}}$ соответственно, а через $X {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} H$ обозначим рациональный фактор по действию группы H (который может быть получен с помощью выбора k‑модели для поля рациональных инвариантных функций K(X)^H).

Определение 1. Напомним, что $k$-плотное $G$-многообразие $X$, т.е. такое, что ${{\bar {X}}_{k}} = X$, называется $k$-сферическим, если $P$ имеет открытую орбиту в $X$.

Цель настоящей работы – построить действие ограниченной группы Вейля ${{W}_{k}} = {{N}_{G}}(A){\text{/}}{{Z}_{G}}(A)$, т.е. соответствующей системе корней максимального расщепимого тора над $k$, на семействах главных орбит минимальной параболической подгруппы над алгебраически незамкнутым полем, что обобщает соответствующие результаты [2]. Заметим, что упомянутое действие будет транзитивным, что даст описание множества главных $P$-орбит. В случае $k$-сферических многообразий ранее авторами [4] была доказана теорема о конечности числа $k$-плотных $P$-орбит (см. также [5, 7], в случае $k = K$). Мы также определим гипотетическое действие ограниченной группы Вейля на всех $k$-плотных орбитах максимальной сложности. Мы доказали корректность этого определения действия только в случае $k = \mathbb{R}$ с помощью метода, основанного на алгебре Гекке, построенной с помощью сингулярных когомологий с компактным носителем. Конструкция действия на семействах главных $P$-орбит будет построена следующим образом: сначала мы определим действие образующих ${{s}_{\alpha }}$ группы Вейля ${{s}_{\alpha }} \in {{W}_{k}}$ (т.е. простых отражений, соответствующих простым корням $\alpha \in {{\Delta }_{k}} = \Delta (A)$ расщепимого тора $A$), а затем свяжем это действие с естественным действием ${{W}_{k}}$ на компонентах $k$-поляризованного кокасательного расслоения.

Все хорошо известные сведения, необходимые для понимания настоящей работы, содержатся в [1, 3, 4, 6].

Предложение 1. Пусть $Q$ – $k$-параболическая подгруппа $G$, содержащая $P$, а $Y$ – $P$-инвариантное $k$-плотное подмногообразие $X$. Тогда $QY$ также $k$-плотное замкнутое подмногообразие $X$.

Определение 2. Назовем сложностью ${{c}_{P}}(X)$ минимальную коразмерность $P$-орбиты в $X$ (совпадающую с коразмерностью орбиты общего положения).

Определение 3. Для $P$-инвариантного многообразия $Y$ назовем (расщепимым) рангом $r{{k}_{k}}(Y)$ – ранг решетки характеров $P$-полуинвариантных $k$-рациональных функций на $Y$.

Определение 4. Для $P$-инвариантного многообразия $Y$ назовем однородностью ${{s}_{k}}(Y)$ – размерность общей ${{L}_{{{\text{an}}}}}$-орбиты в рациональном факторе $Y$ по группе $A{{P}_{u}}$.

Определение 5. Назовем многообразие однородно-неприводимым над $k$, если оно не допускает $G$-эквивариантного $k$-морфизма на нетривиальное многообразие флагов (полное однородное пространство) группы $G$.

Через $\mathfrak{B}(X)$ обозначим множество $k$-плотных подмногообразий максимальной сложности, а через ${{\mathfrak{B}}_{k}}(X)$ подмножество в $\mathfrak{B}(X)$, состоящее из подмногообразий максимального ранга.

Пусть $Q$ – $k$-параболическая подгруппа $G$, собственно содержащая $P$ и не содержащая промежуточных подгрупп. Обозначим через ${{Q}_{u}}$ ее унипотентный радикал. Подгруппа Леви $M$ в $Q$, содержащая $A$, имеет над $k$ полупростой ранг 1. Рассмотрим ${{W}_{Q}} = {{N}_{Q}}{{(A)}_{k}}{\text{/}}{{Z}_{Q}}{{(A)}_{k}}$. Согласно [8, 5.18] группа ${{W}_{Q}}$ порождена одним элементом $s \in {{N}_{Q}}{{(A)}_{k}}$, нормализующим $L$. Для множества $k$-точек разложение Брюа принимает вид

Чтобы сформулировать основные результаты работы, нам понадобятся следующее предложение из [4] и следствие из него.

Предложение 2. Пусть $G$ – редуктивная алгебраическая группа над совершенным полем $k$, действующая на $k$-плотном многообразии $X$. Пусть $Y$ – $P$-инвариантное $k$-плотное подмногообразие $X$. Тогда $({{c}_{P}}(Y),r{{k}_{k}}(Y),{{s}_{k}}(Y)) \leqslant ({{c}_{P}}(X)$, rk_k(X), s_k(X)), где сравнение берется в лексикографическом порядке.

Следствие 1. Пусть $G$ – редуктивная $k$‑группа, действующая на $k$-сферическом многообразии $X$. Тогда $X$ имеет конечное число $P$-орбит с непустым множеством $k$-точек.

Определение 6. Назовем $k$-плотное $P$-инвариантное множество $Y$ главным, если у него максимальная (в лексикографическом порядке) $k$-сложность, расщепимый ранг и однородность.

Для того чтобы определить действие простого отражения ${{s}_{\alpha }} \in {{W}_{k}}$ на представителе $Y \in \mathfrak{B}(X)$, рассмотрим минимальную параболическую подгруппу $Q = \overline {P{{s}_{\alpha }}P} $, содержащую $P$ и ${{s}_{\alpha }}$, и рассмотрим многообразие $QY$. Наша цель для $y \in Y$ – представить $Qy$ в виде объединения $P$-орбит, среди которых $Px$ является открытой

Легко видеть, что все $P$-орбиты, а также $k$-плотные $P$-орбиты находятся в биективном соот-ветствии с $P{\text{/}}Ra{{d}_{u}}Q$-орбитами (соответственно $k$-плотными орбитами) при переходе к фактору по группе $Ra{{d}_{u}}Q$ (сюръективность на множестве $k$-точек следует из существования рационального сечения для унипотентной группы), что позволяет свести ситуацию к случаю, когда $Q = G$ является редуктивной группой полупростого расщепимого ранга 1.

Через $F({{W}_{k}})$ обозначим группу с образующими ${{\tilde {s}}_{i}}$, соответствующими простым отражениям ${{s}_{i}}$ группы ${{W}_{k}}$, удовлетворяющими соотношениям $\tilde {s}_{i}^{2}$ = e. Определим действие $F({{W}_{k}})$ на множестве $\mathfrak{B}(X)$ следующим образом. Пусть снова ${{s}_{\alpha }} \in {{W}_{k}}$ и $Y \in \mathfrak{B}(X)$. Положим, что $dimQY > dimY$ (в противном случае $Y$ можно поменять местами с подмногообразием $Y\,{\text{'}} \subset QY$, таким что $QY\,{\text{'}} = QY$). В предложении 3 приведены типы разнесения $Y$: т.е. описано множество $k$-плотных $P$-орбит в $Qу$, и тем самым множество $\mathfrak{B}(QY)$. Также приведено действие ${{\tilde {s}}_{\alpha }}$ исходя из этой классификации. Заметим, что действие ${{\tilde {s}}_{\alpha }}$ на $\mathfrak{B}(QY)$ совместимо с действием ${{s}_{\alpha }}$ на решетках характеров $P$-полуинвариантных функций соответствующих многообразий.

Предложение 3. Пусть $G$ – редуктивная $k$-группа полупростого расщепимого ранга 1 и пусть $X$ – $k$-плотное однородное $G$-многообразие. Тогда выполнен один из следующих случаев:

1. $X$ – $k$-сферическое однородно-неприводимое многообразие. Тогда $\mathfrak{B}(X) = {\text{\{ }}X,{{Y}_{1}},\; \ldots ,\;{{Y}_{r}}{\text{\} }}$ $r \geqslant 0$; $s \circ [X]$ = [X], $s \circ [{{Y}_{i}}] = [{{Y}_{i}}]$.

2. $X$ – $k$-сферическое однородно-приводимое многообразие.

2.1. $X$ – $k$-орисферическое, т.е. стабилизатор точки общего положения содержит ${{P}_{u}}$. Тогда

$\mathfrak{B}(X)$ = {X, Y}; $s \circ [X] = [Y]$.

2.2. $X$ не является орисферическим:

$\mathfrak{B}(X)$ = {X, Y1, Y2}; $s \circ [{{Y}_{1}}] = [{{Y}_{2}}]$.

3. $X$ не является $k$-сферическим: $\mathfrak{B}(X) = {\text{\{ }}X{\text{\} }}$.

Теперь мы можем сформулировать гипотезу и основной результат работы.

Гипотеза 1. Действие группы $F({{W}_{k}})$ на множестве $\mathfrak{B}(X)$ пропускается через действие группы Вейля ${{W}_{k}}$.

Теорема 1. Гипотеза верна в случае $k = \mathbb{R}$, а также в случае действия на множестве, состоящем из главных семейств $P$-орбит ${{\mathfrak{B}}_{k}}(X)$, которое составляет одну ${{W}_{k}}$-орбиту.

Для $k$-точки $x$ со стабилизатором $H$ имеем соответствие 

Выбор точки $x \in {{(G{\text{/}}H)}_{k}}$ дает вложение множества $k$-плотных $H$-орбит в $G{\text{/}}P$ множество $k$‑плотных $P$-орбит в $G{\text{/}}H$. Несмотря на то, что любая $k$-плотная $P$-орбита определяется выбором точки $x$, на множествах $k$-плотных $P$- и $H$-орбит нет биекции, поскольку возможно строгое включение ${{G}_{k}}{\text{/}}{{H}_{k}} \subset {{(G{\text{/}}H)}_{k}}$.

Предложение 4. Пусть $G$ – редуктивная $k$-группа полупростого расщепимого ранга 1 и пусть $H$ – ее $k$-подгруппа, $X: = G{\text{/}}H$. Тогда для множества $k$-плотных $H$-орбит на $Y = G{\text{/}}P$ выполнен один из случаев:

1. Группа $H$ – сферическая, нередуктивная

(U) $X$ орисферическое;

$\mathfrak{B}(Y{\text{/}}H) = {\text{\{ }}Y > Z{\text{\} ;}}$ $r{{k}_{k}}Z = r{{k}_{k}}Y;$

${{s}_{k}}(Z) = {{s}_{k}}(Y);$ $s \circ [Y] = [Z];$

(TU) $X$ не является орисферическим;

$r{{k}_{k}}{{Z}_{i}} = r{{k}_{k}}Y - 1;$ ${{s}_{k}}({{Z}_{1}}) = {{s}_{k}}({{Z}_{2}});$

$s \circ [Y] = [Y];$ $s \circ [{{Z}_{1}}] = [{{Z}_{2}}].$

2. Группа $H$ – сферическая редуктивная,

(A) $G{\text{/}}H^\circ $ однородно-неприводимо, $H$-анизо-тропна; 

$\mathfrak{B}(Y{\text{/}}H) = {\text{\{ }}Y{\text{\} ;}}$ $s \circ [Y] = [Y];$

(RT) $X$ – однородно-приводимое, $H = {{L}_{0}}A$, где ${{L}_{0}} \subseteq {{L}_{{an}}};$

$r{{k}_{k}}{{Z}_{i}} = r{{k}_{k}}Y - 1;$ $s \circ [Y] = [Y],$ $s \circ [{{Z}_{1}}] = [{{Z}_{2}}].$

(RI) $H$ изотропная ($X$ – однородно-неприво-димо);

$\mathfrak{B}(Y{\text{/}}H) = {\text{\{ }}Y > Z{\text{\} ;}}$ $r{{k}_{k}}Z = r{{k}_{k}}Y - 1;$

$s \circ [Y] = [Y];$ $s \circ [Z] = [Z];$

(N) $X$ однородно-неприводимо, $G{\text{/}}{{H}^{0}}$ – однородно-приводимо. H =  ${{L}_{0}}A\left\langle s \right\rangle $, где $s \in {{N}_{G}}(a){\backslash }{{C}_{G}}(A)$;

$\mathfrak{B}(Y{\text{/}}H) = {\text{\{ }}Y > Z{\text{\} }};$ $r{{k}_{k}}Z = r{{k}_{k}}Y - 1;$

$s \circ [Y] = [Y];$ $s \circ [Z] = [Z].$

3. $X$ не является сферическим: $\mathfrak{B}(Y{\text{/}}H)$ = {Y > Z}.

Опишем теперь связь рассмотренного действия с геометрией кокасательного расслоения. Используя аргумент из [10, раздел 5], мы можем заменить $X$ тотальным пространством некоторого линейного расслоения и после этого можем считать, что $X$ невырождено в смысле [10] или даже квазиаффинно.

Пусть $Y \in {{\mathfrak{B}}_{k}}(X)$ и $\alpha \in {{\Pi }_{k}}$, определим действие ${{\tilde {s}}_{\alpha }}$ на $[Y]$ следующим образом. Для простого отражения ${{s}_{\alpha }} \in {{W}_{k}}$ рассмотрим минимальную параболическую подгруппу $Q$, содержащую $P$ и элемент ${{s}_{\alpha }}$. Рассмотрим тип разнесения $Y$ до многообразия $QY$. Если он является типом $(U)$, положим $\tilde {s} \circ Y = QY$, иначе положим ${{\tilde {s}}_{\alpha }} \circ Y = Y$. Мы покажем, что построенное действие $F({{W}_{k}})$ пропускается через действие группы Вейля ${{W}_{k}}$.

Обозначим через ${{\mu }_{X}}{\text{//}}G$ композицию отображений $T_{X}^{ * } \to \mathfrak{g} \to \mathfrak{g}{\text{*//}}G \cong \mathfrak{t}{\text{*/}}{{N}_{G}}(T)$, где последнее отображение является изоморфизмом Шевалле и рассмотрим морфизм:

${{\tilde {T}}_{X}}$ := $T_{X}^{ * }{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{t}{\text{*}}$ ®  $\mathfrak{g}{\text{*}}{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{t}{\text{*}}$,

совпадающий с отображением моментов на первом сомножителе и с тождественным отображением на втором.

Для алгебраического замкнутого поля хорошо известна следующая

Лемма 1 [2]. Неприводимые компоненты

${{\tilde {T}}_{X}}$ := $T_{X}^{ * }{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{t}{\text{*}}$

имеют одинаковую размерность и соотвеmствуют семействам орбит максимальной сложности и ранга. Эти компоненты отображаются сюръективно на $T_{X}^{ * }$, а W действует на них транзитивно посредством действия на втором сомножителе.

Для алгебраически незамкнутых полей требуется модифицировать указанную конструкцию. Рассмотрим следующую последовательность отображений:

где был использован изоморфизм ${{N}_{G}}(L) = {{N}_{G}}(S)$, $\mathfrak{l}{\text{*}}\, = \,{{(\mathfrak{g}{\text{*}})}^{A}}$. Заметим, что отображение $\mathfrak{l}{\text{*//}}{{N}_{G}}(L)$ → → $\mathfrak{g}{\text{*//}}G$ конечно, что следует из результата Луны [11, теорема 6.16].

Заменой ${{\tilde {T}}_{X}}$ для алгебраически незамкнутого поля будет следующий объект:

Имеем следующую последовательность конечных морфизмов:

Наша цель – сопоставить каждому элементу ${{\mathfrak{B}}_{k}}(X)$ неприводимые компоненты ${{\tilde {T}}_{{X,P}}}$ и показать, что действие W_k на неприводимых компонентах ${{\tilde {T}}_{{X,P}}}$, соответствующее действию на правом сомножителе, соответствует действию $F({{W}_{k}})$ на ${{\mathfrak{B}}_{k}}(X)$, определенному выше.

Для исследования компонент ${{\tilde {T}}_{{X,P}}}$ рассмотрим композицию отображений:

Заметим, что последнее отображение допускает сечение над $\mathfrak{p}_{u}^{ \bot }$, определяемое как

Согласно следующей лемме это отображение определено корректно.

Лемма 2. Пусть $\mathfrak{p} \to \mathfrak{l}$ – $L$-эквивариантное отображение на подгруппу Леви. Тогда для $\xi \in \mathfrak{l}$ слой $\xi + {{\mathfrak{p}}_{u}}$ содержится в слое морфизма факторизации $\mathfrak{g}* \to \mathfrak{g}{\text{*//}}G$. Более того, если ${{\xi }_{0}} \in \xi + {{\mathfrak{p}}_{u}}$ полупрост, то полупрост также и ${{\xi }_{0}} \in {{P}_{u}}\xi $.

Данное сечение $\tau $ позволяет вложить ${{\mu }^{{ - 1}}}(\mathfrak{p}_{u}^{ \bot })$ в ${{\tilde {T}}_{{X,P}}}$ посредством отображения $\tilde {\tau }:\eta \mapsto (\eta ,\mu (\eta ){{{\text{|}}}_{{\mathfrak{l}*}}})$. Заметим, что X также выделяет компоненту $T_{X}^{ * }$  ${{ \times }_{{\mathfrak{t}*/W}}}$ $\mathfrak{l}{\text{*//}}{{N}_{G}}(L)$, обозначаемую $\widehat {{{T}_{X}}{\text{*}}}$. Основным результатом работы является следующая

Теорема 2. Существует действие ${{W}_{k}}$ на множестве ${{\mathfrak{B}}_{k}}(X)$ главных семейств $P$-орбит. При этом $\mathfrak{B}(X)$ ${{W}_{k}}$-эквивариантно изоморфно множеству тех k-неприводимых компонент ${{\tilde {T}}_{{X,P}}}$, которые отображаются в выделенную компоненту множества $T_{X}^{ * }{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{l}{\text{*//}}{{N}_{G}}(L)$ и составляют одну ${{W}_{k}}$-орбиту при действии ${{W}_{k}}$ на втором сомножителе $T_{X}^{ * }{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{l}{\text{*//}}L$.

Многообразие ${{\mu }^{{ - 1}}}(\mathfrak{p}_{u}^{ \bot })$ является объединением конормальных расслоений ко всем ${{P}_{u}}$-орбитам в X. Для H-инвариантного подмногообразия $Y$ через $\mathcal{N}(H,Y)$ (или $\mathcal{N}(Y)$ в случае $H = {{P}_{u}}$) обозначим конормальное расслоение к семейству общих $H$-орбит в $Y$. Через $\tilde {\mathcal{N}}(Y,P)$ обозначим образ $\mathcal{N}(Y,{{P}_{u}})$ в ${{\tilde {T}}_{{X,P}}}$. Поскольку любой элемент из $\mathfrak{g}{\text{*}}$ сопряжен с помощью $G$ элементу в $\mathfrak{p}$, для каждой компоненты ${{\tilde {T}}_{{X,P}}}$ найдется неприводимая компонента $\tilde {\mathcal{N}}$ в ${{\mu }^{{ - 1}}}(\mathfrak{p}_{u}^{ \bot })$ такая, что ее $G$-разнесение плотно. Обозначая через $Y$ проекцию $\tilde {\mathcal{N}}$ на X, получаем, что $\tilde {\mathcal{N}} = \mathcal{N}(Y)$.

Наша следующая цель – исследовать главные семейства ${{P}_{u}}$-орбит, для которых тройка чисел $(c(Y{\text{/}}P),r{{k}_{k}}(Y),{{s}_{k}}(Y))$ максимальна в лексикографическом порядке.

Определение 7. Назовем элементарным радикалом $Ra{{d}_{{{\text{el}}}}}H$ (соответственно анизотропным радикалом $Ra{{d}_{{{\text{an}}}}}H$) наименьшую нормальную подгруппу, такую что группа $H{\text{/}}Ra{{d}_{{{\text{el}}}}}H$ ($H{\text{/}}Ra{{d}_{{{\text{an}}}}}H$) элементарна (соответственно анизотропна).

Легко показать, что $Ra{{d}_{{{\text{el}}}}}H$ порожден $k$-унипотентными подгруппами группы $H$, а $Ra{{d}_{{{\text{an}}}}}H$ порождается $Ra{{d}_{{{\text{el}}}}}H$ и подгруппами H, изоморфными над k группе ${{\mathbb{G}}_{m}}$.

Определение 8.   Пусть   $H$    –    связная $k$-группа, действующая на $k$-плотном многообразии $X$. Действие назовем элементарным (соответственно изотропным), если группа $Ra{{d}_{{{\text{el}}}}}H$ (соответственно $Ra{{d}_{{{\text{an}}}}}H$) действует тривиально на $X$.

Напомним определение нормализатора $P$-орбиты общего положения в $X$, который является параболической подгруппой в $G$:

Нам понадобится следующая версия теоремы о локальной структуре [6, 4.6].

Предложение 5. Пусть $X$ – $k$-плотное $G$‑многообразие и пусть ${{P}_{X}} = {{L}_{X}}{{P}_{{X,u}}}$ – разложение Леви, где ${{L}_{X}}$ нормализуется $A$. Тогда существует гладкое аффинное ${{L}_{X}}$-подмногообразие ${{X}_{{{\text{el}}}}} \subseteq X$, такое что:

1) действие ${{L}_{X}}$ на ${{X}_{{{\text{el}}}}}$ элементарно, все орбиты замкнуты, а категорный фактор ${{X}_{{{\text{el}}}}} \to {{X}_{{{\text{el}}}}}{\text{//}}{{L}_{X}}$ является локально-тривиальным расслоением в этальной топологии. В частности, для этого действия существует стабилизатор общего положения, обозначаемый ${{M}_{X}}$;

2) естественный морфизм ${{P}_{{X,u}}} \times {{X}_{{{\text{el}}}}}$ = = ${{P}_{X}}{{ * }_{{{{L}_{X}}}}}{{X}_{{{\text{el}}}}} \to X$ является открытым вложением.

Сечение ${{X}_{{{\text{el}}}}}$ единственно с точностью до ${{L}_{X}}$-эквивариантного бирационального изоморфизма. Более  точно, его поле рациональных функций изоморфно

Доказательство основной теоремы 2 основано на следующем предложении.

Предложение 6. Определенное ранее действие $\widetilde W$ на множестве $\mathfrak{B}(X)$ пропускается через действие ${{W}_{k}}$, оно изоморфно действию на k-неприводимых компонентах $\mathop {\widetilde T}\nolimits_{X,P} $, отображающихся в выделенную компоненту $T_{X}^{ * }{{ \times }_{{\mathfrak{t}*/W}}}\mathfrak{l}{\text{*//}}{{N}_{G}}(L)$, где биекция на множествах определяется посредством отображения $Y \mapsto G\tilde {\mathcal{N}}(Y,{{P}_{u}})$.

В свою очередь предложение основано на исследовании ситуации, когда подъем от $Y$ до $QY$ имеет тип $(U)$. И в этом случае ключевым является факт о том, что из плотности $G\tilde {\mathcal{N}}(QY,{{P}_{u}})$ в $T_{X}^{ * }$ следует также плотность $G\tilde {\mathcal{N}}(Y,{{P}_{u}})$ в $T_{X}^{ * }$. Доказательство этого факта основано на следующих леммах.

Лемма 3. Пусть $Y$ – главное $P$-инвариантное подмногообразие $X$. Тогда существует последовательность ${{P}_{1}},\; \ldots ,\;{{P}_{l}}$ минимальных параболических подгрупп, содержащих $P$, таких что в последовательности ${{Y}_{i}}: = {{P}_{i}}\; \ldots \;{{P}_{1}}Y$ подъем от ${{Y}_{{i - 1}}}$ к ${{Y}_{i}}$ имеет тип $(U)$ и ${{P}_{l}}\; \ldots \;{{P}_{1}}Y = X$. Более того, существует стабилизатор общего положения для действия $P$ на ${{Y}_{i}}$, а также существует стабилизатор общего положения $L(Y)$ для действия $L$ на ${{Y}_{i}} {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} {{P}_{u}}$, который сопряжен $L(X)$ с помощью элемента w := ${{s}_{l}}\; \ldots \;{{s}_{{i - 1}}} \in {{N}_{G}}{{(S)}_{k}}$.

Доказательство леммы 3 основано на соображении, что при подъеме от $Y$ до ${{P}_{1}}Y$ типа $(U)$ имеет место включение $sPsy \supset Py$, а также на следующей лемме.

Лемма 4. Пусть $X$ – многообразие с действием минимальной параболической подгруппы $P$. Рассмотрим $k$-группу $H$ с анизотропным фактором $H{\text{/}}{{H}_{u}}$, c таким действием на $X$ над полем $k$, что для некоторой точки $x \in {{X}_{k}}$ выполняется $Hx \subset Px$. Тогда ${{H}_{u}}x \subset {{P}_{u}}x$ и $Hx \subset P{\text{'}}x$.

Заметим, что если $Z$ – $L$-инвариантное рациональное сечение для ${{P}_{u}}$-орбит $Y$ (которое всегда существует), то оно также является сечением для семейства $s{{P}_{u}}s$ орбит в $QY$, а значит, $sZ$ является сечением для семейства ${{P}_{u}}$-орбит в $QY$. Принимая во внимание, что $s \in {{N}_{G}}{{(S)}_{k}}$ нормализует $L$, это показывает, что стабилизатор общего положения $L$ на ${{Y}_{i}} {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} {{P}_{i}}$ изоморфен L(Y) = ${{s}_{1}}L({{P}_{1}}Y){{s}_{1}}$ = = wL(X)w^–1.

Следствие 2. Пусть $Q$ – минимальная $k$-параболическая подгруппа, собственно содержащая $P$, $s$ – представитель в нормализаторе соответствующего простого отражения. Пусть $Y \in \mathfrak{B}(X)$ такое подмногообразие, что $QY$ является разнесением типа $(U)$. Тогда для всех $y \in Y$ имеем

Ранее было замечено, что ${{P}_{u}}y \subset s{{P}_{u}}sy$. Таким образом, ограничение $\mathcal{N}(sPsy,s{{P}_{u}}s)$ на $Py$ содержится в $\mathcal{N}(Py,{{P}_{u}})$, и мы имеем $s\mathcal{N}({{P}_{1}}y,{{P}_{u}})$ = = $\mathcal{N}(sPsy,s{{P}_{u}}s) \subset (sPs \cap {{P}_{1}})\mathcal{N}(Py,{{P}_{u}})$.

Согласно [6], для квазиаффинного $X$ существует $\chi \in {{\Lambda }_{k}}(X)$, удовлетворяющее $\left\langle {\chi ,\alpha } \right\rangle \ne 0$ для всех $\alpha \in {{\Delta }_{{{{\mathfrak{p}}_{{X,u}}}}}}$. Такие $\chi $ могут быть также охарактеризованы эквивалентным образом: ${{s}_{\alpha }}\chi \ne \chi $ для ${{s}_{\alpha }} \in {{N}_{G}}(A){\backslash }{{L}_{X}}$. Вложим ${{\Lambda }_{k}}(X)$ в качестве подрешетки $\mathfrak{a}_{X}^{ * }$. Множество $\mathfrak{a}_{X}^{{pr}}$ таких $\chi \in \mathfrak{a}_{X}^{ * }$, которое удовлетворяет данному условию, плотно по Зарисскому $\mathfrak{a}_{X}^{ * }$. Через ${{A}_{0}}$ обозначим общее ядро в $A$ характеров $P$‑полуинвариантных функций ($\mathfrak{a} = {{\mathfrak{a}}_{0}} + {{\mathfrak{a}}_{X}}$). Рассмотрим ${{P}_{X}}$-полуинвариантную функцию ${{f}_{\chi }} \in k(X)_{\chi }^{{(Q)}}$, следуя [10], определим ${{P}_{X}}$-эквивариантное отображение

Отображение ${{\Psi }_{\chi }}{\text{:}}\;X^\circ \to T_{X}^{ * }$, где $X^\circ \, = \,X{\backslash div}({{f}_{\chi }})$, отображает точку $y \in X^\circ $ в значение соответствующего сечения $f_{\chi }^{{ - 1}}(d{{f}_{\chi }})$ в y, дает следующую коммутативную диаграмму:

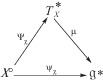
Заметим, что ${{\Psi }_{\chi }}(X)$ является подмножеством $\mathcal{N}(X)$, поскольку дифференциальная 1-форма $f_{\chi }^{{ - 1}}(d{{f}_{\chi }})$ аннулируется векторным полем ${{\mathfrak{p}}_{u}}$. Также согласно [6, (4.5)] образ ${{\psi }_{\chi }}(X^\circ )$ равен $\xi + {{\mathfrak{p}}_{{X,u}}}$. Многообразие ${{\mathcal{K}}_{\chi }} = \psi _{\chi }^{{ - 1}}(\chi ) \subset X^\circ $ (или более кратко $\mathcal{K}$) дает рациональное сечение для ${{P}_{u}}$-орбит (которые также являются ${{P}_{{X,u}}}$-орбитами) в $X^\circ $. ${{P}_{X}}$-эквивариантное отображение ${{\Psi }_{\chi }}$ вкладывает $\mathcal{K}$ в $\mathcal{N}(X)$, этот образ обозначим $\tilde {\mathcal{K}}): = {{\Psi }_{\chi }}(\mathcal{K})$.

Далее, воспользовавшись редуктивностью $L$, зафиксируем $L$-эквивариантный изоморфизм $\mathfrak{l} \cong \mathfrak{l}{\text{*}}$ и расщепление $\mathfrak{g}* \cong \mathfrak{l}{\text{*}} \oplus {{\mathfrak{l}}^{ \bot }}$.

Предложение 7. Пусть $G$ – $k$-группа, действующая на k-плотном квазиаффинном $X$. Для ${{X}_{{{\text{el}}}}}$, которое бирационально $X {\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}} {{P}_{u}}$, рассмотрим ${{\mu }_{\mathfrak{l}}}{\text{:}}\;T{\text{*}}{{X}_{{{\text{el}}}}} \to \mathfrak{l}{\text{*}}$, соответствующее отображение моментов. Пусть $Y \in \mathfrak{B}(X)$, для разложения элемента $w: = {{s}_{1}}\; \ldots \;{{s}_{l}} \in W$ положим ${{Y}_{i}}: = {{P}_{i}}\; \ldots \;{{P}_{1}}Y$, а также предположим, что подъем от ${{Y}_{i}}$ до ${{Y}_{{i + 1}}}$ имеет тип $(U)$. Тогда

(i) $G\mathcal{N}(Y)$ плотно $T{\text{*}}X;$

(ii) $\overline {\mu (\mathcal{N}(Y,{{P}_{u}}))} = Pw{{\mu }_{l}}(T{\text{*}}{{X}_{{{\text{el}}}}})$,

$\overline {\mu (\mathcal{N}(Y,P{\text{'}}))} $ = $Pw{{\mathfrak{a}}_{X}}$;

(iii) $w\mathcal{K}$ – $L$-инвариантное рациональное сечение для множества общих ${{P}_{u}}$-орбит в $Y$.

Доказательство предложения 7 мы опустим, поскольку оно достаточно технично. Предложение 6 существенно опирается на предложение 7, на следствие 2, а также на соображение, что для подъема от $Y$ до $QY$, отличного от типа $(U)$, расщепимый ранг любого необщего семейства $P$-орбит $Y\,{\text{'}} \subset QY$ строго меньше расщепимого ранга $QY$. Дело в том, что согласно предложению 7 (ii) образ отображения моментов выражается через ${{\mathfrak{a}}_{X}}$, а образ отображения моментов конормального расслоения $\mathcal{N}(Y\,{\text{'}},P)$ выражается через алгебру Ли расщепимого подтора в $A$, действующего эффективно на $P$-полуинвариантных функциях $Y\,{\text{'}}$, если расщепимый ранг $Y\,{\text{'}}$ строго меньше $r{{k}_{k}}(X)$, это дает строгое включение для образа отображения моментов. Тем самым, $G\mathcal{N}(Y\,{\text{'}},P)$ не может быть плотно в $T_{X}^{ * }$.