Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 42-46

Цель исследования – распространение результатов работы [1] для групп Карно на пространства Карно–Каратеодори. Напомним, что локально такие структуры похожи, однако они существенно различаются в тонких свойствах. В [2] показано, что вид полиномиального субриманова дифференциала ${{\hat {D}}_{P}}{{\varphi }_{\Gamma }}$ графика φ_Γ, построенного по отображению $\varphi $, является более сложным сравнительно с группами Карно: в каждой точке x матрица его дифференциала (при перегруппировке полей по степеням) является суммой блочно-нижнетреугольной матрицы и матрицы, все элементы которой сравнимы с $\rho (x,{{\varphi }_{\Gamma }}(x))$, где $\rho $ – расстояние, эквивалентное риманову. Для вывода формулы вычисления внутренней меры поверхностей-графиков в [2] использовались два разных адаптированных, или внутренних, базиса в образе: первый позволял получить “классический” вид формулы, когда “диагональные” блоки матрицы $D({{\hat {D}}_{P}}{{\varphi }_{\Gamma }})$ совпадают с суммой единичной матрицы и “диагонального” блока $D({{\hat {D}}_{P}}\varphi )$ (или $\hat {D}\varphi $), а второй – “общий”, когда в каждой точке $x$ эти блоки отличаются от классического варианта на элементы, сравнимые с $\rho (x,{{\varphi }_{\Gamma }}(x))$. В силу специфики строения сублоренцевых шаров (в частности, их неограниченности) форма и мера их сечения плоскостями-образами $D({{\hat {D}}_{P}}{{\varphi }_{\Gamma }})$ зависит от вида такого дифференциала; кроме того, этот вид влияет на свойство пространственноподобия поверхности. Так как ограничения, обеспечивающие это свойство, на внедиагональных элементах не формулируются явно и, следовательно, труднопроверяемы (в силу зависимости от структурных функций, матриц перехода и многих других параметров), то в данной работе мы будем использовать первый вид внутреннего базиса, приводящий матрицу $D({{\hat {D}}_{P}}{{\varphi }_{\Gamma }})$ к блочно-диагональному виду. В таком случае требования будут накладываться на блоки hc-дифференциала отображения (если $\varphi $ гладкое и контактное) или на диагональные блоки дифференциала полиномиального hc-дифференциала (если $\varphi $ гладкое и неконтактное).

Определение 1 (см., например, [4]; ср. [3]). Фиксируем связное риманово ${{C}^{\infty }}$-многообразие $\mathbb{M}$ топологической размерности $N$. Пусть в его касательном расслоении $T\mathbb{M}$ существует фильтрация ${{H}_{1}}\mathbb{M} \subsetneq \ldots \subsetneq {{H}_{i}}\mathbb{M} \subsetneq \ldots \subsetneq {{H}_{M}}\mathbb{M} = T\mathbb{M}$ подрасслоениями такая, что для каждого $p \in \mathbb{M}$ найдется окрестность $U \subset \mathbb{M}$ с набором полей ${{X}_{1}}, \ldots ,{{X}_{N}}$ класса C¹, обладающая следующими свойствами:

1) подпространство ${{H}_{i}}\mathbb{M}({v})$ = ${\text{span\{ }}{{X}_{1}}({v})$, ... ... ${{X}_{{dim{{H}_{i}}}}}({v}){\text{\} }} \subset {{T}_{{v}}}\mathbb{M}$ имеет размерность $dim{{H}_{i}}$ независимо от ${v}$, $i = 1,2,\; \ldots ,\;M$;

2) верны включения $[{{H}_{i}},{{H}_{j}}] \subset {{H}_{{i + j}}}$, i, j = = $1,2, \ldots ,M$, $i + j \leqslant M$.

В этом случае набор $(\mathbb{M},{{H}_{1}},\; \ldots ,\;{{H}_{M}})$ называется пространством Карно–Каратеодори. Если, кроме того, выполнено 3), то набор $(\mathbb{M},{{H}_{1}},\; \ldots ,\;{{H}_{M}})$ – многообразие Карно:

3) H_{j + 1} = ${\text{span\{ }}{{H}_{j}},[{{H}_{1}},{{H}_{j}}],[{{H}_{2}},{{H}_{{j - 1}}}]$, ..., [H_k, ${{H}_{{j + 1 - k}}}]{\text{\} }}$, где $k = \left[ {\tfrac{{j + 1}}{2}} \right]$, ${{H}_{0}} = {\text{\{ }}0{\text{\} }}$, $j = 1,2,\; \ldots ,\;M - 1$.

Для упрощения обозначений пространство Карно–Каратеодори (или многообразие Карно) будем обозначать символом $\mathbb{M}$. Подрасслоение ${{H}_{1}}\mathbb{M}$ называется  горизонтальным. Число $M$ называется  глубиной многообразия $\mathbb{M}$.

Определение 2. Степень поля $deg{{X}_{k}}$ равна $min{\text{\{ }}m|{{X}_{k}} \in {{H}_{m}}{\text{\} }}$.

Замечание 1. Из условия 2) определения 1 следует, что

Опишем локальную однородную группу и ее главные свойства.

Теорема 1 ([5]). Фиксируем $u \in \mathbb{M}$. Набор

определяет нильпотентную градуированную алгебру Ли.

Для фиксированного $u \in \mathbb{M}$ построим [5] алгебру Ли ${{\mathfrak{g}}^{u}}$ со структурными постоянными теоремы 1 как нильпотентную градуированную алгебру Ли векторных полей ${\text{\{ }}(\hat {X}_{i}^{u}){\text{'\} }}_{{i = 1}}^{N}$ на ${{\mathbb{R}}^{N}}$ такую, что экспоненциальное отображение $({{x}_{1}}, \ldots ,{{x}_{N}})$ $ \mapsto $ $ \mapsto $ $exp\left( {\sum\limits_{i = 1}^N {{{x}_{i}}} (\hat {X}_{i}^{u}){\text{'}}} \right)(0)$ тождественно [6]. В силу этого x_i= ${\text{exp}}({{x}_{i}}(\hat {X}_{i}^{u}){\text{'}})(0)$. Следовательно, e_i = = $(\hat {X}_{i}^{u}){\text{'}}(0)$. Соответствующую группу Ли обозначим ${{\mathbb{G}}_{u}}\mathbb{M}$.

Определение 3. Пусть $u \in \mathbb{M}$ и $({{{v}}_{1}}, \ldots ,{{{v}}_{N}})\, \in \,{{B}_{E}}(0$, r), где ${{B}_{E}}(0,r)$ – евклидов шар в ${{\mathbb{R}}^{n}}$. Определим ${{\theta }_{u}}{\text{:}}\;{{B}_{E}}(0,r) \to \mathbb{M}$ следующим образом: ${{\theta }_{u}}({{{v}}_{1}}, \ldots ,{{{v}}_{N}}) = exp\left( {\sum\limits_{i = 1}^N {{{{v}}_{i}}} {{X}_{i}}} \right)(u)$. Известно, что ${{\theta }_{u}}$ является ${{C}^{1}}$-гладким диффеоморфизмом, если $0 < r \leqslant {{r}_{u}}$ для некоторого ${{r}_{u}} > 0$. Набор ${\text{\{ }}{{{v}}_{i}}{\text{\} }}_{{i = 1}}^{N}$ называется нормальными координатами (относительно $u \in \mathbb{M}$) точки ${v} = {{\theta }_{u}}({{{v}}_{1}}$, ..., ${{{v}}_{N}})$.

Используя отображение ${{\theta }_{u}}$, перенесем поля $(\hat {X}_{i}^{u}){\text{'}}$ на $\mathcal{U}\,\, \Subset \,\,\mathbb{M}$: $\hat {X}_{i}^{u} = {{({{\theta }_{u}})}_{ * }}(\hat {X}_{i}^{u}){\text{'}}$.

Определение 4. Группа, ассоциированная с алгеброй Ли ${\text{\{ }}\hat {X}_{i}^{u}{\text{\} }}_{{i = 1}}^{N}$ в точке $u \in \mathbb{M}$, называется локальной однородной группой ${{\mathcal{G}}^{u}}\mathbb{M}$. Определим ее так, чтобы отображение ${{\theta }_{u}}$ было  локальным групповым изоморфизмом окрестностей единиц ${{\mathbb{G}}_{u}}\mathbb{M}$ и ${{\mathcal{G}}^{u}}\mathbb{M}$.

Определение 5. Если $y = exp\left( {\sum\limits_{i = 1}^N {{{y}_{i}}} {{X}_{i}}} \right)(x)$, то положим ${{d}_{\infty }}(x,y) = \mathop {max}\limits_{i = 1, \ldots ,N} \left\{ {{{{\left| {{{y}_{i}}} \right|}}^{{1/{\text{deg}}{{X}_{i}}}}}} \right\}$. Величина $d_{\infty }^{u}({v}{\text{,}}w)$ для $w = exp\left( {\sum\limits_{i = 1}^N {{{w}_{i}}} \hat {X}_{i}^{u}} \right)({v})$ определяется аналогично; см. подробности в [5].

Определение 6 (ср. [7]). Пусть $\mathbb{M}$ и $\tilde {\mathbb{M}}$ – пространства Карно–Каратеодори, $E \subset \mathbb{M}$, ψ : $E \to \tilde {\mathbb{M}}$, и функция $\tilde {\mathfrak{d}}:\psi (E) \times \tilde {\mathbb{M}} \to {{\mathbb{R}}_{ + }}$ непрерывна, равна нулю только на одинаковых элементах и симметрична. Отображение $\psi $ полиномиально субриманово дифференцируемо, или полиномиально hc-дифференцируемо, в (предельной) точке $x \in E$ относительно $\tilde {\mathfrak{d}}$, если существует ${{\mathcal{L}}_{x}}:{{\mathcal{G}}^{x}}\mathbb{M} \to {{\mathcal{G}}^{{\psi (x)}}}\tilde {\mathbb{M}}$ такое, что

1) $\tilde {\mathfrak{d}}(\psi (w),{{\mathcal{L}}_{x}}\langle w\rangle ) = o({{d}_{\infty }}(x,w))$, $E \ni w \to x$;

2) ${{\mathcal{L}}_{x}}(w) = {{\theta }_{{\psi (x)}}} \circ {{L}_{x}} \circ \theta _{x}^{{ - 1}}(w)$, где L_x – полином от ${{w}_{1}},\; \ldots ,\;{{w}_{N}}$, а $exp\left( {\sum\limits_{i = 1}^N {{{w}_{i}}} {{X}_{i}}} \right)(x) = w$.

Отображение ${{\mathcal{L}}_{x}}$ называется полиномиальным субримановым дифференциалом,  или  полиномиальным hc-диф-ференциалом, отображения $\psi $ в x, и обозначается ${{\hat {D}}_{P}}\psi (x)$.

Полиномиальная субриманова дифференцируемость является развитием следующей концепции субримановой дифференцируемости [8].

Определение 7 [8]. Пусть $\mathbb{M}$ и $\tilde {\mathbb{M}}$ – пространства Карно–Каратеодори, $E \subset \mathbb{M}$ – измеримое множество, и $\varphi {\text{:}}\;\Omega \to \tilde {\mathbb{M}}$. Отображение $\varphi $ является hc-дифференцируемым, или дифференцируемым в субримановом смысле, в (предельной) точке $x \in E$, если существует горизонтальный гомоморфизм ${{\mathcal{L}}_{x}}$: ${{\mathcal{G}}^{x}}\mathbb{M}$ → → ${{\mathcal{G}}^{{\varphi (x)}}}\tilde {\mathbb{M}}$ такой, что

Теорема 2 [8]. Гладкие контактные отображения, а именно, дифференциал которых переводит горизонтальные поля в горизонтальные, многообразий Карно в пространства Карно–Каратеодори, непрерывно $hc$-дифференцируемы всюду.

Предположение 1. Будем рассматривать $\varphi {\text{:}}\;\Omega \to \mathbb{M}$, где $\Omega \subset \mathbb{M}$ – открытое множество; $\mathbb{M}$ ($\tilde {\mathbb{M}}$) – пространство Карно–Каратеодори топологической размерности N ($\tilde {N}$) с гладкими базисными полями ${{X}_{1}},\; \ldots ,\;{{X}_{N}}$ (${{\tilde {X}}_{1}},\; \ldots ,\;{{\tilde {X}}_{{\tilde {N}}}}$) и фильтрацией ${{H}_{1}},\; \ldots ,\;{{H}_{M}}$ (${{\tilde {H}}_{1}},\; \ldots ,\;{{\tilde {H}}_{{\tilde {M}}}}$); $\varphi \in {{C}^{{\hat {M}}}}(\Omega ,\tilde {\mathbb{M}})$, где $\hat {M} = max{\text{\{ }}M,\tilde {M}{\text{\} }}$; $\mathbb{M},\tilde {\mathbb{M}} \subset \mathbb{U}$, где $\mathbb{U}$ – (эквирегулярное) пространство Карно–Каратеодори топологической размерности $\hat {N} = N + \tilde {N}$ с базисными полями ${{X}_{1}},\; \ldots ,\;{{X}_{N}},\mathop {\tilde {X}}\nolimits_1 ,\; \ldots ,\;{{\tilde {X}}_{{\tilde {N}}}}$, имеющими те же степени, что и на $\mathbb{M}$ и $\tilde {\mathbb{M}}$, соответственно, распределение ${\text{\{ }}{{{\tilde {X}}}_{1}},\; \ldots ,\;{{\tilde {X}}_{{\tilde {N}}}}{\text{\} }}$ интегрируемо, и $0 = \mathbb{M} \cap \tilde {\mathbb{M}}$; рассматриваемая окрестность пространства Карно–Каратеодори $\mathbb{U}$ и значения $\varphi (x)$ таковы, что все необходимые понятия: экспоненциальные отображения и обратные к ним, локальные однородные группы ${{\mathcal{G}}^{u}}\mathbb{U}$, а также значения ${{\varphi }_{\Gamma }}$, определены корректно.

Замечание 2. Здесь $0$ – некоторая точка, являющаяся единственным пересечением $\mathbb{M}$ и $\tilde {\mathbb{M}}$, принятая за начало координат при построении графиков.

Введем определение отображения-графика на пространствах Карно–Каратеодори.

Определение 8 (ср. [7]). Пусть 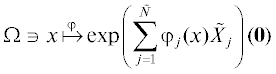. Положим действие отображения-графика ${{\varphi }_{\Gamma }}:\Omega \to \mathbb{U}$ равным

В [2] установлен следующий результат для отображений-графиков.

Теорема 3. Пусть выполнены условия предположения 2, и $\varphi \in {{C}^{{\hat {M}}}}(\Omega ,\tilde {\mathbb{M}})$. Отображение-график ${{\varphi }_{\Gamma }}{\text{:}}\;\Omega \to \tilde {\mathbb{M}}$ полиномиально субриманово дифференцируемо всюду, и ${{\hat {D}}_{P}}{{\varphi }_{\Gamma }}(x)$ сопоставляет элементу $y = exp\left( {\sum\limits_{i = 1}^N {{{y}_{i}}} {{X}_{i}}} \right)(x)$ в нормальных координатах относительно ${{\varphi }_{\Gamma }}(x)$ набор $({{\Delta }_{1}}(x,y),\; \ldots ,\;{{\Delta }_{{N + \widetilde N}}}(x,y))$, где

где ${{\mathcal{D}}_{{\hat {M}}}}{{\varphi }^{\Delta }}({{x}_{ \to }}y)(x)\langle y\rangle \, = \,{{\hat {D}}_{P}}\varphi (x)\langle y\rangle $ – аппроксимация с точностью до $o({{d}_{\infty }}{{(x,y)}^{{\hat {M}}}})$ величины $\theta _{{\varphi (x)}}^{{ - 1}}(\varphi (y))$, а ${{\mathcal{P}}_{k}}(x,y)$ – полиномы от ${{y}_{1}},\; \ldots ,\;{{y}_{N}}$ и величин, сравнимых с $\rho (x,{{\varphi }_{\Gamma }}(x))$. Такой набор аппроксимирует ${{\varphi }_{\Gamma }}(y)$ с точностью до $o({{d}_{\infty }}{{(x,y)}^{{\widehat M}}})$ при любой невырожденной замене базиса.

При ограничениях на $\rho (0,\varphi (x)) = \rho (x,{{\varphi }_{\Gamma }}(x))$ отображение-график ${{\varphi }_{\Gamma }}$ взаимно-однозначно и  $D({{D}_{P}}{{\varphi }_{\Gamma }}(x))(x)$ невырожден. Следовательно (см.  [2]), существует адаптированный базис {^xX₁, ..., $^{x}{{X}_{N}},{{\,}^{x}}{{\tilde {X}}_{1}}, \ldots ,{{\,}^{x}}{{\tilde {X}}_{{\tilde {N}}}}{\text{\} }}$, при перегруппировке полей по степеням приводящий матрицу $D({{D}_{P}}{{\varphi }_{\Gamma }}(x))(x)$ к блочно-диагональному виду (ср. [9]; см. описание и принцип построения в [10, определение 4.1, теорема 4.3, шаги 3–4]).

Опишем сублоренцеву структуру на $\mathbb{U}$. Положим ${{\hat {H}}_{k}} = {\text{span\{ }}{{H}_{k}},{{\tilde {H}}_{k}}{\text{\} }} = {\text{span\{ }}\hat {H}_{k}^{ + },\hat {H}_{k}^{ - }{\text{\} }}$, $\hat {H}_{k}^{ - } \subset {{\tilde {H}}_{k}}$, причем каждое базисное поле степени k принадлежит либо $\hat {H}_{k}^{ + }$, либо $\hat {H}_{k}^{ - }$, $k = 1,2,\; \ldots ,\;\hat {M}$. Напомним, что по выбору внутреннего базиса дифференциалы полиномиальных субримановых дифференциалов (при перегруппировке полей по степеням) имеют блочно-диагональный вид, где каждый блок состоит из единичной матрицы размерности dimH_i – $dim{{H}_{{i - 1}}}$ и либо $((\dim {{\tilde {H}}_{i}} - dim{{\tilde {H}}_{{i - 1}}})$ × × $(dim{{H}_{i}} - dim{{H}_{{i - 1}}}))$-блока $D{{({{\hat {D}}_{P}}\varphi )}_{i}}$ матрицы $D({{\hat {D}}_{P}}\varphi )$, либо $((\dim {{\tilde {H}}_{i}} - dim{{\tilde {H}}_{{i - 1}}})$ × (dimH_i – ‒ $dim{{H}_{{i - 1}}}))$-блока ${{(\hat {D}\varphi )}_{i}}$ матрицы $\hat {D}\varphi $, поэтому, перегруппируя при необходимости поля в образе, представим эти блоки как объединение частей $D({{\hat {D}}_{P}}\varphi )_{i}^{ + }$ и $D({{\hat {D}}_{P}}\varphi )_{i}^{ - }$ (соответственно $(\widehat D\varphi )_{i}^{ + }$ и $(\hat {D}\varphi )_{i}^{ - }$), где “минусовые” части состоят из строк, соответствующих полям из $\hat {H}_{i}^{ - }$, $i = 1,2, \ldots ,\tilde {M}$, dimH₀ = = $\dim {{\tilde {H}}_{0}}$ = 0.

Обозначим адаптированный базис символом ${{{\text{\{ }}}^{x}}{{Y}_{j}}{\text{\} }}_{{j = 1}}^{{\hat {N}}}$ и опишем в его терминах расстояние, понятие пространственноподобия и меру на поверхностях-графиках. Отметим, что все вышеперечисленное можно определить и для исходного базиса ${\text{\{ }}{{Y}_{1}},\; \ldots ,\;{{Y}_{{\tilde {N}}}}{\text{\} }}$ = ${\text{\{ }}{{X}_{1}},\; \ldots ,\;{{X}_{N}},{{\tilde {X}}_{1}},\; \ldots ,\;{{\tilde {X}}_{{\tilde {N}}}}{\text{\} }}$ непосредственной заменой наборов базисных полей.

Определение 9 (ср. [1]). Пусть w = = exp$\left( {\sum\limits_{i = 1}^{\hat {N}} {w{{{_{i}^{{}}}}^{x}}{{Y}_{i}}} } \right)({v})$. Определим величину $^{x}\mathfrak{d}_{2}^{2}(v,w)$ следующим образом:

Множество ${\text{\{ }}w \in \mathbb{U}:{{\,}^{x}}\mathfrak{d}_{2}^{2}({v},w) < {{r}^{2}}{\text{\} }}$ называется шаром относительно $^{x}\mathfrak{d}_{2}^{2}$ радиуса r > 0 с центром в точке ${v}$ и обозначается символом $^{x}\mathop {{\text{Box}}}\nolimits_2^\mathfrak{d} ({v},r)$.

Определение 10 (ср. [1]). Поверхность-график ${{\varphi }_{\Gamma }}(\Omega )$ называется пространственноподобной, если локально для всех ${v} \in {{\varphi }_{\Gamma }}(\Omega )$ она лежит вне множества

за исключением точки ${v} \in {{\varphi }_{\Gamma }}(\Omega )$.

Следующее утверждение описывает классы рассматриваемых отображений.

Лемма 1 (ср. [1]). Пусть длины строк $(\hat {D}\varphi )_{j}^{ - }$ (для контактных отображений) и $D({{\hat {D}}_{P}}\varphi )_{j}^{ - }$ (для неконтактных отображений) не превосходят величину $\tfrac{1}{{dim{{H}_{j}} - dim{{H}_{{j - 1}}}}}$ – c, c > 0, j = 1, 2, ..., $min{\text{\{ }}M,\tilde {M}{\text{\} }}$. Тогда поверхность ${{\varphi }_{\Gamma }}(\Omega )$ пространственноподобна.

Определение 11 (ср. [7]). Значение  внутренней меры $\mathcal{H}_{\Gamma }^{\nu }$ для подмножеств $A\, \subset \,{{\varphi }_{\Gamma }}(\Omega )$, где $\nu = \sum\limits_{i = 1}^M i (dim{{H}_{i}} - dim{{H}_{{i - 1}}})$, $dim{{H}_{0}} = 0$, равно

Здесь точная нижняя грань берется по всем покрытиям множества A.

Сформулируем основной результат сообщения о внутренней мере поверхностей-графиков.

Теорема 4. Пусть выполнено одно из следующих условий:

1) $\varphi \in {{C}^{{\hat {M}}}}(\Omega ,\tilde {\mathbb{M}})$, где $\varphi $ – контактное отображение, а $\Omega $ – открытое подмножество многообразия Карно $\mathbb{M}$;

2) $\varphi \in {{C}^{{\hat {M}}}}(\Omega ,\tilde {\mathbb{M}})$, где $\varphi $ – неконтактное отображение, а Ω – открытое подмножество пространства Карно–Каратеодори $\mathbb{M}$.

Кроме того, пусть $\varphi $ удовлетворяет условиям леммы 1. Тогда $\mathcal{H}_{\Gamma }^{\nu }$-мера поверхности-графика равна

гдедля первого случая, идля второго случая.

Одним из основных шагов доказательства является

Лемма 2 (ср. [7, лемма 1] и др.). Функция множества $\Phi :{{\varphi }_{\Gamma }}(\Omega ) \to \mathbb{R}$, равная

обладает следующими свойствами:

1) она абсолютно непрерывна относительно ${{\mathcal{H}}^{\nu }}$ на $\Omega \subset \mathbb{M}$;

2) она (локально) аддитивна на удаленных шарах.