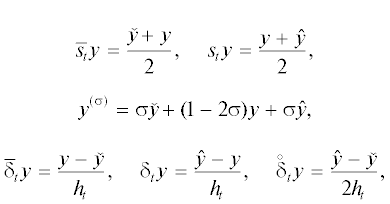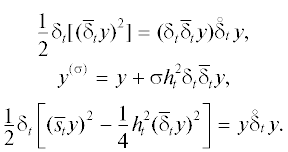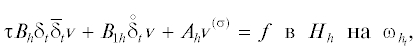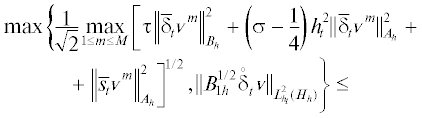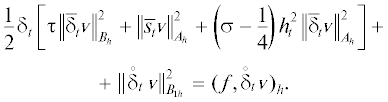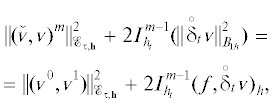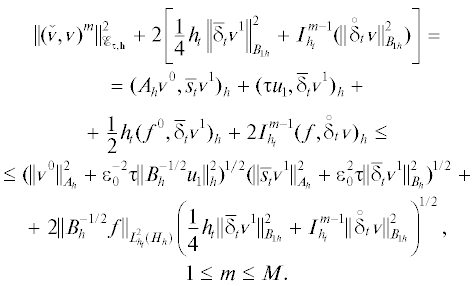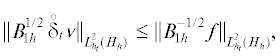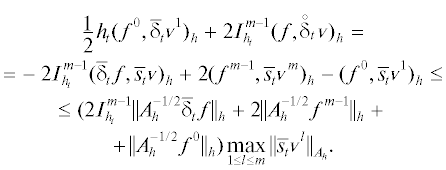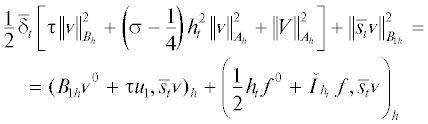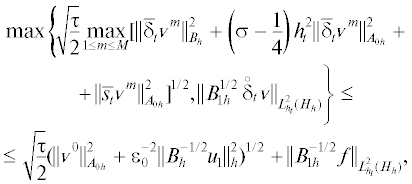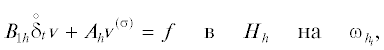Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 490, № 1, стр. 35-41

Рассмотрим линейную гиперболическую 2-го порядка начально-краевую задачу

являющуюся возмущением с (малым) параметром $\tau > 0$ параболической задачи

Здесь $\Omega $ – ограниченная область в ${{\mathbb{R}}^{n}}$ с границей $\partial \Omega $, ${{\Gamma }_{T}} = \partial \Omega \times (0,T)$ и ${\mathbf{f}} = ({{f}_{1}},\; \ldots ,\;{{f}_{n}})$ – вектор-функция; операторы $div$ и $\nabla = ({{\partial }_{1}},\; \ldots ,\;{{\partial }_{n}})$ берутся по $x \in \Omega $. Коэффициенты задач подчиняются стандартным условиям α, ρ, $\mathcal{A} = {\text{\{ }}{{a}_{{ij}}}{\text{\} }}_{{i,j = 1}}^{n} \in {{L}^{\infty }}(\Omega )$ и $\alpha (x) \geqslant \nu $, $\rho (x) \geqslant \nu $, $\mathcal{A}(x) = {{\mathcal{A}}^{T}}(x) \geqslant \nu I$ для почти всех $x \in \Omega $ с $\nu > 0$ и единичной матрицей I. Недавно в [1] был указан набор оценок ${{u}_{\tau }}$ и выведены оценки разности $u - {{u}_{\tau }}$ в терминах данных.

Целью данной работы является анализ устойчивости численных методов решения начально-краевой задачи (1). Такой анализ представляет интерес как в связи c применением в последнее десятилетие гиперболической квазигазодинамической системы уравнений [2–4] для решения ряда задач аэродинамики, астрофизики, теории фильтрации и т.д., так и с классических позиций [5].

В работе доказываются теоремы устойчивости решений симметричных трехслойного с весом и векторного двухслойного по $t$ методов в энергетической и более слабой нормах по начальным данным и правой части уравнения. Соответствующие оценки равномерны как по $\tau $, так и по T. При $\tau = 0$ из них следуют оценки решений соответствующих методов для задачи (2). Охвачен также случай, когда параметр $\tau $ стоит в (1) и перед $div(\mathcal{A}\nabla {{u}_{\tau }})$. Дополнительно выведена оценка порядка $O(\tau )$ для разности решений трехслойных методов с весом $\sigma = \tfrac{1}{4}$ для задач (1) и (2). Все результаты применимы при дискретизации задач по пространству как разностным методом, так и методом конечных элементов (МКЭ), в том числе с сосредоточенными матрицами масс. Техника анализа опирается на развитую в случае МКЭ в [6]. Некоторые другие результаты даны в [7] и цитированных там работах.

Пусть H_h – семейство евклидовых пространств со скалярным произведением ${{( \cdot , \cdot )}_{h}}$ и нормой ${{\left\| {\, \cdot \,} \right\|}_{h}}$, где h – параметр (связанный с дискретизацией $\Omega $). Пусть линейные операторы ${{D}_{h}} = {{B}_{h}},{{B}_{{1h}}},{{A}_{h}}$ действуют в H_h и обладают свойством ${{D}_{h}} = D_{h}^{ * }$ > 0; введем норму ${{\left\| w \right\|}_{{{{D}_{h}}}}} = ({{D}_{h}}w,w)_{h}^{{1/2}} = {\text{||}}D_{h}^{{1/2}}w{\text{|}}{{{\text{|}}}_{h}}$.

Предположим, что ${\text{||}}w{\text{|}}{{{\text{|}}}_{{{{A}_{h}}}}}\, \leqslant \,{{\alpha }_{h}}{\text{||}}w{\text{|}}{{{\text{|}}}_{{{{B}_{h}}}}}$ для всех $w \in {{H}_{h}}$ (эквивалентно, ${{A}_{h}} \leqslant \alpha _{h}^{2}{{B}_{h}}$). В приложении к методам численного решения эллиптических уравнений 2-го порядка обычно ${{\alpha }_{h}} = \frac{{{{c}_{0}}}}{{{{h}_{{min}}}}}$, где ${{h}_{{min}}}$ – минимальный размер ячейки сетки по пространству.

Зададим равномерную сетку ${{\bar {\omega }}_{{{{h}_{t}}}}} = {\text{\{ }}{{t}_{m}} = m{{h}_{t}}{\text{\} }}_{{m = 0}}^{M}$ с шагом ${{h}_{t}} = T{\text{/}}M > 0$. Пусть ${{\omega }_{{{{h}_{t}}}}} = {\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 1}}^{{M - 1}}$. Введем сеточные усреднения, в том числе с весом $\sigma $, и разностные отношения

где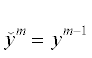 , $\mathop {\hat {y}}\nolimits^m = {{y}^{{m + 1}}}$, $\mathop y\nolimits^m = y({{t}_{m}})$. Доопределим 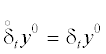. Введем сеточный оператор суммирования с переменным верхним пределом

Ниже используются следующие известные непосредственно проверяемые формулы:

Запишем абстрактный симметричный трехслойный метод с весом σ для задачи (1):

с искомой функцией ${v}$: ${{\bar {\omega }}_{{{{h}_{t}}}}} \to {{H}_{h}}$ и заданными ${{{v}}^{0}},{{u}_{1}} \in {{H}_{h}}$, $f$: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 0}}^{{M - 1}} \to {{H}_{h}}$; для краткости их зависимость от $h$, h_t не указываем. В МКЭ операторам ${{B}_{h}}$, ${{B}_{{1h}}}$ соответствуют матрицы масс (которые могут быть и диагональными после их сосредоточения), а A_h – матрица жесткости.

Пусть ниже выполнены условия либо $\sigma \geqslant \frac{1}{4}$ и ${{\varepsilon }_{0}} = 1$, либо

Тогда можно ввести норму

${{\left\| w \right\|}_{{0,\tau ,{\mathbf{h}}}}}$ = $\left[ {\tau {\text{||}}w{\text{||}}{{{_{{{{B}_{h}}}}^{2}}}_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}} \right.$ + + ${{\left. {\left( {\sigma \, - \,\frac{1}{4}} \right)h_{t}^{2}{\text{||}}w{\text{||}}_{{{{A}_{h}}}}^{2}} \right]}^{{1/2}}}$

с ${\mathbf{h}}: = (h,{{h}_{t}})$, причем верно неравенство ${{\varepsilon }_{0}}\sqrt \tau {{\left\| w \right\|}_{{{{B}_{h}}}}} \leqslant {{\left\| w \right\|}_{{0,\tau ,{\mathbf{h}}}}}$ для всех $w \in {{H}_{h}}$.

Замечание 1. Если операторам ${{B}_{h}}$ и ${{B}_{{1h}}}$ отвечают диагональные матрицы, то при σ = 0 метод (4), (5) становится явным. При $\sigma = 0$ условие (6) принимает вид ${{h}_{t}}{{\alpha }_{h}} \leqslant 2{{\varepsilon }_{1}}{{\tau }^{{1/2}}}$ с $0 < {{\varepsilon }_{1}}: = \sqrt {1 - \varepsilon _{0}^{2}} $ < 1. Если взять $\tau = {{c}_{1}}{\text{/}}{{\alpha }_{h}}$, то имеем ${{h}_{t}}\alpha _{h}^{{3/2}} \leqslant 2{{\varepsilon }_{1}}\sqrt {{{c}_{1}}} $, или  h_t ≤ $2{{\varepsilon }_{1}}(c_{1}^{{1/2}}{\text{/}}c_{0}^{{3/2}})h_{{min}}^{{3/2}}$ при ${{\alpha }_{h}} = {{c}_{0}}{\text{/}}{{h}_{{min}}}$ и τ = = $({{c}_{1}}{\text{/}}{{c}_{0}}){{h}_{{min}}}$. Условие такого типа известно из [8].

Введем норму

${{\left\| y \right\|}_{{L_{{{{h}_{t}}}}^{p}({{H}_{h}})}}}$ = $\left[ {\frac{1}{4}{{h}_{t}}{\text{||}}{{y}^{0}}{\text{||}}_{h}^{p}} \right.$ + + ${{\left. {_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}I_{{{{h}_{t}}}}^{{M - 1}}({\text{||}}y{\text{||}}_{h}^{p})} \right]}^{{1/p}}}$,

p = 1, 2, для y: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 0}}^{{M - 1}} \to {{H}_{h}}$. Следующая теорема о равномерной по $\tau $ и T устойчивости является аналогом [6, теорема 2.1, п. 2] (см. также раздел 6 там). Родственные утверждения можно найти в [9]. Кроме того, дифференциальный прототип теоремы приведен в [1, оценка (8)].

Теорема 1. Для решения метода (4), (5) справедлива оценка

Указанную норму f можно заменить на

$\sqrt 2 I_{{{{h}_{t}}}}^{{M - 1}}{\text{||}}A_{h}^{{ - 1/2}}{{\bar {\delta }}_{t}}f{\text{|}}{{{\text{|}}}_{h}}$ + $\frac{3}{{\sqrt 2 }}\mathop {max}\limits_{0 \leqslant m \leqslant M - 1} {\text{||}}A_{h}^{{ - 1/2}}{{f}^{m}}{\text{|}}{{{\text{|}}}_{h}}$.

Доказательство. Скалярное умножение уравнения (4) на 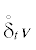с учетом формул (3) приводит к энергетическому равенству

Применив к нему оператор $2I_{{{{h}_{t}}}}^{{m - 1}}$, получим

где ${\text{||}}{{(\mathop {v}\limits^ ,{v})}^{m}}{\text{|}}{{{\text{|}}}_{{{{\mathcal{E}}_{{\tau ,{\mathbf{h}}}}}}}}: = {{({\text{||}}{{\bar {\delta }}_{t}}{{{v}}^{m}}{\text{||}}_{{0,\tau ,{\mathbf{h}}}}^{2} + \,{\text{||}}{{\bar {s}}_{t}}{{{v}}^{m}}{\text{||}}_{{{{A}_{h}}}}^{2})}^{{1/2}}}$. Заметим, что

Эта формула и результат cкалярного умножения уравнения (5) на ${{\delta }_{t}}{{{v}}^{0}} = {{\bar {\delta }}_{t}}{{{v}}^{1}}$ дают

Поэтому равенство (8) влечет соотношения

При f = 0, взяв максимум левой части по m, с учетом неравенства $\varepsilon _{0}^{2}\tau \left\| w \right\|_{{{{B}_{h}}}}^{2} \leqslant \left\| w \right\|_{{0,\tau ,{\mathbf{h}}}}^{2}$ выведем оценку (7). При ${{{v}}^{0}} = {{u}_{1}} = 0$, взяв m = M, получим сначала оценку

а затем, взяв максимум по m, выведем и оценку (7).

Чтобы вывести эту оценку с другой указанной в условии теоремы нормой f, достаточно с помощью формулы 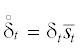и суммирования по частям при ${{{v}}^{0}} = 0$ записать

Установим также оценку ${v}$ в более слабой норме через более слабые нормы данных типа [6, теорема 2.1, п. 1], с иным доказательством. Дифференциальный прототип оценки связан с [1, теорема 1]. Пусть ${{\left\| y \right\|}_{{\mathop {\tilde {L}}\nolimits_{{{h}_{t}}}^p ({{H}_{h}})}}} = {{[I_{{{{h}_{t}}}}^{M}(\left\| y \right\|_{h}^{p})]}^{{1/p}}}$, p = 1, 2.

Теорема 2. Для решения метода (4), (5) с $f = {{\delta }_{t}}g$ справедлива оценка

Указанную в ней норму $f = {{\delta }_{t}}g$ можно заменить на $\sqrt 2 {\text{||}}A_{h}^{{ - 1/2}}f{\text{|}}{{{\text{|}}}_{{L_{{{{h}_{t}}}}^{1}({{H}_{h}})}}}$.

Доказательство. При $1 \leqslant m \leqslant M$ применение оператора $I_{{{{h}_{t}}}}^{{m - 1}}$ к уравнению (4) дает

Положим $V = {{I}_{{{{h}_{t}}}}}{{\bar {s}}_{t}}{v}$. Непосредственно проверяется формула

Также ${{{v}}^{{(\sigma )}}} = {{{v}}^{{(1/4)}}} + \left( {\sigma - \tfrac{1}{4}} \right)h_{t}^{2}{{\delta }_{t}}{{\bar {\delta }}_{t}}{v}$ (см. (3)) и 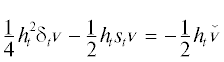, поэтому

Подставив эту формулу в (10) и учитывая, что ${{s}_{t}}{v}$ = ${v} + \tfrac{1}{2}{{h}_{t}}{{\delta }_{t}}{v}$, в силу уравнения (5) выведем

Скалярное умножение выведенного уравнения на ${{\bar {s}}_{t}}{{{v}}^{m}} = {{\bar {\delta }}_{t}}V$ приводит к “слабому” энергетическому равенству

на ${\text{\{ }}{{t}_{m}}\} _{{m = 1}}^{M}$, где $\mathop {I_{{{{h}_{t}}}}^{m}}\limits^ {\kern 1pt} f = I_{{{{h}_{t}}}}^{{m - 1}}f$. Применим к нему оператор $2I_{{{{h}_{t}}}}^{m}$ и получим так как $\tfrac{1}{2}{{h}_{t}}{{f}^{0}} + \mathop {I_{{{{h}_{t}}}}^{{}}}\limits^ {\kern 1pt} f = g - {{s}_{t}}{{g}^{0}}$ при $f = {{\delta }_{t}}g$. При f = 0 отсюда следуют оценки и тем более оценка (9). При ${{{v}}^{0}} = {{u}_{1}} = 0$ она выводится так же, как и в теореме 1.

Для вывода этой оценки с другой указанной в условии нормой f с помощью формулы

достаточно записать

Замечание 2. В оценке (9) каждое из слагаемых $\sqrt 2 ({\text{||}}A_{h}^{{ - 1/2}}{{B}_{{1h}}}{{{v}}^{0}}{\text{|}}{{{\text{|}}}_{h}} + \tau {\text{||}}A_{h}^{{ - 1/2}}{{u}_{1}}{\text{|}}{{{\text{|}}}_{h}})$ можно заменить на $\sqrt T {\text{||}}{{{v}}^{0}}{\text{|}}{{{\text{|}}}_{{{{B}_{{1h}}}}}}$, $\sqrt T \tau {\text{||}}B_{{1h}}^{{ - 1/2}}{{u}_{1}}{\text{|}}{{{\text{|}}}_{h}}$ соответственно. Для обоснования этого вместо использованной в доказательстве оценки надо воспользоваться другой:

Известно, что каждая из оценок (7) и (9) влечет существование и единственность решения метода (4), (5) при любых ${{{v}}^{0}},{{u}_{1}} \in {{H}_{h}}$, f: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 0}}^{{M - 1}} \to {{H}_{h}}$ (см. подобное, например, в [10, следствие 9.1]). Это же относится к оценкам для других методов ниже.

Представляет интерес также случай, когда в уравнении в (1) параметр $\tau $ стоит и перед $div(\mathcal{A}\nabla {{u}_{\tau }})$. Тогда в уравнениях (4), (5) имеем ${{A}_{h}} = \tau {{A}_{{0h}}}$ с ${{A}_{{0h}}} = A_{{0h}}^{ * }$ > 0, ${{A}_{{0h}}} \leqslant \alpha _{h}^{2}{{B}_{h}}$. Теоремы 1 и 2 можно применить, и оценки (7), (9) (с учетом замечания 2) принимают вид

во второй оценке можно заменить $\sqrt {2\tau } {\text{||}}A_{{0h}}^{{ - 1/2}}{{u}_{1}}{\text{|}}{{{\text{|}}}_{h}}$ на $\sqrt T \tau {\text{||}}B_{{1h}}^{{ - 1/2}}{{u}_{1}}{\text{|}}{{{\text{|}}}_{h}}$. В условии (6) следует убрать множитель ${{\tau }^{{1/2}}}$, и при σ = 0 оно принимает вид ${{h}_{t}}{{\alpha }_{h}} \leqslant 2{{\varepsilon }_{1}}$, или ${{h}_{t}} \leqslant 2({{\varepsilon }_{1}}{\text{/}}{{c}_{0}}){{h}_{{min}}}$ при ${{\alpha }_{h}} = {{c}_{0}}{\text{/}}{{h}_{{min}}}$, что типично для явных схем для гиперболических уравнений.

Кроме того, при τ = 0 метод (4), (5) переходит в трехслойный метод с весом $\sigma $ для параболической задачи (2):

с искомой функцией ${v}$: ${{\bar {\omega }}_{{{{h}_{t}}}}} \to {{H}_{h}}$ и заданными ${{{v}}^{0}} \in {{H}_{h}}$, $f$: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 0}}^{{M - 1}} \to {{H}_{h}}$ (слагаемые с B_h и ${{u}_{1}}$ исчезают). При τ = 0 и $\sigma \geqslant \tfrac{1}{4}$ результаты теорем 1, 2 сохраняют силу и упрощаются, а именно, для решения метода (11), (12) верны оценки (во второй из оценок $f = {{\delta }_{t}}g$), причем возможность замен норм f также сохраняет силу.

Остановимся отдельно на случае $\sigma = \tfrac{1}{4}$, когда слагаемые с множителем $\sigma - \tfrac{1}{4}$ в выписанных выше нормах в оценках и энергетических равенствах исчезают. Нам потребуется стандартный симметричный двухслойный метод для задачи (2)

с заданными ${{{v}}^{0}} \in {{H}_{h}}$, $\tilde {f}$: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 1}}^{M} \to {{H}_{h}}$. Нетрудно видеть, что он эквивалентен трехслойному методу (11), (12) с весом $\sigma = \tfrac{1}{4}$, а также ${{f}^{m}} = {{s}_{t}}\mathop {\tilde {f}}\nolimits^m $, $1 \leqslant m \leqslant M - 1$ и ${{f}^{0}} = \mathop {\tilde {f}}\nolimits^1 $. В частности, применение s_t к уравнению (13) влечет (11) с $\sigma = \tfrac{1}{4}$, а при m = 1 уравнение (13) эквивалентно (12) с $\sigma = \tfrac{1}{4}$.

Выведем оценку разности решений методов (4), (5) и (11), (12), ср. с [1, оценка (10)].

Теорема 3. Пусть $b{{B}_{h}} \leqslant {{B}_{{1h}}}$ с $b > 0$. При $\sigma = \tfrac{1}{4}$ и ${{f}^{m}} = {{s}_{t}}\mathop {\tilde {f}}\nolimits^m $ на ${{\omega }_{{{{h}_{t}}}}}$, ${{f}^{0}} = \mathop {\tilde {f}}\nolimits^1 $ для разности ${{r}_{\tau }} = {{{v}}_{\tau }} - {{{v}}_{0}}$ решений ${v} = {{{v}}_{\tau }}$ метода (4), (5) и ${v} = {{{v}}_{0}}$ метода (11), (12) справедлива оценка

Доказательство. При b > 0 неравенство $b{{B}_{h}} \leqslant {{B}_{{1h}}}$ эквивалентно $bB_{{1h}}^{{ - 1}} \leqslant B_{h}^{{ - 1}}$. Применение обоих влечет неравенство

Как следует из уравнений (4), (5) и (11), (12), разность ${{r}_{\tau }}$ удовлетворяет уравнениям

и ${{({{r}_{\tau }})}^{0}} = 0$. В силу теоремы 2 c $f = {{\delta }_{t}}g$, g^m = = $ - \tau {{B}_{h}}{{\bar {\delta }}_{t}}{{{v}}_{0}}$, $1 \leqslant m \leqslant M$ и $\tfrac{1}{2}{{h}_{t}}{{\delta }_{t}}{{g}^{0}} = - \tau {{B}_{h}}{{\delta }_{t}}{v}_{0}^{0}$, т.е. ${{g}^{0}} = 2\tau {{B}_{h}}{{\delta }_{t}}{v}_{0}^{0} + {{g}^{1}} = - {{g}^{1}}$ и ${{s}_{t}}{{g}^{0}} = 0$, а также неравенства (15) имеем

Для решения метода (13) верна оценка

(напомним, что она следует из энергетического равенства ${\text{||}}{{\bar {\delta }}_{t}}{v}{\text{||}}_{{{{B}_{{1h}}}}}^{2} + \tfrac{1}{2}{{\bar {\delta }}_{t}}(\left\| {v} \right\|_{{{{A}_{h}}}}^{2}) = {{(\tilde {f},{{\bar {\delta }}_{t}}{v})}_{h}}$). Ее применение в (16) завершает доказательство.

Запишем теперь симметричный векторный двухслойный метод решения задачи (1) и изучим его устойчивость, следуя [6, раздел 8]. В нем искомыми являются две функции ${v},{\dot {v}}$: ${{\bar {\omega }}_{{{{h}_{t}}}}} \to {{H}_{h}}$, аппроксимирующие ${{u}_{\tau }}$ и ${{\partial }_{t}}{{u}_{\tau }}$ и удовлетворяющие системе уравнений 1-го порядка по t

при заданных ${{{v}}^{0}},{{{\dot {v}}}^{0}} \in {{H}_{h}}$, $f$: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 1}}^{M} \to {{H}_{h}}$. Его тесная связь с трехслойным методом с весом $\sigma = \frac{1}{4}$ и реализация описаны в [6]. При τ = 0 этот метод переходит просто в симметричный двухслойный метод (13) с $\tilde {f} = f$ для параболической задачи (2).

При анализе устойчивости (и выводе оценок погрешности) второе уравнение (17) следует брать неоднородным вида ${{\bar {\delta }}_{t}}{v} - {{\bar {s}}_{t}}{\dot {v}} = g$ с заданной g: ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 1}}^{M} \to {{H}_{h}}$. Назовем такой двухслойный метод обобщенным.

Теорема 4. Для решения обобщенного двухслойного метода справедлива оценка

Указанную в ней норму f можно заменить на $\sqrt 2 (\mathop {max}\limits_{1 \leqslant m \leqslant M} {\text{||}}A_{h}^{{ - 1/2}}{{f}^{m}}{\text{|}}{{{\text{|}}}_{h}} + \,{\text{||}}A_{h}^{{ - 1/2}}{{\bar {\delta }}_{t}}f{\text{|}}{{{\text{|}}}_{{\mathop {\tilde {L}}\nolimits_{{{h}_{t}}}^1 ({{H}_{h}})}}})$.

В случае ${{B}_{{1h}}} = b{{B}_{h}}$ с b > 0 справедлива также оценка

Доказательство. 1. Скалярное умножение первого уравнения (17) на ${{\bar {s}}_{t}}{\dot {v}}$, уравнения ${{\bar {\delta }}_{t}}{v} - {{\bar {s}}_{t}}{\dot {v}} = g$ на ${{A}_{h}}{{\bar {s}}_{t}}{v}$ и сложение результатов приводит к энергетическому равенству

Применив к нему оператор $2I_{{{{h}_{t}}}}^{m}$, получим

на ${\text{\{ }}{{t}_{m}}{\text{\} }}_{{m = 1}}^{M}$. Поскольку ${{\left\| {{{{\bar {s}}}_{t}}{v}} \right\|}_{{{{A}_{h}}}}} \leqslant {{\bar {s}}_{t}}({{\left\| {v} \right\|}_{{{{A}_{h}}}}})$, то вывод оценки (18) завершается подобно теореме 2.

Чтобы установить эту оценку с другой нормой f, заметим, что при ${{{v}}^{0}} = 0$, g = 0 имеем

2. Скалярное умножение первого уравнения (17) на $A_{h}^{{ - 1}}{{B}_{h}}{{\bar {s}}_{t}}{\dot {v}}$, уравнения ${{\bar {\delta }}_{t}}{v} - {{\bar {s}}_{t}}{\dot {v}} = g$ на ${{B}_{h}}{{\bar {s}}_{t}}{v}$ и сложение результатов приводит при ${{B}_{{1h}}} = b{{B}_{h}}$ с b > 0 к соотношениям

Далее рассуждения уже стандартного типа влекут оценку (19).

Возможно обобщение выведенных оценок на случай неравномерной сетки ${{\bar {\omega }}_{{{{h}_{t}}}}}$ (см. [6]).