Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 102-106

1. ПРОБЛЕМА

Существует немало задач Коши для обыкновенных дифференциальных уравнений, решения которых имеют полюсы. Подавляющее большинство таких задач являются нелинейными. Многие из этих задач формулируются для дифференциального уравнения второго порядка, в котором коэффициент перед старшей производной обращается в нуль в некоторых точках. Такие задачи имеют два линейно независимых решения, из которых одно имеет нули, а другое – полюсы. Примерами являются задачи для цилиндрических функций, классических ортогональных полиномов и др. Много подобных задач возникает в квантовой механике. Другими примерами функций с полюсами являются гамма-функция, эллиптические интегралы и др. Такие решения имеют, как правило, не единственную особую точку, а последовательность полюсов.

Эти задачи за редкими исключениями не решаются в элементарных функциях. Для их решения приходится применять численные методы. Общеупотребительные численные методы решения (например, методы Рунге–Кутты) хорошо позволяют считать гладкие участки решения и широко используются для составления таблиц специальных функций [1] и стандартных программ прямого расчета [2]. Однако в окрестностях особых точек погрешность этих методов сильно возрастает. Непосредственно продолжить решение за полюс практически невозможно. Для этого приходится разрабатывать процедуру, рассчитанную на конкретную задачу. Если требуется пройти не один полюс, а несколько, то точность нахождения каждого последующего полюса значительно ухудшается.

Первые успешные работы по обнаружению единственной сингулярности и установлению ее типа были сделаны в [3, 4] в традиционных переменных. Однако этот алгоритм был сложен и требовал высокой квалификации вычислителя. Выбор длины дуги интегральной кривой в качестве аргумента позволил разработать гораздо более точную диагностику единственной сингулярности [5, 6]. Однако задача продолжения решения за сингулярность оставалась нерешенной.

В данной работе предложен простой метод численного решения задачи Коши для обыкновенных дифференциальных уравнений с полюсами первого порядка. Мы назвали его методом инверсной функции (Reciprocal function method, или RF-метод). Он позволяет найти положение полюса, вычислить решение в малой его окрестности и продолжить решение за полюс. Он пригоден для задач со множественными полюсами. Метод допускает использование практически любых явных и неявных схем интегрирования обыкновенных дифференциальных уравнений. Он легко удобен для реализации в стандартных программах.

Для полюсов порядка выше первого этот метод позволяет определить положение полюса и его порядок. Однако продолжение решения за полюс сопряжено со значительными потерями точности.

2. МЕТОД ИНВЕРСНОЙ ФУНКЦИИ

Для простоты изложения рассмотрим задачу Коши для одного дифференциального уравнения

Предполагаем, что правая часть имеет столько непрерывных производных, сколько потребуется для численных схем интегрирования ОДУ. Пусть решение задачи (1) таково, что оно имеет произвольное число полюсов первого порядка в точках $t = {{T}_{k}}$. Положения этих полюсов нам априори неизвестны.

Трудности. Напомним типичные трудности, возникающие при численном решении таких задач. Возьмем любую явную схему. Для простоты шаг $\tau $ будем считать постоянным. Формально решение существует на каждом шаге ${{t}_{n}} = n\tau $. Однако при приближении к первому полюсу значения $u({{t}_{n}})$ будут стремительно нарастать и быстро выйдут за пределы представимых на компьютере чисел. Переход к переменному шагу ${{\tau }_{n}}$, уменьшающемуся по мере увеличения функции, сохраняет эту качественную картину.

Если взять неявную схему, то описанная картина не меняется, но прибавляется еще одна трудность. Решение на новом шаге находится из нелинейного алгебраического уравнения. При конечном шаге ${{\tau }_{n}}$ у этого уравнения может не существовать вещественного решения. В обоих случаях трудно найти положение полюса и невозможно продолжить решение за него с помощью той же схемы.

RF-метод. Описанные трудности легко преодолевает метод инверсной функции. Рассмотрим инверсную функцию ${v}(t) = {{[u(t)]}^{{ - 1}}}$. Из (1) следует, что она удовлетворяет дифференциальному уравнению

Все полюсы первого порядка функции $u(t)$ становятся простыми нулями функции ${v}(t)$, а нули функции $u(t)$ – полюсами функции ${v}(t)$. Это позволяет предложить следующий алгоритм.

Будем численно интегрировать уравнение (1), пока $\left| {{{u}_{n}}} \right|$ не начнет быстро увеличиваться. Практическим критерием этого может служить условие $\left| {{{u}_{n}}} \right| > A$, где A – некоторая константа. Когда это условие выполнилось, полагаем ${{{v}}_{n}} = {{[{{u}_{n}}]}^{{ - 1}}}$ и решаем задачу (2) с этим начальным условием. Очевидно, на ближайших шагах $\left| {{{{v}}_{n}}} \right|$ будет убывать, затем ${v}(t)$ пройдет через нуль, положение которого будет соответствовать полюсу функции $u(t)$. Далее $\left| {{{{v}}_{n}}} \right|$ будет нарастать. Когда выполнится условие $\left| {{{{v}}_{n}}} \right| > {{A}^{{ - 1}}}$, возвращаемся к расчету функции $u(t)$ по уравнению (1).

В окрестностях полюсов ${{T}_{k}}$ функция ${v}(t)$ имеет столько непрерывных ограниченных производных, сколько их имеет $u(t)$ вне полюсов. Поэтому интегрирование ${v}(t)$ можно продолжать той же схемой.

Положения полюсов. Пусть использована численная схема точности $O({{h}^{p}})$. Найдем интервал $\left[ {{{t}_{n}},{{t}_{{n + 1}}}} \right]$, на концах которого значения ${{{v}}_{n}}$ и ${{{v}}_{{n + 1}}}$ имеют разные знаки. На этом интервале лежит расчетное приближение к полюсу T. В окрестности точки смены знака выберем $p$ точек сетки ${{t}_{j}}$. Очевидно, для p = 2 это будут точки ${{t}_{n}}$ и ${{t}_{{n + 1}}}$, для p = 4 – точки ${{t}_{{n - 1}}}$, ${{t}_{n}}$, ${{t}_{{n + 1}}}$, ${{t}_{{n + 2}}}$.

Рассмотрим значения ${{{v}}_{j}}$ в выбранных узлах как аргумент, а соответствующие значения t_j – как функцию этого аргумента. Проведем ньютоновскую (или иную) интерполяцию по этим значениям ${{{v}}_{j}}$ функции $t({v})$ и вычислим значение ${{t}_{ * }}$ при ${{{v}}_{ * }} = 0$. Это и будет расчетное значение полюса.

Погрешность. Наивное вычисление погрешности как традиционной нормы ($C$, ${{L}_{2}}$ или подобных им) от разности численного и точного решений неконструктивно на задачах с сингулярностями. Причина в том, что расчетное положение полюса заведомо отличается от точного, и поэтому погрешности вблизи полюса оказываются огромными.

В [7] было предложено использовать метрику Хаусдорфа для оценки близости решений, имеющих участки быстрого изменения. Опишем процедуру вычисления расстояния в такой метрике. Возьмем точное решение $u(t)$ на участке до первого полюса или на участке между двумя соседними полюсами. Возьмем сеточное решение ${{u}_{n}}$, относящееся к этому участку; оно состоит из точек с координатами $({{t}_{n}},{{u}_{n}})$. При этом часть значений ${{u}_{n}}$ вычисляется непосредственно решением уравнения (1), а лежащие вблизи полюсов значения восстанавливаются по расчетным величинам ${{{v}}_{n}}$. Опустим из каждой точки $({{t}_{n}},{{u}_{n}})$ перпендикуляр на кривую $u(t)$. Длина этого перпендикуляра ${{l}_{n}}$ есть расстояние от точки до кривой. Беря $l = max{{l}_{n}}$, получим метрику Хаусдорфа. Очевидно, она аналогична норме C. Однако на практике более выгодно построить аналог нормы ${{L}_{2}}$. Для этого возьмем среднеквадратичную величину l_n в расчете на одну точку:

где N – полное число точек на выбранном участке. Далее будем пользоваться определением (3).

3. ПРИМЕР РАСЧЕТА

Тест. Рассмотрим следующую задачу Коши:

Приведем точное решение и его полюсы:

Это решение дано на рис. 1. Приведем также уравнение для функции ${v}(t)$:

Расчеты проводились с разными константами перехода A. Оказалось, что большое значение A приводит к худшей точности. Значение $A \geqslant 100$ давало плохие результаты. Для иллюстративных расчетов было выбрано A = 5. В общем случае A должно служить настроечным параметром программы.

Результаты. Для численной реализации были выбраны явные схемы Рунге–Кутты второго и четвертого порядков (ERK2 и ERK4) и явно-неявная одностадийная схема Розенброка с комплексными коэффициентами (CROS) [8]. Мы пользовались их реализацией в пакете GEABORK [9]. Схемы ERK2 и CROS имеют аппроксимацию $O({{\tau }^{2}})$, а схема ERK4 – $O({{\tau }^{4}})$.

Все расчеты проводились до момента t = 10, что требовало прохождения трех полюсов. Опишем качественные и количественные результаты.

На рис. 1 показано численное решение по схеме ERK2 с шагом $\tau = 0.157$. Шаг демонстрационного расчета выбран так, чтобы он был: а) несоизмерим с расстоянием между полюсами (тогда узел сетки заведомо не попадает в полюс) и б) достаточно велик, чтобы можно было видеть отличие численного решения от точного. Видно, что расчет хорошо проходит через полюсы. Ошибка накапливается с увеличением ${{t}_{n}}$, однако даже при таком крупном шаге можно успешно пройти довольно много полюсов.

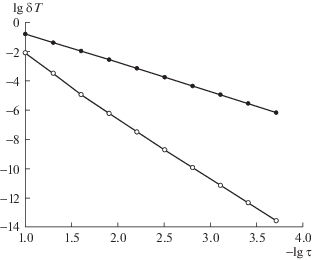
На рис. 2 для всех схем показана зависимость погрешности в метрике Хаусдорфа от величины шага. Для схем ERK2 и CROS кривые практически совпадают. График дан в двойном логарифмическом масштабе. Линии графика прямые начиная уже со второй сетки. Следовательно, зависимость погрешности от шага является степенной. Тангенсы угла наклона этих прямых равны –2 для схем ERK2 и CROS и –4 для ERK4. Таким образом, даже на задаче с полюсами эти схемы реализуют свой теоретический порядок точности. Это свидетельствует о высокой надежности предложенного метода.

Заметим, что для такого количественного определения точности необходим использованный здесь среднеквадратичный аналог метрики Хаусдорфа. Обычные нормы ${{L}_{2}}$ или $C$ и даже традиционная метрика Хаусдорфа (являющаяся аналогом нормы C) не дают конструктивного ответа. Для иллюстрации на рис. 2 показаны также погрешности в норме ${{L}_{2}}$. Сами эти погрешности намного больше погрешностей в метрике Хаусдорфа. Их кривые имеют очень длинные нерегулярные участки: теоретическая сходимость начинается только при чрезмерно малом шаге.

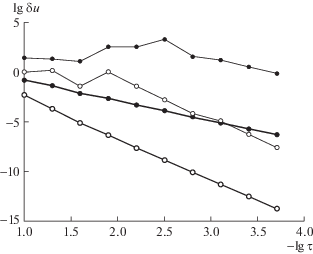
На рис. 3 показана зависимость погрешности определения третьего полюса от шага для всех схем. График также дан в двойном логарифмическом масштабе. Картина полностью аналогична рис. 2: положение полюса вычисляется с точностью $O({{h}^{p}})$.

4. ОБОБЩЕНИЯ

Системы уравнений. Полюсы отдельных компонент решения могут не совпадать. Метод естественно обобщается на этот случай. Нужно для каждой компоненты ${{u}^{k}}(t)$ вектора ${\mathbf{u}}(t)$ вводить свою инверсную функцию ${{{v}}^{k}}(t) = {{[{{u}^{k}}(t)]}^{{ - 1}}}$. Настроечный параметр A^k целесообразно выбирать отдельно для каждой компоненты.

Длина дуги. Для задач с сингулярностями более высокую надежность можно получить, если выбрать в качестве аргумента длину дуги интегральной кривой [10]. Для функций $u(t)$ и ${v}(t)$ интегральные кривые различны, соответственно длина дуги для них тоже различается. Поэтому началом отсчета длины дуги каждый раз следует считать точку перехода.

Выбор шага. Использование длины дуги позволяет применить автоматический выбор шага по кривизне интегральной кривой, который предложен в [11], и его наиболее удачный вариант описан в [7]. Это может существенно уменьшить число шагов, требуемое для достижения заданной точности.

Кратные полюсы. Для полюса первого порядка задача Коши является фактически корректно поставленной. Для полюсов высокого порядка это не всегда выполняется. Поэтому нужно тщательно проверять корректность постановки задачи. Если задача поставлена корректно, то метод инверсной функции позволяет продолжать решение за полюс, хотя и со значительной потерей точности. Для некорректно поставленной задачи продолжение за полюс невозможно, но можно хорошо определить положение первого полюса и его порядок.

БЛАГОДАРНОСТИ

Авторы искренне благодарны М.Д. Малыху за ценные замечания.