Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 111-114

1. ГИПЕРБОЛИЧЕСКАЯ МОДЕЛЬ ДЛЯ ОПИСАНИЯ ЛУЧИСТОЙ ТЕПЛОПРОВОДНОСТИ

Лучистая теплопроводность описывает процесс теплообмена с помощью излучения в оптически толстых средах [1, 2]. Эта модель применяется для описания явлений в астрофизике [3], в некоторых технологических задачах, связанных с использованием плотной лазерной плазмы [4], в процессах, характерных для термоядерного синтеза [5].

В рамках этой модели дивергенция потока тепла за счет излучения $\bar {W}$ описывается в виде

где T – температура, σ – константа Стефана–Больцмана, l(T, ρ) – длина свободного пробега, осредненная по Росселанду. В свою очередь, l определяется с помощью выражения где ν – частота фотона, l_ν(ν, T, ρ) – длина свободного пробега фотона с частотой ν, U_vp – спектральная интенсивность излучения абсолютно черного тела где h – постоянная Планка, k – постоянная Больцмана.

В итоге, упрощенно полагая коэффициент теплоемкости постоянным и пренебрегая движением среды, опишем процесс изменения температуры с помощью параболического уравнения лучистой теплопроводности

где Q – заданный источник тепла, C_v – теплоемкость.

Для решения этого уравнения можно использовать как явные, так и неявные разностные схемы. Неявные схемы, обладая абсолютной устойчивостью, при решении задач, одновременно использующих большое число вычислителей (процессоров, ядер), резко теряют эффективность параллельной обработки. Особенно остро эта проблема стоит для перспективных вычислительных систем, использующих графические платы в качестве ускорителей.

Явные схемы, не снижая эффективности при одновременном использовании большого числа процессоров, обладают очень жестким ограничением на допустимый шаг по времени [6]

где

На подробных пространственных сетках, для моделирования на которых собственно и нужны системы с экстрамассивным параллелизмом, использование явных схем практически невозможно. Проблема здесь еще усугубляется наличием сильного роста коэффициента $\widetilde l$ с ростом температуры, характерного для высокотемпературных газодинамических процессов. Это, как видно из (5), еще больше ограничивает допустимый шаг по времени Δt.

Выход из казалось бы тупиковой ситуации возможен с помощью гиперболической модели теплопроводности:

которая уже достаточно использовалась для описания быстротекущих процессов [7].

Из физических соображений видно, что для того чтобы решения уравнений (4) и (7) слабо различались, необходимо выполнение условия

т.е. где t_проц – характерное время процесса.

Обсудим более подробно свойства решения уравнения (7). Идея сведения параболических уравнений к гиперболическому виду возникла из аналогии с квазигазодинамической системой (QGS), которая, отличаясь от уравнений Навье–Стокса на члены второго порядка малости по числу Кнудсена (O(Kn²)), является гиперболической системой [8].

Эта модель допускает алгоритмы, хорошо адаптируемые к архитектуре вычислительных систем высокой производительности. В работах [9, 10] проводился теоретический анализ решения линейного аналога уравнения (7), его сравнение с решением линейного аналога уравнения (4). В работе [11] обсуждалась формулировка законов сохранения для гиперболического уравнения типа (7).

2. ЯВНЫЕ СХЕМЫ ДЛЯ РЕШЕНИЯ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОЙ ТЕПЛОПРОВОДНОСТИ

В данной работе будет рассмотрено численное решение уравнения (7) с помощью явных схем, обсужден выбор малого параметра ε для этого уравнения, проведено сравнение с решением аналогичного параболического уравнения (4) при различных значениях коэффициента лучистой теплопроводности $\widetilde l$.

В качестве малого параметра ε выбираем величину, пропорциональную отношению пространственного размера сетки h к характерной скорости процесса V:

Такой выбор параметра ε обеспечивает необходимую точность решения уравнения (7) и его близость к решению параболического уравнения (4). С другой стороны, такой выбор ε дает возможность вести расчет уравнения (7) по явной схеме с приемлемым, как показывают теоретические оценки [12], шагом по времени Δt:

Ограничение на Δt (11) является более приемлемым, чем условие (5). Преимущества условия (11) особенно проявляются на подробных пространственных сетках, давая реальную возможность использования явных схем в массивных параллельных вычислениях. Однако следует отметить, что в ряде вычислительных экспериментов, представленных в данной работе, наблюдалось еще более мягкое условие устойчивости типа условия Куранта:

В качестве разностной схемы для решения гиперболического уравнения (7) выберем трехслойную разностную схему, связывающую решение на j – 1, j и j + 1 слое по времени. В случае постоянного Δt аппроксимация производных по времени выглядит следующим образом:

Аппроксимация пространственных производных выполняется на центральном слое по времени t = t ^j.

При этом значения температуры T ^j+1 на слое j + 1 определяются по уже известным значениям температуры T ^j и T ^{j + 1}. Значения коэффициента $\widetilde l$ определяются по известным значениям температуры T ^j. Следует отметить, что сильная нелинейная зависимость коэффициента $\widetilde l$ от температуры вносит дополнительные ограничения на шаг по времени Δt, которые, впрочем, определяются не устойчивостью, а точностью численного решения.

3. ПРИМЕРЫ ЧИСЛЕННОГО РАСЧЕТА

Главной целью вычислительного эксперимента является экспериментальное исследование устойчивости явной трехслойной схемы для решения гиперболического уравнения теплопроводности (7), а также сравнение решений, полученных с помощью уравнения (7) и параболического уравнения (4). Основные расчеты проводились на базе пространственно одномерной постановки (1D), которая предоставляет большие возможности для сгущения сетки. Также были проведены расчеты в двумерной и трехмерной (2D и 3D) пространственных постановках. Расчеты проводились с различными нелинейными коэффициентами лучистой теплопроводности.

Рассматривалась модельная задача

$\frac{{\partial T}}{{\partial t}} + \varepsilon \frac{{{{\partial }^{2}}T}}{{\partial {{t}^{2}}}}$ = ${\text{div}}({{k}_{0}}{{T}^{\alpha }}{\text{grad}}T).$

Расчетная область:

$ - 2.25 \leqslant x \leqslant 2.25$; –2.25 $ \leqslant y \leqslant 2.25$; $ - 2.25 \leqslant z \leqslant 2.25$,

начальные условия: $T\left( {r,0} \right) = \left\{ \begin{gathered} 2,\quad - 1 \leqslant r \leqslant 1; \hfill \\ 0,01,\quad r > 1; \hfill \\ \end{gathered} \right.$

α = 3; k₀ = 1; время счета t_max = 1.

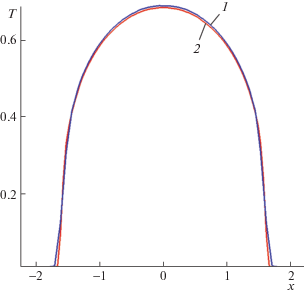
Результаты 3D-расчетов на регулярной сетке из 100 расчетных ячеек на координату (h = 4.5 × 10^–2) с одинаковым шагом по времени Δt = 4.5 × 10^–4 по неявной двухслойной схеме для параболического уравнения (4) – линия 1 на рис. 1 – и по трехслойной схеме для гиперболической модели (7) при ε = 5 × 10^–3 – линия 2 на рис. 1 – различаются в норме С менее чем на 1%. Со сгущением сетки эта разность уменьшается, результаты 1D-расчетов на регулярной сетке из 1000 расчетных ячеек на координату (h = 4.5 × 10^–3, Δt = 10^–4) отличаются не более чем в 5-м знаке.

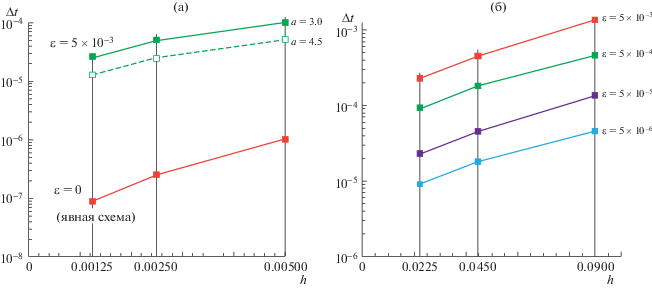
На рис. 2 представлена зависимость максимального допустимого шага интегрирования по времени Δt от шага пространственной сетки h. Для трехслойной схемы (7) выполняется условие $\Delta {{t}_{{\max }}} \leqslant {{a}_{1}}h$, причем константа a₁ зависит от величины параметра ε. Такие же расчеты были проведены для α = 4.5. В этом случае константа a₁ оказалась приблизительно в 2 раза меньше (штриховая линия на графике). Нижний график на рис. 2а соответствует явной двухслойной схеме для параболического уравнения (4), для нее условие устойчивости имеет вид $\Delta {{t}_{{\max }}} \leqslant {{a}_{2}}{{h}^{2}}$. На рис. 2б приведены результаты численных экспериментов в 3D-случае. Аналогичные результаты были получены также на тетраэдральных сетках.

Учитывая, что явные схемы хорошо адаптируются к архитектуре многопроцессорных систем, вопросы, связанные с параллельной реализацией, здесь не рассматривались. Также не рассматривались проблемы, связанные с аппроксимацией члена ${\text{div}}\,\widetilde l\,{\text{grad}}\,T$ на различного рода неструктурированных пространственных сетках. В дальнейшем для целей пространственной аппроксимации предполагается использовать уже накопленный обширный опыт.

ЗАКЛЮЧЕНИЕ

Гиперболическая модель теплопроводности (7) с малым параметром ε при старшей производной по времени приводит к результатам, фактически не отличающимся от данных, полученных на основе классической параболической модели (4). Оптимальным представляется выбор параметра ε в виде (10). При этом, с одной стороны, обеспечивается близость решений параболической и гиперболической модели, а с другой, обеспечивается заметный вычислительный эффект при использовании явных схем.

Гиперболическая модель имеет заметные преимущества при использовании явных схем. Особенно ярко эти преимущества по сравнению с параболической моделью (4) проявляются при использовании подробных пространственных сеток, применение которых стало возможным с появлением вычислительных систем сверхвысокой производительности.