Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 29-37

1. ВВЕДЕНИЕ

Доказательства утверждений, приведенных ниже без ссылок, можно найти в работах [2, 3].

2. РЕШЕНИЕ В ВИДЕ ФОРМАЛЬНОГО РЯДА ПО ρ

Мы представляем решение ${{a}_{s}}(\tau )$ уравнения (7), (9) в виде формального ряда (10). Тогда

так что a⁽⁰⁾ является гауссовским процессом

$a_{s}^{{(0)}}(\tau )$ = ${{b}_{s}}\int\limits_{ - T}^\tau {{{e}^{{ - {{\gamma }_{s}}(\tau - l)}}}d{{\beta }_{s}}(l)} .$

Процесс a⁽¹⁾ удовлетворяет уравнению

так что является третьим винеровским хаосом. Аналогично, при $n \geqslant 2$ имеем так что является (2n + 1)-м винеровским хаосом. Итерируя формулу Дюамеля в правой части равенства (14), мы можем выразить ${{a}^{{(n)}}}(l),$ $l \geqslant - T$, через процессы ${{a}^{{(0)}}}(l\,{\text{'}})$, $l\,{\text{'}} \leqslant l$.

Чтобы изучить предельное поведение корреляций решений ${{a}_{s}}(\tau )$ и корреляций энергетического спектра ${{n}_{s}}(\tau )$, записанных в виде формальных рядов (10) и (12), достаточно исследовать предельное поведение корреляций процессов $a_{s}^{{(n)}}(\tau )$. Чтобы продемонстрировать эффекты, которые здесь можно ожидать, предположим сперва, что $T = \infty $, и рассмотрим корреляции процессов $a_{s}^{{(n)}}({{\tau }_{1}})$ и $a_{{s'}}^{{(n')}}({{\tau }_{2}})$ с $n,n{\text{'}} \leqslant 1$. Нетрудно видеть, что

кроме того, можно показать, что $\mathbb{E}a_{s}^{{(0)}}({{\tau }_{1}})a_{{s'}}^{{(1)}}({{\tau }_{2}})$ ≡ ≡ $\mathbb{E}a_{s}^{{(0)}}({{\tau }_{1}})\bar {a}_{{s'}}^{{(1)}}({{\tau }_{2}}) \equiv 0$. Обозначим $B(s) = \frac{{b_{s}^{2}}}{{{{\gamma }_{s}}}},$ $s \in {{\mathbb{R}}^{d}}$. Тогда, используя (13), (15) и формулу Вика, мы видим, что корреляции процессов $a_{s}^{{(1)}}(\tau )$ имеют вид где (детали этого вычисления см. в [2]). Суммы J_s могут быть приближены интегралами

Точнее,

Здесь и далее символом $C_{s}^{\# }$ мы обозначаем различные непрерывные функции от s, убывающие при ${\text{|}}s{\text{|}} \to \infty $ быстрее любой отрицательной степени |s|. Согласно предположению (8), правая часть (16) мала: она не превосходит $C_{s}^{\# }{{\nu }^{{2 + 2\epsilon }}}$.

Асимптотическое поведение интегралов I_s известно (см. [7, 2 ]).

Теорема 1. Интеграл I_s имеет вид I_s = = $\nu I_{s}^{0} + O(C_{s}^{\# }{{\nu }^{2}})$,³³ где

Здесь ${{\Sigma }_{s}}$ – квадрика $\{ ({{s}_{1}},{{s}_{2}}){\kern 1pt} :({{s}_{1}} - s) \cdot ({{s}_{2}} - s) = 0\} $, а $d{{s}_{1}}d{{s}_{2}}{{{\text{|}}}_{{{{\Sigma }_{s}}}}}$ – элемент объема на ней, соответствующий евклидовой структуре на ${{\mathbb{R}}^{{2d}}}$.

Асимптотика, аналогичная найденной в теореме 1, может быть получена для произвольного $ - \infty \leqslant T$ < 0. Подставляя ${{s}_{1}} = s + x,{{s}_{2}} = s + y$ и обозначая $z = (x,y)$, мы переписываем интеграл $I_{s}^{0}$ в виде

Обозначим $F(z): = x \cdot y = - \tfrac{1}{2}\omega _{{3s}}^{{12}}{{{\text{|}}}_{{{{s}_{1}} = s + x,{{s}_{2}} = s + y,{{s}_{3}} = s + x + y}}}$. Тогда $\left| {\nabla F(z)} \right| = \left| z \right|$, так что последний интеграл в точности совпадает с интегралом $\int {B\delta (F)} $ от функции B по дельта-функции от F, см. [13, с. 67]. Так как $F = - \tfrac{1}{2}\omega _{{s + x + ys}}^{{s + xs + y}} = - \tfrac{1}{2}\omega _{{3s}}^{{12}}\delta _{{3s}}^{{12}}$, то пренебрегая минусом, записываем $I_{s}^{0}$ в виде

Рассматривая ${\text{|}}z{{{\text{|}}}^{{ - 1}}}dz{{{\text{|}}}_{\Sigma }} = \delta (F)$ как меру на пространстве ${{\mathbb{R}}^{{2d}}}$, сосредоточенную на квадрике $\Sigma $, в [2] мы показываем, что она дезинтегрируется как ${\text{|}}x{{{\text{|}}}^{{ - 1}}}dx{{d}_{{{{x}^{ \bot }}}}}y,$ где ${{d}_{{{{x}^{ \bot }}}}}$ обозначает меру Лебега на гиперпространстве ${{x}^{ \bot }} = \{ y{\kern 1pt} :y \cdot x = 0\} $. Точнее, для произвольной наблюдаемой f(z) выполнено

Это представление оказывается важным инструментом при анализе интегралов вида $\int {f\delta (F)} $. Оно используется ниже.

3. КВАЗИРЕШЕНИЯ

Мы начинаем наше исследование с анализа квадратичной по ρ части разложения (10), которую мы называем квазирешением A(τ) = $({{A}_{s}}(\tau ;\nu ,L),s \in \mathbb{Z}_{L}^{d})$:

Рассмотрим энергетический спектр квазирешения A, ${{N}_{s}}(\tau ) = \mathbb{E}{{\left| {{{A}_{s}}(\tau )} \right|}^{2}},$ и разложим его по ρ:

где $n_{s}^{j}(\tau ) = n_{s}^{j}(\tau ;\nu ,L)$. Здесь $n_{s}^{0} = \mathbb{E}{\text{|}}a_{s}^{{(0)}}(\tau ){{{\text{|}}}^{2}} \sim C_{s}^{\# }$⁴⁴, и нетрудно видеть, что $n_{s}^{1} \equiv 0$, а $n_{s}^{2}$ = $\mathbb{E}{\text{|}}a_{s}^{{(1)}}{{{\text{|}}}^{2}}$ + $2\Re \mathbb{E}a_{s}^{{(0)}}\bar {a}_{s}^{{(2)}}$. Первое слагаемое $\mathbb{E}{\text{|}}a_{s}^{{(1)}}{{{\text{|}}}^{2}}$ в $n_{s}^{2}$ имеет порядок $\nu $ и в случае $T = \infty $ дается теоремой 1; второй член вычисляется аналогично. Таким образом,

Мы показываем, что имеет место оценка ⁵⁵

при $L \geqslant {{\nu }^{{ - 2 - \varepsilon }}}$ (см. (8)).

При каждом $\tau \geqslant - T$, любых ν, L и произвольном $k = 0, \ldots ,4$ функция $s \mapsto n_{s}^{k}(\tau )$ естественным образом продолжается до шварцевской функции на ${{\mathbb{R}}^{d}}$. Предел

существует, также является шварцевской функцией аргумента $s \in {{\mathbb{R}}^{d}}$ и удовлетворяет (19), (20). Соответственно, предел энергетического спектра квазирешения ${{N}_{s}}(\tau ;\nu ,\infty )$ = $\mathop {lim}\limits_{L \to \infty } {{N}_{s}}(\tau ;\nu ,L)$ существует и является шварцевской функцией от $s \in {{\mathbb{R}}^{d}}$.

Соотношения (19) и (20) показывают, что правильный скейлинг параметра $\rho $ имеет вид ρ ~ ${{\nu }^{{ - 1/2}}},$ так что мы выбираем ρ в виде

Действительно, при таком скейлинге процесс ${{N}_{s}}(\tau )$ является ε-возмущением линейного процесса $n_{s}^{0}$ и не сходится к $n_{s}^{0}$ в пределе (8): разложение (18) принимает вид ${{N}_{s}} = n_{s}^{0} + \varepsilon N_{s}^{1} + O({{\varepsilon }^{2}}),$ где $N_{s}^{1} = {{\nu }^{{ - 1}}}n_{s}^{2}\sim C_{s}^{\# }$.

4. ВОЛНОВОЕ КИНЕТИЧЕСКОЕ УРАВНЕНИЕ

Для действительной функции ${{\mathbb{R}}^{d}} \ni s \mapsto {{y}_{s}}$ рассмотрим соответствующий ей волновой кинетический интеграл:

где для $j = 1,2,3$ мы обозначаем ${{y}_{j}} = {{y}_{{{{s}_{j}}}}}$ и где ${{s}_{3}} = {{s}_{1}} + {{s}_{2}} - s$. В обозначениях, введенных после теоремы 1, интеграл (22) принимает вид

Последний интеграл в точности совпадает с кинетическим интегралом, используемым физиками для описания четырехволнового взаимодействия, см. [13, с. 71; 10, с. 91].

Рассмотрим функциональное пространство ${{C}_{r}}({{\mathbb{R}}^{d}}) = \{ x \in C({{\mathbb{R}}^{d}}):$ ${{\left| x \right|}_{r}} = {{\sup }_{s}}{{(1 + \left| s \right|)}^{r}}\left| {x(s)} \right| < \infty \} $. Представление (17) для меры ${{\left| z \right|}^{{ - 1}}}dz\,{\text{|}}{{\,}_{\Sigma }}$ влечет, что волновой кинетический интеграл $K$ определяет непрерывный оператор

если $r > d$. Рассмотрим теперь волновое кинетическое уравнение:

Существует ${{\varepsilon }_{*}} > 0$, такой что при $0 \leqslant \varepsilon \leqslant {{\varepsilon }_{*}}$ уравнение (23) имеет единственное решение $m{\text{*}}(\tau )$, обнуляющееся при $\tau = - T$ и задающее ограниченную непрерывную кривую $m{\text{*}}{\kern 1pt} :[ - T,\infty ) \mapsto {{C}_{r}}({{\mathbb{R}}^{d}})$ в каждом пространстве ${{C}_{r}}({{\mathbb{R}}^{d}})$. Оно может быть записано в виде

где ${{m}^{{*0}}},{{m}^{{*1}}} \sim 1$, $m_{s}^{{*0}}(\tau )$ совпадает с $n_{s}^{0}(\tau )$ и удовлетворяет линейному уравнению

Далее $\varepsilon $ всегда обозначает фиксированную малую постоянную, не зависящую от $\nu $ и $L$ и удовлетворяющую $\varepsilon \in (0,{{\varepsilon }_{*}}].$ Параметр ε может быть интерпретирован как квадрат амплитуды квазирешения $A(\tau )$, записанного в правильном скейлинге. Следующая теорема – главный результат работы [2].

Теорема 2. Рассмотрим уравнение (4) с $L \geqslant {{\nu }^{{ - 2 - \epsilon }}}$ и $\rho = {{\nu }^{{ - 1/2}}}{{\varepsilon }^{{1/2}}}$. Энергетический спектр ${{N}_{s}} = {{N}_{s}}(\tau ;\nu ,L)$ его квазирешения A_s приближается с точностью ε²решением m* уравнения (23) в том смысле, что для произвольного $r$

с некоторым ${{C}_{r}} > 0$, если $0 < \nu \leqslant {{\nu }_{{\varepsilon ,r}}}$ для подходящего ${{\nu }_{{\varepsilon ,r}}} > 0$. Предельный энергетический спектр ${{N}_{s}}(\tau ;\nu ,\infty )$ также удовлетворяет этой оценке для каждого r и $0 < \nu \leqslant {{\nu }_{{\varepsilon ,r}}}$.

Уравнение (24) имеет единственное стационарное решение m⁰, $m_{s}^{0} = \frac{{b_{s}^{2}}}{{{{\gamma }_{s}}}}$, и оно является асимптотически устойчивым. Согласно теореме о неявной функции, для достаточно малого $\varepsilon $ уравнение (23) имеет единственное стационарное состояние m^ε, близкое к m⁰, и оно асимптотически устойчиво. Уменьшая при необходимости ${{\varepsilon }_{*}}$, можно считать, что единственное стационарное состояние m^ε определено для всех $\varepsilon \leqslant {{\varepsilon }_{*}}$. Вместе с теоремой 2 этот результат определяет асимптотическое по времени поведение энергетического спектра ${{N}_{s}}(\tau )$: для каждого r > d,

Подходящая модификация теоремы 1 и оценки (16) влечет, что существует и отличен от нуля последовательный предел $\mathop {lim}\limits_{\nu \to 0} \,\mathop {lim}\limits_{L \to \infty } {{\nu }^{{ - 1}}}n_{s}^{2}(\tau ;\nu ,L).$ Трудно усомниться в том, что аналогичный последовательный предел существует и для ${{\nu }^{{ - 2}}}n_{s}^{4}$ (однако это пока не доказано). В этом случае, ввиду оценки (20), при $\rho = {{\nu }^{{ - 1/2}}}{{\varepsilon }^{{1/2}}}$ существует последовательный предел N_s(τ; 0, ∞ ) = $\mathop {lim}\limits_{\nu \to 0} \,\mathop {lim}\limits_{L \to \infty } {{N}_{s}}(\tau ;\nu ,L).$ Тогда он также удовлетворяет утверждению теоремы 2 и асимптотике (25).

В быстром времени t уравнение (4) с $\rho $, выбранным как выше, и $\lambda = {{(\nu \varepsilon )}^{{1/2}}}$ имеет вид

где $\left\| {u(t)} \right\| \sim 1$ при $\nu \to 0$, $L \to \infty $, согласно (6). Таким образом, мы получаем, что

1) для существования кинетического предела коэффициент λ при нелинейности должен быть порядка $\sqrt \nu $, при $\nu \to 0,L \to \infty $;

2) время, необходимое, чтобы “сесть” на кинетический режим, имеет порядок $t \sim {{\lambda }^{{ - 2}}}$. Соответствующий временной масштаб (размер нелинейности)^–2 совпадает с временным масштабом, обычно рассматриваемым физиками, см. [10, 11, 13].

5. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР РЕШЕНИЙ ${{a}_{s}}(\tau )$, ЗАПИСАННЫХ В ВИДЕ ФОРМАЛЬНОГО РЯДА ПО $\rho $

Вернемся к разложению (10). Как было упомянуто в разделе 2, итерируя формулу (14), можно выразить $a_{s}^{{(n)}}({{l}_{0}})$ через процессы ${{a}^{{(0)}}}(l\,{\text{'}})$ с $l\,{\text{'}} \leqslant {{l}_{0}}$. Тогда $a_{s}^{{(n)}}$ представляется в виде суммы

в которой смысл индекса $\mathcal{T}$, по которому ведется суммирование, будет объяснен ниже, а ${{I}_{s}}(\mathcal{T})$ := := ${{I}_{s}}({{l}_{0}};n,\mathcal{T})$ обозначает интеграл

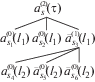
Интегрирование здесь ведется по некоторому выпуклому многограннику в ${{[ - T,{{l}_{0}}]}^{n}}$. Суммирование берется по всем векторам ${{s}_{1}} \ldots ,{{s}_{{3n}}} \in \mathbb{Z}_{L}^{d}$, удовлетворяющим линейным соотношениям, соответствующим множителю $\delta _{{3s}}^{{'12}}$ из определения ${{\mathcal{Y}}_{s}}$. Член, обозначенный через (…), состоит из произведения функций ${{e}^{{ - {{\gamma }_{{s'}}}({{l}_{k}} - {{l}_{j}})}}}$, $exp( \pm i{{\nu }^{{ - 1}}}\omega _{{s_{3}^{'}s_{4}^{'}}}^{{\mathop {s{\text{'}}}\nolimits_1 s_{2}^{'}}})$ и процессов $[a_{{s{\text{''}}}}^{{(0)}}({{l}_{r}})]{\text{*}}$, где $a{\text{*}}$ обозначает либо a, либо $\bar {a}$, с различными индексами $k,j,r$ и различными $s{\text{'}},s_{i}^{'},s{\text{''}}$, принадлежащими множеству $\{ {{s}_{1}}, \ldots ,{{s}_{{3n}}}\} $. Это произведение имеет степень 2n + 1 по отношению к процессу a⁽⁰⁾. Каждый интеграл ${{I}_{s}}({{l}_{0}};n,\mathcal{T})$ соответствует ориентированному дереву $\mathcal{T}$ из класса $\Gamma (n)$ деревьев, имеющих корень $a_{s}^{{(n)}}$, случайные величины $[a_{{s'}}^{{(0)}}({{l}_{j}})]{\text{*}}$ в качестве листьев и величины $[a_{{s'}}^{{(n')}}({{l}_{r}})]{\text{*}}$ с $1 \leqslant n{\text{'}} < n$ в качестве вершин, см. рис. 1. В каждую вершину дерева входит одно ребро, а выходит три. Три ребра, выходящие из какой-нибудь вершины $a_{{s{\text{'}}}}^{{(\bar {n})}}(l\,{\text{'}})$, $\bar {n} \geqslant 1$, соответствуют выбору трех членов ${{a}^{{({{n}_{1}})}}},{{a}^{{({{n}_{2}})}}},{{a}^{{({{n}_{3}})}}}$ в разложении (14) для $a_{s}^{{(n)}}(\tau ): = a_{{s{\text{'}}}}^{{(\bar {n})}}(l\,{\text{'}})$.

Запишем энергетический спектр решения a в виде формального ряда (12). Тогда $n_{s}^{0} \sim 1$, члены $n_{s}^{1}$ = 0 и $n_{s}^{2}$ те же, что и в (18), а $n_{s}^{3}$ и $n_{s}^{4}$ немного отличаются от соответствующих членов из (18); эта неаккуратность в обозначениях не должна вызвать трудностей. Новые члены $n_{s}^{3}$ и $n_{s}^{4}$ по-прежнему удовлетворяют оценке (20) (см. ниже). Рассмотрим $n_{s}^{k}(\tau )$ с произвольным $k \geqslant 0$. Имеем $n_{s}^{k}(\tau )$ = = $\mathbb{E}\sum\limits_{{{k}_{1}} + {{k}_{2}} = k} {a_{s}^{{({{k}_{1}})}}(\tau )\bar {a}_{s}^{{({{k}_{2}})}}(\tau )} ,$ где каждый член $a_{s}^{{(k)}}(\tau )$ дается конечной суммой (26), параметризованной деревьями $\mathcal{T} \in \Gamma (k)$. Тогда

Здесь

а матожидание берется от произведения скобок из формулы (27) для интегралов ${{I}_{s}}({{\mathcal{T}}_{1}})$ и $\overline {{{I}_{s}}({{\mathcal{T}}_{2}})} $. Так как $a_{s}^{{(0)}}(l),\;s \in \mathbb{Z}_{L}^{d}$, – гауссовские случайные величины с корреляциями (15) (в случае $T < \infty $ вторая корреляция немного меняется), то, согласно формуле Вика, каждое матожидание $\mathbb{E}{{I}_{s}}({{\mathcal{T}}_{1}})\overline {{{I}_{s}}({{\mathcal{T}}_{2}})} $ представляется в виде (конечной) суммы по всевозможным виковским спариваниям не сопряженных величин $a_{{{{s}_{j}}}}^{{(0)}}({{l}_{m}})$ с сопряженными величинами $\bar {a}_{{{{s}_{r}}}}^{{(0)}}({{l}_{q}})$. Так как эти случайные величины являются листьями деревьев ${{\mathcal{T}}_{1}}$ или ${{\bar {\mathcal{T}}}_{2}}$, эта сумма может быть параметризована фейнмановскими диаграммами, полученными спариванием деревьев ${{\mathcal{T}}_{1}}$ и ${{\bar {\mathcal{T}}}_{2}}$ по их листьям.⁶⁶ Так как для $s{\text{'}} \ne s{\text{''}}$ гауссовские величины $a_{{s'}}^{{(0)}}$ и $\bar {a}_{{s{\text{''}}}}^{{(0)}}$ некоррелированы, суммирование $\sum\limits_{{{s}_{1}}, \ldots ,{{s}_{{3k}}}} {\kern 1pt} $ в (28) нужно брать только по таким векторам $({{s}_{1}}, \ldots ,{{s}_{{3k}}})$, для которых у каждой пары спаренных по Вику листьев $a_{{s'}}^{{(0)}}$ и $\bar {a}_{{s{\text{''}}}}^{{(0)}}$ индексы $s{\text{'}}$ и $s{\text{''}}$ равны. Таким образом, во всех фейнмановских диаграммах, соответствующих (28), каждый лист $a_{s}^{{(0)}}({{l}_{m}})$ дерева ${{\mathcal{T}}_{1}}$ спарен либо с листом $\bar {a}_{s}^{{(0)}}({{l}_{q}})$ дерева ${{\mathcal{T}}_{1}}$, либо с листом $\bar {a}_{s}^{{(0)}}({{l}_{q}})$ дерева ${{\bar {\mathcal{T}}}_{2}}$, и т.д. Таким образом, мы показали, что где суммирование ведется по множеству $\mathfrak{F}(k)$ фейнмановских диаграмм, соответствующих всевозможным спариваниям между листьями деревьев ${{\mathcal{T}}_{1}} \in \Gamma ({{k}_{1}})$ и ${{\bar {\mathcal{T}}}_{2}} \in \overline \Gamma ({{k}_{2}})$, ${{k}_{1}} + {{k}_{2}} = k$.

Разрешая все соотношения, наложенные на индексы s_j в (28) с помощью подходящего аффинного преобразования, мы находим, что среди 3k индексов s_j имеется в точности k линейно независимых. Обозначая через ${{z}_{1}}, \ldots ,{{z}_{k}} \in \mathbb{Z}_{L}^{d}$ независимые переменные, полученные из индексов s_j посредством этого преобразования, мы переписываем сумму в (28) в виде ${{L}^{{ - kd}}}\sum\limits_{{{z}_{1}}, \ldots ,{{z}_{k}} \in \mathbb{Z}_{L}^{d}} {\kern 1pt} $. Приближая последнюю сумму интегралом $\int\limits_{{{\mathbb{R}}^{{kd}}}} { \ldots dz} $, где z = $({{z}_{1}}, \ldots ,{{z}_{k}}),$ мы находим, что интегралы ${{\mathcal{I}}_{s}}(\tau ;k,\mathcal{F})$ принимают сравнительно простой явный вид. А именно, для любого $s \in \mathbb{Z}_{L}^{d}$

где $l = ({{l}_{1}}, \ldots ,{{l}_{k}})$, функция ${{F}_{\mathcal{F}}}$ – гладкая по (s, z) ∈ ∈ ${{\mathbb{R}}^{{(k + 1)d}}}$ и быстро убывает по s, z и l, а ${{\alpha }^{\mathcal{F}}} = (\alpha _{{ij}}^{\mathcal{F}})$ – кососимметричная (постоянная) матрица без нулевых строк и столбцов. Ее ранг не меньше двух, и для некоторых диаграмм $\mathcal{F}$ он равен двум. Кроме того, все функции $s \mapsto {{\mathcal{I}}_{s}}(\tau ;k,\mathcal{F})$ естественно продолжаются до шварцевских функций на ${{\mathbb{R}}^{d}}$, и после этого продолжения (30) выполняется для каждого $s \in {{\mathbb{R}}^{d}}$. Следовательно, для любого фиксированного $\nu > 0$,

Тогда, ввиду (29),

для всех k, s и $\tau $.

Соотношения (19) и (20) наводят на мысль, что

и всех k, если L достаточно велико в терминах ν^–1 и k. В этом направлении мы имеем два нижеследующих результата.

Теорема 3. Для любого k и любого $\mathcal{F} \in \mathfrak{F}(k)$,⁷⁷

где $\left\lceil {k{\text{/}}2} \right\rceil $ обозначает наименьшее целое $ \geqslant \,\,{\kern 1pt} k{\text{/}}2$.

Если L настолько велико, что

то, согласно (30), ${{\mathcal{I}}_{s}}$ также удовлетворяет (32), и ввиду (29) член $n_{s}^{k}(\tau )$ ограничен правой частью (32), умноженной на ${\text{|}}\mathfrak{F}(k){\text{|}}$. Таким образом, неравенство (31) выполняется для $k \leqslant 4$, так как $d \geqslant 2$. Однако для больших k (в зависимости от d) оценка (32) существенно слабее, чем желаемая оценка (31). Наш следующий результат показывает, что оценка (32) точна в том смысле, что показатель $min(\left\lceil {k{\text{/}}2} \right\rceil ,d)$ в правой части (32) не может быть заменен на $\left\lceil {k{\text{/}}2} \right\rceil $.

Обозначим через ${{\mathfrak{F}}_{2}}(k) \subset \mathfrak{F}(k)$ множество фейнмановских диаграмм $\mathcal{F}$, для которых матрица ${{\alpha }^{\mathcal{F}}}$ из (30) имеет в точности одну ненулевою строку (и, соответственно, один ненулевой столбец). Это множество не пусто.

Теорема 4. Если $k > 2d$, то для любой диаграммы $\mathcal{F} \in {{\mathfrak{F}}_{2}}(k)$ имеет место оценка ${{J}_{s}}(\tau ;k,\mathcal{F})$ ~ ~ ${{\nu }^{d}}C_{s}^{\# }(k) \gg {{\nu }^{{\left\lceil {k{\text{/}}2} \right\rceil }}}C_{s}^{\# }(k)$. В то же время

Предположение о том, что сокращения, влекущие неравенство (34), типичны, представляется правдоподобным, и мы ставим следующую задачу.

Задача 1. Доказать, что $\left| {\sum\limits_{\mathcal{F} \in \mathfrak{F}(k)} {{J}_{s}}(\tau ;k,\mathcal{F})} \right|$ ≤ ≤  $C_{s}^{\# }(k){{\nu }^{{k/2}}}$ для всех k и $\nu $. В частности, ${\text{|}}n_{s}^{k}(\tau ;\nu ,\infty ){\text{|}}$ ≤ ≤  $C_{s}^{\# }(k){{\nu }^{{k/2}}}$ и неравенство (31) выполняется, если L достаточно велико в терминах ${{\nu }^{{ - 1}}}$ и $k$.

Если гипотеза, высказанная в задаче, верна, то при подстановке (21) предельное разложение ${{n}_{s}}(\tau ;\nu ,\infty ) = n_{s}^{0}(\tau ;\nu ,\infty ) + \rho n_{s}^{1}(\tau ;\nu ,\infty )$ + ... превращается в формальный ряд по $\sqrt \varepsilon $, равномерно по ν. Тогда его срезка в произвольном порядке $M \geqslant 2$, ${{n}_{{s,M}}}(\tau ;\nu ,\infty )$ = $n_{s}^{0}(\tau ;\nu ,\infty ) + \ldots + {{\rho }^{M}}n_{s}^{M}(\tau ;\nu ,\infty ),$ ε²-близка к ${{N}_{s}}(\tau ;\nu ,\infty )$ и, следовательно, также удовлетворяет утверждению теоремы 2. Мы не знаем, верно ли, что при больших M срезка ${{n}_{{s,M}}}(\tau )$ удовлетворяет уравнению (23) с погрешностью меньшей, чем ε².

С другой стороны, если гипотеза, высказанная в задаче 1, неверна в том смысле, что

для некоторого k⁸⁸ и для всех достаточно малых $\nu $ и больших L, тогда (12) с $\rho = {{\nu }^{{ - 1/2}}}{{\varepsilon }^{{1/2}}}$ не является равномерным по ν формальным рядом по $\sqrt \varepsilon $. Мы не исключаем возможность, что такая ситуация действительно имеет место, так как НУШ появляется в физике при моделировании малых колебаний в разнообразных средах, и при его выводе отбрасываются члены высоких порядков по амплитуде. Поэтому не кажется невозможным, что кинетический предел имеет место для энергетического спектра квазирешений, но не для энергетического спектра точных решений или энергетического спектра срезок ряда (10) высоких порядков.