Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 68-72

Введение. Плоскими кривыми Пеано нередко называют любые непрерывные отображения отрезка на плоские фигуры (квадрат, треугольник, прямоугольник). В англоязычной литературе для такого типа отображений принят термин “space filling curves”. Все известные “заполняющие плоскость” кривые не просто непрерывны, а $\frac{1}{2}$-гёльдерово непрерывны. Гёльдерова, с показателем $\frac{1}{2}$, непрерывность кривой $p(t)$ равносильна ограниченности следующего квадратно-линейного отношения:

Верхняя грань по всем парам ${{t}_{1}} < {{t}_{2}}$ этого отношения называется (следуя [1]) квадратно-линейным отношением (КЛО) кривой. В англоязычной литературе принят термин локальность кривой.

В отличие, от обычной непрерывности, гёльдерова непрерывность имеет смысл для дискретных структур. В частности, заполняющие плоскость кривые позволяют так перенумеровать двумерную решетку, что расстояние между узлами решетки оценивается сверху произведением константы (квадратного корня из КЛО кривой) на квадратный корень из разности номеров узлов решетки. Таким образом, узлы с близкими номерами оказываются расположены по возможности недалеко друг от друга. Это свойство “локальности” нумерации востребовано в приложениях (см. [2]). Наибольший интерес для приложений представляют кривые с наилучшей локальностью (т.е. с наименьшим КЛО). В качестве расстояния применяются следующие три основные метрики: манхэттенская (L₁), евклидова (L₂) и мажоритарная (чебышевская) (L_∞). Поиски кривых наилучшей локальности уже имеют немалую историю (см. [3]).

Большинство исследованных кривых относятся к введенному в 2004 г. Е.В. Щепиным [1] классу так называемых правильных фрактальных кривых Пеано. Эти кривые самоподобны и имеют квадрат своим образом. Наименьшее число кусков, подобных целому, на которое разбивается кривая, называется ее фрактальным родом. Фрактальный род квадратной кривой сам является квадратом. Так что квадратные самоподобные кривые бывают родов 4, 9, 16, 25, 36, …

Правильная кривая фрактального рода 4 единственна (с точностью до подобия). Это самая популярная из заполняющих плоскость кривых – кривая Гильберта. Ее евклидово КЛО (L₂-локальность), как доказал К. Бауман [4], равно 6.

Правильные кривые Пеано фрактального рода 9 были подробно исследованы в работах Е.В. Щепина и К. Баумана [5, 6]. Оказалось, что наименьшее евклидово КЛО для кривых рода 9 равно $5\frac{2}{3}$. С другой стороны, Е.В. Щепиным [1] и К. Бауманом [7] было доказано, что для любой правильной фрактальной кривой Пеано евклидово КЛО не может быть меньше 5.

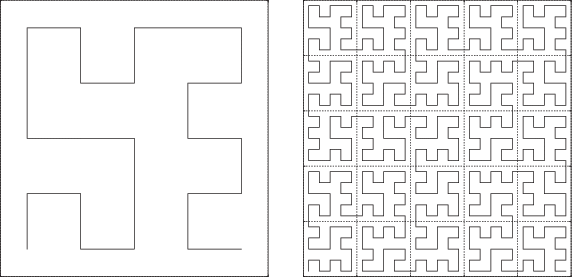
Основной результат данного сообщения заключается в нахождении правильной фрактальной плоской кривой Пеано с КЛО меньшим, чем $5\frac{2}{3}$. Найденная кривая фрактального рода 25 изображена на рис. 1. Точнее, на рис. 1 изображены центральные ломаные ее первого (прототип) и второго подразделений, которые однозначно ее определяют. Прототип этой кривой напоминает слипшиеся буквы У и Е, поэтому мы предлагаем для этого прототипа название УЕ. Доказано, что для изображенной на рис. 1 кривой евклидово КЛО равно $5\frac{{43}}{{73}}$, и проведенные доказательные вычисления (computer-assisted proofs) позволяют утверждать, что все другие кривые фрактального рода ≤36 имеют строго большее КЛО. Поэтому мы будем называть ее минимальной (5 × 5)-кривой. К тому же эта кривая имеет наименьшее мажоритарное КЛО $\left( {5\frac{1}{3}} \right)$ среди правильных фрактальных кривых рода 25.

Терминология. Две кривые $p(t){\text{:}}\,{{I}_{1}} \to {{Q}_{1}}$, q(t): ${{I}_{2}} \to {{Q}_{2}}$ называются изометричными, если существуют изометрии $\alpha {\text{:}}\,{{I}_{1}} \to {{I}_{2}}$ и β: ${{Q}_{1}} \to {{Q}_{2}}$, такие что $\beta (p(t)) = q(\alpha (t))$. Кривые p и q назовем подобными с коэффициентом k, если $\sqrt k p\left( {\frac{t}{k}} \right)$ изометрична $q(t)$. Подобные кривые имеют одинаковое КЛО.

Правильной фрактальной кривой Пеано рода $g = {{q}^{2}}$ называется непрерывное отображение отрезка на квадрат, допускающее разбиение области определения на $g$ равных отрезков (фрактальных периодов), таких, что ограничение кривой на любой из ее фрактальных периодов (фракция кривой первого подразделения) подобно всей кривой с коэффициентом q.

Для правильной кривой площадь образа любого отрезка прямо пропорциональна его длине. Поэтому соответствующим выбором масштаба можно добиться, чтобы коэффициент пропорциональности был равен единице. То есть правильную кривую Пеано всегда можно считать параметризованной площадью и это свойство сохраняется при подобии.

Правильная кривая рода $g$ делится на $g$ фракций первого подразделения. Каждая фракция, в свою очередь, делится на $g$ фракций второго подразделения и т.д. Все фракции s-го подразделения изометричны друг другу и подобны всей кривой. Фракции кривой мы нередко обозначаем прописными латинскими буквами, так же как и их образы.

Пара последовательно проходимых фракций $F,G$ (т.е. ограничение кривой на пару соседних фракций) k-го подразделения называется стыком k-го порядка. Для стыка k-го порядка $F,G$ производный стык $F\,{\text{'}}G\,{\text{'}}$ определяется как стык (k + 1)-го порядка, образованный последней фракцией (k + 1)-го подразделения из $F$ и первой – из $G$.

Приведенным квадратно-линейным отношением стыка $F,G$ называется максимум квадратно-линейных отношений для пар точек из $F \times G{\backslash }F\,{\text{'}} \times G\,{\text{'}}$. Приведенное КЛО кривой $F$ определяется как максимум квадратно-линейных отношений пар точек, не принадлежащих соседним фракциям ее первого подразделения. Очевидно, что КЛО правильной фрактальной кривой равно максимуму из ее приведенного КЛО и максимума приведенных КЛО стыков любого порядка.

Базовым преобразованием для фракции назовем пару $(\alpha ,\beta )$ изометрий [0, 1] и [0, 1]², соответственно, которые переводят всю кривую в ее фракцию (конечно, нужно еще применить сжатие в k раз).

Прототипом кривой называется последовательность квадратов – образов фракций первого подразделения, перечисленных в порядке их следования на кривой.

Входом кривой $p[a,b] \to Q$ называется точка $p(a)$, а выходом – $p(b)$. Общее название для точек входа-выхода – точки перехода.

Последовательность входов-выходов фракций назовем переходной ломаной; для кривой рода g это $\left\{ {p\left( {a + \frac{{(b - a)j}}{g}} \right)} \right\}_{{j = 0}}^{g}$.

Поиск оптимальной кривой. Наши расчеты представляют собой оптимизированный перебор всех возможных кривых заданного рода и оценку их квадратно-линейного отношения. Код можно найти по ссылке [8].

Опишем на примере, в чем состоит трудность такого перебора. Рассмотрим кривые рода $g = {{5}^{2}}$ со входом (0, 0) и выходом (1, 1) (т.е. диагональные). Зафиксируем прототип и переходную ломаную для этого прототипа. Чтобы задать правильную фрактальную кривую, нужно выбрать базовое преобразование для каждой фракции. Ясно, что есть четыре варианта допустимых базовых преобразований: тождественное, симметрия относительно диагонали вход-выход, обращение времени + симметрия относительно второй диагонали, обращение времени + центральная симметрия. Всего это дает 2⁵⁰ возможных кривых, перебирать каждую отдельно слишком долго. Наш алгоритм позволяет рассмотреть все кривые, соответствующие фиксированной переходной ломаной, одновременно.

Алгоритм оценки квадратно-линейного отношения кривой. Для кривой $p(t)$ через $\varkappa (p)$ обозначаем ее КЛО. Для описания алгоритма полезно сначала рассмотреть случай полностью заданной кривой. Опишем алгоритм, который для кривой $p$ и порогов ${{\varkappa }_{L}} < {{\varkappa }_{U}}$ либо находит пару точек на кривой, показывающую, что $\varkappa (p) > {{\varkappa }_{L}}$, либо гарантирует, что $\varkappa (p) < {{\varkappa }_{U}}$.

Ясно, что квадратно-линейное отношение кривой равно максимуму приведенных КЛО по всем стыкам и приведенного КЛО кривой. Для нахождения приведенных КЛО нужно составить все возможные пары не соседних подфракций стыков. Для каждой пары непересекающихся фракций F, $G$ мы можем получить верхнюю $U$ и нижнюю $L$ оценки КЛО на этой паре:

Далее возможны варианты:

(А) Если $L > {{\varkappa }_{L}}$, то и $\varkappa (p) > {{\varkappa }_{L}}$, работа закончена.

(Б) Если $U < {{\varkappa }_{U}}$, то пару можно дальше не рассматривать.

(В) Если же $L \leqslant {{\varkappa }_{L}} \leqslant {{\varkappa }_{U}} < U$, то подразбиваем обе фракции на подфракции и продолжаем оценивать пары подфракций.

Рано или поздно $U - L$ будет достаточно мало и мы не будем попадать в B. Тем самым, мы либо придем к А, либо исчерпаем все пары – это означает, что $\varkappa (p) < {{\varkappa }_{U}}$.

Оценка минимального КЛО в классе кривых с заданной переходной ломаной. Теперь опишем алгоритм, который для класса кривых $\mathcal{P}$ с фиксированным прототипом и переходной ломаной, а также порогов ${{\varkappa }_{L}} < {{\varkappa }_{U}}$ либо гарантирует, что для всех кривых данного класса выполнено $\varkappa (p) > {{\varkappa }_{L}}$, либо находит кривую с $\varkappa (p) < {{\varkappa }_{U}}$.

Отличие от предыдущего алгоритма состоит в следующем: на шаге В, при подразбиении фракций, нужно знать базовое преобразование на соответствующей фракции. Поэтому на этом шаге происходит ветвление в соответствии со всеми возможными вариантами. Далее, на шаге А при получении конфигурации с $L > {{\varkappa }_{L}}$ мы еще не можем быть уверены, что все кривые в классе имеют $\varkappa (p) > {{\varkappa }_{L}}$. Оценка $L > {{\varkappa }_{L}}$ дает лишь запрет на кривые, в которых выбранные нами базовые преобразования (на шагах В) привели к такой конфигурации.

Как понять, что запреты, полученные в А, исчерпывают все кривые класса? Мы можем описать кривые булевыми переменными. А именно, для каждого номера фракции i и для каждого допустимого базового преобразования $b$ мы заводим булеву переменную ${{x}_{{i,b}}}$, которая истинна тогда и только тогда, когда для i-й фракции выбрано преобразование $b$. Множество запретов можно записать в виде КНФ-формулы над этими булевыми переменными.

Задача выполнимости булевых формул (SAT от Satisfability) хорошо изучена (см. [9]). Имеется множество программных библиотек для решения этой задачи (так называемые SAT-solver). Поскольку задача SAT принадлежит классу NP, для SAT-solver нет доказанных полиномиальных оценок скорости работы. Эмпирический факт, обнаруженный нами, состоит в том, что на КНФ-формулах, возникающих в задаче поиска оптимальных кривых, хорошо работают современные SAT-solver.

Для решения нашей задачи использовалась библиотека Glucose3 [10] и обертка pysat [11].

Доказательные вычисления. Согласно теореме 7 из [5], максимум евклидова КЛО достигается на паре вершин $k$-го подразделения, где k удовлетворяет неравенству

Здесь d – глубина кривой, $g$ – фрактальный род, $Q$ – евклидово КЛО, ${{Q}_{\infty }}$ – мажоритарное КЛО. Напомним, что глубиной фрактальной кривой, согласно [1], называется наибольший номер подразделения, на котором возникают стыки фракций, не подобные стыкам меньшего порядка. В случае минимальной кривой прототипа УЕ нетрудно проверить, что производные ее стыков первого подразделения подобны стыкам первого подразделения. Таким образом, для этой кривой d = 1, $g = 25$, $Q = 5\frac{{43}}{{73}}$, ${{Q}_{\infty }} = 5\frac{1}{3}$. Поэтому целая часть от логарифма дроби в правой части равна единице и можно утверждать, что $k \leqslant 5$. То есть точными являются уже вычисления КЛО на пятом подразделении.

Точнее, строгое доказательство равенства Q = $5\frac{{43}}{{73}}$, основанное на компьютерных вычислениях, выглядит следующим образом: во-первых, мы устанавливаем, что Q и ${{Q}_{\infty }}$ мало отличаются от своих предполагаемых точных значений $5\frac{{43}}{{73}}$ и $5\frac{1}{3}$, например, не более чем на 0.01. Эти приближенные вычисления позволяет точно определить целую часть логарифма дроби в неравенстве (2) как равную единице и на основании упомянутой теоремы сделать доказательное заключение о точности проделанных на пятом подразделении вычислений.

Проведенные доказательные вычисления позволяют утверждать, что наименьшее КЛО среди плоских правильных фрактальных кривых рода 16 больше, чем 5.9.

Проведенные вычисления показали, что кривые рода 25, имеющие прототип, отличный от $YE$, имеют евклидово КЛО не менее чем 5.7.

Кривых, имеющих прототип УЕ, очень много: 2²⁵, потому что для каждой фракции имеются два возможных базовых преобразования. Поэтому доказательство того, что построенная кривая – единственная с данным КЛО, основано на следующих вычислениях. Для каждой из 25 фракций прототипа по очереди фиксировалось базовое преобразование, отличное от того, которое имеется у рассматриваемой кривой, и проводилось вычисление КЛО для класса кривых с этим прототипом и выбранной ориентацией фракции. Оказалось, что во всех таких классах нет кривых с КЛО меньшим, чем 5.64.

Для кривых рода 36 вычисления были проведены только для кривых без диагональных стыков. Оказалось, что среди таких кривых нет имеющих КЛО меньше, чем 5.6. Для кривых с диагональными стыками удалось получить теоретическую нижнюю оценку КЛО как $5\frac{2}{3}$.

Таким образом, на основе проведенных вычислений мы можем доказательно утверждать следующее.

Теорема 1. Среди плоских правильных фрактальных кривых Пеано фрактального рода $ \leqslant 36$ существует единственная кривая, которая имеет наименьшее евклидово КЛО, равное $5\frac{{43}}{{73}}$.

Дальнейшие перспективы. Разработанные методы поиска минимальных кривых в дальнейшем естественно применить для поиска минимальных кривых в больших размерностях. Если в размерности 3 уже многое известно (см. [12, 13]), то размерность 4 почти не исследована. Другое перспективное направление поиска – полифрактальные (в смысле [14]) и прежде всего бифрактальные кривые. Здесь систематический машинный поиск ранее не велся, но эвристически найденные кривые, например известная $\beta \Omega $-кривая Wierum’a, обладают прекрасными характеристиками (евклидово КЛО 5), недостижимыми для монофрактальных кривых, которым посвящено настоящее исследование.

ИСТОЧНИК ФИНАНСИРОВАНИЯ

Авторы частично поддержаны программой Президиума РАН № 26 “Фундаментальные основы создания алгоритмов и программного обеспечения для перспективных сверхвысокопроизводительных вычислений” (проект “Многомерные фрактальные кривые Пеано”).