1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 491, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 491, № 1, стр. 107-110

Решение задач обнаружения трещин в среде методами машинного обучения

М. В. Муратов 1, *, В. А. Бирюков 1, член-корреспондент РАН И. Б. Петров 1

1 Московский физико-технический институт (национальный исследовательский университет)
Московская обл., Долгопрудный, Россия

* E-mail: max.muratov@gmail.com

Поступила в редакцию 28.06.2019
После доработки 05.12.2019
Принята к публикации 24.01.2020

Полный текст (PDF)

Аннотация

Работа посвящена решению обратных задач сейсморазведки трещин с использованием методов машинного обучения. Рассматривается одиночная трещина фиксированного размера субвертикальной ориентации в двумерном случае. С помощью нейронной сети производится распознавание пространственного положения этой трещины в геологической среде и ее угла наклона. Обучающая выборка формируется из решений прямых задач с использованием сеточно-характеристического метода на регулярных прямоугольных сетках в виде расчетных сейсмограмм, полученных на поверхности среды с регистрацией вертикальной компоненты скорости.

Ключевые слова: математическое моделирование, сеточно-характеристический метод, машинное обучение, нейронные сети, обратная задача сейсморазведки, трещина

За последние годы методы машинного обучения и, в частности, глубокие нейронные сети показали впечатляющие результаты во многих областях, таких как компьютерное зрение [1–3] – классификация, распознавание и генерация изображений, распознавания речи и машинный перевод. Одним из существенных преимуществ методов глубокого обучения является то, что эти методы могут быть перенесены на многие другие области, связанные с обработкой большого количества данных. В сообщении с помощью данного подхода рассматривается задача распознавания пространственного положения и ориентации трещины в упругой среде. Эта задача является частью более глобальных исследований, таких как изучение разрушения ледового острова и изучение трещиноватых пластов в задачах сейсморазведки. Использованию нейронных сетей для распознавания структуры геологических пластов в задачах сейсморазведки посвящены работы [4, 5]. Большое преимущество подобных работ состоит в том, что входные данные для алгоритмов глубокого обучения не требуют специальной обработки и, следовательно, такие методы могут быть проще в применении, чем стандартные методы сейсморазведки. С помощью нейронных сетей также решены задачи обнаружения выбросов СО2 [6] и обнаружения и классификации дефектов в композитных материалах [7].

ПОСТАНОВКА ЗАДАЧИ

Рассматривается двумерная задача, в которой предлагается найти пространственное положение и угол наклона одиночной трещины фиксированного размера (100 м) с использованием сейсмических данных. Трещина находится в однородной упругой среде со следующими упругими характеристиками: c1 = 4500 м/с, c2 = 2500 м/с, ρ = 2500 кг/м3. Размеры расчетной области 2 × 2 км. Положение трещины варьируется в диапазоне 1000 м по вертикали и горизонтали. Угол наклона – в диапазоне ±15° (трещина субвертикальная). В середине верхней границы исследуемой области возбуждается синусоидальный упругий импульс, состоящий из 5 периодов (длина волны 100 м). Фиксируются значения вертикальной компоненты скорости отраженных волн на сейсмоприемниках, равномерно расположенных на поверхности возбуждения волнового импульса (всего 65 приемников) – сейсмические данные, которые используются в распознавании.

МЕТОДИКА РЕШЕНИЯ

Процесс решения задачи распознавания пространственного положения трещины в упругой среде состоит из двух этапов: обучения нейронной сети и, непосредственно, распознавание контрольного образца сейсмических данных.

Для создания обучающей выборки решаются прямые задачи с различными параметрами трещины [8].

РЕШЕНИЕ ПРЯМЫХ ЗАДАЧ

Определяющая система уравнений линейно-упругой среды может быть представлена в виде

(1)
$\begin{gathered} \rho \frac{{\partial {{V}_{i}}}}{{\partial t}} = \frac{{\partial {{\sigma }_{{ji}}}}}{{\partial {{x}_{j}}}}, \\ ~\frac{{\partial {{\sigma }_{{ij}}}}}{{\partial t}} = \lambda \left( {\mathop \sum \limits_k \frac{{\partial {{V}_{k}}}}{{\partial {{x}_{k}}}}} \right){{I}_{{ij}}} + \mu \left( {\frac{{\partial {{V}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{V}_{j}}}}{{\partial {{x}_{i}}}}} \right),~ \\ \end{gathered} $
где Vi – компонента скорости, σij – компонента тензора напряжений, ρ – плотность среды, λ и μ – коэффициенты Ламе, Iij – компонента единичного тензора. Рассмотрим двумерный случай. Введя вектор переменных ${\mathbf{u}} = \{ {{V}_{x}},{{V}_{y}},{{\sigma }_{{xx}}},{{\sigma }_{{yy}}},{{\sigma }_{{xy}}}\} $, систему (1) приводим к виду

(2)
$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + \mathop \sum \limits_{i = 1,2} {{{\mathbf{A}}}_{i}}\frac{{\partial {\mathbf{u}}}}{{\partial {{\xi }_{i}}}} = 0.~$

Численное решение находится с применением сеточно-характеристического метода [9, 10]. Аппроксимация проводится на структурной прямоугольной сетке. Значения в каждой точке находятся с использованием значений в опорных точках сетки ${\mathbf{u}}({{{\mathbf{r}}}_{{ijkl}}})$ и весов этих точек ${{p}_{{ijkl}}}({\mathbf{r}})$ по формуле

${\mathbf{u}}\left( {\mathbf{r}} \right) = \mathop \sum \limits_{i,j,k,l} {{p}_{{ijkl}}}\left( {\mathbf{r}} \right){\mathbf{u}}\left( {{{{\mathbf{r}}}_{{ijkl}}}} \right).$

Граничное условие можно записать в общем виде как

(3)
$D{\mathbf{u}}\left( {{{\xi }_{1}},{{\xi }_{2}},t + \tau } \right) = {\mathbf{d}},$
где D – некоторая матрица размера 9 × 3 для трехмерного случая (5 × 2 – для двумерного), d – вектор, ${\mathbf{u}}\left( {{{\xi }_{1}},{{\xi }_{2}},t + \tau } \right)$ – вектор искомых значений скорости и компонент тензора напряжений в граничной точке на следующем временном шаге.

На границах расчетной области задавалось условие свободной границы

${\mathbf{Tn}} = 0.$

Для задания трещины использовалась модель бесконечно-тонкой трещины с условием флюидонасыщенной трещины [11, 12]. Такая трещина задается как контактная граница с условием свободного скольжения:

${{{\mathbf{v}}}_{a}} \cdot {\mathbf{n}} = {{{\mathbf{v}}}_{b}} \cdot {\mathbf{n}},\quad {\mathbf{f}}_{n}^{a} = - {\mathbf{f}}_{n}^{b},\quad {\mathbf{f}}_{\tau }^{a} = {\mathbf{f}}_{\tau }^{b} = 0.$

Такая контактная граница полностью пропускает продольные колебания без отражения и полностью отражает поперечные волны.

МЕТОД ОБУЧЕНИЯ НЕЙРОСЕТИ ДЛЯ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ

Использовалась библиотека глубокого обучения Keras, основанная на библиотеке Tensorflow и архитектуре параллельных вычислений CUDA. Библиотека Keras была выбрана в связи простотой ее использования и возможностями, достаточными для решения поставленной задачи. В данной работе решалась двумерная обратная задача, но предложенный метод может быть распространен и на случай трех измерений. Для решения задачи была предложена нейросеть, состоящая из трех свёрточных слоев и двух полносвязных слоев. Обучающая выборка состояла из пар (X, y): X – это сейсмограмма (матрица вещественных чисел размером 65 × 65), y – некоторый набор параметров, задающий положение трещины. В рассматриваемом случае y задавался 4 вещественными числами – координатами концов трещины (при этом высота трещины оставалась постоянной). Параметры слоев сети следующие: первый свёрточный слой: (63, 63, 64), второй свёрточный слой: (29, 29, 128), третий свёрточный слой: (12, 12, 256), первый полносвязный слой: (9216, 256), второй полносвязный слой: (256, 4). Размеры всех фильтров в свёрточных слоях – 3 × 3, функция активации – ReLU. Общее число параметров сети: 2.7 × 106. В качестве оптимизатора нейросети был выбран Adam с коэффициентом скорости обучения (learning rate) равным 0.001.

РАСПОЗНАВАНИЕ

Распознавание контрольного образца представляет собой процесс минимизации функционала

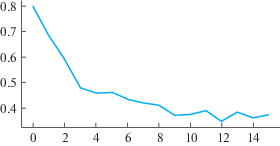
$J = \sqrt {\mathop \sum \limits_i {\text{||}}y_{i}^{{{\text{real}}}} - y_{i}^{{{\text{pred}}}}{\text{|}}{{{\text{|}}}_{{{{L}_{2}}}}}} .$

С каждой новой эпохой в обучении значение функционала уменьшается и стремится к некоторому значению (рис. 1). Следовательно, метод может быть использован для решения данного класса задач.

Рис. 1.

График зависимости значения функционала J от эпохи обучения.

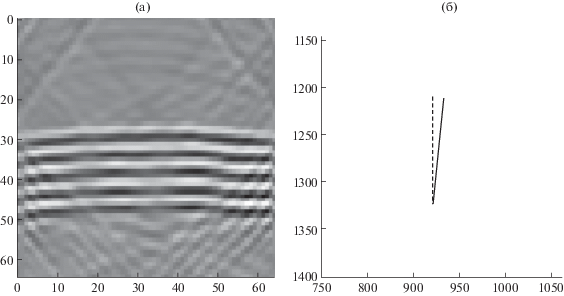
Был произведен контрольный расчет одиночной трещины случайного пространственного расположения и ориентации (в пределах возможных значений постановки задачи). Результаты распознавания контрольного образца изображены на рис. 2. На рис. 2а представлена синтетическая сейсмограмма волнового отклика, полученная на сейсмоприемниках, расположенных на верхней поверхности исследуемой области. На ней видны волны отклика от исследуемой трещины. С использованием разработанной нейронной сети было произведено распознавание пространственного положения и угла наклона трещины на основании сейсмограммы отклика и сопоставление с действительными данными по положению трещин. На рис. 2б изображено расположение и ориентация реального (пунктир) положения трещины и предсказанного (сплошная линия) для контрольного образца – видно достаточно хорошее соответствие.

Рис. 2.

Сейсмограмма (а) и расположение трещины в пространстве (б) – реальное (пунктир) и предсказанное (сплошная линия).

Список литературы

  1. Krizhevsky A., Sustskever I., Hinton G.E. Imagenet Classification with Deep Convolutional Neural Networks // Advances in Neural Information Processing Systems. 2012. P. 1097–1105. https://doi.org/10.1145/3065386

  2. Szegedy C., Toshev A., Erhan D. Deep Neural Networks for Object Detection // Proc. NIPS'13 Proceedings of the 26th Intern. Conf. on Neural Information Processing Systems. 2013. V. 2. P. 2553–2561.

  3. Goodfellow I., Pouget-Abadie J., Mirza M., Xu B., Warde-Farley D., Ozair S., Courville A., Bengio Y. Generative adversarial nets // Advances in Neural Information Processing Systems. 2014. P. 2672–2680.

  4. Zhang C., Frogner C., Araya-Polo M., Hohl D. Machine-Learning Based Automated Fault Detection in Seismic Traces // EAGE Conference and Exhibition 2014. https://doi.org/10.1190/tle36030208.1

  5. Araya-Polo M., Dahlke T., Frogner C., Zhang C., Poggio T., Hohl D. Automated Fault Detection without Seismic Processing // The leading eadge. 2017. V. 36. Iss. 3. P. 194–280. https://doi.org/10.1190/tle36030208.1

  6. Wu Yu., Lin Yo., Zhou Zh., Delorey A. Seismic-Net: A Deep Densely Connected Neural Network to Detect Seismic Events // CoRR. 2018. abs/1802.02241.

  7. Menga M., Chua Y.J., Woutersonb E., Ong C.P.K. Ultrasonic Signal Classification and Imaging System for Composite Materials via Deep Convolutional Neural Networks // Neurocomputing. 2017. V. 257. P. 128–135. https://doi.org/10.1016/j.neucom.2016.11.066

  8. Petrov I.B., Muratov M.V. The Application of Grid-Characteristic Method in Solution of Fractured Formations Exploration Seismology Direct Problems (Review Article) // Matem. Mod. 2019. V. 31. № 4. P. 33–56. https://doi.org/10.1134/S0234087919040038

  9. Магомедов К.М, Холодов А.С. Сеточно-характеристические численные методы. М.: Наука, 1988. 288 с.

  10. Ivanov A.M., Khokhlov N.I. Parallel Implementation of the Grid-Characteristic Method in the Case of Explicit Contact Boundaries // Computer Research and Modeling. 2018. V. 10. № 5. P. 667–678. https://doi.org/10.20537/2076-7633-2018-10-5-667-678

  11. Muratov M.V., Petrov I.B. Application of Fractures Mathematical Models in Exploration Seismology Problems Modeling // Smart Innovation, Systems and Technologies. 2019. P. 120–131. https://doi.org/10.1007/978-3-030-06228-6_11

  12. Favorskaya A., Petrov I., Grinevskiy A. Numerical Simulation of Fracturing in Geological Medium // Procedia Computer Science. 2017. V. 112. P. 1216–1224. https://doi.org/10.1016/j.procs.2017.08.042

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал