1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 492, № 1, 2020

Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 92-96

О задаче акустической диагностики прискважинной зоны

Член-корреспондент РАН И. Б. Петров 1, 2, *, В. И. Голубев 1, 2, А. В. Шевченко 1

1 Московский физико-технический институт (национальный исследовательский университет)
Московская обл., Долгопрудный, Россия

2 Федеральный научный центр Научно-исследовательский институт системных исследований Российской академии наук
Москва, Россия

* E-mail: petrov@mipt.ru

Поступила в редакцию 24.01.2020
После доработки 24.01.2020
Принята к публикации 29.02.2020

Полный текст (PDF)

Аннотация

Рассматривается задача распространения сейсмических волн от источника, расположенного в скважине. Для описания динамического поведения флюида используются акустические уравнения. Прискважинная зона описывается пористой флюидонасыщенной средой в рамках модели Доровского. На удалении от скважины для описания динамического поведения геологического массива используется упругое приближение. Предложен алгоритм, позволяющий в рамках единого сеточно-характеристического подхода на криволинейных расчетных сетках провести полноволновое моделирование во всем расчетном объеме. Его отличительной особенностью является постановка в явном виде необходимых контактных условий на границе между средами с различной реологией. Численно исследована возможность акустической диагностики неоднородности прискважинной зоны.

Ключевые слова: математическое моделирование, сеточно-характеристический метод, сейсморазведка, пористые среды, модель Доровского, прискважинная зона, трещиноватая среда

ВВЕДЕНИЕ

Сейсмические методы исследования активно применяются на практике в задачах разведки и разработки залежей нефти и газа: наземная и морская сейсморазведка, полноволновая инверсия, межскважинное просвечивание. С открытием нетрадиционных и истощением запасов традиционных месторождений актуальным является повышение точности восстановления внутренней структуры среды. Это должно позволить выбирать оптимальную схему разработки, например, для повышения коэффициента извлечения нефти. В разработке новых технологий может существенно помочь математическое моделирование, способное предоставить синтетические волновые поля для различных расстановок источников и приемников и моделей с заданной сложной внутренней структурой.

Благодаря развитию многопроцессорных систем  были достигнуты значительные успехи в разработке современных вычислительных методов решения сейсмических задач [1, 2]. Для численного решения прямой задачи о распространении волн в гетерогенной среде может быть успешно применен сеточно-характеристический численный метод [3], учитывающий внутреннюю математическую структуру гиперболической задачи – распространение разрывов вдоль характеристик. С его помощью ранее был решен ряд прямых задач в акустических, упругих, слоистых и трещиноватых средах [4, 5] как в двумерной, так и в трехмерной постановках, а также обратная задача миграции [6].

В настоящей работе рассматривается задача акустического зондирования прискважинной зоны. Целью исследования является разработка подхода, позволяющего явно учесть ее флюидонасыщенность, а также возможную неоднородность, например, наличие зоны повышенных пористости и проницаемости. В работе строится двумерная цилиндрическая модель скважины, окружающей ее зоны кольматации и геологического массива. При этом флюид внутри скважины описывается в рамках акустических уравнений. Для описания поведения поврежденной пористой среды могут быть использованы модели двухскоростных сред [7, 8]. В работе рассматривалась модель Доровского [9]. Окружающий скважину геологический массив описывается в рамках теории линейной упругости. В расчетном алгоритме в явном виде используются контактные условия между средами с различной реологией [10–13]. Для численного решения системы уравнений используется сеточно-характеристический метод на криволинейных расчетных сетках.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Уравнения, описывающие динамическое поведение бесконечно малого объема акустической среды, могут быть записаны в виде

(1)
${{\rho }_{a}}\frac{\partial }{{\partial t}}{{{\mathbf{v}}}_{a}} = - \nabla {{p}_{a}},$
(2)
$\frac{\partial }{{\partial t}}{{p}_{a}} = - c_{a}^{2}{{\rho }_{a}}\nabla \cdot {{{\mathbf{v}}}_{a}},$
где ρa – плотность жидкости, ca – скорость распространения акустической волны, ${{{\mathbf{v}}}_{a}}$ – вектор скорости жидкости, pa – давление в жидкости.

Уравнения, описывающие динамическое поведение бесконечно малого объема изотропной линейно-упругой среды, могут быть записаны в виде

(3)
${{\rho }_{e}}\frac{\partial }{{\partial t}}{{{\mathbf{v}}}_{e}} = \nabla \cdot {{\sigma }_{e}},$
(4)
$\frac{\partial }{{\partial t}}{{\sigma }_{e}} = \lambda \left( {\nabla \cdot {{{\mathbf{v}}}_{e}}} \right)I + \mu \left( {\nabla \otimes {{{\mathbf{v}}}_{e}} + {{{\mathbf{v}}}_{e}} \otimes \nabla } \right),$
где ρe – плотность среды, σe – тензор напряжений, ${{{\mathbf{v}}}_{e}}$ – вектор скорости среды, λ и μ – упругие параметры Ламе.

Пористая среда, окружающая ствол скважины, повреждается в процессе бурения, в основном за счет проникновения в нее грязи и цементного раствора. Для корректного описания динамических процессов, происходящих в ней под действием акустического источника, в работе используется модель Доровского. Уравнения, описывающие динамическое поведение бесконечно малого объема насыщенной пористой среды, могут быть записаны в виде

(5)
${{\rho }_{s}}\frac{\partial }{{\partial t}}{{{\mathbf{v}}}_{s}} + \nabla \cdot {{h}_{s}} + \frac{{{{\rho }_{s}}}}{{{{\rho }_{0}}}}\nabla {{p}_{f}} = 0,$
(6)
${{\rho }_{0}}\frac{\partial }{{\partial t}}{{{\mathbf{v}}}_{f}} + \nabla {{p}_{f}} = 0,$
(7)
$\begin{gathered} \frac{\partial }{{\partial t}}{{h}_{s}} + \mu \left( {\nabla \otimes {{{\mathbf{v}}}_{e}} + {{{\mathbf{v}}}_{e}} \otimes \nabla } \right) + \\ + \,I\left( {\left( {\frac{{{{\rho }_{f}}}}{{{{\rho }_{0}}}}K - \frac{2}{3}\mu } \right)\nabla \cdot {{{\mathbf{v}}}_{s}} - \frac{{{{\rho }_{f}}}}{{{{\rho }_{0}}}}K\nabla \cdot {{{\mathbf{v}}}_{f}}} \right) = 0, \\ \end{gathered} $
(8)
$\frac{\partial }{{\partial t}}{{p}_{f}} - \left( {K - \alpha {{\rho }_{0}}{{\rho }_{s}}} \right)\nabla \cdot {{{\mathbf{v}}}_{s}} + \alpha {{\rho }_{0}}{{\rho }_{f}}\nabla \cdot {{{\mathbf{v}}}_{f}} = 0,$
где ${{h}_{s}}$ и ${{{\mathbf{v}}}_{s}}$ – величина, равная минус тензору напряжений скелета σs, и вектор скорости скелета, pf и ${{{\mathbf{v}}}_{f}}$ – давление и вектор скорости флюида, ${{\rho }_{0}} = {{\rho }_{s}} + {{\rho }_{f}}$, ${{\rho }_{f}}$ и ${{\rho }_{s}}$ – удельные плотности флюида и скелета, K, μ, α – упругие характеристики насыщенной пористой среды.

Все приведенные выше системы уравнений являются гиперболическими и могут быть записаны в каноническом виде. После проведения расщепления по направлениям каждая из них может быть решена сеточно-характеристическим методом с переходом в инварианты Римана.

На границе между акустической и пористой средами должно быть задано необходимое число контактных условий – по количеству выходящих из сред на границу характеристик. В работе [14] контактные условия приводятся в явном виде, а также проведен численный расчет контактной задачи на прямоугольных расчетных сетках. На границе между пористой и упругой средами в двумерном случае должно быть задано пять контактных условий, в трехмерном – семь. Они формулируются в следующем виде:

(9)
${{{\mathbf{v}}}_{s}} = {{{\mathbf{v}}}_{e}},$
(10)
$\left( { - {{h}_{s}} \cdot {\mathbf{n}}} \right) \cdot {\mathbf{n}} - {{p}_{f}} = \left( {{{\sigma }_{e}} \cdot {\mathbf{n}}} \right) \cdot {\mathbf{n}},$
$\left( { - {{h}_{s}} \cdot {\mathbf{n}}} \right) \cdot {\mathbf{\tau }} = \left( {{{\sigma }_{e}} \cdot {\mathbf{n}}} \right) \cdot {\mathbf{\tau }},$
(12)
${{{\mathbf{v}}}_{s}} \cdot {\mathbf{n}} - {{{\mathbf{v}}}_{f}} \cdot {\mathbf{n}} = 0,$
где ${{{\mathbf{v}}}_{f}}$ – вектор скорости флюида, ${{{\mathbf{v}}}_{s}}$ – вектор скорости скелета, pf – давление флюида, ${{\sigma }_{e}}$ – тензор напряжений упругой среды, ${{{\mathbf{v}}}_{e}}$ – вектор скорости упругой среды, ${\mathbf{n}}$ – нормаль, направленная из пористой среды в упругую среду, а τ – вектор, касательный к поверхности контакта сред.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

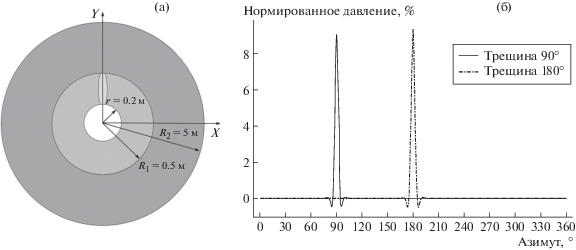
В работе рассматривалась задача распространения акустической волны от высокочастотного источника, помещенного в заполненную водой скважину. Вся область моделирования представляла собой круг радиусом 5 м, а радиус скважины был равен 0.2 м. Мощность прискважинной зоны составляла 0.3 м. Остальная часть области описывалась моделью линейно-упругого тела. Для описания динамического поведения жидкости использовались акустические уравнения со следующими параметрами: скорость акустических волн – 1500 м/с, плотность – 1000 кг/м3. Прискважинная зона описывалась в рамках модели Доровского с параметрами μ = 3.042 × 109 Н/м2, α = 1974.355496 м5/кг/с2, K = 3.710918832 × 109 Н/м2, ρs = 1800 кг/м3, ρf = = 100 кг/м3, φ = 10%. Они соответствуют следующим скоростям распространения волн: ${{C}_{{p1}}}$ = 2000 м/с, ${{C}_{{p2}}}$ = 400 м/с, Cs = 1300 м/с. Рассматривались случаи наличия трещины (зоны повышенной пористости) вблизи скважины, ориентированной вдоль радиуса и направленной на 90° и 180° (см. рис. 1а). В данной области использовались параметры μ = 1.1 × 109 Н/м2, α$~$= 2017.983999 м5/кг/с2, K = = 1.524554690 × 109 Н/м2, $~{{\rho }_{s}}$ = 1100 кг/м3, ${{\rho }_{f}}$ = 450 кг/м3, φ = 45%. Отношение раскрытости трещины к ее протяженности составляло 1 : 10. Геологический массив описывался следующими характеристиками: скорость продольных волн – 2000 м/с, скорость поперечных волн – 1300 м/с, плотность – 2000 кг/м3.

Рис. 1.

Постановка задачи о распространении волны в прискважинной зоне (а). Обозначены характерные размеры. На рисунке трещина ориентирована на 90°. Распределение нормированного отклонения давления по периметру скважины через 0.152 мс после начала расчета (б).

На границе между водой и прискважинной зоной, а также между ней и окружающим геологическим массивом в явном виде задавались контактные условия. На границе области моделирования использовались неотражающие граничные условия. Для моделирования импульса, испускаемого источником, в работе использовался точечный источник, расположенный в центре скважины, со временной зависимостью в виде импульса Пузырёва [15] с несущей частотой 40 кГц. В расчетах записывалось значение давления в жидкости по периметру скважины. Расчет проводился на криволинейной расчетной сетке с максимальным размером ячейки 5 мм, шаг по времени был выбран из условия Куранта равным 0.435 мкс. При решении отдельных уравнений переноса на инварианты Римана использовалась схема Русанова с монотонизатором minimax третьего порядка точности.

На рис. 1б представлено распределение нормированного отклонения давления в воде по периметру скважины в момент времени, соответствующий приходу прямой волны от источника. Видно, что на азимутах, соответствующих местам расположения зон повышенной пористости, фиксируются отклонения в амплитуде порядка 10% по сравнению с однородной прискважинной зоной.

Дополнительно по результатам численного моделирования было выявлено, что при наличии неоднородности свойств среды по азимуту от нее инициируются поверхностные (контакт флюид–насыщенная среда) волны, распространяющиеся со скоростью 1620 м/с. На рис. 2а представлен их вид для двух случаев ориентации трещины. Сплошной линией изображен случай ориентации трещины на 90°, а штрихпунктирной – на 180°.

Рис. 2.

Распределение нормированного отклонения давления по периметру скважины через 0.2 мс после начала расчета (а) и 0.462 мс (б).

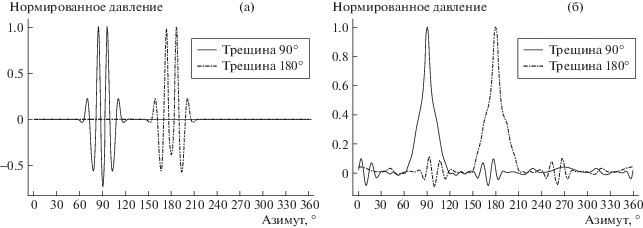
От границы геологического массива, из-за отличия в упругих свойствах, инициируется отраженная волна, распространяющаяся обратно к центру скважины. Ввиду того, что неоднородное включение обладает пониженной скоростью ${{C}_{{p1}}}$, на датчики сигнал в этой апертуре приходит с задержкой порядка 30 мкс. На рис. 2б представлено распределение нормированного отклонения давления по периметру скважины в момент времени, соответствующий приходу на датчики отклика от границы геологического массива. Сплошной линией изображен случай ориентации трещины на 90°, а штрихпунктирной – на 180°. Кроме временной задержки сигнала присутствует также и разница в амплитуде отраженного сигнала порядка 20%.

ЗАКЛЮЧЕНИЕ

В работе в рамках единого сеточно-характеристического подхода проведено моделирование распространения сейсмических волн в акустической, пористой и упругой средах в двумерной цилиндрической постановке. В явном виде приведены контактные условия, достаточные для однозначного разрешения задачи контактного разрыва на контактной границе. Применительно к задаче акустического зондирования прискважинной зоны показано, что при наличии неоднородности свойств среды по азимуту инициируется поверхностная волна, распространяющаяся вдоль границы раздела сред. Для локализации направления на неоднородность могут быть использованы данные гидрофонов, расположенных по периметру скважины.

Список литературы

  1. Virieux J., Calandra H., Plessix R.E. A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging // Geophysical Prospecting. 2011. V. 59. № 5. P. 794–813.

  2. Carcione J. M., Herman C.G., Kroode P. E. Y2K Review Article: Seismic Modeling // Rev. Lit. Arts Amer. 2002. V. 67. № 4. P. 1304–1325.

  3. Breus A., Favorskaya A., Golubev V., Kozhemyachenko A., Petrov I. Investigation of Seismic Stability of High-Rising Buildings Using Grid-Characteristic Method // Procedia Computer Science. 2019. V. 154. P. 305–310.

  4. Беклемышева К.А., Васюков А.В., Голубев В.И., Журавлёв Ю.И. Об оценке сейсмостойкости элементов современных композитных нефтепроводов // ДАН. 2018. Т. 479. № 1. С. 14–17.

  5. Golubev V., Khokhlov N., Grigorievyh D., Favorskaya A. Numerical simulation of destruction processes by the grid-characteristic method // Procedia Computer Science. 2018. V. 126. P. 1281–1288.

  6. Golubev V.I. The usage of grid-characteristic method in seismic migration problems // Smart Innovation, Systems and Technologies. 2019. V. 133. P. 143–155.

  7. Biot M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range // J. Acoustical Society of America. 1956. V. 28. № 2. P. 168–178.

  8. Dorovsky V.N., Perepechko Y.V., Podberezhnyy M.Y., Romenski E.I. Thermodynamic compatible model of microfractured porous media and Stoneley waves // J. Engineering Thermophysics. 2016. V. 25. № 2. P. 182–196.

  9. Доровский В.Н., Перепечко Ю.В., Федоров А.И. Волны Стоунли в теории Био-Джонсона и континуальной теории фильтрации // Геология и геофизика. 2012. Т. 53. № 5. С. 621–632.

  10. Синев А.В., Роменский Е.И., Доровский В.Н. Влияние глинистой корки на волновое поле вблизи скважины в пористой насыщенной среде // Геология и геофизика. 2012. Т. 53. № 8. С. 1070–1077.

  11. Chiavassa G., Lombard B. Wave propagation across acoustic / Biot's media: A finite-difference method // Commun. Comput. Phys. 2012. V. 13. P. 985–1012.

  12. Rosenbaum J.H. Synthetic microseismograms – logging in porous formations // Geophysics. 1974. V. 39. P. 14–32. https://doi.org/10.1190/1.1440407

  13. Winkler K.W., Liu H.L., Johnson D.L. Permeability and borehole Stoneley waves: Comparison between experiment and theory // Geophysics. 1989. V. 54. P. 66–75.

  14. Голубев В.И., Шевченко А.В., Петров И.Б. Об учете водонасыщенности донных осадков в задаче морской сейсмической разведки // ДАН. 2019. Т. 488. № 3. С. 248–252.

  15. Боганик Г.Н., Гурвич И.И. Сейсморазведка // Тверь: АИС, 2006. 744 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал