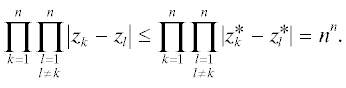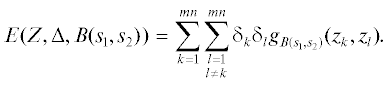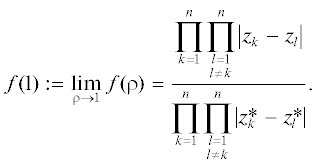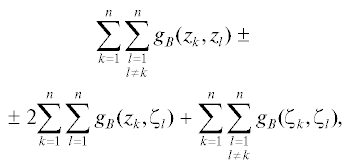Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 24-26

Пусть z_k, $k = 1,\; \ldots ,\;n$, – произвольные точки на  окружности $\left| z \right|$ = 1 и пусть $z_{k}^{ * } = exp\left( {\frac{{2\pi ik}}{n}} \right)$, k = = 1, ..., n, – симметричные точки. В связи с изучением дискриминантов алгебраических полиномов Шур [1] приводит следующее неравенство

В [1, c. 385] отмечается, что это неравенство “было указано автору” Полиа. Неравенство (1) можно интерпретировать как свойство минимальности дискретной логарифмической энергии [2] в случае симметричной конфигурации точек ${\text{\{ }}z_{k}^{ * }{\text{\} }}_{{k = 1}}^{n}.$ В последнее время появилось немало работ, посвященных изучению аналогов (1) и смежных проблем для различных ядер как на плоскости, так и в пространствах большего числа измерений (см., например, [3–8]). Вместе с тем, экстремальные свойства энергии, порожденной ядром Грина ${{g}_{B}}(z,\zeta )$, изучены в меньшей степени [9]. Здесь ${{g}_{B}}(z,\zeta )$ означает классическую функцию Грина области $B \subset \bar {\mathbb{C}}$, доопределенную нулем вне B. Заметим, что логарифмическая энергия является в некотором смысле предельной для гриновой энергии, а интерес к поведению гриновой энергии мотивируется приложениями в геометрической теории голоморфных функций. Естественным образом возникают следующие вопросы. Для каких областей B гриновая энергия дискретного заряда, сосредоточенного в симметричных точках, минимальна? Как меняется разность между энергией произвольного и экстремального зарядов при изменении области B? Что можно сказать об энергии дискретного заряда, сосредоточенного в точках семейства концентрических окружностей, причем заряда, принимающего значения разных знаков? Какими экстремальными свойствами обладает взаимная энергия дискретных зарядов? Отвечая частично на перечисленные выше вопросы, мы даем далеко идущее обобщение неравенства (1).

Рассмотрим следующую конфигурацию. Фиксируем произвольное натуральное число $m \geqslant 1$ и неотрицательные числа

Для произвольных вещественных чисел θ_j, $j = 1$, ..., n, $n \geqslant 2$, удовлетворяющих условию

обозначим через $Z = {\text{\{ }}{{z}_{k}}{\text{\} }}_{{k = 1}}^{{mn}}$ совокупность всевозможных различных точек плоскости $\mathbb{C}$, по которым окружности $\left| z \right| = {{\rho }_{l}}$, $l = 1,\; \ldots ,\;m$, пересекаются с лучами $argz = {{\theta }_{j}}$, $j = 1,\; \ldots ,\;n$. Пусть $\Delta = {\text{\{ }}{{\delta }_{k}}{\text{\} }}_{{k = 1}}^{{mn}}$ – произвольный дискретный заряд, принимающий в точках z_k значения δ_k и такой, что δ_k = ${{\delta }_{{k'}}}$ при $\left| {{{z}_{k}}} \right| = \left| {{{z}_{{k'}}}} \right|$, $1 \leqslant k$, $k{\text{'}} \leqslant mn$. Гринову энергию этого заряда относительно кругового кольца B(s₁, s₂) := := $\{ z{\text{:}}\;{{s}_{1}} < {\text{|}}z{\text{|}} < {{s}_{2}}\} $ обозначим через

Теорема 1. Если заряд Δ принимает значения одного знака, то

где $Z* = {\text{\{ }}z_{k}^{ * }{\text{\} }}_{{k = 1}}^{{mn}}$, ${\text{|}}z_{k}^{ * }{\text{|}} = \left| {{{z}_{k}}} \right|$, $arg{{(z_{k}^{ * })}^{n}} = 0$, $k = 1$, ..., mn.

Для четного числа точек на каждой окружности $\left| z \right| = {{\rho }_{l}}$, $l = 1,\; \ldots ,\;m$, и произвольного заряда $\Delta $ справедлива

Теорема 2. В принятых выше условиях пусть n = 2p, $p \geqslant 2$, и пусть

Тогда

где различные симметричные точки совокупности $Z(\eta ) = {\text{\{ }}{{z}_{k}}(\eta ){\text{\} }}_{{k = 1}}^{{2mp}}$ определены соотношениями:

В отличие от исследователей, изучающих энергию, порожденную другими ядрами, мы рассматриваем заряды, принимающие значения разных знаков и, кроме того, сосредоточенные не на одной, а на нескольких окружностях. Для четного числа точек на каждой окружности (2p) обнаружена новая экстремальная конфигурация, не обладающая, вообще говоря, 2p-кратной симметрией.

Доказательство теорем опирается на диссимметризацию конденсаторов [9, часть 4.4] и асимптотическую формулу для емкости обобщенного конденсатора [9, часть 2.2].

Положив в (2) ${{s}_{1}} = 0$ либо ${{t}_{1}} = 0,$ получим неравенства для разностей дискретных гриновых энергий относительно круга и кольца, либо круга и другого круга. Ограничимся сравнением энергий, порожденных ядрами Грина двух различных кругов, и неравенствами для 2n комплексных чисел, вытекающими из этого сравнения. Для фиксированных чисел θ_k, $k = 1,\; \ldots ,\;n$, $n \geqslant 2$, θ₁ < θ₂ < ... < < ${{\theta }_{n}} < {{\theta }_{1}} + 2\pi $, и $\rho $, $1 < \rho < \infty $, рассмотрим функцию

где ${{z}_{k}} = exp(i{{\theta }_{k}})$, ${{\zeta }_{k}} = \rho exp(i{{\theta }_{k}})$, $z_{k}^{ * } = exp\left( {\frac{{2\pi ik}}{n}} \right)$, $\zeta _{k}^{ * } = \rho exp\left( {\frac{{2\pi ik}}{n}} \right)$, $k = 1, \ldots ,n$, и пусть

Следствие 1. Функция $f(\rho )$ – неубывающая на промежутке $1 \leqslant \rho < \infty $.

Поскольку $f(\rho ) \to 1$ при ρ → $\infty $, то следствие 1 дает обобщение неравенства Полиа–Шура:

Неравенство (1) получается из (3) делением обеих частей (3) на (ρ – 1)ⁿ и предельным переходом при ρ → 1. Другие обобщения неравенства Полиа–Шура, полученные с помощью диссимметризации конденсаторов, представлены в [9, часть 5.1].

Из следствия 1 легко получить

Следствие 2. Пусть $0 < {{\rho }_{1}} < {{\rho }_{2}} < 1$; ${{z}_{k}}$, $k = 1$, ..., n, – произвольные различные точки на окружности $\left| z \right| = {{\rho }_{1}}$ и ${{\zeta }_{k}}$, $k = 1$, ..., n, – точки на окружности $\left| z \right| = {{\rho }_{2}}$, удовлетворяющие условию $arg{{\zeta }_{k}} = arg{{z}_{k}}$, $k = 1$, ..., n. Тогда

где $z_{k}^{ * } = {{\rho }_{1}}{\text{exp}}\left( {\frac{{2\pi ik}}{n}} \right)$, $\zeta _{k}^{ * } = {{\rho }_{2}}{\text{exp}}\left( {\frac{{2\pi ik}}{n}} \right)$, $k = 1$, ..., n.

Неравенство (3) означает, что взаимная логарифмическая энергия двух дискретных зарядов, один из которых сосредоточен в точках окружности |z| = 1, а другой на окружности |z| = ρ, достигает наименьшего значения в случае симметрично расположенных точек. Аналогично неравенство (4) можно интерпретировать как уменьшение (неувеличение) взаимной гриновой энергии относительно круга |z| < 1 двух дискретных зарядов на окружностях $\left| z \right| = {{\rho }_{1}}$ и $\left| z \right| = {{\rho }_{2}}$ при переходе от произвольных точек к симметричным. Положив в (4) ${{\rho }_{1}} = \rho $ и устремив ${{\rho }_{2}} \to \rho $, приходим к заключению, что логарифмическая энергия дискретного заряда, сосредоточенного на окружности $\left| z \right|$ = ρ, минус взаимная энергия этого заряда и заряда на окружности $\left| z \right| = 1{\text{/}}\rho $ при переходе к симметричному случаю не возрастает. Естественно предположить, что последнее утверждение справедливо при замене логарифмической энергии на гриновую относительно круга $\left| z \right| < 1$ и для окружностей $\left| z \right| = {{\rho }_{k}}$, $k = 1,2$, $0 < {{\rho }_{1}} < {{\rho }_{2}} < 1$. Однако это предположение неверно, в чем несложно убедиться, рассматривая энергию заряда на окружности $\left| z \right| = {{\rho }_{2}}$ минус взаимную энергию этого заряда и заряда на $\left| z \right| = {{\rho }_{1}}$ и устремляя ${{\rho }_{2}} \to 1$.

Из нерешенных проблем выделим следующую задачу. Пусть $0 < s < {{\rho }_{1}} < {{\rho }_{2}} < t < \infty $, B = ${\text{\{ }}z{\text{:}}\,s < {\text{|}}z{\text{|}}$ < < t}, z_k, $k = 1, \ldots ,n$, – произвольные различные точки на окружности $\left| z \right| = {{\rho }_{1}}$, и пусть ${{\zeta }_{k}}$, $k = 1$, ... ..., n, – произвольные различные точки на окружности $\left| z \right| = {{\rho }_{2}}$. Верно ли, что хотя бы одна из трех величин

принимает наименьшее значение в случае симметричных точек $z_{k}^{ * }\, = \,{{\rho }_{1}}{\text{exp}}\left( {\frac{{2\pi ik}}{n}} \right)$, $\zeta _{k}^{ * }$ = = ${{\rho }_{2}}{\text{exp}}\left( {i\left( {\frac{\pi }{n}\, + \,\frac{{2\pi k}}{n}} \right)} \right)$, $k = 1, \ldots ,n$? Верно ли это хотя бы в предельном случае при s → 0, t → ∞ (т.е. для логарифмической энергии)?