Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 43-48
О точности схем типа MUSCL при расчете ударных волн
О. А. Ковыркина 1, *, В. В. Остапенко 1, 2, **
1 Институт гидродинамики им. М.А. Лаврентьева Сибирского отделения Российской академии наук
Новосибирск, Россия
2 Новосибирский национальный исследовательский государственный университет
Новосибирск, Россия
* E-mail: olyana@ngs.ru
** E-mail: ostapenko_vv@ngs.ru
Поступила в редакцию 15.06.2019
После доработки 09.04.2020
Принята к публикации 10.04.2020
Аннотация
Рассматривается центрально-разностная NT-схема (Nessyahu–Tadmor scheme), при построении которой используется MUSCL-реконструкция потоков второго порядка. Изучается точность NT-схемы при расчете ударных волн, распространяющихся с переменной скоростью. Показано, что эта схема имеет первый порядок интегральной сходимости на интервалах, одна из границ которых находится в области влияния ударной волны. В результате в этих областях локальная точность NT-схемы существенно снижается. Приведены тестовые расчеты, демонстрирующие эти свойства NT-схемы.
1. Поскольку в классической работе [1] было показано, что среди линейных двухслойных по времени схем нет монотонных схем повышенного порядка аппроксимации, то развитие теории численных методов сквозного счета для гиперболических систем законов сохранения в значительной степени было направлено на преодоление этого “запрета Годунова”. В результате были разработаны различные классы как разностных, так и проекционных схем, в которых повышенный порядок аппроксимации на гладких решениях и монотонность достигались за счет нелинейной коррекции потоков. Перечислим основные классы таких схем, которые будем сокращенно называть NFC (Nonlinear Flux Correction) схемами: MUSCL-схемы [2], TVD-схемы [3], ENO-схемы [4], WENO-схемы [5], DG-схемы [6], CABARET-схемы [7]. Основное достоинство этих схем заключается в том, что они с высокой точностью локализуют ударные волны при отсутствии существенных нефизических осцилляций.
В дальнейшем для NFC-схем типа TVD, WENO, DG и CABARET было показано [8–11], что эти схемы (независимо от их точности на гладких решениях) имеют не более чем первый порядок интегральной сходимости на интервалах, одна из границ которых находится в области влияния ударной волны, что приводит к существенному снижению их точности в этой области. В настоящей работе аналогичный результат получен для центрально-разностной NT-схемы второго порядка [12], при построении которой используется MUSCL-реконструкция численных потоков. Эта схема представляет особый интерес, поскольку лежит в основе целого класса монотонных центрально-разностных схем повышенной точности [13], при реализации которых не применяется решение задачи Римана на границе смежных ячеек разностной сетки (в отличие от стандартных MUSCL-схем [2]).
2. Рассмотрим квазилинейную гиперболическую систему законов сохранения
где ${\mathbf{u}}(x,t)$ – искомая, а f(u) – заданная гладкие вектор-функции. Поставим для системы (1) задачу Коши с гладкими периодическими начальными даннымиПредположим, что задача (1), (2) при t > 0 имеет единственное ограниченное обобщенное решение $u(x,t)$, в котором в некоторый момент времени ${{T}_{0}} > 0$ в результате градиентной катастрофы возникают ударные волны. Пусть $v_{j}^{n} = v({{x}_{j}},{{t}_{n}})$ – численное решение этой задачи, полученное по NT-схеме [12], заданной на равномерной прямоугольной сетке ${{x}_{j}} = jh$, ${{t}_{n}} = n\tau $, в которой временной шаг τ выбирается из условия устойчивости Куранта
где ${{a}_{k}}(u)$ – собственные значения матрицы Якоби fu системы (1), z = 0.5 – коэффициент запаса.Зафиксируем пространственный шаг h базисной сетки и рассмотрим последовательность разностных решений $({{v}_{i}})_{j}^{n} = v(x_{j}^{i},t_{n}^{i})$ на последовательности сжимающихся сеток $x_{j}^{i} = j{{h}_{i}}$, $t_{n}^{i} = n{{\tau }_{i}}$ с шагами ${{h}_{i}} = \tfrac{h}{{{{2}^{i}}}}$, ${{\tau }_{i}} = \tfrac{\tau }{{{{2}^{i}}}}$. Зададим натуральное число $m \gg 1$ и целые числа ${{m}_{1}} < {{m}_{2}}$. Для момента времени $T = m\tau $ путем линейной интерполяции доопределим разностные решения $({{v}_{i}})_{j}^{n}$ до непрерывных по x функций ${{v}_{i}}(x,T)$ и рассмотрим интегралы
Предположим, что последовательность интегралов ${{V}_{i}}(a,b,T)$ от разностных решений ${{v}_{i}}(x,T)$ сходится с порядком ρ, где $0 < \rho \leqslant 2$, к интегралу $U(a,b,T)$ от точного решения $u(x,T)$. Это означает, что с точностью $o(h_{i}^{\rho })$ выполнено условие
где вектор-функция $C \ne 0$ не зависит от hi. Ограничение $\rho \leqslant 2$, с одной стороны, следует из того, что NT-схема имеет второй порядок аппроксимации на гладких решениях, а с другой стороны, из того, что с учетом линейной интерполяции интегралы ${{V}_{i}}(a,b,T)$ вычисляются по формуле трапеций, которая имеет второй порядок точности на гладких функциях. Если рассчитываемое точное решение u не имеет особенностей, то порядок $\rho $ интегральной сходимости (3) будет равен двум. Порядок такой сходимости на отрезках $[a,b]$, содержащих сильные разрывы точного решения или пересекающихся с их областями влияния, может снижаться ниже двух, что зависит от точности передачи схемой условий Гюгонио через размазанные фронты ударных волн.Для приближенного определения порядка интегральной сходимости ρ в случае, когда точное решение u заранее неизвестно, необходимо провести три расчета с достаточно малыми шагами ${{h}_{0}}$ = h, ${{h}_{1}} = \tfrac{h}{2}$, ${{h}_{2}} = \tfrac{h}{4}$ и воспользоваться правилом Рунге. Вычитая из (3) эту же формулу, в которой индекс i заменен на i + 1, получаем
(4)
$\begin{gathered} \delta {{V}_{{i,i + 1}}}(a,b,T) = \\ = {{V}_{i}}(a,b,T) - {{V}_{{i + 1}}}(a,b,T) = C(h_{i}^{\rho } - h_{{i + 1}}^{\rho }). \\ \end{gathered} $Рассматривая отношение модулей равенств (4) при i = 1 и i = 0, находим
Отсюда получаем искомую формулу
(5)
$\rho = \rho (a,b,T) = lo{{g}_{{1/2}}}\frac{{{\text{|}}\delta {{V}_{{1,2}}}(a,b,T){\text{|}}}}{{{\text{|}}\delta {{V}_{{0,1}}}(a,b,T){\text{|}}}}.$Пусть $\varphi (x,T) = \varphi (u(x,T))$ некоторая скалярная функция от точного решения $u(x,T)$, а ψi(x, T) = = $\varphi ({{v}_{i}}(x,T))$ – соответствующая ей последовательность функций от разностных решений ${{v}_{i}}(x$, T). Предположим, что последовательность ${{\psi }_{i}}(x$, T) в некотором пространственном узле $x = jh$ базисной сетки сходится с порядком α к функции $\varphi (x,T)$, т.е. с точностью $o(h_{i}^{\alpha })$ выполнено условие
где функция $c \ne 0$ не зависит от hi. Для приближенного определения порядка локальной сходимости α, по аналогии с (5), получаем следующую формулу:(7)
$\alpha = \alpha (x,T) = lo{{g}_{{1/2}}}\frac{{{\text{|}}\delta {{\psi }_{{1,2}}}(x,T){\text{|}}}}{{{\text{|}}\delta {{\psi }_{{0,1}}}(x,T){\text{|}}}},$(8)
$\delta {{\psi }_{{i,i + 1}}}(x,T) = {{\psi }_{i}}(x,T) - {{\psi }_{{i + 1}}}(x,T),\quad i = 0,1.$Из формулы (8) при i = 0 с учетом формулы (6) при i = 0, 1 имеем
Отсюда с учетом (7) находим
Подставляя это значение функции c в формулу (6), в которой i = 0, получаем приближенное выражение
(9)
$\begin{gathered} \delta \varphi (x,T) = \delta {{\psi }_{0}}(x,T) = \\ = \delta {{\psi }_{{0,1}}}(x,T)\mathop {\left( {1 - \frac{{{\text{|}}\delta {{\psi }_{{1,2}}}(x,T){\text{|}}}}{{{\text{|}}\delta {{\psi }_{{0,1}}}(x,T){\text{|}}}}} \right)}\nolimits^{ - 1} \\ \end{gathered} $3. В качестве конкретной гиперболической системы выберем систему уравнений первого приближения теории мелкой воды, дивергентная форма записи которой в случае прямоугольного горизонтального русла без учета донного трения имеет вид (1), где
(10)
${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} H \\ q \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} q \\ {\frac{{{{q}^{2}}}}{H} + \frac{{g{{H}^{2}}}}{2}} \end{array}} \right).$Здесь $H(x,t)$ и $q(x,t)$ – глубина и расход жидкости, g – ускорение свободного падения. Рассмотрим для системы (1), (10) задачу Коши (2) с начальными данными
(11)
$\begin{gathered} {v}(x,0) = asin\left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right), \\ H(x,0) = \frac{1}{{4g}}\mathop {\left( {asin\left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + b} \right)}\nolimits^2 , \\ \end{gathered} $Точное решение этой задачи моделируется численным расчетом по NT-схеме на мелкой сетке с пространственным шагом $h = 0.005$. Профили глубины, получаемые в этом расчете, показаны сплошными линиями на отрезке [0, X] длины периода в моменты времени T = 0.5 (рис. 1а) и T = 1 (рис. 1б). Результаты расчета данной задачи по NT-схеме на сетке с пространственным шагом $h = 0.1$ приведены на рис. 1 кружками. Порядки интегральной сходимости ρj разностного решения на отрезках $[{{x}_{j}},X]$, изображены на рис. 1 точками. На рис. 2 на момент времени T = 1 приведены графики сеточных функций
(12)
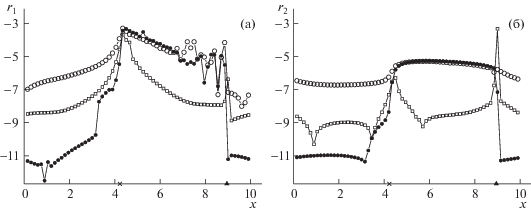
${{({{r}_{i}})}_{j}} = lg\left| {\Delta {{w}_{i}}({{x}_{j}},T)} \right|,\quad \Delta {{w}_{i}} = \frac{{\delta {{w}_{i}}}}{{{{w}_{i}}}},\quad i = 1,2,$Рис. 1.
Глубина жидкости ($ \circ $) и интегральные порядки сходимости ($ \bullet $) в моменты времени $T = 0.5$ (а) и T = 1 (б), получаемые по NT-схеме. Сплошная линия – “точное решение”, которое моделируется расчетом по NT-схеме на мелкой сетке.
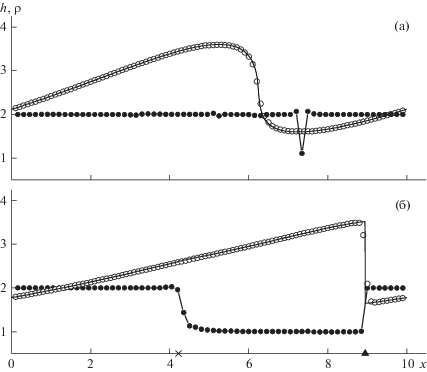
Рис. 2.
График сеточной функции (ri)j = $lg{\text{|}}\Delta {{w}_{i}}({{x}_{j}},T){\text{|}}$, где $\Delta {{w}_{i}}({{x}_{j}},T)$ – относительные локальные дисбалансы вычисления модулей инвариантов w1 (а) и w2 (б) на момент времени T = 1, получаемые по NT-схеме ($ \circ $), по WENO-схеме ($ \bullet $) и по схеме Русанова ($\square $).
Из рис. 1а следует, что в момент времени T = 0.5, когда точное решение является гладким и ударная волна еще не сформировалась, NT-схема имеет второй порядок интегральной сходимости ${{\rho }_{j}}$ почти на всех отрезках $[{{x}_{j}},X] \in [0,X]$. Заметное локальное падение порядка интегральной сходимости на отрезке, левая граница которого лежит в окрестности минимума точного решения, объясняется тем, что NT-схема [12], подобно TVD-схеме [3], имеет лишь первый порядок аппроксимации на локальных экстремумах, расположенных в гладких частях рассчитываемого решения. Из рис. 1б видно, что подобно NFC-схемам других типов (TVD [8], WENO [9], DG [10] и CABARET [11]) и в отличие от немонотонной схемы Русанова с гладкими функциями численных потоков [8], NT-схема имеет первый порядок интегральной сходимости на интервалах $[{{x}_{j}},X]$, левая граница которых лежит в области влияния ударной волны. Причина этого заключается в том, что коррекция потоков, характерная для NFC-схем, приводит к снижению их гладкости, что, в свою очередь, приводит к снижению порядка аппроксимации условий Гюгонио на фронтах ударных волн [14].
Сравнение рис. 2а и 2б показывает, что во всех трех схемах точность вычисления в области влияния ударной волны инварианта ${{w}_{2}} = {v} + 2c$, приходящего в эту область из гладкой части точного решения, существенно выше, чем инварианта ${{w}_{1}} = {v} - 2c$, приходящего с фронта ударной волны и приносящего информацию об аппроксимации схемой условий Гюгонио. Причем максимальное снижение точности вычисления инварианта w1 происходит не на правой границе области влияния, которая примыкает к фронту ударной волны, а в окрестности ее левой границы, где точное решение является достаточно гладким. В работах [8, 11, 14] показано, что аналогичное снижение точности на границе области влияния ударной волны, противоположной ее фронту, демонстрируют и другие разностные схемы повышенной точности: как NFC-схемы, так и немонотонные схемы с гладкими функциями численных потоков. Связано это с тем, что в точном решении задачи Коши (1), (10), (11) из малой окрестности точки градиентной катастрофы выходят расходящиеся характеристики первого семейства, распространяющиеся в расширяющейся окрестности левой границы области влияния ударной волны и переносящие в эту окрестность значения инварианта w1. Поэтому такое снижение точности разностных схем сквозного счета аналогично снижению их точности при расчете центрированных волн разрежения.
Из рис. 2 следует, что вне области влияния фронта ударной волны точность вычисления инвариантов в NT-схеме, схеме Русанова и схеме WENO5 является различной и полностью согласуется с порядком их аппроксимации на гладких решениях. Однако в области влияния ударной волны, где порядок интегральной сходимости схем NT и WENO5 снижается до первого, точность вычисления инвариантов по этим схемам резко падает, становится сравнимой, и на несколько порядков меньшей, чем в схеме Русанова, сохраняющей второй порядок интегральной сходимости [8, 14]. Отсюда с учетом результатов работ [8, 11] следует, что снижение точности NFC-схем в областях влияния ударных волн слабо зависит от типа схемы и порядка ее аппроксимации на гладких решениях, а связано с характерной для этих схем нелинейной коррекцией потоков.
До последнего времени в теории разностных схем сквозного счета имела место следующая альтернатива: невозможно одновременно с высокой точностью локализовать сильные разрывы и сохранить повышенный порядок сходимости в областях их влияния. При этом на практике NFC-схемы (и особенно MUSCL, WENO и DG-схемы) широко применяются при численном моделировании сложных газо- и гидродинамических течений с большим числом ударных волн различной амплитуды, в силу чего все такие расчеты имеют лишь первый порядок точности. Для решения этой проблемы в [14] был предложен метод построения комбинированных разностных схем сквозного счета, которые сочетают достоинства как NFC-схем, так и классических немонотонных схем, а именно, с повышенной точностью локализуют фронты ударных волн и одновременно сохраняют повышенный порядок сходимости во всех областях гладкости рассчитываемых обобщенных решений.
Список литературы
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Мат. сб. 1959. Т. 47. № 3. С. 271–306.
Van Leer B. Toward the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method // J. Comput. Phys. 1979. V. 32. № 1. P. 101–136. https://doi.org/10.1016/0021-9991(79)90145-1
Harten A. High resolution schemes for hyperbolic conservation laws // J. Comput. Phys. 1983. V. 49. P. 357–393. https://doi.org/10.1016/0021-9991(83)90136-5
Harten A., Osher S. Uniformly high-order accurate nonoscillatory schemes // SIAM J. Numer. Analys. 1987. V. 24. № 2. P. 279–309. https://doi.org/10.1007/978-3-642-60543-7_11
Jiang G.S., Shu C.W. Efficient implementation of weighted ENO schemes // J. Comput. Phys. 1996. V. 126. P. 202–228. https://doi.org/10.1006/jcph.1996.0130
Cockburn B. An introduction to the discontinuous Galerkin method for convection-dominated problems, advanced numerical approximation of nonlinear hyperbolic equations // Lect. Notes Math. 1998. V. 1697. P. 151–268. https://doi.org/10.1007/BFb0096353
Karabasov S.A., Goloviznin V.M. Compact accurately boundary-adjusting high-resolution technique for fluid dynamics // J. Comput. Phys. 2009. V. 228. P. 7426–7451. https://doi.org/10.1016/j.jcp.2009.06.037
Ковыркина О.А., Остапенко В.В. О сходимости разностных схем сквозного счета // ДАН. 2010. Т. 433. № 5. С. 599–603. https://doi.org/10.1134/S1064562410040265
Михайлов Н.А. О порядке сходимости разностных схем WENO за фронтом ударной волны // Матем. моделир. 2015. Т. 27. № 2. С. 129–138. https://doi.org/10.1134/S2070048215050075
Ладонкина М.Е., Неклюдова О.А.,Остапенко В.В., Тишкин В.Ф. О точности разрывного метода Галеркина при расчете ударных волн // ЖВМиМФ. 2018. Т. 58. № 8. С. 148–156. https://doi.org/10.1134/S0965542518080122
Ковыркина О.А., Остапенко В.В. О монотонности и точности схемы КАБАРЕ при расчете обобщенных решений с ударными волнами // Выч. технологии. 2018. Т. 23. № 2. С. 37–54.
Nessyahu H., Tadmor E. Non-oscillatory central differencing for hyperbolic conservation laws // J. Comput. Phys. 1990. V. 87. № 2. P. 408–463.
Kurganov A., Tadmor E. New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations // J. Comput. Phys. 2000. V. 160. № 1. P. 241–282. https://doi.org/10.1006/jcph.2000.6459
Зюзина Н.А., Ковыркина О.А., Остапенко В.В. Монотонная разностная схема, сохраняющая повышенную точность в областях влияния ударных волн // ДАН. 2018. Т. 482. № 6. С. 639–643. https://doi.org/10.1134/S1064562418060315
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


