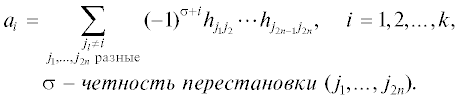Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 108-111

Периодические оптимальные по быстродействию управления на двухступенных свободных нильпотентных группах Ли

Ю. Л. Сачков^1, 2, *

¹ Институт математики им. С.Л. Соболева Сибирского отделения Российской академии наук
Новосибирск, Россия

² Институт программных систем им. А.К. Айламазяна Российской академии наук
Ярославская область, Переславль-Залесский, Россия

^* E-mail: yusachkov@gmail.com

Поступила в редакцию 13.02.2020
После доработки 31.03.2020
Принята к публикации 31.03.2020

DOI: 10.31857/S2686954320030182

Полный текст (PDF)

Аннотация

Для двухступенных свободных нильпотентных групп Ли описаны симплектические слоения и функции Казимира. Рассмотрена левоинвариантная задача быстродействия, для которой множество допустимых скоростей есть строго выпуклый компакт в первом слое алгебры Ли, содержащий начало координат внутри себя. Для вертикальной подсистемы гамильтоновой системы принципа максимума Понтрягина описаны интегралы. Описаны свойства решений этой подсистемы для малых рангов бивектора Пуассона.

Ключевые слова: симплектические слоения, функции Казимира, задача быстродействия, принцип максимума Понтрягина, периодические управления

1. ЗАДАЧА ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Пусть $\mathfrak{g}$ есть двухступенная свободная нильпотентная алгебра Ли с $k \geqslant 2$ образующими:

$\mathfrak{g} = {{\mathfrak{g}}^{{(1)}}} + {{\mathfrak{g}}^{{(2)}}},$

${{\mathfrak{g}}^{{(1)}}} = {\text{span}}\{ {{X}_{i}}\,{\text{|}}\,i = 1,2, \ldots ,k\} ,$

(1)

${{\mathfrak{g}}^{{(2)}}} = {\text{span}}\{ {{X}_{{ij}}}\,{\text{|}}\,1 \leqslant i < j \leqslant k\} ,$

$[{{X}_{i}},{{X}_{j}}] = {{X}_{{ij}}},\quad {\text{ad}}{{X}_{{ij}}} = 0,\quad 1 \leqslant i < j \leqslant k,$

$dim\mathfrak{g} = \frac{{k(k + 1)}}{2}.$

Пусть G есть связная односвязная группа Ли с алгеброй Ли $\mathfrak{g}$. Будем считать X_i, X_ij левоинвариантными векторными полями на G.

Модель для векторных полей X_i, X_ij на G ≅ ≅ ${{\mathbb{R}}^{{k(k + 1)/2}}}$ = $\{ ({{x}_{1}}, \ldots ,{{x}_{k}};{{x}_{{12}}}, \ldots ,{{x}_{{(k - 1)k}}})\} $ можно выбрать в следующем виде [11]:

$\begin{gathered} {{X}_{i}} = \frac{\partial }{{\partial {{x}_{i}}}} - \sum\limits_{j > i} \,\frac{{{{x}_{j}}}}{2}\frac{\partial }{{\partial {{x}_{{ij}}}}} + \sum\limits_{j < i} \,\frac{{{{x}_{j}}}}{2}\frac{\partial }{{\partial {{x}_{{ji}}}}},\quad i = 1,2, \ldots ,k, \\ {{X}_{{ij}}} = \frac{\partial }{{\partial {{x}_{{ij}}}}},\quad 1 \leqslant i < j \leqslant k. \\ \end{gathered} $

Пусть $U \subset {{\mathbb{R}}^{k}}$ есть выпуклый компакт, содержащий начало координат внутри себя. Рассмотрим следующую задачу быстродействия [2]:

(2)

$\dot {q} = \sum\limits_{i = 1}^k \,{{u}_{i}}{{X}_{i}},\quad q \in G,\quad u = ({{u}_{1}}, \ldots ,{{u}_{k}}) \in U,$

(3)

$q(0) = {\text{id}},\quad q({{t}_{1}}) = {{q}_{1}},$

(4)

${{t}_{1}} \to min.$

При $U = - U$ получаем субфинслерову задачу [4–7], а если U есть эллипсоид с центром в нуле, то задача субриманова [1–3].

В случае $k = 2$ $G$ есть группа Гейзенберга, и решение задачи (2)–(4) было получено Х. Буземаном [12] и В.Н. Берестовским [5].

Субриманов случай $U = \left\{ {\sum\limits_{i = 1}^k \,u_{i}^{2} \leqslant 1} \right\}$ был впервые рассмотрен Р. Брокеттом [8] и был полностью исследован для k = 3 О. Мясниченко [9]. Некоторые результаты для k = 4 были получены Л. Рицци и У. Серресом [10].

Существование оптимальных управлений в задаче (2)–(4) следует стандартным образом из теорем Рашевского–Чжоу и Филиппова [2].

2. СИМПЛЕКТИЧЕСКОЕ СЛОЕНИЕ

Перед началом исследования экстремалей в задаче (2)–(4), рассмотрим функции Казимира и симплектическое слоение (разбиение на коприсоединенные орбиты) коалгебры Ли $\mathfrak{g}{\text{*}}$ [13]. Это важно для исследования экстремалей в этой задаче.

Пусть ${{p}^{0}} \in \mathfrak{g}{\text{*}}$. Обозначим через ${{S}_{{{{p}^{0}}}}}$ симплектичекий лист (орбиту коприсоединенного представления) для точки p⁰:

${{S}_{{{{p}^{0}}}}} = \{ {\text{Ad}}_{{{{g}^{{ - 1}}}}}^{*}({{p}^{0}})\,{\text{|}}\,g \in G\} \subset \mathfrak{g}{\text{*}}{\text{.}}$

Далее в теореме 1 получено явное описание листа ${{S}_{{{{p}^{0}}}}}$.

Введем линейные на слоях кокасательного расслоения T*G гамильтонианы, соответствующие левоинвариантному реперу на G:

${{h}_{i}}(\lambda ) = \left\langle {\lambda ,{{X}_{i}}} \right\rangle ,\quad {{h}_{{ij}}}(\lambda ) = \left\langle {\lambda ,{{X}_{{ij}}}} \right\rangle ,\quad \lambda \in T{\text{*}}G.$

Из таблицы умножения для скобки Ли (1) получаем следующую таблицу умножения для скобки Пуассона:

(5)

$\{ {{h}_{i}},{{h}_{j}}\} = {{h}_{{ij}}},\quad \{ {{h}_{{ij}}},{{h}_{l}}\} = \{ {{h}_{{ij}}},{{h}_{{lm}}}\} = 0.$

Гамильтонианы h_i, ${{h}_{{ij}}}$ будем считать координатами на коалгебре Ли $\mathfrak{g}{\text{*}}$.

Бивектор Пуассона (т.е. матрица попарных скобок Пуассона между базисными гамильтонианами h_i, ${{h}_{{ij}}}$) определяется кососимметрической матрицей

(6)

$M = ({{h}_{{ij}}}) = \left( {\begin{array}{*{20}{c}} 0&{{{h}_{{12}}}}& \ldots &{{{h}_{{1k}}}} \\ { - {{h}_{{12}}}}&0& \ldots &{{{h}_{{2k}}}} \\ \vdots & \vdots & \vdots & \vdots \\ { - {{h}_{{1k}}}}&{ - {{h}_{{2k}}}}& \ldots &0 \end{array}} \right) \in {\text{so}}(k).$

Для вектора $a = ({{a}_{1}}, \ldots ,{{a}_{k}}) \in {{\mathbb{R}}^{k}}$ рассмотрим линейную функцию

${{I}_{a}} = \sum\limits_{i = 1}^k \,{{a}_{i}}{{h}_{i}},\quad {{I}_{a}}{\kern 1pt} :\;\mathfrak{g}{\text{*}} \to \mathbb{R}.$

Далее, для любого ${{p}^{0}} \in \mathfrak{g}{\text{*}}$ рассмотрим аффинное подпространство

$\begin{gathered} {{L}_{{{{p}^{0}}}}} = \{ p \in \mathfrak{g}{\text{*}}\,{\text{|}}\,{{h}_{{ij}}}(p) = {{h}_{{ij}}}({{p}^{0}}), \\ {{I}_{a}}(p) = {{I}_{a}}({{p}^{0}})\;\forall a \in ker{{M}_{{{{p}^{0}}}}}\} \subset \mathfrak{g}{\text{*}}, \\ \end{gathered} $

где ${{M}_{{{{p}^{0}}}}} = ({{h}_{{ij}}}({{p}^{0}}))$ есть соответствующая матрица (6). Очевидно, что

$dim{{L}_{{{{p}^{0}}}}} = dim{{S}_{{{{p}^{0}}}}} = {\text{rank}}{{M}_{{{{p}^{0}}}}}.$

Теорема 1. Для любого ${{p}^{0}} \in \mathfrak{g}{\text{*}}$ выполнено равенство ${{S}_{{{{p}^{0}}}}} = {{L}_{{{{p}^{0}}}}}$.

3. ФУНКЦИИ КАЗИМИРА НА $\mathfrak{g}{\text{*}}$

Напомним, что функцией Казимира называется такая функция $h \in {{C}^{\infty }}(\mathfrak{g}{\text{*}})$, что

(7)

$\{ h,{{h}_{i}}\} = \{ h,{{h}_{{ij}}}\} = 0\quad \forall i,j.$

Имеется $\tfrac{{k(k - 1)}}{2}$ очевидных функций Казимира

(8)

${{h}_{{ij}}},\quad 1 \leqslant i < j \leqslant k.$

Теорема 2.

1. Если $k = 2n$, $n \in \mathbb{N}$, то на коалгебре $\mathfrak{g}{\text{*}}$ существуют всего $\tfrac{{k(k - 1)}}{2}$ независимых функций Казимира (8).

2. Если $k = 2n + 1$, $n \in \mathbb{N}$, то на коалгебре $\mathfrak{g}{\text{*}}$, кроме функций Казимира (8), существует еще одна, не зависящая от них:

$C(p) = {{I}_{{a(p)}}}(p) = \sum\limits_{i = 1}^k {{{a}_{i}}(p){{h}_{i}}(p)} ,$

где

Функция Казимира C есть однородный полином степени $n + 1 = \frac{{k + 1}}{2}$ на $\mathfrak{g}{\text{*}}$.

4. ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА И ИНТЕГРАЛЫ ГАМИЛЬТОНОВОЙ СИСТЕМЫ

Применим принцип максимума Понтрягина (ПМП) [2] к задаче (2)–(4). Гамильтониан принципа максимума равен $\sum\limits_{i = 1}^k \,{{u}_{i}}{{h}_{i}}(\lambda )$, $\lambda \in T{\text{*}}G$. Гамильтонова система ПМП имеет вид

(9)

${{\dot {h}}_{i}} = - \sum\limits_{j = 1}^k \,{{u}_{j}}{{h}_{{ij}}},\quad i = 1,2, \ldots ,k,$

(10)

${{\dot {h}}_{{ij}}} = 0,\quad 1 \leqslant i < j \leqslant k,$

(11)

$\dot {q} = \sum\limits_{i = 1}^k \,{{u}_{i}}{{X}_{i}},$

а условие максимальности есть

(12)

$\sum\limits_{i = 1}^k \,{{u}_{i}}(t){{h}_{i}}({{\lambda }_{t}}) = \mathop {\max }\limits_{v \in U} \sum\limits_{i = 1}^k \,{{v}_{i}}{{h}_{i}}({{\lambda }_{t}}) = H(h({{\lambda }_{t}})),$

где

$H({{h}_{1}}, \ldots ,{{h}_{k}}): = \mathop {\max }\limits_{v \in U} \sum\limits_{i = 1}^k \,{{{v}}_{i}}{{h}_{i}}$

есть опорная функция множества U [14]. Функция H выпукла, положительно однородна и непрерывна.

Вдоль экстремальных траекторий $H \equiv {\text{const}} \geqslant 0.$ Анормальный случай

$H \equiv 0 \Leftrightarrow {{h}_{1}} = \ldots = {{h}_{k}} \equiv 0$

можно опустить, так как распределение Δ = = ${\text{span}}({{X}_{1}}, \ldots ,{{X}_{k}})$ удовлетворяет равенствам Δ² = Δ + + $[\Delta ,\Delta ] = TG$, поэтому по условию Гоха [2] все локально оптимальные анормальные траектории одновременно нормальны. Поэтому рассмотрим нормальный случай $H \equiv {\text{const}} > 0$. В силу однородности H можно считать H = 1.

Будем далее предполагать дополнительно, что множество U строго выпукло. Тогда максимизированный гамильтониан H является C¹-гладким на ${{\mathbb{R}}^{k}}{\backslash }\{ 0\} $, а максимум в (12) достигается на управлении $u = \nabla H = \left( {\tfrac{{\partial H}}{{\partial {{h}_{1}}}}, \ldots ,\tfrac{{\partial H}}{{\partial {{h}_{k}}}}} \right)$ [14]. Обозначим H_i = = $\tfrac{{\partial H}}{{\partial {{h}_{i}}}}$, $i = 1,2, \ldots ,k$. Тогда вертикальная подсистема (9), (10) гамильтоновой системы ПМП принимает вид

(13)

${{\dot {h}}_{i}} = - \sum\limits_{j = 1}^k \,{{h}_{{ij}}}{{H}_{j}},\quad {{\dot {h}}_{{ij}}} = 0,\quad 1 \leqslant i < j \leqslant k.$

Замечание. Если M = 0, то все решения ${{h}_{i}}(t)$ системы (13) постоянны, поэтому управления u(t) постоянны и оптимальны.

Теорема 3. Система (13) имеет следующие интегралы:

1) функции Казимира h_ij, $1 \leqslant i < j \leqslant k$, а также гамильтониан H при k = 2n, $n \in \mathbb{N}$,

2) функции Казимира ${{h}_{{ij}}}$, $1 \leqslant i < j \leqslant k$, и C, а также гамильтониан H при $k = 2n + 1$, $n \in \mathbb{N}$.

Для любого ${{p}^{0}} \in \mathfrak{g}{\text{*}}$ симплектический лист ${{S}_{{{{p}^{0}}}}}$ есть инвариантное множество системы (13). В частности, любая функция I_a, $a \in ker{{M}_{{{{p}^{0}}}}}$, постоянна на решениях этой системы.

Теорема 4. Пусть ${{p}^{0}} \in {{H}^{{ - 1}}}(1)$ и ${\text{rank}}{{M}_{{{{p}^{0}}}}} = 2$. Тогда решение $p(t)$ системы (13) с начальным условием $p(0) = {{p}^{0}}$ существует и единственно для любого $t \in \mathbb{R}$.

1) Если $\nabla H({{p}^{0}}) \in kerM$, то $p(t) \equiv {{p}^{0}}$. Соответствующее управление u(t) оптимально.

2) Если 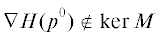, то p(t) есть регулярная C¹-гладкая периодическая плоская кривая. Соответствующее управление u(t) периодическое.

Теорема 5. Пусть $U = \left\{ {\sum\limits_{i = 1}^k \,u_{i}^{2} \leqslant 1} \right\}$. Тогда:

1) помимо интегралов, указанных в теореме 3, имеется еще $n = [k{\text{/}}2]$ независимых интегралов,

2) если $k \geqslant 4$, то решения системы (13) общего вида непериодические.

Список литературы

Montgomery R. A Tour of Subriemannian Geometries, Their Geodesics and Applications. AMS, 2002
Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит, 2005.
Agrachev A., Barilari D., Boscain U. A comprehensive introduction to sub-Riemannian geometry. Cambridge: Cambridge University Press, 2019.
Берестовский В.Н. Однородные многообразия с внутренней метрикой II // Сиб. матем. журн. 1989. Т. 30. № 2. С. 14–28.
Берестовский В. Н. Геодезические неголономных левоинвариантных внутренних метрик на группе Гейзенберга и изопериметриксы плоскости Минковского // Сиб. матем. журн. 1994. Т. 35. № 1. С. 3–11.
Barilari D., Boscain U., Le Donne E., and Sigalotti M. Sub-Finsler structures from the time-optimal control viewpoint for some nilpotent distributions // J. Dyn. Control Syst. 2017. V. 23. № 3. P. 547–575.
Ardentov A., Le Donne E., Sachkov Yu. Sub-Finsler geodesics on Cartan group // Regular and Chaotic Dynamics. 2019. V. 24. № 1. P. 36–60.
Brockett R. Nonlinear Control and Differential Geometry // Proc. Intern. Congress of Mathematicians. August 16–24, 1983. Warszawa. P. 1357–1368.
Myasnichenko O. Nilpotent (3, 6) sub-Riemannian problem // J. Dyn. Control Syst. 2002. V. 8. № 4. P. 573–597.
Rizzi L., Serres U. On the cut locus of free, step two Carnot groups // Proc. Amer. Math. Soc. 2017. V. 145. P. 5341–5357.
Le Donne E., Speight G. Lusin approximation for horizontal curves in step 2 Carnot groups // G. Calc. Var. 2016. V. 55. P. 111.
Busemann H. The isoperimetric problem in the Minkowski plane // AJM. 1947. V. 69. P. 863–871.
Kirillov A.A. Lectures on the Orbit Method. AMS. 2004.
Rockafellar R.T. Convex Analysis. Princeton University Press, 1970.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал