Доклады Российской академии наук. Математика, информатика, процессы управления, 2020, T. 492, № 1, стр. 70-74

Работа посвящена спектральному анализу динамической системы, представляющей собой кинетическую модель двухкомпонентной разреженной плазмы, состоящей из двух типов частиц – электронов и ионов, находящихся в электромагнитном поле. Распределение частиц в фазовом пространстве характеризуется плотностями распределения, зависящими от времени $t,$ координат и скоростей частиц. Система, описывающая динамику плазмы, составлена из уравнений Максвелла для компонент электромагнитного поля, и кинетических уравнений Больцмана для плотностей распределения.

В рассматриваемом здесь бесстолкновительном приближении взаимодействие заряженных частиц осуществляется посредством самосогласованного электромагнитного поля, которое, с одной стороны, индуцируется движением заряженных частиц, а с другой, оказывает воздействие на эволюцию плотностей их распределения. Указанная математическая модель позволила в [1] обнаружить эффект, описывающий неожиданное явление – затухание волн в бесстолкновительной плазме. Данной тематике посвящено значительное количество работ как физиков, так и математиков (см. [2–6], а также имеющуюся там библиографию). Наша цель – спектральный анализ интегро-дифференциального оператора, порождающего эволюционную полугруппу, задающую динамику начального возмущения стационарного решения системы (ср. [7] и [8]).

Для простоты изложения ограничимся случаем двумерного одночастичного фазового пространства $(x,v)$, когда магнитная индукция $B(t,x)$ вырождена и рассматриваемая система уравнений имеет вид

где e и Ze – заряды, m и M – массы электронов и ионов соответственно, ${{f}^{{( \mp )}}}$ – плотности их распределения, а $E = E(t,x)$ – напряженность электрического поля. Каждое из кинетических уравнений допускает запись в форме Лиувилля (см. [9]) и выражает тот факт, что полная производная плотности распределения вдоль траектории частицы соответствующего типа равна нулю. Стационарные решения кинетических уравнений имеют вид где $\phi (x)$ – электростатический потенциал, т.е. $E = - \frac{{\partial \phi }}{{\partial x}}.$ Ниже в качестве невозмущенного выбирается (ср. [10]) стационарное решение системы, не зависящее от пространственной координаты.

Следуя [4], будем считать, что плотность распределения ионов $f_{0}^{{( + )}}\left( {\frac{{m{{v}^{2}}}}{2}} \right)$ фиксирована, и линеаризуем систему относительно соответствующего стационарного решения. В результате получаем систему

где $f = f(t,x,{v})$ – возмущение стационарного распределения электронов ${{f}_{0}}({v})$ = $f_{0}^{{( - )}}\left( {\frac{{m{{{v}}^{2}}}}{2}} \right),$ а $E(t,x)$ – напряженность индуцированного электрического поля. Предполагается, что возмущение плотности распределения частиц и напряженность электрического поля достаточно быстро убывают к нулю на бесконечности.

Генератор возникающей при этом операторной полугруппы действует по формуле

где функция $\varphi ({v}) = \frac{{4\pi {{e}^{2}}}}{m}f\,{{{\text{'}}}_{0}}({v})$ удовлетворяет условию

В качестве основного пространства, в котором действует оператор T, выбирается согласующееся с физической постановкой задачи пространство вектор-функций $(f(x,{v}),g(x))$ с конечной нормой

Явное описание структуры и локализации спектра оператора T в терминах функционального параметра φ рассматриваемой задачи содержит

Теорема 1. При условии конечности момента

спектр $\sigma (T)$ оператора T состоит из следующих двух компонент: где

Доказательство использует известный (см., например, [11]) теоретико-операторный факт: для действующих в прямой сумме банаховых пространств $X \oplus Y$ операторных матриц справедлива формула

где $A{\kern 1pt} :\;X \to X$ – обратимый, $B{\kern 1pt} :\;Y \to X$ и C: $X \to Y$ – ограниченные операторы, I и J – единичные операторы в X и Y соответственно, а выражение $D - C{{A}^{{ - 1}}}B$ называется дополнением Шура, ассоциированным с $A.$

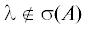Предложение 1. Точка принадлежит резольвентному множеству действующей в $X \oplus Y$ операторной матрицы (3) в том и только том случае, когда в Y ограниченно обратимо соответствующее дополнение Шура

Применительно к рассматриваемой здесь ситуации положим

и определим компоненты действующей в $X \oplus Y$ блочной матрицы следующим образом: оператор $A = - v\frac{\partial }{{\partial x}}$ действует в X с плотной областью определения $\{ f \in X{\text{:}}\,\,f( \cdot ,v)$ – абсолютно непрерывна, $\frac{{v\partial f}}{{\partial x}} \in X\} ,$ $C = \int\limits_\mathbb{R} {\; \cdot \;vdv} $, B – оператор умножения на локально ограниченную функцию $\varphi (v)$, удовлетворяющую условиям (1) и (2). Ключевым элементом доказательства теоремы 1 является следующее

Предложение 2. При условиях (1) и (2) спектр оператора $T$ состоит из двух компонент:

где $\sigma (A) = i\mathbb{R}$, а нормированное дополнение Шурав представлении Фурье по переменной $x$ действует как умножение на функцию $\Delta (k,\lambda ).$

Информацию о локализации спектра задачи, установленную в [4], дополняет и уточняет

Следствие 1. Резольвентное множество оператора T содержит область

В физической литературе (см., например, [2]) уравнение $\Delta (k,\lambda ) = 0$ известно под названием дисперсионного соотношения Ландау. Оно определяет значения спектрального параметра $\lambda $ и волнового числа k, при которых у рассматриваемой системы существуют решения типа плоской волны, зависящие от t и x по закону $exp(\lambda t + ikx).$ Если ${\text{Re}}\lambda > 0,$ то такие решения порождают неустойчивые моды, отвечающие незатухающим колебаниям плазмы. Эффективный способ подсчета индекса неустойчивости (ср. [12]) применительно к рассматриваемой задаче дает

Теорема 2. Пусть $\varphi \in {{{\text{L}}}_{1}}(\mathbb{R})$, $\varphi (v) \to 0$ при $v \to \pm \infty ,$ производная $\varphi {\text{'}}(v)$ ограничена, а все нули функции $\varphi $ невырождены. Если для каждого нуля s функции $\varphi $ параметр $k \in \mathbb{R}{\backslash }\{ 0\} $ удовлетворяет условию

то число N(k) корней $\lambda = \lambda (k)$ уравнения $\Delta (k,\lambda ) = 0,$ расположенных в правой полуплоскости, совпадает с разностью ${{N}_{ + }}(k) - {{N}_{ - }}(k),$ где

Схему доказательства удобно изложить переходя к функции

граничные значения которой на вещественной оси вычисляются по формулам Сохоцкого–Племеля

В соответствии с принципом аргумента (см., например, [13]) для произвольного замкнутого контура $\gamma \subset {{\mathbb{C}}_{ + }},$ содержащего внутри себя все нули функции $w(z),$ расположенные в ${{\mathbb{C}}_{ + }},$ суммарное их количество $N = N(k)$ равно сумме логарифмических вычетов $w(z)$ в области, ограниченной контуром γ. Эта величина представляет собой индекс точки w = 0 относительно кривой $\Gamma = w(\gamma )$ и совпадает с числом вращения, т.е. числом оборотов вокруг нуля радиус-вектора w при обходе кривой Γ в положительном направлении:

Данный способ подсчета количества корней дисперсионного соотношения вполне согласуется с известным (см. [2]) критерием Найквиста, применимость которого в проблеме устойчивости/неустойчивости плазмы была строго обоснована в работе [14].

В рассматриваемой здесь ситуации в качестве γ выбирается  контур,  составленный  из  отрезка [–R, R] и дуги полуокружности радиуса R такого, что образ полуокружности принадлежит достаточно малой окрестности точки w = 1, отделенной от нуля. При движении точки w вдоль замкнутой кривой $\Gamma = w(\gamma )$ участок между двумя последовательными ее пересечениями отрицательной полуоси, отвечающими нулям $s = {{s}_{j}} \in [ - R,R]$, $j = 1, \ldots ,n$, функции $\varphi (s)$, занумерованным в порядке возрастания, дает приращение аргумента

и, следовательно, индекс точки $w = 0$ относительно замкнутой кривой Γ вычисляется по формуле

Условие (4) означает отсутствие на мнимой оси корней дисперсионного соотношения $\Delta (k,\lambda ),$ отвечающих данному $k \in \mathbb{R}{\backslash }\{ 0\} $.

Следствие 2. В предположениях теоремы уравнение $\Delta (k,\lambda ) = 0$ не имеет корней в правой полуплоскости, если

Известно (см. [2, 4]) формулируемое в терминах функции ${{f}_{0}}(v)$ простое достаточное условие, гарантирующее отсутствие неустойчивых плазменных колебаний. А именно, если ${{f}_{0}}(v)$ имеет единственный экстремум (максимум) $v = a$, то дисперсионное соотношение не имеет корней $\lambda = \lambda (k)$ в правой полуплоскости. В самом деле, при этом $\frac{{\varphi (v)}}{{v - a}} < 0$ и, следовательно, ${{N}_{ + }}(k) = {{N}_{ - }}(k) = 0$ для $k \ne 0,$ поскольку

В случае, когда ${{f}_{0}}(v)$ имеет два максимума может возникнуть так называемая двухпучковая неустойчивость (см. [2]). В качестве модельного рассмотрим случай, когда ${{f}_{0}}(a) = {{f}_{0}}(b) = M$ – максимальное значение функции ${{f}_{0}}(v)$, а $c \in (a,b)$ – ее точка минимума, причем ${{f}_{0}}(c) = 0.$ В рассматриваемой ситуации ${{N}_{ - }}(k) = 0$ и критерием двухпучковой неустойчивости служит следующее

Предложение 3. Для заданного $k \in \mathbb{R}{\backslash }\{ 0\} $ имеем $N(k) = {{N}_{ + }}(k) = 1$ в том и только том случае, когда

Имея в виду сформулировать достаточные условия существования неустойчивых мод в терминах расположения и величины максимумов невозмущенной функции распределения, для точки экстремума $v = a$ и фиксированного $\xi \in (0,M)$ положим

Отметим, что величина $({{a}_{ > }}(\xi ) - {{a}_{ < }}(\xi ))$ – ширина локального максимума на уровне ξ. Аналогичные обозначения ${{b}_{ < }}(\eta )$ и ${{b}_{ > }}(\eta )$ вводятся для точки экстремума ${v} = b.$

Следствие 3. Пусть для некоторых ξ, $\eta \in (0,M)$ выполняется неравенство

где ${{a}_{ > }} = {{a}_{ > }}(\xi )$, ${{a}_{ < }} = {{a}_{ < }}(\xi )$, ${{b}_{ > }} = {{b}_{ > }}(\eta )$, ${{b}_{ < }} = {{b}_{ < }}(\eta )$ и $k \ne 0.$ Тогда $N(k) = 1.$

Несколько иное по форме достаточное условие неустойчивости дает

Следствие 4. Если для некоторых $\sigma \in (0$, c – a) и $\tau \in (0,b - c)$ выполнено неравенство

то в полуплоскости ${\text{Re}}\lambda > 0$ имеется ровно один корень $\lambda = \lambda (k)$ уравнения $\Delta (k,\lambda ) = 0,$ отвечающий данному $k \in \mathbb{R}{\backslash }\{ 0\} $.

Результаты настоящей работы распространяются на случай шестимерного одночастичного фазового пространства, когда дисперсионное соотношение Ландау имеет вид

где k – волновой вектор, а λ – спектральный параметр.